为进一步降低编队卫星的运行与管理成本, 提高编队工作的实时性和灵活性, 亟待寻找一种利用在轨决策的编队运行与管理方法, 以增强编队系统鲁棒性和可靠性, 并尽可能减少编队卫星能量消耗, 提高反应速度。而基于微推力的卫星编队能完成更高精度的飞行任务, 提高对地观测的精度等, 可广泛应用于地球重力场观测、地磁观测等需要超高精度对地观测的科学任务中。
NASA的Deep Space 1和ESA的SMART-1都将微推力器卫星应用于深空探测领域中[1-5]; 美国普兰尼特公司拥有148颗在轨微纳卫星时刻进行对地观测, 其中于2017年2月发射的88颗卫星可由人单手托举[6]。而当前在轨微小卫星编队系统, 或不进行控制, 或采用电磁推进器作为动力源进行控制, 但电磁推进器复杂、成本较高, 限制了微纳卫星控制系统的发展。中国现有微推力系统仍不能满足微纳卫星编队的需求, 已发射的微纳卫星均无推力控制系统。而由北京控制工程研究所研究的MEMS微推力器阵列可以产生10-5~10-4 N·s的脉冲推力, 且结构简单, 成本低廉, 为中国微纳卫星在轨控制的发展提供了有力的技术支持和保证[7]。
从软件上来说, 由于采用微推力器, 则表明控制系统不能修正过大的误差, 因此就对卫星编队控制系统的可靠性和快速性提出了要求。快速稳定的信息交流是卫星编队系统运行的重要保证, 而具有高度可靠性和快速性的信息拓扑结构则是信息交流的前提。由于承载卫星编队成员信息交流任务的拓扑网络结构对卫星编队系统有着重要的影响, 从信息拓扑网络结构的角度对卫星编队控制系统的性能进行分析, 并据此设计出有效的编队构型、拓扑结构和控制策略就成了一个很有意义的研究方向。
本文以光学干涉成像卫星为背景, 设计了一个低轨卫星编队控制系统, 包括编队构型、拓扑结构以及控制系统, 可以完成地形三维测绘和地面目标的跟踪定位, 具有极高的科学意义和军事价值。由于卫星对地成像系统的测量要求编队卫星之间必须保证严格的相对位置关系, 因此必须使用高精度的导航系统和控制系统。
1 Cartwheel构型编队飞行动力学 Cartwheel构型[8]是法国空间中心(CNES)提出的概念, 其编队由处于同一轨道平面、相对运动相位角差为120°的3颗绕飞小卫星和1颗中心主星构成。Cartwheel构型小卫星编队利用编队间的稳定几何关系, 通过彼此通信协作, 可以实现卫星编队测高、对地观测等多项功能。研究发现, Cartwheel构型所形成的编队, 垂直基线稳定, 在各个轨道周期中变化极小, 所以对其编队的设计和优化问题十分有意义。本节以Cartwheel编队构型为基础, 建立卫星编队系统相对运动模型。
如图 1所示, 相对运动的坐标系采用主星T的轨道坐标系, y轴垂直于轨道平面, z轴指向地心, x轴指向卫星T的运动方向。经过分析推导可以得到描述从星F的C-W方程如下:
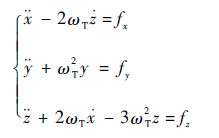 | (1) |
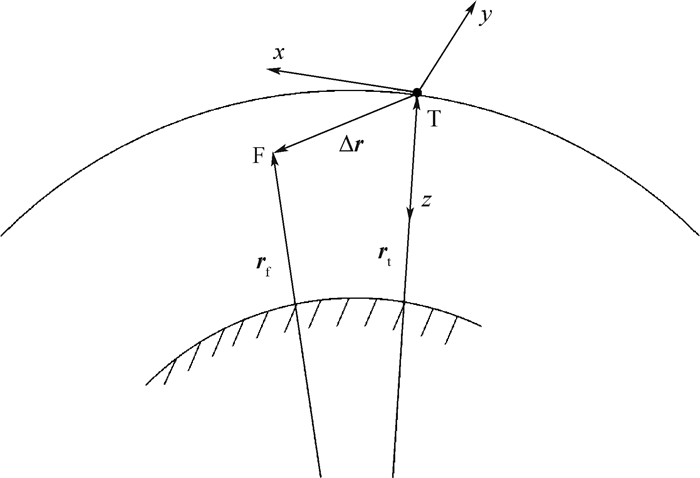 |
| 图 1 主从星间的相对运动 Fig. 1 Relative motion of target and follower |
| 图选项 |
式中:ωT为主星的轨道角速度; fx、fy、fz为所受摄动力或控制力。
式(1)是本文的研究基础。卫星构型的摄动分析、导航算法以及轨道保持控制均基于此方程。解此方程就可以得到卫星相对运动轨迹。设定合理的初值, 就可以得到卫星编队的构型。
取状态变量
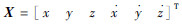
 | (2) |
式中:
 | (3) |
求解可知, 当
 | (4) |
此时, Cartwheel编队的相对运动为2种运动的叠加, 即为在主星T轨道平面内的椭圆绕飞轨道(长短轴为2 : 1)和沿主星T法线方向的简谐运动, 可以严格证明二者的叠加运动为与主星轨道平面xo-yo夹角为30°或150°的圆轨道平面xc-yc, 如图 2所示[9]。
 |
| 图 2 Cartwheel构型空间示意图 Fig. 2 Space schematic diagram of Cartwheel configuration |
| 图选项 |
2 卫星编队拓扑结构设计与分析 卫星编队系统稳定运行的关键在于编队卫星之间信息的交互, 而其拓扑结构就是信息交互的渠道。在微推力器作用下的卫星编队系统中, 由于卫星编队的高精度要求和微推力器作用效果不足之间的矛盾, 又对卫星节点间信息传递的快速性提出了要求。研究与分析卫星编队系统的拓扑结构, 可以有效提高卫星编队的快速性和稳定性。本节将对基于Cartwheel构型的卫星编队系统的信息拓扑结构进行分析和比较, 并据此选择4节点卫星最优拓扑结构。
2.1 适用于微推力卫星编队的拓扑结构分析 卫星编队系统的拓扑结构是实现信息交换和共享的基础。而卫星编队系统长时间在太空中进行高精度编队保持, 系统要实时对各卫星进行轨道控制, 以保证编队构型[10]。
第1节中已确定采用主星沿太阳同步轨道, 从星对主星进行圆轨道绕飞的Cartwheel编队构型。下面对针对此编队构型的几种常用信息拓扑结构进行分析。
网络拓扑结构指网络中各节点相互连接的方式, 在卫星编队系统网络应用中, 主要的拓扑结构包括星形拓扑、环形拓扑和网形拓扑。
研究网络拓扑结构性能的最常见手段是通过图论知识研究拓扑结构的特征参数, 分析信息网络的性能, 其中平均最短路径(Average Shortest Path, ASP)和拓扑可靠性可用于对卫星编队飞行系统进行快速性和可靠性分析。
1) 平均最短路径
平均最短路径表示网络中2个信息节点的信息交互需要经过的最短中介路程, 可以表示为
 | (5) |
式中:N为节点的集合; n为集合中节点的个数; d(i, j)为节点i和节点j之间的最短路径。
平均最短路径越大, 网络中信息传递的路程越长, 信息传输时间就越久, 因此平均最短路径越小越好。
2) 拓扑可靠性
拓扑可靠性主要分析信息网络中有节点或信息链路被破坏或暂时故障时, 信息网络是否仍能正常运作, 或者因之产生如时滞、丢包、噪声等因素对系统带来的影响等。通常, 对拓扑G(N, E)的可靠性RG可定义为
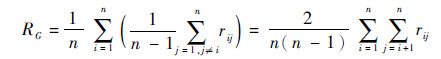 | (6) |
式中:rij为节点i到节点j之间的可靠性。
现综合两方面分析本节中确定的编队构型在不同拓扑结构下的快速性和可靠性。分析由4个节点, 即1颗中心主星和3颗环绕星做成的卫星编队系统构成的星形、环形、网形(全连通)拓扑结构参数, 如图 3所示。设拓扑结构中节点和链路的可靠性k都为0.8。
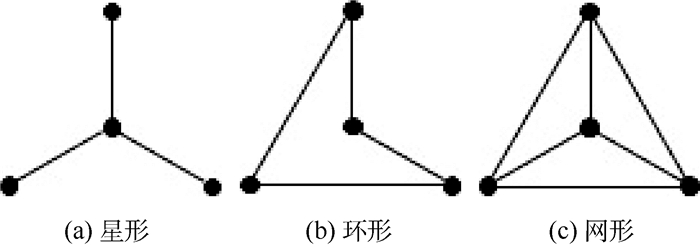 |
| 图 3 4节点卫星编队常用拓扑结构 Fig. 3 Common topological structure of satellite formation with four nodes |
| 图选项 |
根据表 1中计算结果分析可知, 在Cartwheel构型卫星编队系统中, 节点数较少, 故每种拓扑构型的平均最短路径值都很小, 信息传递的效率很高, 时滞较小。但由于星形结构和网形结构的信息传递过程中都需要经过中心节点, 对中心节点处卫星的通信系统要求提出了更大的要求。且星形结构中一旦中心节点发生通信故障, 则系统通信无法继续进行。而网形结构存在过多的冗余通信链路, 虽然为通信网络提供了更高的可靠性和容错性, 但同时也提高了网络搭建成本和对通信设备的要求。环形结构与星形结构相比可靠性略胜一筹, 当某一链路或节点损坏时, 经由之传递的信息可从另一方向的节点和链路传递, 只是有可能使信息传递路径变长, 增加信息传递的时滞; 而与网形结构相比, 组网成本和难度大大降低。
表 1 Cartwheel构型编队4节点拓扑结构性能比较 Table 1 Topological structure performance comparison of Cartwheel configuration formation with four nodes
| 结构 | 平均最短路径 | 拓扑可靠性 |
| 星形 | 1.5 | 0.72 |
| 环形 | 1.33 | 0.891 7 |
| 网形 | 1 | 0.892 |
表选项
针对本文微推力卫星编队系统快速性和可靠性的需求, 既要求卫星编队系统中信息的快速有效传递, 又要求卫星编队系统有发生局部通信故障时持续工作的能力。综合几种适用于卫星编队的拓扑结构的优缺点, 环形拓扑结构具有较高的快速性和可靠性; 同时, 相比于网形拓扑结构, 又具有结构简单、易于实现、减轻对星载通信系统的要求。
2.2 基于拓扑结构对编队构型修正 当伴飞轨道与主轨道相差很小且为近圆轨道时, 通过对其动力学模型线性化, 得到C-W方程, 当初始条件满足一定关系时, 其运动是稳定的。但C-W方程的稳定解是必须严格满足初始条件并对环境理想化, 且卫星间相对距离比较小的情况下才能得到, 与实际情况略有差别。
卫星间通过信息拓扑系统可以进行信息交互, 互换彼此的状态信息。拓扑结构中的相邻星可以利用彼此的相对状态信息(相对距离、方位角)对编队构型进行修正。
根据自然编队构型以及环形拓扑结构, 如图 4所示, 根据其相对几何关系, 每颗卫星可根据其相邻2颗卫星的运动状态推算出本星的运动状态。
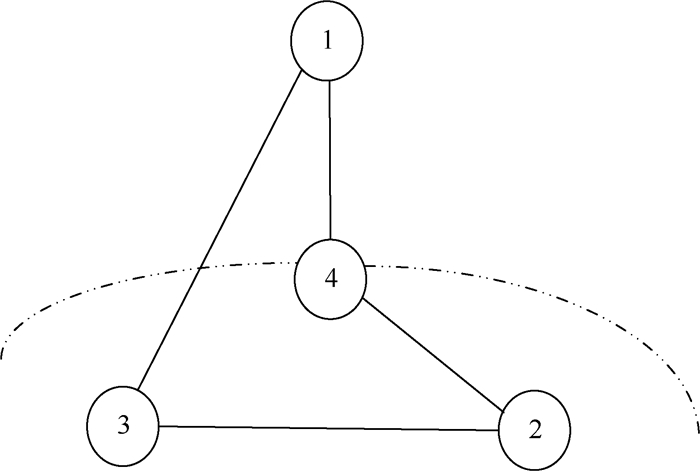 |
| 图 4 拟采用的环形拓扑结构 Fig. 4 Annular topologital structure to be used |
| 图选项 |
以卫星j1、j2推导卫星i的运动状态为例。
由1.2节可知, 自然编队空间圆轨道平面与编队整体绕地球轨道平面夹角为30°, 在编队轨道坐标系中, 由卫星导航系统可实时获得卫星的位置和速度信息Rs和V, 以及环绕星在编队轨道坐标系中的角速度ω。
在编队轨道坐标系中, 由卫星j1、j2将自身状态信息传递给卫星i, 卫星i进行实时结算, 可得出卫星i相对于卫星j1、j2的目标位置矢量Rj1i、Rj2i, 如图 5所示。
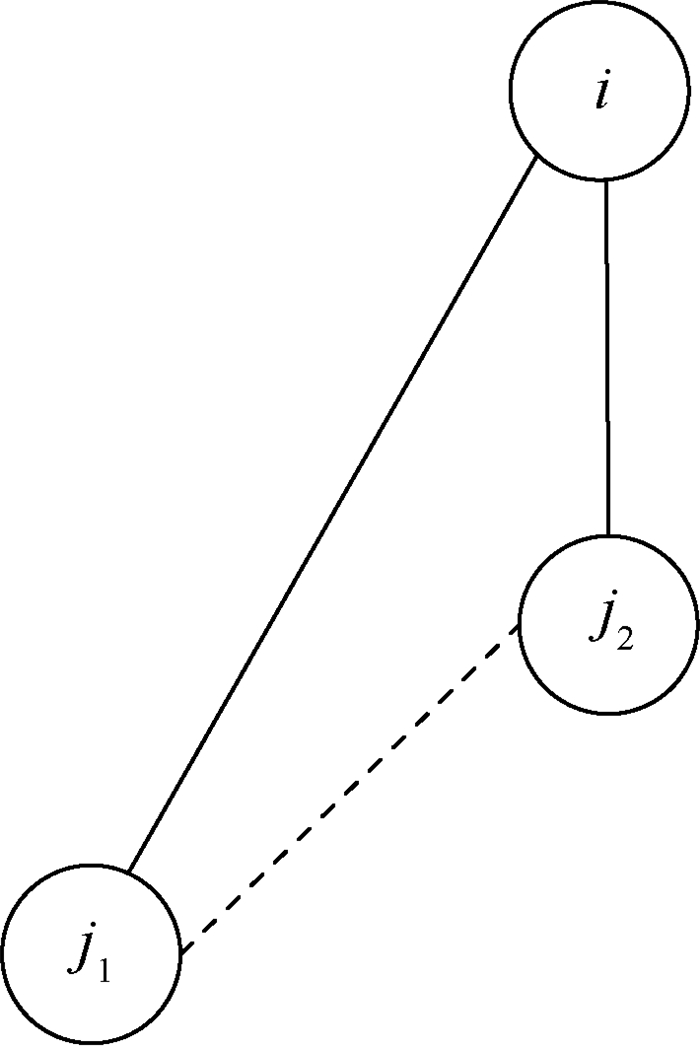 |
| 图 5 卫星j1、j2推导卫星i的相对几何关系图 Fig. 5 Relative geometric diagram for satellite i deduced by satellite j1 and j2 |
| 图选项 |
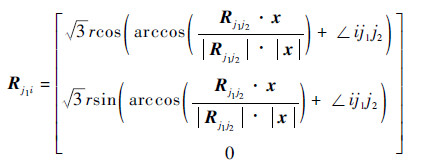 | (7) |
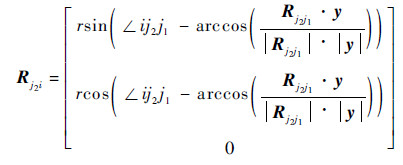 | (8) |
式中:x、y为编队轨道坐标系x、y方向单位向量; r为自然编队圆半径。
将卫星i在编队轨道坐标系中的旋转角速度ωi叉乘Rj1i、Rj2i, 即可得到卫星i相对于卫星j1、j2的目标速度矢量Vj1i、Vj2i。
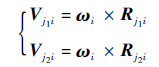 | (9) |
综合考虑2颗目标星j1、j2在卫星编队系统中的重要性及其各自的实际可靠性后, 选取合适的权值kj1、kj2, 加权到式(9)求得的相对位置速度矢量中, 即可求得本星的目标状态矢量。
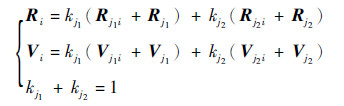 | (10) |
将其转换到编队整体绕地球飞行的轨道坐标系中, 如下:
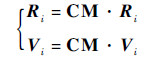 | (11) |
式中:CM为编队轨道坐标系到编队整体绕地球的轨道坐标系的转换矩阵, 即
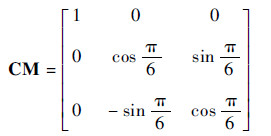 |
当考虑到信息传递以及处理的时滞影响, 假设时滞δt已知, 则时滞后的位置矢量可结算得出Rdt= R0+δt· V0, 在短时滞内速度变化量可忽略不计。
表 2为加入1 s时滞, 随机导航误差(0.03 mm), 经过式(7)~式(11)结算后得到的目标运动状态与事先设计好的理想自然编队轨道比较。
表 2 拓扑结构对编队构型的修正效果 Table 2 Effect of topological structure on formation configuration modification
| 系统所受干扰 | 位置误差量级/m | 速度误差量级/(m·s-1) |
| 仅加入时滞 | 10-12 | 10-15 |
| 仅加入导航误差 | 10-6 | 10-6 |
| 加入时滞和导航误差 | 10-6 | 10-6 |
表选项
综合比较各种影响因素, 模型的计算误差主要来源于随机导航误差, 但仍能经过结算后将导航误差对目标运动状态的影响减小一个量级。时间延迟对计算精度有一定影响, 但影响不大。
3 卫星编队协同控制 卫星编队飞行系统的编队构型和拓扑结构的设计分析, 以及相应的编队构型和拓扑结构的选取只能为其提供一个好的初始及期望状态, 而卫星编队系统能长期稳定运行并完成空间任务, 则必须对卫星编队系统进行有效控制。对于卫星编队飞行系统的保持控制是精密控制, 控制的频度较高, 所以必须进行实时的闭环控制, 因此需采用自主轨道保持的控制方式。另外, 由于系统的控制精度要求, 需要使用精细的微推力器, 不能提供大推力用于修正较大的轨道误差, 因此对系统的快速性需求大大提高[11-13]。
3.1 基于LQR的卫星编队保持协同控制策略 卫星编队系统的协同控制主要分为控制编队整体相对于预期轨道的保持, 以及卫星编队中各子星的构型保持。卫星编队协同控制的工作主要如下:
1) 根据导航信息规划编队整体在惯性坐标系中的位置矢量[xoi yoi zoi]T。
2) 根据导航信息为编队卫星规划任务, 使其满足围绕编队中心的期望构型。
2部分工作产生带控制的2部分误差, 即为保证编队整体不偏离预定轨道, 编队整体相对于标准轨道的误差eformation和每颗从星为了保持编队构型的误差estructure, 如图 6所示。2部分误差矢量相加即为待控量eused。
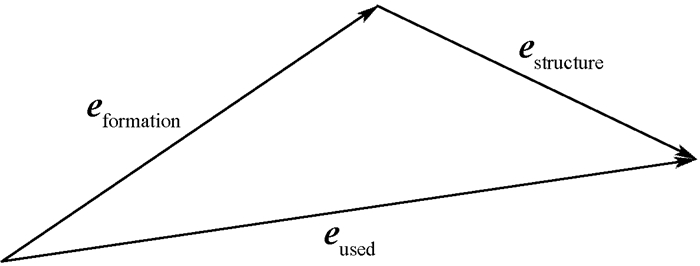 |
| 图 6 卫星编队构型协同控制任务规划 Fig. 6 Satellite formation configuration collaborative control mission planning |
| 图选项 |
卫星编队控制方法采用线性二次最优控制(LQR)[14]。在编队卫星相对运动状态漂移的情况下, 设计推进器冲量需求, 使在其作用下, 把系统由偏离理想轨迹的状态驱动到满足编队构型的目标相对运动状态, 同时使性能指标J取为最小值。
将上面得到待控误差e= eused=eformation+estructure代入误差状态方程:
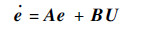 | (12) |
取LQR控制的优化指标为
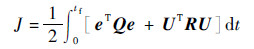 | (13) |
式中:Q和R分别为优化过程中误差和控制量的权值, 它们分别决定于控制精度和燃料消耗在控制系统中的重要程度。对确定的Q和R, 最优控制有唯一解:
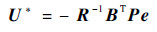 | (14) |
式中:P为Riccati方程的解。
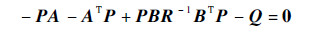 |
本文中的编队保持显然是一个精度要求高的控制, 因此, 应选择较大的R。但同时也要考虑到系统的动态品质和稳定度, 调整Q和R参数, 在保证控制有效性的情况下尽量节省燃料。
3.2 基于粒子群优化算法的能量优化策略 粒子群优化(Particle Swarm Optimization, PSO)算法也称鸟群觅食算法[15], 是目前应用最为广泛的群体智能优化算法。PSO算法是一种元启发式算法, 利用群体中的个体对信息的共享, 从而使得整个群体的运动在问题求解空间中产生从无序到有序的演化过程, 从随机解出发, 经过迭代寻觅最优解, 其解的品质由适应度来评价。
运用3.1节中LQR控制, 只能保证单颗卫星对修正与目标运动状态之间的偏差, 使得能量最优。但在卫星编队飞行协同控制系统中, 并没有综合考虑到整个系统的能量消耗。
考虑卫星编队构型保持系统整体的任务分配, 以保证卫星编队构型为第一目标, 以减少整体能量消耗为优化指标。如图 7所示, 若简单采用LQR控制, 则为修正每颗卫星实际运动状态与目标运动状态之间的偏差。现考虑合理地将修正任务重新分配给每颗卫星, 以减少能量消耗。将某颗卫星的目标运动状态放大到误差允许范围内在轨道圆上的一个弧段, 为了严格保持编队构型, 编队中其他星的目标运动状态同时随之改变。运用PSO算法, 以卫星编队系统整体能量消耗为搜索函数, 寻找在误差允许范围内这一弧段上的最优点, 即为能量最优点。
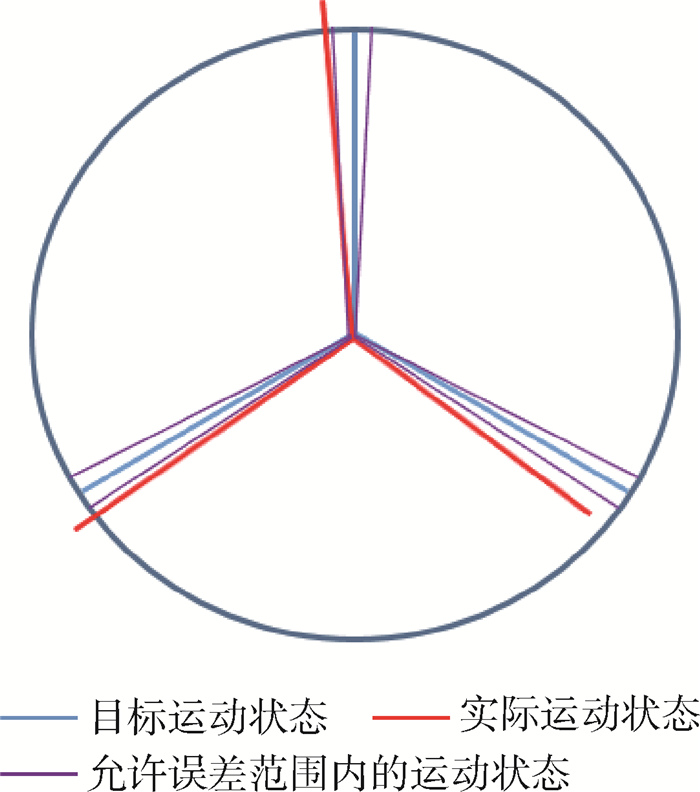 |
| 图 7 基于PSO算法将控制任务重分配 Fig. 7 Control task redistribution based on PSO algorithm |
| 图选项 |
假设绕飞卫星位于同一相对运动轨迹圆上, 3颗卫星相对均匀分布, 则3颗卫星在虚拟中心轨道坐标系中的相位可表示为
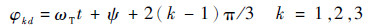 | (15) |
观察式(15)可发现, 只有一个参数ψ可供优化, 将ψ设为0.01°幅值的扇形空间。将优化函数Jψ设为
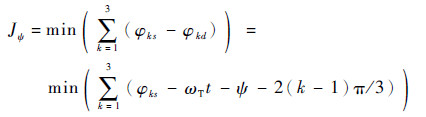 | (16) |
运用PSO算法, 求得可使优化函数Jψ取得最小值时的ψ。与之对应, 则可求得3颗卫星在虚拟中心轨道坐标系中的期望位置向量[xkd ykd zkd]T, 从而求得待控误差e, 代入3.1节的控制方法中用于求解。
4 仿真校验 本文中仿真采用边长为20 cm、质量为1 kg的立方星, 考虑大气阻力、太阳光压、日月引力等摄动因素。编队整体沿太阳同步轨道运动, 编队内部3颗卫星沿半径为1.5 m的圆绕中心领航星运动, 编队内部轨道面与太阳同步轨道面成30°夹角, 微推力器单个比冲为10-5 N·s。控制过程中, 领航星不受控制, 对于3颗环绕星分别运用第2节和第3节中提到方法, 使用PSO算法搜索对控制任务进行重分配后控制进行仿真, 仿真效果如图 8和图 9所示。
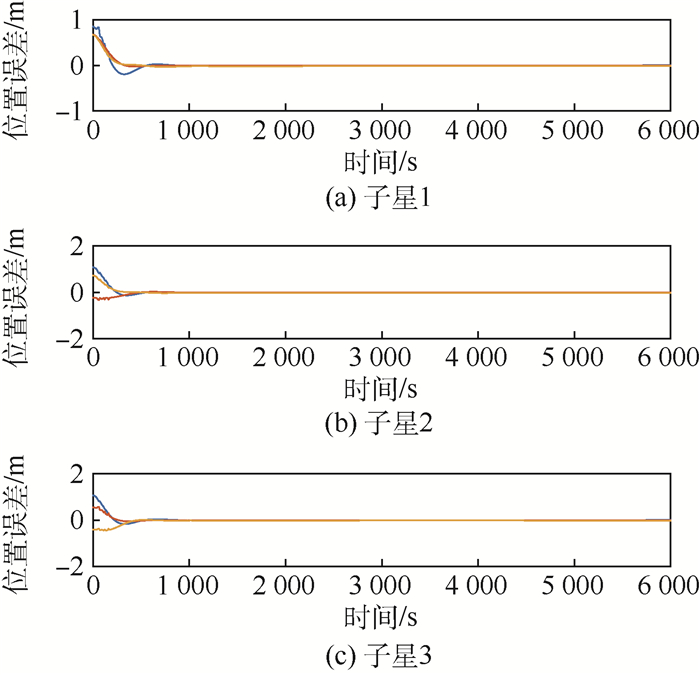 |
| 图 8 Cartwheel构型编队三轴位置误差 Fig. 8 Triaxial position error of Cartwheel Configuration formation |
| 图选项 |
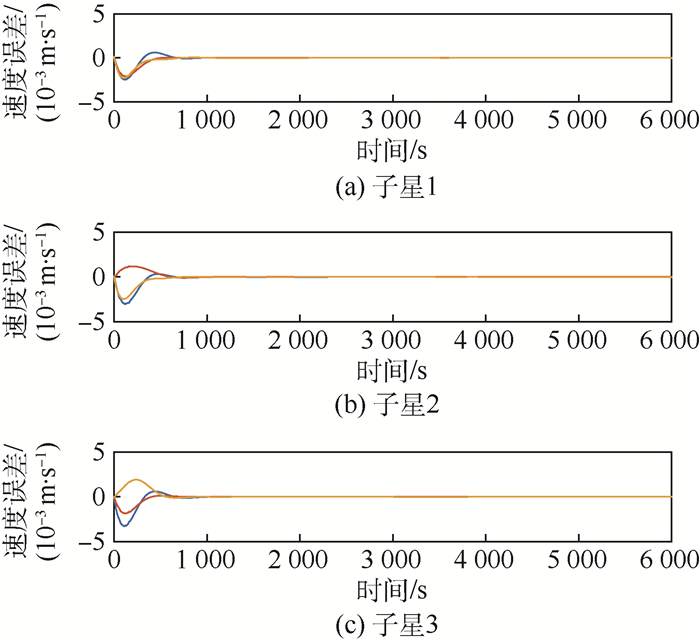 |
| 图 9 Cartwheel构型编队三轴速度误差 Fig. 9 Triaxial velocity error of Cartwheel Configuration formation |
| 图选项 |
3颗环绕卫星执行编队建立和编队保持的整体误差变化如图 8和图 9所示, 图中蓝、红、橙线分别表示卫星三轴的误差信息。利用PSO算法对控制任务进行重新分配, 编队能够在约500~600 s的时间完成高精度重构; 在轨道保持阶段, 位置误差可保持在0.002 m(3σ), 速度误差可保持在4×10-5 m/s(3σ)以下, 能够较精确地完成控制任务。
4.1 能量优化仿真算例 对3颗环绕星分别进行地面事先规划所有目标点和实时PSO搜索目标点的控制策略, 从能量消耗和控制精度2方面进行对比, 如表 3所示。
表 3 地面事先规划所有目标点和实时PSO搜索目标点控制效果对比 Table 3 Control effect comparison between ground planning of all targets in advance and real-time searching of targets by PSO
| 控制策略 | 位置精度/m | 推力器消耗/(10-5N·s) |
| 地面事先规划 | 0.001 715 | 101 120 135 |
| 0.001 833 | ||
| 0.001 539 | ||
| 实时PSO搜索 | 0.001 265 | 554 739 |
| 0.001 517 | ||
| 0.001 864 |
表选项
如表 3所示, 应用PSO算法可在尽量不影响控制精度的前提下, 大幅度减少微推力器消耗, 以提高卫星在轨寿命。
4.2 导航误差对编队保持系统影响仿真算例 当卫星在轨飞行时, 需要通过导航系统实时获得自身的运动状态信息, 同时通过拓扑信息网络获得网络中相邻卫星的运动状态信息, 高精度的导航信息是高精度控制的前提和保证。但是卫星实际运行过程中的导航误差是不可避免的, 2.2节中, 基于拓扑结构对编队构型的修正算法已经可以有效减小导航误差的影响, 然而并不能完全消除。利用基于拓扑结构的控制算法, 并在PSO算法将控制任务重新分配后, 能有效减小导航误差对控制系统精度的影响。如在4.1节的仿真中, 在每一次获取导航信息时加入随机误差, 分析导航误差对编队保持系统的影响。
如图 10和图 11所示, 实时在线规划算法可有效减小导航信息对编队保持的影响, 能保持较高的控制精度, 但当导航误差过大时, 由于所使用的微推力器单个冲量太小, 能量消耗过多。因此, 这种应用微推力器的卫星编队保持系统应同时具备较高精度的导航系统。
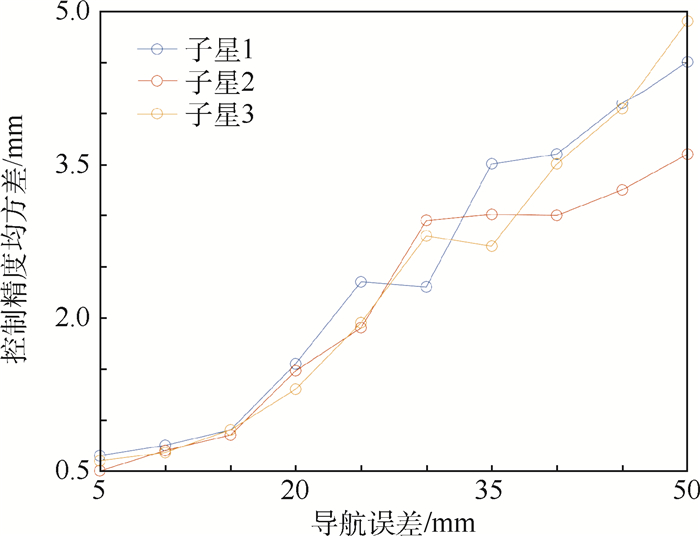 |
| 图 10 不同导航误差对控制精度的影响 Fig. 10 Influence of different navigation errors on control precision |
| 图选项 |
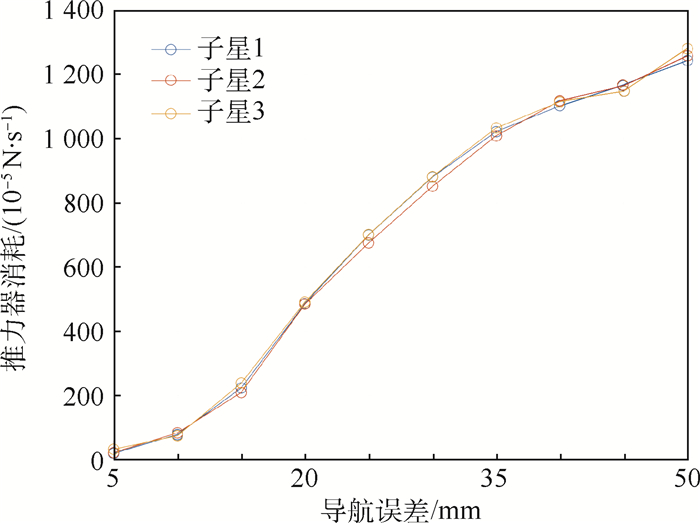 |
| 图 11 不同导航误差对推力器消耗的影响 Fig. 11 Influence of different navigation errors on thrust consumption |
| 图选项 |
4.3 拓扑结构容错仿真算例 卫星在轨运转过程中, 难免会受到干扰, 通信链路暂时中断, 甚至永久无法使用。若采用星形结构, 不难发现, 发生通信链路损坏的卫星将完全处于失联状态, 从而失去控制。当采用环形拓扑结构时, 当某一条通信链路损坏时, 原信息可经由另一条链路传递, 只是由于其信息传递路径变长, 会造成更长的时滞; 只有当与某一颗卫星连接的2条通信链路同时损坏时, 该颗卫星才会失联, 与星形结构相比, 大大提高了系统的可靠性。
环形拓扑结构通信链路的损坏分为以下2种情况, 即与中心领航星无关的链路损坏和与中心领航星有关的链路损坏, 如图 12所示。现分别对这2种情况进行仿真, 如表 4所示。
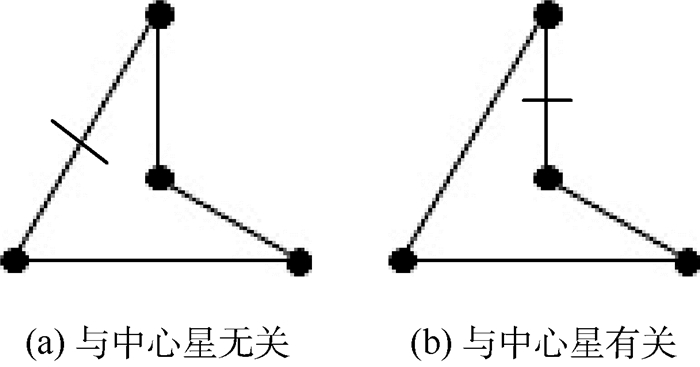 |
| 图 12 2种通信链路损坏示意图 Fig. 12 Schematic diagram of two types of communication link damage |
| 图选项 |
表 4 在线搜索算法对于解决通信链路损坏问题的效果 Table 4 Effect of online search algorithm on problem solution of communication link damage
| 通信链路损坏情况 | 位置误差/m | 推力器消耗/(10-5N·s) |
| 无通信损坏 | 0.001 265 | 554 739 |
| 0.001 517 | ||
| 0.001 864 | ||
| 通信损坏1 (与中心星无关) | 0.003 387 | 149 158 162 |
| 0.003 451 | ||
| 0.001 793 | ||
| 通信损坏2 (与中心星有关) | 0.002 755 | 265 258 269 |
| 0.003 723 | ||
| 0.002 245 |
表选项
由以上仿真可知, 当考虑到拓扑结构中通信链路的损坏时, 虽然系统仍能较正常的运转, 而由于时滞变长使得误差积累以及由于信息滞后造成的计算误差, 使得整个系统的控制精度会有不同程度的下降, 推力器消耗也会大大提高。由于中心领航星在系统中占据较重要的地位, 故3.2节提到的基于拓扑结构的修正算法中所占用的权值也较大, 所以当与之有关的通信链路发生故障时, 对系统也会产生更大的影响。
5 结论 本文研究了微推力下的卫星编队保持问题及其应用, 并进一步做出了一定优化。
1) 设计了适用于光学干涉测量和对地观测的Cartwheel编队构型, 并针对此编队构型分析了其各种拓扑结构的特性, 选取环形拓扑结构, 并设计了基于环形拓扑结构对卫星编队构型的修正算法。
2) 在此基础上, 利用LQR控制, 并加入PSO算法对控制任务进行重分配, 实现了微推力下的高精度卫星编队保持任务。
仿真表明, 所设计的控制器能较好地完成对预定编队构型的保持, 保持较高的精度的同时尽可能减少能量的消耗; 在加入随机导航误差或模仿通信链路损坏时, 仍能较好地完成控制任务; 兼顾了快速性和可靠性。然而当控制过程受到影响时, 控制精度不可避免地会有些降低, 能量消耗有所提高, 如何降低这些因素对控制系统的影响, 将是下一步的研究方向。
参考文献
| [1] | REICHBACH J, SEDWICK R J, MARTINEZ-SANCHEZ M. Micropropulsion system selection for precision formation flying satellites[D]. Cambridge: Massachusetts Institute of Technology, 2001. |
| [2] | SCHARF D P, KEIM J A, HADAEGH F Y. Flight-like ground demonstrations of precision maneuvers for spacecraft formations-Part Ⅰ[J].IEEE Systems Journal, 2010, 4(1): 84–95.DOI:10.1109/JSYST.2010.2042532 |
| [3] | SCHARF D P, KEIM J A, HADAEGH F Y. Flight-like ground demonstrations of precision maneuvers for spacecraft formations-Part Ⅱ[J].IEEE Systems Journal, 2010, 4(1): 96–106.DOI:10.1109/JSYST.2010.2044281 |
| [4] | RAYMAN M D, VARGHESE P. The Deep Space 1 extended mission[J].Acta Astronautica, 2001, 48(5-12): 693–705.DOI:10.1016/S0094-5765(01)00044-3 |
| [5] | RACCA G D, MARINI A, STAGNARO L, et al. SMART-1 mission description and development status[J].Planetary & Space Science, 2002, 50(14): 1323–1337. |
| [6] | 刘博, 特日格乐, 王聪, 等. 印度"一箭104星"任务简析[J].国际太空, 2017(4): 55–61. LIU B, TERGEL, WANG C, et al. Analysis on the mission of India's launching of 104 Satellites on a single rocket[J].Space International, 2017(4): 55–61.(in Chinese) |
| [7] | 杨灵芝, 魏延明, 刘旭辉. MEMS固体微推力器阵列发展研究[J].空间控制技术与应用, 2016, 42(1): 13–19. YANG L Z, WEI Y M, LIU X H. Development of MEMS solid propellant micro-thruster array[J].Aerospace Control and Application, 2016, 42(1): 13–19.(in Chinese) |
| [8] | MASSONNET D. Capabilities and limitations of the interferometric Cartwheel[J].IEEE Transactions on Geoscience & Remote Sensing, 2001, 39(3): 506–520. |
| [9] | 范林东, 杨博, 苗峻, 等. 基于SiC MEMS阵列的高精度微纳卫星编队保持[J].中国空间科学技术, 2016, 36(2): 37–45. FAN L D, YANG B, MIAO J, et al. High precision micro-nano satellite formation keeping based on SiC MEMS micro thruster array[J].Chinese Space Science and Technology, 2016, 36(2): 37–45.(in Chinese) |
| [10] | 张安慧. 大规模航天器编队协同控制性能分析与信息拓扑设计[D]. 哈尔滨: 哈尔滨工业大学, 2013. ZHANG A H. Performance analysis and information topology design for large scale spacecraft formation coordinated control[D]. Harbin: Harbin Institute of Technology, 2013(in Chinese). |
| [11] | TILLERSON M, INALHAN G, HOW J P. Coordination and control of distributed spacecraft systems using convex optimization techniques[J].International Journal of Robust & Nonlinear Control, 2002, 12(2-3): 207–242. |
| [12] | ALFRIEND K, VADALI S R, GURFIL P, et al. Spacecraft formation flying:Dynamics, control and navigation[M].Oxford: Butterworth-Heinemann, 2009. |
| [13] | JOHNSON L B, CHOI H L, PONDA S S, et al. Decentralized task allocation using local information consistency assumptions[J].Journal of Aerospace Information Systems, 2017, 14(2): 103–122.DOI:10.2514/1.I010461 |
| [14] | ULYBYSHEV Y. Long-term formation keeping of satellite constellation using linear-quadratic controller[J].Journal of Gui-dance, Control, and Dynamics, 1998, 21(1): 109–115.DOI:10.2514/2.4204 |
| [15] | FERNANDEZ-MARQUEZ J L, SERUGENDO G D M, MONTAGNA S, et al. Description and composition of bio-inspired design patterns:A complete overview[J].Natural Computing, 2013, 12(1): 43–67.DOI:10.1007/s11047-012-9324-y |
