一般地,非平稳信号建模算法分为两类:一类是自适应递归估计算法,如卡尔曼滤波、最小均方估计、递归最小二乘(Recursive Least Squares,RLS)算法等,由于自适应算法的收敛较慢,该类算法难以对变化较快、噪声较大的时变系统进行有效估计[2]。另一类是基于基函数逼近的参数建模算法,即把时变参数表示为一系列基函数的线性或非线性组合,从而将时变参数建模问题转化为关于基函数的时不变回归模型辨识问题。与自适应估计算法相比,基函数展开更适合于对具有较强非平稳性的时变信号进行辨识[3]。目前有大量可供选择的基函数,常用的主要有:多项式基函数(切比雪夫基函数和勒让德基函数等)、傅里叶基、小波基、Walsh和Haar函数等,每组基函数均有自身的逼近特性,如多项式和小波基对平滑缓慢变化的系统辨识效果较好,而Walsh和Haar函数,适于估计急剧或分段式变化的时变参数[4]。目前,基函数的选取没有完整的体系算法,是展开式算法要考虑的主要问题之一。
基于传统的基函数展开式算法,难以准确辨识不同类型的时变参数变化,为使参数辨识结果更加灵活,大多数研究人员采用多小波基函数[5-6],利用多种类型小波基函数构成多分辨率小波分解,充分结合平滑及分段小波基函数的逼近性能,能够同时准确跟踪缓慢平滑的慢变以及快速急剧的突变,与传统基函数展开相比,多小波基函数算法更适合于非平稳信号的建模分析。
时变参数通过基函数扩展后得到的时不变回归模型包含大量高度相关的待估参数,针对该高维病态矩阵求解问题,许多研究证明正交最小二乘(Orthogonal Least Squares,OLS)[7]算法能够有效稀疏原始冗余模型,构建合理的模型结构,进而实现参数辨识。然而,当信号背景噪声较大时,OLS算法容易出现过拟合现象,为克服过拟合,一般可采用正则化处理。正则化正交最小二乘(Regularized Orthogonal Least Squares,ROLS)[8]算法在OLS算法的基础上进一步引入正则项作为误差准则,一定程度缓解了过拟合现象,提高了对噪声的鲁棒性,使得展开后模型结构的稀疏构建及参数估计过程快速有效。与经典OLS算法相比,ROLS算法更适合于辨识复杂背景噪声下的时变系统。
综上所述,本文选择多小波B样条基函数对非平稳时变系统进行参数展开,同时,考虑到真实信号中含有大量的噪声,通过ROLS算法,对展开后的回归模型进行模型项的选择及参数估计。仿真实验说明,与RLS、基于多小波基函数展开的经典OLS算法相比,该算法估计性能最优。通过该算法对真实EEG信号建立时变自回归模型,基于辨识的时变参数可进行高时间、高频率分辨率的时频能量分析[9],能够准确获得能量在时间、频率轴上的动态变化过程,进而对运动想象任务下EEG信号事件相关去同步(Event-Related Desynchronization,ERD)及事件相关同步(Event-Related Synchronization,ERS)规律实现有效地分析。ERD/ERS分析结果定量客观地揭示了运动想象EEG信号所包含的频率分量及变化规律,有助于认识运动想象状态下大脑各区域神经活动的能量变化特点及脑活动机制。另外,该结果作为一种高分辨率、高灵敏度的时频特征,能够有效提高运动想象脑机接口(Brain Computer Interface,BCI)系统的判断精度。
1 多小波基函数的时变模型辨识 1.1 时变自回归模型 非平稳信号可用时变自回归模型描述,p阶时变自回归模型表示如下:
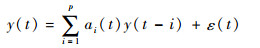 | (1) |
式中:y(t)为待估计的时变信号,t为离散采样时间序列;ε(t)为均值为0,方差为σε2的高斯白噪声序列; ai(t)为时变参数。为估计时变参数ai(t),本文基于基函数展开式算法,将时变参数表示为一组基函数{ωm(t):m=1, 2, …, L}的线性组合:
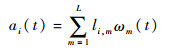 | (2) |
其中:li, m为基函数的时不变权系数。
则式(1)可写为
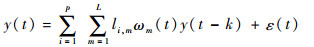 | (3) |
定义:
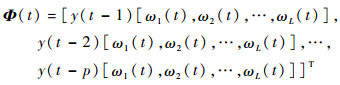 | (4) |
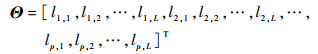 | (5) |
式中:Φ(t)和Θ分别为展开后的回归项向量和参数向量。
将式(3)改写为如式(6)向量形式:
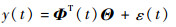 | (6) |
引入基函数后,时变自回归模型式(1)转化为时不变标准线性回归模型式(6),时变参数ai(t)辨识问题转化为时不变参数Θ的求解。令Θ的估计值为
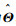
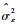
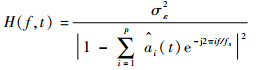 | (7) |
式中:f和fs分别为频率和采样频率。时频谱函数式(7)关于频率f是连续的,故可用于对任何低于奈圭斯特频率fs/2的频率点进行频谱估计,频率分辨率高,频率分辨率上限与模型阶数以及相关参数有关。
如本节所述,基函数的选取是展开式算法要考虑的主要问题之一,每组基函数均有其自己的逼近特点。EEG信号作为典型的生物医学信号,能量微弱复杂,常包含多种快速及缓慢变化,为使建模算法更加灵活,实现同时跟踪各种变化趋势,本文采用多小波基函数扩展算法,组合利用各类小波的逼近性能,构成多分辨率分解。
1.2 多小波基函数 根据小波理论[10-11],一平方可积的标量函数f(x)∈L2(R),L2(R)表示实数上平方可积的函数空间可用多分辨率小波分解任意逼近:
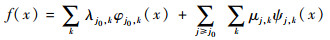 | (8) |
式中:小波族ψj, k(x)=2j/2ψ(2jx-k)和φj0, k(x)=2j/2φ(2jx-k)分别为母小波ψ及尺度函数φ的伸缩和移位,j和k分别为尺度因子和位移因子,j, k∈Z;λj0, k、μj, k为小波分解系数,j0∈Z为最低的分辨率或尺度水平。同时,根据多分辨率分析的性质,当分辨率尺度水平j0足够大时,任意平方可积函数f可用尺度基函数估计,即存在整数J,使得
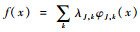
小波基函数的类型有多种,基本B样条作为一类重要的基函数,可以构成多分辨率小波分解,本文选择基本B样条函数作为基函数[12]。根据基本B样条函数的定义式[5],m阶B样条定义在[0,m],假设待估计函数f(x)定义在[0, 1],则对于任意尺度因子j,位移因子k的有效范围被约束于集合Γm={k:-m≤k≤2j-1}。B样条基函数该独特的性质使得多分辨率分解计算变得更加简洁方便。自回归模型(1)中的时变参数ai(t)可用多小波基函数展开为
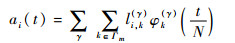 | (9) |
式中:t=1, 2, …, N,N为观测序列的长度。关于B样条基函数阶数的选取,仿真结果证明,对于大多数时变辨识问题,阶数选择3、4、5,可以达到较好的估计效果[5]。将式(2)中{ωm(t):m=1, 2, …, L}用{φk(γ)(t):k∈Γm}表示,则式(9)可转化为式(2)的形式,进一步迭代可得到标准线性回归模型式(6)。
初始回归方程式(6)涉及到大量待估参数,关联的回归项可能高度相关,对于该高维病态回归问题,普通最小二乘难以得到可靠的结果。为解决该问题,本文采用ROLS算法,可有效地选择出重要的模型回归项,构建稀疏合理的模型结构,并估计相应回归参数。
2 时变自回归模型参数估计 2.1 ROLS算法 对于涉及大量候选模型回归项的动态回归问题,OLS算法[7, 13-14]被证明可有效地进行模型项的选择及参数估计。然而,由于OLS算法中用到的误差准则为完全平方误差εTε(ε为误差向量),在数据噪声背景较大的情况下,该最小平方准则会出现过拟合现象[7]。
为克服过拟合现象,常用的算法是对模型进行正则化处理。本文采用将0阶正则项与OLS算法相结合的ROLS算法[8],增强参数估计的鲁棒性,防止过拟合现象,且计算量与OLS算法相当。
考虑模型式(6)的矩阵形式:
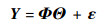 | (10) |
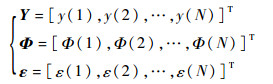 | (11) |
定义回归矩阵Φ的正交分解为
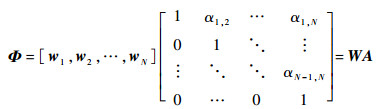 | (12) |
式中:正交列满足wiTwj = 0, i≠j。
模型式(10)可改写为
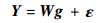 | (13) |
式中:正交权重向量g=[g1, g2, …, gN]T,参数向量Θ满足AΘ=g。
ROLS算法考虑0阶正则化误差项,其标准化后的误差准则为
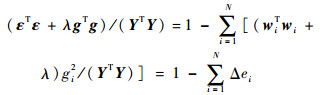 | (14) |
式中:λ≥0为正则化参数;Δei为正则化误差减小率。为选择合理的正则化参数λ,对ROLS算法进行贝叶斯解释,获得λ的迭代计算过程如下[15]:
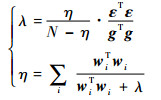 | (15) |
给定λ一初始值,经过若干次迭代计算即可获得稳定且符合算法要求的λ值。依据Δei,利用前向回归算法可逐步选择出重要的回归项,直到
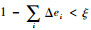
2.2 模型阶数确定 关于模型阶数的确定问题,可根据常用的模型定阶准则,本文采用AIC(Akaike Information Criterion)准则[16]定义如下:
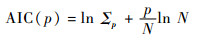 | (16) |
式中:Σp为p阶模型估计误差的方差,使得AIC最小的p为最佳模型阶数,该准则可较好地平衡模型估计精度和复杂度。
3 仿真实例 为验证提出的多小波B样条基函数展开及ROLS算法对时变参数估计的有效性,进行仿真测试实验,分别采用RLS算法、基于B样条展开的OLS(B样条-OLS)估计法及基于多小波B样条和ROLS(B样条-ROLS)建模算法,辨识仿真时变模型,比较并评估了不同算法的估计性能。仿真的二阶时变模型为
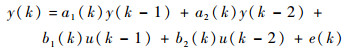 | (17) |
相关参数如下:
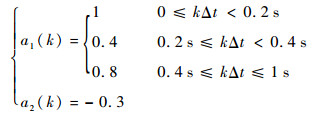 | (18) |
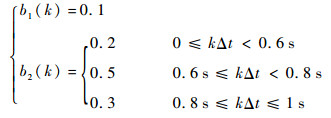 | (19) |
输入项u(k)为方差为1的高斯随机序列,采样频率fs=1 700 Hz,采样间隔时间Δt=1/fs,e(k)为均值为0,方差为0.008的高斯白噪声序列。
利用本文提出的B样条-ROLS建模算法建立时变回归模型,模型阶数取2,B样条阶数取3、4、5,尺度因子j取4,正则化参数λ取1。分别采用RLS算法(遗忘因子取0.96)、B样条-OLS估计法及提出的B样条-ROLS建模算法,对仿真时变参数进行辨识,3种算法的估计结果如图 1所示。
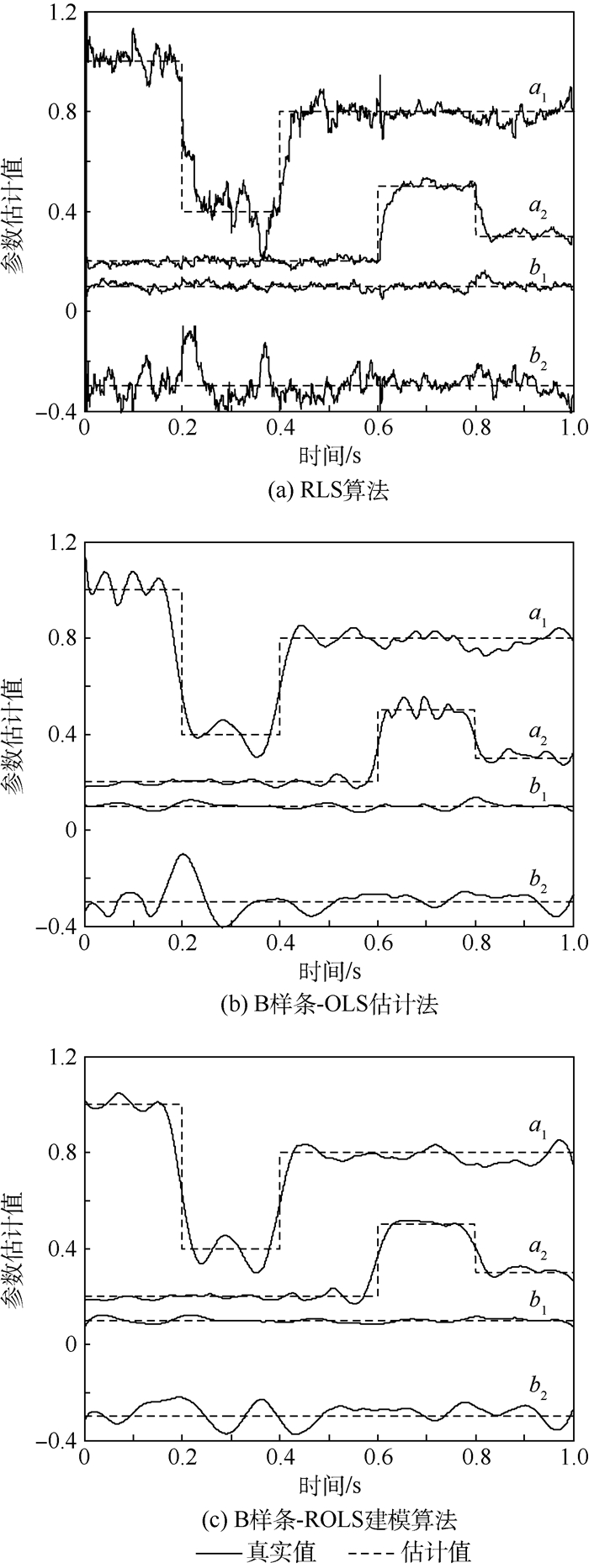 |
| 图 1 基于3种算法的参数辨识结果 Fig. 1 Parameter identification results based on three algorithms |
| 图选项 |
图 1(a)表明,RLS算法由于迭代收敛过程慢,极易受噪声影响,因而难以准确跟踪参数的阶跃性快速变化,且估计参数波动较大。图 1(b)中,多小波B样条基函数良好局部逼近性能,使得该展开算法可以较好地跟踪参数变化,但OLS算法对噪声比较敏感,容易过度捕捉噪声信息,导致出现过拟合现象,造成估计延迟。从图 1(c)得知,B样条-ROLS建模算法结合了多小波B样条基较强的逼近特性和正则化误差准则,因而能够迅速跟踪参数变化,同时对噪声的鲁棒性较好,参数波动较小,一定程度上缓解了过拟合现象。
为进一步定量评估提出算法的参数估计性能,计算比较了上述3种算法参数估计值与真实值之间的平均绝对误差(Mean Absolute Error,MAE),以及标准均方根误差(Root Mean Squared Error,RMSE)分别为
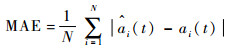 | (20) |
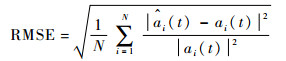 | (21) |
MAE与RMSE越小,表明误差越小,参数估计性能越好。3种算法MAE和RMSE的对比结果如表 1所示。由表 1可知,B样条-OLS估计法效果优于RLS算法,而B样条-ROLS建模算法MAE及RMSE均最小,估计效果最优。该结果表明,本文提出的算法对于参数中快速或缓慢的变化,均可较好地跟踪辨识,且对噪声有一定的鲁棒性,更适用于真实非平稳时变过程的分析及特征提取。
表 1 3种辨识算法估计结果对比 Table 1 Comparison of estimation results among three identification algorithms
| 辨识算法 | 估计参数 | MAE | RMSE |
| RLS算法 | a1(t) | 0.044 8 | 0.142 7 |
| a2(t) | 0.042 2 | 0.263 4 | |
| b1(t) | 0.011 4 | 0.149 6 | |
| b2(t) | 0.017 6 | 0.107 7 | |
| B样条-OLS估计法 | a1(t) | 0.040 6 | 0.101 0 |
| a2(t) | 0.037 7 | 0.178 9 | |
| b1(t) | 0.008 9 | 0.121 7 | |
| b2(t) | 0.016 8 | 0.102 4 | |
| B样条-ROLS建模算法 | a1(t) | 0.039 2 | 0.097 5 |
| a2(t) | 0.035 0 | 0.136 5 | |
| b1(t) | 0.007 9 | 0.099 0 | |
| b2(t) | 0.015 4 | 0.102 0 |
表选项
4 EEG数据建模及时频特征分析 将B样条-ROLS建模算法用于对真实EEG数据建模及时频分析。EEG数据来源于PhysioNet数据库[17],其中包含109位健康被试在执行相同运动想象任务时采集的EEG数据。EEG信号采样频率为160 Hz,记录了64通道数据,电极放置位置以国际10-20导采集系统为标准。每名被试执行4类实验:打开握紧左拳或右,想象打开握紧左拳或右拳,打开握紧双拳或双脚,想象打开握紧双拳或双脚。
运动想象,指想象肢体运动而没有实际的肢体动作[18]。由于在想象左右手运动时产生的脑电信号具有ERD及ERS特征,即大脑异侧主感觉运动皮层α节律(8~13 Hz)和β节律(18~25 Hz)幅度明显减小(ERD),而同侧相应区域α、β节律幅度明显增大(ERS)[19],故通过分析运动想象脑电信号,可以判断想象者的运动意图,从而实现对外部设备的控制。因此运动想象脑电信号成为BCI系统最常使用的一种特征信号,对于有运动障碍患者来说更具有实际意义[20-22]。为对运动想象EEG信号进行分析,本文选择PhysioNet数据库中第2类实验任务数据,包含每名被试想象左、右拳运动实验各21次,每次想象时间持续4 s。大量关于运动想象EEG的研究表明,与想象左右手运动相关的神经活动主要分布在通道位置覆盖了主感觉运动皮层的C3、C4、Cz通道[19, 23],因而本文通过多小波B样条展开以及ROLS算法,对想象左右手任务下,预处理后C3、C4通道的EEG信号进行建模及时频特征提取。
对原始数据进行离散小波滤波,滤除高、低频噪声及眼动伪迹,得到5~15 Hz频带数据,预处理后被试1想象左手运动任务下,第一次实验C3通道EEG信号时域波形如图 2所示。用多小波B样条-ROLS建模算法对该信号建立时变模型,由AIC准则求得模型最佳阶数为5[24],B样条阶取3、4、5,尺度因子j取4,正则化参数λ取1。为清晰表示模型辨识效果,图 3显示了0.5~3.0 s时间段的信号估计结果。由图 3可知,所建模型准确跟踪了处理后真实EEG信号的变化,证明了B样条-ROLS建模算法对真实非平稳时变信号的适用性。
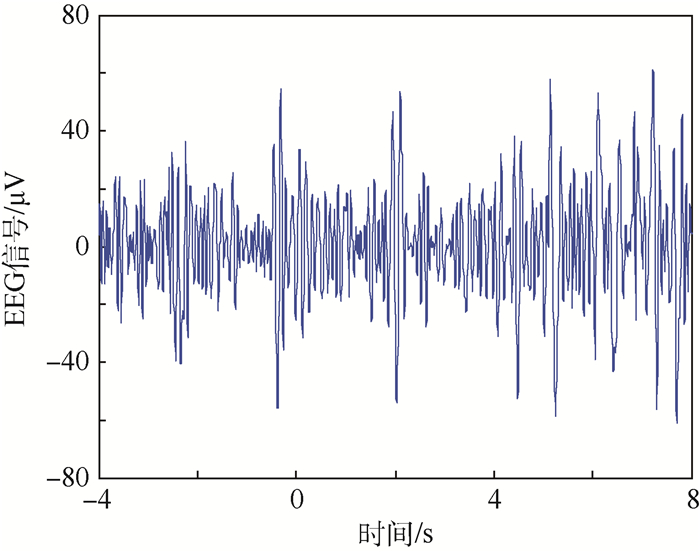 |
| 图 2 预处理后EEG信号时域波形 Fig. 2 Time domain waveform of preprocessed EEG signals |
| 图选项 |
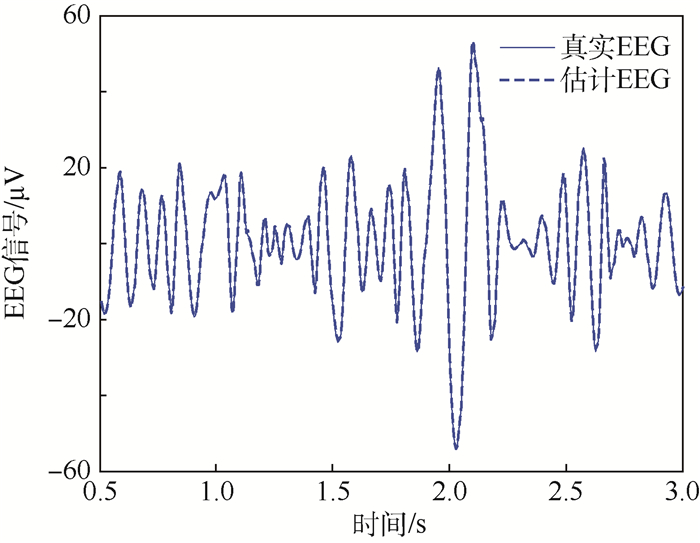 |
| 图 3 5阶时变自回归模型估计结果与真实EEG信号对比 Fig. 3 Comparison between estimation results from TVAR(5) time-varying autoregressive model and real EEG signal |
| 图选项 |
对被试1想象左右手任务下,各21次实验数据均进行上述预处理及建模运算,根据式(7)计算各单次实验EEG信号的时频能量分布,叠加平均后,取任务开始前2s作为基线,得到不同任务下C3、C4通道相对时频能量变化如图 4所示。其中,黑色实线框标明5~15 Hz频率段范围,根据该黑色框区域可获得任务开始后α节律下ERS及ERD规律:想象左手运动,同侧C3通道相对能量增强,异侧C4通道相对能量减弱;想象右手运动,同侧C4通道相对能量增强,异侧C3通道相对能量减弱。该规律表明大脑皮层运动感觉区在左右手运动想象任务下,α频带内同侧区域神经活动同步性增强,与运动想象EEG研究结论及解剖学理论相符合[19]。同时,与传统时频分析算法相比,该算法能够准确量化每个时间采样点、任意频率点上的能量,反映出运动想象过程中时频能量的动态变化过程。
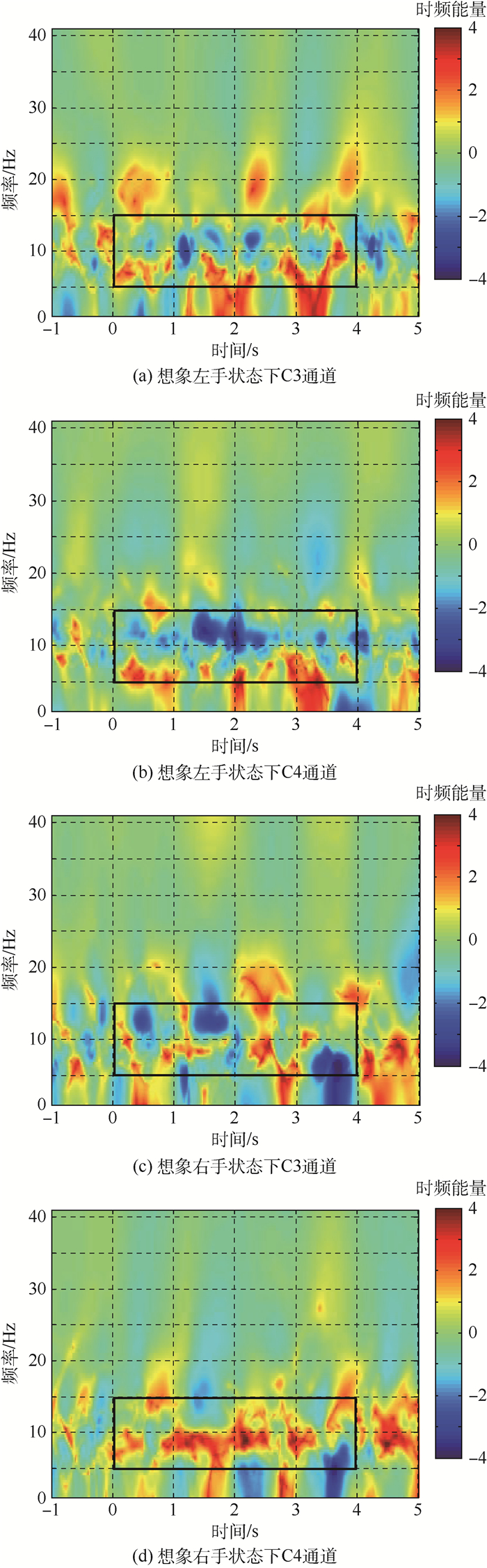 |
| 图 4 不同任务下C3、C4通道相对时频能量变化图 Fig. 4 Relative time-frequency power spectrum of channel C3 and C4 during motor imagery |
| 图选项 |
进一步从时间-频率-空间域上分析EEG信号的相对能量变化过程,每隔0.05 s计算各类任务下α节律相对能量脑头皮地形图,如图 5所示。由图 5(a)可知,想象左手运动,任务开始后0.40~0.75 s期间,α频带下同侧C3相对能量持续高于对侧C4;图 5(b)表明,想象右手运动,想象开始后0.65~1 s期间,α节律下同侧C4相对能量持续高于对侧C3。图 5从时间-频率-空间3个方面分析EEG信号,揭示了运动想象状态下大脑各区域实时动态的神经活动能量分布,能够准确提取出相应任务下大脑作出反应的瞬时时-频特征分布。提出的算法能够对运动想象EEG信号提取时域-频域-空间域特征,具有较高的时间、频率分辨率,充分利用EEG信号采集时间分辨率高、频率信息丰富的特点,可有效提高运动想象BCI系统的判断正确率,提升对运动想象脑活动机理的认识。
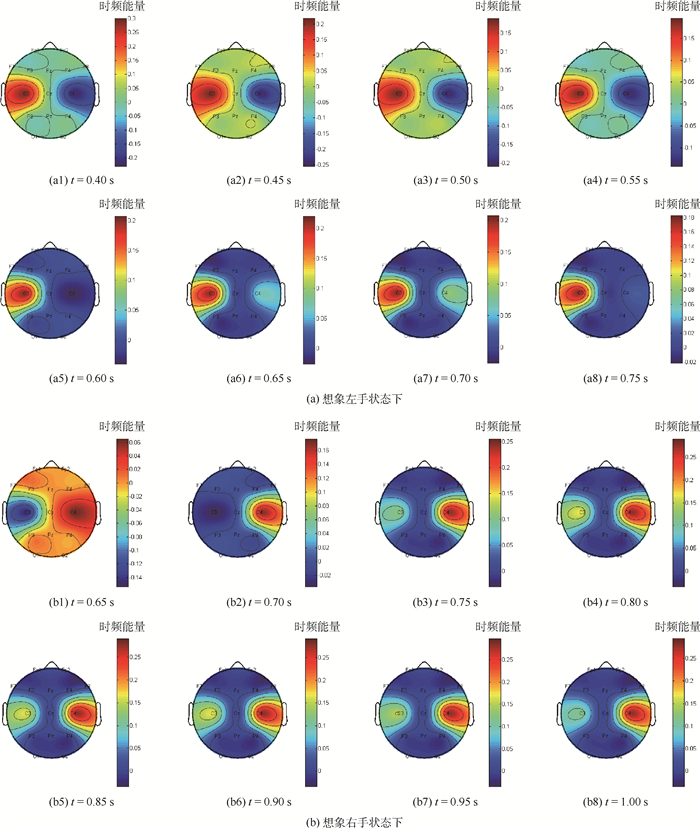 |
| 图 5 各类任务下不同时间点相对能量头皮地形图 Fig. 5 Topographic maps of time-dependent power during motor imagery tasks |
| 图选项 |
5 结论 1) 针对时变系统辨识问题,本文提出了一种新的B样条-ROLS建模算法。该算法结合多小波基的良好局部逼近特性以及ROLS算法的正则化误差准则,可准确、迅速地辨识时变参数,对时变系统具有良好的动态跟踪能力,适用于包括EEG等非平稳复杂时变信号进行估计及时频特征分析。
2) 仿真实例结果验证了本文算法对时变参数估计的有效性,对于噪声干扰下的时变系统,与传统的RLS及B样条-OLS估计法相比,本文算法估计性能最优。对于真实运动想象EEG数据,本文算法同样能够准确快速地跟踪辨识,进一步进行的时频分析可准确反映出α节律下的ERS及ERD规律,提取的具有高分辨率的时域-频域-空间域特征有助于提高运动想象BCI系统判别准确度,同时加深对运动想象脑活动机制的理解。
3) 本文算法可有效辨识复杂时变非平稳信号,具有普遍适用性,可用于分析各类不同状态下的EEG信号,包括用于研究基于自发脑电的飞行员脑力负荷检测[25]。人机系统作业过程中的脑力负荷评估是工效学的重要研究内容,基于生理信号实时脑力负荷监测能够实现根据脑力负荷在飞行员与自动化系统之间动态分配任务,进而优化人机系统设计,避免过高脑力负荷,降低人误风险,在模拟飞行、模拟无人机控制等任务中已被证明可改善作业绩效和飞行员的主观感受[26]。基于自发脑电的研究是脑力负荷研究中使用最多的算法,在接下来的研究工作中,可继续通过本文提出的时频分析算法对飞行员在不同脑力负荷水平下自发脑电各个频段的能量变化进行分析,进而利用模式识别算法建立脑力负荷识别模型,实现对脑力负荷的实时准确监测。
参考文献
| [1] | COBURN K L, LAUTERBACH E C, BOUTROS N N, et al. The value of quantitative electroencephalography in clinical psychiatry:A report by the committee on research of the american neuropsychiatric association[J].The Journal of Neuropsychiatry and Clinical Neurosciences, 2006, 18(4): 460–500.DOI:10.1176/jnp.2006.18.4.460 |
| [2] | SKRETTING K, ENGAN K. Recursive least squares dictionary learning algorithm[J].IEEE Transactions on Signal Processing, 2010, 58(4): 2121–2130.DOI:10.1109/TSP.2010.2040671 |
| [3] | 于开平, 庞世伟, 赵婕. 时变线性/非线性结构参数识别及系统辨识算法研究进展[J].科学通报, 2009, 54(20): 3147–3156. YU K P, PANG S W, ZHAO J. Advances in method of time-varying linear/nonlinear structural system identification and parameter estimate[J].Chinese Science Bulletin, 2009, 54(20): 3147–3156.(in Chinese) |
| [4] | LI B, CHEN X. Wavelet-based numerical analysis:A review and classification[J].Finite Elements in Analysis and Design, 2014, 81(4): 14–31. |
| [5] | LI Y, WEI H L, BILLINGS S A. Identification of time-varying systems using multi-wavelet basis functions[J].IEEE Transactions on Control Systems Technology, 2011, 19(3): 656–663.DOI:10.1109/TCST.2010.2052257 |
| [6] | LI Y, WEI H L, BILLINGS S A, et al. Time-varying model identification for time-frequency feature extraction from EEG data[J].Journal of Neuroscience Methods, 2011, 196(1): 151–158.DOI:10.1016/j.jneumeth.2010.11.027 |
| [7] | WEI H L, BILLINGS S A. Model structure selection using an integrated forward orthogonal search algorithm assisted by squared correlation and mutual information[J].International Journal of Modelling, Identification and Control, 2008, 3(4): 341–356.DOI:10.1504/IJMIC.2008.020543 |
| [8] | WANG N, ER M J, HAN M. Parsimonious extreme learning machine using recursive orthogonal least squares[J].IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(10): 1828–1841.DOI:10.1109/TNNLS.2013.2296048 |
| [9] | WEI H L, BILLINGS S A, LIU J J. Time-varying parametric modelling and time-dependent spectral characterisation with applications to EEG signals using multiwavelets[J].International Journal of Modelling, Identification and Control, 2010, 9(3): 215–224.DOI:10.1504/IJMIC.2010.032802 |
| [10] | GUO L, RIVERO D, PAZOS A. Epileptic seizure detection using multiwavelet transform based approximate entropy and artificial neural networks[J].Journal of Neuroscience Methods, 2010, 193(1): 156–163.DOI:10.1016/j.jneumeth.2010.08.030 |
| [11] | SCHNEIDER K, VASILYEV O V. Wavelet methods in computational fluid dynamics[J].Annual Review of Fluid Mechanics, 2010, 42: 473–503.DOI:10.1146/annurev-fluid-121108-145637 |
| [12] | CHUI C K. An introduction to wavelets[M].Amsterdam: Elsevier, 2016: 49-74. |
| [13] | GUO Y, GUO L, BILLINGS S A, et al. An iterative orthogonal forward regression algorithm[J].International Journal of Systems Science, 2015, 46(5): 776–789.DOI:10.1080/00207721.2014.981237 |
| [14] | GUO Y, GUO L Z, BILLINGS S A, et al. Identification of nonlinear systems with non-persistent excitation using an iterative forward orthogonal least squares regression algorithm[J].International Journal of Modelling, Identification and Control, 2015, 23(1): 1–7.DOI:10.1504/IJMIC.2015.067496 |
| [15] | CHEN S, CHNG E, ALKADHIMI K. Regularized orthogonal least squares algorithm for constructing radial basis function networks[J].International Journal of Control, 1996, 64(5): 829–837.DOI:10.1080/00207179608921659 |
| [16] | AKAIKE H. A new look at the statistical model identification[J].IEEE Transactions on Automatic Control, 1974, 19(6): 716–723.DOI:10.1109/TAC.1974.1100705 |
| [17] | GOLDBERGER A L, AMARAL L A, GLASS L, et al. Physiobank, physiotoolkit, and physionet[J].Circulation, 2000, 101(23): e215–e220.DOI:10.1161/01.CIR.101.23.e215 |
| [18] | YUAN H, HE B. Brain-computer interfaces using sensorimotor rhythms:Current state and future perspectives[J].IEEE Transactions on Biomedical Engineering, 2014, 61(5): 1425–1435.DOI:10.1109/TBME.2014.2312397 |
| [19] | PFURTSCHELLER G, BRUNNER C, SCHL?GL A, et al. Mu rhythm (de) synchronization and EEG single-trial classification of different motor imagery tasks[J].NeuroImage, 2006, 31(1): 153–159.DOI:10.1016/j.neuroimage.2005.12.003 |
| [20] | TAKAHASHI M, TAKEDA K, OTAKA Y, et al. Event related desynchronization-modulated functional electrical stimulation system for stroke rehabilitation:A feasibility study[J].Journal of Neuroengineering and Rehabilitation, 2012, 9(1): 56–1.DOI:10.1186/1743-0003-9-56 |
| [21] | LONG J, LI Y, WANG H, et al. A hybrid brain computer interface to control the direction and speed of a simulated or real wheelchair[J].IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2012, 20(5): 720–729.DOI:10.1109/TNSRE.2012.2197221 |
| [22] | ZHANG R, YAO D, VALDéS-SOSA P A, et al. Efficient resting-state EEG network facilitates motor imagery performance[J].Journal of Neural Engineering, 2015, 12(6): 066024.DOI:10.1088/1741-2560/12/6/066024 |
| [23] | YANG H, GUAN C, CHUA K S G, et al. Detection of motor imagery of swallow EEG signals based on the dual-tree complex wavelet transform and adaptive model selection[J].Journal of Neural Engineering, 2014, 11(3): 035016.DOI:10.1088/1741-2560/11/3/035016 |
| [24] | HESSE W, MLLER E, ARNOLD M, et al. The use of time-variant EEG Granger causality for inspecting directed interdependencies of neural assemblies[J].Journal of Neuroscience Methods, 2003, 124(1): 27–44.DOI:10.1016/S0165-0270(02)00366-7 |
| [25] | CHAOUACHI M, JRAIDI I, FRASSON C. Modeling mental workload using EEG features for intelligent systems[J].User Modeling, Adaption and Personalization, 2011, 6787(1): 50–61. |
| [26] | TIBERIO L, CESTA A, OLIVETTI BELARDINELLI M. Psychophysiological methods to evaluate user's response in human robot interaction:A review and feasibility study[J].Robotics, 2013, 2(2): 92–121.DOI:10.3390/robotics2020092 |
