为了抑制基线漂移,最常用的方法是通过一个高通滤波器去除采样数据中的漂移噪声[2-3]。但是当基线漂移非常严重时,这种方法的去噪效果并不理想。潘超等[4]将传统的多项式算法进行改进,用于校正长周期加速度信号中的基线漂移,但是在进行降维时,这种方法容易丢失信号的有用成分。Morita和Kitagawa[5]利用一系列模拟光谱研究了扰动相关移动窗口二维基线漂移的影响。王远等[6]利用改进的小波变换对信号进行10层分解,然后通过预测相消的方法有效抑制了ATEM (Array Transient Electromagnetic)数据中的基线漂移,虽然这种方法的去噪效果优于插值算法,但是需要对被测信号的细节信息十分了解。庞宇等[7]利用改进的形态学算法抑制了ECG信号中的基线漂移。此外,罗玉荣等[8]利用陷波滤波器和盲源分离法实现了对微弱信号基线漂移的抑制。在光谱研究方面,很多研究者根据实际的应用背景和信号特征,也提出了许多适用于抑制光谱基线漂移的算法[9-12]。本文则是根据振动信号的特点,将形态学去噪思想应用到了具体的工程实践中。
形态学滤波器是一种非线性信号滤波器,有着严格的数学理论基础。这种方法的局部修正能力较好,去噪过程相对简单,不需要信号的频域信息,只需通过简单的闭-开、开-闭运算即可达到提取信号、抑制噪声的目的[13]。近年来,这种方法被广泛应用于图像处理[14-15]、电力系统[16]以及振动信号处理[17]领域。因此,通过比较上述方法的优缺点,本文基于形态学基本原理和粒子群优化(PSO)算法,提出了一种用于振动信号去噪处理的3级形态学滤波方法,并对3种自动驾驶仪的实测振动信号进行了处理,效果较好。
1 基础理论 数学形态学最初是由数学家Matereron和Serra创立的一种信号分析方法,其基本思想主要包括2部分:①目标信号由集合来描述;②通过预先设计的结构元素来局部地修正被测信号的几何结构。这种方法在结构上较为简单,其基本变换仅有2种:腐蚀和膨胀。其他运算(如形态开-闭和形态闭-开)都是这2种基本变换的线性组合。以一维离散信号f(n)为例,数学描述如下。
设g(n)为形态学滤波中所用结构元素,其定义域为G={0, 1, …, M-1},F={0, 1, …, N-1}则是f(n)的定义域,且N?M,则f(n)关于g(n)的腐蚀和膨胀运算定义如下[18]:
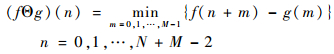 | (1) |
 | (2) |
式中:Θ与⊕分别代表腐蚀、膨胀运算。腐蚀运算和膨胀运算分别代表了一个收缩过程和一个膨胀过程。收缩过程对于减少信号峰值、加宽谷域方面效果良好;而膨胀过程则起到了相反的作用。形态学滤波中,通常是将这2种运算进行级联得到开、闭运算,其定义如下:
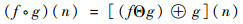 | (3) |
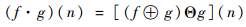 | (4) |
式中:符号“°”表示开运算,“·”表示闭运算。开运算和闭运算是形态学滤波中最基本的滤波方式,分别用于抑制信号的正、负脉冲噪声。但是单独使用的去噪效果不好,通常将两者级联使用,形成形态开-闭(OC)和形态闭-开(CO)运算,其定义如下[18]:
 | (5) |
 | (6) |
据上述定义,开-闭、闭-开运算可以同时起到抑制信号中正、负脉冲干扰的作用。实际应用中,为了抑制形态开的反扩展性和形态闭的扩展性, 尽可能降低滤波过程中统计偏移所造成的影响,通常将这2种滤波器组合使用,组合滤波器的输出形式为
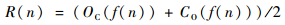 | (7) |
式中:R(n)为组合滤波器的输出信号;f(n)为输入信号,即待滤波信号。
2 滤波器设计 2.1 滤波器实现方式 对于实测信号y(n)而言,其信号成分可以表示为
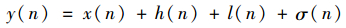 | (8) |
式中:x(n)为有用信号;h(n)为高频干扰;l(n)为基线漂移噪声;σ(n)为随机干扰。h(n)在时域上表现出很窄的波形,利用形态学去噪时,可以通过较窄的形态滤波器予以滤除; 基线漂移噪声l(n)变化缓慢,其特征接近于低频线性变化,可以通过较宽的形态滤波器予以滤除; σ(n)则可以通过适当的平滑处理进行解决。
基于上述分析,振动信号形态学级联滤波器的数学模型可以表示为如图 1所示的基本结构。根据图 1,去噪步骤共有3步。
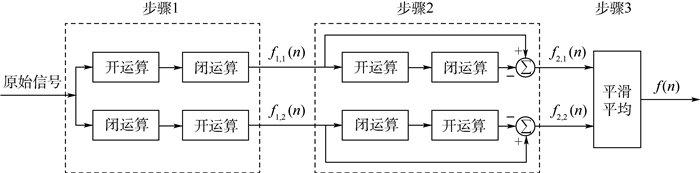 |
| 图 1 级联滤波器结构模型 Fig. 1 Structure model of cascading filter |
| 图选项 |
步骤1????利用式(5)、式(6)对输入信号x(n)进行去噪,其目的是滤除背景杂波及高频脉冲干扰,滤波器数学模型为
 | (9) |
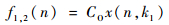 | (10) |
式中:f1, 1(n)和f1, 2(n)分别为2种运算方式步骤1滤波后的输出信号;x(n,k1)为待滤波信号x(n)通过结构元素k1进行形态滤波。步骤1的目的是去除h(n)。滤波后所剩信号包含x(n)、l(n)和σ(n)。
步骤2????将步骤1滤波后的信号再次进行处理。步骤2选择较宽的结构元素滤除有用信号x(n),该级滤波器的结构形式为
 | (11) |
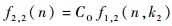 | (12) |
式中:f2, 1(n)和f2, 2(n)分别为采用2种运算方式进行步骤2滤波后的输出信号。步骤2滤波后,所剩信号只有l(n)和σ(n)。
步骤3????将步骤1和步骤2滤波所得信号进行相消与平滑处理,得到最终的去噪信号,其表达式为
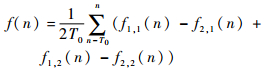 | (13) |
式中:T0为滑动滤波周期。
2.2 滤波器关键元素选取 h(n)和l(n)滤除的关键在于形态学滤波器形状的选择,而该形状可由形态学结构元素来决定。结构元素种类繁多,常见的有直线形、矩形、菱形、抛物线形等规则或不规则曲线,去噪时往往根据需要进行选择。滤波结构元素k1、k2的选择对于去噪结果有很大影响,其形状、尺寸决定了去噪的效果[11]。但是,越复杂的结构元素,如圆盘结构元素和抛物线结构元素,计算量较大,直接影响信号处理速度,难以适应实时性要求较高的自动驾驶仪振动测试。因此,本文选用简单实用的直线形结构元素。
对于直线形结构元素而言,决定其形状的元素有2个,即宽度L和角度θ,L决定了滤波器的宽度,θ决定了滤波器的方向。图 2为直线形结构元素的示意图,其中L={3, 5}, θ={0, 45, 90}。这2个元素的选取会对去噪效果产生一定的影响,如果选取不当,甚至可能使去噪失败。
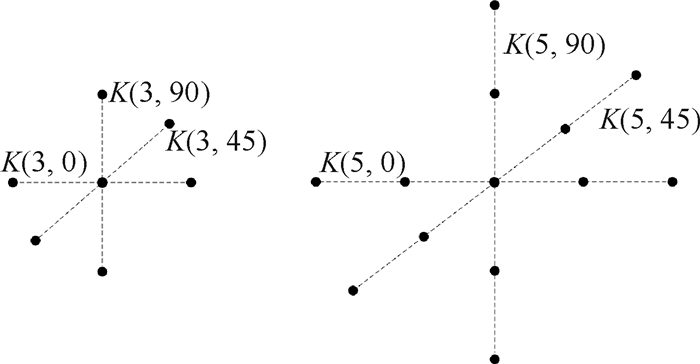 |
| 图 2 直线形结构元素基本模型 Fig. 2 Basic model of linear structural elements |
| 图选项 |
因此,考虑到L和θ对去噪的影响,并将其代入式(13),得到最终的输出信号表达式为
 | (14) |
式中:L1和θ1分别为第1级滤波器中所使用结构元素的宽度和角度;L2和θ2分别为第2级滤波器中所使用结构元素的宽度和角度。
为了合理选择直线形结构元素K(L, θ)的2个参数L和θ,本文采取以下方式:如果考虑结构元素所有可能的情况,那么由其组成的集合可以称为全方位结构元素,即
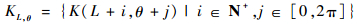 |
但是在实际的去噪过程中,不同的样本信号需要采用不同的结构元素才能实现较好的去噪效果。因此,为了提高本节所述滤波器的自适应能力,本文又进一步引入了PSO算法来实现对结构元素的最优化选择。
PSO算法是一种解决工程优化问题的有效方法,经典的PSO算法可以表示为
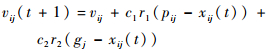 | (15) |
式中:c1和c2为学习因子;r1和r2为随机变量;xij为个体最佳位置, i = 1, 2, …, NP,j = 1, 2, …, N, NP为种群大小,N为节点数;vij为用于更新个体的最佳位置(pij)和最佳位置的全局自适应值(gj)。
为了优化滤波器的参数,目标函数定义为
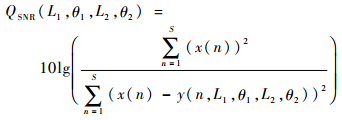 | (16) |
式中:x(n)表示原始信号, y(n)表示滤波后的信号;S为信号长度, 且n=1, 2, …, S。
3 应用实验 为了验证本文方法在去除自动驾驶仪振动信号基线漂移噪声方面的优越性,将现场采集到的信号作为去噪样本,利用小波阈值去噪、传统形态学去噪和本文方法分别进行去噪处理。图 3(a)为现场采集到A型号导弹自动驾驶仪在静止状态时的反馈信号,图 3(b)为振动测试时的反馈信号。由图 3可知,在静止状态下,信号虽然也受到了一定的干扰,但是不存在基线漂移噪声,经过振动试验,同一反馈信号出现了漂移噪声。
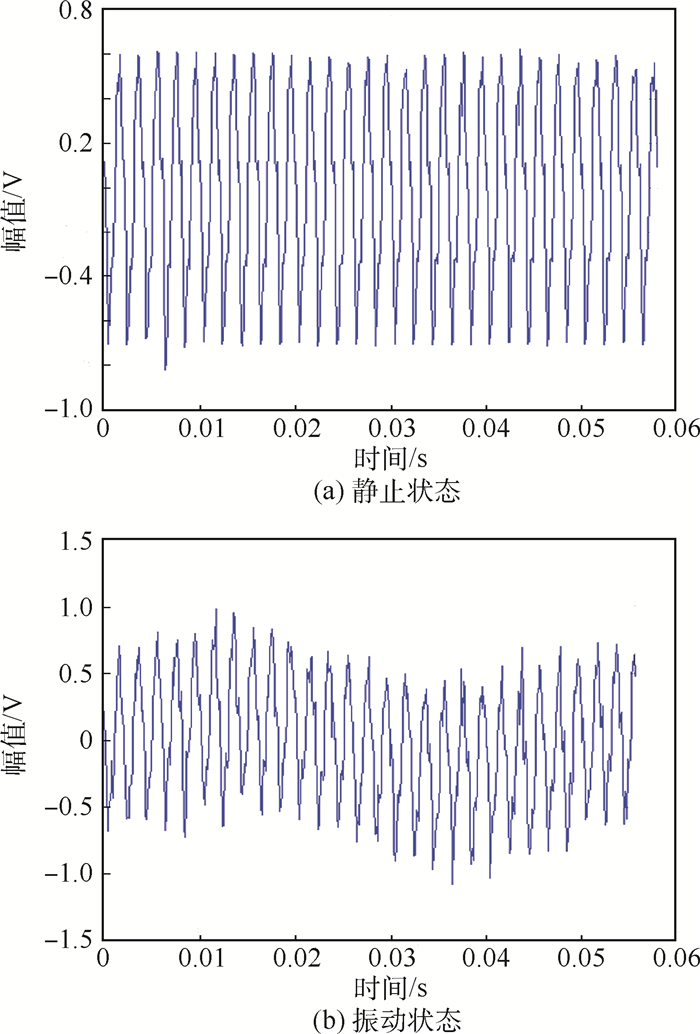 |
| 图 3 静止和振动状态实测信号 Fig. 3 Measured signals in static and vibration states |
| 图选项 |
3.1 传统形态学去噪 为了对图 3(b)所示的信号进行处理,首先采用式(7)所示的传统形态学去噪方法进行处理。消噪后的信号波形如图 4所示。
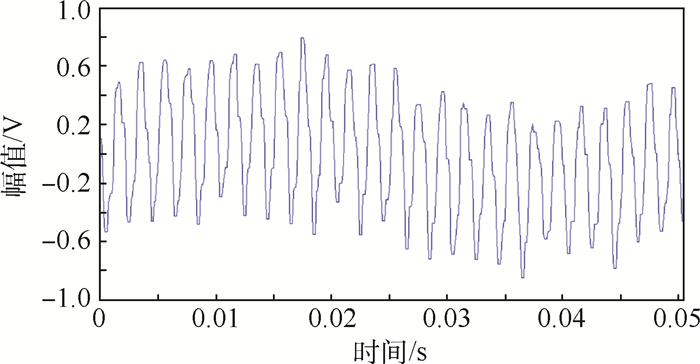 |
| 图 4 传统形态学方法去噪结果 Fig. 4 Denoising results of traditional morphological method |
| 图选项 |
利用传统形态学去噪后,信噪比(Signal to NoiseRatio, SNR)提高到了15.17,均方差(Root Mean Square Error, RMSE)为0.164,对振动信号的噪声起到了一定的抑制作用,但是根据图 4所示的去噪结果来看,基线漂移噪声仍然存在。
3.2 小波阈值去噪 本文利用小波变换同样对该实测振动信号进行了去噪处理。选择常用的“db”小波和“sym”小波作为小波基,分别进行去噪处理。表 1为2种小波基经过不同分解层数(2, 3, 4)后的去噪指标。
表 1 不同分解层数下小波阈值去噪结果 Table 1 Denoising results of wavelet transformation with different wavelet-bases
| 小波基 | 分解层数 | 均方差 | 信噪比 | 波形相似比 |
| sym8 | 2 | 0.151 | 20.80 | 0.94 |
| sym8 | 3 | 0.202 | 13.82 | 0.89 |
| sym8 | 4 | 0.428 | -21.84 | 0.32 |
| db3 | 2 | 0.165 | 18.71 | 0.93 |
| db3 | 3 | 0.254 | 7.76 | 0.83 |
| db3 | 4 | 0.428 | -21.42 | 0.32 |
表选项
由表 1所示的去噪指标可知,当分解层数大于3时,信噪比变为负值,而且波形相似比急速下降至0.3左右,说明有用信号丢失严重,因此分解层数不能大于3层。此外,比较表 1中数据可知,当分解层数为2时,去噪效果较好,此时去噪后的波形如图 5所示。可知,“sym8”小波去噪后的信号光滑度较好,但2种小波基去噪后都存在一个问题,即基线漂移噪声仍然存在。
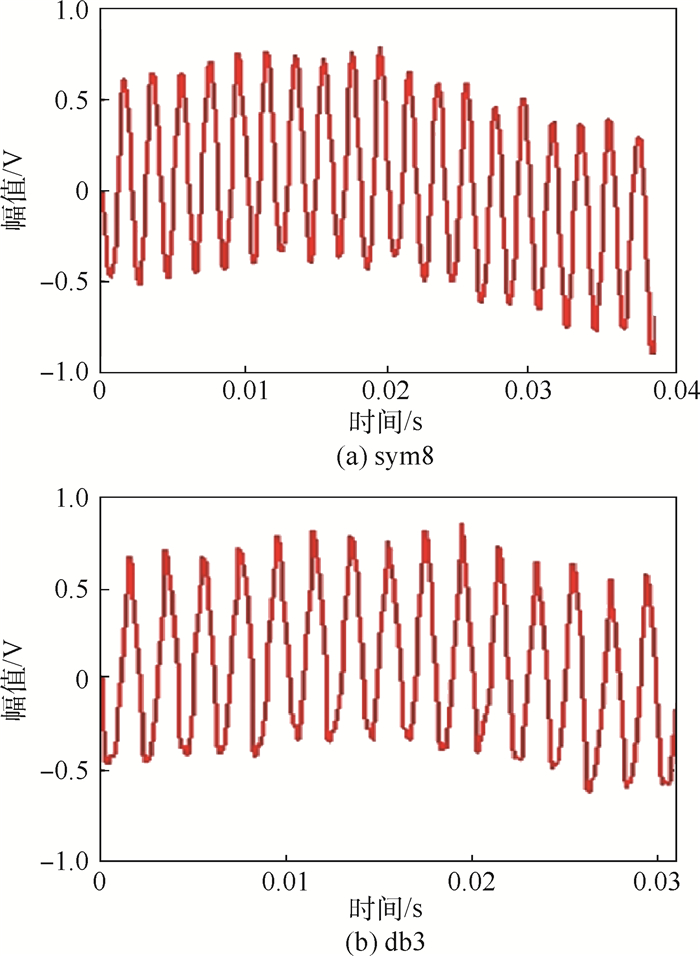 |
| 图 5 小波阈值方法去噪结果 Fig. 5 Denoising results of wavelet threshold method |
| 图选项 |
3.3 本文方法去噪 在利用本文方法进行去噪之前,需确定第1级和第2级滤波器的结构元素。根据2.2节对全方位结构元素的定义,由式(16)可得L1、L2和θ1、θ2的取值对去噪效果的影响。由图 6可知,当信噪比达到最大时,L1 < 5, L2 >28,θ1 < 22, θ2>40。
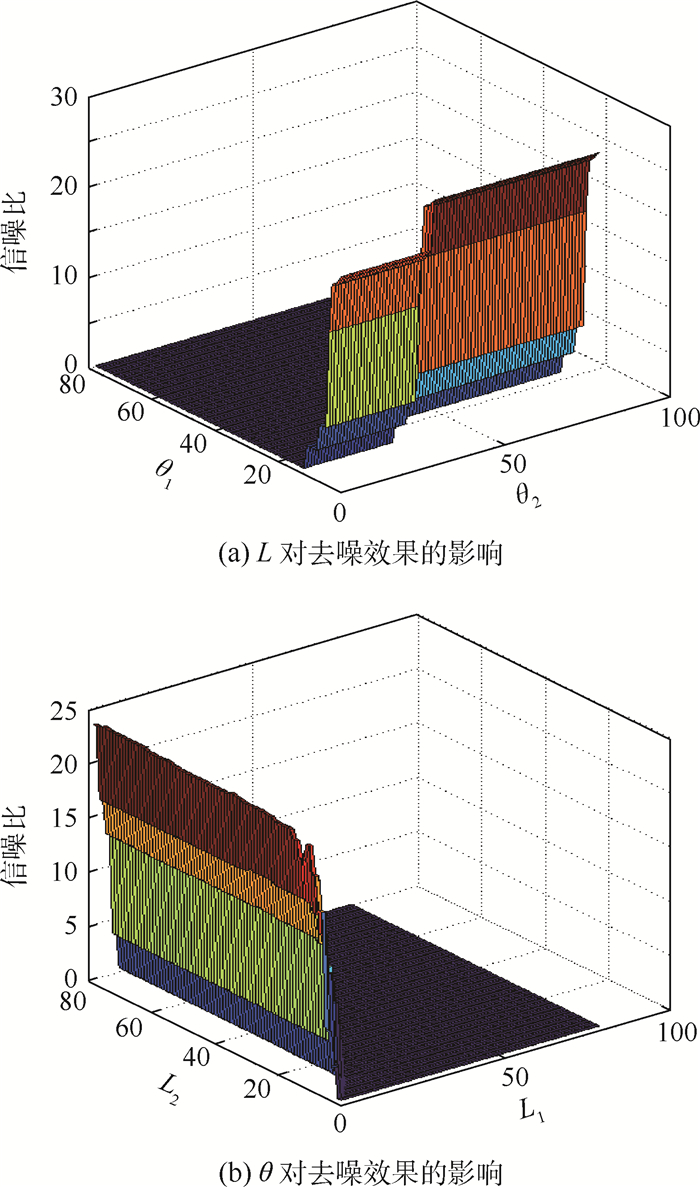 |
| 图 6 L和θ对去噪效果的影响 Fig. 6 Influence of L and θ on denoising |
| 图选项 |
利用PSO算法进行6次优化实验,优化结果如表 2所示。信噪比最终达到28左右,此时优化所得结构元素的具体取值如表 2所示。
表 2 PSO算法优化结果 Table 2 Optimization results using PSO algorithm
| 实验次数 | L1 | θ1 | L2 | θ2 | 信噪比 |
| 1 | 2 | 2 | 29 | 40 | 28.7 |
| 2 | 3 | 3 | 30 | 80 | 28.7 |
| 3 | 3 | 2 | 78 | 72 | 28.7 |
| 4 | 3 | 5 | 68 | 65 | 27.6 |
| 5 | 3 | 5 | 76 | 40 | 27.6 |
| 6 | 2 | 3 | 36 | 72 | 28.1 |
表选项
由表 2的优化结果可知,6次优化实验所得结果符合图 6所得结构元素的取值范围,进一步说明PSO算法的引入增加了本文方法的健壮性和鲁棒性。
结构元素确定之后,根据式(9)~式(13),得到本文方法滤波后的结果,如图 7所示。由滤波结果可知,本文方法能够对基线漂移进行校正。
 |
| 图 7 本文方法对自动驾驶仪实测振动信号的去噪结果 Fig. 7 Denoising results of measured vibration signal of autopilot using proposed method |
| 图选项 |
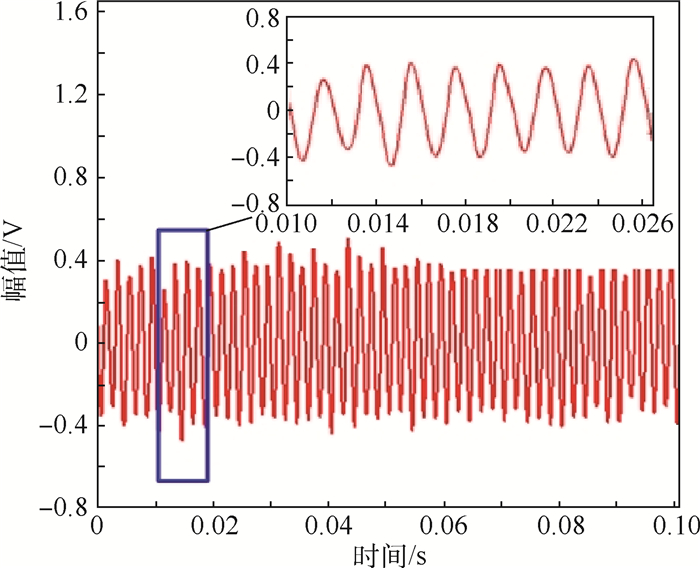
3.4 第2种振动信号去噪 为了进一步验证本文方法适用于处理导弹自动驾驶仪振动测试信号,将B型号导弹自驾仪振动过程中的某实测信号进行滤波处理,处理后的结果如图 8所示。
 |
| 图 8 本文方法和对比方法对B型号导弹自动驾驶仪实测振动信号的去噪结果 Fig. 8 Denoising results of measured vibration signal of Type B missile autopilot by proposed method and reference method |
| 图选项 |
由图 8(a)可知,理论上被测信号应当为正/余弦形式的波形,但是振动过程中测得的原始信号波形失真严重,且含有基线漂移噪声,此时无法有效提取信号特征,直接影响对自动驾驶仪相关性能的分析。利用本文方法去噪后,根据图 8(b)可明显看出,此时基线漂移噪声被有效抑制,而且背景杂散噪声也被消除,有效信号得到了恢复。而另外2种对比方法虽然对噪声有一定的抑制作用,但是无法消除根本性的基线漂移噪声。
4 对比实验 医学心电信号(ECG)是一种常见的非周期振动信号,该类信号经常伴有基线漂移。为了验证本文方法在矫正基线漂移时的自适应能力,本文从MIT-BIH心率失常数据库中随机选择了一种含有基线漂移成分的心电信号,其编号为12431_04,利用本文方法和对比方法分别对该样本信号进行了去噪分析,结果如图 9所示。
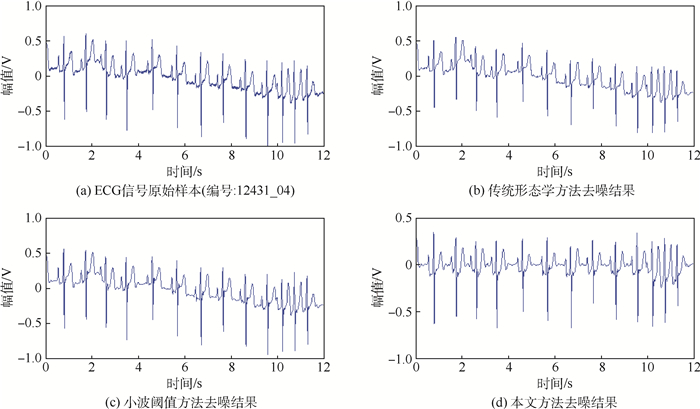 |
| 图 9 含有基线漂移噪声的ECG信号去噪结果 Fig. 9 Denoising results of ECG signals containing baseline drift noise |
| 图选项 |
5 结论 本文分析了工程应用背景,根据形态学基本原理提出了适用于自动驾驶仪振动信号去噪处理的具体方法, 通过对实测数据进行处理,得到如下结论:
1) 不同的振动信号,其基线漂移噪声不同,需选择不同的结构元素进行基线漂移校正。线性结构元素的2个参数,即宽度和角度的取值对去噪结果有很大影响。
2) 与传统的小波阈值去噪和形态学去噪相比,本文方法能够有效抑制基线漂移,降低样本信号的均方差,提高信噪比。
3) 通过对典型的含有基线漂移的ECG信号进行处理,进一步验证了本文方法在去除同类型振动信号时具有较强的自适应能力。
参考文献
| [1] | EVANS J W, KUNDU P, HOROVITZ S G, et al. Separating slow BOLD from non-BOLD baseline drifts using multi-echo FMRI[J].NeuroImage, 2015, 105: 189–197.DOI:10.1016/j.neuroimage.2014.10.051 |
| [2] | CHIU H C. Stable baseline correction of digital strong-motion data[J].Bulletin of Seismological Society of America, 1997, 87(4): 932–944. |
| [3] | BOORE D M, BOMMER J J. Processing of strong-motion accelerograms:Needs, options and consequences[J].Soil Dynamics and Earthquake Engineering, 2005, 25(2): 93–115.DOI:10.1016/j.soildyn.2004.10.007 |
| [4] | PAN C, ZHANG R F, LUO H, et al. Baseline correction of vibration acceleration signals with inconsistent initial velocity and displacement[J].Advances in Mechanical Engineering, 2016, 8(10): 1–11. |
| [5] | MORITA S, KITAGAWA K. Effect of baseline drift on perturbat-correlation moving-window two-dimensional correlation spectroscopy[J].Vibrational Spectroscopy, 2012, 60: 217–219.DOI:10.1016/j.vibspec.2011.10.003 |
| [6] | WANG Y, JI Y J, LI S Y. A wavelet-based baseline drift correction method for grounded electrical source airborne transient electromagnetic signals[J].Exploration Geophysics, 2013, 44(4): 229–237.DOI:10.1071/EG12078 |
| [7] | 邓璐, 庞宇, 赵艳霞, 等. 基于形态学的心电信号基线漂移矫正方法[J].数字通信, 2013, 40(3): 14–16. DENG L, PANG Y, ZHAO Y X, et al. Removal method of baseline drift from ECG signals based on morphology filter[J].Digital Communication, 2013, 40(3): 14–16.(in Chinese) |
| [8] | LUO Y R, HARGRAVES R H, BELLE A, et al. A hierarchical method for removal of baseline drift from biomedical signals:Application in ECG analysis[J].Scientific World Journal, 2013, 2013: 896056. |
| [9] | DU Y G, CHAMBERS S A. Etalon-induced baseline drift and correction in atom flux sensors based on atomic absorption spectroscopy[J].Applied Physics Letters, 2014, 105(16): 163113.DOI:10.1063/1.4898638 |
| [10] | LOPATKA M, BARCARU A, SJERPS M J, et al. Leveraging probabilistic peak detection to estimate baseline drift in complex chromatographic samples[J].Journal of Chromatography A, 2016, 1431: 122–130.DOI:10.1016/j.chroma.2015.12.063 |
| [11] | LIU G F, LUO X L, YANG J. Baseline drift effect on the performance of neutron and γ ray discrimination using frequency gradient analysis[J].Chinese Physics C, 2013, 37(6): 63–69. |
| [12] | ZHU F, QIN B J, FENG W Y, et al. Reducing Poisson noise and baseline drift in x-ray spectral images with bootstrap Poisson regression and robust nonparametric regression[J].Physics in Medicine and Biology, 2013, 58(6): 1739–1758.DOI:10.1088/0031-9155/58/6/1739 |
| [13] | WANG R Q, LI Q, ZHANG M. Application of multi-scaled morphology in denoising seismic data[J].Applied Geophyiscs, 2008, 5(3): 197–203.DOI:10.1007/s11770-008-0033-3 |
| [14] | SALEMBIER P, WILKINSON M H F. Connected operators:A review of region-based morphological image processing techniques[J].IEEE Signal Processing Magazine, 2009, 26(6): 136–157.DOI:10.1109/MSP.2009.934154 |
| [15] | 赵于前, 王小芳, 李桂源. 基于多尺度多结构元素的肝脏图像分割[J].光电子·激光, 2009, 20(4): 563–566. ZHAO Y Q, WANG X F, LI G Y. Liver image segmentation based on multi-scale and multi-structure elements[J].Journal of Optoelectronics·Laser, 2009, 20(4): 563–566.(in Chinese) |
| [16] | GAUTAM S, BRAHMA S M. Overview of mathematical morphology in power systems-A tutorial approach[C]//2009 IEEE Power & Energy Society General Meeting. Piscataway, NJ: IEEE Press, 2009: 3523-3529. |
| [17] | KOZUMPLíK J, PROVAZNíK I. Fast timevarying linear flters for suppression of baseline drift in electrocardiographic signals[J].Biomedical Engineering Online, 2017, 16: 24.DOI:10.1186/s12938-017-0316-0 |
| [18] | SERRA J. Image analysis and mathematical morphology[M].New York: Academic Press, 1982. |
