FPA与经典的粒子群优化(PSO)算法、人工蜂群算法、布谷鸟算法等仿生算法相同,也存在易陷入局部最优、易早熟和后期收敛速度慢等典型缺点。为了克服这些缺点,国外许多****(中国当前研究较少)在FPA的基础上进行一些针对性的研究与创新。如Wang和Zhou[10]引入邻域搜索策略、维度评价及更改策略和动态切换概率策略对算法进行改进,提高算法在高维函数优化问题的全局勘探与开发能力;Abdel-Raouf等[11]针对定积分的求解问题结合混沌优化技术提出一种改进花朵授粉算法(IFPCH),针对数独问题并结合和声搜索算法提出一种混合花朵授粉算法(FPCHS)[12],从不同侧面改善FPA的收敛性能;El-Henawy和Ismail[13]将粒子群优化算法与FPA相融合提出一种混合算法,并将其应用到求解整数规划问题及带约束的全局优化问题[14];?ukasik和Kowalski[15]对FPA进行更加详尽的描述以及对其所涉及的参数进行了研究,并与经典的粒子群优化算法进行了对比,得出FPA前期收敛速度不如粒子群优化算法,但其后期种群的多样性要优于粒子群优化算法的结论。
上述的各种研究改进算法,在某些方面提高了FPA的寻优性能,但FPA在其他领域仍存在一些不足,需要不断地改进与创新。如在多模复杂函数寻优问题上,FPA的全局勘探与局部开采能力表现不是很理想。为此,本文针对这一问题进行研究,首先从单峰函数寻优入手探究FPA的寻优机理,再结合多峰函数寻优分析FPA在多模寻优时存在的问题,最后结合模拟退火(Simulated Annealing,SA)及Nelder-Mead单纯形法提出一种改进的花朵授粉法——NS-FPA。
1 花朵授粉算法及其寻优分析 1.1 花朵授粉算法 Yang[1]通过对自然界显性花朵授粉的分析与研究,将花朵授粉分为两大基本形式:生物异花授粉与非生物自花授粉。并依据花朵的常性与授粉行为抽象出以下4条规则:
1) 生物异花授粉被考虑为算法的全局勘探行为,并由传粉者携带花粉通过Levy飞行的机制实现全局授粉。
2) 非生物自花授粉被视为算法的局部开采行为,或称局部授粉。
3) 花朵的常性可以被认为是繁衍概率,它与两朵参与授粉花朵的相似性呈正比例关系。
4) 花朵的全局授粉与局部授粉通过转换概率p∈[0,1]进行调节。由于物理上的邻近性和风等因素的影响,在整个授粉活动中,转换概率p是一个非常重要的参数。文献[1]中对该参数的试验研究认为,取p=0.8更利于算法寻优。
实际情况下,每棵显花植物拥有许多花朵,并且每朵花都有成千上万的花朵配子。为了算法的实现,Yang[1]假设每棵显花植物仅有一朵花,每朵花仅包含一个配子,每个配子被视为解空间中的一个候选解。FPA寻优的伪代码如下:
Code:FPA()
Objective:minf(x)/max f(x),x=(x1, x2, …, xd)
Input:N, Kmax, p, λ
随机初始化N个候选解x01, x02, …, x0N
计算相应的函数值y01, y02, …, y0N;
计算最优解xbest、最优值ybest;
while(t < Kmax)
????for i=1, 2, …, N do
????????if rand < p then
????????????依据式(1)执行全局授粉;
????????else
????????????依据式(2)执行局部授粉;
????????endif
????????计算子代花粉的函数值;
????????更新花粉的位置;
????endfor
????更新最优解xbest、最优值ybest;
endwhile
Output:xbest, ybest
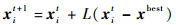 | (1) |
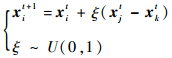 | (2) |
式中:xit+1和xit分别为第t+1和t代的候选解;xjt和xkt为相同植物种类的不同花粉配子;ξ为局部授粉系数;U为均匀分布;L为飞行步长,服从Levy分布:
 | (3) |
其中:Γ(λ)为伽马函数,λ=1.5;s为步长;s0为最小步长。文献[1]中采用Mantegna’s算法生成Levy飞行步长L。
1.2 寻优分析 为了定性分析FPA在寻优过程中花粉种群多样性的变化及寻优特性,本文针对FPA定义如下2个基本参数。
定义1??多样性(diversity)是指每一代花粉的离散程度,简记为Div。则第t代离散程度Divt计算式为
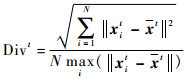 | (4) |
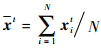 | (5) |
式中:N为花粉种群规模;xt为第t代花粉在解空间中分布的几何中心。
定义2??差异性(difference)是指花粉种群子代与父代的差异程度,简记为Dif。则第t代差异程度Dift计算式为
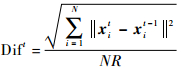 | (6) |
式中:R为花粉最大移动半径(即解空间的半径)。
在FPA寻优过程中,通过对花粉多样性Div与差异性Dif的联合刻画以分析花粉种群多样性的动态变化,再结合寻优迭代过程中花粉位置的动态变化分析FPA的寻优特点。
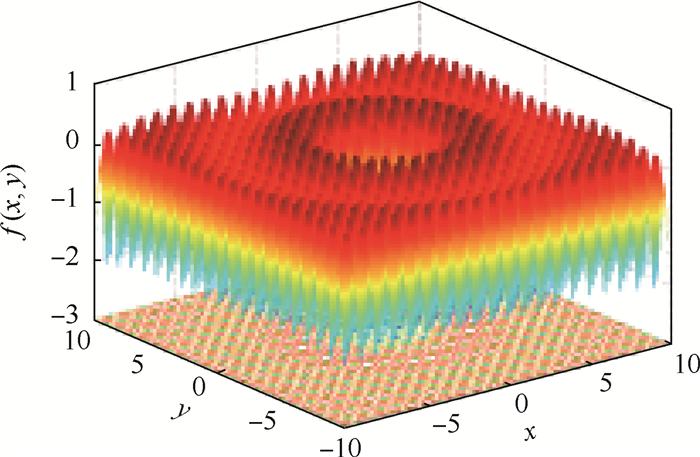
首先,从单峰函数寻优入手。图 1为二维Sphere函数的3D图,该函数是典型的单峰函数。
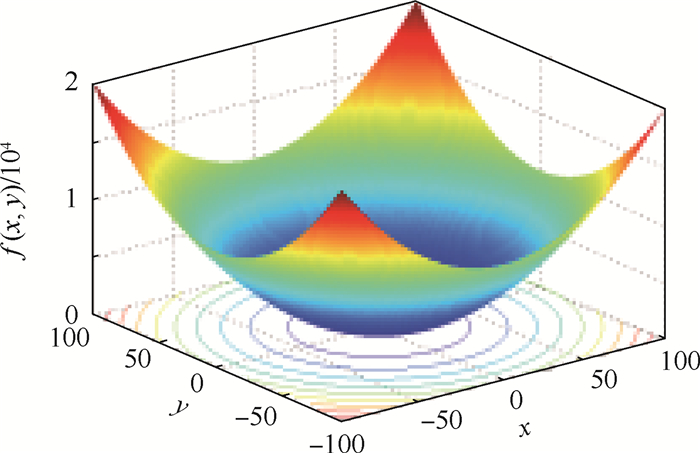 |
| 图 1 Sphere函数3D图 Fig. 1 3D figure of Sphere function |
| 图选项 |
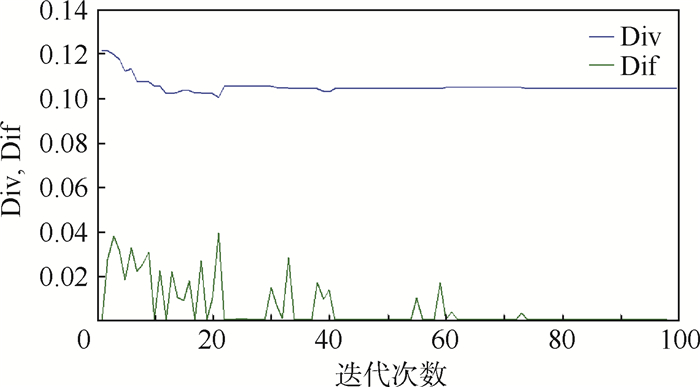
依据参考文献[1, 3]的算法流程及参数设定(花粉数量取30)对该Sphere函数进行100次迭代寻优,其多样性Div与差异性Dif变化曲线如图 2所示。
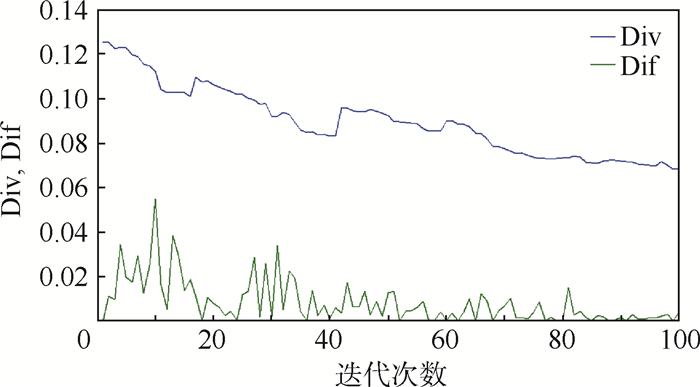 |
| 图 2 Sphere函数FPA寻优参数变化曲线 Fig. 2 Parameter variation curves of Sphere function using FPA optimization |
| 图选项 |
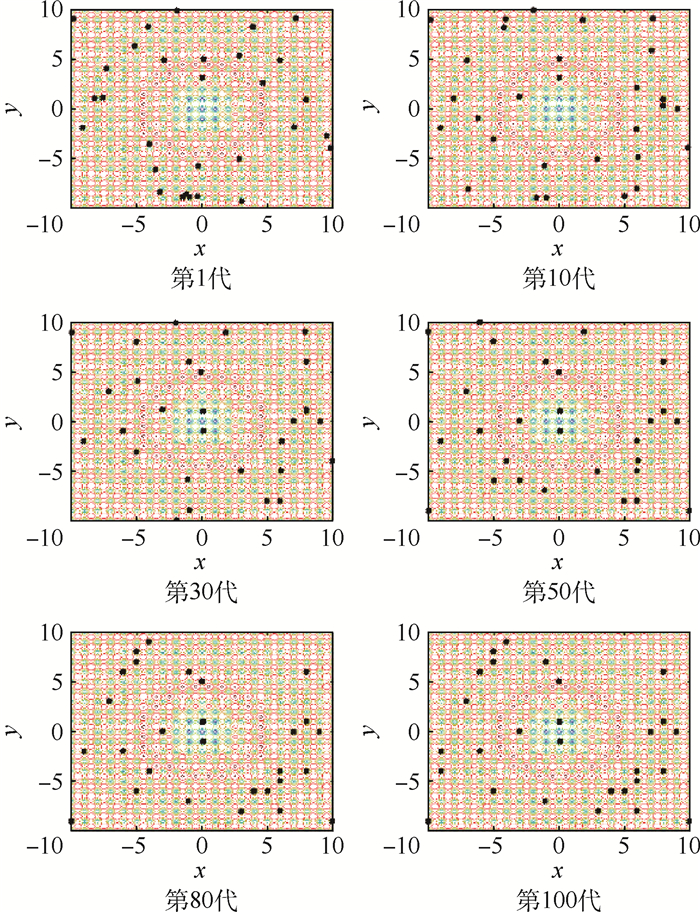
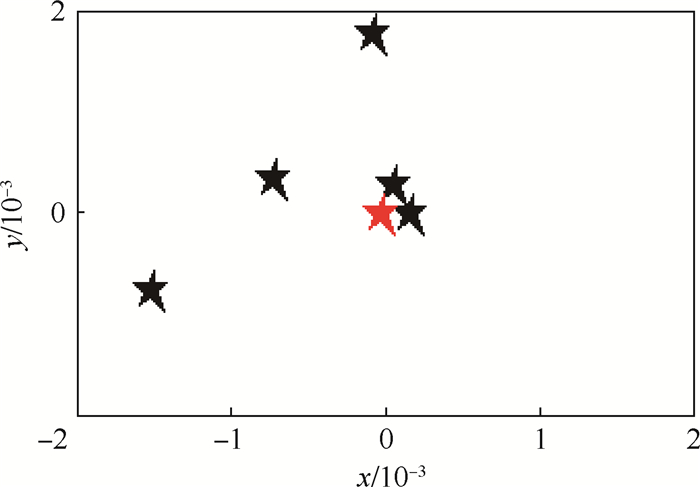
图 3为FPA进化过程中花粉配子在解空间内的动态分布图。图中,从第1、10、30、50、80、100代花粉种群在解空间中分布,可以直观的看出随着种群的进化,花粉种群在解空间的分布趋于集中,直至全部集中在全局最优位置;而反映在图 2中的则是花粉种群的多样性指标Div随着进化代次的增加基本呈衰减走势,这说明花粉的空间多样性在不断锐减。从图 3中还能够看出,第50代以后,花粉种群基本都已聚集到全局最优值附近;表现在图 2中的则是差异性指标Dif在第50代之后波动较小且基本趋于0,这说明算法后期花粉在广阔解空间区域的全局勘探能力基本丧失,这对多模复杂函数寻优是极其不利的,很可能会致使算法陷入局部最优。另外,单峰函数不会存在陷入到局部最优的情况,能够集中体现算法的局部开采能力,将图 3中第100代的花粉分布图进行局部放大,如图 4(红星代表最小值点)所示。可以看出当x、y坐标放大到0.1等级时,花粉已经远离最小值点,这说明FPA的局部开采能力较为薄弱。
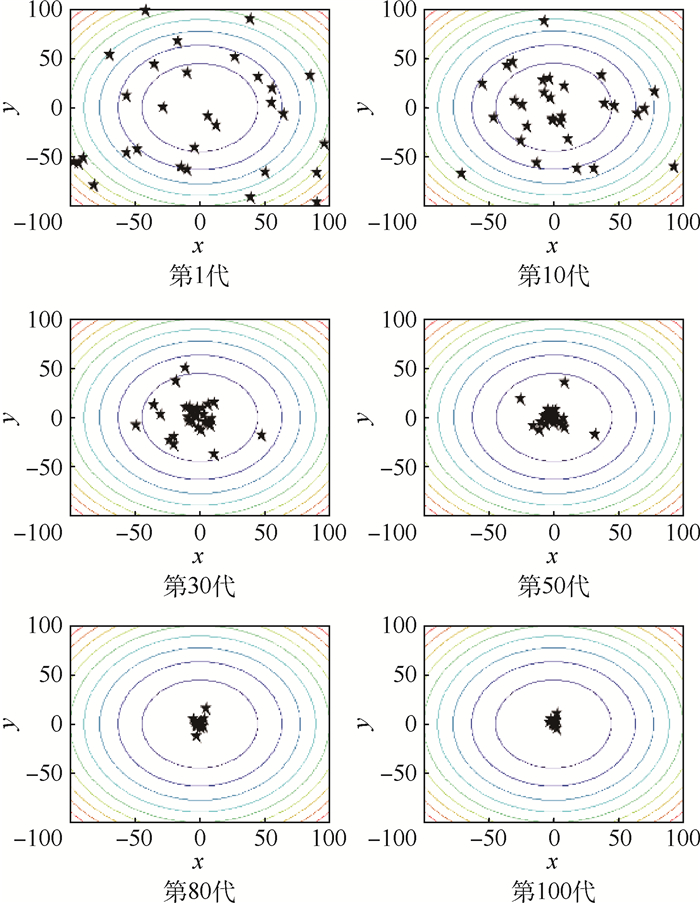 |
| 图 3 Sphere函数FPA寻优花粉分布 Fig. 3 Pollen distribution of Sphere function using FPA optimization |
| 图选项 |
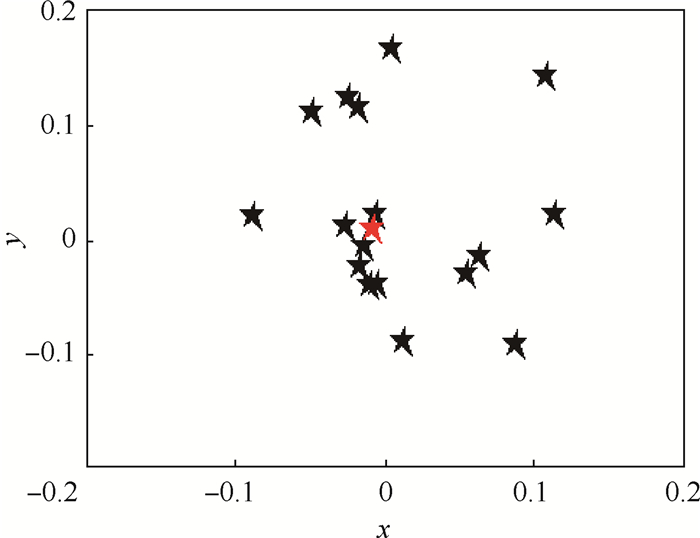 |
| 图 4 图 3第100代的局部放大 Fig. 4 Partial enlargement of Fig. 3 the 100th generation |
| 图选项 |
其次,对多模函数进行寻优,分析FPA对多模复杂函数的寻优缺点。图 5为Bridge函数的3D图,该函数峰值较多,是较为复杂的多模函数。同样依据文献[1, 3]对该函数进行100次迭代寻优实验,给出参数变化曲线(见图 6)及花粉种群的空间分布图(见图 7)。
 |
| 图 5 Bridge函数3D图 Fig. 5 3D figure of Bridge function |
| 图选项 |
 |
| 图 6 Bridge函数FPA寻优参数变化曲线 Fig. 6 Parameter variation curves of Bridge function using FPA optimization |
| 图选项 |
 |
| 图 7 Bridge函数FPA寻优花粉分布 Fig. 7 Pollen distribution of Bridge function using FPA optimization |
| 图选项 |
图 7中,单从第1、10、30、50、80、100代花粉种群在解空间中的分布看,每代的花粉种群分布都较为松散,没有一部分花粉集中的现象。再对比第1、10、30、50、80、100代花粉的空间分布,可以看出第50、80、100代的花粉种群在解空间的位置分布基本一致。从图 6可以看出多样性指标Div在第50代之后无波动、基本趋于平稳,差异性指标Dif在第50代之后基本为0、无明显的波动。这说明50代之后大部分花粉已陷入到局部最优位置无法进行位置更新,这使得算法的全局勘探能力下降,以至于无法探索到全局最优位置,证实了上述的可能性。同时,也检验了2个参数指标(Div、Dif)联合分析的合理性与有效性。
最后结合FPA的具体流程,笔者认为造成FPA后期花粉差异性为0的主要原因在于FPA的贪婪式进化机制(子代的函数值比父代优才能进化),使算法贪婪过度,长期无法进行位置更新,从而导致多数的花粉陷入到局部最优位置,致使FPA的全局开拓能力削弱。理想状态的种群分布状况应该是:部分种群在不断聚集,即算法的局部开采性;而另一部分种群在全局空间内不断的探索,即算法的全局勘探性。而表现在Div、Dif上应当是:种群多样性的保持及算法后期差异性的延续(不为0)。
2 改进策略及改进的花朵授粉算法 2.1 改进策略 针对FPA在多模复杂函数寻优的缺点,对算法进行改进。在全局授粉过程中引入模拟退火的思想,采取Metropolis准则对新状态进行更新。模拟退火的Metropolis准则[16]是依概率的形式对新状态进行更新,在FPA的全局授粉中引入该准则,将改善算法的过度贪婪情况,从而提高全局勘探能力。另外,为了进一步提高FPA的局部开采能力,结合改进的Nelder-Mead单纯形法对FPA的局部授粉行为进行重构。
Nelder-Mead单纯形法是由Nelder和Mead[17]于1965年提出的一种用于优化多维无约束问题的搜索算法。此算法通过在D维空间中取D+1个点构成一个单纯形,计算其顶点函数值;然后对最差点进行内部压缩、外部压缩、映射和扩展等操作,以获得更好的点取代最差点,重构单纯形,从而不断的逼近最优点。此算法是一种直接的搜索算法,其寻优不受目标函数的连续性与可导性影响,具备精细的局部开采能力。为此,本文类比该算法的优势对FPA的局部授粉进行重构,以增强FPA的收敛精度。重构的局部授粉过程如下:
首先,利用花粉i及其周围最近的m-1个花粉的位置信息构建单纯形(见图 8),并根据式(7)计算单纯形的中心:
 | (7) |
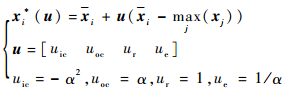 | (8) |
 |
| 图 8 Nelder-Mead单纯形法 Fig. 8 Nelder-Mead simplex method |
| 图选项 |
然后,根据式(8)分别对单纯形进行内部压缩、外部压缩、映射和扩展操作,计算4种操作所对应的位置坐标xiic、xioc、xir、xie,并进行越界处理(依据文献[18]的分析与证明,这里取α=0.618)。
最后,计算4个位置的目标函数值yi*(u)=f(xi*(u))并与花粉i的目标函数值yi进行对比,若比其优,将对花粉i进行位置更新。
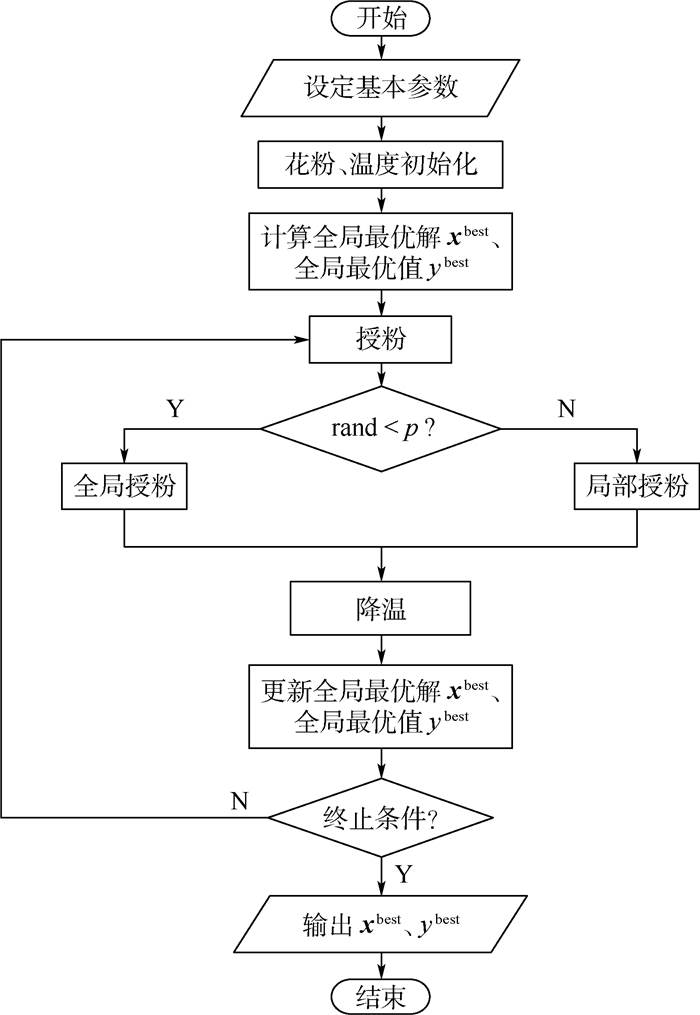
2.2 改进的花朵授粉算法 结合改进策略及基本FPA的计算流程,给出NS-FPA的基本实现步骤(以寻最小值为例)及其流程图(见图 9)。
 |
| 图 9 NS-FPA流程 Fig. 9 Flowchart of NS-FPA |
| 图选项 |
步骤1??初始参数,设定花粉种群规模N、最大迭代次数Kmax、转换概率p、初温概率p0、温度衰减系数γ等。
步骤2??在解空间里随机初始化花粉位置x0,并计算目标函数值y0;初始温度T0可由式(9)计算:
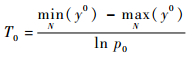 | (9) |
式中:p0通常取0.7~0.9[19]。
步骤3??计算当前的全局目标函数最小值,并记录对应得最优解xbest。
步骤4??若条件(rand < p)成立,转步骤5;否则,转步骤6。
步骤5??全局授粉:依据式(1)计算子代花粉位置,并计算目标函数值;由式(10)计算可接受概率pr;若条件(rand < pr)成立,则进行位置更新。
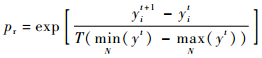 | (10) |
步骤6??局部授粉:依据2.1节中重构的局部授粉过程进行。
步骤7??降温:按式(11)进行降温操作:
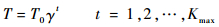 | (11) |
式中:γ通常取0.7~0.99[19]。
步骤8??计算全局目标函数值的最小值,并更新最优解xbest。
步骤9??若满足终止条件,则输出全局最优解;否则,转至步骤4。
3 仿真计算 为了验证NS-FPA的有效性,首先结合1.2节对NS-FPA进行定性仿真分析,验证算法改进后的全局勘探能力;其次,选取多个多模复杂函数进行寻优仿真实验,定量分析NS-FPA的收敛速度与收敛精度,从而分析NS-FPA的局部开采能力及综合性能;然后,对NS-FPA中新增的2个参数p0、γ进行探讨,以确定其取值范围;最后,对比NS-FPA、FPA的时间复杂度,探讨NS-FPA的缺失。
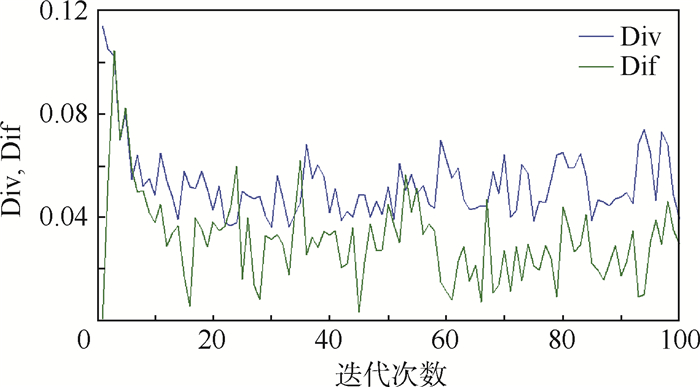
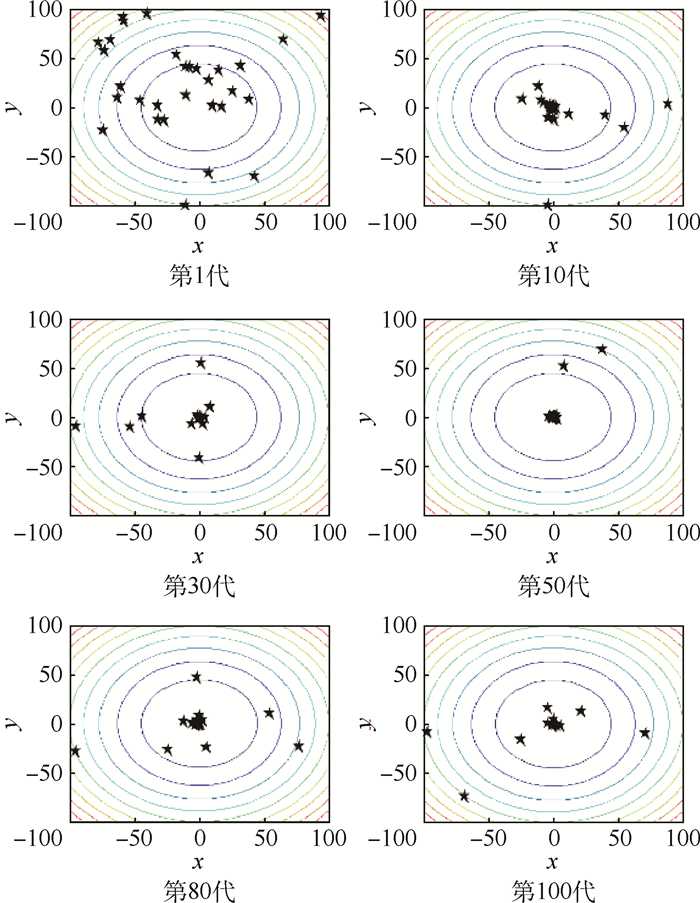
3.1 定性仿真分析 为了与1.2节形成鲜明对比,本节同样针对二维Sphere函数及Bridge函数采用NS-FPA在同样参数下进行100次迭代寻优,并给出寻优过程中花粉多样性Div指标与差异性Dif指标变化曲线及花粉的动态分布图(见图 10~图 14)以定性分析NS-FPA的寻优特性。
 |
| 图 10 Sphere函数NS-FPA寻优参数变化曲线 Fig. 10 Parameter variation curves of Sphere function using NS-FPA optimization |
| 图选项 |
 |
| 图 11 Sphere函数NS-FPA寻优花粉分布 Fig. 11 Pollen distribution of Sphere function using NS-FPA optimization |
| 图选项 |
 |
| 图 12 图 11第100代的局部放大 Fig. 12 Partial enlargement of Fig. 11 the 100th generation |
| 图选项 |
 |
| 图 13 Bridge函数NS-FPA寻优参数变化曲线 Fig. 13 Parameter variation curves of Bridge function using NS-FPA optimization |
| 图选项 |
 |
| 图 14 Bridge函数NS-FPA寻优花粉分布 Fig. 14 Pollen distribution of Bridge function using NS-FPA optimization |
| 图选项 |
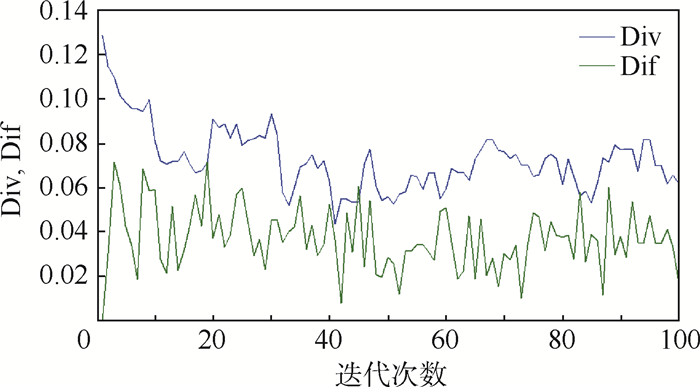
从图 11和图 14中可以直观地看出:无论对Sphere函数还是Bridge函数寻优,第10、30、50、80、100代花粉种群在空间的分布均呈现一部分种群聚集、另一部分种群松散的特征(由于第1代是随机初始化,因此整体较为松散、种群差异性最大)。另外,各代之间的种群分布除全局最优值附近的集中种群分布相似,这是说明部分花粉正在逐步向全局最优位置聚拢,体现了算法的导向性;分散的那部分种群分布有较大的差异,这是说明另外一部分花粉在不断的开拓新区域,体现了种群的全局勘探性。而从图 10和图 13中则可以看出:种群的多样性指标Div及差异性指标Dif在算法的1~10代(起始阶段)有略微的下降,因为这是算法由完全的随机性逐渐地向算法兼顾随机性与导向性转变的过程;第10代之后Div与Dif基本呈平稳的波动状态,无整体的锐减趋势。这说明NS-FPA在算法运行的中后期能够很好的保持花粉种群的多样性与差异性,从而增加花粉跳出局部最优的几率,这对多模函数寻优是有利的。
与图 2~图 4、图 6和图 7相对比,可以得出以下结论:改进的FPA在多模函数寻优过程中能够保证花粉的多样性及差异性,从而能够避免算法陷入局部最优,有效地保证了FPA的全局勘探能力,基本达到了1.2节中所述的种群分布的理想状态。最后,结合图 4和图 12可看出NS-FPA的局部开采能力得到了明显的改善。
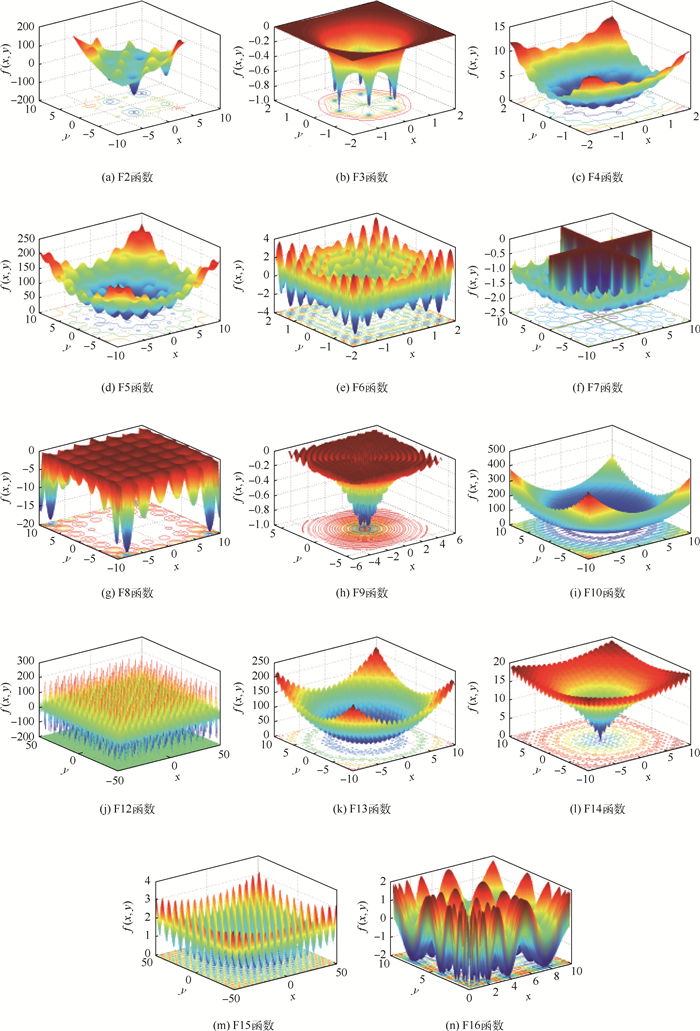
3.2 定量仿真分析 选择15个多模复杂测试函数、1个单峰函数进行仿真实验并与FPA、布谷鸟算法(CS)[20]、萤火虫算法(FA)[21]进行对比(见表 1)。16个标准测试函数的基本信息如表 2所示。为了更加直观地表现测试函数的复杂性,图 1(F1)、图 5(F11)和图 15给出了F1~F16的二维函数3D图。
表 1 4个算法的参数设置 Table 1 Parameter setup for four algorithms
| 算法 | 参数设置 |
| FPA | 转换概率p=0.8;参数λ=1.5 |
| CS | 发现概率pa=0.25;步长调节量α=0.01; 参数β=1.5 |
| FA | 步长因子α=0.25;吸引度因子β=0.2; 光强吸收强度γ=1 |
| NS-FPA | 转换概率p=0.8;温度衰减系数γ=0.7; 初温概率p0=0.8;参数λ=1.5 |
| 注:公共参数:种群规模N=50;最大迭代次数Kmax,F1~F13取100,F14~F16取10 000。 | |
表选项
表 2 16个标准测试函数 Table 2 16 standard test functions
| 代号 | 函数 | 表达式 | 解空间 | 最小值 |
| F1 | Sphere |  | [-100, 100]2 | 0 |
| F2 | Brid |  | [-2π, 2π]2 | -106.764 5 |
| F3 | Roots |  | [-2, 2]2 | -1 |
| F4 | Bohachevsky | 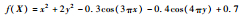 | [-100, 100]2 | 0 |
| F5 | Eggcrate | 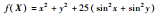 | [-10, 10]2 | 0 |
| F6 | Guichi-f4 | 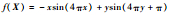 | [-2, 2]2 | -3.253 9 |
| F7 | Cross-in-Tray | 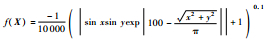 | [-10, 10]2 | -2.062 61 |
| F8 | Holder Table | 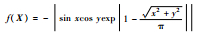 | [-10, 10]2 | -19.208 5 |
| F9 | Drop-Wave | 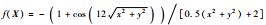 | [-5.12, 5.12]2 | -1 |
| F10 | Levy |  | [-10, 10]2 | 0 |
| F11 | Bridge | 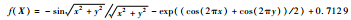 | [-10, 10]2 | -3.005 4 |
| F12 | Shubert | 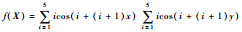 | [-50, 50]2 | -186.730 9 |
| F13 | Rastrigin | 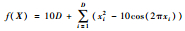 | [-20, 20]4 | 0 |
| F14 | Ackley |  | [-32, 32]30 | 0 |
| F15 | Griewank | 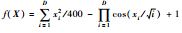 | [-600, 600]40 | 0 |
| F16 | Vincent | 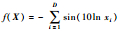 | [0.25, 10]50 | -50 |
表选项
 |
| 图 15 二维函数3D图 Fig. 15 3D figures of 2D functions |
| 图选项 |
通过图 15再结合图 1和图 5,16个测试函数的多模复杂程度有所差异,但基本可以分为3类:F1(单峰),F2~F8(多模),F9~F16(超多模)。为了保证评价的客观性,在测试中分别对16个函数进行50次仿真计算,用50次仿真结果的统计特性对对比结果进行分析。依据文献[1, 22]分别对4种寻优算法进行参数设定,如表 1所示。其仿真对比结果如表 3所示。
表 3 16个标准测试函数优化结果对比 Table 3 Comparison of optimization results of 16 standard test functions
| 函数代号 | FPA | CS | |||||
| 最优值 | 平均值 | 标准差 | 最优值 | 平均值 | 标准差 | ||
| F1 | 2.82 | 5.42 | 1.63 | 9.85×10-7 | 2.37×10-3 | 5.49×10-4 | |
| F2 | -106.764 5 | -106.762 7 | 2.24×10-3 | -106.764 5 | -106.757 0 | 1.64×10-3 | |
| F3 | -0.999 8 | -0.997 0 | 1.88×10-3 | -0.999 7 | -0.994 5 | 1.21×10-3 | |
| F4 | 6.46×10-5 | 2.46×10-2 | 3.49×10-2 | 2.56×10-1 | 1.81 | 3.97×10-1 | |
| F5 | 2.09×10-6 | 2.41×10-3 | 5.07×10-3 | 1.88×10-3 | 0.53 | 1.24×10-1 | |
| F6 | -3.253 9 | -3.253 7 | 3.20×10-4 | -3.253 9 | -3.253 3 | 1.29×10-4 | |
| F7 | -2.062 6 | -2.062 3 | 7.46×10-5 | -2.062 6 | -2.062 5 | 2.11×10-5 | |
| F8 | -19.208 5 | -19.208 3 | 1.73×10-4 | -19.208 5 | -19.208 2 | 7.18×10-5 | |
| F9 | -0.993 3 | -0.947 3 | 1.77×10-2 | -0.986 5 | -0.936 2 | 1.77×10-2 | |
| F10 | 1.24×10-5 | 2.93×10-2 | 3.70×10-2 | 4.06×10-6 | 5.60×10-3 | 1.40×10-3 | |
| F11 | -3.004 1 | -2.877 1 | 8.56×10-2 | -2.928 0 | -2.651 2 | 7.64×10-2 | |
| F12 | -186.730 7 | -186.712 5 | 2.68×10-2 | -186.730 8 | -186.709 8 | 6.13×10-3 | |
| F13 | 6.60 | 15.36 | 5.01 | 2.93 | 8.05 | 1.46 | |
| F14 | 3.87 | 6.34 | 1.17 | 4.66 | 8.35 | 0.92 | |
| F15 | 4.64 | 11.29 | 2.66 | 2.73 | 6.97 | 1.21 | |
| F16 | -49.61 | -49.22 | 0.16 | -49.84 | -49.74 | 9.33×10-2 | |
| F1 | 8.63×10-11 | 5.79×10-9 | 5.66×10-9 | 3.88×10-9 | 1.82×10-5 | 2.89×10-5 | |
| F2 | -106.764 5 | -104.939 3 | 5.23 | -106.764 5 | -106.764 5 | 4.76×10-6 | |
| F3 | -1.000 0 | -0.999 8 | 1.06×10-4 | -1.000 0 | -0.999 9 | 7.81×10-5 | |
| F4 | 6.70×10-7 | 4.88×10-4 | 8.66×10-4 | 8.32×10-9 | 5.00×10-5 | 3.94×10-5 | |
| F5 | 8.34×10-8 | 3.59×10-6 | 5.29×10-6 | 5.15×10-9 | 1.88×10-7 | 1.70×10-7 | |
| F6 | -3.253 9 | -3.253 1 | 8.20×10-4 | -3.253 9 | -3.253 9 | 5.93×10-6 | |
| F7 | -2.062 6 | -2.062 6 | 1.77×10-4 | -2.062 6 | -2.062 6 | 1.30×10-8 | |
| F8 | -19.208 5 | -19.207 9 | 9.73×10-4 | -19.208 5 | -19.208 5 | 4.50×10-10 | |
| F9 | -1.000 0 | -0.994 9 | 1.75×10-2 | -1.000 0 | -0.999 9 | 1.99×10-4 | |
| F10 | 4.68×10-9 | 1.41×10-7 | 2.10×10-7 | 1.26×10-10 | 6.79×10-9 | 7.70×10-9 | |
| F11 | -3.005 4 | -2.933 6 | 0.20 | -3.005 4 | -3.005 1 | 3.18×10-4 | |
| F12 | -186.730 9 | -177.764 8 | 13.30 | -186.730 9 | -186.730 8 | 5.50×10-4 | |
| F13 | 2.38×10-6 | 1.33 | 1.41 | 0 | 1.18×10-7 | 7.42×10-7 | |
| F14 | 1.80×10-3 | 3.83×10-3 | 1.12×10-3 | 6.46×10-12 | 1.62×10-7 | 1.09×10-6 | |
| F15 | 3.00×10-4 | 7.47×10-2 | 0.19 | 2.97×10-4 | 1.32×10-3 | 7.53×10-4 | |
| F16 | -49.87 | -9.62 | 9.83×10-2 | -50.00 | -49.99 | 2.51×10-4 | |
表选项
首先, 分别从多模、超多模函数的寻优结果中对比FPA与NS-FPA的寻优特性。表 3中,从多模函数F2~F8的寻优对比结果中可以看出,F2函数:FPA 50次寻优的最优值能够达到精确解,而平均值却只能够达到小数点后2位;NS-FPA的最优值及平均值都能够达到精确解;再看标准差,FPA值达到10-3,而NS-FPA达到10-6,比FPA高3个数量级,这说明NS-FPA要更稳定。F3函数:FPA的最优值精度达到10-3,平均值精度达到10-2;而NS-FPA的最优值为精确解,平均值精度达到10-4,标准差比FPA高2个数量级。F4函数:FPA的最优值精度达到10-5,平均值精度达到10-2;而NS-FPA的最优值精度达到10-9,平均值精度达到10-5,标准差比FPA高3个数量级。F5函数:FPA的最优值精度达到10-6,平均值精度达到10-3;而NS-FPA的最优值精度达到10-9,平均值精度达到10-7,标准差比FPA高4个数量级。F6函数:FPA的最优值能够达到精确解,平均值精度达到10-3;而NS-FPA的最优值及平均值都达到精确解,标准差比FPA高2个数量级。F7函数:FPA的最优值能够达到精确解,平均值精度达到10-3;而NS-FPA的最优值及平均值都达到精确解,标准差比FPA高3个数量级。F8函数:FPA的最优值能够达到精确解,平均值精度达到10-3;而NS-FPA的最优值及平均值都达到精确解,标准差比FPA高6个数量级。
在超多模函数F9~F16的寻优对比结果中,F9函数:FPA的最优值精度达到10-2,平均值精度达到10-1;而NS-FPA的最优值达到精确解,平均值精度达到10-4,标准差比FPA高2个数量级。F10函数:FPA的最优值精度达到10-5,平均值精度达到10-2;而NS-FPA的最优值精度达到10-10,平均值精度达到10-9,标准差比FPA高7个数量级。F11函数:FPA的最优值精度达到10-2,平均值精度较差;而NS-FPA的最优值达到精确解,平均值精度达到10-3,标准差比FPA高2个数量级。F12函数:FPA的最优值精度达到10-3,平均值精度为10-1;而NS-FPA的最优值达到精确解,平均值精度达到10-4,标准差比FPA高2个数量级。对于高维超多模函数F13~F16,FPA基本失去了寻优精度,而NS-FPA依旧能够寻优且平均寻优精度均达到10-3以上,标准差也达到10-4以上, 这验证了改进方案的有效性。
从整体上看,NS-FPA的寻优精度要比FPA至少高出2个数量级,寻优稳定性(标准差)高出2~7个数量级,这说明相对于FPA,NS-FPA能够更好的处理多峰寻优,且具有较高的稳定性。
其次,与Yang等[20-21]近几年提出的布谷鸟算法、萤火虫算法进行对比。表 3中,对于多模函数F2~F8的寻优,可以看出FPA与CS的最优值、平均值、标准差几乎相当。除F2函数外,FA的最优值、平均值、标准差要略微优于FPA与CS, 但NS-FPA的评价指标都要优于FPA、CS、FA,至少高2个数量级的计算精度。对于超多模函数F9~F16,FPA与CS的寻优效果相当;F8~F9,FA的寻优效果要劣于CS与FPA;F10~F16,FA的寻优效果要优于CS与FPA;但NS-FPA的寻优效果都要明显优于FPA、CS、FA。综合来看,NS-FPA对多模寻优的处理要更优于FPA、CS、FA。
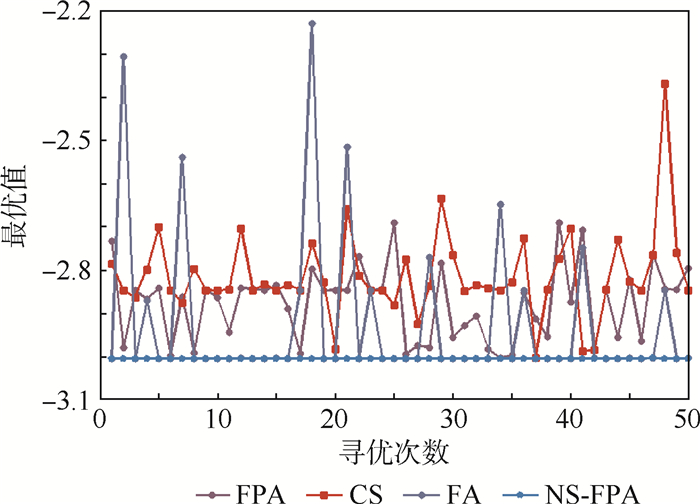
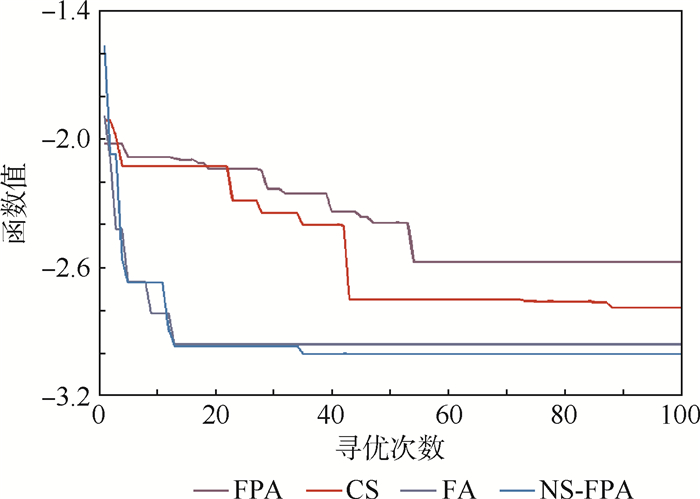
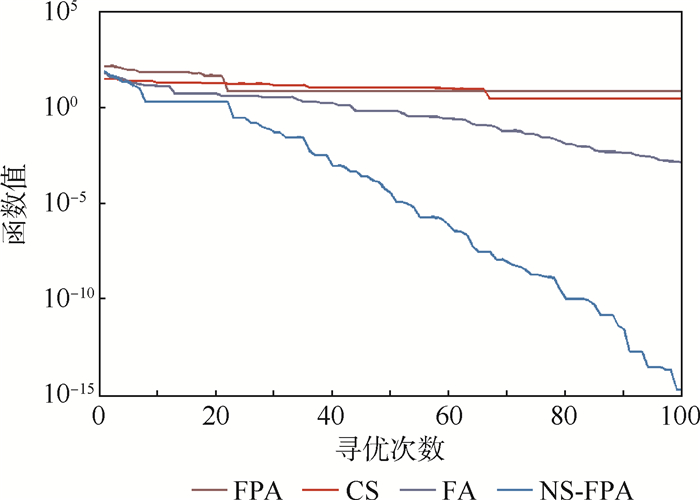
最后,图 16给出F11函数50次优化结果对比,从图中可以直观地看出NS-FPA与FPA、CS、FA相比寻优结果波动性较小、更加稳定,这说明NS-FPA的鲁棒性较好,也间接证实了模拟退火策略能够使得FPA成功避免陷入局部最优,从而保证了算法的全局勘探性。图 17为F11函数优化过程进化曲线对比,从图中可以看出NS-FPA的寻优结果更靠近理论值-3,并且收敛速度也要快于FPA、CS、FA。为了直观地体现各个算法的收敛精度,图 18以对数坐标轴的形式给出F13函数优化过程进化曲线对比,从图中可以看出NS-FPA的终止计算精度达到了10-15,并且仍有下降的趋势,这体现NS-FPA优秀的局部开采能力,也进一步证实了NS-FPA的有效性。
 |
| 图 16 F11函数50次寻优结果对比 Fig. 16 Comparison of 50 times' optimization results of F11 function |
| 图选项 |
 |
| 图 17 F11函数寻优进化曲线 Fig. 17 Optimization evolution curves of F11 function |
| 图选项 |
 |
| 图 18 F13函数寻优进化曲线 Fig. 18 Optimization evolution curves of F13 function |
| 图选项 |
3.3 NS-FPA的参数分析 尽管NS-FPA的寻优效果较好,与FPA相比,NS-FPA多了2个基本参数初温概率p0、温度衰减系数γ。为了讨论其对NS-FPA寻优性能的影响,本节以超多模函数F9为例,进行仿真计算实验。
首先,讨论初温概率p0对算法性能的影响。实验时其他参数不改变,设定不同的p0后, 分别对F9函数进行50次寻优计算,统计结果如表 4所示(左侧三栏)。从表 4中可以看出随着p0的增大,算法的平均值不断逼近理论解,且标准差不断变小(标准差越小,算法的鲁棒性越好),直至p0取0.7时,达到最优,之后有所下降。当p0取0.6~0.9时,平均值、标准差达到高于10-4的精度。因此,在寻优计算时建议p0取0.6~0.9。
表 4 不同p0、γ参数下的NS-FPA寻优结果 Table 4 Optimization results of NS-FPA with different p0 and γ
| p0 | 平均值 | 标准差 | γ | 平均值 | 标准差 | |
| 0.1 | -0.998 08 | 9.20×10-3 | 0.1 | -0.996 70 | 1.28×10-2 | |
| 0.2 | -0.998 44 | 9.19×10-3 | 0.2 | -0.999 11 | 4.04×10-3 | |
| 0.3 | -0.998 61 | 8.57×10-3 | 0.3 | -0.999 15 | 3.27×10-3 | |
| 0.4 | -0.999 14 | 4.14×10-3 | 0.4 | -0.999 65 | 1.40×10-3 | |
| 0.5 | -0.999 35 | 2.73×10-3 | 0.5 | -0.999 72 | 1.21×10-3 | |
| 0.6 | -0.999 81 | 9.14×10-4 | 0.6 | -0.999 78 | 1.14×10-3 | |
| 0.7 | -0.999 99 | 6.52×10-5 | 0.7 | -0.999 83 | 9.39×10-4 | |
| 0.8 | -0.999 93 | 9.59×10-5 | 0.8 | -0.999 98 | 7.47×10-5 | |
| 0.9 | -0.999 86 | 7.12×10-4 | 0.9 | -0.999 89 | 6.15×10-4 |
表选项
其次,讨论温度衰减系数γ对算法性能的影响。同样,在实验时其他参数不改变,设定不同的γ后, 分别对F9函数进行50次寻优计算,统计结果如表 4所示(右侧三栏)。从表 4中可以看出,随着γ增大,算法的平均值和标准差逐渐变小,直至γ=0.8时,达到最小,之后有所增加。当γ取0.7~0.9时,平均值、标准差达到高于10-4的精度。因此,在寻优计算时建议γ取0.7~0.9。
3.4 NS-FPA的时间复杂度分析 与FPA相比,NS-FPA的局部授粉较为复杂,在算法复杂度上要大于FPA。为直观地对比2种算法的时间复杂度,本节从3.2节选择6个测试函数分别用FPA、NS-FPA在同一平台上单独进行50次寻优实验,统计50次实验的平均耗时,结果如表 5所示。
表 5 NS-FPA与FPA的平均消耗时间对比 Table 5 Comparison of mean consumption time between NS-FPA and FPA
| 函数代号 | 平均耗时/s | NS-FPA与FPA平均 耗时的百分比 | |
| NS-FPA | FPA | ||
| F5 | 0.28 | 0.20 | 142.56 |
| F6 | 0.28 | 0.20 | 142.76 |
| F11 | 0.31 | 0.22 | 137.15 |
| F13 | 0.28 | 0.22 | 126.89 |
| F14 | 33.56 | 27.22 | 123.31 |
| F15 | 34.99 | 28.63 | 122.24 |
表选项
表 5中,NS-FPA的平均耗时要大于FPA,且平均高出32.49%。再考虑到3.2节中,对于FPA不能求解的多模函数,NS-FPA却具有较好的寻优性能,笔者认为在时间上多出32.49%的消耗是值得的,它增强了算法的求解性能。
4 结论 本文针对多模复杂函数优化问题对FPA进行研究,首先提出了种群多样性指标与差异性指标,定性分析了基本FPA的寻优缺陷;然后,基于模拟退火的思想解决算法过度贪婪的问题,再结合Nelder-Mead单纯形法对局部授粉过程进行重构,提出一种改进的花朵授粉算法——NS-FPA。通过定性、定量的方式对其进行仿真对比分析得出以下结论:
1) 基于模拟退火思想的全局授粉行为能够避免FPA陷入局部最优,改善了FPA的全局勘探能力,解决了算法早熟的问题。
2) 重构的局部授粉行为改善了算法的局部开采能力,大大提升了算法的收敛速度与收敛精度。
3) NS-FPA可以用来解决多模复杂优化问题。
4) NS-FPA在寻优时需要比FPA多消耗32.49%的时间。
参考文献
| [1] | YANG X S. Flower pollination algorithm for global optimization[C]//International Conference on Unconventional Computation and Natural Computation. Berlin: Springer, 2012: 240-249. |
| [2] | YANG X S, KARAMANOGLU M, HE X. Multi-objective flower algorithm for optimization[J].Procedia Computer Science, 2014, 18(1): 861–868. |
| [3] | YANG X S, KARAMANOGLU M, HE X. Flower pollination algorithm:A novel approach for multiobjective optimization[J].Engineering Optimization, 2014, 46(9): 194–195. |
| [4] | AL-MA'SHUMAH F, PERMANA D, SIDARTO K A. Solving inverse problem for Markov chain model of customer lifetime value using flower pollination algorithm[J].Journal of Molecular Structure, 2015, 1692(1): 7–11. |
| [5] | PRATHIBA R, MOSES M B, SAKTHIVEL S. Flower pollination algorithm applied for different economic load dispatch problems[J].International Journal of Engineering & Technology, 2014, 6(2): 1009–1016. |
| [6] | DUBEY H M, PANDIT M, PANIGRAHI B K. Hybrid flower pollination algorithm with time-varying fuzzy selection mechanism for wind integrated multi-objective dynamic economic dispatch[J].Renewable Energy, 2015, 83: 188–202.DOI:10.1016/j.renene.2015.04.034 |
| [7] | ABDELAZIZ A Y, ALI E S, ELAZIM S M A. Implementation of flower pollination algorithm for solving economic load dispatch and combined economic emission dispatch problems in power systems[J].Energy, 2016, 101: 506–518.DOI:10.1016/j.energy.2016.02.041 |
| [8] | SHARAWI M, EMARY E, IMANE A, et al. Flower pollination optimization algorithm for wireless sensor network lifetime global optimization[J].Applied Soft Computing, 2014, 4(3): 2231–2307. |
| [9] | EMARY E, ZAWBAA H M, HASSANIEN A E, et al. Retinal vessel segmentation based on flower pollination search algorithm[M].Berlin: Springer, 2014: 93-100. |
| [10] | WANG R, ZHOU Y Q. Flower pollination algorithm with dimension by dimension improvement[J].Mathematical Problems in Engineering, 2014, 2014: 481791. |
| [11] | ABDEL-RAOUF O, ABDEL-BASET M, EL-HENAWY I. An improved flower pollination algorithm with chaos[J].International Journal of Education & Management Engineering, 2014, 4(2): 1–8. |
| [12] | ABDEL-RAOUF O, EL-HENAWY I, ABDEL-BASET M. A novel hybrid flower pollination algorithm with chaotic harmony search for solving sudoku puzzles[J].International Journal of Engineering Trends & Technology, 2014, 6(3): 126–132. |
| [13] | EL-HENAWY I, ISMAIL M. An improved chaotic flower pollination algorithm for solving large integer programming problems[J].International Journal of Digital Content Technology & Its Applic, 2014, 8(3): 72–79. |
| [14] | ABDEL-RAOUF O, ABDEL-BASET M, EL-HENAWY I. A new hybrid flower pollination algorithm for solving constrained global optimization problems[J].International Journal of Applied Operational Research, 2014, 3(2): 21–28. |
| [15] | ?UKASIK S, KOWALSKI P A. Study of flower pollination algorithm for continuous optimization[M].Berlin: Springer, 2015: 451-459. |
| [16] | 傅文渊, 凌朝东. 布朗运动模拟退火算法[J].计算机学报, 2014, 37(6): 1301–1308. FU W Y, LING C D. Brownian motion based simulated annealing algorithm[J].Chinese Journal of Computers, 2014, 37(6): 1301–1308.(in Chinese) |
| [17] | NELDER J A, MEAD R A. A simplex method for function minimization[J].The Computer Journal, 1965, 7(4): 308–313.DOI:10.1093/comjnl/7.4.308 |
| [18] | NAZARETH L, TSENG P. Gilding the lily:A variant of the Nelder-Mead algorithm based on golden-section search[J].Computational Optimization & Applications, 2002, 22(1): 133–144. |
| [19] | YANG X S. Nature-inspired optimization algorithms[M].Beckington: Luniver Press, 2014: 67-75. |
| [20] | YANG X S, DEB S. Cuckoo search:Recent advances and applications[J].Neural Computing and Applications, 2014, 24(1): 169–174.DOI:10.1007/s00521-013-1367-1 |
| [21] | YANG X S, HE X. Firefly algorithm:Recent advances and applications[J].International Journal of Swarm Intelligence, 2013, 1(1): 36–50.DOI:10.1504/IJSI.2013.055801 |
| [22] | KAIPA K N, GHOSE D. Glowworm swarm optimization:Theory, algorithms, and applications[M].Berlin: Springer, 2017: 91-131. |
