目前,基于统计性能退化监测数据的寿命预测是研究的热门[5-6],并且已经研究出多种性能退化模型,例如随机系数模型[7]、随机过程模型[8-9]和随机滤波模型[10]等。基于统计性能退化监测数据的寿命预测方法,利用退化过程的随机性求出剩余寿命的概率分布情况,便于反映预测结果的随机性。在基于随机过程模型中,最常采用Wiener过程。Wiener过程便于描述系统因受到外部环境影响、内部的状态改变以及负载情况,而具有随机的非单调独立增量过程[11]。由于Wiener过程可以用来描述随机的非单调独立增量过程,目前大量采用Wiener过程对复杂系统进行性能退化建模[12]。通常所说的Wiener过程是指具有线性漂移系数的一类随机过程[13-14]。Wang[15]提出了基于期望最大化(Expectation-Maximization,EM)算法的性能退化模型参数估计方法。
上述研究丰富了Wiener过程在剩余寿命预测领域中的应用,但还存在着如下几个问题:
1) 假设系统的性能退化过程是关于时间的线性函数,或运用某些尺度转换方法将非线性关系转化为线性关系[16]。例如Gebraeel[17]采用取对数方法将指数退化模型转变为一般的线性退化模型。然而,还有很多非线性退化过程无法转换为线性的,例如航空发动机性能退化过程具有明显的非线性特点,直接建立非线性退化模型更满足实际情况。司小胜等[18]采用非线性Wiener过程对复杂系统的剩余寿命进行研究。
2) 在目前的剩余寿命预测研究中,鲜有研究多阶段退化的情况。刘君强等[19]在发动机的寿命预测中研究了多阶段的情况,实验结果表明发动机的退化过程具有多阶段性。
3) 如何体现个体性能退化的差异性。由于环境、材料和误差等的影响,同类型产品的性能退化过程存在差异性,在产品的剩余寿命预测中需要考虑个体性能退化的差异性。刘君强等[19]提出性能退化模型参数具有随机性,服从高斯-伽马分布,从而反映出个体退化的差异性。
针对以上问题,本文根据航空发动机性能退化具有非线性、多阶段的性质,用多阶段非线性Wiener过程构建出性能退化模型。根据多个同类产品历史性能退化监测数据,利用极大似然估计与一维搜索方法,进行参数先验分布的估计,在先验分布和实时获取的个体发动机退化数据的基础上,用贝叶斯方法求得参数的后验分布,从而实现对个体发动机剩余寿命的实时精确预测。
1 剩余寿命预测模型 1.1 模型分析与假设 通过分析航空发动机具有复杂多阶段非线性的性能退化特点,本文将采用多阶段非线性的Wiener过程建立性能退化模型。在该非线性Wiener过程中漂移系数不再与时间无关,而是关于时间的非线性函数。基于非线性Wiener过程的性能退化模型可以表示为
 | (1) |
式中:X(t)为在时刻t的性能退化量;u(t; θ)为非线性Wiener过程的漂移系数,θ为漂移系数的非线性函数中的未知参数;σ为扩散系数;B(t)为标准布朗运动。当u(t; θ)=u时,上述非线性性能退化模型转化为一般线性Wiener退化模型。
为了通过实际发动机监测数据进行实例的验证, 根据文献[8],本文假设u(t; θ)=urtr-1,此时的非线性退化模型变为
 | (2) |
式中:r为漂移系数的非线性函数中的未知参数。
利用Wiener过程进行多阶段非线性的退化建模需要做出以下假设:
假设1??当性能退化量没有超过失效阈值时,发动机处于正常状态;超过失效阈值时,则发动机处于失效状态。
假设2??为描述航空发动机性能退化的个体差异性,将模型参数u, σ2视为随机变量,设w=1/σ2, 可得u, w的联合分布是高斯-伽马分布:
 | (3) |
式中:a、b、c、d为u和w组成的联合分布中的参数。
1.2 多阶段性能退化模型 多阶段的性能退化模型可以表示为
 | (4) |
式中:I(t)为示性函数;X(0)为性能退化模型的初始值;X(ti)为ti时的性能退化值,ti为到达每个性能退化分界值的时间;Xn(t-tn-1)为第n阶段的退化函数。
根据1.1节分析与假设,本文将使用多阶段非线性的Wiener随机过程构建出性能退化模型。此时,X(t)表示为
 | (5) |
式中:Wn-1为第n-1个性能退化阶段的分界值。
1.3 寿命分布 剩余寿命Lt′定义为产品自t′时的退化量X(t′)到其第一次超出失效阈值Wn所用的时间,剩余寿命Lt′表达式为
 | (6) |
式中:X(t′)和X(t+t′)分别为在t′和t′+t时刻的性能退化量;Wn为失效阈值。
因为本文构建的退化模型考虑了非线性的性质,很难计算求得Lt′的准确分布。为此,Si等[8]给出了剩余寿命概率密度函数的一个近似表达式。航空发动机的剩余寿命Lt′的概率密度函数为
 | (7) |
1.4 剩余寿命预测的多阶段性 令ξk为航空发动机性能退化量X(t)从初始时刻到其第一次超过第k个性能退化阶段分界值Wk的时间,ξk为
 | (8) |
根据Wiener过程的齐次马尔可夫性质,则ξk可以改写为
 | (9) |
式中:X′(t)为第k个阶段的性能退化模型;X′(t)= uktrk+σkB(t),其中uk、rk和σk表示第k个阶段性能退化模型的参数。
令Δξk=ξk-ξk-1,ΔWk=Wk-Wk-1,则式(9)可以改写为
 | (10) |
根据式(7)可得第k个性能退化阶段的寿命分布函数为
 | (11) |
由式(11)可以推导出航空发动机寿命T为
 | (12) |
由于

 | (13) |
当t′时刻的性能退化量X(t′)满足要求X(ξk-1)≤X(t′)≤X(ξk),Lt′表达式为
 | (14) |
2 参数估计 由于很难直接估算出未知超参数a、b、c和d的值,本文将采用两阶段方法进行估计。首先,根据现有的航空发动机的历史退化监测数据,利用极大似然估计与一维搜索方法估算出一组u, σ2的值。然后,根据估算出的一组u, σ2的值,再利用极大似然估计方法估算出a、b、c和d的值。
2.1 第1阶段参数估计 假设现在共有m个同类型的航空发动机的性能退化监测数据,其中第i个发动机的第k个阶段的监测时刻记为tik|1, tik|2, …, tik|n,与此时刻相对应的性能退化监测数据记为yik|1, yik|2, …, yik|n。
根据多阶段非线性Wiener过程的性质,可知Xik~N(uiktrk, σik2t),其中uik、rk、和σik为第i个发动机的第k个阶段的Wiener过程的未知参数,可求得参数Θ=[uik, rk, σik]基于第i个发动机的第k个阶段的退化监测数据的对数似然函数为
 | (15) |
式中:yik|j为第i个发动机在第k个阶段的第j次监测值;ti|k-1为第i个发动机到达第k-1个阶段分界值的时间;nik为第i个发动机在第k个阶段的监测次数;tik|j为第i个发动机在第k个阶段的第j次监测时间。
先固定未知参数rk,对uik,σik2(i = 1, 2, …, m)求偏导,计算结果为
 | (16) |
根据式(15)进一步可求得m个航空发动机的退化模型参数Θ=[uik, rik, σik]的完全对数似然函数为
 | (17) |
将式(16)求得的uik,σik(i=1, 2, …, m)代入式(17),可求得关于rk的轮廓似然函数,然后利用一维搜索方法可得rk的估计值,然后将rk再代入式(16),可得uik,σik2(i = 1, 2, …, m)的一组估计值。
2.2 第2阶段参数估计 利用第1阶段求得的一组(u1k, w1k),(u2k, w2k), …, (umk, wmk)来估计参数ak, bk, ck, dk,其中wik=1/σik2。由式(3)可得ak, bk, ck, dk的似然函数为
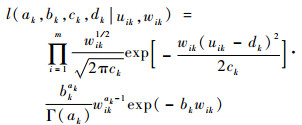 | (18) |
极大化l(ak, bk, ck, dk|uik, wik ),求得估计值为
 | (19) |
式中:

3 基于贝叶斯方法的模型参数更新 由于材料、环境等外界因素的影响,同一型号发动机的性能退化路径存在着个体的差异性。ΔYk=(Δy1, k, Δy2, k, …, Δyn, k)为个体发动机处于第k个退化过程的监测数据。
当获得个体发动机实时性能退化数据后,根据贝叶斯方法可得第k个性能退化阶段的参数uk和wk的后验分布为
 | (20) |
式中:f(uk, wk|ΔYk)为个体发动机第k性能退化阶段模型参数的后验分布函数;f(uk, wk)为第k性能退化阶段的模型参数uk和wk的先验分布函数;l(ΔYk|uk, wk)为似然函数。
根据文献[20]中共轭先验分布的性质,个体发动机第k个性能退化阶段中的模型参数uk和wk更新后的后验分布表达式为
 | (21) |
式中:
 | (22) |
其中:ak′、bk′、ck′、dk′分别为ak、bk、ck、dk更新后的值;tk-1为发动机到达第k-1个性能退化阶段分界值的时间;A、B和C为多项式。
由于参数u和w的联合分布是高斯-伽马分布,更新后的uk和wk的后验分布期望为
 | (23) |
此时σk2=bk′/ak′。
4 个体发动机的实时剩余寿命预测 根据发动机的历史性能监测数据和单台发动机的实时监测数据,建立多阶段航空发动机性能退化模型。首先利用极大似然估计和一维搜索方法,进行参数先验分布的估计。在先验分布和实时获取的个体发动机退化数据的基础上,采用贝叶斯方法对参数分布更新。从而实现对个体发动机剩余寿命的实时精确预测。剩余寿命预测的具体步骤如图 1所示。
 |
| 图 1 剩余寿命的预测流程 Fig. 1 Prediction process of residual life |
| 图选项 |
步骤1??基于历史性能退化数据,根据式(14)建立退化模型的对数似然函数,利用极大似然与一维搜索方法估算出模型参数的先验分布。
步骤2??当获取到个体发动机的实时性能退化监测数据后,运用贝叶斯方法,根据式(20)~式(22)对发动机性能退化模型参数进行实时更新。
步骤3??根据式(23)可以求得发动机性能退化模型中的参数u, σ2的后验分布的期望估计值。
步骤4 ??根据式(11)~式(14)多阶段非线性Wiener过程的寿命预测方法,求得个体发动机实时的剩余寿命。
5 实例验证 排气温度裕度(Exhaust Gas Temperature Margin,EGTM)是监测发动机性能的关键指标。7台同类型的航空发动机在全寿命周期内监测的EGTM数据如表 1所示。为了验证多阶段非线性Wiener过程在航空发动机剩余寿命预测中的准确性,选择表 1中前5台发动机的EGTM历史监测数据用作先验参数估计,后2台发动机的EGTM监测数据用作实时更新。根据经验,EGTM的失效阈值定义为0℃。
表 1 某型号发动机EGTM监测数据 Table 1 EGTM monitoring data of a certain model of engine
| 当前时间/ cycle | 发动机编号 | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 100 | 69 | 70.8 | 74 | 67 | 67 | 61 | 69 |
| 200 | 63.3 | 56.2 | 70 | 65 | 61.4 | 65.3 | 63 |
| | | | | | | | |
| 3 600 | 21.6 | 19 | 8 | -0.3 | 15 | 13.9 | 19.4 |
| 3 700 | 18.7 | 17.1 | 5.6 | 10.4 | 12.5 | 16.5 | |
| 3 800 | 9.5 | 16.4 | -0.1 | 12.8 | 6.8 | 13.6 | |
| 3 900 | 1.2 | 10.4 | -0.9 | 10.7 | |||
| 4 000 | -0.8 | 6.8 | |||||
表选项
图 2给出了该7台发动机的性能退化路径。从图中可知,在大于35℃时,EGTM的上升速度较慢,0~35℃时,EGTM的退化速度较快。将发动机的退化分界值定义为ξ=35℃。此时,可采用两阶段非线性的Wiener过程进行退化建模。
 |
| 图 2 航空发动机退化路径 Fig. 2 Degradation path of aeroengines |
| 图选项 |
根据表 1中给出的航空发动机历史EGTM监测数据,利用极大似然估计方法和一维搜索方法,即可得到发动机性能退化模型各阶段参数先验分布的估计值,超参数的估计结果如表 2所示。
表 2 超参数的先验估值 Table 2 Prior estimates of hyper parameter
| 阶段 | a | b | c | d | r |
| 1 | 1.875 8 | 0.045 7 | 0.561 3 | -1.000 7 | 0.443 8 |
| 2 | 0.971 1 | 0.019 6 | 0.069 8 | -0.166 5 | 0.791 9 |
表选项
从图 2中可知,该型号发动机在不同阶段的退化速率存在着明显的差异,进一步说明了发动机的退化过程具有多阶段的特点。
在计算求得航空发动机各阶段性能退化模型参数的先验分布后,可以运用贝叶斯方法,基于实时性能退化数据对模型参数的后验分布进行更新。以编号为6的发动机为例,在获得实时性能退化监测数据后,经贝叶斯更新后的模型参数第1阶段和第2阶段估计结果分别如表 3和表 4所示。
表 3 贝叶斯更新后的参数第1阶段估计结果 Table 3 Bayes updated parameter estimation results at the first stage
| 当前时间/ cycle | 超参数 | 估计 | |||||
| a | b | c | d | u | σ2 | ||
| 1 000 | 6.875 8 | 0.830 3 | 0.382 5 | -1.126 2 | -1.126 2 | 0.120 8 | |
| 1 500 | 9.375 8 | 6.996 6 | 0.377 3 | -1.212 3 | -1.212 3 | 0.756 2 | |
| 2 000 | 11.876 | 7.208 6 | 0.377 4 | -1.224 4 | -1.224 4 | 0.607 0 | |
表选项
表 4 贝叶斯更新后的参数第2阶段估计结果 Table 4 Bayes updated parameter estimation results at the second stage
| 当前时间/ cycle | 超参数 | 估计 | |||||
| a | b | c | d | u | σ2 | ||
| 2 500 | 3.471 1 | 0.452 3 | 0.022 1 | -0.080 3 | -0.080 3 | 0.130 3 | |
| 3 000 | 5.971 1 | 1.988 4 | 0.015 3 | -0.083 4 | -0.083 4 | 0.333 0 | |
| 3 500 | 8.471 1 | 3.298 6 | 0.012 2 | -0.095 8 | -0.095 8 | 0.389 3 | |
表选项
在得到了参数更新后的估计值后,可以对发动机性能退化各阶段的剩余寿命进行实时预测。
图 3和图 4分别给出了编号为6的航空发动机在第1和第2阶段的实时剩余寿命概率密度分布图。
 |
| 图 3 第1阶段剩余寿命概率密度分布 Fig. 3 Probability density distribution of residual life at the first stage |
| 图选项 |
 |
| 图 4 第2阶段剩余寿命概率密度分布 Fig. 4 Probability density distribution of residual life at the second stage |
| 图选项 |
为直观反映出基于多阶段非线性Wiener的退化模型与传统的单阶段线性Wiener随机过程在寿命预测问题中的精确性,定义相对误差(Relative Error, RE)指标为
 | (24) |
式中:L为预测剩余寿命;T为实际剩余寿命。
2种模型的相对误差计算结果如表 5所示。
表 5 2种模型相对误差对比结果 Table 5 Relative error comparison results of two models
| 当前时间/ cycle | 相对误差 | |
| 单阶段线性 | 多阶段非线性 | |
| 1 000 | 0.046 6 | 0.018 6 |
| 1 500 | 0.072 1 | 0.037 9 |
| 2 000 | 0.076 8 | 0.264 2 |
| 2 500 | 0.182 1 | 0.175 |
| 3 000 | 0.624 4 | 0.49 |
| 3 500 | 1.235 0 | 0.518 |
表选项
根据表 5的相对误差对比结果,可计算得到单阶段线性与多阶段非线性的平均误差分别为0.372 8和0.250 6。基于多阶段非线性Wiener过程的剩余寿命预测平均误差值小于传统的预测,证实本文方法用于航空发动机剩余寿命预测的结果更精确。产生以上误差对比结果的原因是航空发动机性能退化具有多阶段非线性特点,基于多阶段非线性Wiener过程构建的性能退化模型更加符合实际航空发动机的性能退化路径。此外,同类型发动机由于环境和材料等因素的影响会产生个体的差异性,考虑个体差异性的航空发动机剩余寿命预测结果更加精确。
6 结论 1) 本文采用了基于多阶段非线性的Wiener过程来建立航空发动机的性能退化模型,能够较好地满足航空发动机的实际退化路径。
2) 与不考虑个体差异的Wiener过程的性能退化模型相比,考虑个体差异性的Wiener过程更能描述复杂系统的退化过程,剩余寿命的估算结果更加的准确。
3) 当获取个体发动机的实时监测数据后,能够结合历史性能退化监测数据,运用贝叶斯方法对模型参数的后验分布进行实时更新,实现对个体发动机剩余寿命的实时精确预测。
参考文献
| [1] | PECHT M G. Prognostics and health management of electronics[M].Hoboken: Wiley Online Library, 2008: 1-19. |
| [2] | GUAN Q, TANG Y, XU A. Objective Bayesian analysis accelerated degradation test based on Wiener process models[J].Applied Mathematical Modelling, 2016, 40(4): 2743–2755.DOI:10.1016/j.apm.2015.09.076 |
| [3] | 谢吉伟, 刘君强, 王小磊. 应用交互式多模型算法的设备剩余寿命预测[J].空军工程大学学报(自然科学版), 2016, 17(2): 98–102. XIE J W, LIU J Q, WANG X L. A residual usefual lifetime prediction based on interacting multiple model algorithm[J].Journal of Air Force Engineering University(Natural Science Edition), 2016, 17(2): 98–102.(in Chinese) |
| [4] | SI X S, WANG W, HU C H, et al. Remaining useful life estimation-A review of the statistical data driven approaches[J].European Journal of Operational Research, 2011, 213(1): 1–14.DOI:10.1016/j.ejor.2010.11.018 |
| [5] | FENG L, WANG H L, SI X S, et al. A state-space-based prognostic model for hidden and age-dependent nonlinear diffusion degradation process[J].IEEE Transactions on Automation Science and Engineering, 2013, 10(4): 1072–1086.DOI:10.1109/TASE.2012.2227960 |
| [6] | 彭宝华, 周经伦, 孙权. 基于退化与寿命数据融合的产品剩余寿命预测[J].系统工程与电子技术, 2011, 33(5): 1073–1078. PENG B H, ZHOU J L, SUN Q. Residual lifetime prediction of products based on fusion of degradation data and lifetime data[J].Systems Engineering and Electronic, 2011, 33(5): 1073–1078.(in Chinese) |
| [7] | GEBRAEEL N Z, ELWANY A H, JING P. Residual life predictions in the absence of prior degradation knowledge[J].IEEE Transactions on Reliability, 2009, 58(1): 106–117.DOI:10.1109/TR.2008.2011659 |
| [8] | SI X S, WANG W, HU C H, et al. Remaining useful life estimation based on nonlinear diffusion degradation process[J].IEEE Transactions on Reliability, 2012, 61(1): 50–67.DOI:10.1109/TR.2011.2182221 |
| [9] | PENG W, LI Y F, YANGY J, et al. Inverse Gaussian process models for degradation analysis:A Bayesian perspective[J].Reliability Engineering & System Safety, 2014, 130(1): 175–189. |
| [10] | WANG W. A two-stage prognosis model in condition based maintenance[J].European Journal of Operational Research, 2007, 182(3): 1177–1187.DOI:10.1016/j.ejor.2006.08.047 |
| [11] | 王小林, 程志君, 郭波. 基于维纳过程金属化模电容器的剩余寿命预测[J].国防科技大学学报, 2011, 33(4): 146–151. WANG X L, CHENG Z J, GUO B. Residual life forecasting of metallized film capacitor based on Wiener process[J].Journal of National University of Defense Technology, 2011, 33(4): 146–151.(in Chinese) |
| [12] | 王小林, 郭波, 程志君. 融合多源信息的维纳过程性能退化产品的可靠性评估[J].电子学报, 2012, 40(5): 977–982. WANG X L, GUO B, CHENG Z J. Reliability assessment of products with Wiener process degradation by fusing multiple information[J].Acta Electronica Sinica, 2012, 40(5): 977–982.(in Chinese) |
| [13] | WANG W, CARR M, XU W, et al. A model for residual life prediction based on Brownian motion with an adaptive drift[J].Microelectronic Reliability, 2011, 51(2): 285–293.DOI:10.1016/j.microrel.2010.09.013 |
| [14] | SI X S, WANG W, HU C H, et al. Estimating remaining useful life with three-source variability in degradation modelling[J].IEEE Transactions on Reliability, 2014, 63(1): 167–190.DOI:10.1109/TR.2014.2299151 |
| [15] | WANG X. Wiener processes with random effects for degradation data[J].Journal of Multivariate Analysis, 2010, 101(2): 340–351.DOI:10.1016/j.jmva.2008.12.007 |
| [16] | PARK C, PADGETT W J. Accelerated degradation models for failure based on geometric Brownian motion and Gamma processes[J].Life Time Data Analysis, 2005, 11(4): 511–527.DOI:10.1007/s10985-005-5237-8 |
| [17] | GEBRAEEL N Z. Sensory-updated residual life distributions for components with exponential degradation patterns[J].IEEE Transactions on Automation Science and Engineering, 2006, 3(4): 382–392.DOI:10.1109/TASE.2006.876609 |
| [18] | 司小胜, 胡昌华, 周东华. 带测量误差的非线性退化过程建模与剩余寿估计[J].自动化学报, 2013, 39(5): 530–541. SI X S, HU C H, ZHOU D H. Nonlinear degradation process modeling and remaining useful life estimation subject to measurement error[J].Acta Automatica Sinica, 2013, 39(5): 530–541.(in Chinese) |
| [19] | 刘君强, 谢吉伟, 左洪福, 等. 基于随机Wiener过程的航空发动机剩余寿命预测[J].航空学报, 2015, 36(2): 564–574. LIU J Q, XIE J W, ZUO H F, et al. Residual lifetime prediction for aeroengines based on Wiener process with random effects[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 564–574.(in Chinese) |
| [20] | 茆诗松, 汤银才. 贝叶斯统计[M].北京: 统计出版社, 2012: 10-16. MAO S S, TANG Y C. The Bayesian statistics[M].Beijing: China Statistics Press, 2012: 10-16.(in Chinese) |
