无线电引信抗干扰性能的客观科学评价是确保引信有效使用、弹药威力有效发挥的基础与前提[5-6]。目前,针对无线电引信抗干扰性能的研究主要包括模糊函数切割法[7-8]、干扰信号作用下引信启动概率[9-11]和处理增益方法等[12-16]。文献[8]提出了一种基于模糊函数切割法的无线电引信抗干扰性能测度方法,能够测度同一体制不同工作参数下引信的抗干扰性能,但无法获取不同干扰波形对引信的干扰效果。文献[9]提出了基于启动概率的压制性干扰效果评估方法,仅适用于评估满足高斯随机过程的压制性干扰信号干扰效果。文献[12]定量研究了脉冲多普勒引信抗压制式有源噪声干扰的能力,缺乏对引信威胁更大的周期调制干扰的抗干扰性能研究。
本文以处理增益为表征参量,理论推导了典型周期调制干扰信号作用下脉冲多普勒引信处理增益量化表达式,定量分析了脉冲多普勒引信抗调幅和调频类信号干扰性能,明确了引信抗周期调制干扰的影响因素,为引信抗干扰性能设计提供了理论依据。
1 脉冲多普勒引信工作原理 本文以脉冲对连续波相干检测脉冲多普勒引信为例进行说明,其工作原理如图 1所示。脉冲产生器产生调制脉冲对振荡器产生调制,已调脉冲信号经过功率放大器,由天线向空间辐射。目标回波信号由接收天线进入接收机,经过带通滤波器滤除带外噪声后进入混频器,与振荡器产生的连续波本振信号进行混频,得到幅度受多普勒信号调制的视频脉冲信号,再经过视频放大器后,送入距离门选通电路。经距离门选通后的有用信号通过多普勒信号处理,提取目标信息,推动执行级输出点火信号。
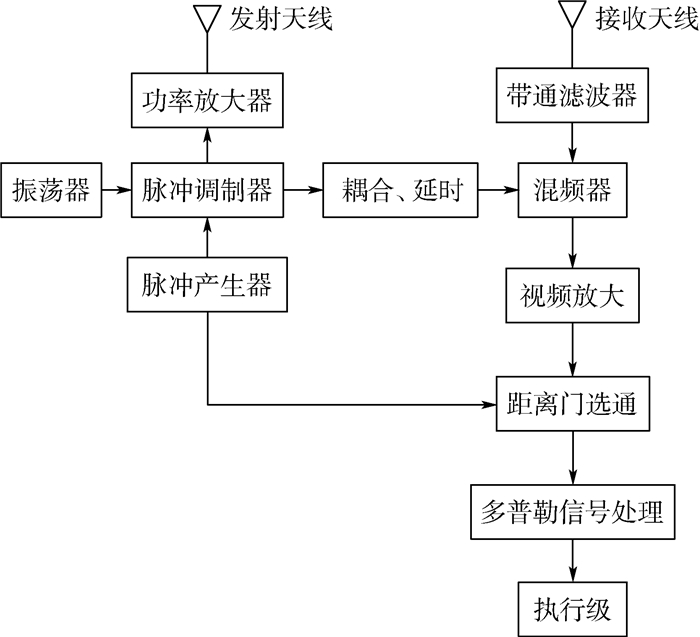 |
| 图 1 脉冲多普勒引信原理框图 Fig. 1 Block diagram of PD fuze principle |
| 图选项 |
脉冲多普勒引信发射脉冲信号为
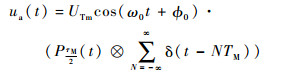 | (1) |
式中:UTm为射频脉冲幅度;ω0为载波频率;
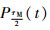
发射信号遇目标后,部分能量被反射,目标回波信号为
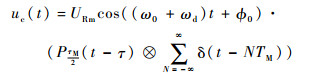 | (2) |
式中:URm为目标回波信号幅度;ωd为多普勒频率;τ为回波信号延迟。
由式(2)可知,目标回波信号的平均功率为
 | (3) |
回波信号经天线接收,通过等效带宽为[ω0-ωoff,ω0+ωoff]的带通滤波器,输出信号为
 | (4) |
其中:ω为角频率;n为谐波次数;ωoff为带通滤波器截止频率,通常选定为π/τM;ΩM=2π/TM;a为满足式(5)的最大整数,
 | (5) |
回波信号通过带通滤波器后,进入混频器与本振信号U0cos(ω0t+?d)混频,滤除高次频率分量,得到视频脉冲信号:
 | (6) |
式中:K为混频器系数;U0为本振信号幅度。
视频脉冲信号经过放大处理后,送至距离门选通电路。设距离门脉宽与引信发射信号脉宽相等,则视频脉冲信号通过距离门后的频谱为
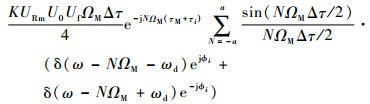 | (7) |
式中:?i为距离门;Uf为距离门信号幅值;Δτ=τM+τi-τ为距离门输出脉冲宽度, τi为距离门信号延迟。
由式(7)可知,多普勒滤波器输出基带多普勒信号功率为
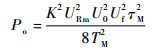 | (8) |
2 周期调制干扰信号作用下脉冲多普勒引信处理增益 干扰信号通过混频器后,信号载频ωj被滤除,干扰信号载频变为原调制频率ωc,为了使干扰信号能够完全通过多普勒滤波器,实际使用中通常将调制频率ωc设置为近似等于引信多普勒频率ωd。因此,干扰信号参数满足:
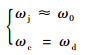 | (9) |
引信处理增益定义为引信输出信干比与输入信干比的比值,它是衡量引信抗干扰性能的重要指标,因此本文采用处理增益定量计算和表征脉冲多普勒引信抗周期调制干扰性能。
2.1 正弦波调幅信号干扰下引信处理增益 正弦波调幅干扰信号表达式为
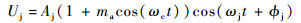 | (10) |
式中:Aj为干扰信号幅值;ma为调制度;?j为干扰信号初始相位。
由式(10)得干扰信号的输入功率为
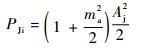 | (11) |
干扰信号被引信天线接收后,首先通过一个等效带宽为

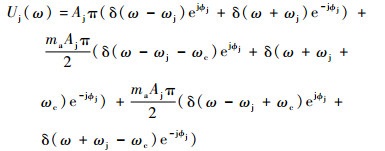 | (12) |
干扰信号通过带通滤波器后,进入混频器,与本振信号U0cos(ω0t+?0)混频,得到中频信号:
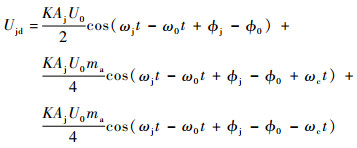 | (13) |
式中:距离门选通脉冲表示为
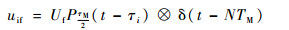 | (14) |
中频信号Ujd通过距离门后得到输出信号为
 | (15) |
对式(15)进行傅里叶变换, 并令ωj=ω0得:
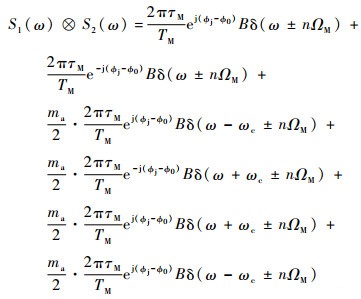 | (16) |
式中:

当且仅当式(16)中n=0时所有频率成分能够通过多普勒滤波器;n≠0时,对应的频率成分被多普勒滤波器滤除。因此,式(16)通过多普勒滤波器后,剩余项为
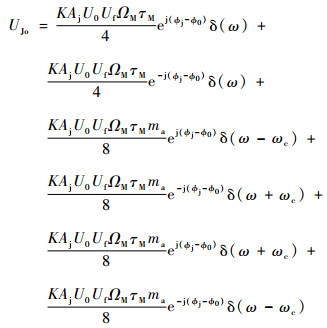 | (17) |
多普勒滤波器输出信号功率为
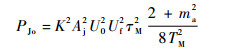 | (18) |
综上,正弦波调幅干扰信号作用下,脉冲多普勒引信处理增益为
 | (19) |
2.2 方波调幅信号干扰下引信处理增益 方波调幅干扰信号时域表达式为
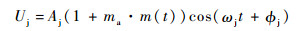 | (20) |
式中:m(t)为方波时域表达式,满足:
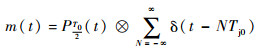 | (21) |
式中:T0为方波宽度;Tj0为方波重复周期。
由式(20)和式(21)得干扰信号的输入功率为
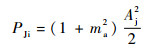 | (22) |
干扰信号通过带通滤波器后,进入混频器,与本振信号U0cos(ω0t+?0)进行混频,滤除低频分量,得到中频信号
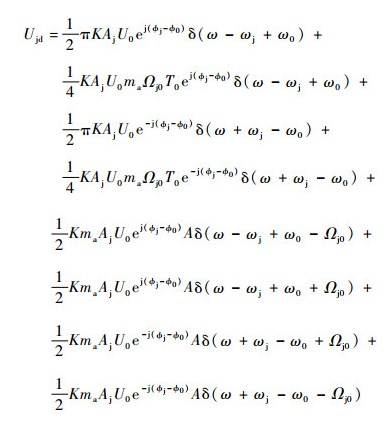 | (23) |
式中:

中频信号通过距离门后,进入多普勒滤波器,滤除带外频谱。令
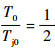
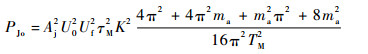 | (24) |
综上,方波调幅干扰信号作用下,脉冲多普勒引信的处理增益为
 | (25) |
2.3 正弦波调频信号干扰下引信处理增益 正弦波调频干扰信号时域表达式为
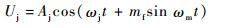 | (26) |
式中:mf为调制指数;ωm为调制角频率。
由式(26)得正弦波调频干扰信号的功率为
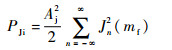 | (27) |
式中:Jn(mf)为第一类n阶贝塞尔函数。
根据贝塞尔函数的性质
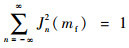
 | (28) |
干扰信号通过多普勒滤波器后输出功率为
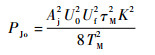 | (29) |
综上,正弦波调频干扰信号作用下,脉冲多普勒引信的处理增益为
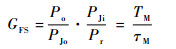 | (30) |
2.4 方波调频信号干扰下引信处理增益 方波调频干扰信号在时域上表现为两种频率的载波按调制周期交替出现,因此方波调频干扰信号可以用式(31)表示:
 | (31) |
式中:Ts为调制周期;τj0为在一个调制周期中,频率成分ωj0持续的时长,通常满足τj0=Ts/2。Δω=ωj0-ω0为调制频偏。
由式(31)得方波调频信号的输入功率为
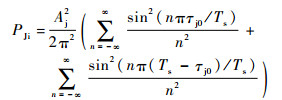 | (32) |
当τj0=Ts/2时,式(32)简化为
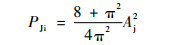 | (33) |
干扰信号通过距离选通门,并进行多普勒滤波后,得到输出功率为
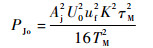 | (34) |
综上,方波调频干扰信号作用下,脉冲多普勒引信的处理增益为
 | (35) |
3 处理增益影响因素分析 以正弦波调幅干扰信号为例,研究影响处理增益的主要因素。正弦波调幅干扰信号由引信天线接收后,进入混频器,与本振信号混频得
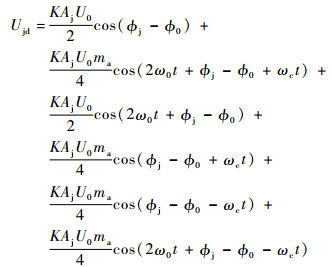 | (36) |
滤除高频分量后的干扰信号为
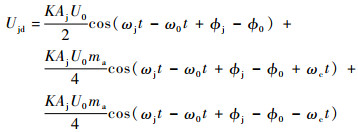 | (37) |
上述信号经过距离门可得
 | (38) |
式(38)单边谱如图 2所示。
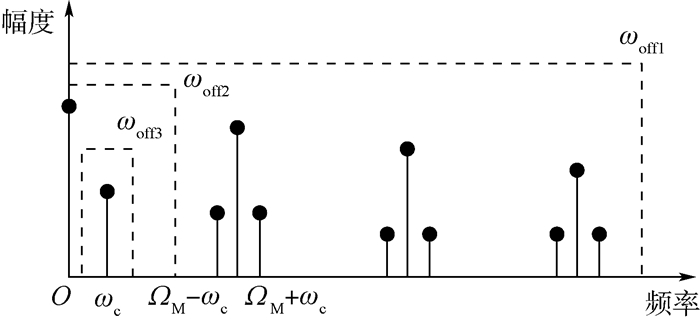 |
| 图 2 距离门输出单边谱 Fig. 2 One-sided spectrum of range gate output |
| 图选项 |
当多普勒滤波器截止频率为ωoff1时,干扰信号大量频率分量能够通过多普勒滤波器。随着多普勒滤波器截止频率降低至ωoff2时,仅有基带(n=0)处的干扰信号和直流分量能够通过多普勒滤波器,干扰信号功率得到有效抑制。当多普勒滤波器由低通滤波器改变为带通滤波器,且带宽减小至ωoff3时,仅有基带干扰信号能够通过多普勒滤波器,直流分量被滤除,干扰信号功率进一步得到抑制。此时,干扰信号输出功率为
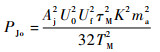 | (39) |
此时的引信处理增益为
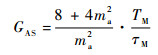 | (40) |
由上述理论分析可知,引信处理增益主要受多普勒滤波器类型和带宽、距离门脉冲宽度影响。通过替换多普勒滤波器为带通滤波器,同时减小多普勒滤波器带宽和距离门脉冲宽度,可以抑制干扰信号输出功率,提高引信处理增益和抗干扰性能。
脉冲多普勒引信距离门脉冲宽度通常与调制脉冲宽度相同,调制脉冲宽度要求取式(41)的2个分式中较小值[17]:
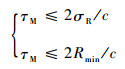 | (41) |
式中:σR为距离分辨率;Rmin为引信最小作用距离;c为光速。调制脉冲宽度越窄,测距精度越高[2],因此,减小距离门脉冲宽度在提升引信抗干扰性能的同时不会降低引信的探测性能。
4 仿真与讨论 根据脉冲多普勒引信工作原理,基于MATLAB建立了脉冲多普勒引信干扰模型,针对6种干扰源进行仿真,对理论推导结果进行了验证。仿真参数设置如下:脉冲重复周期TM=4 000 ns;发射脉冲宽度τM=20 ns;多普勒频率fd=40 kHz;多普勒滤波器截止频率Fd=66.7 kHz;仿真距离30 m;预定炸高15 m;距离门延迟τi=100 ns;距离门脉冲宽度与发射信号脉冲宽度相等;信号幅值1 V;干扰信号输入功率0.5 W,调制度为1。
在上述工作参数下,引信回波信号输入功率为0.002 5 W,距离门选通后输出功率为3.125×10-6 W。典型周期调制干扰信号作用下,脉冲多普勒引信处理增益,如表 1所示。
表 1 周期调制干扰信号作用下脉冲多普勒引信处理增益仿真结果 Table 1 Simulation results of PD fuze processing gain under interference of periodic modulation jamming signal
| 干扰信号 样式 | 干扰波性参数 | 处理增益 | |||||
| 载波幅值/V | 调制周期/kHz | 调制频偏/MHz | 理论值/dB | 仿真值/dB | 表达式 | ||
| 正弦波调幅 | 0.816 5 | 40 | 20.000 | 20.525 |  | ||
| 方波调幅 | 0.707 1 | 40 | 19.114 | 19.550 | 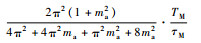 | ||
| 正弦波调频 | 1 | 40 | 20 | 23.010 | 23.319 | 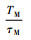 | |
| 方波调频 | 1.050 8 | 40 | 20 | 25.590 | 24.901 |  | |
表选项
图 3、图 4分别给出了干扰信号参数不变的情况下,引信处理增益与引信距离门脉冲宽度、多普勒低通滤波器带宽的量化关系。图 5为将多普勒低通滤波器替换为多普勒带通滤波器后,滤波器带宽与处理增益量化关系。如图 3所示,周期调制干扰信号作用下处理增益在距离门脉冲宽度由20 ns增加至100 ns的过程中均降低了约7 dB。如图 4所示,引信处理增益受多普勒滤波器带宽变化影响较为明显。当滤波器带宽由50 kHz增加至350 kHz时,各类干扰信号作用下的引信处理增益减小值均在4.5 dB以上。如图 5所示,在多普勒滤波器带宽不变,滤波器类型由低通滤波器变为带通滤波器的情况下,不同干扰信号作用下处理增益变化差距较大,其中方波调幅作用下处理增益增加值达到10 dB,而正弦波调频信号作用下处理增益仅增加0.1 dB。
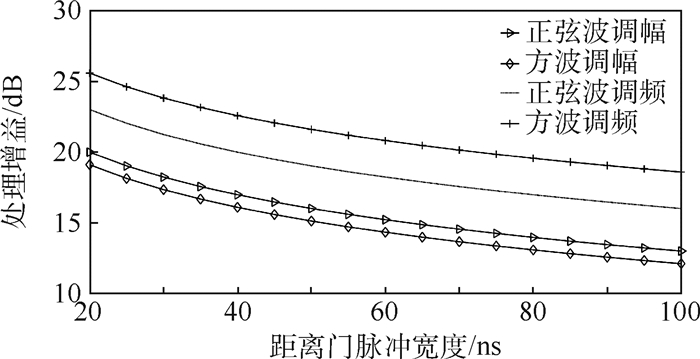 |
| 图 3 距离门脉冲宽度与处理增益量化关系 Fig. 3 Quantitative relationship between range gate pulse width and processing gain |
| 图选项 |
 |
| 图 4 多普勒低通滤波器通带宽度与处理增益量化关系 Fig. 4 Quantitative relationship between Doppler low pass filter bandwidth and processing gain |
| 图选项 |
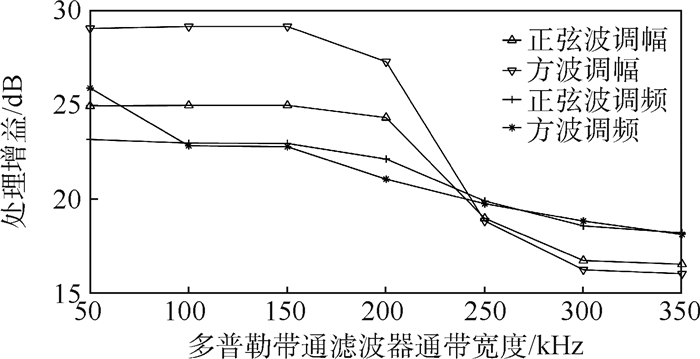 |
| 图 5 多普勒带通滤波器通带宽度与处理增益量化关系 Fig. 5 Quantitative relationship between Doppler band pass filter bandwidth and processing gain |
| 图选项 |
综上,脉冲多普勒引信抗干扰性能的影响因素主要包括距离门选通和多普勒滤波。减小距离门脉冲宽度和多普勒滤波器带宽,并将多普勒低通滤波器替换为带通滤波器可以在不影响引信信号输出功率的情况下减小干扰信号通过距离门和滤波器的功率,进而提高引信抗干扰性能。
表 2给出了不同距离门脉冲宽度条件下下使引信启动的最小干扰功率实测值。由表 2可以看出,随着距离门脉冲宽度的增加,引信启动的最小干扰功率逐渐减小。表 3给出了不同滤波器带宽条件下使引信启动的最小干扰功率实测值。由表 3可以看出,随着多普勒滤波器带宽的增加,引信启动的最小干扰功率逐渐减小。在相同多普勒滤波器带宽条件下,调幅类干扰信号作用下,引信启动的最小干扰功率小于调频类干扰信号作用下,引信启动的最小干扰功率。
表 2 不同距离门脉冲宽度条件下使引信启动最小干扰功率实测值 Table 2 Measured value of minimum interference power of fuze starting at different range gate pulse width
| dBm | |||
| 干扰信号 样式 | 最小干扰功率 | ||
| 400 ns脉冲宽度 | 800 ns脉冲宽度 | 1 200 ns脉冲宽度 | |
| 方波调幅 | -13 | -16 | -17 |
| 方波调频 | -12 | -13 | -15 |
表选项
表 3 不同多普勒滤波器通带宽度条件下使引信启动最小干扰功率实测值 Table 3 Measured value of minimum interference power of fuze starting at different Doppler filter bandwidth
| dBm | |||
| 干扰信号 样式 | 最小干扰功率 | ||
| 10 kHz通带宽度 | 20 kHz通带宽度 | 30 kHz通带宽度 | |
| 方波调幅 | -16 | -23 | -25 |
| 正弦波调幅 | -20 | -21 | -23 |
| 方波调频 | -13 | -14 | -14 |
| 正弦波调频 | -14 | -14 | -15 |
表选项
理论推导、仿真和实测结果表明:
1) 仿真和实测结果与理论推导结果吻合,验证了脉冲多普勒引信在周期调制干扰信号作用下,脉冲多普勒引信处理增益量化表达式的正确性。
2) 干扰信号功率相同的情况下,脉冲多普勒引信抗调幅信号干扰能力弱于抗调频干扰能力。
3) 干扰信号功率保持不变的情况下,随着距离门脉冲宽度增加,脉冲多普勒引信处理增益相应降低,不同干扰信号作用下,引信处理增益受距离门脉冲宽度变化影响的变化趋势一致。
4) 干扰信号功率保持不变的情况下,随着多普勒滤波器带宽增加,脉冲多普勒引信处理增益相应降低。不同干扰信号作用下,引信处理增益变化受多普勒滤波器带宽变化影响的程度不同,但变化趋势一致。
5) 干扰信号功率保持不变的情况下,将多普勒低通滤波器替换为带通滤波器,脉冲多普勒引信处理增益得到明显提升。随着带通滤波器带宽增加,脉冲多普勒引信处理增益降低。不同干扰信号作用下,引信处理增益变化受多普勒滤波器带宽变化影响的程度不同,但变化趋势一致。
5 结论 本文以引信处理增益为表征参量,定量研究了脉冲多普勒引信抗周期调制干扰性能。
1) 获取了脉冲多普勒引信抗干扰性能与其影响因素之间的量化关系,既为脉冲多普勒引信抗干扰性能的优化设计提供了理论依据,又为脉冲多普勒引信抗干扰性能评估提供了技术支撑。
2) 理论推导、仿真和实测结果表明脉冲多普勒引信具有较强的抗周期调制干扰性能,抗干扰性能与引信距离门脉冲宽度、多普勒滤波器类型和带宽有关。
参考文献
| [1] | HARTLEY J D. A method for suppression of pulsed interference in a pulse Doppler radar[C]//2008 International Conference on Radar. Piscataway, NJ: IEEE Press, 2008: 265-270. |
| [2] | 赵惠昌. 无线电引信设计原理与方法[M].北京: 国防工业出版社, 2012: 147-161. ZHAO H C. Fundamentals and methodology of radio fuze[M].Beijing: National Defense Industry Press, 2012: 147-161.(in Chinese) |
| [3] | 隋鉴, 李国林. 针对脉冲多普勒引信的二维多假目标干扰[J].电光与控制, 2016, 23(3): 7–10. SUI J, LI G L. Two-dimensional multiple false targets jamming against pulse Doppler fuze[J].Electronic Optics & Control, 2016, 23(3): 7–10.(in Chinese) |
| [4] | 张彪, 闫晓鹏, 栗苹, 等. 基于支持向量机的无线电引信抗扫频式干扰研究[J].兵工学报, 2016, 37(4): 635–640. ZHANG B, YAN X P, LI P, et al. Research on anti-frequency sweeping jamming of radio fuze based on support vector machine[J].Acta Armamentarii, 2016, 37(4): 635–640.(in Chinese) |
| [5] | ZHANG C C, GE J J, SHENG J T. Analysis of ground clutter characteristics of airborne forward looking pulse Doppler radar in high PRF[C]//2006 International Conference on Radar. Piscataway, NJ: IEEE Press, 2006: 1-3. |
| [6] | SKOLNIK M I. Radar handbook[M]. 2nd ed. New York: McGraw-Hill, Inc., 1990: 226-243. |
| [7] | 周新刚, 赵惠昌, 涂友超. 脉冲多普勒引信抗干扰性能评判方法和仿真[J].系统仿真学报, 2011, 23(1): 207–211. ZHOU X G, ZHAO H C, TU Y C. ECCM evaluation and simulation of pulse Doppler fuze[J].Journal of System Simulation, 2011, 23(1): 207–211.(in Chinese) |
| [8] | 赵惠昌, 周新刚. 基于模糊函数切割法的线性调频连续波引信抗干扰性能测度[J].兵工学报, 2009, 30(12): 1591–1595. ZHAO H C, ZHOU X G. Anti-jamming performance evaluation of linear frequency modulated continuous wave fuze based on ambiguity function incision[J].Acta Armamentarii, 2009, 30(12): 1591–1595.DOI:10.3321/j.issn:1000-1093.2009.12.005(in Chinese) |
| [9] | 涂友超. 典型伪码体制引信参数提取及干扰效果研究[D]. 南京: 南京理工大学, 2010. TU Y C. Study on parameter extraction and jamming effective of typical pseudo-random code fuze[D]. Nanjing: Nanjing University of Science and Technology, 2010(in Chinese). |
| [10] | 熊金柱, 曹玉瑞, 涂友超. 基于启动概率的伪码调相引信干扰效果研究[J].河南大学学报, 2010, 40(5): 460–463. XIONG J Z, CAO Y R, TU Y C. Study on jamming effect of pseudo-random binary-phase-coded fuze based on starting probability[J].Journal of Henan University, 2010, 40(5): 460–463.(in Chinese) |
| [11] | 涂友超, 赵惠昌, 周新刚. 噪声调频干扰下伪码调相引信启动概率分析[J].南京理工大学学报, 2011, 35(2): 252–256. TU Y C, ZHAO H C, ZHOU X G. Analysis on starting probability of pseudo-random binary-phase-coded fuze under noise FM jamming[J].Journal of Nanjing University of Science and Technology, 2011, 35(2): 252–256.(in Chinese) |
| [12] | 李泽, 栗苹, 郝新红, 等. 脉冲多普勒引信抗有源噪声干扰性能研究[J].兵工学报, 2015, 36(6): 1001–1008. LI Z, LI P, HAO X H, et al. Anti-active noise jamming performance of pulse Doppler fuze[J].Acta Armamentarii, 2015, 36(6): 1001–1008.(in Chinese) |
| [13] | 涂友超, 赵惠昌, 周新刚. 伪码体制引信抗瞄准式噪声调幅干扰性能研究[J].南京理工大学学报, 2008, 32(3): 350–355. TU Y C, ZHAO H C, ZHOU X G. Performance of anti-noise AM spot jamming of pseudo-random code fuze[J].Journal of Nanjing University of Science and Technology, 2008, 32(3): 350–355.(in Chinese) |
| [14] | 刘己斌, 赵惠昌, 陆建伟. 几种伪码体制引信的抗噪声性能分析[J].兵工学报, 2005, 26(1): 20–24. LIU J B, ZHAO H C, LU J W. Performance analysis concerning anti-noise for several pseudo-random code fuzes[J].Acta Arnamentarii, 2005, 26(1): 20–24.(in Chinese) |
| [15] | 熊刚, 杨小牛, 赵惠昌. 伪码调相与正弦调频复合引信抗干扰性能分析[J].现代雷达, 2007, 29(12): 12–17. XIONG G, YANG X N, ZHAO H C. Performance analysis of anti noise of pseudo-random PM and sine frequency modulation combined fuze[J].Modern Radar, 2007, 29(12): 12–17.DOI:10.3969/j.issn.1004-7859.2007.12.004(in Chinese) |
| [16] | 闫岩, 崔占忠. 超宽带无线电引信抗干扰性能研究[J].兵工学报, 2010, 31(1): 13–17. YAN Y, CUI Z Z. Anti-jamming performance of ultra wideband radio fuze[J].Acta Armanentarii, 2010, 31(1): 13–17.(in Chinese) |
| [17] | 梁棠文. 防空导弹引信设计及仿真技术[M].北京: 宇航出版社, 1995: 233-235. LIANG T W. Design and simulation technology of air defense missile fuze[M].Beijing: China Astronautic Publishing House, 1995: 233-235.(in Chinese) |
