旋翼自由尾迹方法简单高效,适用于桨叶气动载荷分析[2-3]。通过建立共轴刚性双旋翼自由尾迹模型,Yeo和Johnson[4]于2013年采用CAMRADⅡ(Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics Ⅱ)研究高速共轴刚性双旋翼系统桨叶载荷特性。随后Schmaus和Chopra[5]于2015年采用基于自由尾迹模型的UMARC(University of Maryland Advanced Rotor Code)研究高速共轴刚性双旋翼系统结构载荷。Quackenbush等[6]采用基于自由尾迹的CHARM(Comprehensive Hierarchical Aeromechanics Rotorcraft Model)研究新型高速共轴刚性双旋翼复合式直升机性能。此外,Baeder等[7]基于自由尾迹模型的PRASADUM(Parallelized Rotorcraft Analysis for Simulation and Design developed at the University of Maryland)研究高速共轴刚性双旋翼前飞状态下的桨叶载荷。然而,这些方法通过翼型静态气动特性描述旋翼反流区的升力变化,而未考虑高速共轴刚性双旋翼后行边反流区的前缘脱体涡,也未考虑共轴刚性双旋翼桨尖涡对桨叶非定常气动载荷的干扰影响。
计算流体力学(Computational Fluid Dynamics, CFD)方法基于速度-压力形式的Navier-Stokes方程,适用于旋翼流场分析[8]。叶正寅和徐国华等基于嵌套CFD方法研究悬停状态共轴刚性双旋翼非定常流动干扰特性[9-10]。随后招启军等[11]将此方法用于悬停状态共轴刚性双旋翼非定常流动干扰特性研究,但均未针对共轴刚性双旋翼高速状态的非定常气动载荷开展研究。Singh和Kang[12]于2015年采用CFD方法研究了共轴刚性双旋翼桨叶时变载荷,表明共轴刚性双旋翼载荷分析需考虑双旋翼气动干扰因素。Baeder等[7]采用CFD/CSD(Computaional Strutural Dyanmics)研究了高速共轴刚性双旋翼前飞状态下的桨叶载荷,表明桨叶载荷受上、下旋翼气动干扰影响明显,且需考虑后行边反流区影响。此外,Bhagwat等[13]基于Helios (Helicopter overset simulations)和RCAS(Rotorcraft Comprehensive Analysis System)的CFD/CSD混合方法研究了高速刚性共轴双旋翼桨叶载荷,表明共轴刚性双旋翼之间气动干扰影响共轴刚性双旋翼气动特性。虽然上述CFD方法能较好分析高速共轴刚性双旋翼桨叶气动载荷,但计算的共轴刚性双旋翼尾迹耗散较大,且需复杂的网格和较多的计算资源[14]。
黏性涡粒子法基于速度-涡量形式的Navier-Stokes方程,适用于旋翼尾迹、旋翼气动载荷[15-16]、旋翼与平尾[17]以及旋翼与尾桨气动干扰分析[18]。为降低高速共轴刚性双旋翼前飞状态下的需要功率,高速状态下的X2旋翼转速下降20%,最大前飞速度下的桨尖Ma数Mtip约为0.82,抑制桨叶压缩性的影响[7],因此,涡方法仍可适用于共轴刚性双旋翼桨叶气动特性分析,且已得到成功应用[4-7]。然而,此方法未考虑高速共轴刚性双旋翼后行边反流区以及共轴刚性双旋翼之间桨尖涡干扰影响。为此,本文基于非定常面元法建立满足桨叶前缘和后缘边界条件的旋翼反流区气动模型以体现高速共轴刚性双旋翼后行边反流区影响,且增加共轴刚性双旋翼桨尖涡-桨叶气动干扰模型以体现共轴刚性双旋翼非定常气动干扰的影响,并结合基于黏性涡粒子法的共轴刚性双旋翼尾迹模型,构建高速共轴刚性双旋翼气动干扰下的时变气动载荷分析方法。
1 计算方法 1.1 共轴刚性双旋翼桨叶气动基本原理 与单旋翼不同,前飞状态下的共轴刚性双旋翼系统存在较大反流区和升力偏置,且共轴刚性双旋翼系统的上、下旋翼桨尖涡干扰也将影响桨叶的非定常气动载荷。此外,共轴刚性双旋翼采用非线性弦长、非线性负扭、多段翼型桨叶,其中X2高速共轴刚性双旋翼桨叶采用钝头翼型DBLN-526、SC1012-R8以及SSCA-09翼型(见图 1(a),其中R为桨叶半径),且各段翼型之间光滑过渡。基于非定常面元法和翼型曲线插值,将共轴刚性双旋翼桨叶离散为光滑表面单元,得到X2桨叶离散网格如图 1(b)所示,且根据非定常面元法求得桨叶表面压力分布,从而获得桨叶各截面的气动特性,而无需通过翼型气动特性查表修正,因而更好体现桨叶非定常气动特性。
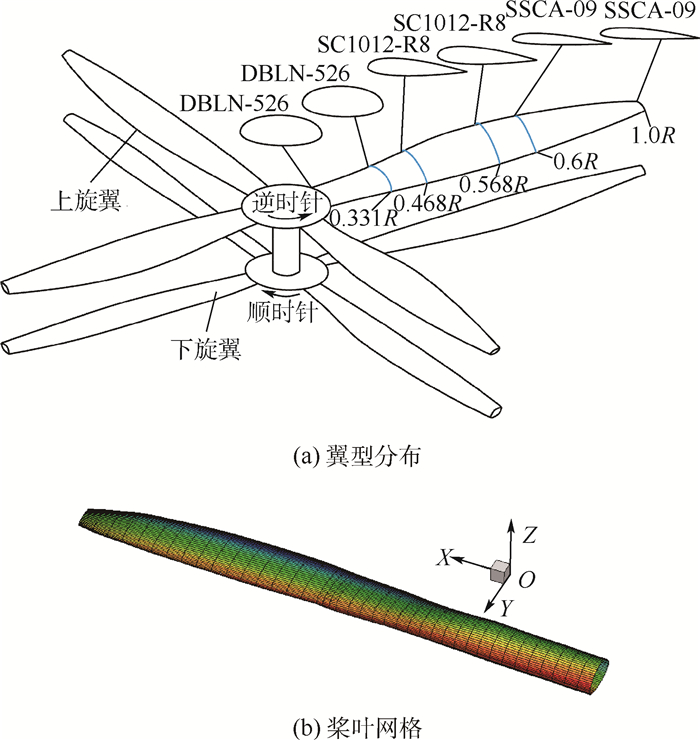 |
| 图 1 X2高速共轴刚性双旋翼桨叶翼型和网格 Fig. 1 Airfoil and grid of X2 high-speed rigid coaxial rotor blade |
| 图选项 |
根据非定常面元法基本理论,定义共轴刚性双旋翼流场速度势函数?v由共轴刚性双旋翼桨叶和尾迹涡面的汇σs和偶极子μd构成[15, 17-18]:
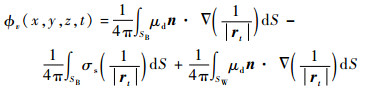 | (1) |
式中:SB为共轴刚性双旋翼桨叶表面;SW为共轴刚性双旋翼尾迹涡面;n为共轴刚性双旋翼桨叶和尾迹涡面外法线;rt为共轴刚性双旋翼桨叶和尾迹涡面位置;S为面积积分变量。
根据共轴刚性双旋翼桨叶表面无穿透和远场无扰动边界条件,则
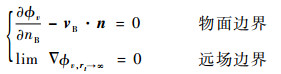 | (2) |
式中:vB为共轴刚性双旋翼桨叶速度; nB为桨叶表面单位法向。
1.2 共轴刚性双旋翼桨叶反流区气动模型 大速度前飞状态,共轴刚性双旋翼均存在较大的后行边反流区。前行边的空气从桨叶前缘向后缘移动,并满足后缘Kutta条件,根据桨叶Neumann和后缘Kutta条件,后缘处形成脱体涡(见图 2),涡面偶极子μwTE为
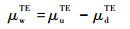 | (3) |
 |
| 图 2 高速共轴刚性双旋翼反流区气动模型 Fig. 2 Reverse flow aerodynamic model of high-speed rigid coaxial rotor |
| 图选项 |
式中:μuTE和μdTE分别为桨叶后缘上、下表面偶极子强度。
与前行边不同,共轴刚性双旋翼后行边反流区的空气从桨叶后缘向前缘移动,并在前缘形成脱体涡(见图 2),满足前缘Kutta条件,因此桨叶前缘尾迹涡面偶极子μwLE为
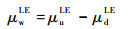 | (4) |
式中:μuLE和μdLE分别为桨叶前缘上、下表面偶极子强度。
将式(3)和式(4)代入式(1),并根据Neumann和前后缘Kutta条件,得到共轴刚性双旋翼桨叶偶极子求解方程:
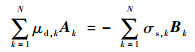 | (5) |
式中:μd, k和σs, k分别为共轴刚性双旋翼桨叶第k个面元偶极子和汇强度;Ak为共轴刚性双旋翼桨叶与从前缘或后缘脱出的尾迹偶极子影响系数之和;Bk为共轴刚性双旋翼桨叶的汇影响系数。
 | (6) |
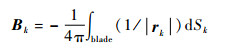 | (7) |
其中:nTE和nLE分别为后缘和前缘法向矢量;rTE和rLE分别为后缘和前缘位置矢量;Sk为第k个单元面积; 下标blade表示桨叶面元,下标TEwake表示桨叶后缘涡面,下标LEwake表示桨叶前缘涡面; rk为第k个面元的位置矢量。
求解式(5)得到共轴刚性双旋翼桨叶偶极子μd分布。与前行边桨叶相似,根据式(4)得到反流区桨叶前缘的尾迹涡面面元强度μwLE,而后由尾迹涡面速度求出下一个时间步t+Δt的涡面位置,并根据涡量等效原则积分得到在尾随偶极子面元中心的涡粒子涡量(见图 2)。通过速度-涡量形式的Navier-Stokes方程确定共轴刚性双旋翼尾迹涡量的空间分布,从而体现共轴刚性双旋翼反流区对共轴刚性双旋翼尾迹结构的影响。
1.3 共轴刚性双旋翼桨尖涡-桨叶气动干扰模型 共轴刚性双旋翼系统的上旋翼桨尖涡将穿过下旋翼桨叶表面,从而改变下旋翼桨叶表面压力分布,并影响下旋翼桨叶气动载荷的时变非线性特性。与此相同,下旋翼也将影响上旋翼桨叶非定常气动载荷。根据伯努利方程,共轴刚性双旋翼桨尖涡干扰下的上、下旋翼桨叶非定常压力系数Cpu和Cpd为
 | (8) |
式中:pref和ρ分别为参考压力和空气密度;vBu、pu、vrefu、?up blade和?up wake分别为上旋翼桨叶表面空气速度、表面压力、当地参考速度以及上旋翼桨叶诱导速度势和尾迹诱导速度势;vBd、pd、vrefd、?down blade和?down wake分别为下旋翼桨叶表面空气速度、表面压力、当地参考速度以及下旋翼桨叶诱导速度势和尾迹诱导速度势。
式(8)中??up blade/?t描述上旋翼桨叶时变气动载荷对下旋翼桨叶表面压力的影响;而??down blade/?t表示下旋翼桨叶时变气动载荷对上旋翼桨叶表面压力的影响,以体现共轴刚性双旋翼桨叶交叠时存在的载荷干扰。
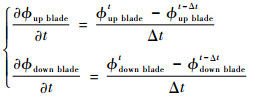 | (9) |
式(8)中??up wake/?t表述上旋翼桨尖涡对下旋翼桨叶表面压力的影响,可转变为上旋翼桨尖涡对下旋翼桨叶的诱导速度与上旋翼桨尖涡速度的乘积;而??down wake/?t描述下旋翼桨尖涡对上旋翼桨叶表面压力的影响,可转变为下旋翼桨尖涡对上旋翼桨叶诱导速度与下旋翼桨尖涡速度的乘积。
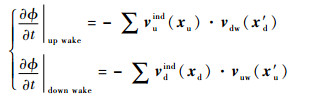 | (10) |
式中:xu、vuw和x′u分别为上旋翼桨叶位置、桨尖涡速度和位置;xd、vdw和x′d分别为下旋翼桨叶位置、桨尖涡速度和位置;vuind和vdind分别为下旋翼桨尖涡对上旋翼桨叶的诱导速度和上旋翼桨尖涡对下旋翼桨叶的诱导速度。
共轴刚性双旋翼桨尖涡干扰下的双旋翼桨叶气动载荷为
 | (11) |
式中:ΔFk和ΔSk分别为气动力和面积;Cp, k为面元压力系数;nk为面元外法线矢量。
1.4 共轴刚性双旋翼尾迹模型 与单旋翼不同,共轴刚性双旋翼系统的上、下旋翼桨叶均脱出桨尖涡,受到双旋翼桨尖涡之间的相互干扰作用,桨尖涡几何特征将发生改变,且上旋翼桨尖涡将穿过下旋翼旋转平面(见图 3(a)),从而改变共轴刚性双旋翼非定常气动载荷。
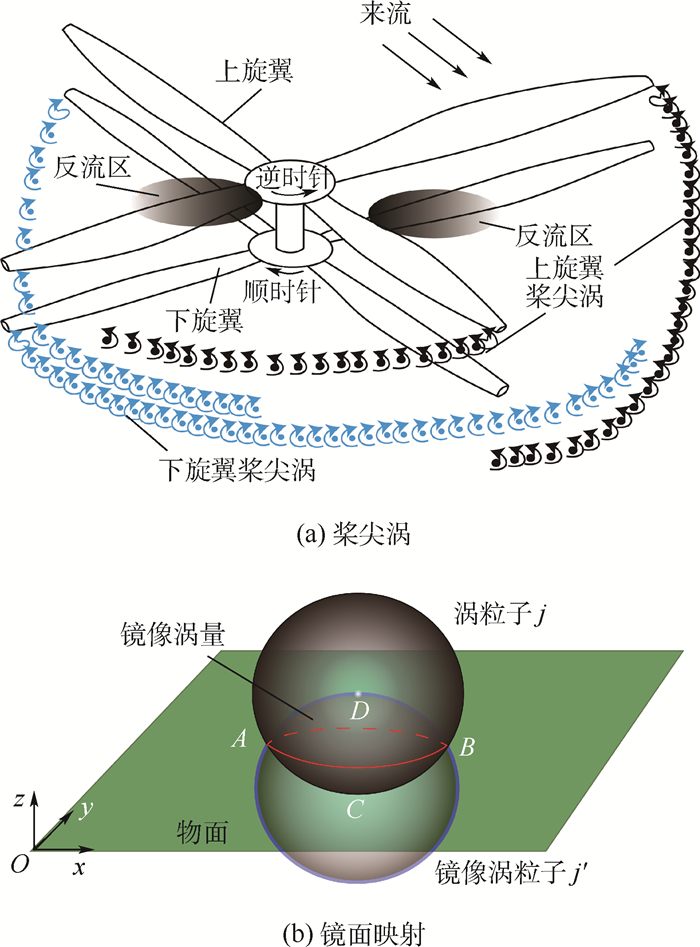 |
| 图 3 X2高速共轴刚性双旋翼桨尖涡和镜面映射 Fig. 3 Tip vortex of X2 rigid coaxial rotor and mirror mapping of vorticity |
| 图选项 |
基于黏性涡粒子法[15-18],共轴刚性双旋翼涡量分布由速度-涡量(u, ω)形式的Navier-Stokes方程确定:
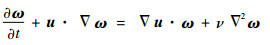 | (12) |
式中:ν为运动黏性系数。
采用四阶Runge-Kutta、PSE(Particle Strength Exchange)、直接求解法求解式(12)获得共轴刚性双旋翼涡量场空间分布,得到共轴刚性双旋翼桨尖涡结构。
共轴刚性双旋翼系统的上旋翼桨尖涡将穿过下旋翼旋转平面,从而改变下旋翼气动载荷,但上旋翼桨尖涡靠近下旋翼桨叶表面,并进入下旋翼桨叶内部,从而改变上旋翼桨尖涡对下旋翼桨叶气动载荷的干扰影响。为体现上、下旋翼桨叶对共轴刚性双旋翼桨尖涡的影响,基于镜面映射法,进入桨叶的涡强为涡量与体积VACB之积(见图 3(b)),则镜面涡量为
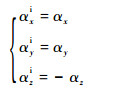 | (13) |
式中:αx、αy和αz分别为涡量在桨叶表面的2个切分量和法分量;αxi、αyi和αzi分别为镜面涡量在桨叶表面的2个切分量和法分量。
1.5 共轴刚性双旋翼配平 与常规旋翼系统不同,由于共轴刚性双旋翼之间存在总距、纵、横向周期操纵差异,因此定义双旋翼操纵量为
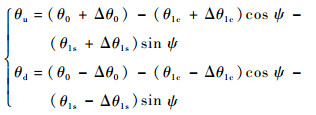 | (14) |
式中:θu、θd分别为上、下旋翼桨距;θ0、θ1c和θ1s分别为双旋翼系统总距、纵向和横向操纵量平均值;Δθ0、Δθ1c和Δθ1s分别为双旋翼系统总距、纵向和横向操纵量差值;ψ为旋翼桨叶方位角。
根据共轴刚性双旋翼系统力矩和力平衡要求,稳定状态下的加速度均为零,因此平衡方程为
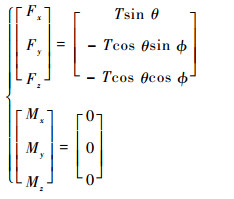 | (15) |
式中:Fx、Fy、Fz和Mx、My、Mz分别为共轴刚性双旋翼的气动力和力矩;T为重力;θ为双旋翼系统俯仰角;?为双旋翼系统滚转角。
与常规直升机配平不同,由于共轴刚性双旋翼操作量多于平衡方程,因而配平较为复杂。为此,文献[19]建立基于目标函数和约束条件的优化方法实现共轴刚性双旋翼飞行器全机配平。此外,文献[20]通过建立共轴刚性双旋翼飞行器飞行动力学模型,给定提前操纵角和纵、横向周期变距差动值实现整机配平。针对共轴刚性双旋翼系统,给定旋翼系统俯仰姿态,通过旋翼系统力和力矩平衡,从而实现双旋翼系统配平,并已应用于共轴刚性双旋翼系统性能和桨叶结构载荷分析[5-6, 12-13]。为此,针对共轴刚性双旋翼系统,上述双旋翼系统平衡方程为6个,而变量为8个,双旋翼配平变量多于平衡方程数目,为实现对共轴刚性双旋翼系统配平方程封闭,基于文献[7]给定机体俯仰角θ和滚转角?,减少双旋翼系统操作变量,而后在给定飞行状态下,给定初始操纵量,通过计算共轴刚性双旋翼系统气动载荷,判定是否满足平衡方程。若不满足,则通过差分计算共轴刚性双旋翼系统Jacobian矩阵,并通过牛顿迭代法计算双旋翼操纵量,直到满足平衡方程为止,完成共轴刚性双旋翼系统配平。
为验证共轴刚性双旋翼系统配平的可靠性,计算得到Harrington共轴双旋翼悬停状态[21]和前飞状态下的性能[22]如图 4所示。图中P为双旋翼功率,hp, 1 hp=745.7 W;CT为旋翼系统拉力系数;CQ为旋翼系统扭矩系数;μ为前进比。
 |
| 图 4 Harrington共轴双旋翼性能 Fig. 4 Performance of Harrington coaxial rotor |
| 图选项 |
从图 4中可以看出,计算得到的Harrington共轴双旋翼悬停状态下的CT-CQ曲线与实验测量结果[21]吻合的很好,悬停状态下,共轴双旋翼之间存在一定的总距差动。此外,计算得到Harrington共轴双旋翼在CT=0.004 8下各前飞速度的功率与实验测量结果[22]基本吻合,其中共轴双旋翼之间的总距、纵横向周期变距均存在差动,由此表明本文共轴刚性双旋翼气动载荷配平方法的可行性。
2 高速共轴刚性双旋翼非定常气动干扰特性 2.1 X2高速共轴刚性双旋翼非定常气动载荷 本算例计算前飞状态下X2TD(X2 Technology Demonstrator)高速共轴刚性双旋翼桨叶非定常气动载荷[7, 23]。上、下旋翼均由4片非均匀弦长和非线性负扭桨叶构成,旋翼半径为4.023 m,桨尖Mtip为0.554,桨叶翼型分布如图 1所示。计算模型桨叶弦向为60段,展向为40段,双旋翼系统由19 200个面元构成,方位角步长为2.5°,双旋翼系统操纵量如表 1所示。
表 1 共轴刚性双旋翼系统操纵量(185 km/h) Table 1 Control variables of rigid coaxial rotor system (185 km/h)
| (°) | |||
| 变量 | PRASADUM[7] | CFD[7] | 本文 |
| θ0 | 5.84 | 6.38 | 8.87 |
| Δθ0 | 0.32 | 0.1 | 0.1 |
| θ1c | 3.38 | 1.77 | 0.27 |
| Δθ1c | 0 | 0 | 0 |
| θ1s | 0.21 | 0.34 | 0.33 |
| Δθ1s | 4.29 | 4.1 | 5.7 |
表选项
计算得到前飞速度为102、185和278 km/h状态下的旋翼特征剖面非定常气动载荷如图 5所示。图中:Cn为截面法向升力系数;ψ为方位角。图中同时给出基于自由尾迹的综合分析方法PRASADUM计算结果[7]以及基于NASA OVER-FLOW和CREATE AV Helios的CFD/CSD计算结果[7],其中PRASADUM耦合了共轴刚性双旋翼自由尾迹模型和桨叶气动弹性模型,CFD/CSD耦合了共轴刚性双旋翼CFD模型和桨叶气动弹性模型。由于共轴刚性双旋翼桨叶挥舞运动由桨叶弹性变形产生,为体现挥舞运动的影响,基于铰接式旋翼挥舞运动方程,通过等效挥舞外伸量和等效挥舞约束弹簧刚度[20, 24],保证挥舞频率满足旋翼弹性挥舞频率1.42,并近似一阶弹性挥舞。3种前飞状态下,本文分析方法计算得到特征剖面非定常气动载荷变化特征与CFD/CSD计算结果均吻合地较好,体现了上、下旋翼在前行侧和后行侧由干扰引起的非定常载荷减小特性,并较好计算X2共轴刚性双旋翼非定常气动载荷。由于PRASADUM的共轴刚性双旋翼自由尾迹模型通过桨尖涡模拟共轴刚性双旋翼系统尾迹结构,暂未考虑双旋翼桨叶整体涡结构对桨叶非定常气动载荷的干扰以及后行边反流区的前缘脱体涡特性,PRASADUM计算结果总体偏大,且前行边和后行边升力系数均出现较大振荡。相比于PRASADUM计算结果,本文方法计算的上、下旋翼非定常气动载荷随时间变化幅值、相位均与CFD/CSD计算结果吻合地更好,且更好体现各前飞速度上、下旋翼在前行边和后行边升力系数下降特性。此外,由于在低速前飞状态下,后行边反流区较小,因而增加桨叶后行边反流区气动模型的计算结果改善不明显;然而,大速度前飞状态下,旋翼后行边反流区逐渐增大,增加桨叶后行边反流区气动模型的计算结果明显与CFD/CSD计算结果更吻合。上旋翼后行边桨叶根部截面涡量如图 6所示。增加桨叶后行边反流区气动模型后,后行边的桨叶内段前缘脱出涡,从而增加桨根区域涡量强度,并与之后的桨叶干扰,增加方位角300°桨叶非定常气动载荷变化幅度。而未考虑桨叶后行边反流区气动模型,涡量则从桨叶后缘脱出,而后叠加在桨叶表面,削弱桨根区域涡量强度,减小与之后桨叶干扰产生的非定常气动载荷。因此,后行边涡量截面分布和气动载荷变化均可体现后行边反流区气动模型的可行性。
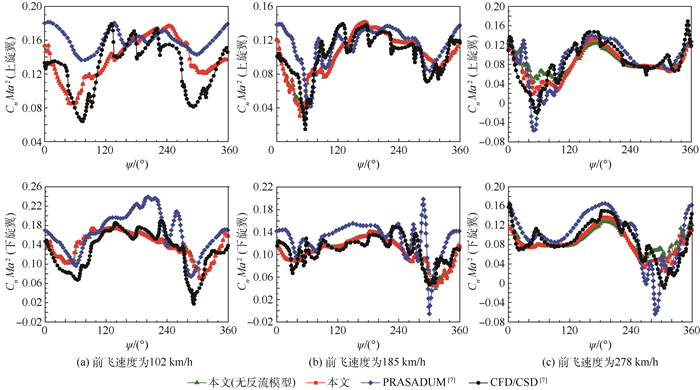 |
| 图 5 不同前飞速度下的X2旋翼截面载荷 Fig. 5 Sectional load of X2 rotor at different forward speeds |
| 图选项 |
 |
| 图 6 上旋翼后行边桨叶截面涡量(278 km/h) Fig. 6 Vorticity of blade section at retreating side of upper rotor (278 km/h) |
| 图选项 |
2.2 上、下旋翼之间的非定常气动干扰特性 图 7给出3种前飞速度状态下X2共轴刚性双旋翼系统上、下旋翼特征剖面非定常气动载荷变化历程(按上旋翼时间历程)。前飞速度102km/h状态,相比于上旋翼,下旋翼非定常气动载荷在方位角60°和300°处明显下降,且在后行边300°处下降更显著。主要原因在于下旋翼受到上旋翼桨尖涡干扰的影响。上旋翼桨尖涡将穿过下旋翼后半部分(见图 8(a),其中上旋翼桨尖涡采用红色表示,下旋翼桨尖涡采用淡蓝色表示),且在方位角60°和300°处受到上旋翼卷起桨尖涡干扰显著,因而导致下旋翼诱导入流λ在方位角60°和300°处明显大于上旋翼(见图 9(a1)、(a2))。随着前飞速度的增加,双旋翼桨尖涡向下速度逐渐减小,上旋翼桨尖涡沿着上旋翼桨盘平面移动,而下旋翼桨尖涡沿着下旋翼桨盘平面移动(见图 8(b)、(c)),从而对下旋翼干扰减弱,因此下旋翼的非定常气动载荷时间历程与上旋翼基本相似(见图 7(b)、(c)),上旋翼诱导速度分布与下旋翼诱导速度分布也基本相似(见图 9(b1)、(b2))。因此上、下旋翼气动干扰对桨盘诱导速度和非定常气动载荷影响明显。
 |
| 图 7 不同前飞速度下上、下旋翼截面载荷 Fig. 7 Sectional load of upper and lower rotor at different forward speeds |
| 图选项 |
 |
| 图 8 不同前飞速度下的X2旋翼尾迹结构 Fig. 8 Wake structure of X2 rotor at different forward speeds |
| 图选项 |
 |
| 图 9 X2旋翼诱导入流分布 Fig. 9 Induced flow distribution of X2 rotor |
| 图选项 |
2种前飞速度的上、下旋翼总距分别为(8.85°、9.08°)和(11.5°、11.4°),且均存在一定的横向周期操纵量,分别为(7.9°、-7.9°)和(5.2°、-4.7°),因此图 10中2种前飞速度下的拉力主要分布在前半侧。低速状态下,共轴刚性双旋翼与常规旋翼相似,旋翼反流区较小,升力偏置较小,因而旋翼前半部分和后部分为旋翼主要升力区域(见图 10(a1)、(a2))。上、下旋翼前半部分均受到旋翼桨尖涡的干扰影响(见图 8(a)),由此引起上、下旋翼载荷波动,且上、下旋翼桨尖涡位置存在交叉,因而上、下旋翼载荷波动交叉出现,并导致上、下旋翼升力差表现出由桨尖涡干扰导致的丝带特性;此外,上旋翼桨尖涡将穿过下旋翼后部(见图 8(a)),因而上、下旋翼升力差表现出60°与300°处卷起桨尖涡干扰特性(见图 10(a3))。随着前飞速度增加,与常规旋翼不同,共轴刚性双旋翼反流区增大,升力偏置明显向前行边移动,因而前行边为双旋翼主要升力区域(见图 10(b1)、(b2))。此外,上、下旋翼升力差呈现出与桨叶片数相关的辐射状特性,而桨尖涡干扰导致的丝带特性和60°与300°处卷起桨尖涡干扰特性减弱(见图 10(b3))。主要原因在于高速前飞状态下,上旋翼桨尖涡远离下旋翼(见图 8(c)),桨尖涡干扰效应降低,而旋翼载荷增加,上旋翼对下旋翼时变干扰载荷增加(见式(9)),因而升力特性表现出8片桨叶的辐射状干扰。
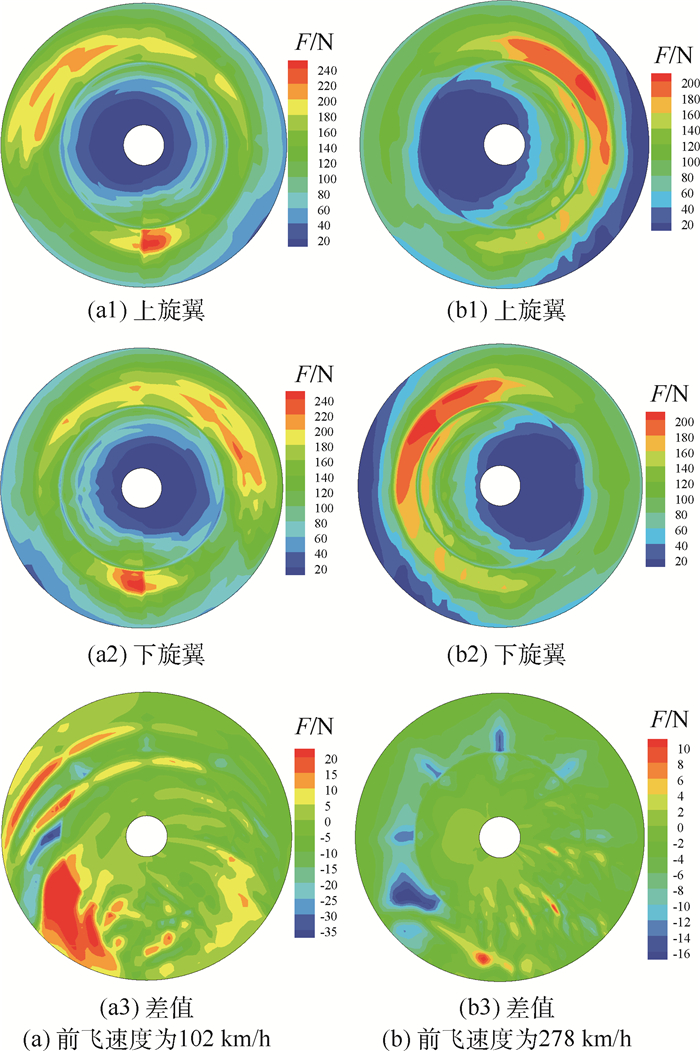 |
| 图 10 X2旋翼截面升力分布 Fig. 10 Sectional force distribution of X2 rotor |
| 图选项 |
前飞状态下的共轴刚性双旋翼尾迹结构与单旋翼略有不同。受下旋翼后行边和前行边卷起桨尖涡的诱导影响,上旋翼前行边和后行边桨尖涡向内侧和下方移动,并与下旋翼桨尖涡位置互换(见图 11(a),其中上旋翼桨尖涡采用红色表示,下旋翼桨尖涡采用橙色表示)。在x=0.25R处上旋翼前行边和后行边脱出桨尖涡①,下旋翼后行边和前行边桨叶脱出桨尖涡②(见图 11(b))。受桨尖涡之间的相互干扰作用,在x=0.5R~0.75R处,上旋翼桨尖涡①开始向旋翼内侧和下方移动,而下旋翼桨尖涡②则向上旋翼方向移动(见图 11(c)、(d));在x=1.0R处,下旋翼桨尖涡②达到上旋翼旋转平面高度,并在上旋翼桨尖涡①之上,实现桨尖涡①和②位置互换(见图 11(e))。图 12给出了此状态下桨叶特征剖面处诱导速度随方位角的变化历程和频率分布。上、下旋翼诱导速度在方位角80°~240°之间基本相似,然而上、下旋翼桨尖涡位置互换导致下旋翼桨尖涡上移,从而使得前行边0°~80°和后行边240°~360°的下旋翼诱导速度显著大于上旋翼。此外,相比于上旋翼诱导速度谐波分量,下旋翼诱导速度不仅1 Ω谐波分量增加17.5%,且3 Ω、4 Ω、5 Ω谐波分量显著增大(其中Ω为旋翼转速的频率单位),分别为30.9%、144.2%、194.7%。与此同时,上、下旋翼特征剖面非定常气动载荷总体差异小于诱导速度差异,但非定常气动载荷的3 Ω、4 Ω、5 Ω谐波分量却显著增大。
 |
| 图 11 X2旋翼桨尖涡位置互换(102 km/h) Fig. 11 Interchange of tip vortex position of X2 rotor (102 km/h) |
| 图选项 |
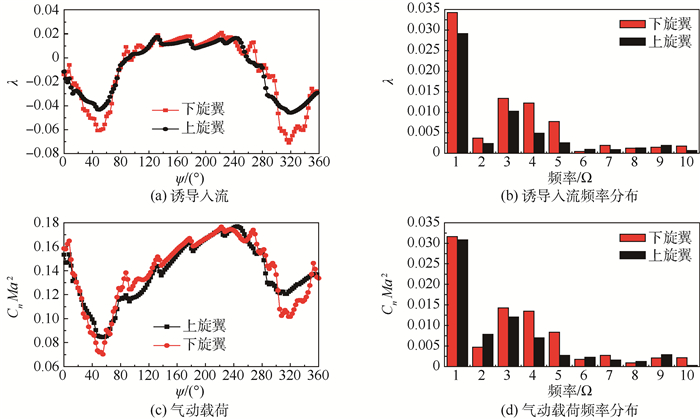 |
| 图 12 上、下旋翼诱导入流和截面载荷的频谱特性 Fig. 12 Frequency spectrum of induced flow and sectional load of upper and lower rotor |
| 图选项 |
2.3 共轴刚性双旋翼与单旋翼气动载荷特性差异 图 13给出3种前飞速度状态下单旋翼和共轴刚性双旋翼截面载荷与频率。前飞速度为102 km/h状态,共轴刚性双旋翼在60°和300°处升力明显小于孤立旋翼,主要原因为下旋翼在方位角60°和300°处受上旋翼卷起桨尖涡的干扰影响(见图 9(b)),同时下旋翼卷起桨尖涡向上旋翼上方移动,并对上旋翼也存在较明显的干扰。随着前飞速度的增加,由于上、下旋翼桨尖涡向下移动速度减小,双旋翼桨尖涡之间干扰作用减弱,因而共轴刚性双旋翼和单旋翼之间的气动载荷时间历程差异减小。
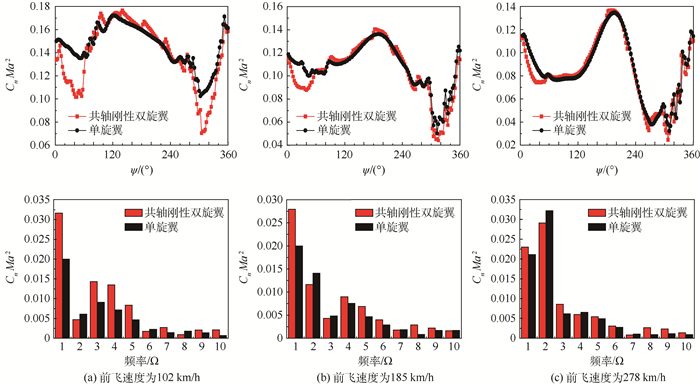 |
| 图 13 共轴刚性双旋翼和单旋翼截面载荷与频率 Fig. 13 Sectional load and frequency of rigid coaxial rotor and single rotor |
| 图选项 |
相比于单旋翼,共轴刚性双旋翼升力系数1 Ω、3~10 Ω谐波分量增大。受上旋翼卷起桨尖涡对下旋翼在60°和300°处显著干扰作用影响,共轴刚性双旋翼升力系数1 Ω分量明显增加,且随前飞速度的增加而减小。但共轴刚性双旋翼升力系数8 Ω谐波分量随前飞速度增加而增加,主要原因为下旋翼桨叶受到上旋翼桨叶干扰作用增强(见式(9)),且下旋翼旋转一周将与上旋翼桨叶叠加8次,因而产生8 Ω谐波分量。
图 14给出共轴刚性双旋翼与单旋翼的诱导速度和截面升力差值。各种状态下,诱导速度和截面升力差值均表现出桨叶片数的辐射特征和旋翼后部干扰特性。低速前飞状态,受上旋翼卷起桨尖涡的显著影响,双旋翼诱导速度和截面升力差值均表现出显著的卷起桨尖涡干扰和桨叶片数整数倍(8Ω)的辐射状干扰特性。随着前飞速度增加,由于上、下旋翼桨尖涡干扰作用减小,共轴刚性双旋翼和单旋翼之间的诱导速度和截面升力差异所呈现的卷起桨尖涡干扰特征逐渐减弱,而受到上、下旋翼桨叶干扰更加明显,因而呈现桨叶片数整数倍辐射状的桨叶干扰特征更加突出。
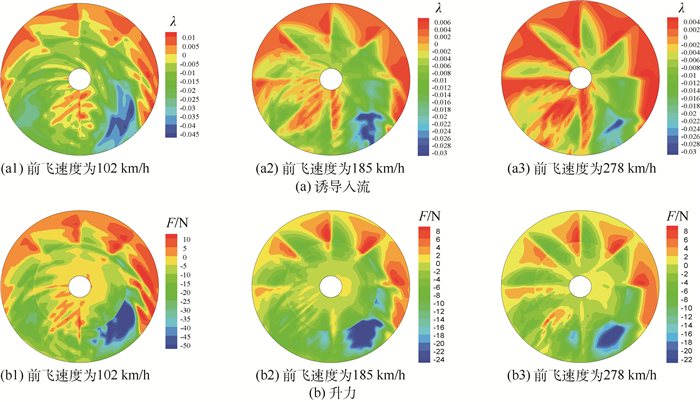 |
| 图 14 单旋翼与共轴双旋翼的诱导速度和截面升力差异 Fig. 14 Change in induced velocity and sectional force due to single rotor and rigid coaxial rotor |
| 图选项 |
上述研究分析表明,本文分析方法能较好分析共轴刚性双旋翼复杂干扰下的非定常气动载荷,且共轴刚性双旋翼系统的桨尖涡干扰和桨叶干扰对双旋翼桨叶非定常气动载荷存在明显的影响。由于推进螺旋桨也将处于共轴刚性双旋翼桨尖涡干扰区域,为此,将进一步研究共轴刚性双旋翼桨尖涡干扰下的推进螺旋桨性能和载荷,以及由此产生的全机操作特性变化。
3 结论 1) 建立满足桨叶前缘和后缘边界条件的高速共轴刚性双旋翼反流区气动模型,并结合共轴刚性双旋翼桨尖涡-桨叶气动干扰模型,构建高速共轴刚性双旋翼非定常气动载荷分析方法,相比于基于自由尾迹的PRASADUM,本文方法计算更好地体现上、下旋翼在前行边和后行边非定常气动载荷的变化特性,与CFD/CSD计算结果更吻合。
2) 低速状态,下旋翼桨叶载荷在60°和300°方位角出明显下降,但随着前飞速度增加,上、下旋翼气动载荷特性差异缩小。
3) 低速状态,上、下旋翼气动载荷差异呈现出由桨尖涡干扰导致的丝带特性和卷起桨尖涡干扰特性,而高速前飞状态则呈现出桨叶片数相关的辐射状特性。
4) 受双旋翼桨尖涡相互诱导作用,共轴刚性双旋翼出现桨尖涡位置互换现象。
5) 相比于单旋翼,低速状态的共轴刚性双旋翼升力系数1Ω谐波分量显著增加,并随前飞速度增加而减小,而高速状态8Ω谐波分量增加明显,且桨叶片数整数倍辐射状的桨叶干扰特征更加突出。
参考文献
| [1] | ELLER E. X2TM load alleviating controls[C]//The American Helicopter Society 68th Annual Forum. Fairfax, VA: AHS, 2012: 1578-1587. |
| [2] | TAN J F, WANG H W. Highly efficient unsteady panel time-marching free wake for aerodynamics of rotorcraft[J].Journal of Aircraft, 2014, 51(1): 54–61.DOI:10.2514/1.C031807 |
| [3] | GOVINDARAJAN B M, LEISHMAN J G. Curvature corrections to improve the accuracy of free-vortex methods[J].Journal of Aircraft, 2016, 53(2): 378–386.DOI:10.2514/1.C033392 |
| [4] | YEO H, JOHNSON W. Investigation of maximum blade loading capability of lift-offset rotors[C]//The AHS 69th Annual Forum. Fairfax, VA: AHS, 2013: 782-797. |
| [5] | SCHMAUS J, CHOPRA I. Aeromechanics for a high advance ratio coaxial helicopter[C]//The AHS 71st Annual Forum. Fairfax, VA: AHS, 2015: 1139-1153. |
| [6] | GAFFEY T M, ZHANG C, QUACKENBUSH D T, et al. Aeromechanics of the coaxial compound helicopter[C]//56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2015: 1-19. |
| [7] | PASSE B, SRIDHARAN A, BAEDER J. Computational investigation of coaxial rotor interactional aerodynamics in steady forward flight[C]//33rd AIAA Applied Aerodynamics Conference. Reston: AIAA, 2015: 1-29. |
| [8] | CAO Y H, ZHAO M. Numerical simulation of rotor flowfields based on several spatial discretization schemes[J].Journal of Aircraft, 2012, 49(5): 1535–1539.DOI:10.2514/1.C031786 |
| [9] | 许和勇, 叶正寅. 悬停共轴双旋翼干扰流动数值模拟[J].航空动力学报, 2011, 26(2): 453–457. XU H Y, YE Z Y. Numerical simulation of interaction unsteady flows around co-axial rotors in hover[J].Journal of Aerospace Power, 2011, 26(2): 453–457.(in Chinese) |
| [10] | 叶靓, 徐国华. 共轴式双旋翼悬停流场和气动力的CFD计算[J].空气动力学学报, 2012, 30(4): 437–442. YE L, XU G H. Calculation on flow field and aerodynamic force of coaxial rotors in hover with CFD method[J].Acta Aerodynamic Sinica, 2012, 30(4): 437–442.(in Chinese) |
| [11] | 朱正, 招启军, 李鹏. 悬停状态共轴刚性双旋翼非定常流动干扰机理研究[J].航空学报, 2016, 37(2): 568–578. ZHU Z, ZHAO Q J, LI P. Investigations on unsteady flow interaction mechanism of coaxial rigid rotors in hover[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 568–578.(in Chinese) |
| [12] | SINGH R, KANG H. Computational investigations of transient loads and blade deformations on coaxial rotor systems[C]//33rd AIAA Applied Aerodynamics Conference. Reston: AIAA, 2015: 101-111. |
| [13] | SINGH R, KANG H, BHAGWAT M, et al. Computational and experimental study of coaxial rotor steady and vibratory loads[C]//54th AIAA Aerospace Sciences Meeting. Reston: AIAA, 2016: 1-10. |
| [14] | KOMERATH N M, SMITH M J, TUNG C. A review of rotor wake physics and modeling[J].Journal of the American Helicopter Society, 2011, 56(2): 022006-1–022006-21. |
| [15] | TAN J F, WANG H W. Simulating unsteady aerodynamics of helicopter rotor with panel/viscous vortex particle method[J].Aerospace Science and Technology, 2013, 30(1): 255–268.DOI:10.1016/j.ast.2013.08.010 |
| [16] | HE C J, ZHAO J G. Modeling rotor wake dynamics with viscous vortex particle method[J].AIAA Journal, 2009, 47(4): 902–915.DOI:10.2514/1.36466 |
| [17] | 谭剑锋, 王浩文, 吴超, 等. 基于非定常面元/黏性涡粒子混合法的旋翼/平尾非定常气动干扰研究[J].航空学报, 2014, 35(3): 643–656. TAN J F, WANG H W, WU C, et al. Rotor/empennage unsteady aerodynamic interaction with unsteady panel/viscous vortex particle hybrid method[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 643–656.(in Chinese) |
| [18] | 谭剑锋. 直升机旋翼对尾桨非定常气动载荷的影响[J].航空学报, 2015, 36(10): 3228–3240. TAN J F. Influence of helicopter rotor on tail rotor unsteady aerodynamic loads[J].Acta Aeronauica et Astronautica Sinica, 2015, 36(10): 3228–3240.(in Chinese) |
| [19] | 陈全龙, 韩景龙, 员海玮. 前行桨叶概念旋翼动力学分析方法[J].航空学报, 2014, 35(9): 2451–2460. CHEN Q L, HAN J L, YUN H W. Analytical method for advancing blade concept rotor dynamics[J].Acta Aeronautica et Astronautica Sincia, 2014, 35(9): 2451–2460.(in Chinese) |
| [20] | 袁野, 陈仁良, 李攀. 共轴刚性旋翼飞行器配平特性及验证[J].南京航空航天大学学报, 2016, 48(2): 186–193. YUAN Y, CHEN R L, LI P. Trim characteristics and verification of coaxial rigid rotor airfraft[J].Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(2): 186–193.(in Chinese) |
| [21] | HARRINGTON R D. Full-scale-tunnel investigation of the static-thrust performance of a coaxial helicopter rotor: TN-2318[R]. Washington, D. C. : NASA, 1951. |
| [22] | DINGELADEIN R C. Wind-tunnel studies of the performance of multirotor configurations: TN-3236[R]. Washington, D. C. : NASA, 1954. |
| [23] | WALSH D, WEINER S, ARIFIAN K, et al. High airspeed testing of the Sikorsky X2 technology TM demonstrator[C]//The 67th Annual Forum of the AHS International. Fairfax, VA: AHS, 2011: 2999-3010. |
| [24] | 高正, 陈仁良. 直升机飞行动力学[M].北京: 科学出版社, 2003: 40-42. GAO Z, CHEN R L. Flight dynamics of helicopter[M].Beijing: Science Press, 2003: 40-42.(in Chinese) |
