对干扰资源分配决策的研究很多,文献[1]提出一种多波束干扰系统干扰资源综合管理算法,对雷达进行筛选,对干扰机进行聚类,提高了资源分配的效率;文献[2]提出一种零和竞争理论的雷达干扰网干扰功率分配方法,采用零和竞争理论对干扰功率在各雷达间进行分配,达到比按比例分配更好的干扰效果;文献[3]提出一种基于变效能因子的Lanchester协同干扰最优功率分配算法,通过建立变效能因子Lanchester平方律扩展模型,并以战斗状态方程作为目标函数,求解出最佳功率协同分配策略。传统的干扰资源分配方法还包括模拟退火算法(Simulated Annealing Algorithm, SAA)[4]、贴近度[5]、贝叶斯推理算法[6]以及0-1规划[7]等。
实现质量高的干扰资源分配,关键包括3个部分:①对敌方雷达实现威胁评估;②建立己方干扰机与敌方雷达之间的决策矩阵;③选择合适的优化算法实现最佳干扰。对雷达威胁等级的评估是实施高效干扰的基础,直觉模糊集(Intuitionistic Fuzzy Sets, IFS)[8-11]增加了一个非隶属度函数的概念,能够描述“非彼非此”的“模糊概念”,更加细腻地刻画了客观世界的模糊性本质。IFS无论在表达能力和推理精度上都优于传统的评估算法,本文在选取几个典型雷达参数指标的基础上,利用IFS对雷达威胁系数进行威胁评估;建立敌方雷达与己方干扰机之间的关系才能够更好地“对症下药”。本文从频域、空域、极化方式和干扰样式4个方面建立己方干扰机与敌方雷达之间的匹配度矩阵,作为建立目标方程的基础;针对传统模拟退火算法、蚁群算法(Ant Colony Algorithm, ACA)易陷入局部最优等问题,提出一种改进粒子群优化(Improved Particle Swarm Optimization, IPSO)算法[12-15]。本文对权重和学习因子作出改进,提高了全局搜索能力、局部改良能力和收敛能力,引入补偿粒子实现对盲区的搜索,增强了粒子的多样性,并将其引入到离散问题的求解,依据目标函数得到最优干扰资源分配方法。
1 研究框架 如图 1所示,现代电子战中作战双方均涉及各类装备,是系统对系统的对抗。
 |
| 图 1 空战图 Fig. 1 Air battle picture |
| 图选项 |
如何利用有限的干扰资源实现对敌方雷达实施最大限度的干扰,主要思路如图 2所示,包括以下3个部分:第1步是根据己方无源探测系统以及雷达系统获得的敌方雷达参数,科学评估敌方雷达威胁系数;第2步是根据己方干扰系统参数和整合的敌方雷达参数,计算整个战场中所有己方干扰系统与敌方雷达系统之间的契合程度;第3步则是确定目标函数,利用智能优化算法确定最优干扰资源分配方法。
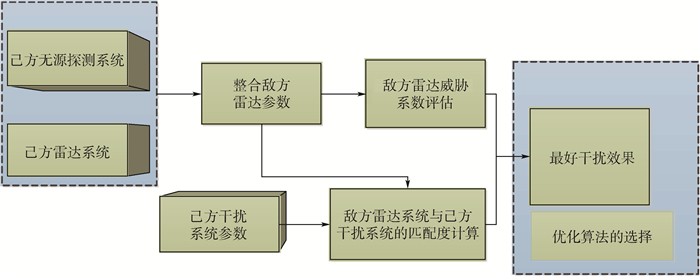 |
| 图 2 资源分配框架 Fig. 2 Resource distribution frame |
| 图选项 |
2 雷达威胁评估 在复杂的空战环境中,如何对雷达实施有效而不过度的干扰,首先要完成的任务就是对雷达的威胁等级做科学的评价。通过己方无源探测系统以及雷达系统获得的敌方雷达参数(包括速度、距离、来波方位、重频、载频和脉宽), 采用IFS算法对雷达威胁等级进行评估的主要步骤如下:
步骤1 ?威胁指标隶属度确定。
1) 速度。敌方雷达速度直接决定防空武器的系统反应时间和毁伤概率,其隶属度函数为
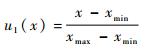 | (1) |
式中:xmin和xmax分别为数据集合内的最小值和最大值;x为单次测量值。
2) 距离。敌方雷达距离反映了敌方的攻击企图和达成攻击的可能性,其隶属度函数为
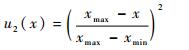 | (2) |
3) 载频。当前雷达大都工作于0.8~40 GHz频段。雷达载频越高,威胁等级越高,其隶属度函数为
 | (3) |
4) 脉宽。敌方雷达脉宽越窄,其威胁程度就越高,其隶属度函数为
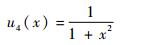 | (4) |
步骤2 ?确定犹豫度矩阵。对于经济型指标,如速度、雷达载频,其犹豫度计算公式为:y=(0.5+k)(1-u),k为测量变化率。对于成本型指标,如平台距离威胁、雷达脉宽,其犹豫度计算公式为:y=(0.5+k)(1+u)。
步骤3 ?根据式(5)确定非隶属度函数:
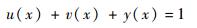 | (5) |
式中:u(x)为隶属度函数;v(x)为非隶属度函数;y(x)为犹豫度函数。
步骤4?确定第j部雷达的威胁系数:
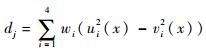 | (6) |
式中:wi为敌方雷达指标权重。
3 干扰系统和雷达系统的匹配度矩阵 干扰机对雷达实施有效干扰的必要条件为频率、方向、极化方式的对准,以及有效的干扰调制信号样式。
频率对准的程度用δij(f)表示,其表达式如下:
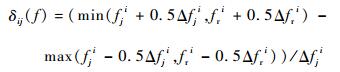 | (7) |
式中:fji为干扰机i的中心频率;Δfji为干扰机i的频带宽度;frj为雷达j的中心频率;Δfrj为雷达j接收机的频带宽度。
方向对准的程度可用雷达相对于干扰信号最大增益值方向的偏离程度来衡量,定义如下:
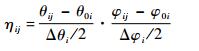 | (8) |
式中:θij和φij分别为雷达j相对于干扰波束i指向的俯仰角和方位角;θ0i和φ0i为干扰波束i增益最大值G的方向;Δθi和Δφi为干扰波束i的半功率波束宽度。
极化方式对准是发射的干扰信号的极化方向与雷达接收天线的极化方式一致,使得干扰信号可以进入雷达接收机,避免极化失配引起干扰信号衰减。干扰机多采用圆极化,这样干扰信号均能进入到各雷达接收机中去,但存在一个极化损失系数γij,取0.5。
对某一雷达,即使干扰功率相同,但用不同的干扰调制信号样式其干扰效果也会大不一样,定义干扰样式合适度如下:
 | (9) |
定义敌方雷达与己方干扰机的匹配度为
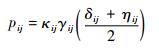 | (10) |
匹配度表示的是干扰机对雷达的干扰效率,匹配度越大,则说明干扰机对雷达实施干扰会有更好的效果。求出整个战场所有的己方干扰系统(m部)和敌方雷达系统(n部)的匹配度,构建匹配度矩阵:
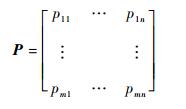 | (11) |
4 干扰资源分配方法 干扰资源的分配方法直接决定着最终干扰效果,为实现好的干扰效果,首先确定干扰效果目标函数:
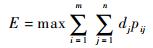 | (12) |
本文假设一个干扰系统最多对一部雷达实施干扰,而一部雷达可以同时被多个干扰系统干扰,即
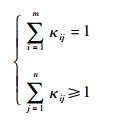 | (13) |
针对传统PSO算法易陷入局部最优的问题,本文提出一种IPSO算法,以实现干扰资源的最优分配。算法步骤如下:
步骤1 ?随机初始化种群中各微粒的位置和速度。例如:微粒位置为x=[3, 4, 2, 5, 1, 6],表示干扰机3对雷达1实施干扰,干扰机4对雷达2实施干扰,干扰机2对雷达3实施干扰……依次类推。
步骤2 ?评价各微粒的适应度。将当前各微粒的位置和适应度值存储于各微粒的pbest中,将所有pbest中适应度最优个体的位置和适应度值存储于gbest中。
步骤3 ?更新微粒的速度和位置:
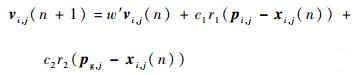 | (14) |
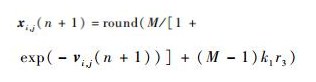 | (15) |
式中:vi, j为微粒速度;xi, j(n)为微粒位置;round()为取整函数;k1、r3为常数;pi, j为个体极值;pg, j为全局极值;M为常数;w′为权重;c1和c2为学习因子;r1和r2为[0, 1]之间的随机数。
步骤4?更新权重。为增强传统PSO算法的平衡能力和局部改良能力,采用非线性的动态惯性权重系数公式,其表达式如下:
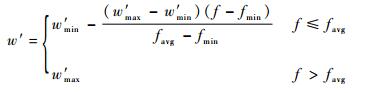 | (16) |
式中:w′max和w′min分别为权重w′的最大值和最小值;f为粒子当前的目标函数值;favg和fmin分别为当前微粒的平均目标值和最小目标值。
步骤5?更新学习因子。学习因子的公式如下:
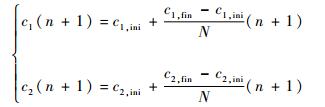 | (17) |
式中:c1, ini和c2, ini分别为c1和c2的初始值;c1, fin和c2, fin分别为c1和c2的终值;N为最大迭代次数。令2个学习因子在优化过程中随时间进行不同的变化,使得在优化的初始阶段,粒子具有较大的自我学习能力和较小的社会学习能力,加强全局搜索能力,在后期粒子具有较大的社会学习能力和较小的自我学习能力,有利于收敛到全局最优解。
步骤6 ?更新粒子适应度值以及种群适应度值。对粒子的适应度值排序,剔选出表现最差的h个粒子,为增强粒子的多样性,避免陷入局部最优,对这部分粒子速度做高斯调整:
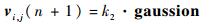 | (18) |
式中:k2为常数;gaussion为满足标准整台分布的随机数。根据式(15)、式(18)更新粒子位置,得到适应度值。
步骤7 ?比较得到最优适应度值,当前的粒子位置对应的干扰机分配序列为最优干扰资源分配决策。
步骤8 ?若达到一定的精度要求(通常为预设的精度阈值或迭代次数),输出结果;否则返回步骤3继续搜索。
IPSO算法流程图如图 3所示。
 |
| 图 3 IPSO算法流程图 Fig. 3 IPSO algorithm flowchart |
| 图选项 |
5 实例仿真 模拟退火算法、蚁群算法都是常用的优化算法,故将IPSO算法与这2种算法对比。为公平起见,模拟退火算法和蚁群算法都是在固定参数条件下采用经典的基础算法。仿真硬件平台均为Inter(R) Core(TM) i7-3770 CPU 3.40 GHz,在Windows 7操作系统下进行。
仿真参数设置如下。模拟退火算法:Markov链长度为200,衰减参数为0.998,步长因子为0.01,初始温度为100,容差为10-8;蚁群算法:蚂蚁个数为50,信息素重要程度参数为1,启发式因子重要程度参数为5,信息蒸发系数为0.01,最大迭代次数为150,信息素增加强度系数为100;本文IPSO算法:最大迭代次数取150,粒子群规模为50,c1, ini取2.5,c1, fin取0.5,c2, ini取0.5,c2, fin取2.5,wmax取0.9,wmin取0.3,Monte Carlo仿真次数200次。雷达威胁指标权重均取1/4。干扰机8部,雷达6部。雷达仿真参数如表 1所示。干扰机参数设置如表 2所示。
表 1 雷达仿真参数 Table 1 Radar parameters for simulation
| 编号 | 速度/ Ma | 距离/ km | 载频/ GHz | 脉宽/ μs | 俯仰角/ (°) | 方位角/ (°) | 频率宽度/ GHz |
| 1 | 2.1 | 55 | 14 | 0.5 | 3.8 | 0.5 | 2.1 |
| 2 | 1.7 | 109 | 11 | 1.5 | 0.5 | 25 | 2.6 |
| 3 | 1.3 | 155 | 1.9 | 0.7 | 15 | -18 | 0.1 |
| 4 | 1.5 | 136 | 3.5 | 5 | 20.5 | 18.5 | 0.7 |
| 5 | 0.9 | 164 | 13 | 0.8 | 15.8 | 32 | 2.1 |
| 6 | 0.8 | 180 | 3.5 | 2.1 | -25.8 | -40 | 1.1 |
表选项
表 2 干扰机仿真参数 Table 2 Jamming system parameters for simulation
| 编号 | 俯仰角/(°) | 方位角/(°) | 中心频率/GHz | 频率宽度/GHz | |||
| 波束中心 | 波束宽度 | 波束中心 | 波束宽度 | ||||
| 1 | 3.1 | 2 | 3.5 | 1.1 | 10.8 | 2.1 | |
| 2 | 0.1 | 0.2 | 0.9 | 0.1 | 9.3 | 1.7 | |
| 3 | 14.7 | 3.8 | 14.3 | 2 | 1.1 | 0.2 | |
| 4 | 19.4 | 5.1 | 20 | 3.1 | 2.5 | 0.4 | |
| 5 | 16.3 | 2.4 | 36 | 5.2 | 10 | 2.1 | |
| 6 | -27 | 3.2 | -42 | 1.8 | 3.3 | 1.1 | |
| 7 | 15.3 | 2.9 | -37 | 2.4 | 11.1 | 2.3 | |
| 8 | 1.8 | 0.7 | 23 | 4 | 3.2 | 1.1 | |
表选项
8部干扰机对6部雷达的合适度如下:
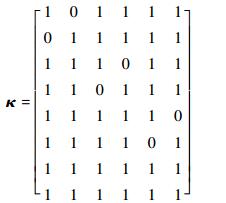 | (19) |
从最优解正确率和实时性2个方面衡量本文算法(IPSO)性能,与模拟退火算法(SAA)、蚁群算法(ACA)对比。仿真结果分别如图 4和图 5所示。
 |
| 图 4 最优解正确率对比 Fig. 4 Comparison of accuracy of best solution |
| 图选项 |
 |
| 图 5 运算时间对比 Fig. 5 Comparison of computation time |
| 图选项 |
由图 4和图 5可知,在同样迭代次数下,本文的优化算法可以达到的最优解正确率水平要优于模拟退火算法、蚁群算法以及PSO算法,且没有奇异值;在运算时间方面,本文算法也具有更好的实时性。因此综合来看,本文提出的IPSO算法在求解最佳干扰资源分配决策时性能更优。
由图 6可知,IPSO算法达到最优解的速度最快,在迭代次数为150次时达到最优解,之后增大迭代次数其最优解也保持稳定。相较于模拟退火算法的185次和蚁群算法的170次有了提高。
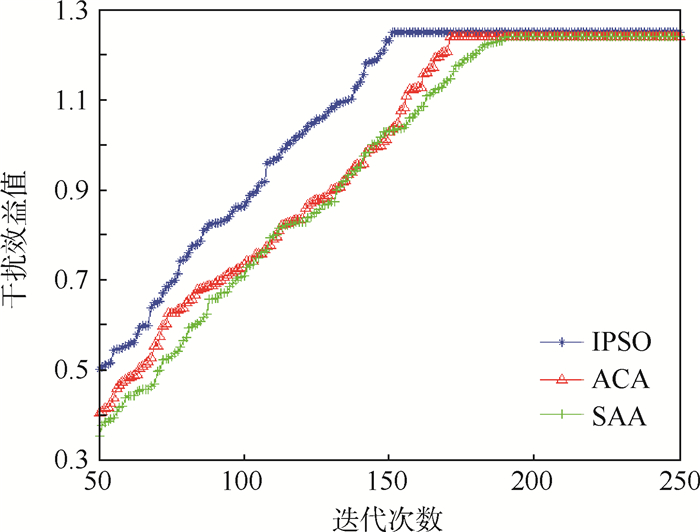 |
| 图 6 干扰增益值变化情况 Fig. 6 Jamming benefit changing situation |
| 图选项 |
6 结论 本文针对复杂战场态势,在结合IFS和IPSO基本原理的基础上,提出一种干扰资源分配方法。
1) 以IFS对敌方雷达威胁系数进行评估、己方干扰系统与敌方雷达系统匹配度为基础,定义目标函数,充分考虑了敌方雷达的危险程度,以及己方配备装备的情况,有利于实施合理的干扰资源分配方法。
2) 与传统模拟退火算法、蚁群算法进行对比,本文算法的最优解正确率最高,达到了96.9%,相较于模拟退火算法和蚁群算法分别提高了0.04%和0.07%;在运算时间方面,本文算法的平均耗时最少,为0.95 s,相较于模拟退火算法和蚁群算法分别提高了0.03%和0.04%。且本文算法在多次实验中变现稳定,没有出现奇异值。
3) 本文算法达到最优解需要150次迭代,优于模拟退火算法和蚁群算法的185次和170次,说明本文算法具有较好的收敛性。
为使本文方法更加合理,可以扩充对敌方雷达的指标分析,在雷达指标的权重确定上作更加科学的处理。
参考文献
| [1] | 宋海方, 吴华, 程嗣怡, 等. 多波束干扰系统干扰资源综合管理算法[J].兵工学报, 2013, 34(3): 332–338. SONG H F, WU H, CHEN S Y, et al. Integrated management algorithm of jamming resources in multi-beam jamming systems[J].Acta Armamentarii, 2013, 34(3): 332–338.(in Chinese) |
| [2] | 李先茂, 董天临, 黄高明. 基于零和竞争理论的雷达干扰功率分配方法[J].四川大学学报(工程科学版), 2016, 48(3): 129–135. LI X M, DONG T L, HUANG G M. Distribution method of jamming power to radar net based on two-person zero-sum game[J].Journal of Sichuan University(Engineering Science Edition), 2016, 48(3): 129–135.(in Chinese) |
| [3] | 万开方, 高晓光, 刘宇. 基于变效能因子的Lanchester协同干扰最优功率分配[J].系统工程与电子技术, 2011, 33(7): 1544–1548. WAN K F, GAO X G, LIU Y. Optimal power partitioning for cooperative electronic jamming based on Lanchester with variable efficiency factors[J].Systems Engineering and Electronics, 2011, 33(7): 1544–1548.(in Chinese) |
| [4] | 刘以安, 倪天权, 张秀辉, 等. 模拟退火算法在雷达干扰资源优化分配中的应用[J].系统工程与电子技术, 2009, 31(8): 1914–1917. LIU Y A, NI T Q, ZHANG X H, et al. Application of simulated annealing algorithm in optimizing allocation of radar jamming resources[J].Systems Engineering and Electronic, 2009, 31(8): 1914–1917.(in Chinese) |
| [5] | 吕永胜, 王树宗, 王向伟, 等. 基于贴近度的雷达干扰资源分配策略研究[J].系统工程与电子技术, 2005, 27(11): 1893–1894. LU Y S, WANG S Z, WANG X W, et al. Study on the allocation tactics for radar jamming resources based on close degree[J].Systems Engineering and Electronic, 2005, 27(11): 1893–1894.DOI:10.3321/j.issn:1001-506X.2005.11.022(in Chinese) |
| [6] | 高晓光, 胡明, 郑景嵩. 突防任务中的单机对多目标干扰决策[J].系统工程与电子技术, 2010, 32(6): 1239–1243. GAO X G, HU M, ZHENG J S. Jaming strategy for single plane to multi-target of penetration[J].Systems Engineering and Electronic, 2010, 32(6): 1239–1243.(in Chinese) |
| [7] | 沈阳, 陈永光, 张秀辉, 等. 基于0-1规划的雷达干扰资源分配研究[J].兵工学报, 2007, 28(5): 528–532. SHEN Y, CHEN Y G, ZHANG X H, et al. Research on optimal distribution of radar jamming resource based on zero-one programming[J].Acta Armamentarii, 2007, 28(5): 528–532.(in Chinese) |
| [8] | ZHANG H D, XIONG L L, MA W Y. Generalized intuitionistic fuzzy soft rough set and its application in decision making[J].Journal of Computational Analysis and Applications, 2016, 20(4): 750–766. |
| [9] | SAHIN R. Fuzzy multicriteria decision making method based on the improved accuracy function for interval-valued intuitionistic fuzzy sets[J].Soft Computing, 2016, 20(7): 2557–2563.DOI:10.1007/s00500-015-1657-x |
| [10] | JAIN A, PARDASANI K R. Fuzzy soft set model for mining amino acid associations in peptide sequences of mycobacterium tuberculosis complex(MTBC)[J].Journal of Intelligent & Fuzzy Systems, 2016, 31(1): 259–273. |
| [11] | AGARWAL M, BISWAS K K, HANMANDLU M. Generalized intuitionistic fuzzy soft sets with applications in decision-making[J].Applied Soft Computing, 2013, 13(8): 3552–3566.DOI:10.1016/j.asoc.2013.03.015 |
| [12] | FU X, LI A Q, WANG L P, et al. Short-term scheduling of cascade reservoirs using an immune algorithm-based particle swarm optimization[J].Computers & Mathematics with Applications, 2011, 62(6): 2463–2471. |
| [13] | CHE Z H. A particle swarm optimization algorithm for solving unbalanced supply chain planning problems[J].Applied Soft Computing, 2012, 12(5): 1279–1287. |
| [14] | ZHOU X C, ZHAO Z X, ZHOU K J, et al. Remanufacturing closed-loop supply chain network design based on genetic particle swarm optimization algorithm[J].Journal of Central South University of Technology, 2012, 19(2): 482–487.DOI:10.1007/s11771-012-1029-y |
| [15] | NEDJAH N, CALAZAN R D, MOURELLE L D, et al. Parallel implementtions of the cooperative particle swarm optimization on many-core and multi-core architectures[J].International Journal of Parallel Programming, 2016, 44(6): 1173–1199.DOI:10.1007/s10766-015-0368-3 |
