齿轮传动系统在可靠度意义上可视为串联系统，系统中任意轮齿疲劳失效则系统失效。齿轮传动系统作为设备中造价昂贵的关键部件，其疲劳可靠度评估十分重要。
目前，科研人员针对齿轮传动系统可靠度评估问题进行了许多研究，研究方法有通过对产品寿命直接分析，通过状态监测手段评估，以及基于应力-强度干涉模型的评估方法。
通过对产品寿命直接分析^[1]得到寿命分布，通过寿命分布预测可靠度。该方法适用于已经投入使用的齿轮产品，可以更全面地体现环境随机性和复杂性。但是对处于设计、研发或只有少量生产的产品，往往难以获得足够的失效数据。
通过状态监测手段评估系统可靠度。例如对齿轮箱润滑油的监测以及振动情况的监测^[2-3]，在线监测信号可以很好地反映当前系统的磨损状态，但齿轮属于无初始裂纹零件，其疲劳失效具有突然性，多数疲劳失效在破坏前并不能发出异常信号。
基于应力-强度干涉模型^[4]评估系统可靠度。Dong等^[5]基于裂纹扩展理论研究了齿轮轮齿的齿面接触疲劳寿命。Place等^[4]以扩展的应力-强度干涉模型研究了直升机齿轮箱系统的可靠度，并以2个零件的串联系统为例，通过多元累积分布函数的轮廓线方法计算了考虑失效相关的系统可靠度。Nejad等^[6]以经验公式方法计算了风力发电机齿轮箱内各轮齿对输入轴扭矩的应力响应，并使用线性累积损伤方法计算了随机载荷下各轮齿的寿命。笔者团队^[7]运用全概率思想建立了考虑失效相关的风力发电机齿轮箱串联系统可靠度函数。此外，经典的结构可靠度评估方法^[8-10]和较新的系统可靠度评估方法^[11-13]都是在应力-强度干涉模型的基础上的不同扩展。然而齿轮系统存在多部件，多失效模式且失效相关，同时具有变构特性，现有的基于应力-强度干涉模型的可靠度评估方法^[4-13]尚未完全考虑影响可靠度的因素(失效相关、系统变构特性)。
针对上述问题，本文提出系统PSN曲线的思想，在此基础上通过蒙特卡罗仿真方法建立齿轮串联系统的寿命评估模型，以提高仿真效率且兼顾齿轮传动系统共因失效。
1 齿轮箱结构及零件PSN曲线 1.1 齿轮箱结构 齿轮系统结构选用750 kW级风力发电机常用增速齿轮箱，该齿轮箱由一级行星轮系与两级固定轴斜齿轮齿轮副组成，如图 1所示。

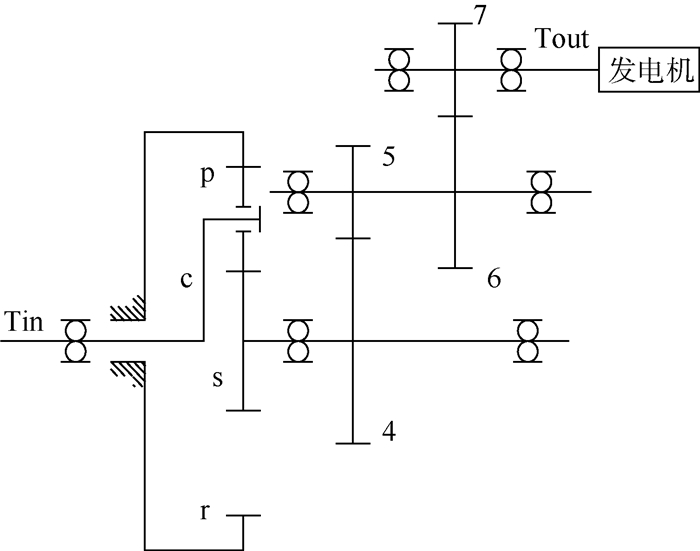图 1 齿轮箱传动原理图 Fig. 1 Schematic of gearbox transmission

图选项

图 1中Tin为输入轴，r为固定的内齿圈，s为太阳轮，c为行星架，p为行星轮，4、5为互相啮合的中速级斜齿轮，6、7为互相啮合的高速级斜齿轮，Tout为输出轴。
由文献[14]获知风力发电机常用齿轮箱各齿轮轮齿几何参数如表 1所示。
表 1 齿轮箱零件参数 Table 1 Gearbox component parameters

参数	太阳轮	行星轮	内齿圈	齿轮4	齿轮5	齿轮6	齿轮7
Z	21	38	99	84	23	92	24
Mn	10	10	10	8	8	5	5
αn/(°)	20	20	20	20	20	20	20
β/(°)	7.5	7.5	7.5	14	14	14	14
αt′/(°)	22.6	22.6	22.6	21.5	21.5	21.5	21.5

表选项






表 1中Z为齿数，M_n为齿轮模数，α_n为齿轮法向压力角，β为齿轮螺旋角，α_t′为端面压力角。
根据齿轮传动系统结构和各齿轮轮齿参数，按照机械设计手册中斜齿轮齿根强度校核相关理论，计算各轮齿所受尺面接触应力σ_H与输入轴扭矩关系如表 2所示。表中，K_A为使用系数，K_V为动载系数；K_Hβ为纵向载荷分布系数；K_Hα为横向载荷分布系数；T_in为输入轴扭矩。
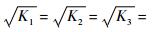
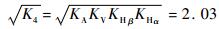
表 2 齿面接触应力 Table 2 Gear surface contact stress

啮合齿轮	太阳轮/行星轮	行星轮/内齿圈	齿轮1/齿轮2	齿轮3/齿轮4
σH/MPa	0.052 1	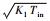0.022 5	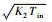0.030 9	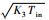0.031 6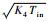

表选项






1.2 零件PSN曲线 文献[15]中PSN曲线不包含寿命在10⁴~10⁷循环之外的寿命所对应的载荷，因此大载荷造成的损伤不能根据该曲线定量。近些年超高周疲劳研究发现很多小的载荷仍能对材料造成损伤，且大、小载荷均会出现在随机载荷历程中。因此，本文在文献[15]的基础上重新构建了零件PSN曲线。零件在恒幅循环载荷下的寿命服从对数正态分布^[15]，其对数寿命中值PSN曲线为μ(s)=ln(c)+m·ln(s), 其中c=5.632 2×10³¹, m=－8.451 7，c和m为参数。本文将不同应力下的对数寿命的标准差σ均设为其对数寿命均值的3.5%，即σ(s)=0.035μ(s)。通过计算多级恒幅载荷下相同失效概率对应的寿命值，然后拟合应力与寿命值关系，得到该失效概率下的零件PSN曲线如图 2所示。

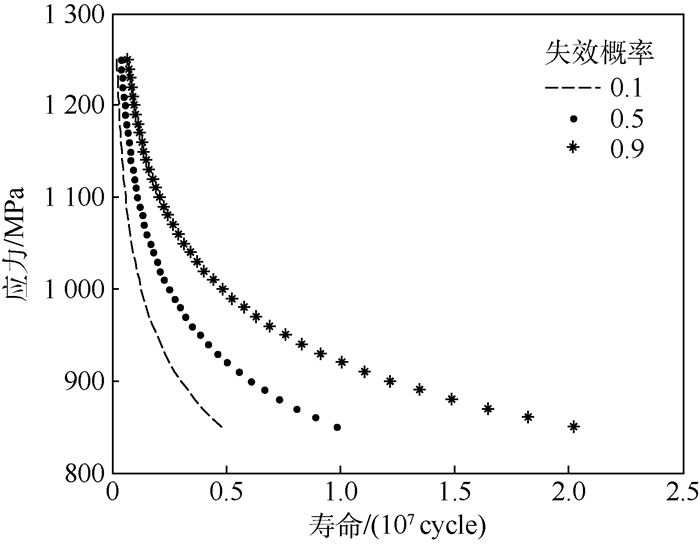图 2 零件PSN曲线 Fig. 2 PSN curves of components

图选项

经过比较，该曲线在寿命10⁴~10⁷cycle部分接近文献[15]的曲线, 其中cycle为循环次数。
2 系统寿命评估的蒙特卡罗仿真 蒙特卡罗仿真计算寿命的关键是零件所受载荷的抽样是否正确，零件疲劳性能的抽样是否合理，以及零件受载后的损伤计算。假设零件所受载荷为假设零件所受载荷为服从某种分布的随机变量，当载荷作用一次时，即从分布中随机抽取一个载荷值。零件的疲劳性能抽样是靠对零件的PSN曲线的随机生成实现的：首先对1 000 MPa恒幅应力下的寿命进行随机抽样得到一个寿命样本，然后计算该寿命样本对应的累积概率P₁(P₁为第1次失效概率P的计算样本值)，则P₁所对应的PSN曲线抽样完为常数c₁和m₁，s为确定性应力，N_s为确定性寿命变量：

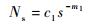(1)

当第i次载荷作用时，产生确定的应力，该载荷产生的损伤1/N_s(s_i)为确定值，即1/(c₁s_i^-m₁)。在多次载荷作用后，应用线性累积损伤法则计算总的轮齿损伤，当任意轮齿的损伤大于1时，系统失效。
每个轮齿都相当于串联系统的一个零件，表 1显示该系统共有457个零件。齿轮系统每次啮合时都有若干轮齿参与啮合，而参与啮合的轮齿所受应力均来源于相同的外部输入载荷——输入轴扭矩，参与啮合的轮齿损伤为共因损伤。齿轮系统每次啮合时参与啮合的轮齿不同，所以从抵抗疲劳载荷的能力上看，齿轮系统是时变的。本文编制蒙特卡罗数值仿真流程(见图 3)计算齿轮传动系统可靠度。

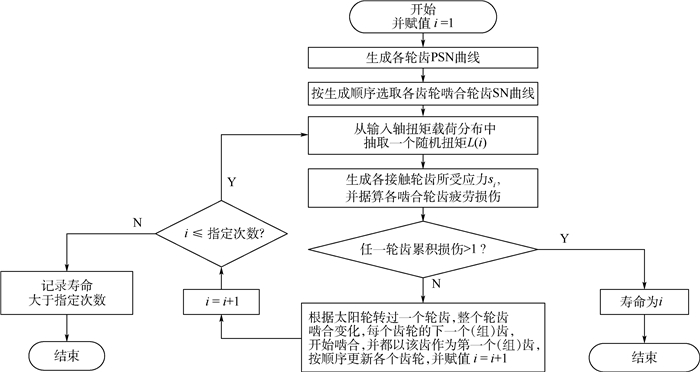图 3 齿轮传动系统可靠度仿真流程 Fig. 3 Gear transmission system reliability simulation process

图选项

假设输入轴扭矩载荷为随机变量且服从威布尔分布W(1.25×10⁸, 1.63)，50次仿真得到50个系统寿命数据，以对数正态分布对寿命数据进行拟合，得到对数正态分布参数为(11.485 7, 0.348 0)，其统计分布如图 4所示。

图 4 基于零件PSN，随机载荷下齿轮系统寿命概率分布 Fig. 4 Gear system life probability distribution under random load based on component PSN

图选项

使用MATLAB拟合优度KS检验模块进行假设检验，检验统计量的观测值ksstat为0.062 8。由于ksstat小于1，证明在显著水平0.05下接受系统寿命服从参数为(11.485 7, 0.348 0)的对数正态分布的假设。
当串联系统寿命较短或受载次数较少时，仿真次数较少，上述方法是简单有效的。当设计寿命较长时(例如风力发电机齿轮箱中值设计寿命通常为20年)，例如90%可靠度下的寿命为1×10¹⁰次以上时，采用上述的直接的蒙特卡罗仿真方法需要耗费大量时间。
为此本文在串联系统寿命的直接仿真基础上，进行了提升效率的研究。定义系统的恒幅循环下的疲劳特性(串联系统PSN曲线)，这样就能够避免仿真时频繁使用多个零件的PSN曲线，从而达到把系统看成一个零件的目的，把复杂的系统问题变成简单的零件可靠度评估问题。
3 齿轮传动系统PSN曲线 将已经建立的蒙特卡罗特仿真程序中随机载荷变为指定的确定性载荷，用于计算系统在恒幅载荷下的寿命。本文系统PSN曲线为PSN曲线的扩展，其中的“S”不是应力而是扭矩，亦可以写为系统PTN曲线(T代表扭矩)，表示不同失效概率P下寿命N与扭矩S的函数关系。在确定性的3~4级扭矩或者更多级恒幅扭矩下，将得到的寿命进行统计分析，可以得到各恒幅扭矩下的寿命拟合分布，进而获得串联系统PSN曲线。
3.1 齿轮传动系统恒幅应力下寿命生成 根据国标GB/T 24176—2009^[16]所述，为获得材料的PSN曲线，一般选定3~5级应力，且每级应力不低于8个试样。
齿轮系统内部的不同轮齿受应力不同，而输入轴扭矩一致，所以针对齿轮串联系统的蒙特卡罗仿真实验设计为在输入轴扭矩为2×10⁸，3×10⁸，5×10⁸，6×10⁸ N·mm下，各做50次仿真实验，寿命计算结果如表 3所示。
表 3 各级恒幅扭矩下齿轮系统寿命统计及统计矩 Table 3 Gear system life andstatistics moment under various constant torque

输入轴扭矩/(108 N·mm)	寿命标准差/cycle	寿命均值/cycle
2	3.3×105	6.6×105
3	6.2×104	1.1×105
5	4.2×103	1.2×104
6	2.2×103	5.9×103

表选项






3.2 串联系统恒幅应力下寿命统计矩分析 将表 3中齿轮串联系统的寿命均值和标准差与输入轴扭矩的关系画成散点图，从散点图中可以看出寿命均值和标准差与载荷呈现幂函数规律，所以选用形式为y=ax^b的方程进行非线性回归，其散点图与回归曲线如图 5所示。

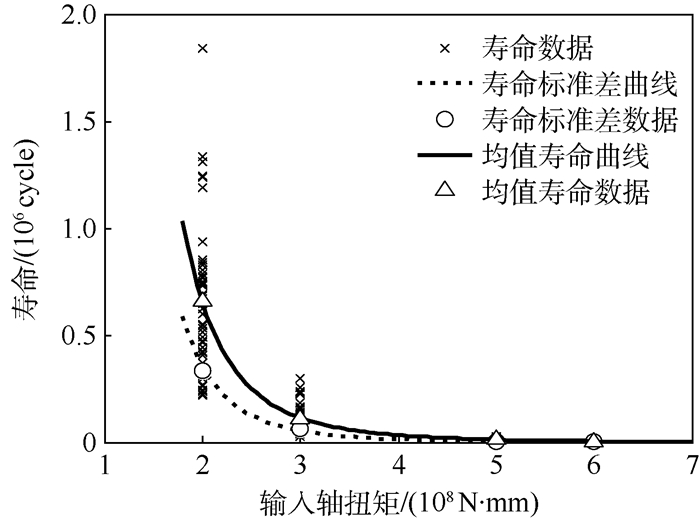图 5 各级恒幅扭矩下齿轮系统寿命及统计矩 Fig. 5 Gear system life and statistical moment under various constant torque

图选项

齿轮串联系统的恒幅输入轴扭矩下标准差与应力函数关系、寿命均值与输入轴扭矩函数关系分别为

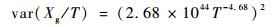(2)

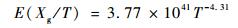(3)

式中：X_g为齿轮系统寿命随机变量；T为恒幅输入轴扭矩；var(X_g/T)为恒幅输入轴扭矩T下的寿命X_g的方差；E(X_g/T)为恒幅输入轴扭矩T下的寿命X_g的均值。
3.3 齿轮传动系统恒幅扭矩下寿命曲线 一般情况下，产品的寿命服从对数正态分布。本文按照对数正态分布对齿轮传动串联系统的恒幅载荷下的寿命进行分布拟合，拟合结果通过了对数正态分布的假设检验。多级输入轴扭矩下的经验分布与对数正态分布曲线如图 6所示。

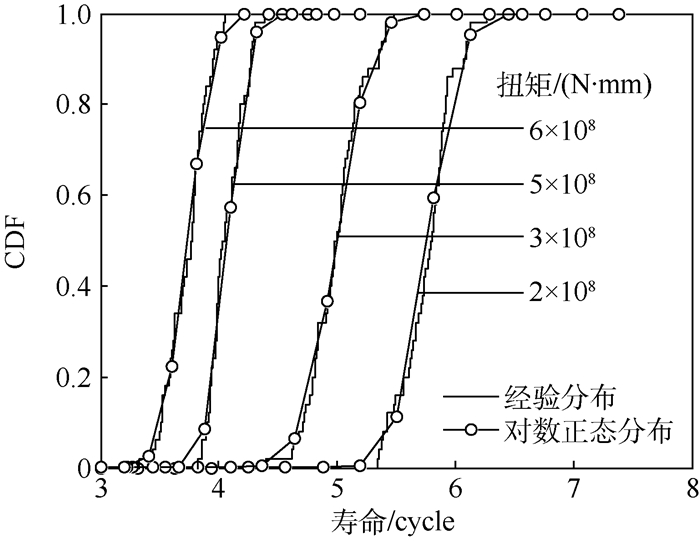图 6 齿轮系统各级扭矩下对数寿命分布正态拟合 Fig. 6 Normal fitting of gear system logarithmic life distribution under various torque

图选项

从图 6可以看出，齿轮串联系统在不同恒幅循环输入扭矩下的寿命的对数值的经验分布与取对数后的正态拟合分布之间的差异，可见齿轮系统拟合很好。
如果随机变量服从对数正态分布，则其概率密度函数可以表达如式(4)所示，且其分布参数μ和σ与随机变量的数学期望和方差满足式(5)和式(6)的函数关系。

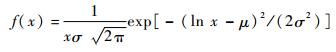(4)

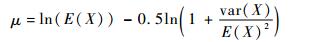(5)

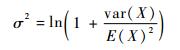(6)

结合式(2)~式(6)推导出齿轮串联系统恒幅扭矩下寿命分布参数与扭矩T的关系为

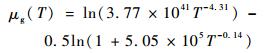(7)

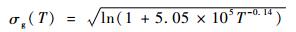(8)

由此可得任意恒幅载荷下链条系统的寿命分布。通过各级载荷下的相同寿命分位点对载荷关系的拟合可以得到系统PSN曲线，其拟合结果如图 7所示。

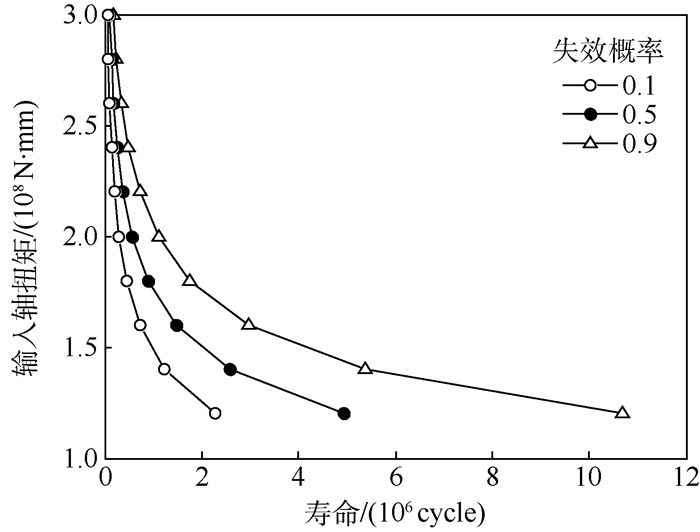图 7 齿轮系统PSN曲线 Fig. 7 Gear system PSN curves

图选项

4 系统寿命评估方法 以系统PSN曲线代表系统的疲劳性能进行蒙特卡罗仿真时，系统寿命计算就简化为从已知分布中抽取一个载荷，从PSN曲线中随机抽取一条SN曲线代表系统疲劳性能，基于该SN曲线，每抽取一个载荷，系统产生Miner累积损伤，当疲劳损伤之和为1时，系统破坏，此时的载荷抽样次数即为系统寿命。
通过上述方法，求得齿轮传动系统寿命服从对数正态分布，其分布参数为11.401 4和0.358 4。
对于变幅载荷下的零件疲劳寿命的计算，一个方便、可行的方法是根据疲劳累积损伤等效原则，把复杂变幅载荷历程转换为损伤等效的恒幅循环载荷^[17-18]，在工程中可以认为在该等效恒幅载荷下的寿命分布与变幅载荷下的寿命分布近似。以齿轮串联系统为例，在得到齿轮串联系统的PSN曲线之后，将该系统视为一个“零件”，进一步得到失效概率为0.5的中值PSN曲线为

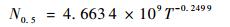(9)

基于该曲线，“零件”在任意载荷T一次作用下将产生损伤1/N_0.5(T)。当T服从某分布，密度函数为g(T)时，其作用一次产生损伤的期望为

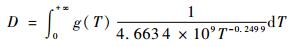(10)

由此可以计算出在该载荷分布下的平均寿命，该平均寿命对应于中值系统PSN曲线中的扭矩T即为等效载荷。通过该等效载荷求取“零件”恒幅寿命分布(见图 8)。

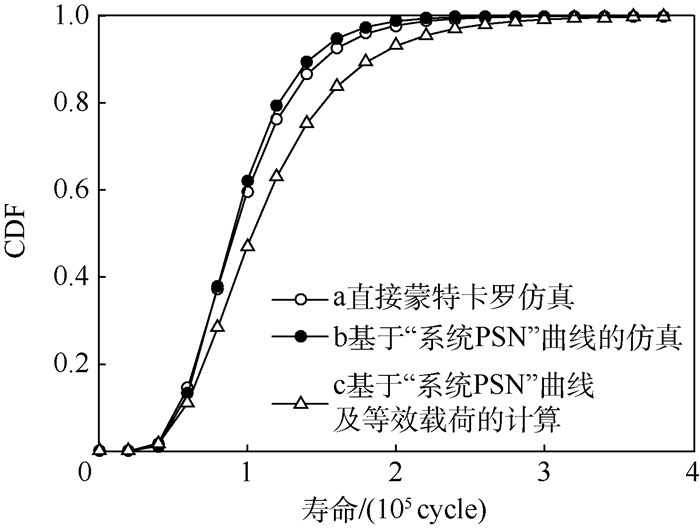图 8 齿轮串联系统寿命分布 Fig. 8 Life distribution of gear series system

图选项

从图 8中可以看出, 在3种方法下，无论是链条串联系统还是齿轮串联系统的寿命分布都很相近。而以效率来看，无疑基于“串联系统PSN”和等效载荷的模型最高，在针对设计寿命较长的系统时，可以通过在几级大载荷下获得其PSN曲线，将其等效为“零件”；而根据中值SN曲线可以很轻易的获得等效载荷，在等效载荷下求“零件”的寿命分布非常简单。
采用3种方法获得的寿命特征值及相对误差如表 4所示。
表 4 3种方法寿命特征值比较 Table 4 Comparison of characteristic life of three methods

方法	系统寿命均值/(104cycle)	系统寿命标准差/(104cycle)	以a为参照的均值相对误差/%	以a为参照的标准差相对误差/%
a	9.8	4.0	0	0
b	9.5	3.5	3.1	12.5
c	11	5.3	12.2	32.5

表选项






方法b寿命分布与方法a寿命分布的误差为引入系统PSN曲线代替复杂的齿轮系统结构所产生；方法c的寿命分布与方法a寿命分布的相对误差产生原因在于系统PSN曲线和等效载荷代替了随机载荷的双重误差。
从图 8和表 4中可以看出，基于系统PSN曲线的和随机载荷的方法可以大大降低结构复杂程度对计算效率的影响，且能保持一个数量级左右的精度。可见系统PSN曲线的概念对于复杂结构的共因失效可靠度评估有一定工程意义。
基于系统PSN及等效载荷的系统可靠度(寿命分布)计算以损失一定计算精度获得计算效率显著提升，尤其在高设计寿命产品评估中，直接仿真方法由于过低的运算效率没有实用价值，提升效率往往会带来精度的降低符合一般科学规律。基于系统PSN及等效载荷的计算方法效率不受系统结构大小和载荷分布的影响，对于长设计寿命和短设计寿命的可靠度评估都是一种稳定的工程计算方法。
5 结论 1) 根据寿命统计矩与载荷的函数关系，得到了寿命分布参数-载荷之间的幂函数回归方程，即在任意给定恒幅载荷下可以得到串联系统寿命的对数分布参数，通过对多级载荷下的寿命分布计算得到了系统PSN曲线。
2) 提出了基于系统PSN曲线和等效载荷的串联系统寿命评估方法。通过齿轮传动系统的3种寿命计算方法(在随机载荷下基于零件PSN曲线的直接仿真方法，在随机载荷下基于系统PSN的仿真方法，在等效载荷下基于系统PSN曲线的计算方法)的比较，证明了本文方法对齿轮传动系统寿命评估简单高效，具有普遍适用性。

参考文献

[1]	ASTRIDGE D G. Helicopter transmissions-design for safety and reliability[J].Proceedings of the Institution of Mechanical Engineers Part G:Journal of Aerospace Engineering, 1989, 203(27): 123–138.
[2]	SHENG S W, Investigation of oil conditioning, real-time monitoring and oil sample analysis for wind turbine gearboxes: NREL/PR-5000-50301[R]. Golden: National Renewable Energy Laboratory, 2011.
[3]	SHENG S, OYAGUE F, BUTTERFIELD S. Investigation of various wind turbine drive train condition monitoring techniques: NREL/CP-500-46160[R]. Golden: National Renewable Energy Laboratory, 2010.
[4]	PLACE C S, STRUTT J E, ALLSOPP K, et al. Reliability prediction of helicopter transmission systems using stress-strength interference with underlying damage accumulation[J].Quality & Reliability Engineering International, 1999, 15(2): 69–78.
[5]	DONG W, XING Y, MOAN T, et al. Time domain-based gear contact fatigue analysis of a wind turbine drivetrain under dynamic conditions[J].International Journal of Fatigue, 2013, 48(1): 133–146.
[6]	NEJAD A R, GAO Z, MOAN T. On long-term fatigue damage and reliability analysis of gears under wind loads in offshore wind turbine drivetrains[J].International Journal of Fatigue, 2014, 61(2): 116–128.
[7]	谢里阳, 周金宇, 李翠玲, 等. 系统共因失效分析及其概率预测的离散化建模方法[J].机械工程学报, 2006, 42(1): 62–68. XIE L Y, ZHOU J Y, LI C L. Common cause failure analysis and discretely modeling for system probability prediction[J].Journal of Mechanical Engineering, 2006, 42(1): 62–68.(in Chinese)
[8]	DITLEVSEN O, MADSEN H O. Structural reliability methods[M].New York: John Wiley & Sons, 1996.
[9]	ZHAO Y G, ONO T. Moment method for structural reliability[J].Structural Safety, 2001, 23(6): 47–75.
[10]	NAESS A, LEIRA B J, BATSEVYCH O. Reliability analysis of large structural systems[J].Probabilistic Engineering Mechanics, 2012, 28(3): 164–168.
[11]	XIE L Y, ZHOU J Y, HAO C Z. System-level load-strength interference based reliability modeling of k-out-of-n system[J].Reliability Engineering & System Safety, 2004, 84(3): 311–317.
[12]	谢里阳, 王正. 随机恒幅循环载荷疲劳可靠度异量纲干涉模型[J].机械工程学报, 2008, 44(1): 1–6. XIE L Y, WANG Z. Dissimilar-dimension interference model of fatigue reliability under uncertain cyclic load[J].Journal of Mechanical Engineering, 2008, 44(1): 1–6.(in Chinese)
[13]	谢里阳, 刘建中, 吴宁祥, 等. 风电装备传动系统及零部件疲劳可靠度评估方法[J].机械工程学报, 2014, 50(11): 1–8. XIE L Y, LIU J Z, WU N X. Fatigue reliability evaluation method for gear component and system of wind turbine[J].Journal of Mechanical Engineering, 2014, 50(11): 1–8.(in Chinese)
[14]	OYAGUE F. Gearbox reliability collaborative (GRC) description and loading: NREL/TP-5000-47773[R]. Golden: Office of Scientific & Technical Information, 2011: 9.
[15]	朱孝录. 调质钢齿轮接触疲劳强度可靠度试验研究[J].齿轮, 1983, 7(3): 1–9. ZHU X L. The study of quenched and tempered steel gear contact fatigue strength reliability tests[J].Gear, 1983, 7(3): 1–9.(in Chinese)
[16]	中华人民共和国国家质量监督检验总局. 金属材料疲劳试验数据统计方案与分析方法: GB/T 24176-2009[S]. 北京: 中国标准出版社, 2009. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Metalic materials-fatigue testing-statistical planning and analysis of data: GB/T 24176-2009[S]. Beijing: Standards Press of China, 2009(in Chinese).
[17]	GARDNER E D. Reliability of components subject to cumulative fatigue[D]. Arizona: University of Arizona, 1971: 35-45.
[18]	CHEN D. New approaches to the estimation of cumulative fatigue reliability[J].Reliability Engineering and System Safety, 1991, 33(2): 231–247.DOI:10.1016/0951-8320(91)90061-B