EHA本质上是一种泵控的静液传动系统,采用旋转电机驱动柱塞泵,然后由柱塞泵输出的流体介质来推动作动筒[8]。EHA的变量控制方式有3种:变转速电机+定排量泵、定转速电机+变排量泵和变转速电机+变排量泵方案[9-11]。由于变排量泵的结构复杂,并且双变量控制难度高,因此目前一般不采用双变量控制结构。变转速电机+定排量泵的配置是主流的EHA方案,通过控制电机的旋转速度和方向来控制泵的输出流量大小和吸排油方向,从而控制液压作动筒的输出位移。对于变转速控制的EHA,受电机的驱动力矩和旋转部件的惯量比的限制,目前研制成功的EHA动态特性不如电液伺服作动器[12-14]。
针对小功率驱动场合,Anderson和Lindler[15]面向无人机舵面的作动需求开发了功能材料驱动的固液复合作动器,具有结构简单、体积小的优势。这种功能材料驱动的固液复合作动器的设计核心在于开发新原理的直线泵[16],现有单向阀配流的直线泵[17-19]及完全主动配流的直线泵[20]。由于功能材料的变形率低,上述采用功能材料驱动的直线泵输出流量小,因此以其构成的固液复合作动器输出功率偏小,并且输出速度低。
针对旋转电机+柱塞泵驱动EHA的动态特性问题和功能材料驱动固液复合作动器的功率不足问题,文献[21]提出了一种基于直线驱动及互配流原理的新型EHA,简称直线驱动电静液作动器(Linear-driven Electro-Hdrostatic Actuator, LEHA),LEHA的核心创新点在于提出了一种具有多个单元的主动配流直线泵原理,采用直线电磁元件直接驱动直线泵的吸排油和配流部件,构成EHA。
文献[21]主要给出了直线泵的配流机理的证明,给出了直线泵的多单元拓扑连接方式,说明了协同配流直线泵相对于单向阀配流直线泵具有的优势。LEHA是一种具有新原理的电静液作动器,还没有形成完善的设计方法,本文将研究LEHA的参数设计问题,给出LEHA中关键参数的匹配设计约束规则。
1 直线驱动电静液作动器原理 LEHA与传统EHA的主要区别在于其所采用的直线驱动方式,LEHA利用直线振荡电机驱动直线泵的吸排油和配流部件,在直线泵的输出口得到稳定的流量,进而驱动液压作动筒以构成静液传动作动器,其原理如图 1所示,图中:xc为作动筒位移;Q1和Q2分别为流入2个容腔的流量;p1和p2分别为2个容腔的压力;Fl为负载力。
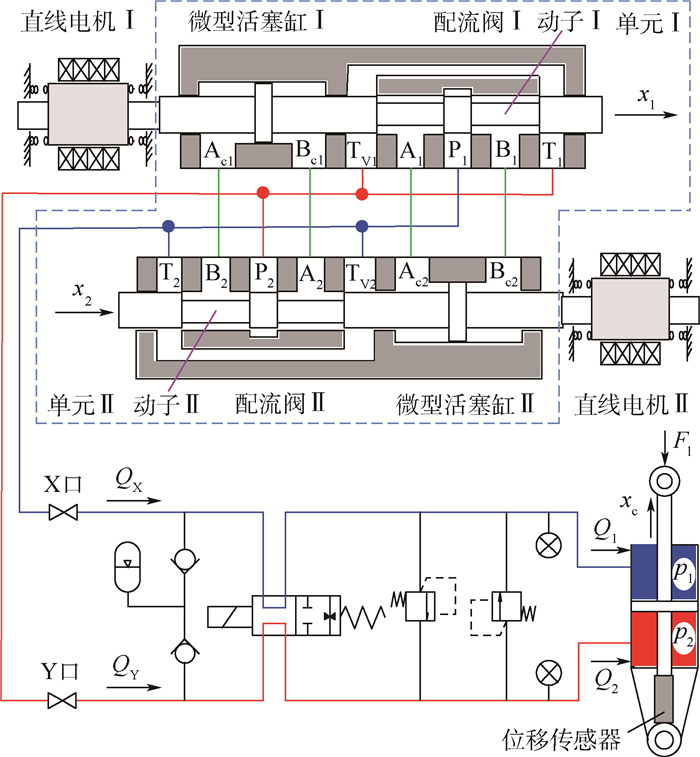 |
| 图 1 LEHA原理 Fig. 1 Schematic of LEHA |
| 图选项 |
LEHA中的直线泵具有2个相似的单元,一个单元包含一个微型活塞缸和一个三位四通配流阀,微型液压缸的活塞与滑阀阀芯在结构上整合为一个轴状零件,微型液压缸的两腔分别与另一个单元配流阀的A口及B口相连、一个单元配流阀的P口与另一个单元配流阀的TV口相连。根据上述油路连接规则,可以看出直线泵的单元之间具有协同配流的特征,即一个单元的吸排油部件产生的流量由另一个单元的滑阀进行配流,因此该直线泵定义为协同配流直线泵。
为描述直线泵的几何流量,定义符号函数
 | (1) |
对于图 1所示的由2个单元构成的直线泵,不考虑油液的压缩性、泵的泄漏等因素,其输出流量与2个单元的位移x1、x2的关系,即直线泵的几何流量为[21]
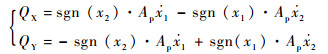 | (2) |
式中:QX为直线泵X口的输出流量;QY为直线泵Y口的输出流量;Ap为直线泵的吸排油活塞面积;
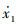
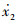
可以看出,在交互配流原理的作用下,一个单元的阀芯位置决定了由另一个单元吸排油活塞运动速度产生的流量的方向。为讨论在正弦函数作用下的双单元直线泵几何流量,定义2个单元的运动函数为
 | (3) |
式中:φ为2个单元的相位差; ω为角频率;Sp为吸排油活塞振幅。
则2个单元的运动速度为
 | (4) |
将式(3)及式(4)代入式(2),得到直线泵的几何流量为
 | (5) |
对式(5)给出几何流量在时域上的表达式在一个周期T内进行积分,得到泵在一个运行周期内的排油体积为
 | (6) |
定义fm为2个单元的往复运动频率,则单位时间内的排油体积为
 | (7) |
从式(7)可以看出泵的排量与吸排油活塞面积和振幅成正比,与相位差有正弦运算的关系;要改变直线泵流量的方向,只能调节单元动子的相位差。
2 LEHA的指标需求和参数设计 LEHA作为一种高度集成的电静液作动器,其参数设计涉及到系统与外界交互作用的参数匹配问题,根据LEHA的系统性能指标条件得到其元部件的工作范围约束条件;同时也涉及到系统内部元部件之间的匹配问题,如直线电机输出力、振幅、频率和直线泵的吸排油活塞面积的匹配问题,定义其主要性能指标如表 1所示。
表 1 LEHA性能指标 Table 1 Performance parameter of LEHA
| 参数 | 符号 |
| 作动器最大空载速度 | vact-max |
| 作动器最大静态输出力 | Fact-max |
| 作动器最大角功率 | Pact-max |
| -3 dB, -90°频宽 | fband |
| 系统最高压力 | pmax |
表选项
根据LEHA的原理图可以得到LEHA的主要设计参数包括直线电机的输出力、振幅和谐振频率,还包括直线泵的吸排油活塞面积,以及作动筒的活塞面积和行程,定义LEHA中需要设计的参数如表 2所示。
表 2 LEHA的关键参数 Table 2 Key parameters of LEHA
| 参数 | 符号 |
| 直线泵吸排油活塞面积 | Ap |
| 吸排油活塞振幅 | Sp |
| 直线电机振荡频率 | fm |
| 直线电机最大电磁力 | Fe-max |
| 作动筒活塞面积 | Acyl |
| 作动筒行程 | Scyl |
表选项
3 LEHA的参数匹配设计规则 LEHA的设计规则推导过程为:首先分析静态指标匹配设计问题,然后根据系统模型分析系统各参数对频宽的影响,得到LEHA的动态性能匹配设计规则,最后从系统功率的充足性和匹配性上讨论负载带来的设计约束条件。
3.1 静态指标设计规则
3.1.1 最大空载速度约束条件 考虑到相位差不理想带来的影响,直线泵在单位时间内的排油体积如式(7)所述。实际上由于间隙的存在,直线泵还必然存在一定的泄漏,将直线泵本身的内泄漏利用直线泵的容积效率ηp来表示,则可以定义直线泵的平均流量为
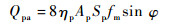 | (8) |
对于作动筒而言,若不考虑其外泄漏和两腔之间的内泄漏,则作动筒速度vcyl与直线泵平均流量之间的关系为
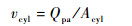 | (9) |
实际上对于作动筒内泄漏的建模,部分文献将其内泄漏流量Qleak简单建模为
 | (10) |
式中:Cleak为泄漏系数;Δp为两腔压差。
定义作动筒的容积效率为ηc,则有
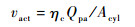 | (11) |
式中:vact为作动筒速度。
则作动筒最大空载速度为
 | (12) |
式(12)给出了LEHA的速度约束条件,即根据作动器最大空载速度得到Ap、Sp、fm和Acyl之间的约束关系。定义式(12)为LEHA参数设计的第1项约束条件。
3.1.2 系统最高压力约束条件 直线泵的出口压力与负载大小和直线泵本身的能力有关,在此只考虑负载充足的情况,即只考虑电机和泵组合系统的指标对直线泵输出压力的影响。直线电机的最大电磁力为Fe-max,若按照直线泵输出压力与电机输出力静态对应的关系,系统最高压力为
 | (13) |
实际上由于直线泵的主动配流作用,直线电机的位置闭环控制效果会影响直线泵的输出性能,因此从一个周期内能量转换的角度来分析系统压力与设计变量的关系。考虑[0, T]时间段的工作周期,若2个直线电机的振荡波形为三角函数曲线,定义电机位移为
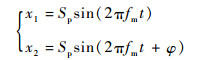 | (14) |
则电机速度为
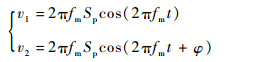 | (15) |
假设电机始终工作在第一象限,即电磁力与动子速度始终同方向,则2个电机在一个周期内输出的机械能为
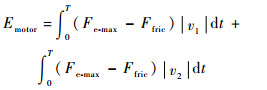 | (16) |
将摩擦力Ffric的影响转换为效率ηm来考虑,定义电机输出力
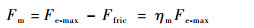 | (17) |
当相位差φ=π/2,结合式(14)~式(17),得到2个电机在一个周期内输出的机械能为
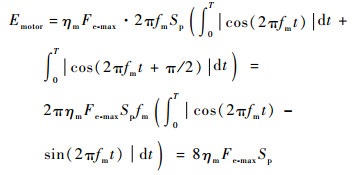 | (18) |
假设直线泵的输出压力为恒定值pmax,结合式(8),在一个周期内直线泵输出的液压能为
 | (19) |
当相位差φ=π/2,有
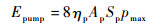 | (20) |
定义直线泵输出液压能量与输入机械能量Ep-in的关系为Epump=ηm-pEp-in,ηm-p为直线泵效率系数,因此得
 | (21) |
则系统最高压力pmax可以表达为
 | (22) |
式(22)给出了pmax与Fe-max和Ap的关系,可以看出直线泵的输出压力与电机驱动力、吸排油活塞面积与驱动及配流过程中的效率相关,效率系数受配合间隙、直线电机的位移控制效果影响。
定义系数Kη=ηm-pηm/ηp,显然根据物理意义可知其值域为[0, 1)。定义式(22)为LEHA参数设计的第2项约束条件。
3.1.3 最大静态输出力约束条件 得到了直线泵的输出压力与设计参数之间的约束表达式,然后考虑作动器的最大静态输出力Fact-max与设计参数之间的约束关系。在堵转情况下,作动筒输出力与系统最高压力的关系为
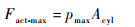 | (23) |
结合式(22),有
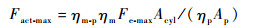 | (24) |
式(24)描述了作动器最大静态输出力对Fe-max、Ap和Acyl的设计约束条件,定义式(23)为LEHA参数设计的第3项约束条件。
3.2 动态性能匹配设计规则
3.2.1 LEHA的线性化模型 1) 直线振荡电机模型
根据电压平衡方程、电磁力与电流的关系和动子质量力平衡方程,直线振荡电机的模型为
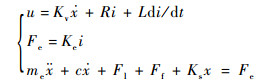 | (25) |
式中:Kv为电机的反电动势系数,由电机的几何结构及永磁体材料特性决定;R为线圈电阻;L为线圈电感;Ke为电机的力系数;me为电机动子质量;c为电机的黏性摩擦系数;Ff为除黏性摩擦力外的其他摩擦项;Ks为弹簧刚度系数;u为绕组电压;i为绕组电流;Fe为电磁力。
若不考虑除黏性摩擦力外的其他摩擦项,根据式(25)得到直线振荡电机输出位移xm关于控制变量u和干扰变量Fl的传递函数为
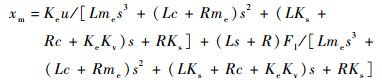 | (26) |
首先不考虑负载的作用,即令Fl=0,以电压u为输入,以位移xm为输出,得到电机的线性传递函数为
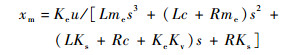 | (27) |
实际上,由于直线电机的电感为毫亨级,因此传递函数分母的三次项系数很小,可以将三阶系统简化为二阶系统,简化传递函数为
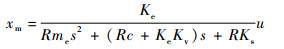 | (28) |
式(28)二阶系统的标准形式表达式为
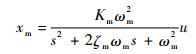 | (29) |
式中:自然角频率

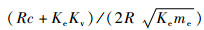
考虑实际的电机及其驱动系统模型,电机驱动器运行在电流模式,采用运算放大器搭建增益电路和积分电路来实现PI控制器,对电机进行流闭环控制,驱动器的输入指令为电压,电压指令到电流指令的增益为Kdr。
2) 液压作动筒模型
作动筒输出位移关于输入流量和负载力的传递函数为
 | (30) |
式中:β为油液弹性模量;Bcyl为作动筒黏性摩擦系数;Vt为两腔容积;Qcyl为作动筒油口流量;Flcyl为作动筒活塞杆所受负载力;mcyl为作动筒动子质量。
为分析设计参数对LEHA的频率特性影响,先不考虑负载力的影响,则有
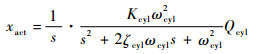 | (31) |
式中:自然角频率
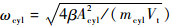
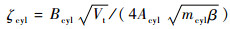
3) LEHA系统模型
对LEHA的控制框图而言,可以将直线泵简化描述为一个比例环节,其输入变量对输出变量的影响“瞬时”完成,不具有时延特性,实际上是将直线泵作为一项传动比环节。直线电机和作动筒的线性化模型都是三阶系统,输入变量对输出变量的影响需要经过储能环节的延迟作用。
综合直线电机的控制框图模型和作动筒的框图模型,并且将直线泵表示为变增益的比例环节,得到LEHA的控制框图模型如图 2所示。
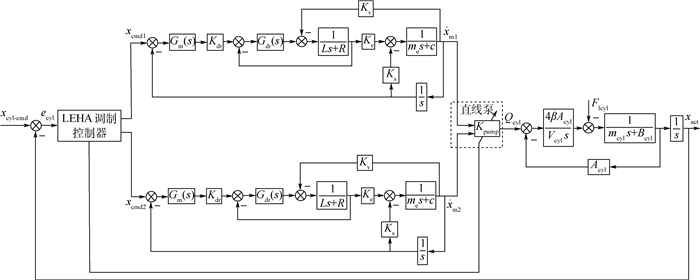 |
| 图 2 LEHA控制框图 Fig. 2 Control block diagram of LEHA |
| 图选项 |
3.2.2 LEHA频宽与调制频率的关系 为分析调制频率对LEHA频率特性的影响,统计不同频率的结果得到作动器在该调制频率时的频率特性;为了对比不同电机振荡频率时的作动器频宽,以作动器行程的5%作为正弦位移指令的幅值,仿真计算电机振荡频率为10 ~100 Hz时的作动器频率特性。对于给定的2 mm、5 Hz正弦位移指令,在调制频率为30、100 Hz时,LEHA的位移响应和直线电机位移响应分别如图 3和图 4所示。
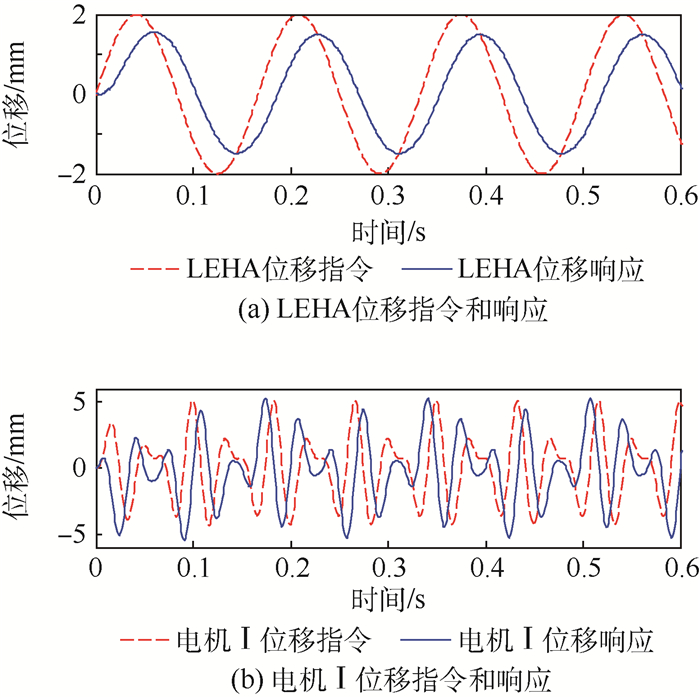 |
| 图 3 30 Hz调制频率的LEHA位移响应 Fig. 3 Displacement response of LEHA when modulation frequency is 30 Hz |
| 图选项 |
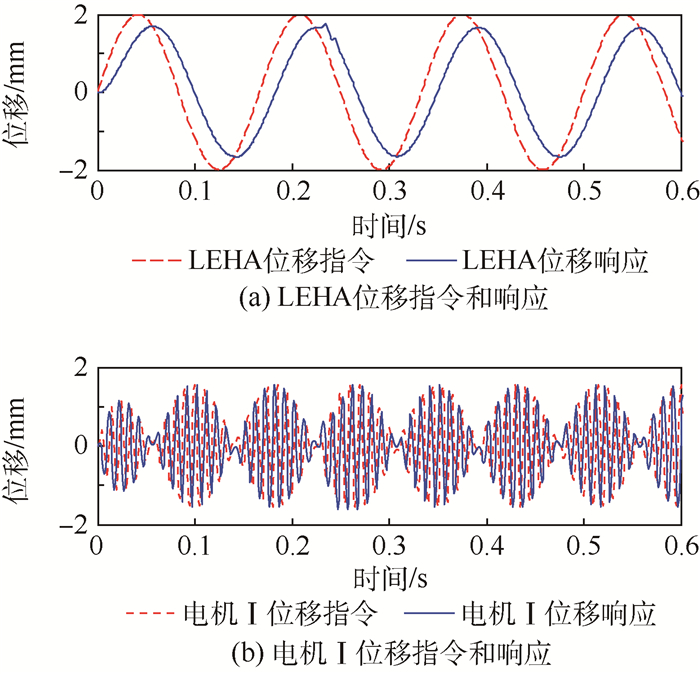 |
| 图 4 100 Hz调制频率的LEHA位移响应 Fig. 4 Displacement response of LEHA when modulation frequency is 100 Hz |
| 图选项 |
从图 3和图 4可以看出,调制频率越高,在一个作动器运动周期内直线泵的吸排油周期数越多,从图 4(b)可以看出电机振荡曲线的幅值包络线为正弦曲线,相邻周期的振幅变化小,振荡电机的调幅控制效果好。根据LEHA的调制工作原理,调制频率越高,直线泵的流量调节速度越快,作动器的输出调节速度越快,LEHA具有更好的位移响应特性。
统计在10~100 Hz调制频率范围内LEHA的-3 dB,-90°频宽,在不同调制频率下LEHA的频宽如图 5所示。可以看出调制频率越高,LEHA的频宽越高,但是增长速率随着调制频率的增加而下降(见图 5)。
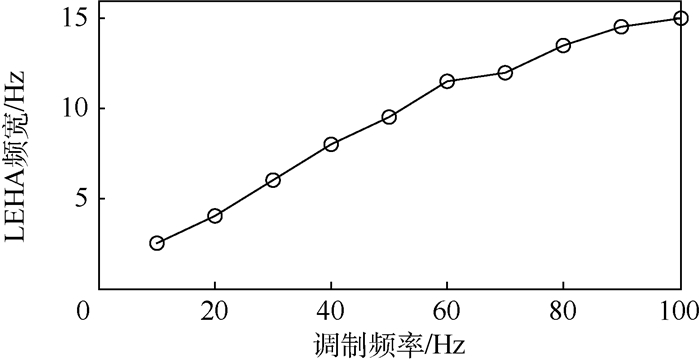 |
| 图 5 LEHA频宽与调制频率的关系 Fig. 5 Relationship between bandwidth of LEHA and modulation frequency |
| 图选项 |
3.2.3 动态性能设计规则 本节将在适度简化的基础上,分析LEHA中各项参数对系统动态性能的影响,得到基于LEHA的频宽性能需求的直线电机振荡频率约束条件。
在图 2所示的LEHA线性化框图模型中,直线泵被简化为变增益的比例环节,其作用是将直线电机的输出位移转换为泵的输出流量信号。由于泵内的容腔很小,因此不考虑油液的可压缩性,可以忽略油液弹性带来的直线泵模型中的时延特性,其对系统动态性能的影响在于增益系数会影响整个系统前向通道的增益,从而影响系统的响应特性。
对于LEHA而言,由于直线电机、作动筒等子系统的叠加作用,其频率特性比任何单独的子系统都差;因此要使得LEHA系统的频宽达到期望值fband,则直线电机和液压作动筒的固有频率都应该明显高于fband。引入增益系数Kfrep和Kfrec,因此有ωm≥Kfrepωband及ωcyl≥Kfrecωband。
 | (32) |
式中:油液弹性模量β的取值与油液空气溶解量密切相关,按工程经验可以取400 MPa。
实际上作动筒的液压固有频率一般很高,对于LEHA需求的10 Hz左右的频宽,液压固有频率不会成为限制作动器频宽的主要因素,因此式(32)只需要考虑直线电机的频率约束条件。
系数Kfrep实际上反映了LEHA频宽指标对直线电机振荡频率的最低要求,关于直线电机振荡频率对LEHA性能的影响,与电机的控制器效果密切相关,式(32)中参数Kfrep取值可以从图 5所给出的LEHA频宽与调制频率的关系中得到。结合式(32)和图 5可以得到LEHA频宽指标对直线电机振荡频率的约束条件,定义其为LEHA参数设计的第4项约束条件。
3.3 负载匹配设计规则 作动器作为一种驱动系统,会受到各种类型的负载,典型的负载包括:惯性负载、弹性负载和黏性阻尼负载等,或者以上典型负载的混合作用。作动器在驱动对象时,系统必须具有足够的功率,一般将负载力和负载速度的关系定义为负载特性,以负载力和负载速度为坐标所绘制的关系曲线称为负载轨迹。本节根据LEHA的角功率需求给出一项约束设计规程,然后针对惯性负载、弹性负载和黏性阻尼负载3种情况讨论LEHA的参数设计规则。
3.3.1 作动器最大角功率约束 根据一般舵机的设计规范,作动器的最大角功率定义为最大静态输出力与最大空载速度的积,即
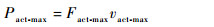 | (33) |
结合式(12)和式(24),有
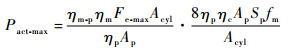 | (34) |
即
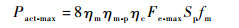 | (35) |
定义式(35)为LEHA参数设计的第5项约束条件。
3.3.2 惯性负载的参数设计约束 作动器驱动的对象惯量定义为mobj,则惯性负载力为
 | (36) |
讨论位移x为三角函数曲线的情况,即x=x0sin(ωlt),则负载轨迹方程为
 | (37) |
式(37)可以等效变形为椭圆方程
 | (38) |
作动器驱动上述惯性负载所需的功率为
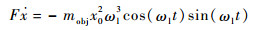 | (39) |
作动器实际的功率特性曲线应该由实验测得,然后根据负载匹配条件:功率特性曲线包络负载曲线,可以得到作动器参数的设计约束条件。但是在设计阶段,无法确定在F-v坐标下LEHA具体的输出功率特性曲线,但是其范围不会超过最大输出力和最大速度的乘积而得到的等功率曲线。根据式(35)得到LEHA角功率对应的等功率曲线为
 | (40) |
显然式(40)所定义的LEHA输出功率不小于式(39)定义的驱动惯性负载的需求功率,因此只需要求式(39)所定义函数的最大值。
定义θ=ωlt,函数f1(θ)=mobjx02ωl3cos θsin θ,则函数f1(θ)在定义域[0, 2π]内的最大值为
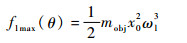 | (41) |
结合式(40)和式(41),得到LEHA对于式(36)所定义惯性负载的功率包络设计约束条件为
 | (42) |
3.3.3 弹性负载的参数设计约束 作动器驱动的弹性负载力为
 | (43) |
式中:K为负载弹性系数。
讨论位移x为三角函数曲线的情况,定义
 | (44) |
则负载方程为
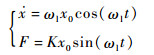 | (45) |
式(45)实质上是一个椭圆方程,等价变换为
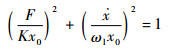 | (46) |
根据相切条件,等功率线方程为
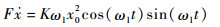 | (47) |
定义θ=ωlt,函数f2(θ)=Kωlx02cos θsin θ,则函数f2(θ)在定义域[0, 2π]内的最大值为
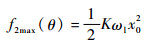 | (48) |
结合式(40)和式(48),得到LEHA对于弹性负载的功率包络设计约束条件为
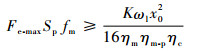 | (49) |
3.3.4 黏性阻尼负载的参数设计约束 黏性阻尼负载力为
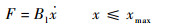 | (50) |
讨论位移x为三角函数曲线的情况,即
 | (51) |
则负载方程为
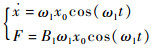 | (52) |
式中:Bl为阻尼系数。
在
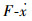
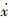
 | (53) |
因此LEHA对黏性阻尼负载的参数设计约束条件为
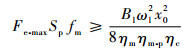 | (54) |
总结得到LEHA的6项参数设计约束条件如表 3所示。
表 3 LEHA参数设计的6项约束条件 Table 3 Six constraint conditions for LEHA parameter design
| 项目 | 约束条件内容 | |
| 条件1:速度约束 | vact-max=8ηpηcApSpfm/Acyl | |
| 条件2:压力约束 | pmax=ηm-pηmFe-max/(ηpAp) | |
| 条件3:输出力约束 | Fact-max=pmaxAcyl | |
| 条件4:频宽约束 | fm≥Kfrepfband, Kfrep=f(fband) | |
| 条件5:角功率约束 | Pact-max=8ηmηm-pηcFe-maxSpfm | |
| 条件6: 负载约束 | 惯性负载 | 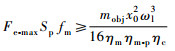 |
| 弹性负载 | 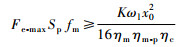 | |
| 黏性阻尼负载 |  | |
表选项
4 LEHA参数设计算例 LEHA的主要参数指标包括最大空载速度、最大静态输出力、系统功率、动态频宽指标和系统工作压力水平等,以小功率的EHA为例,定义如表 4所示的LEHA指标需求,3种负载条件如表 5所示。效率系数取值分别为ηm=0.95, ηm-p=0.8, ηp=0.9, ηc=0.9。
表 4 LEHA性能指标需求 Table 4 Performance parameter requirement of LEHA
| 参数 | 数值 |
| 作动器最大空载速度vact-max/(m·s-1) | 0.06 |
| 作动器最大静态输出力Fact-max/kN | 6 |
| 作动器最大角功率Pact-max/W | 360 |
| -3 dB, -90°频宽fband/Hz | 6 |
表选项
表 5 LEHA负载参数 Table 5 Parameters of LEHA load
| 负载类型 | 参数值 | 负载条件取值 |
惯性负载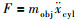 x=x0sin(ωlt) | mobj=60 kg x0=0.002 m ωl=14π | 1.87 N·m·s-1 |
| 弹性负载 F=Kx x=x0sin(ωlt) | K=1.5×105 N·m-1 x0=0.04 m ωl=π | 65.3 N·m·s-1 |
黏性阻尼负载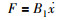 x=x0sin(ωlt) | Bl=600 N·m-1·s x0=0.04 m ωl=4π | 26.3 N·m·s-1 |
表选项
根据Liang等开展的高功率密度直线振荡电机研究[22],根据经验值将吸排油活塞振幅Sp设计为±5 mm,作动筒行程Scyl选取为±40 mm,系统最高压力pmax选取为6 MPa。其他需要设计的参数包括:吸排油活塞面积Ap、电机振荡频率fm、最大电磁力Fe-max、作动筒活塞面积Acyl。
根据输出力约束条件式(23),结合密封件的标准尺寸,选取作动筒的活塞杆直径为33 mm,活塞直径为48 mm,则作动筒活塞面积Acyl为954 mm2。
根据角功率的定义,约束条件1、2和5实际上有一项是重复条件,可以得到设计参数Ap、fm、Fe-max需要满足的约束条件为
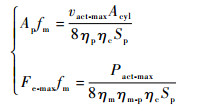 |
代入参数值,得到Ap、fm、Fe-max需要满足的约束如图 6所示。
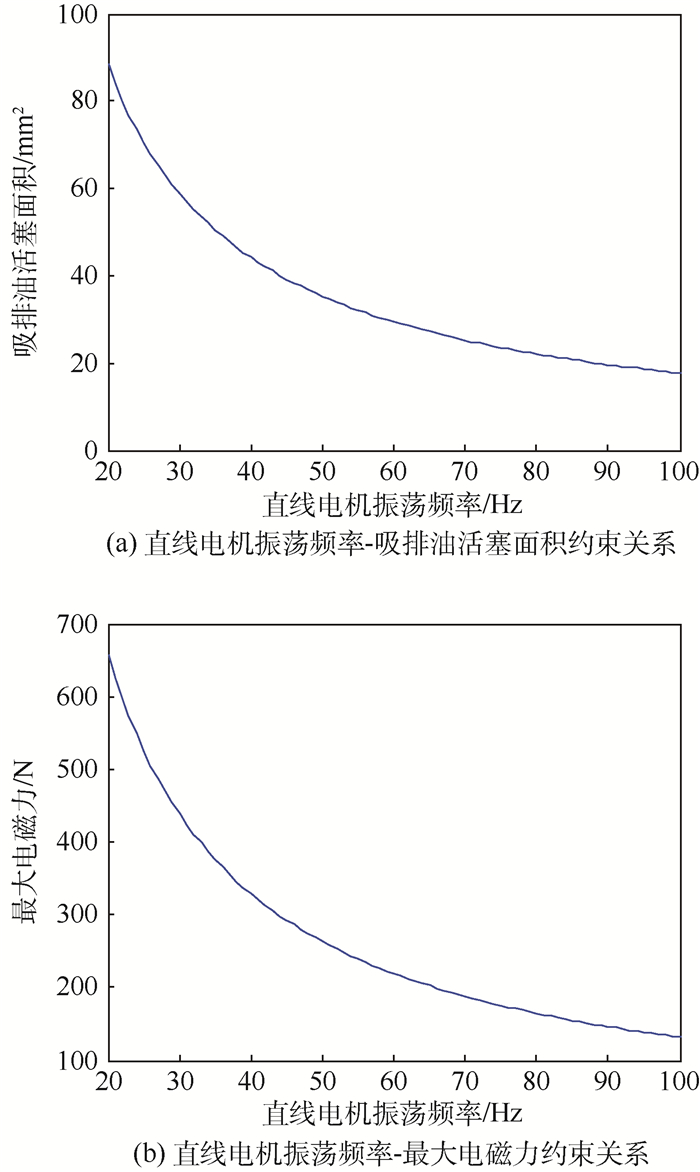 |
| 图 6 直线电机参数约束条件 Fig. 6 Parameter constraint condition of linear motor |
| 图选项 |
从图 6可以看出,提高直线电机的振荡频率,可以在保证充足流量的条件下减小直线泵的吸排油活塞面积,从而减小直线电机的最大电磁力需求,进而减小电机的尺寸和质量,提升直线电机的功率重量比,同时也能提高LEHA的功率重量比。
根据LEHA频宽对直线电机振荡频率的约束条件,当LEHA频宽指标为6 Hz时,根据图 5给出的分析结果,直线振荡电机的谐振频宽不低于30 Hz。针对表 4给出的指标需求,LEHA的关键参数设计结果如表 6所示。
表 6 LEHA的关键参数取值 Table 6 Key parameter values of LEHA
| 参数 | 数值 |
| 直线泵吸排油活塞面积Ap/mm2 | 59 |
| 吸排油活塞振幅Sp/mm | ±5 |
| 直线电机振荡频率Fm/Hz | 30 |
| 直线电机最大电磁力Fe-max/N | 439 |
| 作动筒活塞面积Acyl/mm2 | 954 |
| 作动筒行程Scyl/mm | ±40 |
表选项
根据表 6给出的设计参数,LEHA中直线电机最大电磁力、电机振幅和振荡频率的乘积为
 |
显然表 6给出的设计参数满足负载约束条件,因此根据本文所述的6项参数设计规则,能够针对具体的指标完成LEHA的参数设计。
5 LEHA设计指标实验验证 根据表 6所示的设计参数加工LEHA的原理样机,如图 7所示。
 |
| 图 7 LEHA原理样机 Fig. 7 LEHA prototype |
| 图选项 |
LEHA原理样机中直线电机的振荡频率为30 Hz,直线电机力系数为27.5 N/A。实际LEHA样机中直线泵的参数与表 6所给参数不同,吸排油活塞直径为10.5 mm,活塞杆直径为7 mm,直线泵的吸排油活塞面积为48 mm2。
5.1 作动筒最大空载速度测试 以幅值为±10 mm的低频方波信号为位移指令,测试LEHA的位移跟踪响应,如图 8所示。在上升沿和下降沿时间段内,电机实际输出振幅为6 mm,LEHA的速度为0.057 m/s。根据式(12),LEHA速度与直线泵振幅正相关,因此若直线电机振幅为5 mm,按照直线泵样机48 mm2吸排油活塞面积,LEHA速度为0.047 5 m/s;若按图 6(a)给出的约束条件,当直线电机振荡频率为30 Hz时,将直线泵吸排油活塞面积设计为59 mm2,则LEHA能达到0.06 m/s的最大空载速度。
 |
| 图 8 LEHA最大空载速度 Fig. 8 Maximum no-load velocity of LEHA |
| 图选项 |
5.2 直线泵最高输出压力测试 以节流阀作为直线泵负载,测量直线泵的最高输出压力,电机位移、直线泵的输出压力和电机绕组电流如图 9所示。
 |
| 图 9 直线泵性能测试结果 Fig. 9 Testing results of linear pump performance |
| 图选项 |
直线泵输出压力的平均值为5.6 MPa,电机振荡波形在峰值处存在一定变形,但是过零点时刻2个电机的相位差接近90°,直线泵的配流效率高。图 9中,直线电机电流峰值为13 A,对应电磁力为358 N,当直线泵的吸排油活塞面积为48 mm2时,根据式(22)给出的压力约束条件,直线泵输出压力为5.95 MPa,与实测值5.7 MPa的误差为4.2%,实验结果与按照设计规则给出的参数算例相符合。
5.3 LEHA调制频率特性测试 目前LEHA原理样机中直线电机的振荡频率设计为30 Hz,实验测试调制频率在10~30 Hz范围内LEHA的频率特性,统计结果如图 10所示,A为输出幅值与指定幅值之比。
 |
| 图 10 不同调制频率时的LEHA频率特性 Fig. 10 LEHA frequency response to different modulation frequency |
| 图选项 |
LEHA的频宽随调制频率的增长而增加,如图 11所示,实验结果与图 5仿真结果符合,调制频率为30 Hz时,LEHA频宽为5.5 Hz。
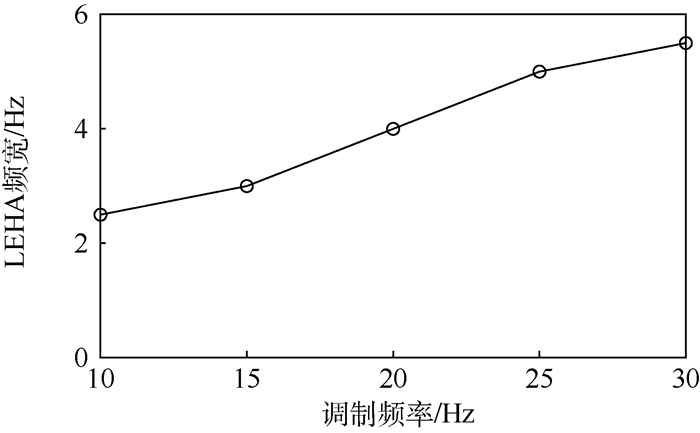 |
| 图 11 LEHA频宽与调制频率的关系(实验结果) Fig. 11 Relationship between bandwidth of LEHA and modulation frequency (experimental result) |
| 图选项 |
LEHA的工作原理本质上是利用直线泵的互配流机制将2个电机的高频调制振荡位移解调成可控的作动筒位移。电机的振荡频率越高,单位时间内调制信号的波形周期数越多,在利用一个包络线进行调幅时,每2个相邻周期的幅值变化率越小,这样使得相邻周期的波形具有更好的相似性。对于不同的电机振荡频率,如果波形的畸变率能保证大致相当,则在高频下电机的响应速度越快;并且调制频率越高,在由直线泵将多个通道的运动整合变换成可控流量时,具有更精密的调节效果;因此提高内部通道的调制频率,即提高直线电机的振荡频率,将使LEHA达到更高的频宽。
6 结论 LEHA作为一种新原理的泵控式电静液作动器,涉及到机械、电气和液压等多个学科,本文研究了LEHA的参数匹配设计规则,得到了LEHA参数设计的6项匹配规则,包括:最大空载速度约束条件、最大静态输出力约束条件、系统最高压力约束条件、动态频宽约束条件、角功率约束条件和负载匹配约束条件,上述设计规则能够为LEHA的设计过程提供充足的理论依据,指导LEHA的参数设计过程;并且通过LEHA原理样机的实验测试验证了其参数设计规则。
根据LEHA的参数设计约束条件可知:
1) 直线电机的振荡频率越高,LEHA频宽越高,因此应该尽量提高直线电机的谐振频率。
2) 在同等的流量需求下,直线电机的振荡频率越高,直线泵的吸排油活塞面积越小;在保证系统压力的前提下,直线电机的最大电磁力需求越小,因此电机体积可以设计得越小,因此可以提升系统的功率重量比。
参考文献
| [1] | WHEELER P, BOZHKO S. The more electric aircraft:Technology and challenges[J].IEEE Electrification Magazine, 2014, 2(4): 6–12.DOI:10.1109/MELE.2014.2360720 |
| [2] | WHEELER P. Technology for the more and all electric aircraft of the future[C]//IEEE International Conference on Automatica. Piscataway, NJ: IEEE Press, 2016: 1-5. |
| [3] | SARLIOGLU B, MORRIS C T. More electric aircraft:Review, challenges, and opportunities for commercial transport aircraft[J].IEEE Transactions on Transportation Electrification, 2015, 1(1): 54–64.DOI:10.1109/TTE.2015.2426499 |
| [4] | DERRIEN J C, SECURITE S D. Electro-mechanical actuator (EMA) advanced technologies for flight controls[C]//28th International Congress of the Aeronautical Sciences, 2012: 1-10. |
| [5] | ALLE N, HIREMATH S S, MAKARAM S, et al. Review on electro hydrostatic actuator for flight control[J].International Journal of Fluid Power, 2016, 17(2): 125–145.DOI:10.1080/14399776.2016.1169743 |
| [6] | BOTTEN S L, WHITLEY C R, KING A D. Flight control actuation technology for next-generation all-electric aircraft[J].Technology Review Journal, 2000, 23(6): 55–68. |
| [7] | CHAKRABORTY I, TRAWICK D R, JACKSON D, et al. Electric control surface actuator design optimization and allocation for the more electric aircraft[C]//2013 Aviation Technology, Integration, and Operations Conference. Reston: AIAA, 2013: 4283. |
| [8] | VAN DEN BOSSCHE D. The A380 flight control electro-hydrostatic actuators, achievements and lessons learnt[C]//25th International Congress of the Aeronautical Sciences, 2006: 1-8. |
| [9] | ANDERSON J A. Variable displacement electro-hydrostatic actuator[C]//IEEE Aerospace and Electronics Conference. Piscataway, NJ: IEEE Press, 1991: 529-534. |
| [10] | SHEN W, MAI Y, SU X, et al. A new electric hydraulic actuator adopted the variable displacement pump[J].Asian Journal of Control, 2016, 18(1): 178–191.DOI:10.1002/asjc.v18.1 |
| [11] | JIANG J H, LIU Q, LIU J L, et al. Performance comparison of displacement and speed control in electro-hydrostatic actuator[J].Applied Mechanics and Materials, 2015, 779: 205–211.DOI:10.4028/www.scientific.net/AMM.779 |
| [12] | HANKAN C, TUNA B, BULENT E P. A complete analysis for single rod electro hydrostatic actuators[C]//10th International Fluid Power Conference. Dresden: IFAS, 2016: 119-132. |
| [13] | NAVARRO R. Performance of an electro-hydrostatic actuator on the F-18 systems research aircraft: NASA/TM-97-206224[R]. Edwards: Dryden Flight Research Center, 1997: 1-37. |
| [14] | MCCULLOUGH. Design and characterization of a dual electro-hydrostatic actuator[D]. Hamilton: McMaster University, 2011: 4-11. |
| [15] | ANDERSON E, LINDLER J. Smart material actuator with long stroke and high power output[C]//43rd Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2002: 1354. |
| [16] | JOHN S, SIROHI J, WANG G, et al. Comparison of piezoelectric, magnetostrictive, and electrostrictive hybrid hydraulic actuators[J].Journal of Intelligent Material Systems and Structures, 2007, 18(10): 1035–1048.DOI:10.1177/1045389X06072355 |
| [17] | KAN J, TANG K, REN Y, et al. Study on a piezohydraulic pump for linear actuators[J].Sensors and Actuators A:Physical, 2009, 149(2): 331–339.DOI:10.1016/j.sna.2008.12.008 |
| [18] | CHAUDHURI A, WERELEY N M. Experimental validation of a hybrid electrostrictive hydraulic actuator analysis[J].Journal of Vibration and Acoustics, 2010, 132(2): 021006.DOI:10.1115/1.4000778 |
| [19] | KIM G W, WANG K W. Helmholtz resonance in a piezoelectric-hydraulic pump-based hybrid actuator[J].Smart Materials and Structures, 2010, 20(1): 015010. |
| [20] | TAN H, HURST W, LEO D. Performance modeling of a piezohydraulic actuation system with active valves[J].Smart Materials and Structures, 2004, 14(1): 91–110. |
| [21] | LI Y, JIAO Z, YAN L, et al. Conceptual design and composition principles analysis of a novel collaborative rectification structure pump[J].Journal of Dynamic Systems, Measurement, and Control, 2014, 136(5): 054507.DOI:10.1115/1.4027504 |
| [22] | LIANG H, JIAO Z, YAN L, et al. Design and analysis of a tubular linear oscillating motor for directly-driven EHA pump[J].Sensors and Actuators A:Physical, 2014, 210: 107–118.DOI:10.1016/j.sna.2014.01.026 |
