国内外关于指令信号振荡方面的研究集中于振荡故障检测功能实现和算法开发上[6-7], 故障模式和影响的数据信息多来源于工业技术报告和军方报告的经验数据等, 鲜有文献对其故障机理及故障影响特征展开系统的研究[8-9]。
机电作动系统(EMA)作为新型电功率作动系统之一, 已应用于空客380和波音787新型民用客机的水平安定面配平及扰流板作动, 成为电传飞控系统的典型特征之一。本文将建立机电作动系统动力学模型并对振荡信号的产生机理进行分析。开展非指令振荡信号故障影响的仿真分析, 对振荡信号的产生位置、不同频率和不同幅值带来的故障影响展开系统化研究, 为机电作动系统非指令振荡信号的审查提供支持。
1 故障机理分析 1.1 振荡信号产生机理 对于采用复杂数字式软硬件实现的电传飞控系统, 电子线路中的传输信号易受到内外干扰源干扰, 形成非指令信号。能够修改指令并产生非指令信号的内外干扰通常包括但不限于数据位丢失、有害的瞬变、异步微处理器对信号的处理、传输延迟、信号畸变、传感器噪声、不可靠的传感器信号、闪电和电磁效应[10-11]。
然而, 电信号在传输过程中往往受到不止一种干扰源的干扰, 而是多种干扰的耦合。振荡信号即为电子元件同时受到2种或2种以上干扰作用, 在故障模式下产生的一种杂散信号。例如, 若两台独立的计算机用于控制同一驱动系统, 为保证信号传输不失真, 计算机异步微处理器对信号的处理时间应大于信号传输延迟时间, 并保持稳定的时间逻辑关系。但是当异步微处理器对信号的处理或传输延迟发生异常时, 异步处理时间就不能与传输延迟时间保持原时间逻辑关系, 信号输出表现为杂散的振荡信号[12]。此外, 传感器阻抗参数波动会引起电流变化, 产生传感器噪声, 由于传输线路阻抗不匹配, 传感器噪声可能发生畸变, 输出通常表现为振荡信号。
1.2 振荡信号表现形式 一般情况下, 电功率作动系统产生振荡信号的频率范围为0.05~50 Hz。频率低于0.2 Hz的振荡信号对舵面产生的影响可以忽略; 舵面作动器存在低通滤波器架构, 高于10 Hz的振荡信号不会传递到舵面。因此, 造成振荡失效的振荡信号频率范围通常为0.2~10 Hz[13]。振荡信号的振荡形式为三角波到正弦波形中的任一形状, 基于工程经验, 常见振荡信号的幅值范围为正常信号幅值的30%~250%[14]。
1.3 振荡信号产生位置 振荡信号的产生部位包括传输给操纵面闭环系统所有的指令与信号:计算机组件及接口、反馈组件(如传感器)、输入组件(如控制舵面信号、大气数据信号)、驱动组件及结构安装组件, 其产生位置如图 1所示, ACE为作动器电子控制装置。
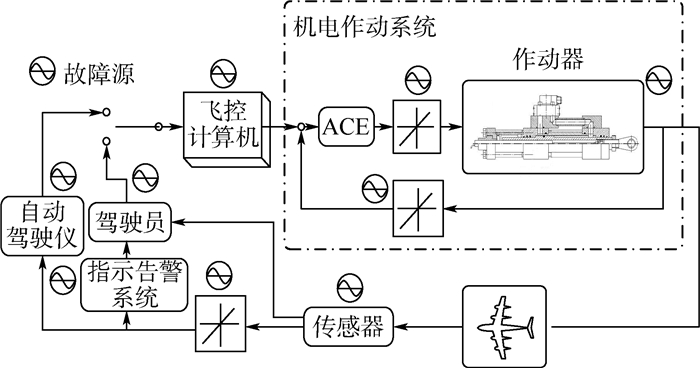 |
| 图 1 振荡信号产生位置 Fig. 1 Oscillation signal generation position |
| 图选项 |
本文研究对象为图 1虚线框内的机电作动系统, 其振荡信号产生位置为控制器输出端、传感器输出端及驱动器输入端[15]。其中, 控制器通过比较舵偏指令与传感器反馈信号调节系统, 使响应跟踪指令信号, 消除误差; 传感器将舵偏角变化量转换为电信号反馈给控制器, 实现闭环控制; 驱动器通过脉宽调制(PWM)模块控制逆变器功率管的导通顺序, 驱动电机作动。
2 机电作动系统 机电作动系统可分为直线式机电作动系统与旋转式机电作动系统2类, 是位置伺服控制系统的总称[16]。图 2为直线式机电作动系统结构, 系统由ACE、无刷直流电机、齿轮减速箱、滚珠丝杠和传感器等部分组成。作动系统驱动电机常采用无刷直流电机, 齿轮减速箱及滚珠丝杠将驱动电机的旋转输入力矩转换为线性输出力, 驱动舵面偏转。此外, 作动系统通过位置传感器、转速传感器输出位置信号和驱动转速信号, 实现闭环控制。
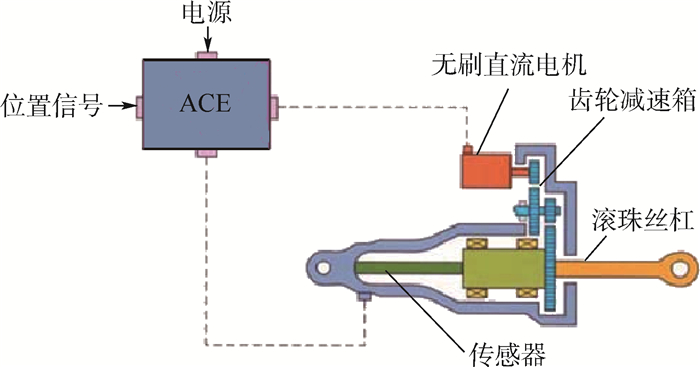 |
| 图 2 直线式机电作动系统结构 Fig. 2 Structure of linear electromechanical actuation system |
| 图选项 |
2.1 机电作动系统建模 对机电作动系统进行系统建模, 分析振荡信号在作动系统中的故障影响。无刷直流电机为二相导通星形三相六状态。为简化分析, 做如下假设:
1) 三相绕组完全对称, 气隙磁场为方波, 定子电流和转子磁场分布皆对称。
2) 3个霍尔元件在空间相隔120°对称布置。
3) 不计电枢反应, 气隙磁场分布近似是平顶宽度为120°电角度的梯形波。
基于上述假设, 无刷直流电机三相电流满足iA+iB+iC=0;三相绕组自感满足LA=LB=LC=L; 各相互感满足MAB=MBA=MBC=MCB=MAC=MCA=M; 无刷直流电机三相绕组任意一相的电压可表示为
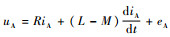
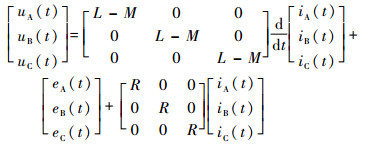 |
式中:uA(t)、uB(t)和uC(t)为电机三相定子绕组的相电压; eA(t)、eB(t)和eC(t)为电机三相定子绕组的反电势; iA(t)、iB(t)和iC(t)为电机三相定子绕组的相电流; R为相电阻; L为定子绕组自感, M为定子绕组互感, 且L-M>0。
电磁功率满足P=eAiA+eBiB+eCiC; 不计转子的机械损耗和杂散损耗, 电磁功率全部转化为转子动能可得
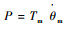
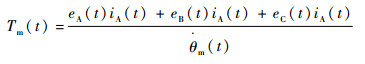 |
式中:Tm(t)为无刷直流电机电磁转矩;
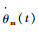
机电作动系统运动方程为
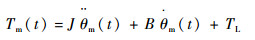 |
式中:J为机电作动系统转动惯量,
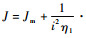
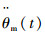
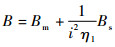
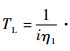
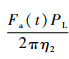
滚珠丝杠输出轴转角θs和无刷直流电机转角θm间的关系为
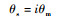 |
系统输出舵偏角θ与丝杠螺母位移xL关系为
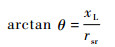 |
式中:rsr为舵面转动半径; θ≈KxL, K为位移角度系数, 其与舵面的转动半径相关。
2.2 仿真分析 已知机电作动系统参数如下[17-18]:额定电压U=270 V, 额定转速n=12 000 r/min, 反电势系数Ke=0.022 9 V/(r·min-1), 滚珠丝杠导程为5 mm, 齿轮减速箱传动比i=20。
给定目标舵偏角为1°, 图 3~图 5为机电作动系统舵偏角、电机转速及转矩输出。电机在0.01 s内完成加速并以额定转速带动齿轮减速箱及滚珠丝杠作动, 转速波动小; 舵偏角响应速度受到齿轮减速箱和机械传动装置限制, 在1.85 s内跟踪指令信号, 完成作动, 电机停转。
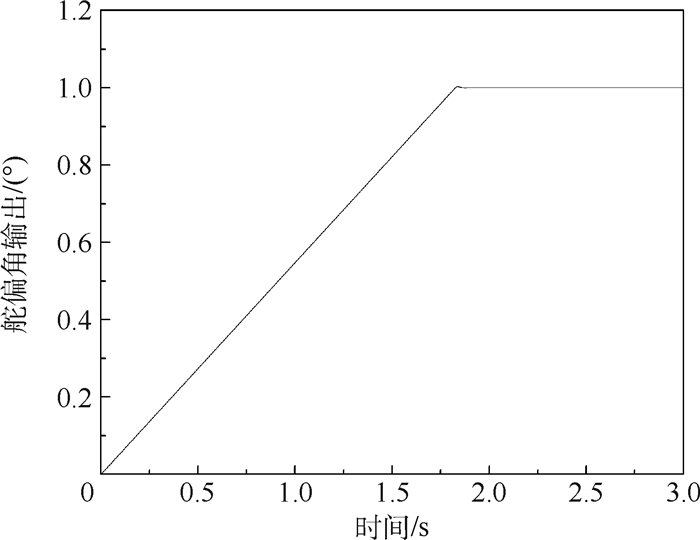 |
| 图 3 机电作动系统舵偏角输出 Fig. 3 Control surface deflection angle output of EMA |
| 图选项 |
 |
| 图 4 机电作动系统电机转速 Fig. 4 Motor speed of EMA |
| 图选项 |
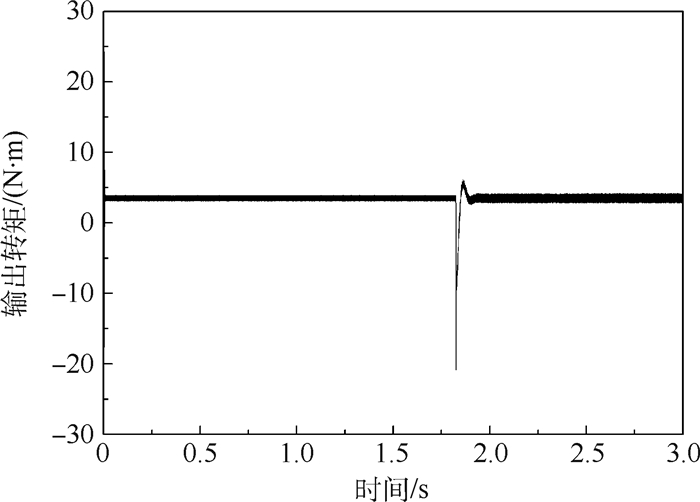 |
| 图 5 机电作动系统输出转矩 Fig. 5 Output torque of EMA |
| 图选项 |
为了验证模型建立的合理性与正确性, 将仿真数据与文献[19]中直线式机电作动系统的无刷直流电机实验数据进行对比, 文献[19]中驱动电机额定功率1.5 kW, 额定转速10 000 r/min。对比如图 6所示, 本文基于模型的电机转速仿真曲线与文献[19]实验数据趋势一致, 并且电机转速及响应性能均符合实验规律。由此, 验证了机电作动系统模型的正确性与有效性。
 |
| 图 6 电机转速对比 Fig. 6 Comparison of motor speed |
| 图选项 |
此外, 已知某机型水平安定面机电作动系统最大偏转速度至少为0.5(°)/s, 最小偏转速度至少为0.1(°)/s, 位移控制精度为0.05 mm。由图 3可知系统输出舵偏角偏转速度达到0.5(°)/s, 由图 6可知电机响应时间为0.01 s, 稳态误差为3%, 其响应性能符合民用客机水平安定面舵面偏转要求。
3 振荡故障分析 由于振荡信号为电信号, 且是电信号在传输过程中受到干扰而发生的畸变, 因此振荡信号的注入方法为故障信号与正常指令信号的叠加, 即液态故障(图 7)。
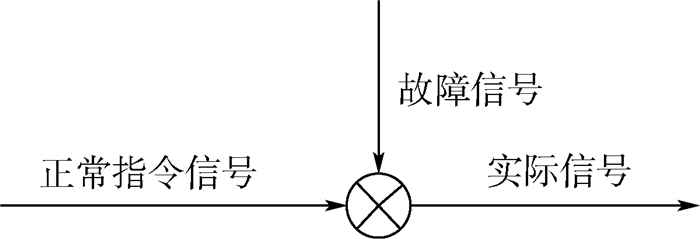 |
| 图 7 液态故障 Fig. 7 Liquid failure |
| 图选项 |
振荡信号的振荡形式为三角波到正弦波中的任一波形, 为便于数值计算, 考虑到正弦曲线的连续性, 本文选取振荡信号波形为正弦波, 且随机选取振荡信号幅值为正常信号幅值的30%~250%。
综上, 振荡信号注入如图 8~图 10所示。
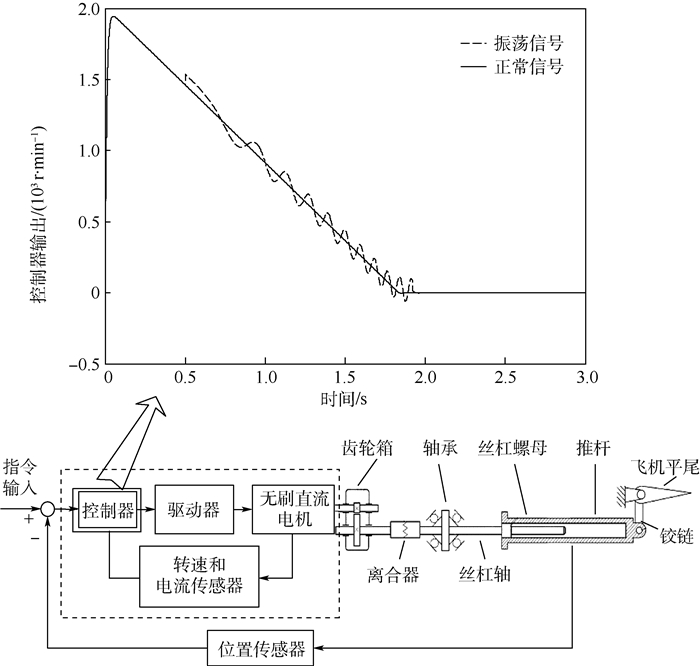 |
| 图 8 控制器输出端注入振荡信号 Fig. 8 Controller output terminal injected with oscillation signal |
| 图选项 |
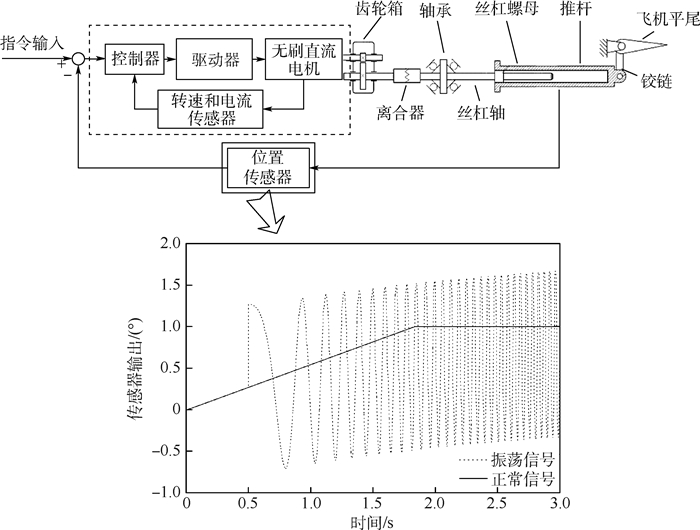 |
| 图 9 传感器输出端注入振荡信号 Fig. 9 Sensor output terminal injected with oscillation signal |
| 图选项 |
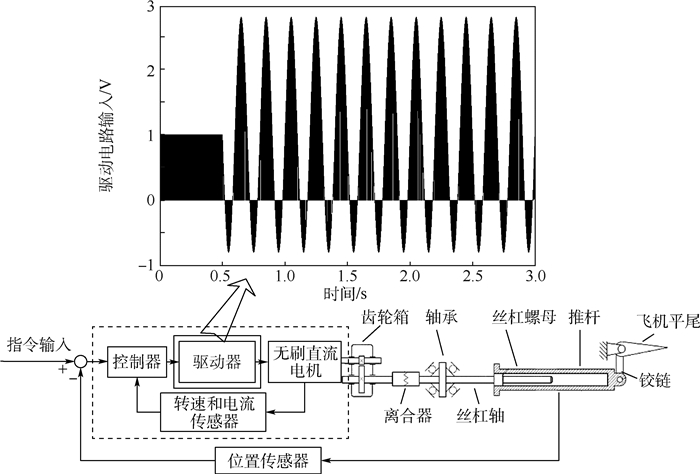 |
| 图 10 驱动器输入端注入振荡信号 Fig. 10 Motor driver input terminal injected with oscillation signal |
| 图选项 |
3.1 定频率定幅值故障分析 由2.2节可知, 振荡信号产生位置分别为机电作动系统控制器输出端、传感器输出端、驱动器输入端。选取正弦振荡信号的频率为5 Hz, 幅值为正常信号幅值的100%。0.5 s时叠加振荡信号, 研究振荡信号不同的产生位置对系统的故障影响。由注入振荡信号后无刷直流电机转速(图 11)、系统输出转矩(图 12)及舵偏角(图 13)变化可知:
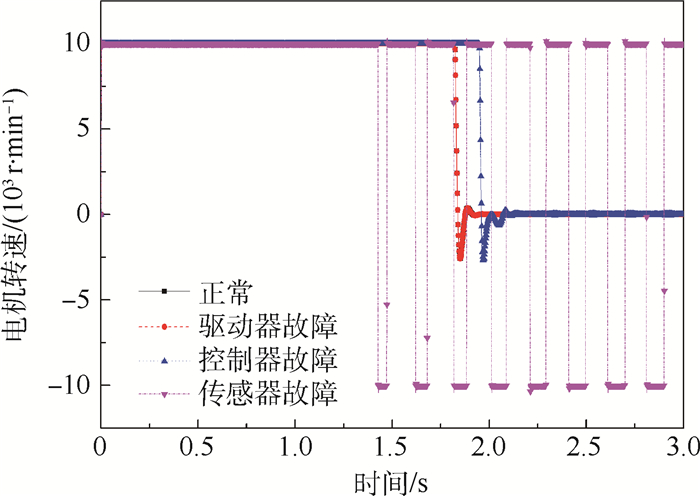 |
| 图 11 不同位置注入振荡信号后的电机转速 Fig. 11 Motor speed after injecting oscillation signal in different positions |
| 图选项 |
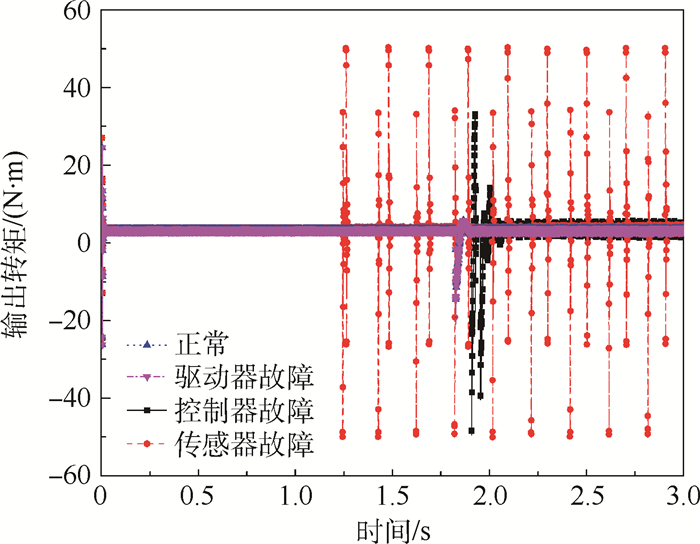 |
| 图 12 不同位置注入振荡信号后的输出转矩 Fig. 12 Output torque after injecting oscillation signal in different positions |
| 图选项 |
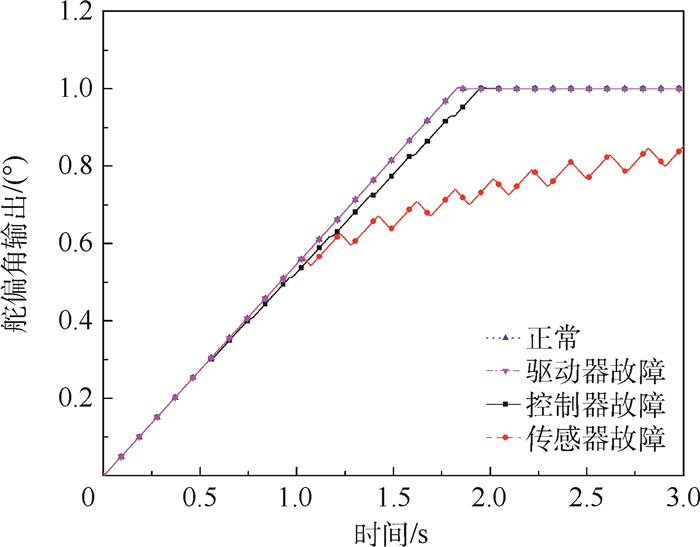 |
| 图 13 不同位置注入振荡信号后的舵偏角输出 Fig. 13 Surface deflection angle output after injecting oscillation signal in different positions |
| 图选项 |
1) 无刷直流电机转速、系统输出转矩及舵偏角波动与振荡信号同频率变化。
2) 振荡信号波形在传输过程中发生变化, 舵偏输出已不为正弦波而为三角波。
3) 故障影响严重程度:传感器输出端>控制器输出端>驱动输入端。
驱动器PWM波周期为50 μs, 功率管导通切换频率为50 kHz远大于振荡信号的频率, 并且功率管为正向导通, 振荡信号基本不影响功率管的导通。无刷直流电机三相绕组中一相导通异常时, 仍有两相绕组能够保持电机正常运行, 因此驱动器突发振荡信号对系统输出影响可忽略。
控制器闭环控制使系统能够跟踪指令信号, 控制器输出信号突发振荡后, 作动系统输出舵偏角跟踪含有振荡的指令信号, 系统仍能正常作动, 只是输出舵偏随振荡信号波动。
传感器输出信号突发振荡时, 控制器根据错误的反馈信号对系统进行错误的控制, 指令信号与反馈信号的偏差值逐渐增大, 系统不能正常跟踪指令信号; 无刷直流电机转速在额定正转、反转间切换, 相比由于控制器输出信号突发振荡引起的电机启停切换, 功率至少增加1倍; 输出转矩随无刷直流电机转速发生同频率抖动, 无刷直流电机以额定功率作动且频繁正反转切换, 电机保持最大功率工作状态易被烧毁, 并可能损伤机械传动机构。
由于控制器存在电流限幅, 无刷直流电机输出转速在额定转速内切换, 振荡信号波形在传输过程中发生变化, 舵偏输出已不为正弦波而为三角尖波。
3.2 定频率变幅值故障分析 由3.1节分析可知, 驱动器输入振荡信号对系统的故障影响可忽略, 本节选取振荡信号的频率为5 Hz, 幅值分别为正常信号幅值的30%、175%与250%, 0.5 s时分别在控制器输出端和传感器输出端叠加振荡信号, 研究振荡信号的幅值大小对作动系统的故障影响。由系统故障响应(见图 14和图 15)可知:
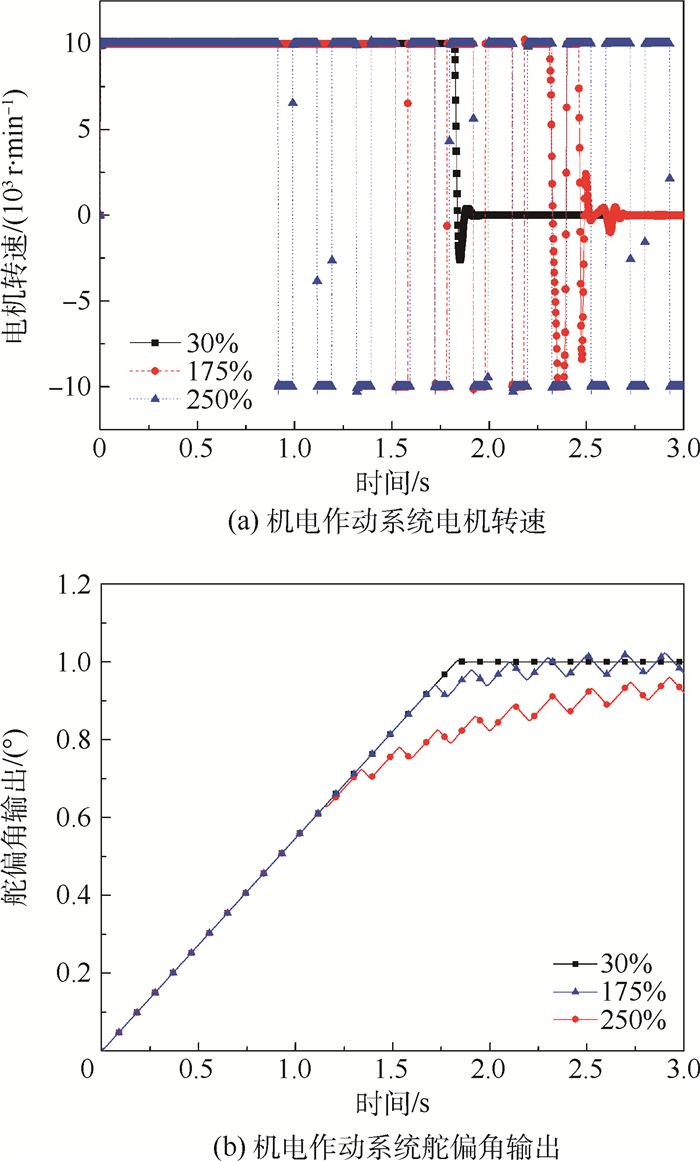 |
| 图 14 控制器输出变幅值振荡信号 Fig. 14 Oscillation signal of varied amplitude injected in controller output |
| 图选项 |
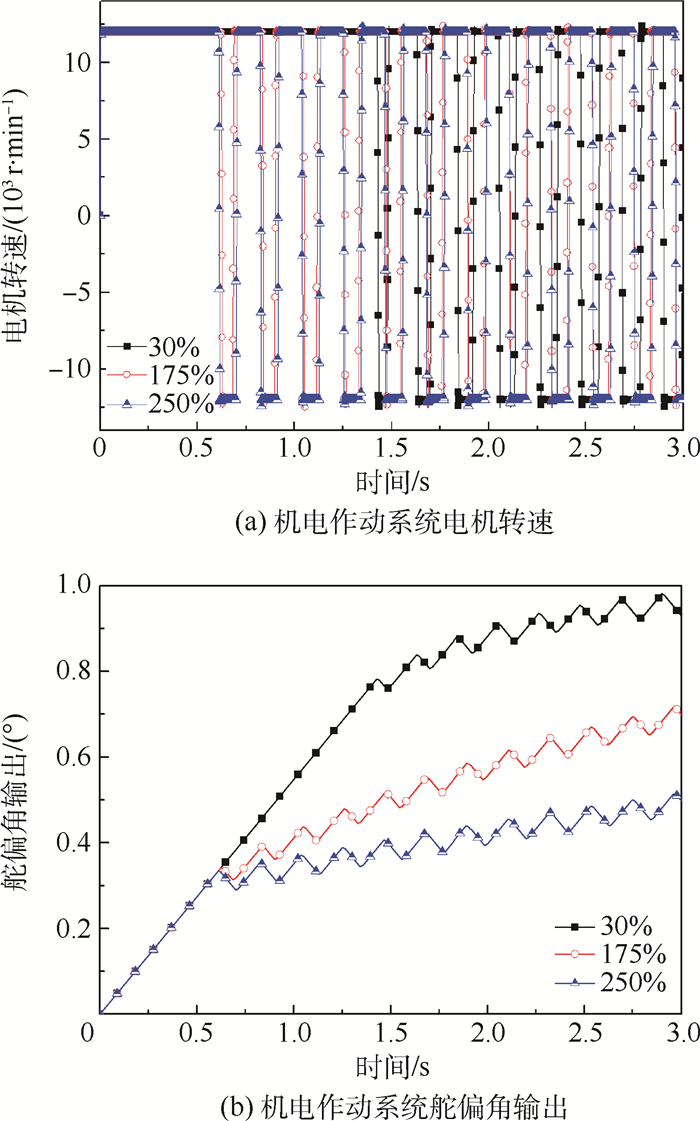 |
| 图 15 传感器输出变幅值振荡信号 Fig. 15 Oscillation signal of varied amplitude injected in sensor output |
| 图选项 |
1) 当控制器输出振荡信号幅值大于100%时, 作动过程中的故障响应时刻与振荡信号幅值有关:幅值越大, 故障响应时间越早; 控制器输出250%的振荡信号时, 虽然其跟踪速度随振荡信号的幅值增大而减小, 但仍远大于传感器输出振荡信号时系统的响应速度(见图 16)。
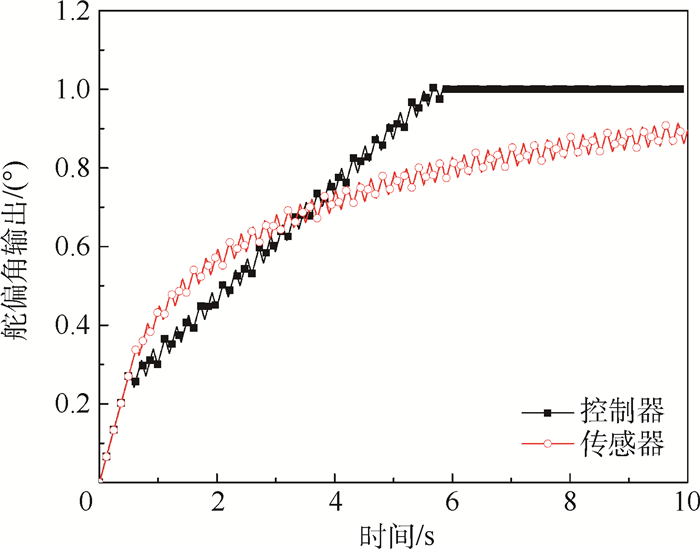 |
| 图 16 控制器与传感器振荡信号故障影响比较 Fig. 16 Comparison of oscillation signal failure effect between controller and sensor |
| 图选项 |
2) 对于传感器输出振荡信号而言, 舵偏波动幅值与振荡信号幅值无关, 与系统性能有关。
3.3 变频率定幅值故障分析 由2.2节知, 造成振荡失效的振荡信号频率范围通常为0.2~10 Hz, 取正弦振荡信号幅值为正常信号幅值的100%, 频率为0.2~10Hz随时间逐渐增大。取舵偏指令信号为幅值0.01°、频率5 Hz的正弦信号, 旨在观察系统对周期时变信号的跟踪能力。由3.1节知, 驱动器突发振荡信号对系统输出影响可忽略, 0.5 s时分别在控制器、传感器输出端叠加振荡信号, 研究不同频率的振荡信号对系统的故障影响。由系统故障响应可知:
1) 系统故障响应(电机转速、输出转矩和舵偏角)的波动与振荡信号同频率变化。
2) 振荡信号频率小于3 Hz时, 系统舵偏角输出波动剧烈, 不能跟踪指令, 且振荡信号频率越小, 对系统干扰越强。
3) 振荡信号频率大于8 Hz时, 电磁转矩振荡明显, 系统输出转矩频繁切换, 易损伤机械传动装置, 且振荡信号频率越高, 输出转矩切换时刻越早。
由图 17和图 18可知, 控制器输出端注入振荡信号, 系统仍能跟踪正弦指令, 但是随着振荡信号频率的增大, 电磁转矩输出振荡明显。传感器输出振荡信号, 输出舵偏完全不能跟踪指令信号, 且转速调节范围约为控制器振荡时的1.5倍, 转矩频繁抖动, 可见传感器故障对系统的影响之大。且由图 18(c)可得, 振荡信号频率越低, 系统输出舵偏角波动幅度越大。
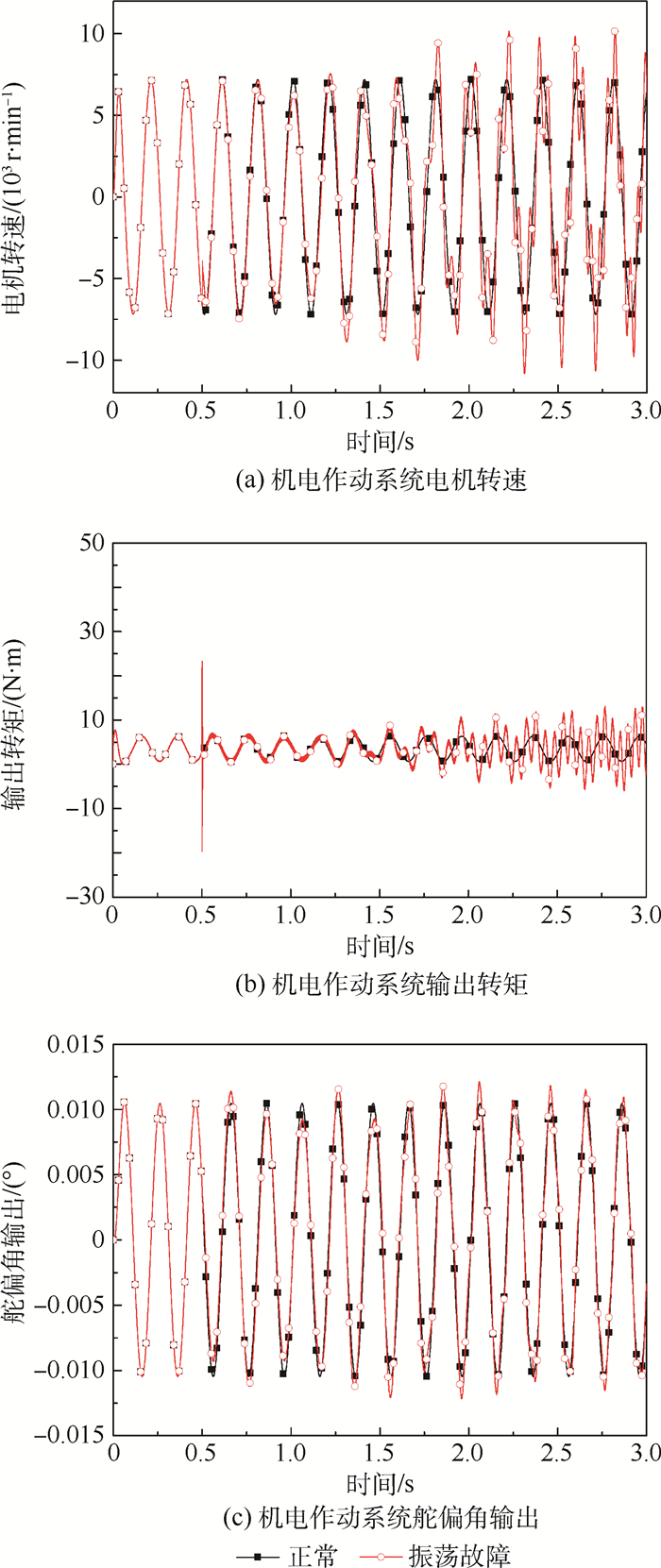 |
| 图 17 控制器输出变频率振荡信号 Fig. 17 Oscillation signal of varied frequency injected in controller output |
| 图选项 |
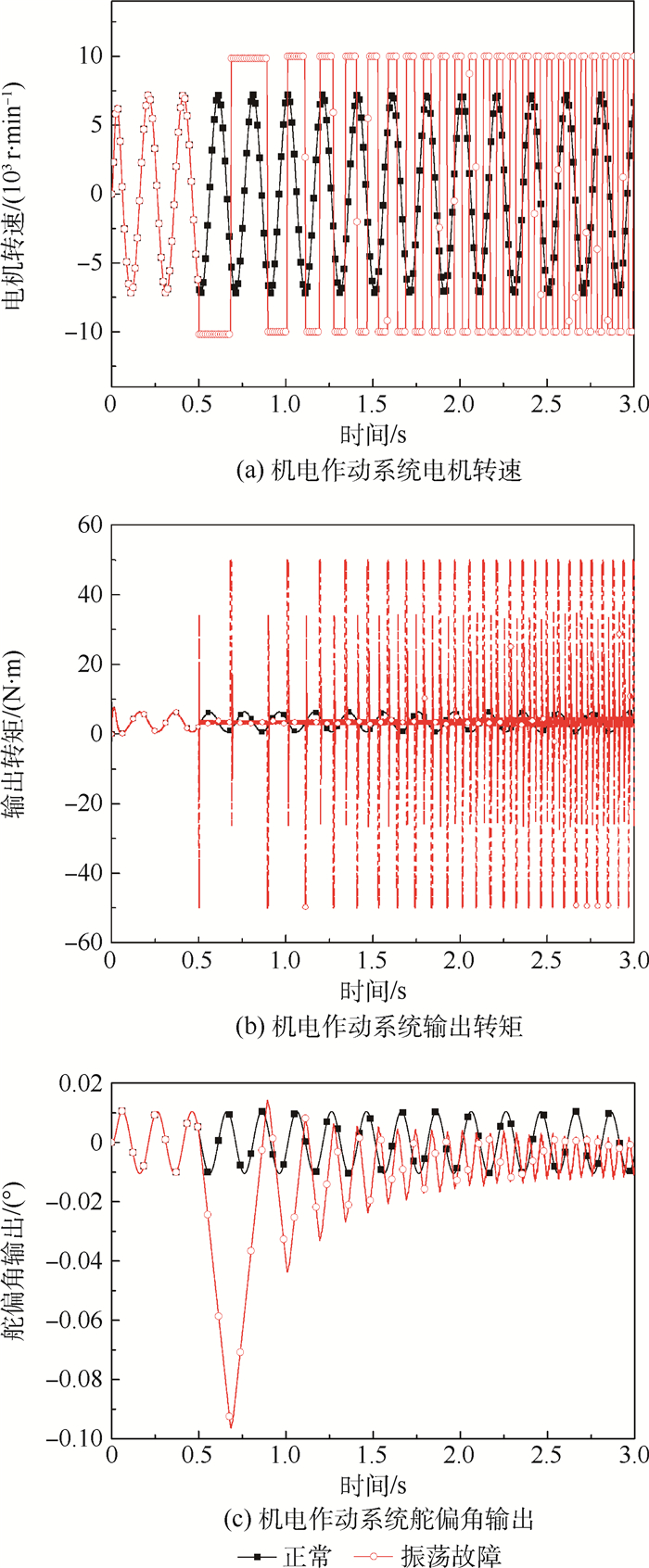 |
| 图 18 传感器输出变频率振荡信号 Fig. 18 Oscillation signal of varied frequency injected in sensor output |
| 图选项 |
综上可知, 输出电磁转矩波动随振荡信号频率的增大而增大, 输出舵偏角随振荡信号频率的减小而增大, 为确定对输出转矩与舵偏影响较大的振荡信号频率带, 基于传感器0.2~10 Hz变频率振荡故障对系统输出转矩与舵偏角输出进行FFT分析:
1) 舵偏角FFT分析
采用FFT进行频域分析[20], 频率小于3 Hz基波幅值为3~10 Hz众数的8倍(见图 19, THD为总谐波失真), 频率小于3 Hz的基波对系统舵偏角输出影响占主要作用。
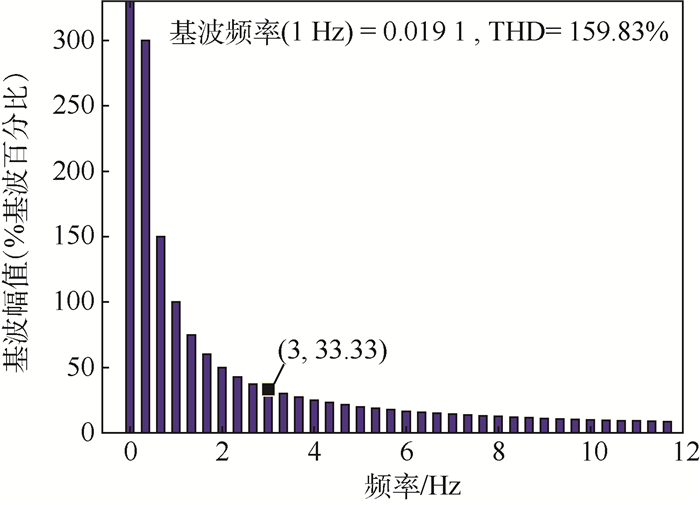 |
| 图 19 机电作动系统舵偏角FFT Fig. 19 FFT of control surface deflection angle of EMA |
| 图选项 |
为验证此结论, 舵偏指令为1°, 0.5 s时在传感器输出端分别注入0.6、2、4和8 Hz振荡信号(见图 20), 可得:①机电作动系统输出舵偏角的波动幅度随振荡信号频率的增大而减小, 振荡信号频率小于3 Hz时, 系统不能跟踪指令, 舵偏角输出波动剧烈; ②振荡信号频率越小, 输出舵偏角波动的增量越大, 大于3 Hz时, 舵偏波动增量基本不变。
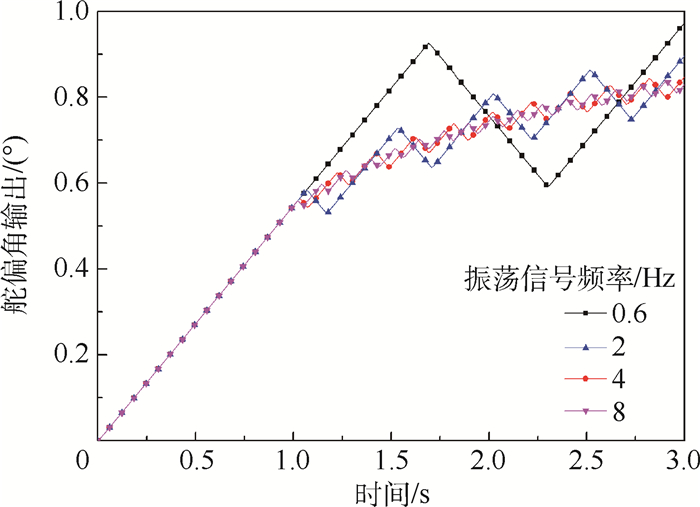 |
| 图 20 不同振荡信号频率对输出舵偏角的影响 Fig. 20 Influence of different oscillation signal frequencies on output control surface deflection angle |
| 图选项 |
2) 输出电磁转矩FFT分析
频率在大于9.6 Hz的基波幅值大于等于0~9.6 Hz的6倍(见图 21), 其可能会使系统输出转矩波动频繁且波动幅值大。
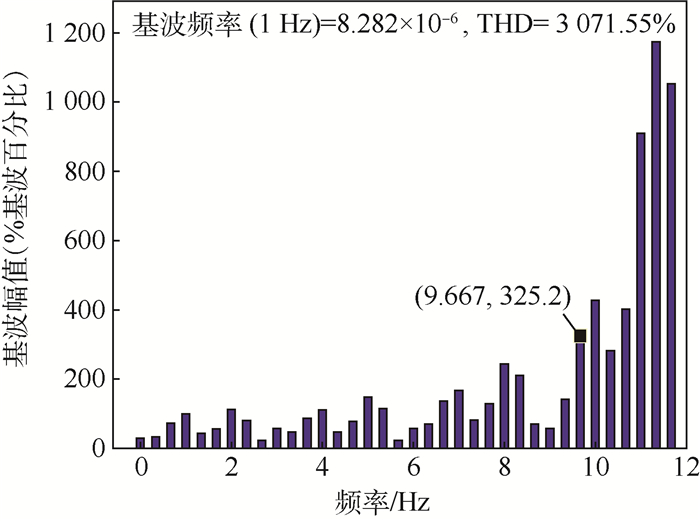 |
| 图 21 机电作动系统电磁转矩FFT Fig. 21 FFT of electromagnetic torque of EMA |
| 图选项 |
为验证此结论, 舵偏指令为1°, 0.5 s时在控制器输出端注入0.2~10 Hz振荡信号(见图 22), 可得:①机电作动系统作动过程中控制器输出端注入振荡信号, 虽能跟踪指令到达目标位置, 但电磁转矩产生, 影响系统作动精度; ②转矩波动幅度随振荡信号频率的增加而增大。作动系统输出舵偏角的波动幅度随振荡信号频率的增大而减小, 振荡信号频率小于3 Hz时, 系统不能跟踪指令, 舵偏角输出波动剧烈。
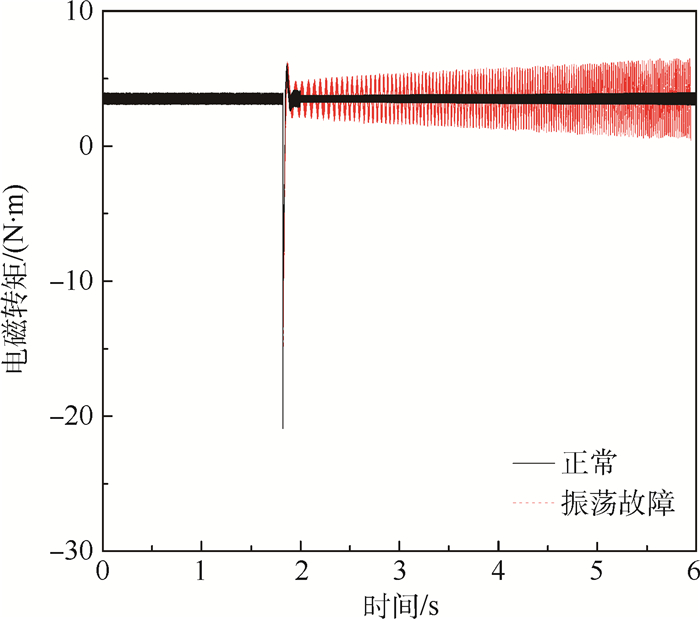 |
| 图 22 不同振荡信号频率对电磁转矩的影响 Fig. 22 Influence of different oscillation signal frequency on electromagnetic torque |
| 图选项 |
通过上述仿真分析, 可得振荡信号对机电作动系统的故障影响如下:
1) 传感器输出振荡信号对系统影响最大。系统舵偏角输出不能在限定时间内跟踪指令信号, 无刷直流电机功率调节范围大, 易烧毁电机且对机械传动装置造成损伤; 控制器输出振荡信号影响系统跟踪指令速度; 驱动器输入振荡信号对系统的故障影响较小, 可不计。适航审查中应着重关注机电作动系统传感器输出信号振荡这一位置处的故障模式。
2) 信号发生正弦振荡时, 舵偏角输出已不为正弦波形, 而为三角波。在振荡信号的传播过程中, 机电作动系统改变了信号的波形。
3) 无刷直流电机转速、系统输出转矩及舵偏角的振荡与振荡信号同频率变化, 振荡信号频率越大, 舵偏角输出抖动越快。
4) 振荡信号频率在0.2~3 Hz时, 舵偏角输出波动剧烈, 不能跟踪指令, 且振荡信号频率越小, 对舵偏角输出干扰越强。
5) 振荡信号频率在8~10 Hz时, 输出转矩频繁切换, 易损伤机械传动装置, 且振荡信号频率越高, 输出转矩切换时刻越早。
6) 当振荡信号幅值大于正常信号100%时, 系统跟踪指令的速度随振荡信号幅值的增大而减小, 振荡信号幅值越大, 系统稳定性与快速性越差。
4 结论 1) 本文建立了机电作动系统的动力学模型, 分析机电作动系统非指令振荡信号的产生机理, 研究了振荡信号的一般表现形式、产生位置及注入方法。
2) 系统架构会改变振荡信号波形, 振荡信号波形由正弦波改变为舵偏角输出的尖波振荡。
3) 传感器输出振荡信号的故障影响最大, 舵偏角不能正常跟踪指令信号, 输出转矩在额定值内抖动, 对机械传动结构造成不可逆转的损伤。
4) 电机转速、系统输出转矩及舵偏角的振荡与振荡信号同频率变化。
5) 振荡信号频率在0.2~3 Hz、8~10 Hz时, 输出舵偏角与转矩波动剧烈, 不能正常跟踪指令, 导致传动机构损伤, 故障影响严重。
6) 当振荡信号幅值大于正常信号100%时, 系统跟踪指令速度随振荡信号幅值增大而减小。
本文结论为机电作动系统故障模式与影响适航审查提供支持。
参考文献
| [1] | CAO W, MECROW B C, ATKINSON G J, et al. Overview of electric motor technologies used for more electric aircraft (MEA)[J].IEEE Transactions on Industrial Electronics, 2012, 59(9): 3523–3531.DOI:10.1109/TIE.2011.2165453 |
| [2] | 王留呆. 电传飞控系统舵面振荡故障检测的一种实现形式和符合性验证[J].科技信息, 2014(11): 40. WANG L D. An implementation and conformance verification of control surface oscillation fault detection in electronic flight control system[J].Science & Technology Information, 2014(11): 40.(in Chinese) |
| [3] | GOUPIL P. Oscillatory failure case detection in the A380 electrical flight control system by analytical redundancy[J].Control Engineering Practice, 2010, 18(9): 1110–1119.DOI:10.1016/j.conengprac.2009.04.003 |
| [4] | 欧旭坡, 朱亮, 徐东光. 民机飞控系统适航性设计与验证[M].上海: 上海交通大学出版社, 2015: 154-155. OU X P, ZHU L, XU D G. Airworthiness design and verification of civil aircraft flight control system[M].Shanghai: Shanghai Jiao Tong University Press, 2015: 154-155.(in Chinese) |
| [5] | OSSMANN D, VAN DER LINDEN F L J. Advanced sensor fault detection and isolation for electro-mechanical flight actuators[C]//NASA/ESA Conference on Adaptive Hardware and Systems (AHS). Piscataway, NJ: IEEE Press, 2015: 1-8. |
| [6] | BALABAN E, SAXENA A, NARASIMHAN S, et al. Experimental validation of a prognostic health management system for electro-mechanical actuators[C]//AIAA Infotech@Aerospace, St. Louis, Missouri. Reston: AIAA, 2013, 12: 329-344. |
| [7] | VINSON G, COMBACAU M, PRADO T. Synchronous machine faults detection and diagnosis for electro-mechanical actuators in aeronautics[J].IFAC Proceedings Volumes, 2012, 45(20): 770–775.DOI:10.3182/20120829-3-MX-2028.00119 |
| [8] | BORELLO L, VILLERO G, VEDOVA M D L D. Redundant hydraulic secondary flight control systems behavior in failure conditions[J].Mechanical Engineering and Automation, 2013, 32(8): 499–506. |
| [9] | 邢琰, 吴宏鑫, 王晓磊, 等. 航天器故障诊断与容错控制技术综述[J].宇航学报, 2003, 24(3): 221–226. XING Y, WU H X, WANG X L, et al. Summary of fault diagnosis and fault-tolerant control technology of spacecraft[J].Acta Aeronautica Sinica, 2003, 24(3): 221–226.(in Chinese) |
| [10] | FAA, Special conditions. Airbus model A380-800 airplane: No. 25-316-SC[S]Washington, D. C. : Federal Aviation Administration, 2006. |
| [11] | FAA, Special conditions. Boeing model 777 series airplanes: No. 25-ANM-78[S]. Washington, D. C. : Federal Aviation Administration, 1993. |
| [12] | SACHS H, CARL U B, THIELECKE F. Impact of oscillatory failure cases in electro-hydraulic actuation systems on an aeroelastic aircraft: 2007-01-3902[R]. Hanburg: SAE Technical Paper, 2007. |
| [13] | LAVIGNE L, ZOLGHADRI A, GOUPIL P, et al. Robust and early detection of oscillatory failure case for new generation airbus aircraft[C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Reston: AIAA, 2008, 98: 715-721. |
| [14] | URBANO S. Early and robust detection of oscillatory failure cases(OFC) in the flight control system: A data driven technique[C]//55th AIAA Aerospace Sciences Meeting. Reston: AIAA, 2017. |
| [15] | GAO Z, CECATI C, DING S X. A survey of fault diagnosis and fault-tolerant techniques-Part Ⅰ:Fault diagnosis with model-based and signal-based approaches[J].IEEE Transactions on Industrial Electronics, 2015, 62(6): 3757–3767.DOI:10.1109/TIE.2015.2417501 |
| [16] | HILL C I, BOZHKO S, YANG T, et al. More electric aircraft electro-mechanical actuator regenerated power management[C]//24th IEEE International Symposium on Industrial Electronics (ISIE). Piscataway, NJ: IEEE Press, 2015: 337-342. |
| [17] | 刘彬. 舵机用无刷直流电机控制系统研究[D]. 西安: 西北工业大学, 2004: 30-31. LIU B. Research on steering engine using brushless DC motor control system[D]. Xi'an: Northwestern Polytechnical University, 2004: 30-31(in Chinese). |
| [18] | 张仁嘉, 吴志刚, 杨超. 电动伺服舵系统动力学建模及颤振分析[J].北京航空航天大学学报, 2016, 42(7): 1368–1376. ZHANG R J, WU Z G, YANG C. Dynamic modeling and flutter analysis of a fin-actuator system[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7): 1368–1376.(in Chinese) |
| [19] | KIM S. Modeling and fault analysis of BLDC motor based servo actuators for manipulators[C]//IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2008: 767-772. |
| [20] | 李璠, 毛海涛. 飞机机电作动系统故障模式分析与故障诊断方法[J].航空维修与工程, 2016(3): 47–50. LI P, MAO H T. The method of failure mode analysis and diagnosis for aircraft electromechanical actuation system[J].Aviation Maintenance and Engineering, 2016(3): 47–50.(in Chinese) |
