此外,虽然多传感器系统通过协作能够从不同角度和视野获得目标信息,但有源传感器在获得持续量测时会不断向外辐射电磁波,容易暴露自身位置。如何合理有效地量化传感器辐射,日益成为国内外****的研究热点。传统算法中采用降低开机次数控制辐射风险[6-8],实际上不同时刻传感器辐射风险是不同的。因此,文献[9-10]提出低截获概率(Low Probability of Intercept,LPI)熵量化不同时刻传感器辐射风险,更具合理性。但是,计算截获概率需要已知窗函数信息,这在实际应用中往往难以获取[11]。近年来,在LPI基础上,文献[12]提出采用辐射度影响(Emission Level Impact,ELI)量化传感器辐射。在此基础上,文献[13-14]研究了目标跟踪中跟踪精度与辐射代价平衡优化问题。然而,该平衡优化问题只能保证加权性能最优,不适用战术需求已知的场景[15],甚至某些时刻跟踪精度过低或辐射风险过高,从而导致目标丢失或传感器被摧毁。
针对上述问题,研究跟踪任务需求下辐射控制问题,本文提出一种多传感器协同跟踪与辐射控制的调度算法。该算法引入ELI量化传感器辐射,构建基于部分可观马尔可夫决策过程(Partially Observable Markov Decision Process,POMDP)的目标跟踪与辐射控制模型;将长时调度问题转化决策树寻优问题,给出基于改进分支定界技术(Improved Branch and Bound,IB & B)的搜索算法。仿真结果验证了本文搜索算法和调度算法的有效性。
1 问题描述及系统建模 为了更好地描述问题,建立如图 1所示的有源传感器调度场景。本文目的是量化传感器辐射风险,考虑跟踪任务需求,寻求跟踪精度约束下,具有最小辐射风险的传感器调度序列。根据POMDP理论,建立基于POMDP的目标跟踪及辐射控制模型,以有效跟踪目标状态、控制系统辐射风险。
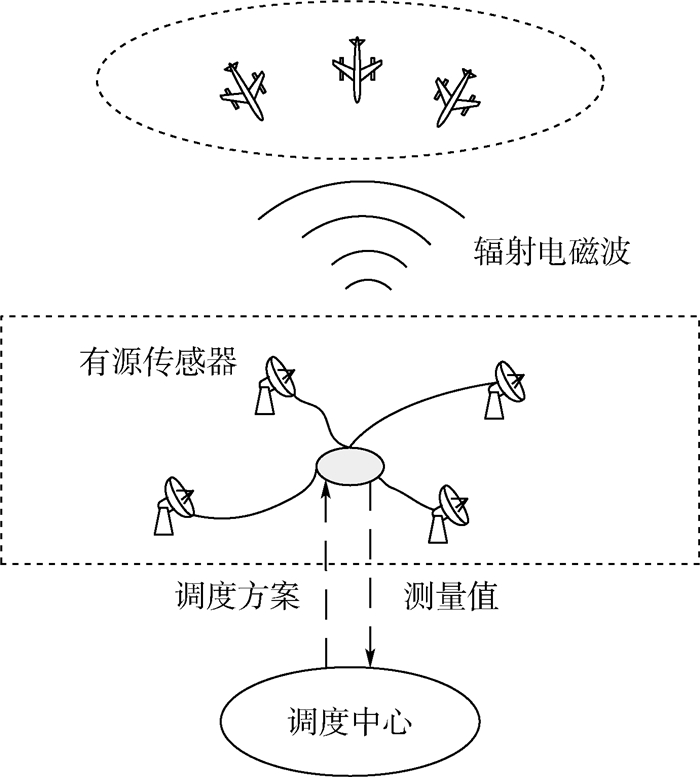 |
| 图 1 有源传感器调度场景 Fig. 1 Active sensor scheduling scenario |
| 图选项 |
1.1 传感器调度动作 假定有N个有源传感器在三维监视空间中协同跟踪一个目标,考虑到多传感器配准的困难性,每个时刻只有一个传感器跟踪目标。定义k时刻调度动作为ak=(ak, n)1×N,其中ak, n=1或0分别表示k+1时刻调度或不调度有源传感器n。
1.2 状态空间及状态转移 k时刻系统状态Sk由目标运动状态Xk和传感器ELI状态Ek组成,即
 | (1) |
式中:[xk, yk, zk]和

目标状态按照状态转移方程转移到下一时刻,即
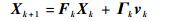 | (2) |
式中:Fk为状态转移矩阵;Γk和vk分别为噪声输入矩阵和零均值高斯噪声。
将传感器ELI状态量化为有限状态集合{1, 2, …, Ns},集合中每个值代表相应的ELI状态真值。考虑到传感器ELI状态会按照状态转移矩阵Tk, n来实现转移[12]。当调度传感器n时,则
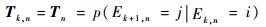 | (3) |
否则,Tk, n为Ns维单位矩阵INs。因此,传感器ELI状态转移矩阵可表示为
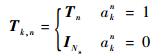 | (4) |
式中:Tn为传感器n的ELI状态转移矩阵。
1.3 观测空间及观测矩阵 k时刻系统观测Zk由目标状态观测ZXk和瞬间观测威胁度ZEk组成,则
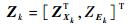 | (5) |
式中:ZXk和ZEk分别为传感器跟踪目标时获得的量测值及其对应的瞬间观测威胁度。
对于有源传感器(如雷达),其量测值由斜距离r、方位角θ及高低角φ组成,即
 | (6) |
式中:
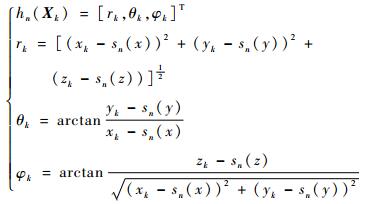 |
hn和wk, n分别为传感器n的非线性量测方程和零均值高斯噪声;sn(x)、sn(y)和sn(z)为传感器n的位置信息。
同理,将瞬间观测威胁度量化为有限状态集合{1, 2, …, Ms},集合中每个值对应真实的瞬间威胁度。考虑到瞬间观测威胁度与真实瞬间威胁度的关系,当调度传感器n时,可用一组观测矩阵来表示,即
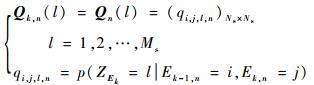 | (7) |
式中:qi, j, l, n为ELI前后状态分别为i和j时,瞬间观测威胁度为l的条件概率。
否则,Qk, n(l)为Ms维单位矩阵IMs。因此,传感器ELI观测矩阵可表示为
 | (8) |
1.4 信念状态 考虑到系统状态不能被完全观测,为了保持对目标运动状态和传感器ELI状态的持续更新,引入信念状态bk=[bXkT, bEkT]T,其中bXk为目标信念状态,bEk为ELI信念状态[16]。则根据所有历史信息及初始状态ηk,得
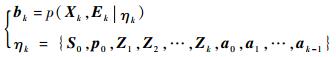 | (9) |
式中:S0和p0为系统初始状态及其分布。
2 辐射风险控制下长时调度算法 2.1 系统长时辐射风险 定义k时刻系统长时辐射风险R为一段时域内所有被调度传感器的ELI信念状态期望之和,则
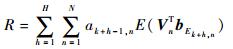 | (10) |
式中:H为时域长度;符号E为取期望操作;Vn=[1, 2, …, Ns]T为ELI实际量化值。
根据隐马尔可夫模型(Hidden Markov Model,HMM)滤波器理论,若已知k+1瞬间观测威胁度,则可以获知k+1时刻ELI信念状态[12]。以调度传感器n为例,其ELI信念状态更新为
 | (11) |
式中:lk+1为k+1时刻瞬间观测威胁度;1为Ns维单位向量;符号⊙表示Hadamard积。
观察式(11),虽然k时刻不能获知k+1的瞬间观测威胁度lk+1,但依据所有历史状态能够获lk+1的分布概率,即
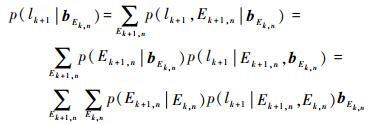 | (12) |
进一步,可得
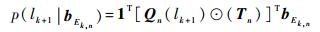 | (13) |
则单步辐射风险为
 | (14) |
因此,代入式(10),长时辐射风险为
 | (15) |
2.2 目标跟踪精度 依据贝叶斯滤波原理,目标信念状态的实时更新包括预测和更新2个阶段,即预测阶段为
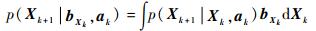 | (16) |
更新阶段为
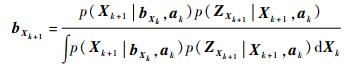 | (17) |
对于任意给定的系统,结合式(16)和式(17)目标信念状态可由粒子滤波(Particle Filter,PF)实时更新[1]。进一步,考虑到过程噪声和量测噪声均为高斯噪声,目标信念状态bXk服从高斯分布,即
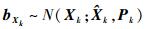
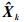

步骤1??初始化。目标信念状态中获取状态均值和方差, bXk的期望值为
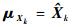
步骤2??时间更新。无迹变换获得2L+1个sigma点,并依据状态转移矩阵传递得χk+1|ki(i=0, 1, …, 2L),则
 |
式中:L为状态维数;ω=[ω0, ω1, …, ω2L]T为权重向量。
步骤3??量测更新。
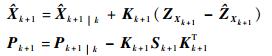 |
式中:Pk+1|k、Kk+1和Sk+1分别为预测协方差、滤波增益和新息协方差[17]。
步骤4??更新目标信念状态,预测跟踪精度ρk+1。
 |
步骤5??k=k+1,转到步骤2直至k+H步结束。
因此,根据上述步骤能够实时更新目标信念状态,估计目标跟踪精度。
2.3 基于改进分支定界技术搜索算法 考虑跟踪任务需求,辐射控制下传感器长时调度问题可描述为
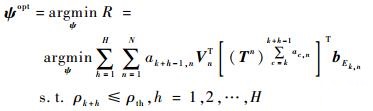 | (18) |
式中:ψ=[ak, ak+1, …, ak+H-1]为H步调度序列;ρth为期望跟踪精度。
将上述H步长时调度问题转化为深度为H的决策树寻优问题,图 2给出了深度H=3,传感器个数N=4的决策树示意图。图中(Rk+h, l, ρk+h, l)表示k+h层第l个节点对应的h步长时辐射风险和目标跟踪精度。图中每个调度动作ak+h将第k+h层节点展开至下一层子节点,从而形成深度为H的决策树。因此,寻找最优的调度序列ψopt就是在决策树中搜索满足跟踪精度约束的最小长时辐射风险及其对应的节点序列。
 |
| 图 2 决策树示意图(H=3, N=4) Fig. 2 An illustrative decision tree (H=3, N=4) |
| 图选项 |
传统的决策树搜索算法中,标准代价搜索(Uniform Cost Search, UCS)以代价为顺序进行搜索,其打开的节点较少,因此搜索效率较高。然而,考虑到搜索节点数随着决策步长H的增加呈指数增长,UCS依然需要耗费大量的时间。分支定界技术能够有效剪除多余分支和节点[18],为此借鉴UCS思想,提出基于IB & B技术的搜索算法,给出各节点的次优下界值,并以此下界值为剪支依据,在不丢失最优解的基础上加快搜索速度。
若已知第k+h层节点的调度序列为ψk:k+h-1=[ak, ak+1, …, ak+h-1],则该节点的下界值[18]为
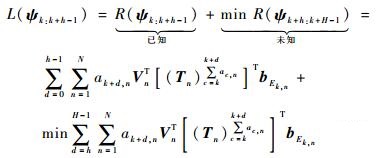 | (19) |
传统的分支定界技术需要精确求解各节点最优下界值,以期最大限度的剪除多余分支,加快搜索速度。然而,对于任意给定的转移矩阵Tn,R(ψk+h:k+H-1)存在NH-h种组合,求解该值的最优下界值难度较大,需要额外采用其他搜索算法,增加了搜索时间和存储空间。为此,结合本文实际,在不增加搜索空间和存储空间的基础上,给出R(ψk+h:k+H-1)的次优下界值。对于任意传感器n,在任意步长d,令
 | (20) |
则存在
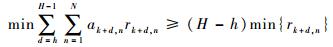 | (21) |
因此,该节点的次优下界值为
 | (22) |
式(22)给出了节点次优下界值,求解该值无需复杂的搜索算法,只需对比各传感器在剩余H-h时域内的辐射风险大小即可。跟踪精度约束下,基于IB & B技术的搜索算法流程如下。
步骤1??从根节点开始搜索,将根节点放入列表,并令初始的最优长时辐射风险为Ropt=+∞。
步骤2??若列表不为空,剔除列表第一个节点,并从该节点向下一深度搜索所有路径,由式(15)预测长时辐射风险,UKF估计目标跟踪精度;剔除不满足跟踪精度约束的节点,由式(22)计算剩余节点的次优下界值;剔除次优下界值大于当前Ropt的节点,并以次优下界值为顺序将剩余节点放入列表。
步骤3??重复打开列表第一个节点,若未到达最大搜索深度H,则转到步骤2;否则,转到步骤4。
步骤4??若节点长时辐射风险小于当前Ropt,则将该长时辐射风险记为Ropt,并记录该节点,转到步骤3。
步骤5??打开列表节点,直至列表为空。
若Ropt小于+∞,搜索成功,从对应节点中获得最优调度序列;否则,搜索失败,即所有调度序列均不满足跟踪精度需求,则下一时刻调度跟踪误差最小的传感器,以快速满足精度需求。
3 仿真验证与分析 考虑N=4的有源传感器系统,协同跟踪一个近似匀速直线(Nearly Constant Velocity,NCV)运动的目标。目标初始位置为(8, 6, 5)km,初始速度为(-280, -220, 0)m/s。传感器坐标分别为(0, -5, 0)km、(-5, 0, 0)km、(5, 0, 0)km和(0, 5, 0)km。将传感器ELI状态量化为{1, 2, 3}(分别表示低辐射状态、中辐射状态和高辐射状态);瞬间观测威胁度量化为{1, 2, 3}(分别表示小增量、中增量和高增量)。不失一般性,假设传感器4具有更好地观测性能,但其更易处于高辐射状态;传感器1观测性能最差,但其更易处于低辐射状态。则对应的量测噪声设置为σr1=200 m, σθ1=σφ1=0.01 rad, σr2=σr3=100 m, σθ2=σθ3=σφ2=σφ3=0.005 rad,σr4=10 m, σθ4=σφ4=0.001 rad,σrn、σθn和σφn分别为传感器n的斜距离、方位角和俯仰角标准差。ELI转移矩阵分别为
 |
3.1 搜索算法性能对比 为了验证IB & B搜索算法的先进性,采用已有的3种搜索算法进行对比,即穷举搜索(Enumerative Search, ES)、UCS[4]和基于UCS的阈值ε近似搜索(记为ε-UCS)[10]。
表 1为不同算法不同决策步长搜索性能对比,图 3为H=3时,不同搜索算法节点打开占比。由图 3可知,ε-UCS算法通过引入阈值剪支能够在一定程度上减少节点打开数,但ε-UCS算法是以丢失最优解为代价的[10]。相比于ε-UCS算法,本文提出的IB & B算法能够在不丢失最优解的情况下,显著降低节点打开数。进一步结合表 1,决策步长H越大,IB & B算法优势越明显。文献[4]指出,系统耗时和系统内存消耗分别与节点打开数和最大存储节点成正比。因此,本文提出的IB & B算法具有较好的实时性和可行性。
表 1 算法搜索性能对比 Table 1 Comparison of search performance among algorithms
| 算法 | H=2 | H=3 | H=4 | H=5 | |||||||
| 节点打开数(占比) | 最大存储节点 | 节点打开数(占比) | 最大存储节点 | 节点打开数(占比) | 最大存储节点 | 节点打开数(占比) | 最大存储节点 | ||||
| ES | 20 | 16 | 84 | 64 | 340 | 256 | 1 364 | 1 024 | |||
| UCS | 17(85%) | 4 | 69(82%) | 16 | 240(70%) | 64 | 856(63%) | 251 | |||
| ε-UCS | 17(85%) | 4 | 62(74%) | 16 | 177(52%) | 64 | 533(39%) | 251 | |||
| IB & B | 9(45%) | 4 | 19(23%) | 12 | 36(11%) | 28 | 73(5%) | 66 | |||
表选项
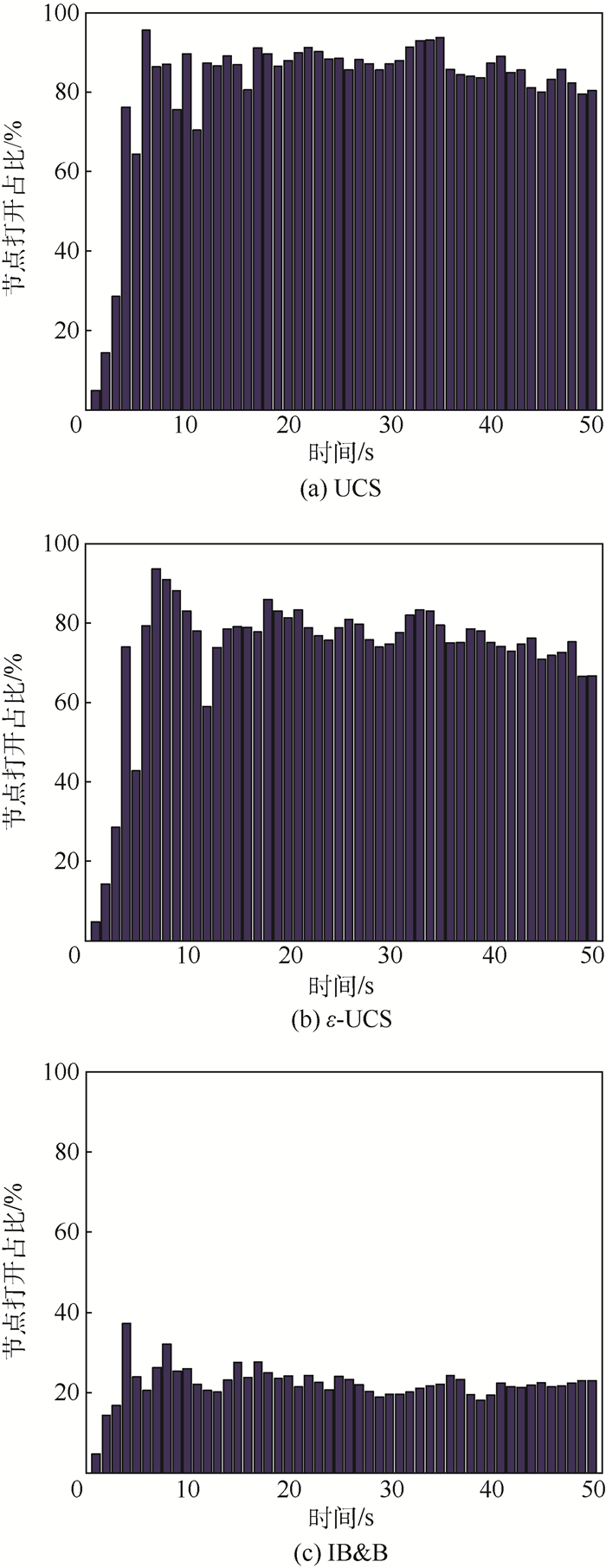 |
| 图 3 不同搜索算法的节点打开占比 Fig. 3 Percentage of opened node of different search algorithms |
| 图选项 |
图 4为不同决策步长下的最优累积辐射风险。由图可知,随着决策步长H增大,系统能够获得更优地调度序列,使得累积辐射风险更低,从而验证了长时调度模型的必要性。结合本文仿真条件,当决策步长H>3,系统累积辐射风险下降幅度变缓(这与仿真条件设置相关)。因此,不失一般性,之后的仿真实验将以H=3为例。
 |
| 图 4 不同决策步长下的最优累积辐射风险 Fig. 4 Optimum cumulative radiation risk versus decision step |
| 图选项 |
3.2 调度算法性能对比 为了验证本文调度算法的有效性,采用已有的4种调度策略进行对比:
1) 固定调度策略(Fixed Scheduling Policy,FSP)[16],整个跟踪过程中一直选择某个传感器。不失一般性,本文以传感器2跟踪目标为例。
2) 最近调度策略(Closest Scheduling Policy,CSP)[1],调度与目标最近距离的传感器。
3) 短时调度策略(Myopic Scheduling Policy, MSP),以单步预测收益进行决策[14, 19]。
4) 基于ε-UCS的长时调度策略,以ε-UCS搜索算法获得调度序列[10]。
采用均方根误差(Root Mean Square Error,RMSE)衡量算法跟踪性能,图 5为不同跟踪精度阈值下,目标RMSE对比。如图 5所示,FSP和CSP在不同跟踪精度阈值下,其目标RMSE均不能满足精度需求。MSP、ε-UCS和本文算法能够根据阈值变化自适应的调度传感器以满足精度需求。进一步,由于初始时刻目标误差较大,根据2.3节搜索策略,当所有传感器均不能满足精度需求时,则调度跟踪误差最小的传感器。图 5给出了跟踪精度阈值ρth为30、50和70 m的目标RMSE,对于其他ρth也同样适用。
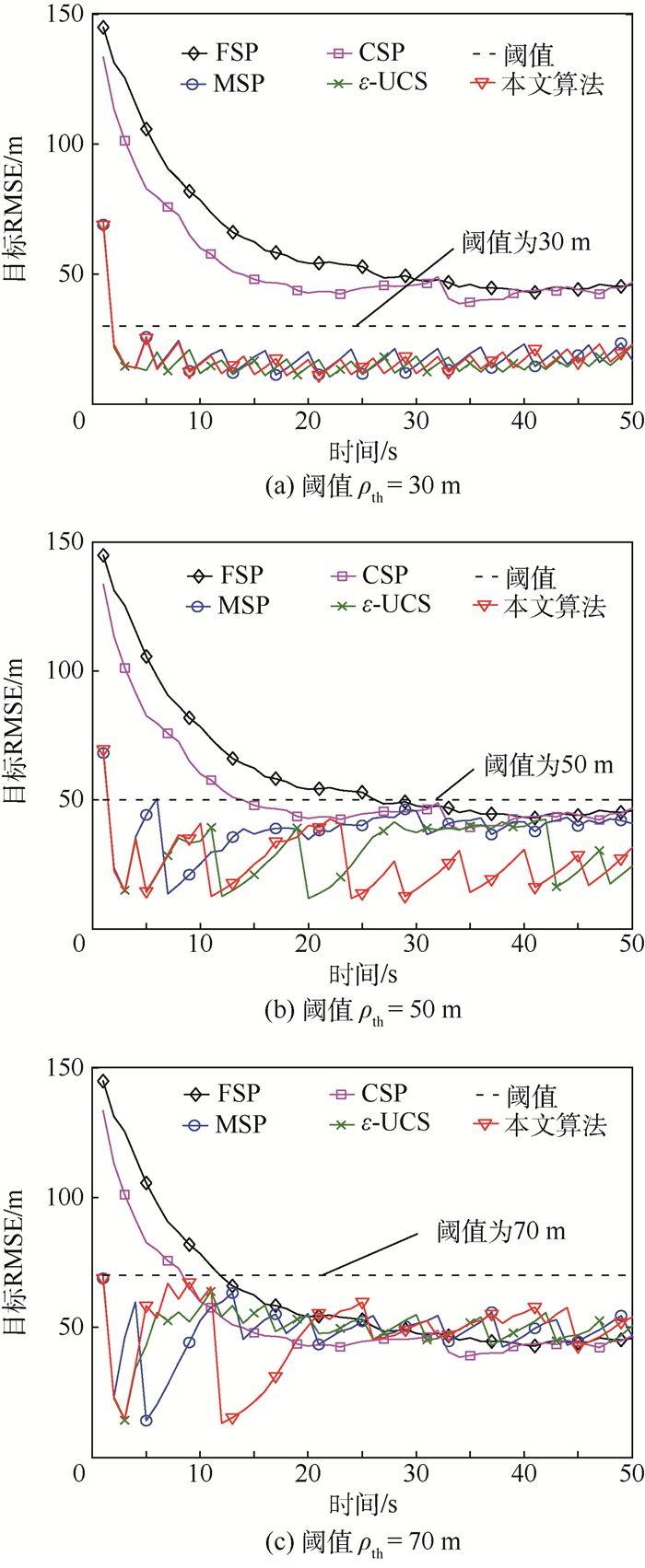 |
| 图 5 不同阈值下的目标RMSE Fig. 5 Target RMSE of different thresholds |
| 图选项 |
以跟踪精度阈值ρth=50 m为例,图 6为不同策略下的累积辐射风险和累积ELI值。以图 6(a)为例,FSP和CSP由于没有控制辐射,选择辐射风险小的传感器,其对应的累积辐射风险均较高。MSP以单步预测收益进行决策,其累积辐射风险得以控制。相比于MSP,以一段时域内预测收益进行决策能够获得更低的累积辐射风险。进一步,由于IB & B搜索算法能够保证不丢失最优解。因此,本文算法的累积辐射风险要更低于ε-UCS。此外,虽然ELI状态不完全可观,但其真实信息包含在ELI信念状态中。因此,结合式(10)和式(18),辐射风险函数中包含了ELI真实信息,通过优化目标函数可以降低系统累积辐射风险和累积ELI值。对比图 6(a)、(b),图中数据验证了辐射风险函数和目标优化函数的合理性和有效性。
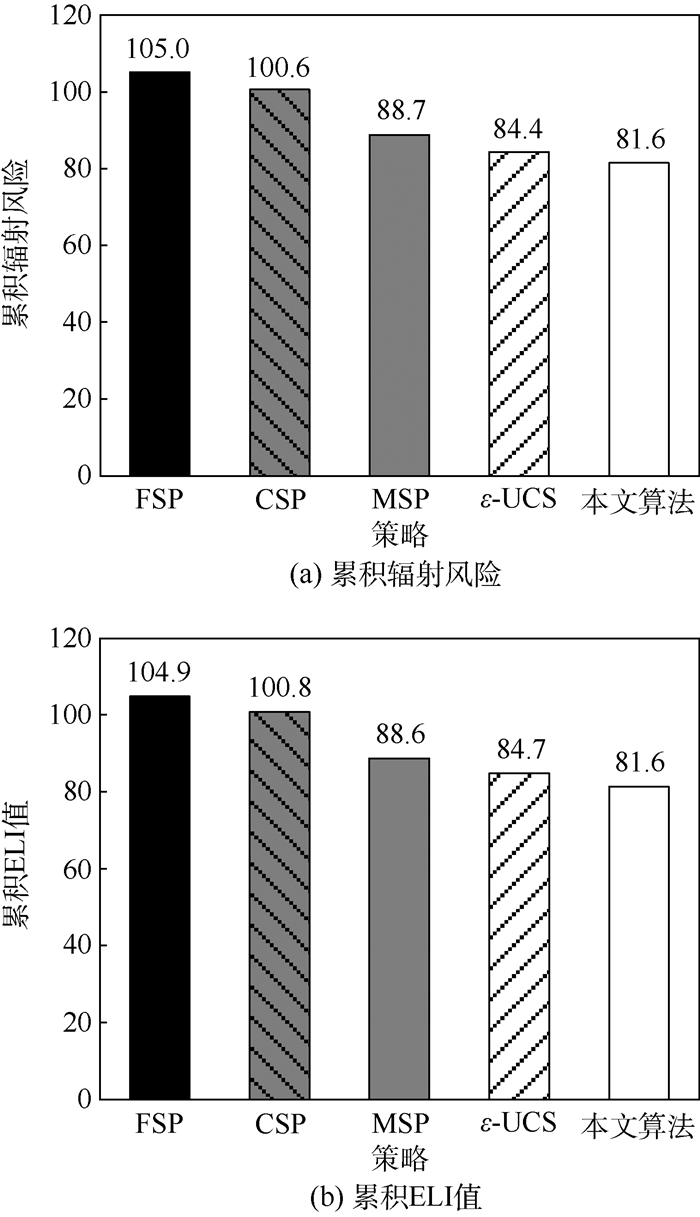 |
| 图 6 不同策略下的累积辐射风险和累积ELI值 Fig. 6 Cumulative radiation risk and cumulative ELI value of different policies |
| 图选项 |
图 7为不同时间下的系统累积辐射风险。由图 7可知,在整个时间范围内,FSP和CSP的辐射风险均较高,以一段时域预测收益进行决策(本文算法和ε-UCS)要优于以单步预测收益进行决策(MSP)。此外,ε-UCS可能会丢失最优解,其对应的累积辐射风险要高于本文算法。因此,验证了本文算法在整个时间范围内的有效性。
 |
| 图 7 不同时间下的累积辐射风险 Fig. 7 Cumulative radiation risk versus time |
| 图选项 |
4 结论 针对有源传感器协同跟踪目标时存在被敌方截获的风险,以目标跟踪任务为需求,提出多传感器协同跟踪与辐射控制的调度算法,经仿真实验表明:
1) 引入ELI量化传感器辐射风险,并设计辐射风险函数,该函数能够有效的衡量传感器真实ELI状态,控制系统辐射风险。
2) 提出基于IB & B技术的搜索算法,与已有的搜索算法相比,该算法能够有效降低节点打开数和最大存储数,提高了搜索实时性。
3) 与已有调度策略相比,本文调度算法能够在满足跟踪任务需求下,获得更优的调度序列,系统辐射风险更低,提高了己方生存能力。
参考文献
| [1] | LI Y, KRAKOW L W, CHONG E K P, et al. Approximate stochastic dynamic programming for sensor scheduling to track multiple targets[J].Digital Signal Processing, 2009, 19(6): 978–989.DOI:10.1016/j.dsp.2007.05.004 |
| [2] | 刘钦, 刘铮. 一种基于Rényi信息增量的机动目标协同跟踪算法[J].控制与决策, 2012, 27(9): 1437–1440. LIU Q, LIU Z. A method of maneuvering target collaboration tracking based on Rényi information gain[J].Control and Decision, 2012, 27(9): 1437–1440.(in Chinese) |
| [3] | 程洪玮, 王博, 安玮. 一种基于信息决策树的低轨星座传感器调度算法[J].电子学报, 2010, 38(11): 2630–2634. CHENG H W, WANG B, AN W. A sensor scheduling method of LEO constellation based on information decision tree[J].Acta Electronica Sinica, 2010, 38(11): 2630–2634.(in Chinese) |
| [4] | CHHETRI A S, MORRELL D, PAPANDREOU S A. Nonmyopic sensor scheduling and its efficient implementation for target tracking applications[J].EURASIP Journal on Advances in Signal Processing, 2006(1): 1–18. |
| [5] | SUNBERG Z, CHAKRAVORTY S, ERWIN R S. Information space receding horizon control for multisensor tasking problem[J].IEEE Transactions on Cybernetics, 2016, 46(6): 1325–1336.DOI:10.1109/TCYB.2015.2445744 |
| [6] | LIU B, JI C L, ZHANG Y Y, et al. Blending sensor scheduling strategy with particle filter to track a smart target[J].Wireless Sensor Network, 2009, 1: 300–305.DOI:10.4236/wsn.2009.14037 |
| [7] | 吴巍, 王国宏, 双炜, 等. 多机载平台多目标跟踪与辐射控制[J].系统工程与电子技术, 2012, 34(3): 495–501. WU W, WANG G H, SHUANG W, et al. Multi-airborne-platform multi-target tracking and radiation control technology[J].Systems Engineering and Electronics, 2012, 34(3): 495–501.(in Chinese) |
| [8] | 吴卫华, 江晶, 高岚. 机载雷达辅助无源传感器对杂波环境下机动目标跟踪[J].控制与决策, 2015, 30(2): 277–282. WU W H, JIANG J, GAO L. Tracking maneuvering target in clutter with passive sensor aided by airborne radar[J].Control and Decision, 2015, 30(2): 277–282.(in Chinese) |
| [9] | ZHANG Z, SHAN G. UTS-based foresight optimization of sensor scheduling for low interception risk tracking[J].International Journal of Adaptive Control and Signal Processing, 2014, 28(10): 921–931.DOI:10.1002/acs.v28.10 |
| [10] | ZHANG Z, SHAN G. Non-myopic sensor scheduling to track multiple reactive targets[J].IET Signal Processing, 2015, 9(1): 37–47.DOI:10.1049/iet-spr.2013.0187 |
| [11] | SHE J, WANG F, ZHOU J. A novel sensor selection and power allocation algorithm for multiple-target tracking in an LPI radar network[J].Sensors, 2016, 16(12): 2193–2206.DOI:10.3390/s16122193 |
| [12] | KRISHNAMURTHY V. Emission management for low probability intercept sensors in network centric warfare[J].IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(1): 133–151.DOI:10.1109/TAES.2005.1413752 |
| [13] | 单甘霖, 张子宁. 面向目标跟踪的单平台主被动传感器长期调度[J].系统工程与电子技术, 2014, 36(3): 458–463. SHAN G L, ZHANG Z N. Non-myopic sensor scheduling in a single platform for target tracking[J].Systems Engineering and Electronics, 2014, 36(3): 458–463.(in Chinese) |
| [14] | SHAN G, ZHANG Z. Non-myopic sensor scheduling for low radiation risk tracking using mixed POMDP[J].Transactions of the Institute of Measurement and Control, 2017, 39(2): 230–243.DOI:10.1177/0142331215604211 |
| [15] | KALANDROS M. Covariance control for multisensor systems[J].IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(4): 1138–1157.DOI:10.1109/TAES.2002.1145739 |
| [16] | SONG H, XIAO M, XIAO J, et al. A POMDP approach for scheduling the usage of airborne electronic countermeasures in air operations[J].Aerospace Science and Technology, 2016, 48: 86–93.DOI:10.1016/j.ast.2015.11.001 |
| [17] | ROY A, MITRA D. Unscented-Kalman-filter-based multitarget tracking algorithms for airborne surveillance application[J].Journal of Guidance, Control, and Dynamics, 2016, 39(9): 1949–1966.DOI:10.2514/1.G001587 |
| [18] | HUBER M F. Optimal pruning for multi-step sensor scheduling[J].IEEE Transactions on Automatic Control, 2012, 57(5): 1338–1343.DOI:10.1109/TAC.2011.2175070 |
| [19] | 宋海方, 肖明清, 陈游, 等. 基于MDP的战机对抗导弹措施优化算法[J].北京航空航天大学学报, 2017, 43(5): 942–950. SONG H F, XIAO M Q, CHEN Y, et al. MDP method for optimization of fighter aircraft's countermeasures against missile[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(5): 942–950.(in Chinese) |
