振动是外力作用于弹性体后产生周期性运动的一种自然现象，0.01~20 Hz的振动被称为低频超低频振动^[1]。低频超低频振动传感器在地震预警、能源勘探、航空航天、核工程、以及生物医学等领域有着非常重要的应用。
目前，发动机振动破坏是造成航空航天飞行器运行故障的主要原因，对航空发动机关键部件振动指标的实时监测，能够为故障的排查提供准确的依据；另外，太空环境下的微振动的频率范围介于0.01~1 Hz之间^[1]，国防工业中核工程的信号检测范围更是低至0.003 Hz。因此，对于具有良好低频响应的低频振动传感器的研制已经成为研究热点。
早期的多轴振动测量实际上是把单轴振动传感器安装在3个垂直的方向分别测量。后来国内外专家****设计出的压阻式、压电式和电容式^[2]振动传感器可以同时进行多轴测量。其中，压阻式^[3]和压电式振动传感器可以实现低频信号的三轴测量，而电容式振动传感器大多用于2个方向的低频信号检测。压电式和压阻式多轴振动传感器在测量低频信号时由于横向效应会使得各方向的结果相互影响^[4]，造成测量误差。目前，在低频振动测量领域磁电式振动速度传感器由于精度高、输出信号大以及抗干扰能力强等特点被广泛应用。但是由于磁电式振动速度传感器采用弹簧结构作为唯一的支承导向元件，系统刚度随机械结构固定，导致传感器本身的固有频率大约在5~30 Hz之间，在测量低于其固有频率的振动信号时，传感器的输出信号信噪比较低，在一定程度上限制了其应用。
因此本文基于磁悬浮效应和惯性式测量原理提出一种新型结构的多轴悬浮式低频振动传感器，并从测量机理、理论分析、仿真验证等方面进行阐述。
1 测量机理 多轴悬浮式低频振动传感器是一种新型的基于磁悬浮效应和惯性测量原理的振动传感器。测量时该传感器固定在被测振动体上，以地球上的惯性系为参考坐标，是一种绝对式测振仪^[5]。
当被测振动体频率远远高于振动传感器的固有频率时，质量块相对于壳体的位移与被测物体的位移数值相等、相位相反^[6]。所以，通过测量悬浮质量块相对于壳体在3个相互垂直方向(X轴、Y轴和Z轴)上的位移即可得到被测物体的多轴振动信号。图 1为多轴悬浮式低频振动传感器整体结构示意图，k为弹簧系数。

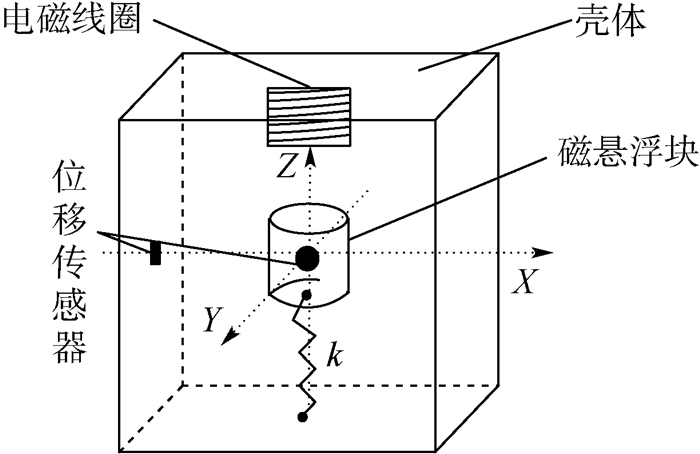图 1 多轴悬浮式低频振动传感器整体结构示意图 Fig. 1 Schematic diagram of overall structure of multi-axis maglev low-frequency vibration sensor

图选项

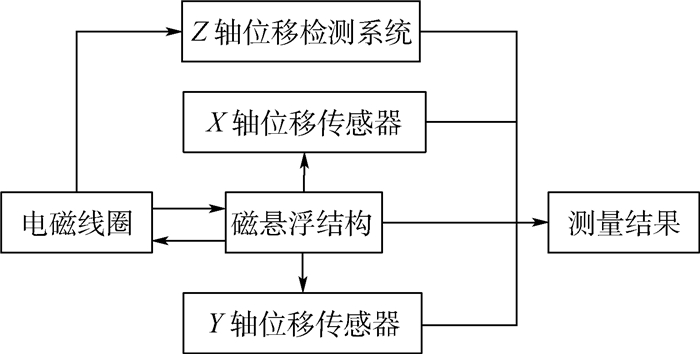
多轴悬浮式低频振动传感器机械结构由电磁线圈、悬浮质量块、光电位移传感器、微弹簧和壳体组成。其中电磁线圈、悬浮质量块和微弹簧同轴心，微弹簧下端固定在壳体底部、微弹簧上端与悬浮质量块底部固定连接。2个光电位移传感器分别用来测量质量块在X轴和Y轴方向上相对于壳体的振动位移。在多轴悬浮式低频振动传感器中，轴向位移检测电路被设计用来检测Z轴方向的振动信号。测量时该电路检测电磁线圈两端的电压变化量并把该电压变化量进行解调从而获得Z轴振动位移。轴向位移检测电路的设计实现了Z轴方向的无传感器位置自检测，有助于减小传感器体积，提高轴向位移检测的精度和稳定性。图 2为Z轴位移自检测原理示意图，m为惯性质量，c为阻尼。

图 2 Z轴位移自检测原理示意图 Fig. 2 Schematic diagram of principle of Z-axial displacement self-sensing

图选项

磁悬浮系统工作时，电磁线圈在驱动电流作用下产生的电磁吸力与质量块重力方向相反实现悬浮。动态测量时，由于电磁线圈产生的电磁吸力随质量块位移的变化而实时改变，无法与重力平衡，致使磁悬浮结构不能保持稳定，因此本系统设计加入微弹簧结构。敏感被测量时，悬浮质量块在电磁力、重力和弹簧弹力的共同作用下可回到平衡位置并实现稳定悬浮。图 3为多轴悬浮式低频振动传感器工作原理示意图。

图 3 多轴悬浮式低频振动传感器工作原理示意图 Fig. 3 Schematic diagram of working principle of multi-axis maglev low-frequency vibration sensor

图选项

综上所述，质量块能够在电磁线圈和微弹簧的共同作用下保持稳定悬浮；通过调整传感器的控制电流，可实现对系统等效刚度和等效阻尼的控制，从而使传感器具有较低的测量下限。
2 理论分析 2.1 典型磁悬浮系统数学模型 磁悬浮系统的力学模型如图 4所示，y为悬浮质量块与电磁铁之间的气隙位移，y₀为振动体位移。可以等效为一个由弹簧系数为k，惯性质量为m和阻尼为c三部分组成的系统^[7]。

图 4 典型磁悬浮系统的等效力学模型 Fig. 4 Equivalent mechanical model of typical maglev system

图选项

典型磁悬浮系统中悬浮质量块受重力和电磁吸力，由合外力与加速度关系可得

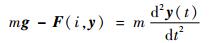(1)

式中：g为重力加速度；F(i, y)为质量块所受电磁力，i为电磁铁中的瞬时电流; 为质量块的加速度。
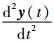
根据电磁力和磁场能量之间的关系^[8]，得到质量块所受的电磁力表达式为

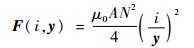(2)

式中：A为气隙的导磁截面积；μ₀=4π×10^-7 H/m为真空磁导率；N为电磁线圈匝数。
由于式(2)中μ₀、A、N均为常数，故定义常数l=μ₀AN²/4，则电磁力可改写为

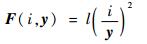(3)

通过式(3)可知：电磁力与气隙距离平方成非线性的反比关系，这也正是磁悬浮系统不稳定的根源所在^[9]。由于磁悬浮系统中存在着复杂的非线性关系，很难用来作为分析系统特性的依据，所以要进行线性简化。
设在平衡点处的电磁力为F(i₀, y₀)，将电磁力在平衡点处进行泰勒级数展开，因为平衡时电流变化量和位移变化量都很小，故忽略高次项得到线性化方程^[10]

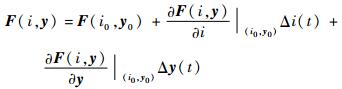(4)

式中：i₀和y₀分别为悬浮质量块处于平衡位置时，电磁线圈电流以及悬浮质量块与电磁铁之间的气隙位移；Δy(t)为气隙位移变化量；Δi(t)为电磁线圈电流变化量。对式(3)求偏导，可得

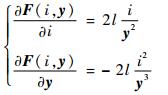(5)

将l=μ₀AN²/4代入式(5)可得

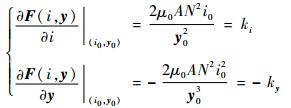(6)

式中：k_i和k_y分别为电流刚度系数和位移刚度系数。
在平衡点处F(i₀, y₀)与重力大小相等，把式(4)代入式(1)化简得到^[11]

(7)

对式(7)进行拉氏变换，得到位移与驱动电流的传递函数为

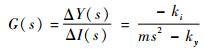(8)

对该传递函数的特征方程进行求解可知磁悬浮系统具有一个正实部极点，所以磁悬浮系统不稳定^[12]，因此本文在磁悬浮系统的基础上设计加入微弹簧结构来实现动态平衡。
2.2 多轴悬浮式低频振动传感器数学模型 加入微弹簧后系统的整体结构如图 1所示，此时重新对传感器中悬浮质量块进行受力分析。由牛顿第二定律可得

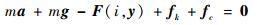(9)

式中：a为悬浮质量块的绝对加速度；f_k为微弹簧产生的弹性力；f_c为阻尼力。
根据2.1节叙述可知振动体的位移为y₀，那么悬浮质量块的绝对位移就是y₁：

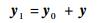(10)

又因式(9)中a为悬浮质量块的绝对加速度，所以可得

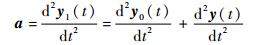(11)

在平衡点处，对处于平衡状态的悬浮质量块进行受力分析，将磁场力表达式(4)代入式(9)并整理得到悬浮质量块平衡点附近的动力学方程为

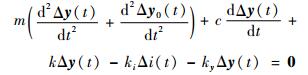(12)

因为该多轴悬浮式低频振动传感器在工作时保持通入电磁线圈的电流恒定不变，所以电流的变化量为零，即Δi(t)为零，代入式(12)并化简得

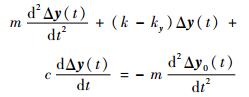(13)

由式(13)可见，多轴悬浮式低频振动传感器中悬浮质量块的动力学方程与质量-弹簧-阻尼系统的动力学方程相同，所以加入微弹簧后该传感器系统能够实现稳定悬浮。
2.3 刚度阻尼特性 本文所设计的多轴悬浮式低频振动传感器采用微弹簧以及永磁、电磁混合结构来取代传统磁电式振动速度传感器中的单一弹簧结构，其正常工作的必要条件就是要具有适当的刚度阻尼特性^[13]。
对式(13)进行拉氏变换，得到由被测振源引起的悬浮质量块与壳体间的位移与振源位移的传递函数H(s)为

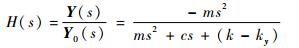(14)

将s=jω代入可得

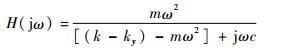(15)

典型的二阶力学系统的频响方程为

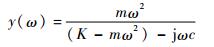(16)

将式(15)与式(16)对比可知，多轴悬浮式低频振动传感器的等效刚度系数为

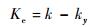(17)

把式(6)代入式(17)得

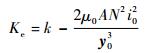(18)

所以，整理得到传感器的固有角频率为

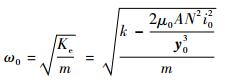(19)

阻尼比为

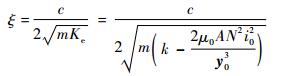(20)

上述理论分析表明：多轴悬浮式低频振动传感器的等效刚度和等效阻尼由敏感结构参数和控制电流共同决定。因此，当该传感器的机械结构参数确定后，通过合理的调整控制电流就可以获得期望的刚度、阻尼，从而有效降低传感器的固有频率。
2.4 轴向位移检测电路 测量振动时，悬浮结构在外力作用下跟随振源振动导致电磁线圈和悬浮质量块之间的气隙产生变化从而使电磁线圈磁阻发生变化。磁阻的变化又直接影响回路的电感，在这个过程中保持通入电磁线圈电流不变，电磁线圈两端电压必然会发生变化。因此，如果测量出回路电压的变化量，就可以反推出气隙长度。
多轴悬浮式低频振动传感器的电磁线圈可以等效为电阻R与电感L串联，由基尔霍夫电压定律可以得到电压u和电流i之间的关系^[14]：

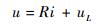(21)

式中：u_L为感应电势, 其表达式为

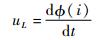(22)

其中：?为磁通量; t为时间。将式(22)代入式(21)可得

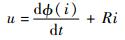(23)

又因为

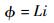(24)

所以，当传感器气隙发生变化导致传感器电感变化时可得到：

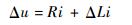(25)

式中：Δu为电磁线圈两端电压变化量；ΔL为电感变化量。
式(25)表明在平衡位置附近电压变化量与电感变化量的函数关系。当通入电磁线圈的电流恒定时，电磁线圈两端电压变化量与电感变化量成正比，又因为电感是位移的函数，所以把电压变化量解调就可以获得悬浮质量块在Z轴方向的振动位移。
在这个过程中电磁线圈既是励磁线圈又是检测线圈，所以Z轴位移测量不需要再额外安装位移传感器，避免了因此带来的故障；同时提高了Z轴位移检测的精度且有助于减小传感器的体积。
3 仿真验证 3.1 有限元磁场分析 当传感器敏感外界振动时，悬浮质量块与电磁线圈间气隙改变会引起径向电磁力与重力不平衡。因此对磁悬浮结构静态下气隙磁场分布的精确分析是该传感器研制的关键部分。有限元法是结构分析中应用最广泛的数值分析方法^[15]，因此采用该方法对传感器结构进行电磁场的三维建模，准确表达了磁感应强度的分布情况。
表 1为多轴悬浮式低频振动传感器的结构参数，在该结构参数下采用ANSYS对传感器建模然后进行有限元分析得到如图 5所示的磁悬浮结构磁力线分布图。从图 5中可以直观地看出磁力线主要分布在电磁线圈、永磁体以及二者之间气隙所组成的磁路中，即电磁线圈能够对圆柱形永磁体提供纵向的吸引力。
表 1 多轴悬浮式低频振动传感器结构参数 Table 1 Structure parameters of multi-axis maglev low-frequency vibration sensor

参数	数值
电磁线圈外径D1/mm	36
电磁线圈内径d1/mm	14
电磁线圈高度h1/mm	20
漆包线线径d2/mm	0.18
电磁线圈匝数N	3 000
圆柱形永磁体直径D2/mm	10
圆柱形永磁体高度h2/mm	12
圆柱形永磁体质量m /g	2.0
微弹簧刚度系数k/(N·m-1)	7.2

表选项

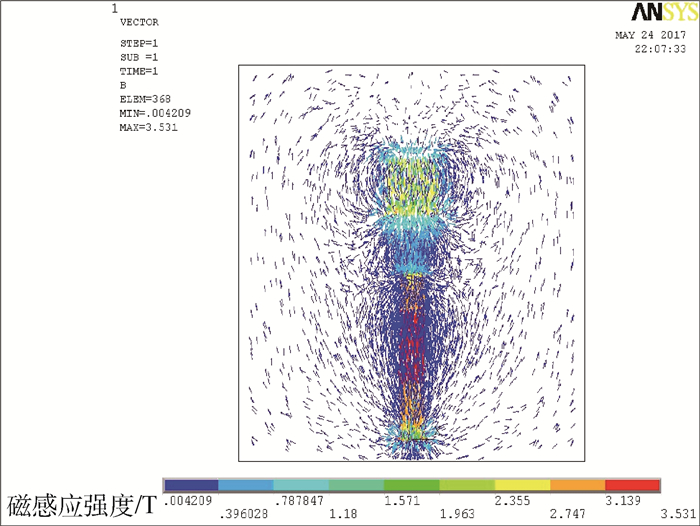图 5 磁悬浮结构磁力线分布图 Fig. 5 Magnetic induction of maglev structure

图选项

本文所设计的传感器中悬浮质量块的质量为2 g，重力约为0.02 N。表 2为ANSYS计算得到的悬浮质量块在磁场中各方向的受力情况。由数值可以看出水平方向(X轴和Y轴)电磁力相比Z轴方向差了2个数量级，所以电磁吸力主要集中在Z轴方向；且Z轴方向电磁力与悬浮质量块的重力大小相等。进一步证明电磁线圈不仅能够对圆柱形永磁体提供纵向吸引力，而且该力能够使质量块克服自身重力实现悬浮。ANSYS分析所得结论对多轴悬浮式低频振动传感器的研制提供了有力的理论依据。
表 2 悬浮体所受电磁力数值 Table 2 Values of electromagnetic attractive force of maglev mass block

N
电磁力	X轴方向	Y轴方向	Z轴方向
虚功力	2.908 8×10-4	1.060 4×10-4	2.055 8×10-2
麦克斯韦力	1.681 4×10-4	2.391 9×10-4	2.420 5×10-2

表选项






3.2 气隙磁场分析 磁悬浮系统不稳定的根本原因在于：电磁力随气隙位移发生改变导致无法与重力保持动态平衡^[16]。因此对电磁力及其影响因素的准确分析是多轴悬浮式低频振动传感器理论研究的重要环节。本文此节采用MATLAB对电磁力进行数值分析，用来指导该传感器的结构设计以及设定合适的平衡位置。
在表 1结构参数下用MATLAB计算得到悬浮质量块所受电磁力与控制电流和悬浮气隙的关系如图 6所示。电磁线圈产生的电磁力不仅跟传感器的机械结构有关还跟控制电流以及气隙位移有关系。

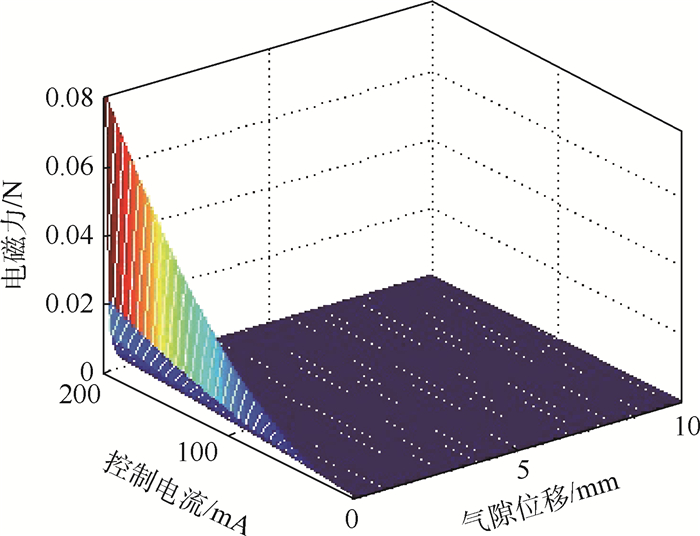图 6 电磁力与控制电流和气隙位移关系 Fig. 6 Relationship between electromagnetic force and control current and air gap displacement

图选项

从图 6可以看出电磁力与控制电流和气隙位移都呈非线性关系：当控制电流一定时，电磁力与气隙位移成反比；当气隙位移一定时，电磁力与控制电流成正比。
悬浮体的质量为2 g，重力约为0.02 N，MATLAB数据显示在控制电流为20~80 mA，气隙位移为4~10 mm区域内，系统的承载力集中在0.02 N左右。所以选取间隙|y₀|=8 mm则对应控制电流为i₀=45.2 mA，工作时该传感器在此平衡位置附近振动。当控制电流和初始位置确定后，位移刚度系数k_y也随之确定代入式(6)得k_y=7.082 N/m。
3.3 传感器低频特性分析 振动传感器的低频特性可用动态性能指标来描述^[17]，动态性能指标分为2类：一类是时域指标，另一类是频率域指标^[18]。但是在进行动态分析之前先要判断系统的稳定性，图 7为多轴悬浮式低频振动传感器的零极点分布图。从图 7上可以看出，此系统的2个极点分别为-2.33+3.1j和-2.33-3.1j，这2个极点均位于S平面的左半平面，所以系统是稳定的。

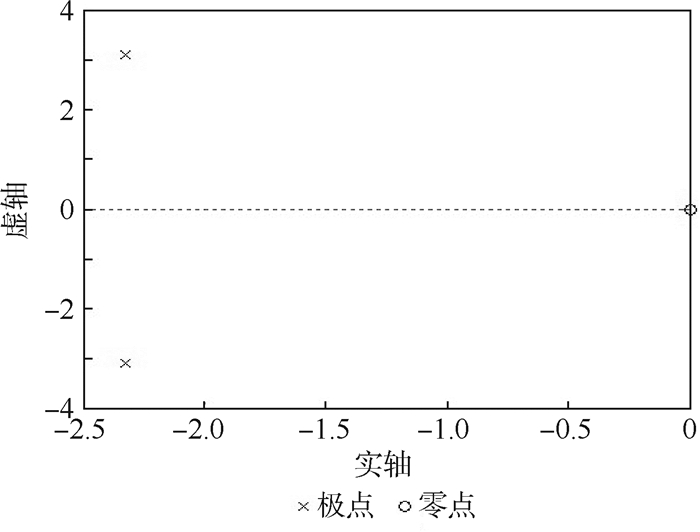图 7 零极点分布图 Fig. 7 Zero-pole distribution diagram

图选项

时域动态性能指标一般都用阶跃过渡过程曲线上某些特征点的数据来表示^[19]。
图 8为多轴悬浮式低频振动传感器在不同阻尼情况下的单位阶跃响应曲线，表 3为该阶跃响应曲线所对应的主要特征点数值。超调量σ用于评价系统的阻尼程度，反应系统响应过程的平稳性^[20]；而响应时间t_s是同时反映响应速度和阻尼程度的综合指标^[21]。

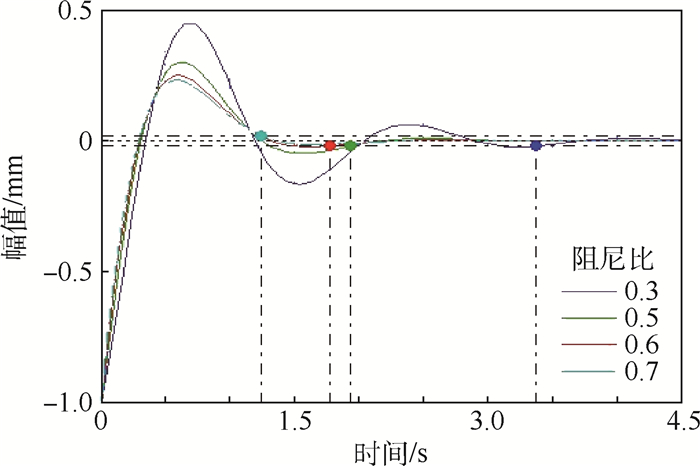图 8 多轴悬浮式低频振动传感器单位阶跃响应曲线 Fig. 8 Unit step response curves of multi-axis maglev low-frequency vibration sensor

图选项

表 3 阶跃响应主要特征 Table 3 Step response main features

阻尼比ξ	响应时间ts/s	超调量σ/%
0.3	3.38	44.5
0.5	1.94	29.8
0.6	1.77	24.7
0.7	1.24	23.0

表选项






表 3数据显示：适当增大阻尼系数，可以提高该传感器系统的响应速度，加快自由振动的衰减，同时降低该系统超调量，使过渡过程更加平稳。第2节通过理论建模分析得出系统Z轴方向阻尼比的表达式，从表达式中可以看出当机械结构固定后，Z轴方向的阻尼比与控制电流成正比，即调整通入电磁线圈的控制电流就可以获得期望的阻尼比。对于惯性式振动传感器比较理想的情况是ξ=0.6~0.7。然而以上结论只适用于调整Z轴方向上的阻尼比，对于X轴和Y轴这2个方向则只能通过设计电路获得较高的阻尼比。
惯性式位移传感器在使用时有下限截止频率，即不允许在低于其固有频率的条件下使用^[22]，所以降低传感器的固有频率，扩大仪器的使用频率范围已经成为该领域研究的关键点。图 9为根据多轴悬浮式低频振动传感器传递函数计算得到的对数幅频和相频特性曲线。图 9中-3dB处对应的频率约为0.6Hz，即该传感器的固有频率约为0.6 Hz，系统具有良好的低频特性。第1节和第2节通过对系统刚度和阻尼特性分析得出了传感器固有频率表达式，当传感器机械结构确定后，根据结论可知固有频率和控制电流成反比关系，即固有频率随着控制电流的增大而降低，所以调整电磁线圈的控制电流就可以降低系统的下限截止频率，扩展了该传感器的使用范围。

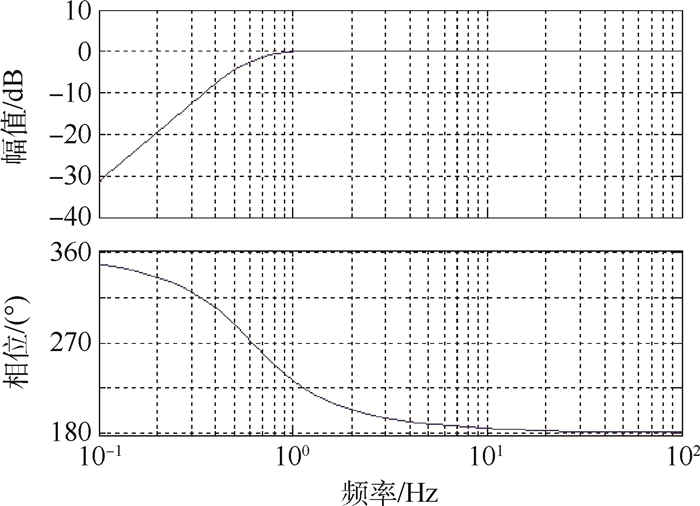图 9 多轴悬浮式低频振动传感器对数频率特性曲线 Fig. 9 Logarithmic frequency characteristic curves of multi-axis maglev low-frequency vibration sensor

图选项

该传感器的固有频率和Z轴方向的阻尼比受控制电流的限制，合理地增大控制电流既可以获得较高的阻尼比又可以降低固有频率，而较高的阻尼比又可以使幅频特性曲线在共振区附近变得平直，这样就可以使传感器的使用下限更低一些，从而扩展了应用范围。
3.4 实验设计 本文在理论建模和仿真分析的基础上，对多轴悬浮式低频振动传感器进行实验研究，验证系统方案的可行性。利用直流电机、滑轨和支撑板搭建运动平台产生激振力，并利用示波器进行振动信号的采集和显示。实际测量得到的信号如图 10所示。

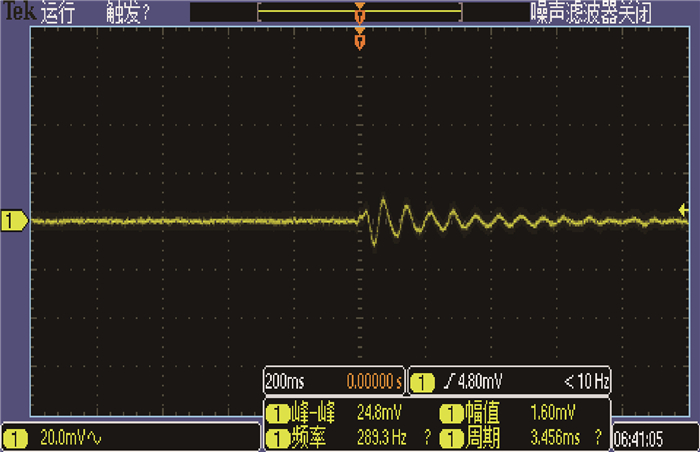图 10 传感器实测Z轴信号 Fig. 10 Measured signal of Z-axis by sensor

图选项

实验结果表明：在激振力作用下，多轴悬浮式低频振动传感器能够跟随外界振动，反映被测振动体的实际情况，实现低频振动信号的测量。并且增大控制电流时，可降低系统的等效刚度，测量更低频率的振动信号。
4 结论 本文采用电磁、永磁混合磁悬浮结构以及微弹簧作为支撑元件设计了一种新型结构的低频振动传感器，通过设计轴向位移检测电路以及使用光电位移传感器实现多轴测量。
1) 该传感器采用轴向位移检测电路测量振动，避免了因为安装位移传感器带来的故障影响，在提高Z轴位移检测精度的基础上使系统更加稳定，同时有助于减小传感器的体积。
2) 该传感器设计加入微弹簧结构，在保证磁悬浮系统稳定性的前提下简化了传感器的结构设计使其更能适应工业应用。
3) 仿真分析得出该传感器的固有频率为0.6 Hz，相比于传统的磁电式低频振动传感器具有更好的低频响应。
实验初步验证该传感器可以通过调整控制电流主动控制系统的刚度和阻尼，进而实现低频振动信号的测量。后期的研究中，可以结合具体实验数据对该传感器进行定量标定。
致谢    
感谢航空航天先进传感技术教育部创新团队和先进惯性仪表与系统技术国家自然基金委创新研究群体的支持。
参考文献

[1]	赵锦春. 低频超低频振动计量技术应用分析[J].信息技术与标准化, 2011(5): 78–81. ZHAO J C. The application prospects of metrology technology of low and super low-frequency vibration measurement[J].Information Technology & Standardization, 2011(5): 78–81.(in Chinese)
[2]	江东, 杨嘉祥. 基于磁悬浮效应的三维振动测量[J].仪器仪表学报, 2011, 32(3): 557–562. JIANG D, YANG J X. Three-dimensional vibration measurement based on magnetic levitation effect[J].Chinese Journal of Scientific Instrument, 2011, 32(3): 557–562.(in Chinese)
[3]	PARASHAR S K, KUMAR A. Three-dimensional analytical modeling of vibration behavior of piezoceramic cylindrical shells[J].Archive of Applied Mechanics, 2015, 85(5): 641–656.DOI:10.1007/s00419-014-0977-0
[4]	YURIN A I, DMITRIEV A V, KRASIVSKAYA M I, et al. Adaptive contactless fiber-optic vibration displacement sensor[J].Measurement Techniques, 2017, 59(11): 1146–1150.DOI:10.1007/s11018-017-1106-6
[5]	袁新江, 姜洋, 汪磊磊, 等. 大型精密测量设备的微振研究[J].电子机械工程, 2012, 28(1): 13–16. YUAN X J, JIANG Y, WANG L L, et al. Research on micro-vibration of large-scale precise measurement equipment[J].Electro-Mechanical Engineering, 2012, 28(1): 13–16.(in Chinese)
[6]	樊尚春. 传感器技术及应用[M].3版北京: 北京航空航天大学出版社, 2016: 308-314. FAN S C. Sensor technology and application[M].3rd edBeijing: Beihang University Press, 2016: 308-314.(in Chinese)
[7]	孙承文. 基于DVD光读取头的超低频振动传感器机理的研究[D]. 合肥: 合肥工业大学, 2009: 5-8. SUN C W. The research on mechanism of ultra-low frequency vibration sensor mechanism based on DVD pickup[D]. Hefei: Hefei University of Technology, 2009: 5-8(in Chinese).http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1509116
[8]	裴雪红. 基于改进RBF神经网络的PID控制[D]. 哈尔滨: 哈尔滨理工大学, 2010: 28-32. PEI X H. Improved PID control based on RBF neural network[D]. Harbin: Harbin University of Science and Technology, 2010: 28-32(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-11914-1011041676.htm
[9]	陈兴华. 高温超导EMS磁浮系统的鲁棒控制器的研究[D]. 成都: 西南交通大学, 2008: 4-8. CHEN X H. Study on robost controller for high-temperature superconductor EMS system[D]. Chengdu: Southwest Jiaotong University, 2008: 4-8(in Chinese).http://d.wanfangdata.com.cn/Thesis/Y1345716
[10]	VENGHI L E, GONZALEZ G N, SERRA F M. Implementation and control of a magnetic levitation system[J].IEEE Latin America Transactions, 2016, 14(6): 2651–2656.DOI:10.1109/TLA.2016.7555233
[11]	USWARMAN R, CAHYADI A I, WAHYUNGGORO O. Control of a magnetic levitation system using feedback linearization[C]//International Conference on Computer, Control, Informatics and Its Applications. Piscataway, NJ: IEEE Press, 2014: 95-98.http://ieeexplore.ieee.org/document/6819156/
[12]	BOONSATIT N, PUKDEBOON C. Adaptive fast terminal sliding mode control of magnetic levitation system[J].Journal of Control Automation & Electrical Systems, 2016, 27(4): 1–9.
[13]	高志华, 胡业发. 磁力轴承刚度阻尼特性研究[J].中国制造业信息化, 2005, 34(2): 130–132. GAO Z H, HU Y F. Research on characteristic of stiffness and damping for active magnetic bearing[J].Machine Design and Manufacturing Engineering, 2005, 34(2): 130–132.(in Chinese)
[14]	江东, 高颖. 磁悬浮效应检振系统设计[J].电机与控制学报, 2008, 12(3): 343–347. JIANG D, GAO Y. Vibration measuring principle and system based on magnetic levitation effect[J].Electric Machines and Control, 2008, 12(3): 343–347.(in Chinese)
[15]	汪龙芳, 贺卫亮. 基于索膜有限元模型的翼伞气动变形仿真[J].北京航空航天大学学报, 2017, 43(1): 47–52. WANG L F, HE W L. Parafoil aerodynamic deformation simulation based on cable-membrane finite element model[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(1): 47–52.(in Chinese)
[16]	LI Z, LUN Q Q. Analysis of magnetic field and levitation force characteristics for 3-DOF deflection type PM motors[J].Journal-Chinese Institute of Engineers, 2016, 39(6): 1–9.
[17]	安建军. 冲击波压力传感器动态灵敏度研究[D]. 太原: 中北大学, 2008: 11-14. AN J J. The research of the dynamic sensitivity of the shock wave pressure sensor[D]. Taiyuan: Zhongbei University, 2008: 11-14(in Chinese).http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1321464
[18]	佘天莉. 测振传感器的动态特性补偿研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2006: 17-18. SHE T L. The research on dynamic characteristics compensation of vibration sensor[D]. Harbin: Institute of Engineering Mechanics China Seismological Bureau, 2006: 17-18(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-85406-2006093733.htm
[19]	KUREK J. Step response identification of inertial model for oscillating system[M]//JANUSZ K. Advanced mechatronics solutions. Berlin: Springer International Publishing, 2016: 51-56.
[20]	朱中华. 微压压力传感器的设计与研究[D]. 镇江: 江苏大学, 2008: 28-29. ZHU Z H. Design and research of micropressure sensor[D]. Zhenjiang: Jiangsu University, 2008: 28-29(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10299-2008095424.htm
[21]	LANG Z Q, BILLINGS S A. Output frequency characteristics of nonlinear systems[J].International Journal of Control, 2015, 64(6): 1049–1067.
[22]	TAN N, ATHERTON D P, YVCE A. Computing step and impulse responses of closed loop fractional order time delay control systems using frequency response data[J].International Journal of Dynamics & Control, 2016, 5(1): 1–10.