20世纪80年代后期,对驻定ODW的数值模拟工作得到了快速发展,由于计算能力的限制,多是采用较为简单的模型进行模拟。Fujiwara等[1-2]用迎风显式TVD格式对驻定ODW进行二维和三维数值模拟;Cambier等[3]用带化学反应的TVD格式对燃烧室的驻定ODW问题进行了数值计算;Dennis[4]和Yungster[5]等都用不同的方法对驻定ODW问题进行研究,并且将计算出的ODW波形与实验得到的照片进行比较。随着计算方法与运算能力的大幅提高,数值模拟已经成为主要的研究手段。Powers和Gonthier[6]采用二步不可逆反应模拟了弱驱斜爆震结构。Pimentel等[7]采用详细反应动力学模型研究了OSW与斜爆震转变区域的不同结构,以及斜劈面角度变化产生的Taylor波对爆震结构的影响,得到的3种不同类型的转换形式:①OSW角逐渐地增大,平滑转换;②ODW形成,OSW角陡峭转换;③ODW形成,OSW角平滑转换。Berlyand等[8]研究了爆震波在斜面上的反射出现的稳态与非稳态2种现象。国内****对ODW的研究起步较晚,但近年来发展迅速,Teng等[9]研究了不同过驱度下OSW向ODW转变的模式特征,得到了诱导区转变形式的临界过驱度,并且指出OSW和ODW面的夹角可以用作判断激波向爆震波转化的有效参考[10],随后的研究模拟了活化能和斜楔面对波面胞格结构的影响[11-12],发现存在2种横波结构:单向横波和双向横波,并探讨了横波由单向到双向的转变规律,在最新发表的文章中[13],运用CVC(Constant Volume Combustion)理论研究了来流动力学参数对诱导区特性的影响。Gui等[14]研究了ODW面胞格结构,同样发现单向横波和双向横波结构,并深入分析了这种微观结构的周期性碰撞现象。Liu等[15]运用R-H(Rankine-Hugoniot)方法分析了ODW向上游传播的诱因是诱导区尾部的压力超过ODW的脱体压力。此外Liu等[16]利用提高部分区域反应进程变量的方法触发ODW,得到了存在着单向横波的完全耦合ODW和存在着双向横波的部分耦合ODW,并且进一步验证了横波对ODW的稳定自持有重要影响。同时Liu等[16]在爆震波不同区域引入局部温度扰动以检验ODW的稳定性,发现稳定传播的ODW在传播过程中稳定性会不断得到增强,但其并未深入讨论温度扰动的传播形式。鉴于此,本文可以被视为对其工作的一项延伸和拓展。
虽然前人对ODW的研究已经进行了大量的工作,但其内部结构的发展规律并不完全清楚,并且绝大部份数值研究都在均匀来流条件下进行。发动机实际工作中,由于燃料掺混不均匀、蒸发不完善、进气道出口压力波动等因素,都可能在燃烧室入口处产生来流物性参数的变化。这些扰动都会对ODW结构产生很大的影响,其中又以温度扰动最为显著。本文出发点在于,通过对燃烧室内的驻定ODW施加来自上游的温度扰动,观察扰动在燃烧室内的传播特点及扰动对ODW结构的影响。本文侧重于ODW大致结构的变化情况,并不对爆震波内部微小结构(胞格结构等)进行分析。
1 计算区域与网格划分方法 计算区域为一个210 mm×120 mm的燃烧室,如图 1所示, RCJ ODW为反射CJ ODW。反应物为混合均匀的氢气和空气,当量比为1,进口来流马赫数Ma=5.95,温度T=796 K,压强P=35.04 kPa,斜楔角为16°,图 1给出了计算域区域及ODW的基本结构,其总体架构与Ghorbanian和Sterling[17]所描述的架构相近。左边界为进口端,进口端边界上来流参数设定为初始值不变。
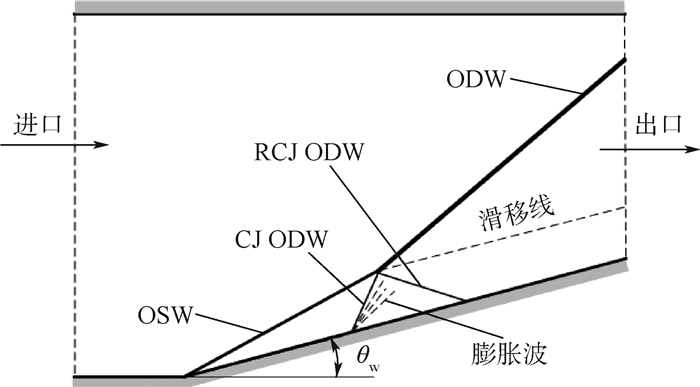 |
| 图 1 计算区域及ODW结构示意图 Fig. 1 Schematic of ODW structure and computational domain |
| 图选项 |
为保证数值结果的收敛,本文选取了3种网格划分的方法,分别为756×400、854×600和1 132×800,3种网格下的库朗特数分别取0.2、0.4和0.8,最大时间步长取5×10-9 s。图 2给出了t=0.09 ms时,3种网格下的温度分布云图,能够看出,3种网格下都得到了能够稳定自持的ODW,随着网格密度加大,ODW的微观结构逐渐显现,图 2(b)中自ODW面向下游产生横波,在图 2(c)这种横波变得更加清晰。
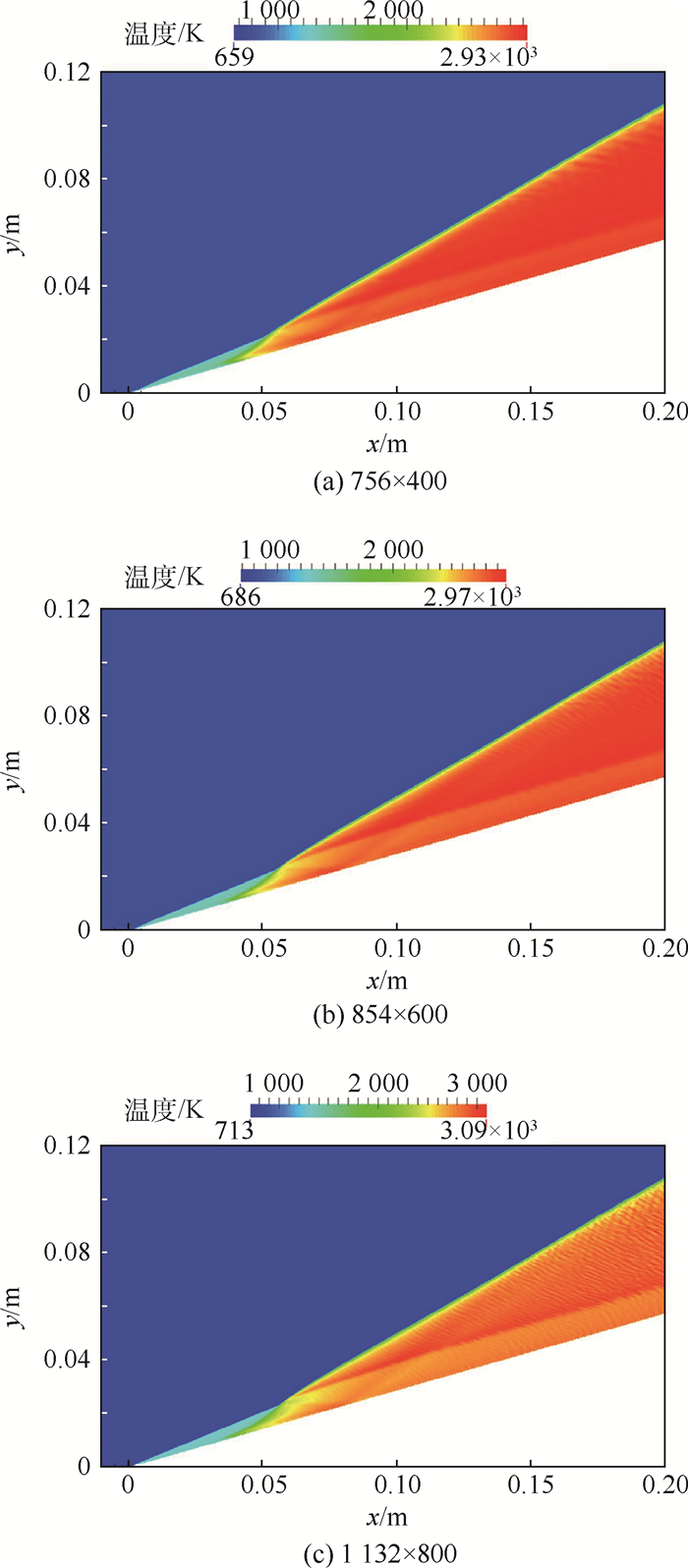 |
| 图 2 t=0.09 ms时3种网格划分下温度分布云图 Fig. 2 Temperature distribution contours of three kinds of mesh density at t=0.09 ms |
| 图选项 |
图 3显示了斜楔面上的压力变化情况,可看出3种网格下CJ ODW后的压力在理论压力(PCJ)附近上下波动,这种波动是自斜爆震产生的横波作用的结果,随着网格密度的增大,数值波动也更为剧烈。由图 3还可看出,854×600和1 132×800下压力的变化趋势基本吻合,而756×400下的压力偏离较大,为进一步比较3种网格下的数值结果,取平行于斜楔面一直线(y=4 mm),得到温度和OH-质量浓度沿该直线的分布情况,如图 4所示。从图 4可看出,854×600和1 132×800下数值结果的变化趋势已基本吻合,数值波动也十分接近。
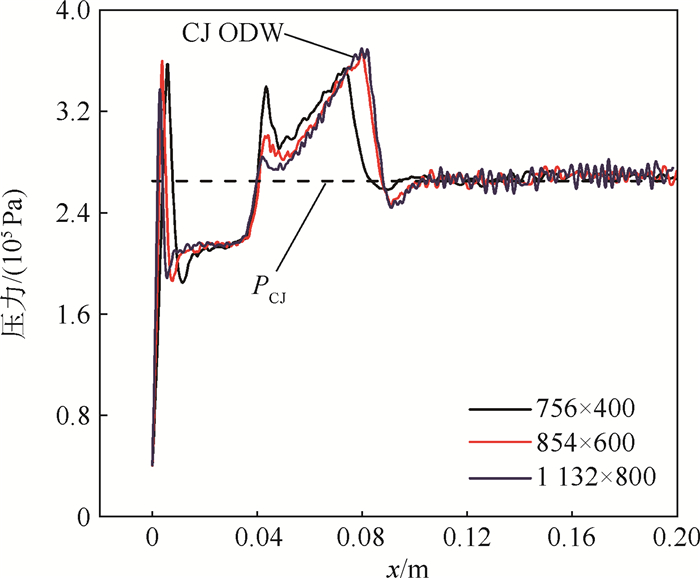 |
| 图 3 t=0.09 ms时3种网格划分下沿斜楔面的压力分布(Ma=5.95,T=796 K,P=35.04 kPa) Fig. 3 Pressure distribution along ramp at t=0.09 ms in three kinds of mesh density (Ma=5.95, T=796 K and P=35.04 kPa) |
| 图选项 |
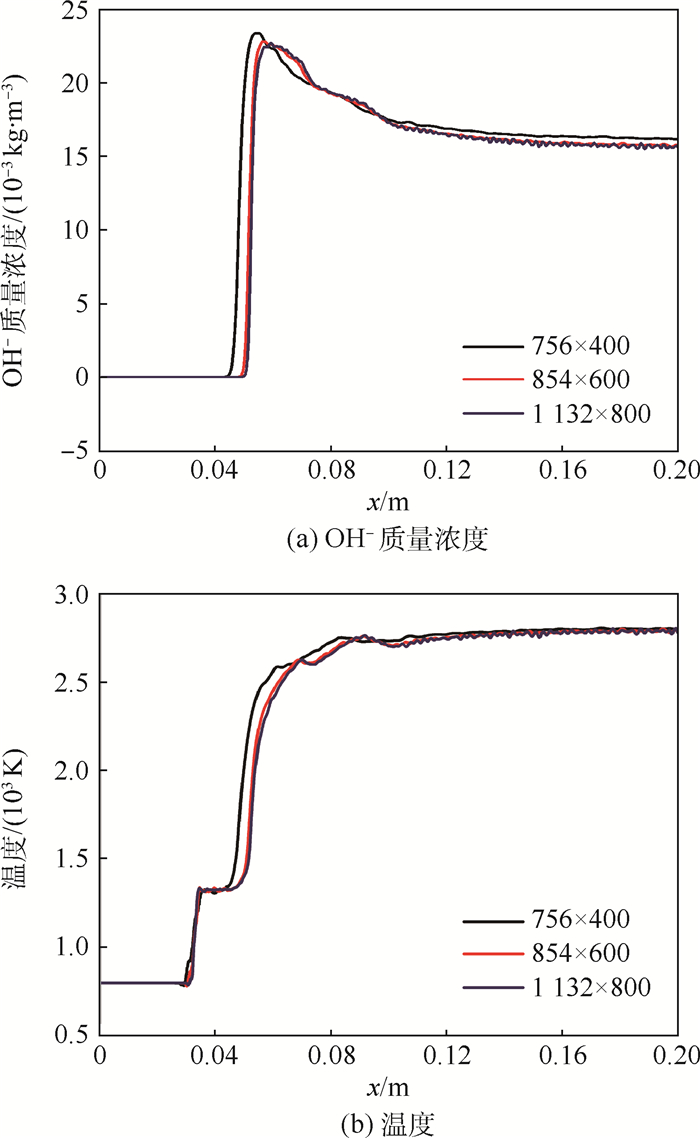 |
| 图 4 t=0.09 ms时3种网格划分下y=4 mm上的温度和OH-质量浓度分布(Ma=5.95,T=796 K,P=35.04 kPa) Fig. 4 Distribution of temperature and OH- mass density at t=0.09 ms measured at y=4 mm in three kinds of mesh density (Ma=5.95, T=796 K and P=35.04 kPa) |
| 图选项 |
本文目的在于研究温度扰动引起的ODW结构的变化,并不要求网格能够精细描述ODW的微观结构。综上所述,854×600下能够得到完整的ODW结构,数值结果与1 132×800下的数值结果接近,并且波后压力能够符合理论预测,故是合适的网格划分。
2 控制方程与数值方法 与bhattraI和Hao [18]相同,本文选取了二维非稳态无黏可压欧拉方程来构建数学模型。采用开源CFD软件OpenFOAM进行运算。控制方程如下:
连续方程
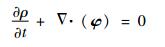 | (1) |
动量方程
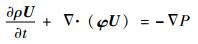 | (2) |
能量方程
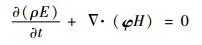 | (3) |
组份方程
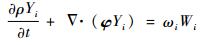 | (4) |
理想气体状态方程
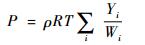 | (5) |
式中:E=e+|U|2/2=∑Yiei+|U|2/2为单位质量气体的内能;H=E+P/ρ为单位质量气体的总焓;φ=ρU为质量通量;R为摩尔气体常数; Yi为化学组份i的质量分数; Wi为相应的相对分子质量; ωi为其摩尔生成速率。反应速率常数k采用Arrhenius定律进行定义:
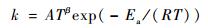 | (6) |
式中:Ea为各分步反应的活化能; A和β为分步反应的2个变量因子,它们决定各分步反应的频率因子ATβ。
本文采用的化学动力模型为氢气/空气9组份[O2, H, OH, O, H2, H2O, N2, HO2, H2O2] 19步可逆反应模型[19],该反应模型在模拟燃烧过程的同时,能够得到的反应中各原子团的变化情况,这可以与实验结果进行直接对比,其可靠性和有效性已被大量研究所验证[20-22],因此在爆震燃烧研究中被广泛应用。具体反应机制如表 1所示,反应速率及摩尔生成速率由CHEMKIN计算而得。
表 1 19步氢气/空气反应模型[19] Table 1 19-step H2-Air reaction model[19]
| 反应 | A | β | Ea/(kJ·mol-1) |
| H+O2=OH+O | 1.91×1014 | 0 | 16 440 |
| H2+O=H+OH | 5.08×104 | 2.67 | 6 292 |
| H2+OH=H+H2O | 2.16×108 | 1.51 | 3 430 |
| O+H2O=OH+OH | 2.97×106 | 2.02 | 13 400 |
| H2+M=H+H+M | 4.57×1019a | -1.40 | 105 100 |
| O+O+M=O2+M | 6.17×1015a | -0.50 | 0 |
| H+O+M=OH+M | 4.72×1018a | -1.0 | 0 |
| H+OH+M=H2O+M | 4.50×1022b | -2.0 | 0 |
| H+O2+M=HO2+M | 1.48×1012c | 0.60 | 0 |
| H+HO2=H2+O2 | 1.66×1013 | 0 | 820 |
| H+HO2=OH+OH | 7.08×1013 | 0 | 300 |
| O+HO2=O2+OH | 3.25×1013 | 0 | 0 |
| OH+HO2=H2O+O2 | 2.89×1013 | 0 | -500 |
| HO2+HO2=H2O2+O2 | 4.20×1014 | 0 | 11 980 |
| H2O2+M =OH+OH+M | 2.95×1014a | 0 | 48 400 |
| H2O2+H=H2O+OH | 2.41×1013 | 0 | 3 970 |
| H2O2+H=HO2+H2 | 6.03×1013 | 0 | 7 950 |
| H2O2+O=HO2+OH | 9.55×106 | 2.0 | 3 970 |
| H2O2+OH=HO2+H2O | 1.00×1012 | 0 | 0 |
| 注:第3体效率:a-f H2O=12.0, f H2=2.5;b-f H2O=12.0, f H2=0.73;c-f H2O=14.0, f H2=1.3。 | |||
表选项
本文数值方法采用AUSM+通量离散格式[18]。每步迭代中,采用黎曼外推法从各网格值推导各网格中心点的左右面通量值,在标量梯度的计算中,采用压力梯度项用以限制数据变化范围,化学反应采用解耦的方式进行处理。进口边界处来流参数保持不变,混气为均匀掺混的氢气和空气,当量比为1,氮气质量分数为0.743 5。出口边界处采用零梯度条件,上下壁面处采用有滑移的绝热边界条件。
3 结果与讨论 3.1 ODW的基本结构 当t=0.1 ms时,燃烧室内部形成了能够稳定自持的ODW结构,如图 5所示,从流场的密度云图能够看出完整的ODW结构。气流撞击楔面产生OSW, 激波诱导混气反应形成一段诱导区,在诱导区末端混气开始剧烈反应生成强烈的燃烧波,燃烧波不断叠加形成ODW,Ghorbanian和Sterling[17]通过数值模拟证明对于在过驱状态下,诱导区末端形成的爆震波为CJ ODW,图 5中CJ爆震波的角度为36.8°,与CJ理论值(βCJ)37.4°很接近。OSW与CJ ODW汇聚形成驻定的ODW,3种波相交于一点,该点被称为三波点,自三波点处向下游延伸产生一条滑移线,在滑移线上下两侧压力相等,但温度、密度和速度等其他参数会发生突跃变化。由于三波点是高温高压的区域,通常CJ ODW在三波点处会发生反射,形成RCJ ODW。
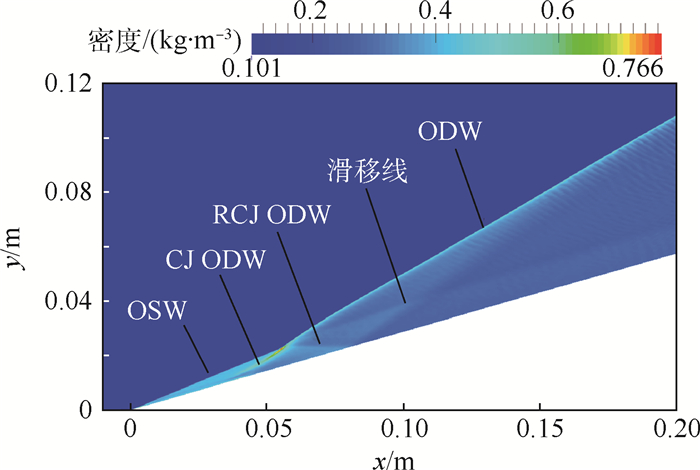 |
| 图 5 t=0.1 ms时密度分布云图 Fig. 5 Density distribution contours at t=0.1 ms |
| 图选项 |
诱导区后的反应区被滑移线分为2个区域,滑移线以上到爆震波间为爆震区(detonation zone),其以下到壁面之间则为爆燃区(deflagration zone)。CJ ODW与其后形成的膨胀波(expansion waves)耦合,形成向诱导区弯曲的低温区域。RCJ ODW在反应区内经壁面和ODW反射传播并不断衰减,Choi等[23]指出,RCJ ODW的传播可能与ODW面的胞格结构变化有关,也可能影响爆震区内的横波传播。自ODW波面形成的横波向下游传播,导致了反应区内微观结构的不断变化,Dupré等[24]指出这种不稳定性对爆震波的自持传播起到本质作用。
3.2 温降扰动在燃烧室内的传播 对于几何结构不可变的燃烧室,进口边界处任一参数动可能会引起其他物性参数的瞬态波动。在t=0.1 ms时,在流场进口边界引入一扰动,即温度突然下降100 K(温降扰动),为保证来流参数物理上的合理性,考虑到燃烧室的实际工作情况,保持进口来流速度不变,压力、密度和来流马赫数等进口参数做出相应调整。扰动在进口边界均匀分布并保持不变,观察温度扰动在燃烧室内传播的过程。R-H分析指出,在弱过驱爆震区间内ODW能够稳定自持,扰动传播过程中ODW波结构必然会经历调整,图 6显示了自扰动传入至ODW重新调整到稳定状态的完整过程。
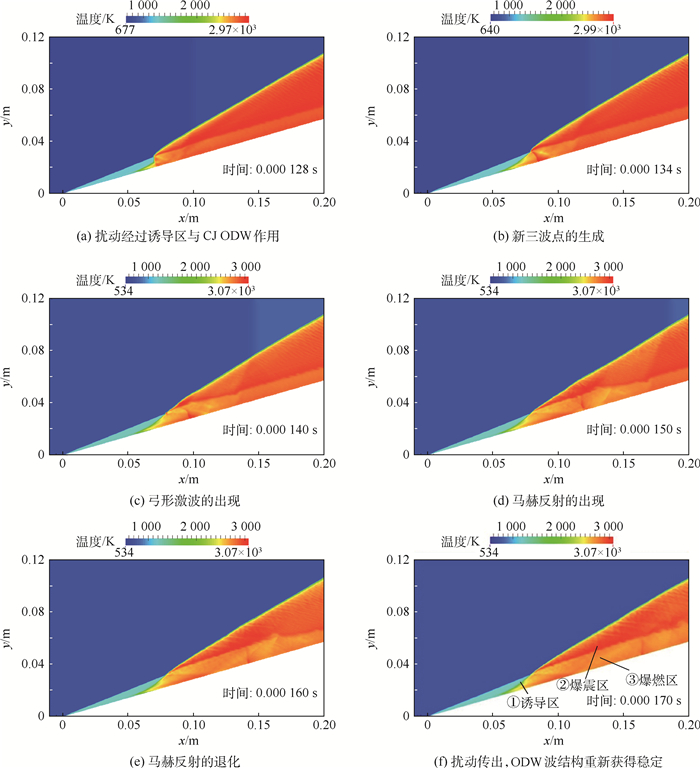 |
| 图 6 温降扰动传入至ODW重新调整到稳定状态的时序图 Fig. 6 Sequence charts for variation of ODW structure from introducing temperature drop disturbance to retrieving stabilization |
| 图选项 |
将扰动前图 6(a)和扰动流出后流场图 6(f)对比,易发现爆震区结构发生了剧烈变化。图 7给出了扰动前后,三波点附近的密度变化情况。由图 7(a)可看出,扰动前爆震区结构变化较平滑,在接近三波点的区域,爆震区胞格结构不明显,直到流场下游,才逐渐显现。然而扰动传播过后,爆震区内结构不再平滑,胞格结构在结构新三波点处不远便十分清晰,火焰波阵面呈现明显周期性波动,并从波阵面生成面向下游的多层横波结构,如图 7(b)所示。
 |
| 图 7 三波点附近扰动前后的密度分布灰度图 Fig. 7 Grayscale images for density nearby triple point before and after disturbance |
| 图选项 |
为了研究扰动在诱导区、爆燃区和爆震区中扰动的传播形式,在3个区域分别选取了3个观测点,如图 6(f)中①、②、③所示。由图 6可看出扰动在反应区中的传波形态复杂,大致可分为3个阶段:弓形CJ ODW及双三波点的形成;新三波点的形成;激波、膨胀波和弱压缩波的组合传播。
3.2.1 第1阶段 图 6(a)和(b)中,在诱导区内扰动引起的膨胀波穿过诱导区,随后与CJ ODW作用使其发生弯曲,形成一道弓形CJ ODW,同时形成新的三波点,为与第2阶段的新三波点相区别,这里称第1阶段的新三波结构为扰动三波点结构。图 8为此阶段的速度局部放大云图,可看出扰动三波点沿新生成的CJ ODW向下游延伸,同时不断改变原结构中CJ ODW的形态。
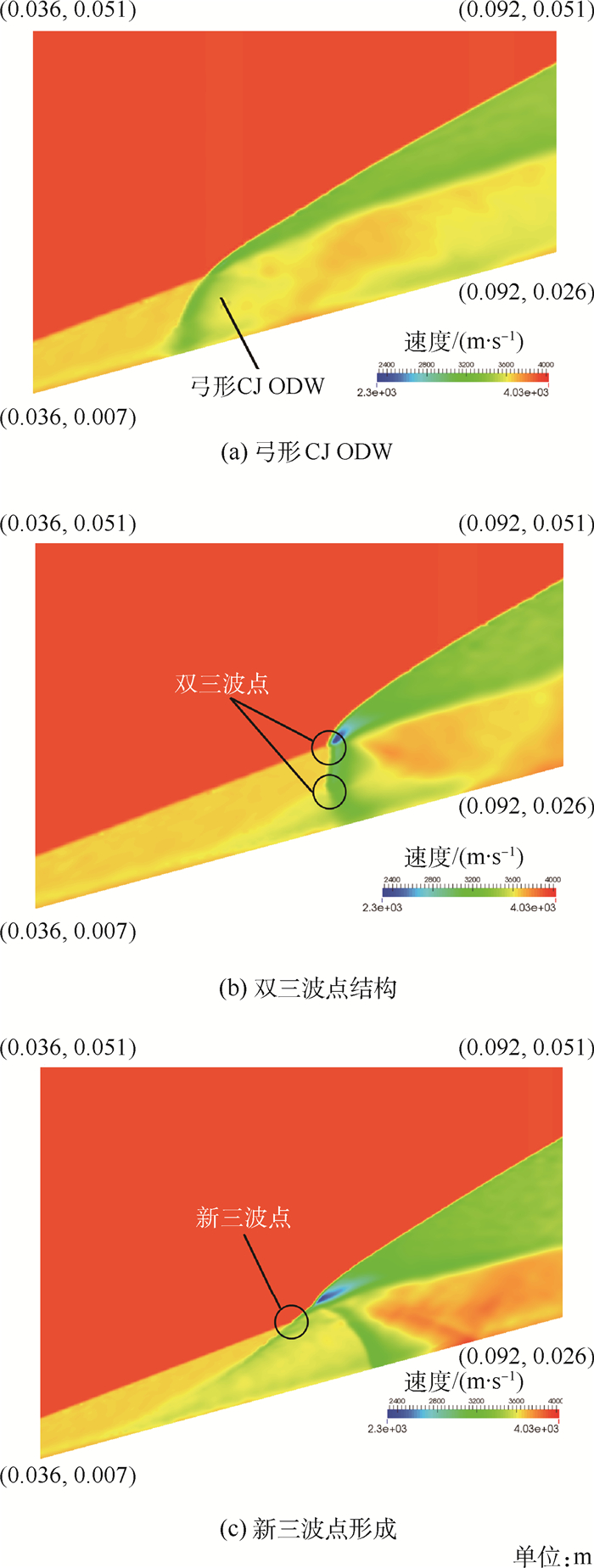 |
| 图 8 第1阶段局部放大速度云图 Fig. 8 Partially amplified velocity contour for the first period |
| 图选项 |
自扰动三波点生成一道近似垂直于壁面的激波,其下游侧生成一组膨胀波,这种激波和膨胀波的组合随扰动三波点向下游传播。在第1阶段,诱导区后段形成了独特的双三波点结构。最终,扰动三波点与原波结构中的三波点汇聚形成新波的三波点。至此诱导区便完成了从原三波至新的三波结构的转变。
3.2.2 第2阶段 在该阶段,第1阶段的双三波点结构完成了汇聚,新的ODW结构逐渐形成。然而数值模拟发现,新形成的结构存在较大的不稳定性,物性参数出现剧烈的变化,如图 9所示。当t=0.134 ms时新三波点形成,此后新三波点处的温度、压力和速度较扰动前都出现了剧烈的数值波动,甚至会产生局部热点。这表明在温降扰动下,虽然ODW波结构能够保持结构的完整性不被破坏,但内部微观结构的不稳定性却被放大了,这与扰动传出后胞格结构更明显的现象一致,这一点后文会进一步阐述。
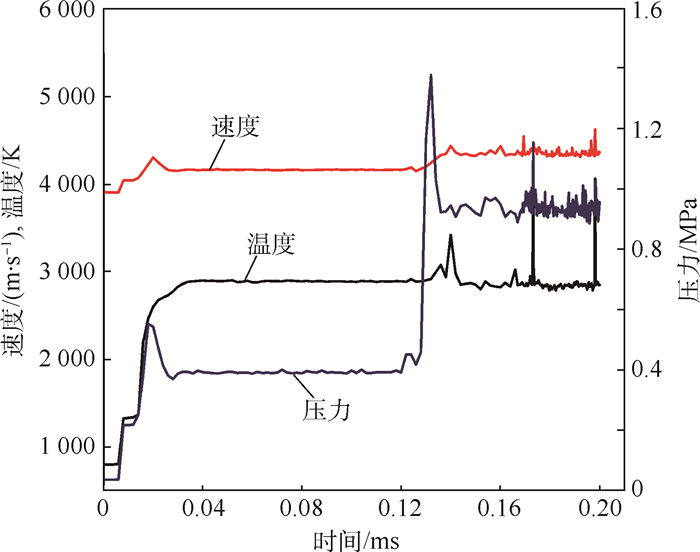 |
| 图 9 新三波点处温度、速度和压力随时间变化曲线 Fig. 9 Profiles for temperature, velocity and pressure nearby new triple point changing with time |
| 图选项 |
3.2.3 第3阶段 在该阶段,ODW的结构变化复杂,存在着不同种类波之间的相互作用,图 10显示了扰动引起的激波、膨胀波及弱压缩波在反应区内的传播过程的简化图,其时序与图 6(c)~(f)对应。
 |
| 图 10 温降扰动引起的激波、膨胀波及弱压缩波在反应区内传播的时序简图 Fig. 10 Sequence sketches for propagation of shock wave, expansion waves and weak compression wave in reaction zone caused by temperature drop disturbance |
| 图选项 |
扰动在进入反应区后,上游新的ODW结构逐渐形成。在第1阶段形成的射向壁面的激波变为弓形激波,激波下游自避免生成一段膨胀区,激波下游气体经膨胀波加速,为平衡上下游两侧的气体状态,自壁面生成一道向下游传播的弱压缩波,如图 10(a)所示。
在壁面中端,弓形激波在壁面发生了明显的马赫反射,在壁面处生成一道马赫杆,但这种马赫反射现象持续时间不长,随着激波向下游传播,马赫杆逐渐变短,反射点向壁面逼近,直至在壁面中后段,马赫反射退化为普通的规则反射,如图 10(b)和(c)所示。由图 10(d)可以看出,在壁面末段,反射激波几乎消失,只以一道近乎垂直于壁面的激波向下游传播,直至扰动传出燃烧室,在此阶段,激波强度变得很弱,不像此前能够引发ODW面和滑移线的强烈的卷曲。
图 11为诱导区、爆燃区和爆震区中3个观测点的Ma的变化情况,在爆燃区③处,膨胀波在激波下游传播,Ma存在上升、下降再上升的过程,而在爆震区②处,Ma先下降后上升,这几乎与前者完全相反。这种现象的原因在于,激波下游的膨胀波在爆燃区能够保持足够强度,但在进入爆震区后迅速减弱,以致并不足以引起观测点②处强烈的参数变化,因此②处Ma的剧烈下降反应的是膨胀波上游的激波的传播,在激波经过②处后,由于在新的ODW结构中,②处的Ma远高此前的最低值,必然存在一组膨胀波以使激波上游的气体压力降低,从而使压力相匹配。在观测点③处,情况则完全不同,贴近壁面处的膨胀波较强,最先引起③处Ma的明显上升,当上游激波经过③处时引起了Ma的骤降,最后激波上游的膨胀波又将此处的气体平衡至新的爆燃区所匹配的状态。
 |
| 图 11 ΔT=-100 K时3个区域内观测点的Ma变化 Fig. 11 Variation of Ma in sampling points from three zones at ΔT=-100 K |
| 图选项 |
在分析爆震区和爆燃区内Ma变化截然相反的现象时需要结合定性和定量的方法。由前文可知,激波、膨胀波和弱压缩波在扰动传播过程中起着不同程度的作用,其中激波和膨胀波的作用能在图 11中明显观察到,而弱压缩波的作用并不明显,这与观测点的选取位置有关。此外,爆震区和爆燃区对扰动的响应也不同,达到稳定状态后,Ma在爆震区波动明显比爆燃区剧烈,这与前文新三波点处的剧烈数值波动一致,侧面体现了不稳定性对爆震波稳定传播起着本质作用。
3.3 温升扰动在燃烧室内的传播 3.2.3节着重研究温度降低情况下的扰动传播情况,为了研究温度上升时的情况,在t=0.1 ms时刻又引入了另一温升扰动,即温度上升100 K,选取了相同位置的观测点,分析方法与3.2.3节相同。
温升扰动同样引发了激波、膨胀波和弱压缩波的复杂组合,图 12(a)为t=0.14 ms时,流场内的Ma分布云图,图 12(b)为其简化图,可看出3种波自爆震波面射出,彼此相互间隔,并且沿ODW面向下游传播,这与前文引入的温降扰动沿壁面传播的情形完全不同。图 13中,爆震区②处Ma数先下降后上升,随后又有一个下降、上升的过程,这与图 12(b)中3种波相互间隔一一对应。
 |
| 图 12 t=0.14 ms时Ma分布云图和温升扰动引起的激波、膨胀波及弱压缩波在反应区内的分布简图 Fig. 12 Distribution contours of Ma and distribution sketches for propagation of shock wave, expansion waves and weak compression wave in reaction zone at t=0.14 ms |
| 图选项 |
 |
| 图 13 ΔT=100 K时3个区域内观测点的Ma变化 Fig. 13 Variation of Ma in sampling points from three zones at ΔT=100 K |
| 图选项 |
图 13给出了3个区域内Ma的变化情况。对比图 13和图 10可知,2种温度扰动下,爆震区(②处)内的Ma的分布形式大体相反,而在爆燃区(③处)内则完全相同,造成这种结果的主要原因是在温升扰动下,弱压缩波的强度明显较温降扰动下强,如图 13局部放大图所示,弱压缩波穿过滑移线同时影响了爆震区和爆燃区,从而引发Ma在2个区域内都出现了小幅度的下降。此外在温升扰动的影响下,爆震区内呈现的不稳定性也较爆燃区强烈,这与3.2.3节一致。
4 结论 本文对温度扰动在斜爆震燃烧室的传播进行了数值模拟,分析了在温度上升和温度下降2种扰动作用下的扰动传播形态,得出以下结论:
1)在温度扰动下,ODW能够顺利完成结构的调整。引入温降扰动后,ODW内部不稳定性被进一步释放,爆震区呈现出多层次的横波结构,胞格结构更为清晰,波后物性参数的波动也更为剧烈,而且对比爆震区和爆燃区内Ma在扰动传播过后的数值波动,发现爆震区内的不稳定性较爆燃区剧烈,这侧面印证了Dupré等[24]的结论,即不稳定性对爆震波的稳定传播起着本质作用。
2)在温降扰动下,ODW的结构调整可分为3个阶段:弓形CJ ODW及双三波点结构的形成;双三波点的汇聚及新三波点的形成;激波、膨胀波和弱压缩波的组合传播。扰动在传播过程中不断衰减,在诱导区和未反应区,扰动以膨胀波的形式传播。在反应区,激波会呈现出弓形激波、马赫反射、规则反射和近乎垂直于壁面的正激波4种形态。
对ODW结构起主要作用的激波和膨胀波。在爆燃区中激波在上游,膨胀波在下游;在爆震区中则相反,膨胀波在上游,激波在下游。这并不意味着在2个区域形成了不同的激波和膨胀波的组合传播形式,这种分布位置矛盾的原因是激波下游的膨胀波在爆燃区内强度较大,对气流状态的影响明显,但其传播到在爆震区内时强度衰减明显,不足以显著改变气体状态,而激波上游膨胀波的强度分布则相反,其在爆震区中的强度要明显大于在爆燃区中的强度。
3)在温升扰动下,激波、膨胀波和弱压缩波对ODW结构调整都起到了重要作用。通过分析扰动的传播形态的分布情况,发现与温降扰动下,弱压缩波对气流状态的影响很弱不同,弱压缩波在温升扰动下强度较大,对ODW的结构调整起到了较大的作用。此外,温降扰动沿壁面向下游传播,而温升扰动则沿ODW面向下游传播,造成这种形态上巨大差异的原因尚不清楚,还需进一步研究。
参考文献
| [1] | FUJIWARA T, MATSUO A, NOMOTO H. A two-dimensional detonation supported by a blunt body or a wedge[C]//26th AIAA Aerospace Sciences Meeting. Reston: AIAA, 1988.https://arc.aiaa.org/doi/abs/10.2514/6.1988-98 |
| [2] | WANG Y Y, FUJIWARA T, AOKI T, et al. Three-dimensional standing oblique detonation wave in a hypersonic flow[C]//26th Aerospace Sciences Meeting. Reston: AIAA, 1988.https://arc.aiaa.org/doi/abs/10.2514/6.1988-478 |
| [3] | CAMBIER J L, ADELMAN H G, MENEES G P. Numerical simulations of oblique detonations in supersonic combustion chambers[J].Journal of Propulsion and Power, 1989, 5(4): 482–491.DOI:10.2514/3.23180 |
| [4] | DENNIS E G, DAVID T D. Numerical modelling of standing oblique detonation waves: AIAA-88-0063[R]. Reston: AIAA, 1988. |
| [5] | YUNGSTER S, EBERHARDT S, BRUCKNER A. Numerical simulation of shock-induced combustion generated by high-speed projectiles in detonable gas mixtures[C]//27th Aerospace Sciences Meeting. Reston: AIAA, 1989.http://html.rhhz.net/BJHKHTDXXBZRB/10.2514/6.1989-673 |
| [6] | POWERS J, GONTHIER K. Reaction zone structure of weak underdriven oblique detonations[C]//Aerospace Sciences Meeting and Exhibit. Reaction Zone Structure of Weak Underdriven Oblique Detonations, 1992.https://arc.aiaa.org/doi/abs/10.2514/6.1992-347 |
| [7] | PIMENTEL C A R, AZEVEDO J L F, SILVA F D, et al. Numerical study of wedge supported oblique shock wave-oblique detonation wave transitions[J].Journal of the Brazilian Society of Mechanical Sciences, 2002, 24(3): 149–157.DOI:10.1590/S0100-73862002000300002 |
| [8] | BERLYAND A T, VLASENKO V V, SVISHCHEV S V. Stationary and nonstationary wave structures that arise in stabilization of detonation over a compression surface[J].Combustion:Explosion, and Shock Waves, 2001, 37(1): 82–98.DOI:10.1023/A:1002876911205 |
| [9] | TENG H H, JIANG Z L, NG H D. Numerical study on unstable surfaces of oblique detonations[J].Journal of Fluid Mechanics, 2014, 744(2): 111–128. |
| [10] | TENG H H, JIANG Z L. On the transition pattern of the oblique detonation structure[J].Journal of Fluid Mechanics, 2012, 713(6): 659–669. |
| [11] | TENG H H, NG H D, LI K, et al. Evolution of cellular structures on oblique detonation surfaces[J].Combustion & Flame, 2014, 162(2): 470–477. |
| [12] | TENG H, NG H D, JIANG Z. Initiation characteristics of wedge-induced oblique detonation waves in a stoichiometric hydrogen-air mixture[J].Proceedings of the Combustion Institute, 2016, 32(2): 2735–2742. |
| [13] | WANG T, ZHANG Y, TENG H, et al. Numerical study of oblique detonation wave initiation in a stoichiometric hydrogen-air mixture[J].Physics of Fluids, 2015, 27(9): 096101.DOI:10.1063/1.4930986 |
| [14] | GUI M Y, FAN B C, DONG G. Periodic oscillation and fine structure of wedge-induced oblique detonation waves[J].Acta Mechanica Sinica, 2011, 27(6): 922–928.DOI:10.1007/s10409-011-0508-y |
| [15] | LIU Y, WU D, YAO S. Analytical and numerical investigations of wedge-induced oblique detonation waves at low inflow mach number[J].Combustion Science and Technology, 2015, 187(6): 843–856.DOI:10.1080/00102202.2014.978865 |
| [16] | LIU Y, HAN X D, YAO S B, et al. A numerical investigation of the prompt oblique detonation wave sustained by a finite-length wedge[J].Shock Waves, 2016, 26(6): 729–739.DOI:10.1007/s00193-016-0626-3 |
| [17] | GHORBANIAN K, STERLING J D. Influence of formation processes on oblique detonation wave stabilization[J].Journal of Propulsion & Power, 2015, 12(3): 509–517. |
| [18] | BHATTRAI S, HAO T. Numerical study of shcramjet combustor characteristic control techniques[J].Frontiers in Aerospace Engineering, 2013, 2(3): 189–198. |
| [19] | MARCUS ó C, CURRAN H J, SIMMIE J M, et al. A comprehensive modeling study of hydrogen oxidation[J].International Journal of Chemical Kinetics, 2004, 36(11): 603–622.DOI:10.1002/kin.v36:11 |
| [20] | 董刚, 范宝春, 谢波. 氢气-空气混合物中瞬态爆震过程的二维数值模拟[J].高压物理学报, 2004, 18(1): 40–46. DANG G, FAN B C, XIE B. Two-dimensional simulation of transient detonation process for H2O2-N2 mixture[J].Chinese Journal of High Pressure Physics, 2004, 18(1): 40–46.DOI:10.11858/gywlxb.2004.01.008(in Chinese) |
| [21] | 姜孝海, 范宝春, 董刚, 等. 旋转爆震流场的数值模拟[J].推进技术, 2007, 28(4): 403–407. JIANG X H, FAN B C, DONG G, et al. Numerical investigation on the flow field of rotating detonation wave[J].Journal of Propulsion Technology, 2007, 28(4): 403–407.(in Chinese) |
| [22] | FUSINA G, SISLIAN J, PARENT B. Computational study of formation and stability of standing oblique detonation waves[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2013.https://arc.aiaa.org/doi/abs/10.2514/6.2004-1125 |
| [23] | CHOI J Y, KIM D W, JEUNG I S, et al. Cell-like structure of unstable oblique detonation wave from high-resolution numerical simulation[J].Proceedings of the Combustion Institute, 2007, 31(2): 2473–2480.DOI:10.1016/j.proci.2006.07.173 |
| [24] | DUPRé G, PERALDI O, LEE J H, et al. Propagation of detonation waves in an acoustic absorbing walled tube[C]//Progress in Astronaut and Aeronaut. Reston: AIAA, 1988, 114: 248-263.https://arc.aiaa.org/doi/abs/10.2514/5.9781600865886.0248.0263 |
