柔性机构以其便于微型化、免装配、免润滑、运动灵敏度高、无噪声、环境适应性强等优点^[1], 越来越多地被运用到航空航天、微操作机器人、精密光学仪器以及工业设备等领域^[2]。而其中的柔性铰链以其小体积、无摩擦和间隙、运动灵敏度高等优点^[3], 可以解决传统刚性铰链间隙带来的冲击、摩擦、润滑等问题。
在柔性铰链的设计方面, 研究者们设计出如圆弧型柔性铰链^[4]、椭圆型柔性铰链^[5]、锥形柔性铰链^[6]等不同切口轮廓的柔性铰链, 以及基于不同切口轮廓的组合型柔性铰链。在柔性铰链的性能优化方面, 文献[7]以工作方向柔度和非工作方向柔度的柔度比为研究对象, 建立了对柔性铰链的多目标优化模型; 文献[8-9]以基于柔度比的多目标优化模型, 研究优化了深切口椭圆弧柔性铰链^[8], 优化设计了杠杆式柔性铰链放大机构^[9]。
随着近年来拓扑优化理论的成熟和其应用的普及, 拓扑优化在柔性铰链的设计和优化工作中也发挥着重要的作用。使用拓扑优化理论设计柔性铰链, 可以得到柔性铰链针对拓扑优化目标的最佳拓扑结构和材料分布方式, 不仅可以给设计者启发, 还可以避免以往通过特异性设计带来的不确定性^[10]。朱本亮和张宪民等^[11]采用二维连续体拓扑优化方法以最小化柔度和为拓扑优化目标, 设计出一种平移柔性铰链和一种转动柔性铰链; 刘敏和张宪民等^[12]采用同样的方法, 以最小归一化处理的柔度和为拓扑优化目标设计出类V型柔性铰链, 并将类V型柔性铰链应用于微位移放大机构^[13], 还改变拓扑优化区域, 以最小归一化处理的柔度比为拓扑优化目标, 设计出多孔洞型柔性铰链^[14]。
二维连续体拓扑优化方法仅限于在柔性铰链的切口轮廓平面寻求最佳的拓扑结构和材料分布方式。而本文基于三维连续体拓扑优化理论, 并以最大化柔度比为拓扑优化目标, 设计出一种具有全新三维拓扑结构的柔性铰链, 对其柔度进行研究, 并与圆弧型柔性铰链进行对比。
1 基于变密度法设计柔性铰链 1.1 拓扑优化模型 在以柔性铰链连接刚性连杆的柔性机构中, 连杆的长度大于其高度, 所以必然存在一个长度等于杆件高度的正方形区域。以此正方形为拓扑优化区域, 设计的柔性铰链不仅具有普遍性, 而且能够使柔性铰链结构更加紧凑。如图 1所示, 连杆尺寸为40 mm×10 mm×10 mm, 为在其末端拓扑优化出柔性铰链, 选取边长等于10 mm的立方体为拓扑优化区域Ω_D, 非拓扑优化区域Ω_N为40 mm×10 mm×10 mm的长方体。利用有限元思想将连杆等分成32 000个边长为0.5 mm的细小立方体单元, 设计区域Ω_D包含可变密度单元8 000个, 其余为非设计区域Ω_N所属的不可变密度单元。拓扑优化过程中, 以设计区域Ω_D中每个单元的单元密度ρ_e为设计变量, 假想材料的原始密度为ρ₀, 单元的相对密度x^e=ρ_e/ρ₀, x^e在0~1之间连续取值; 而在非设计区域Ω_N中, 所有不可变密度单元密度为ρ₀。
如图 1所示, 以设计区域Ω_D左边为固定端, 分别建立5个独立的工况:工况F_x、工况F_y、工况F_z中, 在非设计区域右端加载沿x轴、y轴、z轴方向1 N单位力, 并建立拓扑优化模型中沿坐标轴正方向的拓扑优化响应; 工况F₁、工况F₂中, 在非设计区域右端加载zOy平面内与z轴正方向成±45°角的1 N单位力, 并建立综合考虑对y轴和z轴方向不同柔度需求的拓扑优化响应。下文将详细说明这些拓扑优化响应。

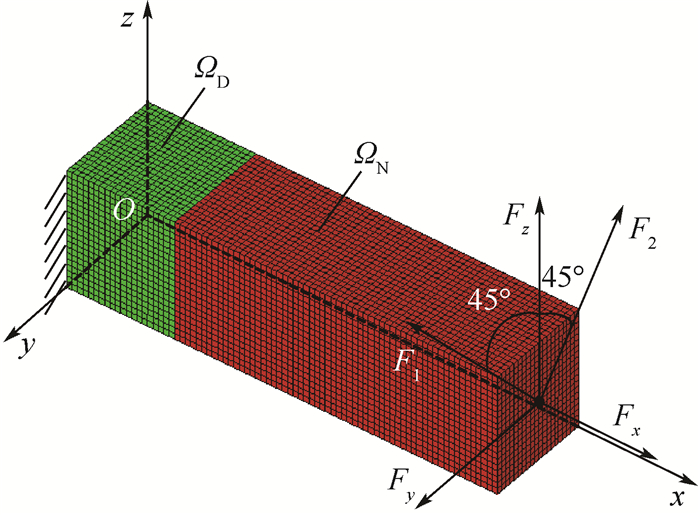图 1 拓扑优化区域与工况示意图 Fig. 1 Schematic of topology optimization area and working conditions

图选项

工况F_x和工况F_z的拓扑优化模型的柔度响应分别表征x轴方向柔度C_x和z轴方向柔度C_z。性能优异的单轴柔性铰链具有较小的x轴方向柔度C_x和较大的z轴方向柔度C_z, 因此以最大柔度比为拓扑优化目标:

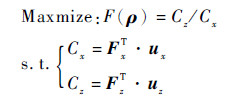(1)

式中:F_x^T为工况F_x柔性铰链末端所受载荷矩阵的转置; u_x为工况F_x柔性铰链末端的位移矩阵; F_z^T为工况F_z柔性铰链末端所受载荷矩阵的转置; u_z为工况F_z柔性铰链末端的位移矩阵^[12]。
中心漂移是一种柔性铰链转动中心随铰链弹性变形发生位置变化的现象, 中心漂移严重影响着转动精度。为提高拓扑优化结果的转动精度, 必须抑制拓扑优化模型的中心漂移。
图 2中, 柔性铰链转动产生的中心漂移为d, d是旋转后中性层反向延长线与原中性层的交点C和理论中心O的距离。由相似三角形原理, 定义式(2)的中心漂移精度ε表征d, 以抑制中心漂移:

(2)

图 2 拓扑优化模型的正视图和中心漂移 Fig. 2 Front view and center drift of topology optimization model

图选项

式中:d_z为非优化区域右侧中点D的z向位移响应; l_z为优化区域右侧中点B的z向位移响应; l_d为优化区域长度; l_n为非优化区域长度; ε^*为设定的中心漂移精度。由相似三角形原理计算可知, 当中心漂移d≤0.085 mm时, 等价ε≤0.1, 故本文ε^*取值0.1。
抗干扰能力更强的单轴柔性铰链工作方向的柔度最大, 非工作方向的柔度小。图 1所示的5种不同工况中, 运动分别为沿x轴、y轴、z轴、1方向、2方向, 而只有z轴是工作方向, 其他方向为非工作方向。因此, z轴方向柔度越大并且其他方向柔度越小的拓扑, 其优化结果越符合单轴柔性铰链对抗干扰能力的要求。
工况F_z、工况F₁、工况F₂中右端中心点的z向位移响应分别为d_z-Fz、d_z-F1、d_z-F2; 工况F_y中右端中心点的y向位移响应为d_y-Fy。其中, d_z-Fz为工作方向位移响应, 其他位移响应是非工作方向位移响应。由几何关系可知:工况F₁、工况F₂右端中心点的实际位移为、。创建3个第2类拓扑优化响应位移比s_z-y=d_z-Fz/d_y-Fy、s_z-1= , 并根据传统单轴柔性铰链柔度的相关经验值确定各位移比最小值:z方向柔度至少是y方向柔度的1 000倍, 是1方向、2方向的100倍。因此, 给定拓扑优化约束s_z-y≥1 000, s_z-1≥100, s_z-2≥100, 以增大拓扑优化结果工作方向柔度, 并减小非工作方向柔度。
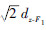
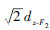
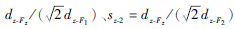
所有单元的相对密度x^e与单元体积v_e的乘积之和等于优化区域拓扑优化后的体积, 与拓扑优化前体积V₀之比为体积分数响应V, 限制体积分数即限制材料用量, 如式(3)所示。根据处理拓扑优化问题保留体积分数的常用经验值, V^*取值0.3。

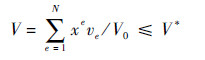(3)

为避免求解刚度矩阵时出现奇异解, 将相对密度下限x_min^e设定为接近0但不等于0的值。

(4)

综上, 基于变密度法的拓扑优化模型为

(5)

1.2 拓扑优化过程和结果 HyperWorks软件中的OptiStruct模块是基于变密度材料插值法进行拓扑优化迭代计算的, 借助该软件将1.1节建立的拓扑优化模型实现求解, 经过38轮迭代计算, 得到满足各限制条件的拓扑优化结果, 终止迭代计算, 完成单轴柔性铰链的拓扑优化设计。输出拓扑优化结果的密度阈值设置为0.3, 即单元的相对密度x^e大于0.3的单元将被保留, 小于0.3的单元将被去除, 得到拓扑优化过程和结果如图 3所示。

图 3 拓扑优化过程和结果 Fig. 3 Process and results of topology optimization

图选项

由此得到新型三维拓扑结构的几何模型如图 4所示。设b为铰链宽度, b=10 mm; t_i(x)为截面高度; b_i(x)为截面宽度。设R为半圆切口轮廓的半径, t为柔性铰链中间最薄处的厚度, r为孔洞域半圆部分的半径, l为孔洞域矩形部分的宽度, 如图 5所示。则拓扑优化结果为:R=4.75 mm, t=0.5 mm, r=1.5 mm, l=5 mm。

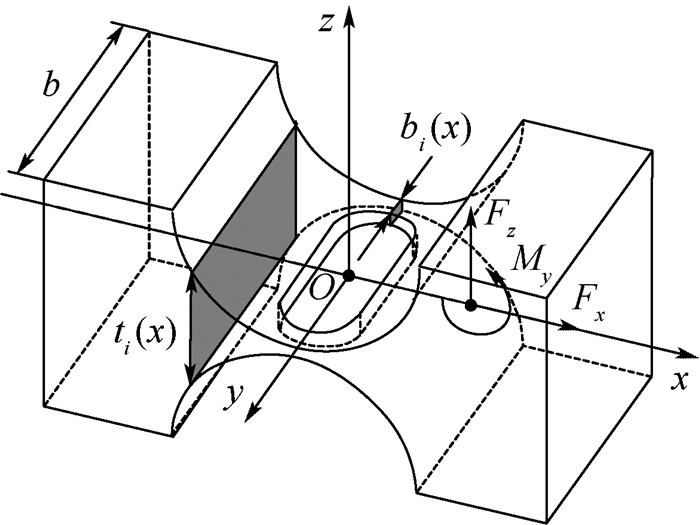图 4 新型柔性铰链三维图 Fig. 4 3D drawing of new flexure hinge

图选项

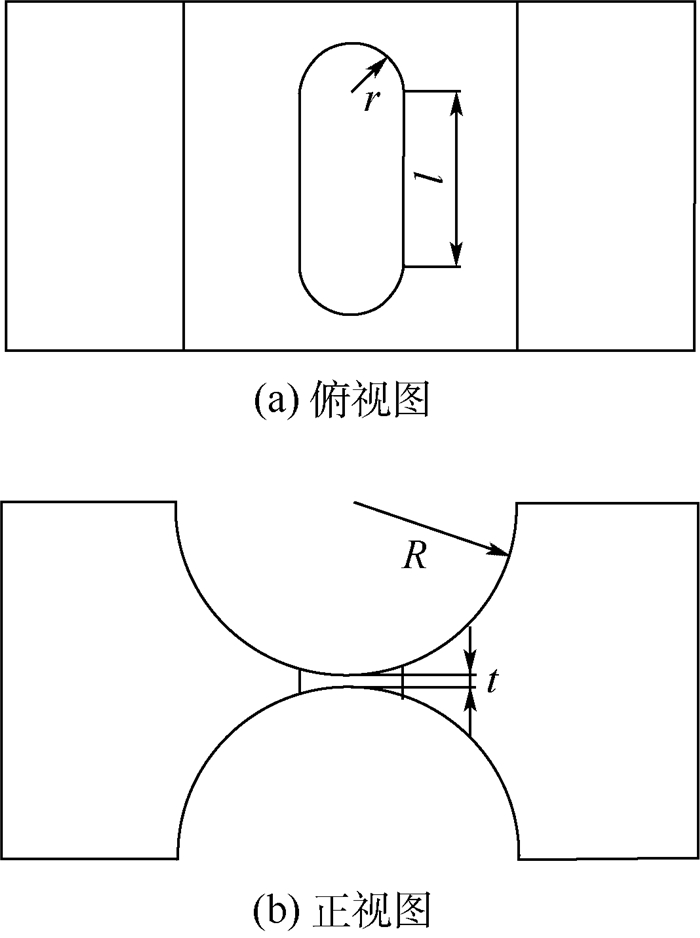图 5 新型柔性铰链俯视图、正视图及参数 Fig. 5 Top and front view of new flexure hinge with parameters

图选项

2 柔度理论分析 如图 6所示, 以平面x=-r和平面x=r为分割面将柔性铰链分割成4个弯曲片段, 按位置对其编号。第i(i=1, 2, 3, 4)个弯曲片段截面高度t_i(x)和宽度b_i(x)的数学表达式为

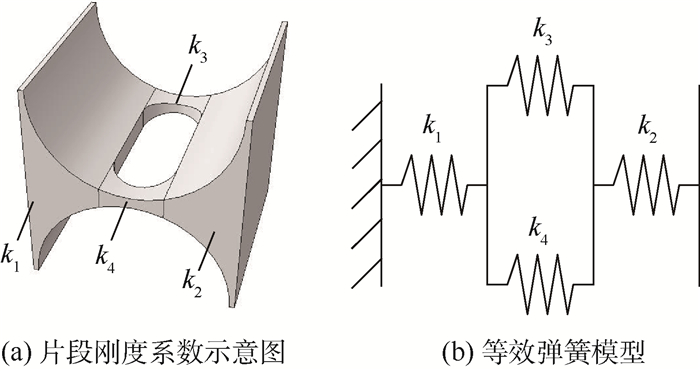图 6 柔性铰链等效弹簧刚度示意图 Fig. 6 Schematic of flexure hinge's equivalent spring stiffness

图选项

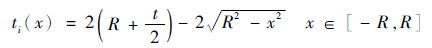(6)

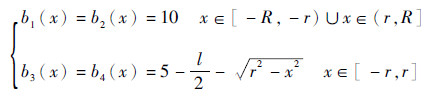(7)

第1个和第2个弯曲片段的截面是高度随切口轮廓变化、宽度不变的矩形, 第3个和第4个弯曲片段的截面是高度随切口轮廓变化、宽度随孔洞域轮廓变化的矩形, 则每个截面的惯性矩为

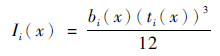(8)

每个截面的面积为

(9)

为求解新型柔性铰链柔度, 使用等效弹簧系统描述新型柔性铰链的拓扑结构。如图 6所示, 4个弯曲片段的刚度系数分别为k₁、k₂、k₃、k₄, 通过弹簧的串并联关系求解等效弹簧刚度系数。k₃和k₄并联后与k₁、k₂串联, 所以等效刚度系数为

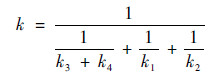(10)

柔度C是刚度系数k的倒数, C=1/k, 由式(10)推导得柔性铰链的等效柔度为

(11)

求解各弯曲片段柔度, 并结合式(11)即可求得该新型柔性铰链柔度, 下面将求解第i个弯曲片段的柔度。
基于微小位移欧拉-伯努利梁理论将各柔性片段简化为一端固定一段自由的悬臂梁^[15]。如图 7所示, 左侧A点为悬臂梁固定端, 右侧B点为自由端, O点为悬臂梁的几何中心, 并以O点为原点建立坐标轴, AB的长度为2a_i。

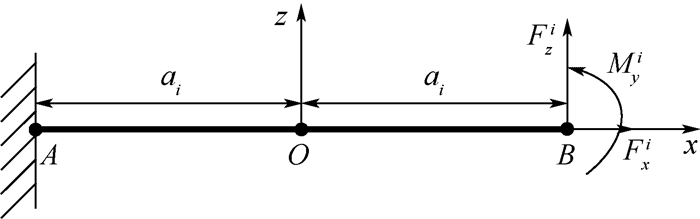图 7 第i个弯曲片段简化悬臂梁示意图 Fig. 7 Schematic of the ith bending segment's simplified cantilever beam

图选项

卡氏第二定理:

(12)

式中:Lⁱ为第i(i=1, 2, 3, 4)个弯曲片段变形量矩阵; Cⁱ为第i个弯曲片段的柔度矩阵; Fⁱ为第i个弯曲片段载荷矩阵, 即

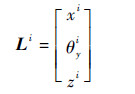(13)

(14)

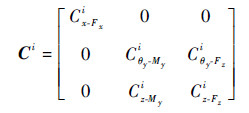(15)

其中:xⁱ为第i个弯曲片段末端x轴方向位移; θ_yⁱ为第i个弯曲片段末端以y轴为轴的转角; zⁱ为第i个弯曲片段末端z轴方向位移; F_xⁱ、M_yⁱ和F_zⁱ分别为第i个弯曲片段末端加载的x轴方向力、y轴方向弯矩和z轴方向力; Cⁱ_x-Fx为B点在F_xⁱ作用下的x轴方向位移; Cⁱ_θy-My和Cⁱ_z-My分别为B点在M_yⁱ作用下y轴转角和z轴方向位移; Cⁱ_θy-Fz和Cⁱ_z-Fz分别为B点在F_zⁱ作用下y轴转角和z轴方向位移。
由卡氏第一定理求解式(13):

(16)

悬臂梁在x轴方向只受F_xⁱ作用, x处所受弯矩为M_yⁱ和F_zⁱ对x点的弯矩之和, 因此简化悬臂梁的变形能Uⁱ的表达式为

(17)

式中:E为弹性模量。
将式(8)和式(9)代入式(16)和式(17)得到Lⁱ, 再将Lⁱ和Fⁱ代入式(12)得到第i个弯曲片段的柔度矩阵Cⁱ。Cⁱ中主对角线柔度项是衡量柔度的关键, 所以只求解主对角线柔度项:

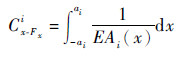(18)

(19)

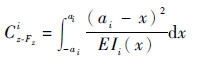(20)

由式(18)~式(20)得到第i个弯曲片段的柔度项表达式具体形式。
C_x-Fxⁱ柔度项表达式:

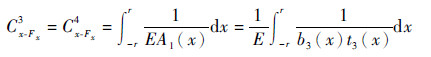(22)

C_θy-Myⁱ柔度项表达式:

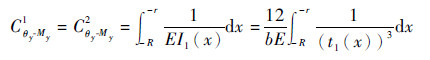(23)

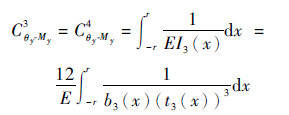(24)

Cⁱ_z-Fz柔度项表达式:

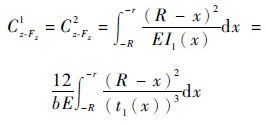(25)

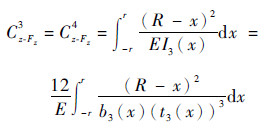(26)

将式(21)~式(26)代入式(11), 可求得新型柔性铰链柔度项C_x-Fx、C_θy-My和C_z-Fz。在MATLAB中编写该新型柔性铰链柔度计算程序, 得到不同参数新型柔性铰链的柔度矩阵主对角柔度项理论值。
3 有限元仿真分析验证 为验证新型柔性铰链柔度矩阵理论分析的正确性, 利用ABAQUS软件对新型柔性铰链进行有限元仿真分析。在仿真分析中, 孔洞域尺寸同拓扑优化结果的孔洞域尺寸, 即r=1.5 mm, l=5 mm。
材料为弹性模量E=110 GPa、泊松比υ=0.3的钛合金。单轴柔性铰链的边界条件和载荷加载情况如图 4所示。模型左侧固定, 在铰链右侧末端中点B点施加y轴方向单位弯矩M_y=1 N·mm得到柔度项C_θy-My; 在铰链右侧末端B点分别施加x和z轴方向单位力F_x=1 N和F_z=1 N得到柔度项C_x-Fx、C_z-Fz。新型柔性铰链的仿真变形结果如图 8所示, 仿真值如表 1中所示。利用第2节理论分析计算得到表 1中理论值, δ为理论值和仿真值的相对误差。

图 8 新型柔性铰链有限元仿真分析 Fig. 8 FEA of new flexure hinge

图选项

表 1 新型柔性铰链柔度理论值与仿真值对比 Table 1 Comparison of theoretical and simulation compliance values of new flexure hinge

R/mm	t/mm	Cθy-My				Cz-Fz				Cx-Fx
		理论值/(10-4rad·(N·mm)-1)	仿真值/(10-4rad·(N·mm)-1)	相对误差/%		理论值/(10-2N-1·mm)	仿真值/(10-2N-1· mm)	相对误差/%		理论值/(10-6N-1· mm)	仿真值/(10-6N-1· mm)	相对误差/%
4	0.2	64.442	66.383	3.01		10.420	10.770	3.36		37.143	38.302	3.12
4	0.3	23.106	23.298	0.83		3.775	3.805	0.79		28.384	28.538	0.54
4	0.4	11.298	11.005	2.59		1.858	1.810	2.58		23.641	22.985	2.77
4	0.5	6.202	6.123	1.27		1.026	1.014	1.17		19.700	19.352	1.77
6	0.2	77.907	78.843	1.20		28.263	28.695	1.53		42.968	43.792	1.92
6	0.3	28.290	27.365	3.27		10.316	10.023	2.84		33.563	32.419	3.41
6	0.4	13.458	12.810	4.81		4.927	4.724	4.12		27.114	26.029	4.00
6	0.5	7.401	7.073	4.43		2.720	2.626	3.46		22.915	21.882	4.51
8	0.2	86.393	88.427	2.35		55.480	57.161	3.03		46.336	47.892	3.36
8	0.3	31.454	30.408	3.33		20.309	19.784	2.59		36.874	35.342	4.15
8	0.4	14.781	14.133	4.38		9.571	9.259	3.26		29.199	28.345	2.92
8	0.5	8.288	7.761	6.36		5.282	5.012	5.11		25.165	23.827	5.32
10	0.2	95.256	96.204	1.00		95.177	97.148	2.07		50.632	51.210	1.14
10	0.3	34.478	32.827	4.79		34.696	33.372	3.82		38.963	37.730	3.16
10	0.4	16.066	15.174	5.55		16.209	15.534	4.16		31.940	30.258	5.27
10	0.5	8.849	8.299	6.22		8.997	8.557	4.89		26.450	25.449	3.78

表选项






表 1中采用控制变量法, 参数R在^{[4, 10]} mm的区间上间隔2取值, 参数t在[0.2, 0.5] mm的区间上间隔0.1取值, 共16组数据。
C_θy-My柔度项相对误差的最大值为6.36%, 最小值为0.83%, 平均值为3.46%;C_z-Fz柔度项相对误差最大值为5.11%, 最小值为0.79%, 平均值为3.05%;C_x-Fx柔度项相对误差最大值为5.32%, 最小值为0.54%, 平均值为3.20%。理论分析和仿真分析数值的相对误差均小于6.36%, 在误差允许范围内, 验证了柔度矩阵理论公式的正确性。
但还存在一定的误差, 是因为使用等效弹簧模型串并联关系描述孔洞域和实体域关系会带来一定误差; 而且柔性铰链是一个空间连续体, 而有限元法的思想是把无限的连续用有限的网格离散变形体近似, 这时将产生离散误差, 并且为使有限元分析同时兼顾精度和效率, 所以单元不能过于细化也是引起误差的一个原因。
4 与圆弧型柔性铰链的对比 通过该新型柔性铰链结构特点可知, 其是以经典的圆弧型柔性铰链的实体域为基础, 在铰链厚度最小处的水平面添加孔洞域而来, 现对比相同参数R和t的2种柔性铰链的柔度与柔度比。
基于第2节新型柔性铰链的理论分析计算出新型柔性铰链的C_x-Fx、C_θy-My和C_z-Fz柔度项, 文献[4]计算出圆弧型柔性铰链的C_x-Fx、C_θy-My和C_z-Fz柔度项, 并定义柔度比χ=C_z-Fz/C_x-Fx。图 9绘制了有相同参数R和t的圆弧型柔性铰链和新型柔性铰链的C_θy-My和C_z-Fz柔度项对比; γ_θy-My为新型柔性铰链与圆弧型柔性铰链的C_θy-My柔度项比值, γ_z-Fz为新型柔性铰链与圆弧型柔性铰链的C_z-Fz柔度项比值, 这2个参数用以衡量2种柔性铰链柔度差异。图 10为2种柔性铰链的柔度比χ对比, γ_χ为2种柔性铰链的柔度比χ的比值。

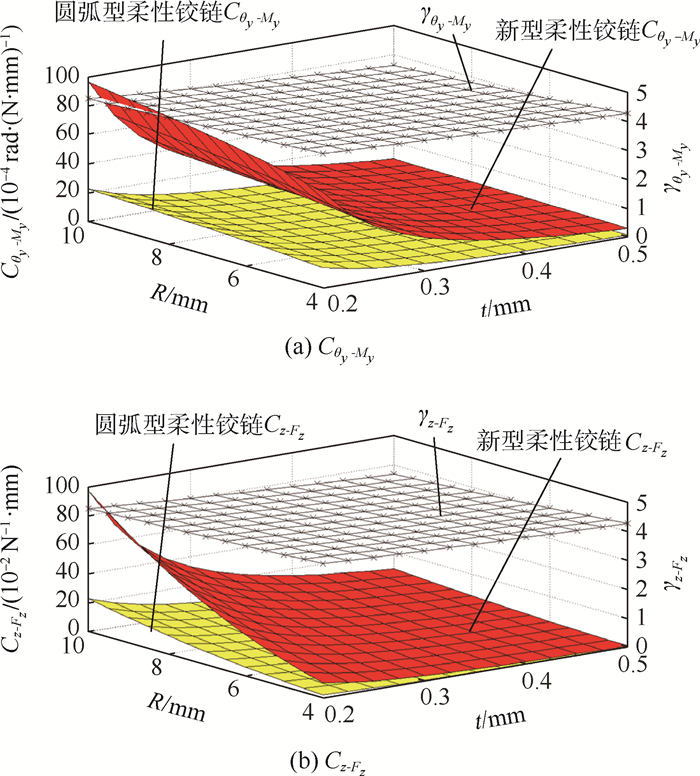图 9 2种柔性铰链Cθy-My和Cz-Fz柔度项对比 Fig. 9 Comparison of compliance item Cθy-My and Cz-Fz between two flexure hinges

图选项

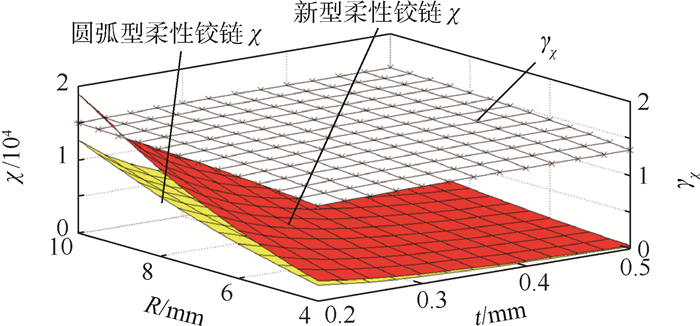图 10 2种柔性铰链柔度比对比 Fig. 10 Comparison of compliance ratio χ between two flexure hinges

图选项

通过图 9可知, 圆弧型柔性铰链和新型柔性铰链的柔度都随参数R的增大和参数t的减小而增大。但新型柔性铰链的柔度明显大于具有相同切口轮廓的圆弧型柔性铰链, 尤其当参数R越大, 参数t越小时, 柔度增大的趋势越明显。γ_θy-My和γ_z-Fz都稳定在γ=4平面, 所以新型柔性铰链的转动性能是圆弧型柔性铰链转动能力的4倍, 新型柔性铰链具有更大的转动能力, 柔度提升300%。
图 10表明, 在柔度比χ的对比中, 新型柔性铰链的柔度比χ也明显大于圆弧型柔性铰链, γ_χ稳定在γ=1.5平面, 证明新型柔性铰链在z轴方向可以获得更大的柔度, 也表明拓扑优化模型正确。
5 结论 1) 本文基于三维连续体拓扑优化的变密度法, 建立了单轴柔性铰链的拓扑优化模型, 设计出一种具有全新三维拓扑结构的单轴柔性铰链。
2) 借助等效弹簧模型描述新型柔性铰链的三维拓扑结构, 推导出其柔度矩阵, 设计16组实例进行有限元仿真分析, 并与理论分析值进行对比, 结果表明有限元仿真分析值和理论计算值的相对误差在6.36%以内, 验证了理论分析的正确性。
3) 对比具有相同参数的新型柔性铰链与圆弧型柔性铰链的柔度和柔度比, 结果表明新型柔性铰链比圆弧型柔性铰链柔度提升300%, 柔度比是其1.5倍。
综上, 本文使用三维连续体拓扑优化方法, 为设计单轴柔性铰链提供了一种在垂直于切口轮廓面的水平面添加孔洞域的思路, 此设计结果可以明显增大单轴柔性铰链的转动能力。

参考文献

[1]	于靖军, 郝广波, 陈贵敏, 等. 柔性机构及其应用研究进展[J].机械工程学报, 2015, 51(13): 53–68. YU J J, HAO G B, CHEN G M, et al. State-of-art of compliant mechanisms and their applications[J].Chinese Journal of Mechanical Engineering, 2015, 51(13): 53–68.(in Chinese)
[2]	余跃庆, 李清清. Y型柔性铰链的设计与实验[J].光学精密工程, 2017, 25(2): 394–400. YU Y Q, LI Q Q. Design and experiment of Y-type flexure hinge[J].Optics and Precision Engineering, 2017, 25(2): 394–400.(in Chinese)
[3]	陈贵敏, 贾建援, 刘小院, 等. 柔性铰链精度特性研究[J].仪器仪表学报, 2004, 25(4): 107–109. CHEN G M, JIA J Y, LIU X Y, et al. Study on the accuracy of flexible hinges[J].Chinese Journal of Scientific Instrument, 2004, 25(4): 107–109.(in Chinese)
[4]	LOBONTIU N, GARCIA E. Analytical model of displacement amplification and stiffness optimization for a class of flexure-based compliant mechanisms[J].Computers and Structures, 2003, 81(32): 2797–2810.DOI:10.1016/j.compstruc.2003.07.003
[5]	SMITH S T, BADAMI V G, Dale J S, et al. Elliptical flexure hinges[J].Review of Scientific Instruments, 1997, 68(3): 1474–1483.DOI:10.1063/1.1147635
[6]	CHEN G M, LIU X Y, GAO H W, et al. A generalized model for conic flexure hinges[J].Review of Scientific Instruments, 2009, 80(5): 106–116.
[7]	邱丽芳, 南铁玲, 柳林. 微柔性铰链转动能力和精度特性研究[J].微纳电子技术, 2007, 44(12): 1068–1072. QIU L F, NAN T L, LIU L. Study on the rotation capacity and the precision of micro flexible hinges[J].Micronanoelectronic Technology, 2007, 44(12): 1068–1072.DOI:10.3969/j.issn.1671-4776.2007.12.008(in Chinese)
[8]	卢倩, 黄卫清, 王寅, 等. 深切口椭圆柔性铰链优化设计[J].光学精密工程, 2015, 23(1): 206–215. LU Q, HUANG W Q, WANG Y, et al. Optimization design of deep-notch elliptical flexure hinges[J].Optics and Precision Engineering, 2015, 23(1): 206–215.(in Chinese)
[9]	卢倩, 黄卫清, 孙梦馨. 基于柔度比优化设计杠杆式柔性铰链放大机构[J].光学精密工程, 2016, 24(1): 102–111. LU Q, HUANG W Q, SUN M X. Optimization design of amplification mechanism for level flexure hinge based on compliance ratio[J].Optics and Precision Engineering, 2016, 24(1): 102–111.(in Chinese)
[10]	于靖军, 裴旭, 毕树生, 等. 柔性铰链机构设计方法的研究进展[J].机械工程学报, 2010, 45(13): 2–13. YU J J, PEI X, BI S S, et al. State-of-arts of design method for flexure mechanisms[J].Journal of Mechanical Engineering, 2010, 45(13): 2–13.(in Chinese)
[11]	ZHU B L, ZHANG X M, FATIKOW S. Design of single-flexure hinges using continuum topology optimization method[J].Science China:Technological Sciences, 2014, 57(3): 560–567.DOI:10.1007/s11431-013-5446-4
[12]	LIU M, ZHANG X M, FATIKOW S. Design and analysis of a high-accuracy flexure hinge[J].Review of Scientific Instruments, 2016, 87(5): 055106.DOI:10.1063/1.4948924
[13]	刘敏, 张宪民. 基于类V型柔性铰链的微位移放大机构[J].光学精密工程, 2017, 25(4): 467–476. LIU M, ZHANG X M. Mico-displacement amplifier based on quasi-V-shaped flexure hinge[J].Optics and Precision Engineering, 2017, 25(4): 467–476.(in Chinese)
[14]	LIU M, ZHANG X M, FATIKOW S. Design and analysis of a multi-notched flexure hinge for compliant mechanisms[J].Precision Engineering, 2017, 48: 292–304.DOI:10.1016/j.precisioneng.2016.12.012
[15]	PAROS J M, WEISBORO L. How to design flexure hinges[J].Machine Design, 1965, 37(27): 151–156.