在尾桨故障中,最严重也是最危险的故障就是尾桨完全失效[2-3],即由尾桨传动轴断裂或者尾桨碰撞而造成的侧力突然消失。此时,尾桨完全失去了作用,旋翼反扭矩无法平衡,直升机向旋翼旋转的相反方向加速偏转。在这种情况下,驾驶员应立即关闭发动机,从而停止向旋翼输出扭矩,防止机身进一步加速偏转。随后通过自转下滑方式着陆,期间倘若处理不当将会导致严重的事故。因此,本文重点对直升机尾桨完全失效后自转着陆的最优轨迹和操纵过程进行研究。
国内外关于尾桨故障后的安全飞行问题已有一定研究。主要包括模拟直升机各类尾桨故障的工程试飞和处理方法[1-3],尾桨受损部件的检测分析[4-6],新的故障监测方法[7-9],以及直升机尾桨完全失效后的飞行仿真[10-11]。在飞行仿真方面,文献[10]建立了直升机尾桨完全失效后的6自由度刚体模型,并设计控制系统,让尾桨完全失效后的直升机重新配平,但没有研究其自转着陆过程;文献[11]设计了控制系统,可以让尾桨完全失效后的小型无人直升机跟踪预定轨迹进行自转着陆,但并未研究其最优自转着陆过程。可以看出,目前对直升机尾桨完全失效后自转着陆的研究尚未涉及到最优轨迹和操纵过程的求解。
直升机尾桨完全失效后的最优着陆轨迹和操纵过程问题可以被描述为:在尾桨完全失效后,从允许的尾桨失效后自转着陆的操纵策略中找出一个最优的操纵策略,使直升机在该操纵策略作用下由初始飞行状态完成自转下滑着陆到允许的目标状态(或范围)的同时,其评价整个自转着陆过程品质优劣的性能指标为最优。该问题可以采用最优控制方法进行求解。最优控制方法广泛应用于直升机发动机失效后轨迹优化的研究,不仅可以得到直升机发动机失效后安全飞行的最优飞行轨迹和操纵[12-16],还能为飞行试验提供理论依据[17-21]。目前尚未有文献将该方法应用于研究直升机尾桨完全失效后的最优自转着陆过程。
因此,本文采用最优控制方法研究直升机尾桨完全失效后的最优自转着陆轨迹和操纵过程。首先,建立直升机6自由度刚体飞行动力学模型,在模型中加入可以描述尾桨完全失效和自转着陆阶段发动机出轴功率以及旋翼转速变化的相关方程。在该模型的基础上,以直升机的状态量和控制量为优化变量,将直升机尾桨完全失效后的自转着陆问题转化为非线性最优控制问题,并采用直接转换法和序列二次规划算法进行求解。然后,以某型号单旋翼带尾桨直升机为样机,计算前飞状态下空中停车后的自转着陆过程,并与飞行试验数据进行对比,以验证所建模型和最优控制方法的准确性。最后,计算并分析该型号直升机在以巡航速度下前飞时,尾桨完全失效后自转着陆的最优轨迹和操纵过程。
1 飞行动力学建模 首先给出常规单旋翼带尾桨直升机的6自由度刚体飞行动力学模型(建模过程见参考文献[19])。其状态量为:体轴系下的速度u、v和w;滚转、俯仰和偏航角速度p、q和r;滚转角、俯仰角和偏航角φ、θ和ψ;水平位移、侧向位移和高度x、y和h。操纵量为:旋翼桨根总距θ0,纵向周期变距θs,横向周期变距θc和尾桨总距θt。主控方程如下:
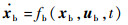 | (1) |
式中:xb为状态向量;ub为操纵向量;t为时间。
本文假设直升机在尾桨完全失效前处于配平状态,故可根据主控方程式(1)给出当前飞行条件下稳定飞行时的状态量和操纵量。
当直升机尾桨完全失效时,尾桨提供的侧向力突然消失,此时原飞行动力学模型中由尾桨产生的力(FXTR、FYTR、FZTR)、力矩(MXTR、MYTR、MZTR)和尾桨需用功率PTR均为零,即
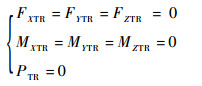 | (2) |
驾驶员在发现直升机尾桨完全失效后,应立即将油门关至慢车状态,从而停止向旋翼输出扭矩,防止机身进一步加速偏转。此时发动机出轴功率PA以及旋翼转速Ω自由度方程可以表示为[20]
 | (3) |
式中:tp为发动机响应时间常数;PMR为旋翼需用功率;η为直升机传动效率因子;IMR为旋翼转动惯量。
在随后的自转着陆过程中,由于尾桨完全失效,驾驶员只能通过操纵旋翼桨根总距θ0,纵向周期变距θs和横向周期变距θc来使直升机安全着陆。考虑到操纵系统特性对这3个操纵量速度的限制,同时为了避免操纵量出现跳跃或者不连续的控制形式[17],使用操纵量关于时间t的导数u0、us和uc作为新的控制变量,并把θ0、θs和θc作为新的状态变量,即
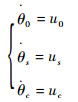 | (4) |
式(1)~式(4)组成了适用于计算直升机尾桨完全失效后轨迹优化的6自由度刚体飞行动力学模型。其状态空间形式为
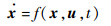 | (5) |
式中:状态量x和控制量u分别为
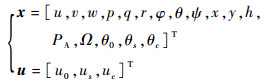 | (6) |
2 最优控制模型和数值解法 2.1 最优控制模型 直升机尾桨完全失效后的最优安全着陆问题可以归结为一种含有状态和控制约束的非线性最优控制问题。最优控制问题一般由优化变量、性能指标、微分方程、边界条件和路径约束组成[21]。
1) 优化变量
按照最优控制问题描述,优化变量为6自由度刚体飞行动力学模型式(5)中的状态量x和控制量u,以及自转着陆初始时刻t0和结束时刻tf。
2) 性能指标
尾桨完全失效后自转着陆的过程中,驾驶员不仅要通过剩余的3个操纵量(θ0、θs和θc)来尽量维持横航向姿态的稳定,同时还要控制俯仰姿态角、前飞速度和下降率以完成安全着陆。此外,还应该考虑到自转下滑所需时间、自转着陆的可操纵性和可实现性等因素,故性能指标J可以定为
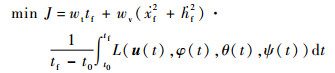 | (7) |
式中:
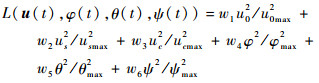 | (8) |
其中:
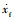
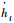
3) 微分方程
采用适用于计算尾桨完全失效后自转着陆过程的6自由度刚体飞行动力学模型式(5)。
4) 边界条件
① 初始边界条件(t0时刻)
假设直升机在标准大气条件下尾桨完全失效时处于稳定飞行状态,根据旋翼飞行器适航条例规定[22],尾桨完全失效后,驾驶员至少延迟1 s开始操纵直升机,因此本文以尾桨完全失效1 s后直升机的飞行状态作为初始边界条件(t0=1 s)。为了求得初始边界条件,需要计算直升机发生尾桨完全失效到驾驶员开始操纵这段时间内的自由响应,即求解操纵量保持不变时,由式(1)和式(2)构成的一阶微分方程(此时驾驶员尚未关闭发动机,旋翼保持正常转速,因此式(3)不发挥作用)。为此,首先对主控方程式(1)进行配平计算得到直升机尾桨完全失效前稳定飞行时的状态量和操纵量,得到一阶微分方程的初值,然后使用向后差分公式算法求解。
② 末端边界条件(tf时刻)
本文根据旋翼飞行器适航条例关于自转下滑的具体要求确定最优控制模型的末端边界条件:
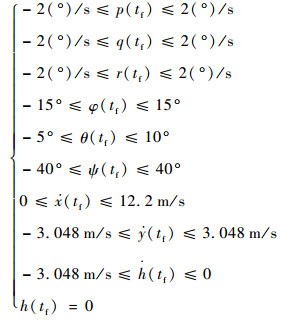 | (9) |
式中:
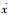
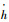
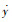
5) 路径约束
为了让直升机尾桨完全失效后自转下滑的轨迹和操纵时间历程在可接受的范围内,本文根据旋翼飞行器适航条例关于自转下滑的要求,结合当前的飞行状态、飞行任务和操纵系统特性来确定最优控制模型的路径约束:
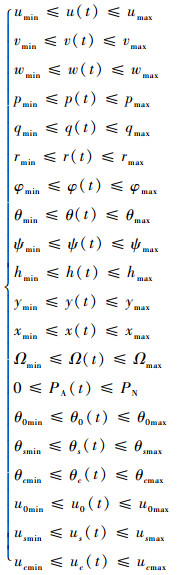 | (10) |
式中:PN为发动机额定功率。路径约束的具体数值将在算例中给出。
2.2 数值解法 直升机尾桨完全失效后最优控制问题的状态和控制变量众多,约束和目标函数非常复杂,故解析求解不可行,需要通过数值求解。本文采用直接转换法将该非线性动态最优控制问题转化为非线性规划问题,并用具有良好鲁棒性和计算效率的序列二次规划算法来求解[19-20]。
2.2.1 无量纲缩放 在求解最优控制问题时,由于优化变量的量纲不同,某些变量之间的数量级相差较大,会引起数值求解困难。所以在数值计算前,首先对飞行动力学模型式(5)中的优化变量进行无量纲缩放。
状态量、控制量和时间的无量纲缩放如下:
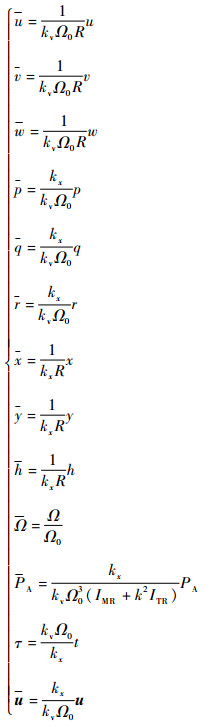 | (11) |
式中:kx和kv为常数;Ω0为直升机标准旋翼转速;R为旋翼半径;k为旋翼和尾桨转速比;ITR为尾桨转动惯量。为了使无量纲缩放后的状态变量和控制变量大小接近1,取kx=10, kv=0.1,则无量纲缩放后飞行动力学模型的主控方程可以表示为
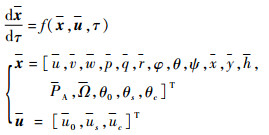 | (12) |
2.2.2 直接转换法 将时间的无量纲τ等分为N-1个时间段:
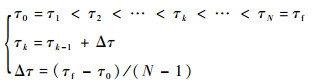 | (13) |
根据时间节点把连续空间下的状态变量和控制变量进行离散可得
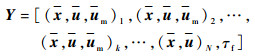 | (14) |
式中:
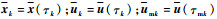
对最优控制问题中的微分方程进行离散,得到缺陷等式约束方程为
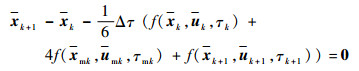 | (15) |
式中:
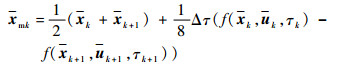 | (16) |
对性能指标进行离散得
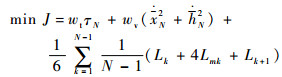 | (17) |
将路径约束作用到所有时间节点和中点处,然后将初始边界条件和末端边界条件分别作用到初始和末端时间节点处,最终可以将最优控制问题离散成非线性规划问题。本文应用稀疏序列二次规划算法[23]进行求解,然后将所有时间节点和中点处的状态变量和控制变量最优解进行分段3次Hermite插值,即可得到原最优控制问题的最优解,从而得到直升机尾桨完全失效后自转着陆的最优轨迹和操纵过程。
3 模型和方法验证 由于目前尚未找到直升机尾桨完全失效后自转着陆的飞行试验数据,为了说明所建模型和采用的最优控制方法的可行性和准确性,本文对模型进行了一些修改,使其能够计算直升机空中停车后的最优自转着陆过程,从而可以和文献[24]中的飞行试验数据进行对比。虽然直升机尾桨完全失效后的自转着陆与空中停车后的自转着陆有一些不同之处:前者只能通过侧滑来稳定航向的姿态,而后者可以通过尾桨来进行航向控制。但两者也有一定的相似之处,即均涉及到发动机关闭后的自转着陆过程。因此,虽然2种自转下滑对应的飞行状态和操纵策略并不完全相同,但是通过与直升机空中停车后自转着陆的飞行试验数据的对比,可以在一定程度上说明本文建立的旋翼和机体模型的准确性。除此之外,在文献[24]中,驾驶员可以根据当前飞行任务自行决定自转着陆过程中的操纵策略和对应的飞行轨迹,而不需要去跟踪预定的飞行轨迹和操纵方案。因此也可以验证本文最优控制方法的准确性。
本文所用样机型号和参数与文献[24]一致,其基本参数如表 1所示。
表 1 某直升机基本参数 Table 1 Basic parameters of a helicopter
| 参数 | 数值 |
| 总质量W/kg | 2 000 |
| 旋翼半径R/m | 5.345 |
| 主桨叶片数nMb | 3 |
| 负扭θ1/(°) | -12 |
| 桨叶弦长c/m | 0.35 |
| 旋翼转速Ω/(r·min-1) | 386 |
| 旋翼实度σ | 0.062 |
| 旋翼方向 | 左旋 |
| 尾桨叶片数nTb | 2 |
| 平尾面积Shs/m2 | 4.67 |
| 平尾安装角ihs/(°) | 0 |
| 垂尾面积/m2 | 1.021 |
| 旋翼位置/m | (-0.09, 0.01, 1.53) |
| 平尾位置/m | (-4.91, 0.01, 0.01) |
| 垂尾位置/m | (-6.90, 0, 0.50) |
| 尾桨位置/m | (-6.35, 0.30, -0.51) |
表选项
该型号直升机的初始状态和飞行任务如下:前飞速度为30 m/s,高度为200 m,航迹角为0°,处于无侧滑稳定飞行状态。随后驾驶员关闭发动机模拟空中停车,并在2 s后操纵直升机进入自转下滑,最后安全着陆。
在该飞行试验中尾桨可以正常工作,故需要在飞行动力学模型式(5)中取消式(2)的作用,并加入尾桨总距θt与其关于时间的一阶导数ut。
由于发动机首先关闭,在求初始边界条件时对应的一阶微分方程改由式(1)和式(3)构成。末端边界条件采用式(9)。具体路径约束如下:
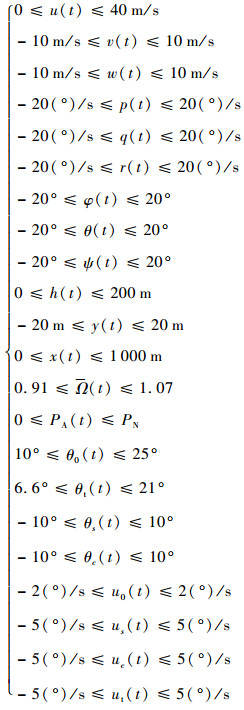 | (18) |
性能指标式(7)中的各项权重系数wt=0.01, wv=0.03, w1=w2=w3=0.15, w4=w5=w6=0.12,其中函数L中加入ut2/utmax2对应权重系数为0.15。
图 1为本文计算得到的某型号直升机空中停车后自转着陆过程与飞行试验数据的对比,图中ud为地轴系下前飞速度。从图 1中可以看出,本文计算的最优自转着陆过程和飞行试验数据吻合较好。在着陆阶段,本文计算得到的总距变化更加柔和,这是因为在飞行试验时,驾驶员采取的操纵策略并不一定是当前飞行任务下最优的,而本文采用了最优控制方法,对操纵速率进行了控制和约束,因此可以得到更好的操纵策略。通过与飞行试验数据的对比可以说明本文建立的飞行动力学模型以及采用的最优控制方法的准确性,可以用来研究直升机尾桨完全失效后自转着陆的最优轨迹和操纵过程。
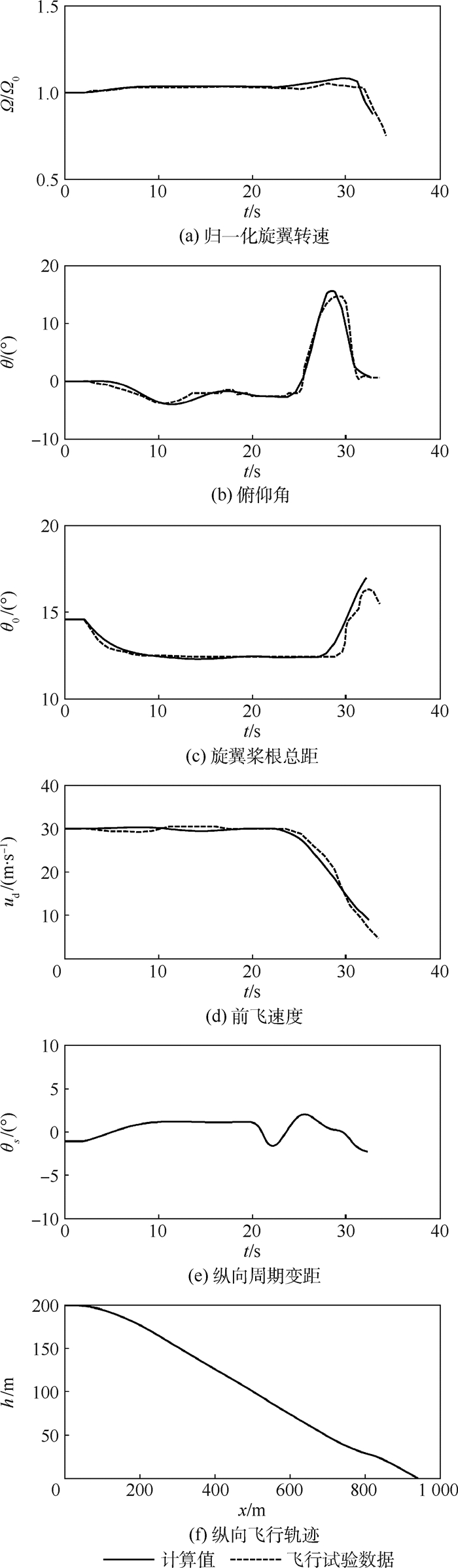 |
| 图 1 空中停车最优自转着陆过程与飞行试验数据对比 Fig. 1 Comparison between optimal autorotation landing procedure and flight test data for in-flight shutdown |
| 图选项 |
4 尾桨完全失效后自转着陆优化 计算分析该型号直升机在以巡航速度下前飞时,尾桨完全失效后自转着陆的最优轨迹和操纵过程。尾桨完全失效时初始状态如下:速度为35 m/s,高度为50 m,航迹角为0°,飞行器处于无侧滑稳定飞行状态。随后尾桨完全失效,尾桨提供侧力突然消失,假设驾驶员在反应1 s以后关闭发动机并自转下滑着陆。
初始边界条件采用第2节介绍的方法计算得到,末端边界条件采用式(9)。尾桨完全失效后自转着陆所需的路径约束如下:
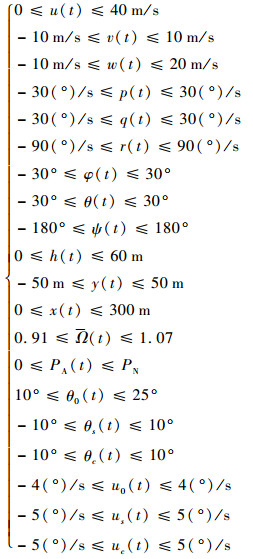 | (19) |
性能指标式(7)中的各项权重系数wt=0.05, wv=0.05, w1=w2=w3=0.18, w4=w5=w6=0.12。
图 2和图 3为本文计算得到的该型号直升机尾桨完全失效后自转着陆的最优轨迹和操纵过程,图中:vd和wd分别为地轴系下侧向速度和下降率,β为机身侧滑角。
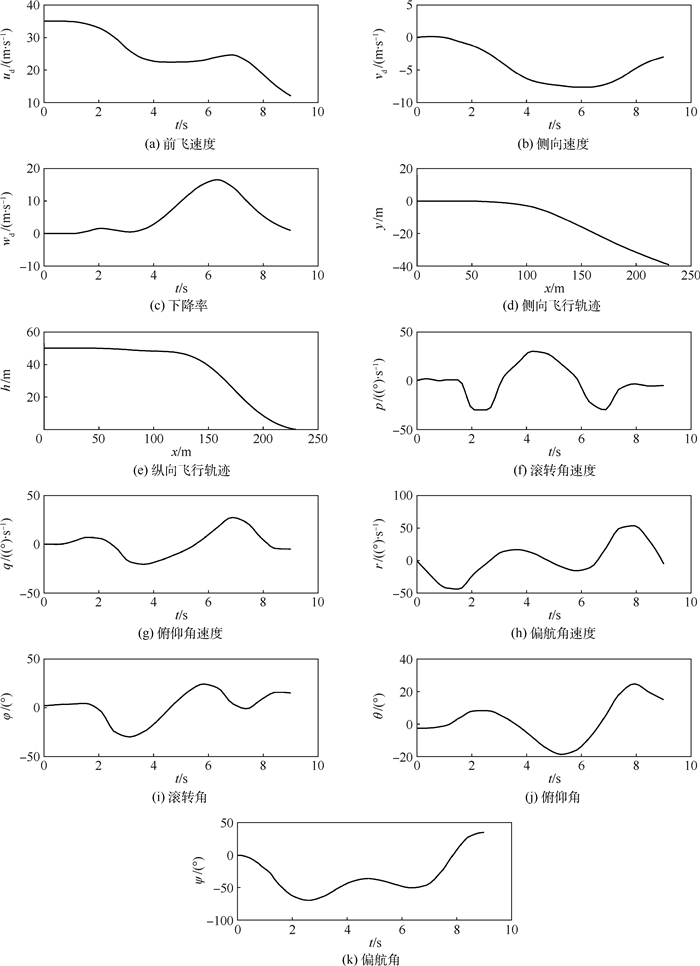 |
| 图 2 最优自转着陆过程的状态量变化 Fig. 2 States in optimal autorotation landing procedure |
| 图选项 |
 |
| 图 3 最优自转着陆过程的功率、转速、侧滑角与操纵量的变化 Fig. 3 Power, rotor speed, sideslip angle and controls in the optimal autorotation landing procedure |
| 图选项 |
从图 2和图 3可以得到以下结论:
1) 尾桨完全失效时,偏航角速度r急剧变化(图 2(h)),在1 s后已接近-50(°)/s,但此时滚转角速度p和俯仰角速度q变化较为稳定(图 2(f)、(g));在1 s之后,驾驶员关闭发动机,偏航角速度变化开始减弱,但偏航角(图 2(k))和侧滑角(图 3(c))继续增大,进而产生复杂的耦合运动,其主要表现为出现了明显的横滚响应(图 2(i)),这主要是由大侧滑角导致直升机垂尾侧向力对全机重心产生很大的滚转力矩所致。
2) 驾驶员延迟1 s后开始操纵直升机,将油门关至慢车进入自转下滑(图 3(a))。自转下滑期间,驾驶员需要降低总距(图 3 (d)),向前推杆通过纵向周期变距(图 3(f))来降低俯仰角(图 2(j))进入下滑,并操纵横向周期变距(图 3(e))稳定滚转角(图 2(i)),然后采用侧滑方式进一步稳定横航向的姿态角(图 2(k))。
3) 在准备着陆阶段,驾驶员开始增总距,同时向后拉杆增大俯仰角(图 3(d)、(f)、图 2(j)),减小直升机的下降率和飞行速度;在俯仰角增大至30°时,驾驶员向前推杆,防止俯仰角继续增大,从而保持直升机的着陆姿态。
4) 着陆时姿态较为平稳,接地侧向速度和下降率接近0(图 2(a)~(c)),前飞速度也在允许的范围之内。
从以上结论可以看出,本文得到的最优轨迹和操纵过程较为合理,且与文献[1-3]中由工程试飞得出的定性的结论和建议相符。
5 结论 1) 本文建立了适用于计算直升机尾桨完全失效后轨迹优化的6自由度刚体飞行动力学模型,并将直升机尾桨完全失效后的自转着陆问题转化为非线性最优控制问题进行求解。从而能够研究并分析直升机尾桨完全失效后自转着陆的最优轨迹和操纵过程。
2) 本文计算的某型号直升机空中停车自转着陆的最优轨迹和操纵与飞行试验数据吻合良好,说明所建模型和采用的最优控制方法的准确性和可行性。
3) 该型号直升机在巡航速度下发生尾桨完全失效时,直升机在旋翼负扭的作用下会产生较大的偏航角速度和侧滑角变化,进而产生复杂的耦合运动,主要表现为明显的横滚响应。因此,驾驶员在关闭发动机进行自转着陆的同时,还需要通过操纵横向周期变距稳定滚转角,并以侧滑的方式来稳定横航向的姿态角,最后安全着陆。利用本文所建模型和最优控制方法得到的整个最优自转着陆过程,与工程试飞得出的定性的结论和建议相符。
参考文献
| [1] | 孙杰, 高艳辉. 直升机尾桨故障及其试飞研究[J].飞行力学, 2001, 19(4): 67–69. SUN J, GAO Y H. The helicopter tail-rotor failure and the flight test[J].Flight Mechanics, 2001, 19(4): 67–69.(in Chinese) |
| [2] | 于琦, 章海红. 直升机尾桨机械性失效及试飞研究[J].飞行力学, 2008, 26(3): 74–77. YU Q, ZHANG H H. Analysis of the tail-rotor failure from mechanical malfunction and research in flight test[J].Flight Mechanics, 2008, 26(3): 74–77.(in Chinese) |
| [3] | 赵敬超. 直升机尾桨失效分析及试飞技术研究[J].航空科学技术, 2015, 26(3): 70–73. ZHAO J C. Helicopter tail rotor failure analysis and flight test technology research[J].Aeronautical Science & Technology, 2015, 26(3): 70–73.(in Chinese) |
| [4] | 张海. 某型直升机尾桨桨距操纵杆断裂故障分析[J].航天制造技术, 2010(4): 29–32. ZHANG H. Fault analysis of an operating lever's rupture in helicopter[J].Aerospace Manufacturing Technology, 2010(4): 29–32.(in Chinese) |
| [5] | 李春光, 舒平, 马晓明, 等. 直升机尾桨连杆组件失效分析[J].失效分析与预防, 2013, 8(6): 346–349. LI C G, SHU P, MA X M, et al. Failure analysis on tailor rotor rod components of a helicopter[J].Failure Analysis and Prevention, 2013, 8(6): 346–349.(in Chinese) |
| [6] | 艾剑波, 黄文俊, 李满福, 等. 直11型机尾桨变距拉杆故障分析与处理[J].直升机技术, 2009(3): 68–71. AI J B, HUANG W J, LI M F, et al. The analysis and treatment on tail rotor pitch-link failure of Z11 helicopter[J].Helicopter Technique, 2009(3): 68–71.(in Chinese) |
| [7] | GOODMAN N, BAYOUMI A, BLECHERTAS V, et al. CBM component testing at the University of South Carolina: AH-64 tail rotor gearbox studies[C]//American Helicopter Society Technical Specialists' Meeting on Condition Based Maintenance. Grapevine, Texas: AHS, 2009: 1-8. |
| [8] | SINGH H K, PAWAR P M, GANGULI R, et al. On the effect of mass and stiffness unbalance on helicopter tail rotor system behavior[J].Aircraft Engineering and Aerospace Technology, 2008, 80(2): 129–138.DOI:10.1108/00022660810859355 |
| [9] | 胡和平. 动力学分析在某直升机尾桨故障分析中的应用[J].直升机技术, 2009(3): 21–24. HU H P. Application of dynamic analysis in helicopter tail rotor failure analysis[J].Helicopter Technique, 2009(3): 21–24.(in Chinese) |
| [10] | O'ROURKE M J. Simulation model for tail rotor failure[J].Journal of Aircraft, 1994, 31(1): 197–205.DOI:10.2514/3.46474 |
| [11] | GARCIA R D, VALAVANIS K P, KANDEL A. Autonomous helicopter navigation during a tail rotor failure utilizing fuzzy logic[C]//Proceedings of the 15th Mediterranean Conference on Control & Automation. Piscataway, NJ: IEEE Press, 2007: 1-6. |
| [12] | JOHNSON W. Helicopter optimal descent and landing after power loss: NASA TM-73244[R]. Washington, D. C. : NASA, 1977. |
| [13] | LEE A Y, BRYSON A E, HINDSON W S. Optimal landing of a helicopter in autorotation[J].Journal of Guidance, Control, and Dynamics, 1988, 11(1): 7–12.DOI:10.2514/3.20262 |
| [14] | CHEN R T N, ZHAO Y. Optimal trajectories for the helicopter in one-engine-inoperative terminal area operations: NASA TM-110400[R]. Washington, D. C. : NASA, 1996. |
| [15] | OKUNO Y, KEIJI K, AKIRA A. Analytical prediction of height-velocity diagram of a helicopter using optimal theory[J].Journal of Guidance, Control, and Dynamics, 1991, 14(2): 453–459.DOI:10.2514/3.20659 |
| [16] | BIBIK P, NARKIEWICZ J. Helicopter optimal control after power failure using comprehensive dynamic model[J].Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1354–1362.DOI:10.2514/1.51371 |
| [17] | BOTTASSO C L, MAISANO G, SCORCELLETTI F. Trajectory optimization procedures for rotorcraft vehicles, their software implementation, and applicability to models of increasing complexity[J].Journal of the American Helicopter Society, 2010, 55(3): 32010.DOI:10.4050/JAHS.55.032010 |
| [18] | 孟万里, 陈仁良. 直升机单发失效后自转着陆轨迹优化[J].航空学报, 2011, 32(9): 1599–1607. MENG W L, CHEN R L. Trajectory optimization of helicopter autorotation landing after one engine failure[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1599–1607.(in Chinese) |
| [19] | MENG W L, CHEN R L. Study of helicopter autorotation landing following engine failure based on a six-degree-of-freedom rigid-body dynamic model[J].Chinese Journal of Aeronautics, 2013, 26(6): 1380–1388.DOI:10.1016/j.cja.2013.07.041 |
| [20] | 孟万里. 直升机单台发动机失效后飞行轨迹优化研究和应用[D]. 南京: 南京航空航天大学, 2014: 27-57. MENG W L. Study and application of trajectory optimization for helicopter flight after one engine failure[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014: 27-57(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10287-1015951833.htm |
| [21] | KIM C J, SUNG S, PARK S H, et al. Numerical time-scale separation for rotorcraft nonlinear optimal control analyses[J].Journal of Guidance, Control, and Dynamics, 2014, 37(2): 658–673.DOI:10.2514/1.59557 |
| [22] | KIM S. Certification of transport category rotorcraft: 29-2C[S]. Washington: Federal Aviation Administration, Department of Transportation, 2014: 57-146. |
| [23] | GILL P E, MURRAY W, SAUNDERS M A. User's guide for SNOPT version 7: Software for large-scale nonlinear programming[D]. San Diego: University of California, 2007: 4-29. |
| [24] | 牛永红, 杨百兴. Z11直升机自转着陆试飞[J].飞行力学, 2001, 19(3): 74–76. NIU Y H, YANG B X. Flight test of Z11 helicopter autorotation landing[J].Flight Dynamics, 2001, 19(3): 74–76.(in Chinese) |
