部分可变刚度驱动器在固锁定刚度调节动力的情况下表现出了随交互力非线性的刚度变化[6-8],这也与柔顺驱动器刚度设计准则相一致。也有****致力于研究和设计非线性刚度弹性体用于柔顺驱动器。代表性的有Nicola和Masafumi采用凸轮和线性弹簧制作的非线性结构[9],Pew和Klute通过改变杠杆支点改变力臂达到非线性效果[10],Austin等通过橡胶达到非线性效果[11]以及Palli等采用平面柔性四杆机构得到负载刚度非线性关系等[12]。笔者课题组设计的非线性刚度驱动器(NSCA)不同于上述非线性结构,首次提出弹性悬臂梁和凸轮原理相结合的机构实现给定的非线性刚度关系。
然而,在人机交互过程中外界干扰和噪声带来的振动以及不柔顺交互感限制了非线性刚度驱动器的控制性能,而此类问题需要通过设计相应的控制器来解决。经典的串联弹性驱动器(SEA)一般采用PID控制,配合使用前馈控制来提高其控制性能。然而,用PID等单一闭环反馈控制器来解决一些未知的外部干扰就显得捉襟见肘了[13]。当系统受外部干扰时,很难设计出一个既保持系统稳定又保持高性能的控制器。Ohnishi等于1987年首次提出了干扰观测器(Disturbance Observer, DOB)用于估计系统中的难以可测量的干扰[14]。干扰观测器还是典型的鲁棒控制工具,在机器人和工业自动化等领域得到了广泛的应用。
普遍认为,基于干扰观测器的控制系统具有2个自由度的控制结构,包括内环反馈和外环反馈[15-16]。内环反馈主要用于抑制外界干扰,增强系统对被控对象不确定性的鲁棒性。干扰观测器的原理是将机器人模型误差以及外部扰动通过引入补偿的形式,把被控系统近似看作无干扰无误差的名义模型(nominal model)[17]。针对轨迹跟踪性能的外环控制器能够与标称模型匹配设计。为此,首先通过输入量和内环反馈量估计外部干扰量作为观测补偿量,再将其加入控制量中对消实际干扰[18]。在实际控制系统中,噪声往往位于高带宽频段,然而干扰观测器的监测频率往往受到硬件系统的采样率限制,这样为了能够消除高频噪声对观测信号的影响以及在反馈信号中的高频振动,在干扰观测器中加入低通滤波器可以更加准确地预测干扰[19]。
干扰观测器自身优越的无模型控制特点为非线性刚度驱动器由于交互力引入的外部干扰难以建立准确数学模型而无法直接补偿的实际问题提供了有效的解决方案。本文首先基于非线性刚度驱动器的结构建立了动力学方程及状态方程并提出了适用于该非线性刚度驱动器的干扰观测控制系统。然后通过稳定性分析确定了系统稳定条件。最后通过未知干扰引入的控制误差补偿的理论分析与实验验证,证明了该干扰观测器对提高非线性刚度驱动器的控制精度有显著效果。
1 非线性弹性体及非线性刚度驱动器结构设计 1.1 非线性弹性体 非线性弹性体结构如图 1所示。非线性弹性体作为非线性刚度驱动器的核心机械结构,由一个滚轮和一个弹性体组成。该弹性体由2个对称的弹性单元组成,每个弹性单元由悬臂梁部分和接触部分组成。虽然制作弹性单元的2部分使用同一材料,但当滚轮与接触部分由于外力发生挤压时,悬臂梁部分受力变形后会产生恢复力,然而接触部分几乎不产生形变,可以将该部分看作刚体。弹性部分的挠度和挠角将导致接触点的位置变化。垂直于悬臂梁部分末端的由挠度产生的接触点位置变化和挤压力存在一定的映射关系。此外,挠角的变化也影响了接触点位置的竖直分量,因此接触点竖直方向上的位置变化与挤压力的关系不再是简单的比例关系,而是挠度和挠角的共同作用的结果。总之,接触部分的接触面轮廓曲线决定了挤压力与接触点位移的变化关系,即刚度变化关系,因此,基于该机构的非线性刚度单元的设计核心为接触面轮廓曲线形状设计。笔者课题组已经就该问题进行了深入研究[20],本文将不再赘述。
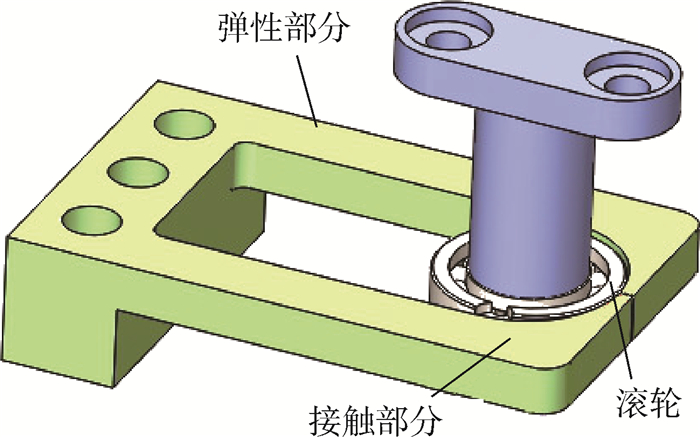 |
| 图 1 非线性弹性体 Fig. 1 A nonlinear elastic component |
| 图选项 |
1.2 非线性刚度驱动器结构设计 非线性刚度驱动器三维模型如图 2所示,主要包括机架、电机组件(直流无刷电机、减速器、旋转编码器)、线轮、内筒、外筒、驱动丝、传感器读头、以及3个非线性弹性元件。线轮和外筒之间通过驱动丝传动,电机作为驱动器动力源驱动线轮,并通过驱动器带动外筒旋转,外筒与滚子固连。内筒为输出轴并与弹性元件固连。内筒与外筒共轴,当内筒与外筒之间没有相对运动时,滚子与弹性元件间无挤压力,反之,则弹性元件变形产生挤压力。为了实现顺、逆时针双向传动,弹性元件采用了对称的结构。这个相对转动通过磁栅尺传感器检测,传感器读头和磁栅尺片分别固定在外筒与内筒表面上。此相对转动角度能够反映施加在驱动器上的外负载力的大小。
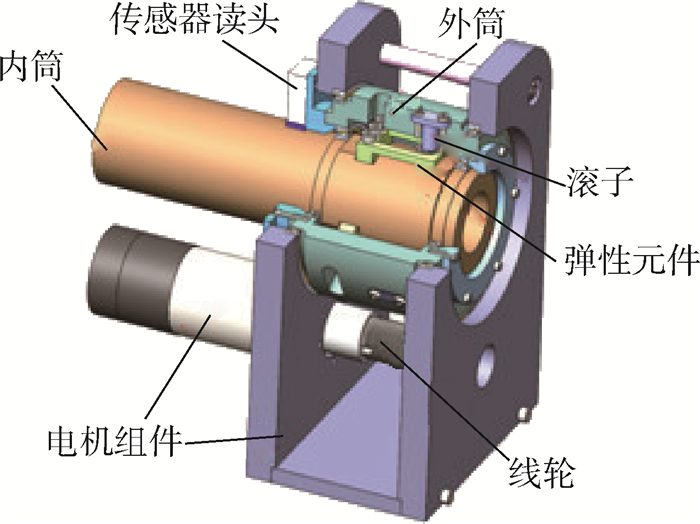 |
| 图 2 非线性刚度驱动器三维模型 Fig. 2 3D model of nonlinear stiffness compliant actuator |
| 图选项 |
2 动力学模型及干扰观测器建立 2.1 动力学模型 非线性刚度驱动器系统可以分为动力系统、传动系统、弹性体和外负载。动力系统即电机组合,主要包括电机转子和齿轮减速器。电机组合的等效转动惯量可以根据电机组合的动力学模型求得。电机转子的动力学方程为
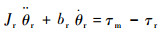 | (1) |
式中:Jr和br分别为电机转子的转动惯量和阻尼;
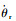
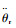
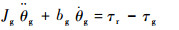 | (2) |
其中:Jg和bg分别为电机减速器的转动惯量和阻尼;
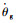
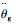
由于电机与减速器刚性连接,因此两者的角度存在如下关系:
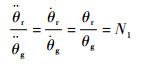 | (3) |
式中:θr和θg分别为电机转子和齿轮减速器转角;N1为电机减速比。联合式(1)~式(3)得到电机组合的动力学模型为
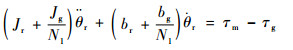 | (4) |
根据图 3模型可以得到传动系统和弹性体部分的动力学简图。外转筒的动力学模型为
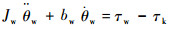 | (5) |
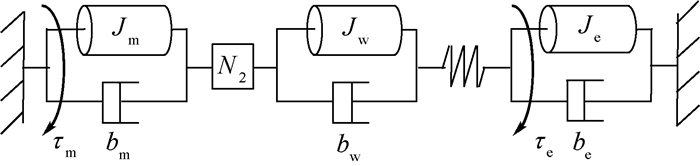 |
| 图 3 带外负载的非线性刚度驱动器模型 Fig. 3 Model of NSCA with external load |
| 图选项 |
式中:Jw和bw分别为外转筒的转动惯量和阻尼;
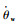
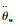
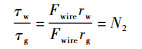 | (6) |
其中:Fwire为钢丝绳拉力;rw和rg分别为外转筒和电机输出轴半径;N2为钢丝绳的传动比。
假设钢丝绳在传动过程中不发生形变,那么电机组合输出轴的角速度与外转筒的角速度的关系为
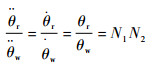 | (7) |
式中:θw为非线性刚度驱动器外转筒转角。
联合式(4)、式(5)、式(7)整理得
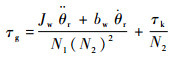 | (8) |
将式(8)代入式(4)得
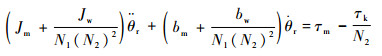 | (9) |
可以令
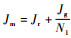
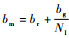
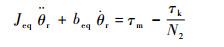 | (10) |
式中:
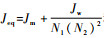
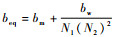
外负载部分的动力学模型为
 | (11) |
式中:Je和be分别为外负载的转动惯量和阻尼;τe为驱动器输出力矩;
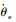
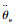
2.2 状态方程建立 由2.1节动力学方程式(10)、式(11)可得控制系统输入输出方程为
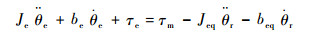 | (12) |
基于非线性刚度驱动器力矩控制下的干扰观测器控制框图如图 4所示。τm可分为以下几部分:
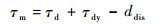 | (13) |
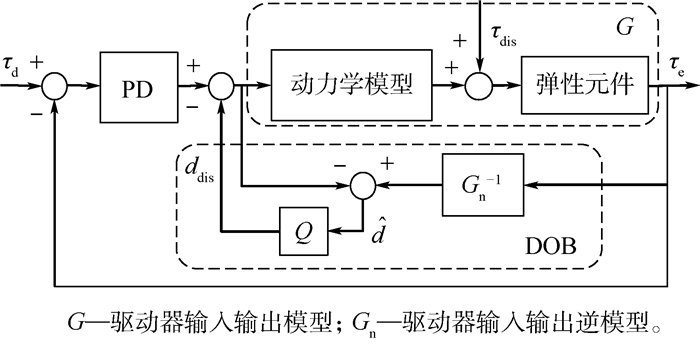 |
| 图 4 基于非线性刚度驱动器力矩控制下的干扰观测器控制框图 Fig. 4 Block diagram of DOB control based on torque control of NSCA |
| 图选项 |
式中:τd为期望驱动器末端的输出力矩,可以由PD控制公式表示为
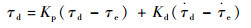 | (14) |
其中:Kp和Kd分别为比例单位系数和微分单位系数。
τdy为平衡动力学消耗力,表示为
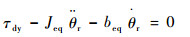 | (15) |
ddis为控制系统消除干扰,表示为
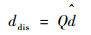 | (16) |
式中:
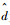
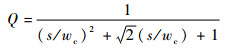 | (17) |
其中:wc=2πfc,fc为截止频率。由此式(12)转化为
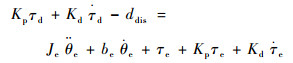 | (18) |
如果将系统外部干扰考虑到输入输出方程中,整理得
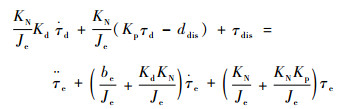 | (19) |
式中:τdis为系统外部干扰;KN为驱动器表现刚度。式(19)可以划归标准输入输出方程
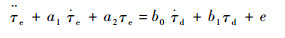 | (20) |
其中:
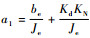
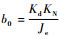
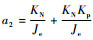
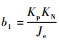

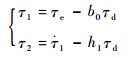 | (21) |
式中:τ1、τ2为系统状态变量;h1=b1-a1b2。
则可列出状态方程一般形式:
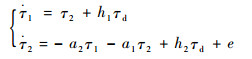 | (22) |
式中:h2=(e-a2b0)-a1h1。
整理状态方程得到矩阵形式
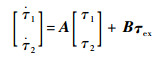 | (23) |
式中:
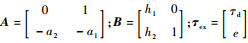
通过式(24)矩阵等式计算出正定矩阵P:
 | (24) |
2.3 干扰观测器建立 实际控制系统中力矩加速度难以测量,此外对力矩变化速度求导会引入大量噪声导致难以获得准确的力矩加速度值。陈文华等[21]提出了一个有效的解决此类问题的办法。因此,采用其所设计的干扰观测器。首先建立一个辅助方程:
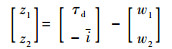 | (25) |
式中:[z1??z2]T∈R2;[w1??w2]T计算公式为
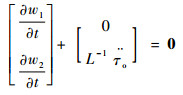 | (26) |
式中:期望力矩τd为控制信号无需测量,可以不设置与其对应的?w1/?t值,L可以认为是实际干扰和观测干扰误差的反馈增益。令
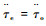
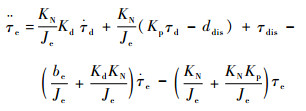 | (27) |
将式(26)、式(27)代入式(25)中求导得到
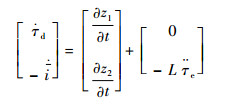 | (28) |
可以将变化向量选取得到
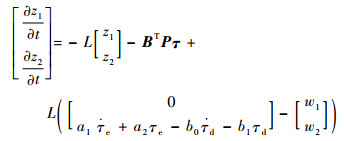 | (29) |
将式(28)代入式(27)中,得到干扰观测器:
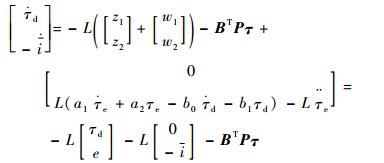 | (30) |
2.4 李雅普诺夫稳定性分析 李雅普诺夫方程是一种有效证明系统稳定性的方法,选取如式(31)的李雅普诺夫函数:
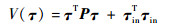 | (31) |
对所选取的李雅普诺夫函数求导:
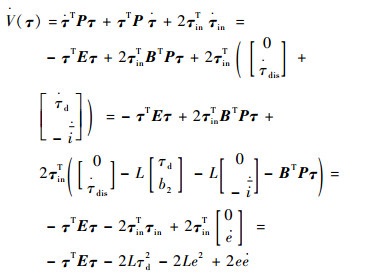 | (32) |
将公理Le2+L-1?2≥2e?代入式(32),可以得到:
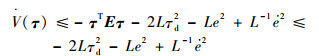 | (33) |
只要:
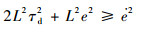 | (34) |
即可满足
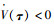
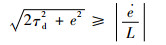 | (35) |
1) 如果干扰信号变化得很慢,即
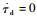
2) 如果干扰信号变化不能忽略,假设其有界,则可以确定|?| < |δ|,调整L大小使之满足不等式。此外,在L大小确定后,增大τd可以减小干扰观测器的误差。
3 实验验证 3.1 实验平台 驱动器的电路平台如图 5所示,分辨率为0.005 mm的磁栅尺传感器(MSR5000)用以检测弹性体的变形,从而获得其接触力。电机组合由MAXON EC伺服电机(型号397172),光电编码器(型号462003512线)和减速齿轮箱(减速比66:1)组成。TI DSP TMS320F28335作为整个控制系统的上位机用以读取、处理、计算来自传感器和电机的信号并发送动作指令。具体而言,通过DSP芯片的QEP模块获取电机的实时位置信息;通过GPIO模块采集磁栅尺传感器的位置变化;通过PWM模块发出PWM波驱动电机。另外,MPS-010062采集卡捕获电机编码器与磁栅尺传感器的读数并通过USB串口发送至PC机,已达到分析和处理实验数据的目的。
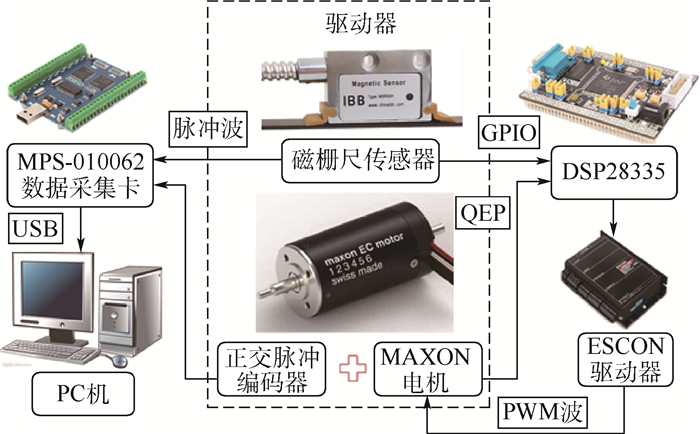 |
| 图 5 实验平台设置简图 Fig. 5 Systematic diagram of experimental platform |
| 图选项 |
3.2 干扰观测器在力矩控制实验中的评定 力矩控制是实现丰富的人机交互体验的前提,驱动器能否实现按期望信号输出的能力直接反映了驱动器的控制性能的好坏。在力矩控制实验环节内,通过对比2组实验结果可以判断干扰观测器能否提高非线性刚度驱动器的控制精度。
首先,使驱动器跟踪给定的频率为1 Hz,幅值为0~8 N·m变化的正弦变化力矩信号。实验持续9 s,其中前4个周期保持驱动器末端固定,即屏蔽了外界所有干扰。在实验的第4个周期末,释放驱动器末端并加入近似正弦波形幅值为[-9°, 9°]变化的干扰信号,操作如图 6所示,干扰信号如图 7(a)所示,直至第9周期末。其中的2组实验唯一的区别是控制算法中是否加入了干扰观测器。
 |
| 图 6 通过转动驱动器末端进行实验 Fig. 6 Experiment via rotating output shaft of actuator |
| 图选项 |
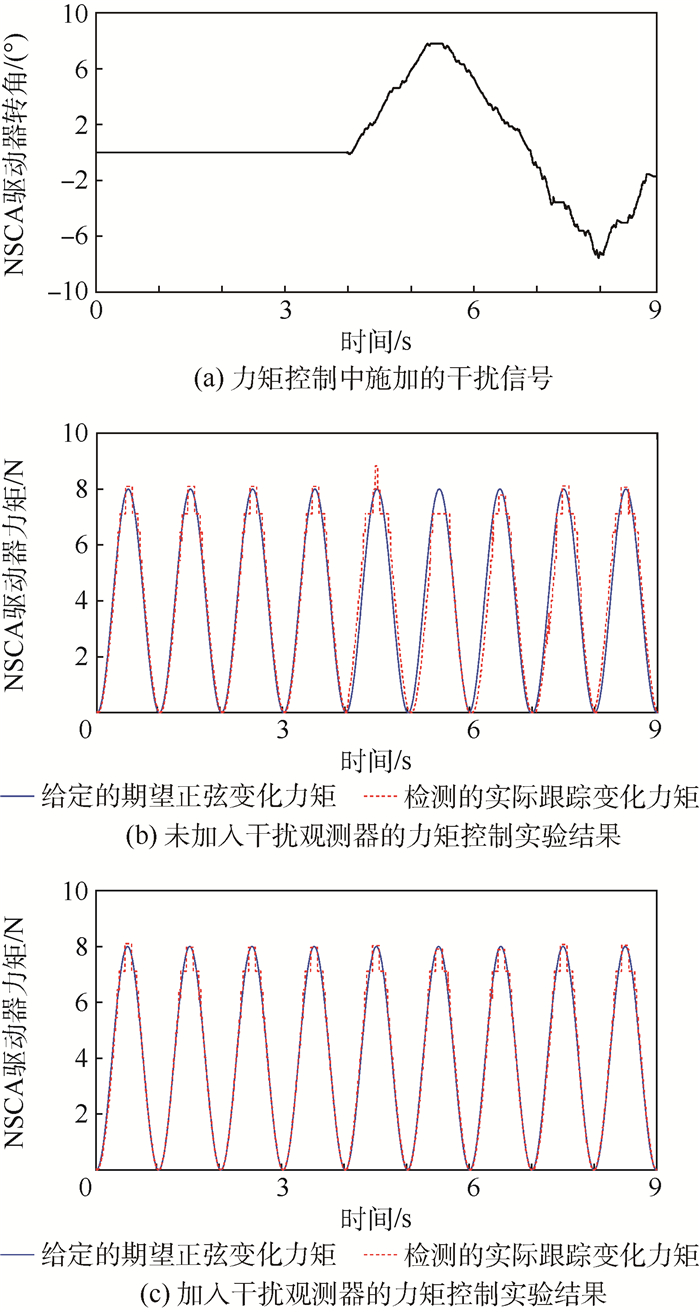 |
| 图 7 力矩控制中施加的干扰信号及未加入和加入干扰观测器的力矩控制实验结果 Fig. 7 Disturbance signal in torque control and torque control experiment results with and without DOB |
| 图选项 |
图 7(b)为未加入干扰观测器的实验结果,通过分析采集到的实验数据可以看出,在没有引入干扰观测器的一组试验中,在前4个周期,驱动器末端固定,跟随信号表现出了滞后。当驱动器末端自由后,由于加入了外部干扰,导致期望力矩与表现力矩相位差增大,可以看出的是跟踪信号当力矩变化方向和干扰方向相同时,相位超前;当力矩变化方向和干扰方向相反时,相位滞后。并且如果经过了力矩峰值,会产生严重误差,尤其在刚加入干扰的前2个周期。4~5 s内,此时力矩变化方向和干扰偏移方向一致,当经过峰值力矩时,单位形变对应输出力矩最大,瞬时产生很大误差(0.9 N·m)。同样地,在5~6 s内,由于相位滞后,导致峰值力矩仅仅达到7.2 N·m。但是在引入干扰观测器之后的图 7(c),驱动器力矩跟踪滞后性明显减小,特别是加入干扰之后,力矩跟踪效果并无明显恶化,证明了干扰观测器提升了控制系统性能。
3.3 干扰观测器在阻抗控制实验中的评定 阻抗控制[22]实验中,给出力矩模型如下:
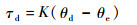 | (36) |
式中:K为阻抗模型的刚度,综合Stienenw、Wang、Vitiello和Malosio[23-26]等选定的应用于肩关节及上肢的康复实验刚度,决定前2组实验取0.5 N·m/(°),后2组取5 N·m/(°)。执行式(36)意味着当驱动器受到外界干扰时,会在一定程度下屈服,即沿干扰方向与期望位置发生一定距离的位置偏移。而θd即期望位置满足式(37):
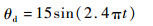 | (37) |
实验记录了位置偏差和驱动器输出力矩,通过计算实验阻抗模型刚度(驱动器输出力矩/位置偏差)与实验设置阻抗模型的刚度K进行分析确定干扰观测器的控制效果。
前2组实验分别加入了-3~3 N·m的力矩交互(图 8(a)、图 9(a)中点划线),此时可以计算出实验刚度K(力矩/位置偏差)并与标准期望刚度进行比较。图 8(b)表示当受到力矩干扰时,没有加入干扰观测器的刚度误差。当干扰发生方向上的变化时,系统抵御干扰的能力大幅度降低,刚度误差最大,最大刚度瞬时达到0.67 N·m/(°)(最小刚度0.34 N·m/(°))。这会在交互过程中产生瞬时冲量,给交互者带来不适应感,甚至导致使用者受伤,不能满足安全的交互需求。但是引入干扰观测器后这一问题能到缓解,如图 9(b)所示,观测器成功估计并消除了绝大部分由于干扰带来的刚度误差,使其最大表现刚度降低至低于0.57 N·m/(°)(最小表现刚度0.45 N·m/(°)),并且最终稳定在0.01 N·m/(°)以内,提高了控制精度。另外,刚度误差的毛刺逐渐减小证明了该干扰观测器在稳定的交互过程中具有收敛误差的功能。在高刚度的情况下,考虑到人机交互的实际力交互范围[23],力矩干扰被扩大至[-10, 10] N·m。图 10(b)表示当受到力矩干扰时,没有加入干扰观测器一组刚度误差,最大刚度瞬时达到5.21 N·m/(°)(最小刚度4.90 N·m/(°))。图 11(b)为加入干扰观测器的刚度误差,其最大刚度降低至5.03 N·m/(°)(最小刚度4.98 N·m/(°),控制精度显著提升。
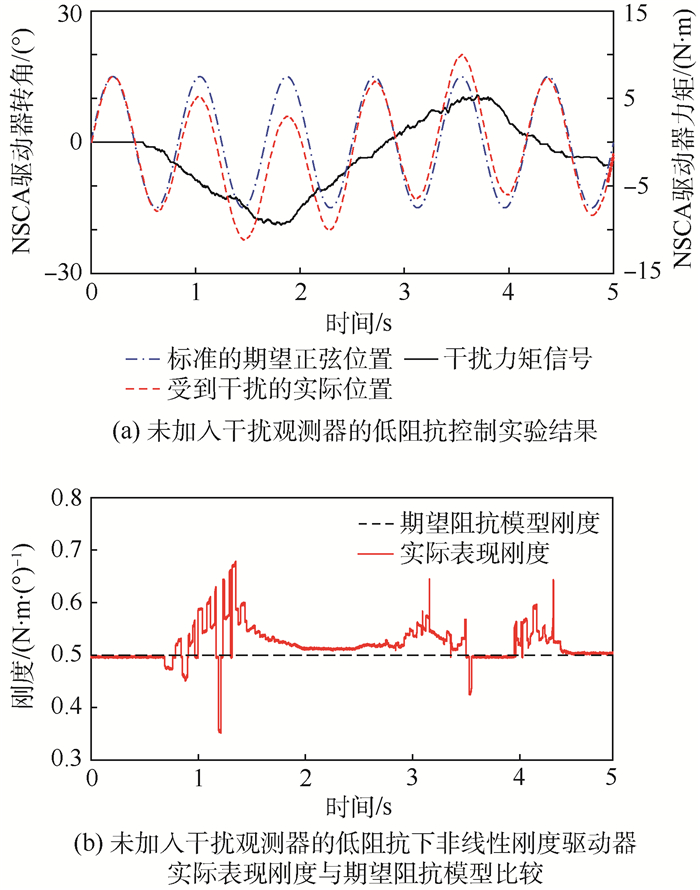 |
| 图 8 未加入干扰观测器的低阻抗控制实验结果及低阻抗下非线性刚度驱动器实际表现刚度与期望阻抗模型刚度比较 Fig. 8 Low impedance control experiment results without DOB and comparison between performed stiffness of NSCA and desired impedance stiffness under low impedance without DOB |
| 图选项 |
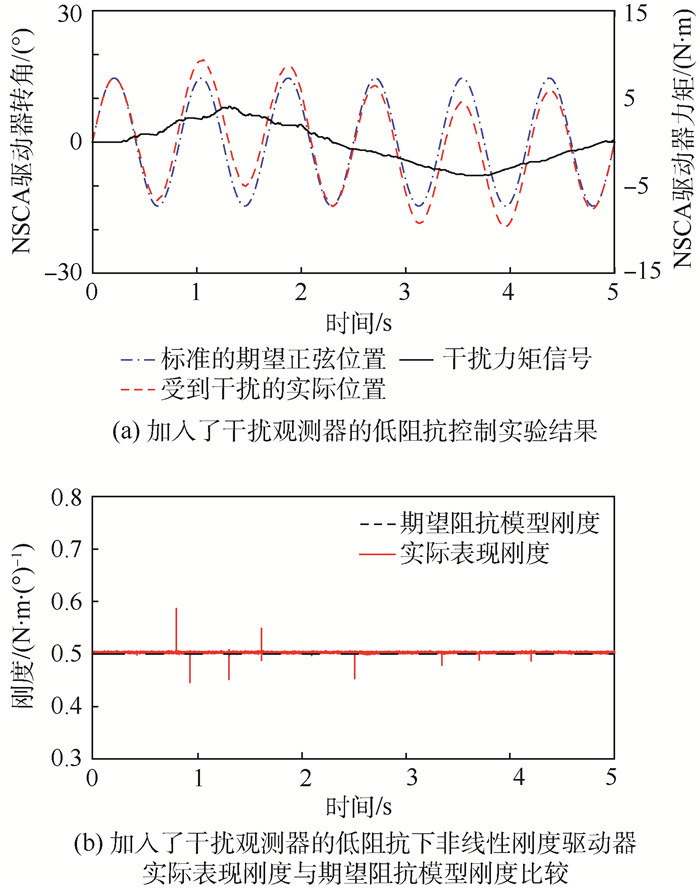 |
| 图 9 加入了干扰观测器的低阻抗控制实验结果和低阻抗下非线性刚度驱动器表现刚度与期望阻抗模型刚度比较 Fig. 9 Low impedance control experiment results with DOB and comparison between performed stiffness of NSCAand desired impedance stiffness under low impedance with DOB |
| 图选项 |
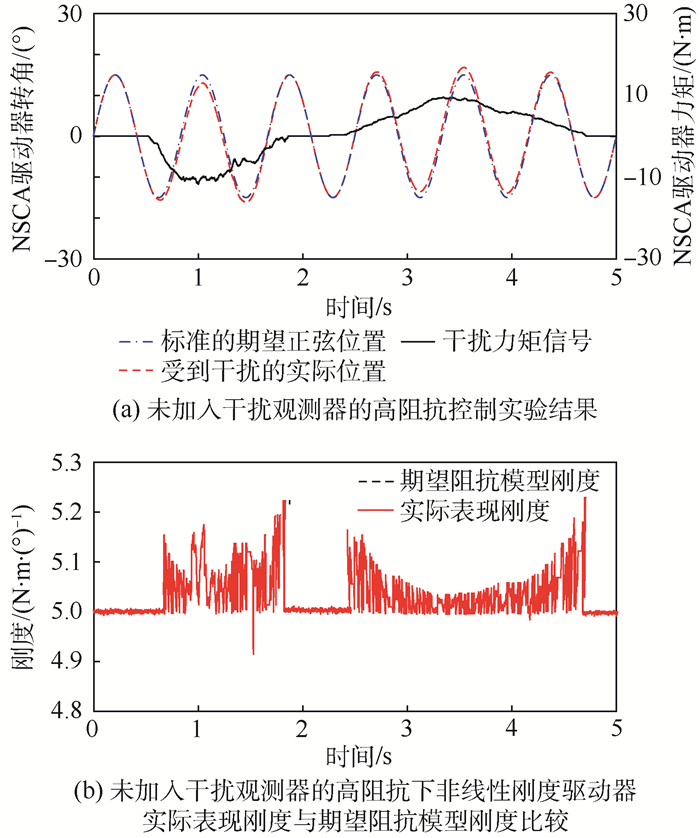 |
| 图 10 未加入干扰观测器的高阻抗控制实验结果及高阻抗下非线性刚度驱动器实际表现刚度与期望阻抗模型刚度比较 Fig. 10 High impedance control experiment results without DOB and comparison between performed stiffness of NSCA and desired impedance stiffness under high impedance without DOB |
| 图选项 |
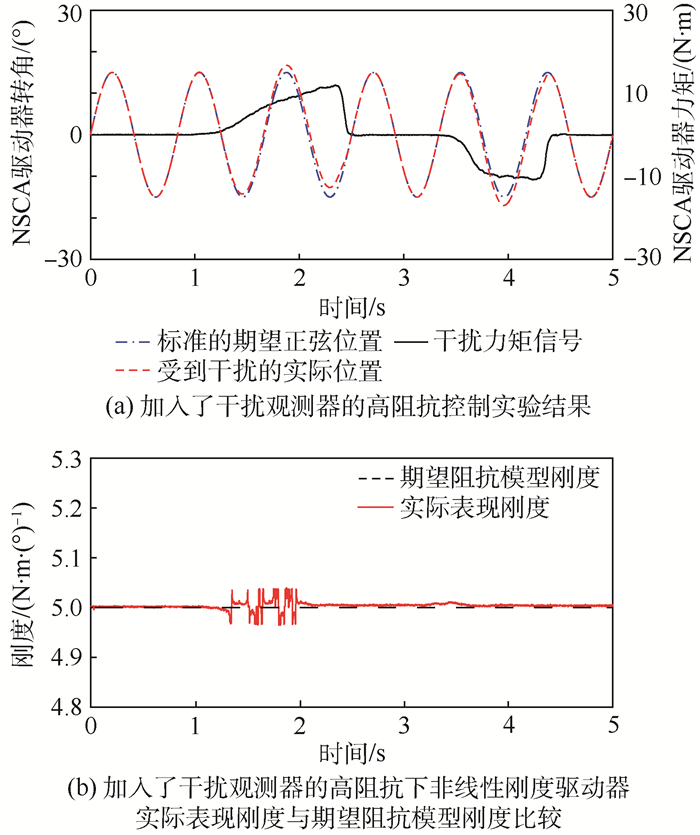 |
| 图 11 加入了干扰观测器的高阻抗控制实验结果及高阻抗下非线性刚度驱动器实际表现刚度与期望阻抗模型刚度比较 Fig. 11 High impedance control experiment results with DOB and comparison between performed stiffness of NSCA and desired impedance stiffness under high impedance with DOB |
| 图选项 |
此外,图 9(b)和图 11(b)的区别在于阻抗刚度系数的不同。阻抗模型刚度发生变化意味着弹性体的工作区域和位置发生改变。在系统稳定的情况下,当非线性刚度驱动器系统刚度大时,即出现同等位置偏差时,τd较大,此时误差e减小。这与式(35)所表达的信息相符合。这是由于,扩大非线性元件的工作范围时,单位形变下的力容纳量变大,这就会降低实验中力矩的瞬时尖点。总体上,将误差率降低了85.71%,提高了控制精度。
4 结论 1) 本文建立了非线性刚度驱动器的动力学模型,并且根据该动力学模型建立了状态方程用于描述控制系统。
2) 根据控制系统状态方程建立了干扰观测器,并针对该控制器进行了李雅普诺夫稳定性分析并给出了稳定条件。然后根据理论将干扰观测器算法应用于非线性刚度驱动器控制系统中。
3) 通过力矩控制和阻抗控制实验验证了干扰观测器在该非线性刚度驱动器中的良好的控制效果。此外通过实验验证,反映了非线性刚度驱动器的特点:在交互力小时,弹性体处于低刚度工作空间,表现出了良好的力分辨率;在交互力大时,弹性体处于高刚度工作区间,表现刚度更加稳定。
4) 该非线性刚度驱动器是作为适用于肩关节康复机器人的一个关节而设计的,单关节驱动器的性能测试不仅能够客观地评价所涉及的非线性弹性体在人机交互中的表现出的特点,而且为机器人整机调试提供了良好的基础和宝贵的经验。
致谢
感谢天津大学机械工程学院蓝绍彬和马天宇在样机研发工作中的贡献。
参考文献
| [1] | GRIOLI G, WOLF S, GARABINI M, et al. Variable stiffness actuators:The user's point of view[J].International Journal of Robotics Research, 2015, 34(6): 727–743.DOI:10.1177/0278364914566515 |
| [2] | SCHIAVI R, GRIOLI G, SEN S, et al. VSA-Ⅱ: A novel prototype of variable stiffness actuator for safe and performing robots interacting with humans[C]//IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2008: 2171-2176. |
| [3] | BYRVAN H, SUGAR T G, VANDERBORGHT B, et al. Compliant actuator design[J].IEEE Robotics & Automation Magazine, 2009, 16(3): 81–94. |
| [4] | ERLER P, BECKERLE P, STRAH B, et al. Experimental comparison of nonlinear motion control methods for a variable stiffness actuator[C]//Biomedical Robotics & Biomechatronics. Piscataway, NJ: IEEE Press, 2014: 1045-1050. |
| [5] | SCHEPELMANN A, GEBERTH K A, GEYER H. Compact nonlinear springs with user defined torque-deflection profiles for series elastic actuators[C]//IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2014: 3411-3416. |
| [6] | WOLF S, HIRZINGER G. A new variable stiffness design: Matching requirements of the next robot generation[C]//IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2008: 1741-1746. |
| [7] | TORREALBA R R, UDELMAN S B. Design of cam shape for maximum stiffness variability on a novel compliant actuator using differential evolution[J].Mechanism & Machine Theory, 2016, 95: 114–124. |
| [8] | JAFARI A, TSAGARAKIS N G, CALDWELL D G. AwAS-Ⅱ: A new actuator with adjustable stiffness based on the novel principle of adaptable pivot point and variable lever ratio[C]//IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2011: 4638-4643. |
| [9] | NICOLA S, MASAFUMI O. Design and Realization of a non-circular cable spool to synthesize a nonlinear rotational spring[J].Advanced Robotics, 2012, 26(3-4): 234–251.DOI:10.1163/156855311X614545 |
| [10] | PEW C, KLUTE G K. Design of lower limb prosthesis transverse plane adaptor with variable stiffness[J].Journal of Medical Devices, 2015, 9(3): 035001.DOI:10.1115/1.4030505 |
| [11] | AUSTIN J, SCHEPELMANN A, GEYER H. Control and evaluation of series elastic actuators with nonlinear rubber springs[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ: IEEE Press, 2015: 6563-6568. |
| [12] | PALLI G, BERSELLI G, MELCHIORRI C, et al. Design of a variable stiffness actuator based on flexures[J].Journal of Mechanisms & Robotics, 2011, 3(3): 034501. |
| [13] | YU H, HUANG S, CHEN G, et al. Human-robot interaction control of rehabilitation robots with series elastic actuators[J].IEEE Transactions on Robotics, 2015, 31(5): 1089–1100.DOI:10.1109/TRO.2015.2457314 |
| [14] | NAKAO M, OHNISHI K, MIYACHI K. A robust decentralized joint control based on interference estimation[C]//IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 1987: 326-331. |
| [15] | SARIYILDIZ E, OHNISHI K. Analysis the robustness of control systems based on disturbance observer[J].International Journal of Control, 2013, 86(10): 1733–1743.DOI:10.1080/00207179.2013.795663 |
| [16] | SARIYILDIZ E, CHEN G, YU H. Robust position control of a novel series elastic actuator via disturbance observer[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ: IEEE Press, 2015: 5423-5428. |
| [17] | SARIYILDIZ E, OHNISHI K. Stability and robustness of disturbance-observer-based motion control systems[J].IEEE Transactions on Industrial Electronics, 2015, 62(1): 414–422.DOI:10.1109/TIE.2014.2327009 |
| [18] | 尹正男. 具有鲁棒性的最优干扰观测器的系统性设计及其应用[D]. 上海: 上海交通大学, 2012: 2-3. YIN Z N. Systematic design of optimal disturbance observer with robust performances and its application[D]. Shanghai: Shanghai Jiao Tong University, 2012: 2-3(in Chinese). |
| [19] | SARIYILDIZ E, OHNISHI K. A guide to design disturbance observer[J].Journal of Dynamic Systems Measurement & Control, 2013, 136(2): 2483–2488. |
| [20] | LAN S B, SONG Z B. Design of a new nonlinear stiffness compliant actuator and its error compensation method[J].Journal of Robotics, 2016, 2016: 7326905. |
| [21] | CHEN W H, BALLANCE D J, GAWTHROP P J, et al. A nonlinear disturbance observer for robotic manipulators[J].IEEE Transactions on Industrial Electronics, 2000, 47(4): 932–938.DOI:10.1109/41.857974 |
| [22] | HOGAN N. Impedance control-An approach to manipulation.Ⅰ-Theory.Ⅱ-Implementation.Ⅲ-Applications[J].ASME Transactions Journal of Dynamic Systems & Measurement Control B, 1984, 107(1): 304–313. |
| [23] | STIENENW A H, HEKMAN E E, TER B H, et al. Design of a rotational hydroelastic actuator for a powered exoskeleton for upper limb rehabilitation[J].IEEE Transactions on Bio-medical Engineering, 2010, 57(3): 728–735.DOI:10.1109/TBME.2009.2018628 |
| [24] | WANG P R, CHIU Y H, TSAI M S, et al. Estimation and evaluation of upper limb endpoint stiffness and joint torques for post-stroke rehabilitation[C]//World Congress on Medical Physics and Biomedical Engineering, 2009. Berlin: Springer, 2009: 44-47. |
| [25] | VITIELLO N, LENZI T, ROCCELLA S, et al. NEUROExos:A powered elbow exoskeleton for physical rehabilitation[J].IEEE Transactions on Robotics, 2013, 29(1): 220–235.DOI:10.1109/TRO.2012.2211492 |
| [26] | MALOSIO M, CAIMMI M, LEGNANI G, et al. LINarm: A low-cost variable stiffness device for upper-limb rehabilitation[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ: IEEE Press, 2014: 3598-3603. |
