高速旋转的MSCSG转子受陀螺效应的影响,因此,LFMB驱动高速转子径向偏转过程中,径向二转动自由度间存在耦合;此外,MSCSG转子偏转响应速度快、抗扰性强的要求难以同时满足。德国的Teldix公司研制了基于洛伦兹力悬浮的全主动磁悬浮飞轮,能够输出3 N·m的控制力矩[7];北京航空航天大学的王春娥和汤继强提出了永磁偏置与LFMB相结合的磁悬浮飞轮,实现了转子的五自由度悬浮[8];在此基础上,向彪等提出采用LFMB实现了飞轮转子最大偏角为1.7°的偏转控制[9-10]。但鲜见对LFMB驱动的转子进行解耦以及高精度快响应偏转控制的研究报道。
为消除转子径向耦合,现有的针对MSCMG的转子解耦算法包括交叉比例-积分-微分(Proportional-Integral-Differential,PID)控制算法[11]、线性二次型调节器(Linear Quadratic Regulator, LQR)控制方法[12]、Cholesky分解降秩方法[13]、最小二乘支持向量积解耦方法[14]、微几何方法[15]等。交叉PID方法在分散PID控制的基础上引入交叉项以补偿偏转通道间耦合,结构简单,但目前缺乏有效的交叉参数设计方法,只能通过根轨迹仿真试凑;LQR控制方法、Cholesky分解降秩方法、最小二乘支持向量积解耦方法结构复杂且运算量大,不易于工程实现;微几何方法可以用于抑制高速转子径向两转动通道间的耦合,但该方法抽象、复杂,需将模型变换到几何域中讨论,且算法模型受映射形式约束。
为实现转子偏转的高精度快响应控制,现有的MSCMG转子偏转控制算法包括交叉PID控制[11, 16]、滑模变结构控制[17]、基于状态观测器的补偿控制[18-19]等。交叉PID算法原理简单便于实现,但是机动性差,对指令信号的跟踪存在相位滞后;滑模变结构控制具有响应迅速、对参数变化不敏感的优点,但在变结构切换过程中容易引起系统的抖振;基于状态观测器补偿算法可以抑制外界扰动,但是观测器存在一定滞后,会影响动态响应速度。因此,这些控制算法无法同时实现对转子偏转的快速响应和扰动抑制。
前馈解耦方法是近年来针对单元机组信号间存在耦合问题提出的一种串联解耦方法,具有物理概念清晰、数学模型简单、便于理解等优点[20];二自由度内模控制器(2-DOF IMC)是一种具备独立调节跟踪性和抗扰性的控制器[21-22],结构简单,容易实现。因此,本文提出针对MSCSG转子偏转的前馈解耦内模控制器,通过前馈解耦矩阵消除MSCSG转子径向偏转二自由度间耦合,采用二自由度内模控制器对解耦的转子偏转系统进行快速响应、抗扰控制。
1 MSCSG转子偏转动力学模型 MSCSG结构如图 1所示,主要由上陀螺房、中陀螺房、下陀螺房、电机组件、转子组件、力矩器、轴向磁轴承、径向磁轴承、位移传感器构成。图 1中,以MSCSG转子质心O为原点建立转子坐标系O-XYZ,其中,Z轴指向转子轴向,转子沿该轴高速转动[23]。MSCSG转子平动通过纯电磁结构的径向磁轴承和轴向磁轴承实现,磁轴承极面位于2个不同半径的球形包络面上,如图 1中虚线所示。由于球面磁极产生的电磁力始终经过磁极球心,当磁极球心与转子质心重合时,无论转子在磁间隙内处于什么位置,都不会产生扭转力矩,从而实现了平动自由度对径向转动自由度的解耦。因此,转子径向偏转只受力矩器控制。
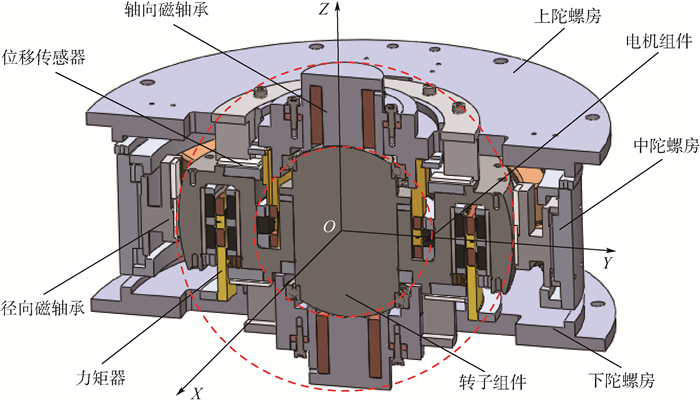 |
| 图 1 MSCSG结构示意图 Fig. 1 Structure diagram of MSCSG |
| 图选项 |
MSCSG采用LFMB为力矩器驱动转子偏转,LFMB产生的电磁力依据安培力定律,即磁感应强度为B的磁场中沿与磁场垂直方向放置长度为L的线圈,当流经线圈中电流为I时,线圈将受到安培力作用,其表达式为
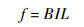 | (1) |
基于LFMB驱动的转子偏转系统结构如图 2所示。图 2中,转子外缘一周狭槽内壁中放置着上、下2层磁钢,2层磁钢中内外磁钢间充磁方向相反,磁钢间磁场分布均匀,从而形成了沿径向的闭合回路。4组匝数相同的定子线圈位于内、外磁钢间的狭缝中,沿LFMB周向均匀分布,成对使用,其中,沿x轴正、负方向上的2组线圈构成一对,沿y轴正、负方向上的2组线圈构成一对。以LFMB几何中心O′为原点定义定子坐标系O′-xyz,其中x轴与y轴分别与相对方向两组线圈中心线重合,z轴方向根据右手定则确定。图中:α、β分别为转子绕x、y轴径向偏转角度;lm为LFMB定子半径;lr为位移传感器到z轴的距离;Ω为转子轴向角速度。
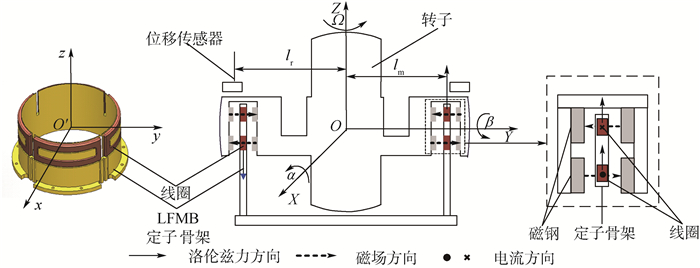 |
| 图 2 转子偏转系统结构示意图 Fig. 2 Structure diagram of rotor tilting system |
| 图选项 |
当与磁场垂直方向放置的线圈通入电流时,线圈的上下两部分将分别产生垂直于线圈及磁场方向的安培力,合力大小为
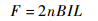 | (2) |
式中:n为线圈匝数。当相对方向线圈通入大小相等、方向相反的电流时,线圈将产生大小相等、方向相反的安培力,形成力偶驱动转子径向偏转。根据式(2)中电流与安培力间线性关系,并依据力矩器结构可知,沿x、y方向的控制力矩px、py表达式为
 | (3) |
其中:iα、iβ分别为线圈中驱动转子绕x、y轴偏转的激励电流。
对于高速旋转的MSCSG的转子,其陀螺技术方程为[24]
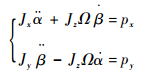 | (4) |
式中:Jx和Jy分别为转子相对于x轴及y轴的转动惯量,大小与转子赤道转动惯量Jr相等;Jz为转子相对于z轴的转动惯量;α、β的数值可通过实时采集y、x轴正、负方向上位移传感器的测量值hy+、hy-、hx+、hx-获得,即
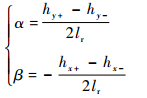 | (5) |
根据式(3)、式(4),并考虑到控制系统存在时延τ,MSCSG转子偏转动力学方程组可以表示为
 | (6) |
对式(6)进行拉普拉斯变换得到
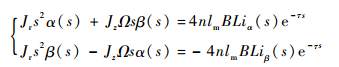 | (7) |
式中:s为算子。
因此,转子径向偏转的状态方程为
 | (8) |
从而确定被控对象传递函数为
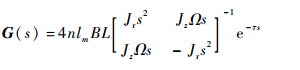 | (9) |
2 基于前馈解耦的内模控制器设计 2.1 前馈解耦网络设计 由式(9)可知,陀螺转子径向两偏转通道间存在耦合。为实现转子径向两偏转角独立控制,需通过矫正网络使其解耦,从而令该系统转化为2个单输入、单输出的系统。
前馈解耦的本质在于将解耦补偿器串联在待解耦对象前端,用于抵消多变量被控对象各通道间的相互关联,从而保证各回路控制系统独立工作。对于式(9)所描述的双输入双输出系统,其前馈解耦方法的核心思想如图 3所示。图中,C(s)为控制器,D(s)为解耦器,G(s)为被控对象,解耦器D(s)将被控对象G(s)解耦为2个独立的单通道回路。解耦器与被控对象构成广义被控对象N(s),即N(s)=D(s)G(s)。前馈解耦的最终目的是通过设计合适的解耦器D(s),使广义被控对象N(s)的表达式为对角矩阵。
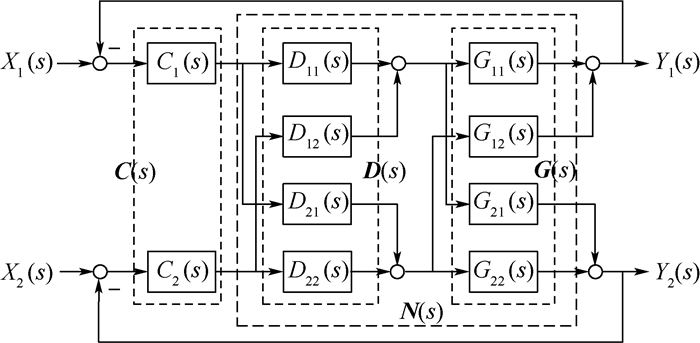 |
| 图 3 前馈解耦系统结构 Fig. 3 Structure of feedforward decoupling system |
| 图选项 |
由图 3可知,X1(s)通过G21(s)对Y2(s)施加作用时,也通过D21(s)和G22(s)进行了补偿;同理,X2(s)通过G12(s)对Y1(s)施加作用时,也通过D12(s)和G11(s)进行了补偿,因此,解耦矩阵具有前馈补偿的性质。为简化解耦矩阵D(s)结构,本文令D11(s)=D22(s)=1。此时,广义被控对象N(s)表达式为
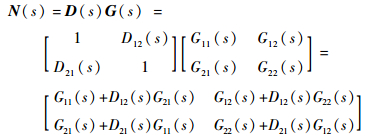 | (10) |
当N(s)中主对角线元素外的项都为0时,可实现解耦控制。此时可求解出:
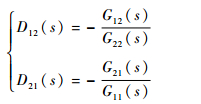 | (11) |
根据式(9)、式(11),确定转子偏转系统前馈解耦矩阵表达式为
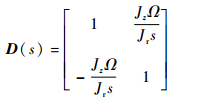 | (12) |
因此,化简为对角矩阵的广义被控对象传递函数为
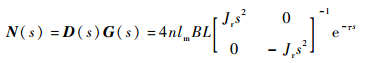 | (13) |
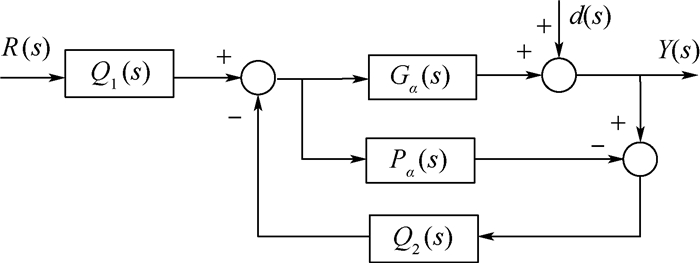
2.2 二自由度内模控制器 由于控制系统时延τ的不确定性、模型误差的客观存在性以及外界扰动因素的影响,导致建立的模型与实际被控对象存在差异。采用PID控制算法、滑模控制算法难以兼顾系统的响应速度及抗扰性。因此,本文将能够同时调节系统响应速度和抗扰性的二自由度内模控制器应用于转子偏转控制。
二自由度内模控制器结构如图 4所示[21]。
 |
| 图 4 二自由度内模控制器结构 Fig. 4 Structure of 2-DOF IMC |
| 图选项 |
图 4中,Gα(s)为实际被控对象,Pα(s)为被控对象的内部模型,Q1(s)和Q2(s)构成二自由度内模控制器,R(s)为给定输入,d(s)为外界干扰,Y(s)为系统输出。根据图 4可知,系统输出Y(s)表达式为
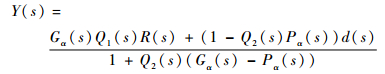 | (14) |
模型精确条件下,式(14)可表述为
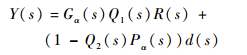 | (15) |
由式(15)可知,系统输出Y(s)由Gα(s)·Q1(s)R(s)和(1-Q2(s)Pα(s))d(s)两部分构成,分别对应着系统的参考输入项以及干扰项,因此系统对参考输入项的响应特性取决于Q1(s),系统对干扰项的抑制性能取决于Q2(s)。为了提高控制器响应速度及抗扰性能,Q1(s)、Q2(s)中分别引入低通滤波器F1(s)、F2(s),使Q1(s)、Q2(s)满足:
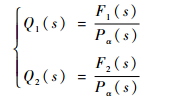 | (16) |
式中:
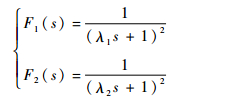 | (17) |
其中:滤波器参数λ1、λ2均为正数。因此,可将图 4等效简化为图 5形式。
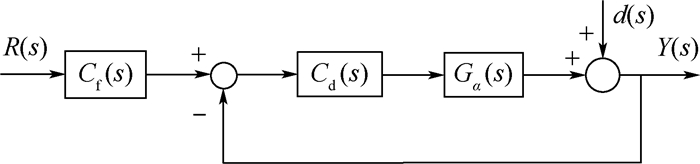 |
| 图 5 简化的二自由度内模控制器结构 Fig. 5 Simplified structure of 2-DOF IMC |
| 图选项 |
进而确定等效二自由度内模控制器的Cf(s)、Cd(s)表达式为
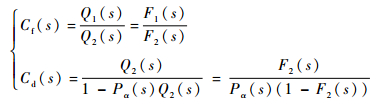 | (18) |
以转子绕x轴径向偏转的α通道为例,根据式(13),经前馈解耦,该通道的被控对象传递函数为
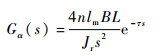 | (19) |
Gα(s)中包含不确定项τ,因此其内部模型Pα(s)的伪线性函数表达式为
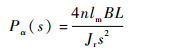 | (20) |
将式(17)、式(20)代入式(18),可确定径向偏转α通道二自由度内模控制器的Cf(s)、Cd(s)表达式为
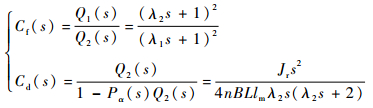 | (21) |
采用同样的方法可以设计出径向偏转β通道的二自由度内模控制器。
2.3 控制器性能分析 定义灵敏度函数为系统误差E(s)与给定输入值R(s)间传递函数:
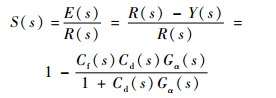 | (22) |
定义补灵敏度函数为系统输出Y(s)与给定输入R(s)间传递函数:
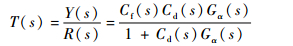 | (23) |
灵敏度函数S(s)是闭环系统对动态性能的度量函数,其增益值越小,系统的跟随性越好;补灵敏度函数T(s)是闭环系统鲁棒性的度量函数,其增益值越小,系统对扰动的抑制能力越强[24]。
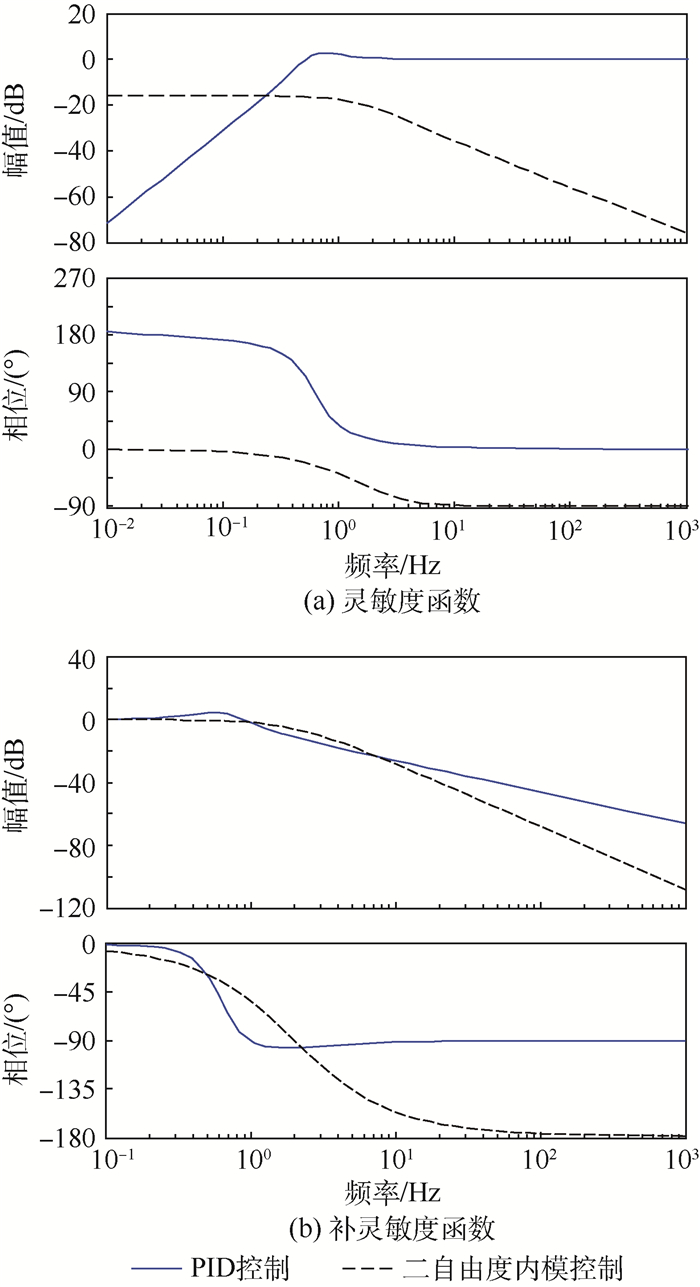
将二自由度内模控制器和PID控制器的灵敏度函数和补灵敏度函数Bode图进行对比,主要参数如表 1所示,其中,和PID控制器相关参数依照文献[25]设定。除前文介绍过参数外,表 1中,Kp、Ki、Kd分别为PID控制器的比例、积分、微分系数,ωL、ωH分别为交叉环节低通、高通滤波器截止频率,kL、kH分别为交叉环节低通、高通系数,kr为总交叉系数。基于表 1中控制器参数,二自由度内模控制器与PID控制器的灵敏度函数及补灵敏度函数Bode图如图 6所示。
 |
| 图 6 灵敏度函数与补灵敏度函数Bode图 Fig. 6 Bode diagrams of sensitivity function and penalty sensitivity function |
| 图选项 |
表 1 转子偏转系统参数 Table 1 Parameters of rotor tilting system
| 参数 | 数值 |
| Jz/ (kg·m2) | 0.016 6 |
| Ω/Hz | 100 |
| λ2 | 0.003 |
| Kp | 15 |
| Kd | 3 |
| n | 200 |
| L/m | 0.115 8 |
| kL | 0.5 |
| kH | 0.2 |
| lr/m | 0.078 |
| Jr/ (kg·m2) | 0.009 7 |
| λ1 | 0.08 |
| τ/s | 0.002 |
| Ki | 0.001 |
| B/T | 0.4 |
| lm/m | 0.059 |
| ωL/Hz | 80 |
| ωH/Hz | 400 |
| kr | 0.05 |
表选项
由图 6(a)可知,二自由度内模控制器在0.01~1 Hz频段范围内灵敏度函数幅值约为-16 dB,在1~ 1 000 Hz范围内,灵敏度函数幅值随频率升高而减小,且远小于0 dB;PID控制器在0.01~0.8Hz范围内,灵敏度函数幅值随频率升高而增加,峰值约为3 dB,随后衰减,在2 Hz左右稳定在0 dB;对比2种控制器灵敏度函数Bode图可知,二自由度内模控制系统在0.3 Hz以上的频段范围内灵敏度增益小于PID控制器,说明设计的二自由度内模控制器与PID控制器相比具有更好的跟踪能力。
由图 6(b)可知,二自由度内模控制器在0.1~1 Hz频段范围内补灵敏度函数增益幅值保持在0 dB,从1 Hz起幅值随频率升高呈衰减趋势;PID控制器在0.1~0.8 Hz频段范围内补灵敏度函数增益幅值保持在0 dB,在0~2.5 Hz频段范围增益幅值随频率升高呈小幅度增加趋势,在2.5 Hz达到峰值4.5 dB,在大于2.5 Hz频段范围内增益幅值呈衰减趋势。
对比2种控制器补灵敏度函数Bode图可知,二者在0~7 Hz频段范围内补灵敏度函数增益幅值大致相等,在7 Hz以上的频段范围内二自由度内模控制系统补灵敏度函数增益小于PID控制系统,且随频率增加,二自由度内模控制器增益幅值衰减速度大于PID控制器,由此可以判断,二自由度内模控制器抗扰性强于PID控制器。
3 仿真分析 为验证本文算法的有效性和优越性,将所提出的前馈解耦内模控制算法和交叉PID算法在MATLAB环境下进行对比仿真,主要参数如表 1所示。
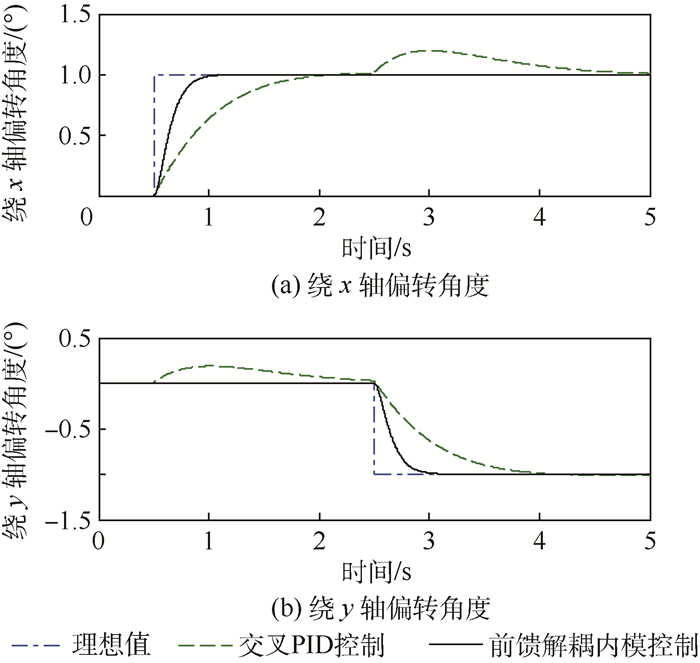
3.1 解耦仿真分析 图 7为t=0.5 s时,令转子绕x轴偏转阶跃1°;t=2.5 s时,令转子绕y轴偏转阶跃-1°,分别采用交叉PID控制和前馈解耦内模控制的条件下,转子径向两偏转通道间耦合关系仿真曲线。由图 7可知,采用交叉PID控制算法条件下,0.5 s时刻转子绕x轴偏转1°引起转子产生绕y轴偏转约0.2°抖动,2.5 s时刻转子绕y轴偏转-1°导致转子同时产生绕x轴偏转约0.2°抖动;采用前馈解耦内模控制算法时,0.5 s时刻x轴偏转对y轴转动状态无影响,2.5 s时刻转子绕y轴偏转对x轴转动状态也无影响;对比可知,与交叉PID控制算法相比,前馈解耦内模控制算法可实现转子径向两偏转自由度完全解耦。
 |
| 图 7 解耦效果仿真对比 Fig. 7 Comparison of decoupling simulation results |
| 图选项 |
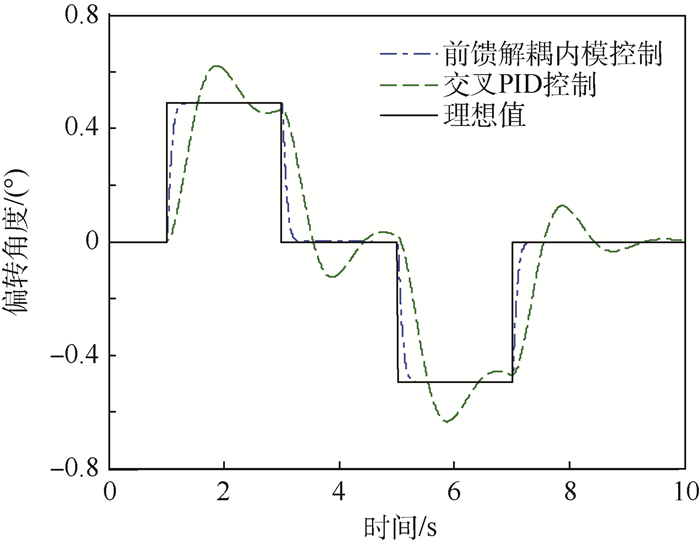
3.2 响应速度仿真分析 转子绕x轴偏转的指令信号如图 8中实线所示,1 s时,令转子正向偏转阶跃0.5°,3 s时令转子偏转角恢复为0°;5 s时令转子反方向偏转0.5°,7 s时刻再令转子偏转角恢复为0°。分别采用交叉PID控制和前馈解耦内模控制算法条件下,转子偏转响应曲线如图 8所示。根据图 8可知,采用交叉PID控制算法在对指令阶跃信号进行跟踪过程中,超调量约为24%,响应时间约为0.7 s;采用前馈解耦内模控制算法的控制系统无超调,响应时间约为0.3 s,较交叉PID控制算法减少57.1%。仿真结果表明,与交叉PID控制算法相比,前馈解耦内模控制算法具有更快的响应速度。
 |
| 图 8 偏转响应曲线对比 Fig. 8 Comparison of tilting response curves |
| 图选项 |
3.3 抗扰性仿真分析 1 s时刻对处于平衡位置的转子施加绕x轴偏转的0.1sin(2πt)°正弦干扰信号时,分别采用交叉PID算法和前馈解耦内模控制算法情况下,干扰信号对转子系统偏转角度的影响如图 9(a)所示。为使交叉PID控制器性能达到最优,其控制器参数参照文献[25]设定,如表 1所示。由图 9(a)可知,采用交叉PID算法的转子系统受0.1sin(2πt)°的正弦信号干扰后产生幅值约为0.02°的往复偏转;采用前馈解耦内模控制算法的控制系统受0.1sin(2πt)°正弦信号干扰后产生幅值约为0.018°的往复偏转。
 |
| 图 9 抗扰性能对比 Fig. 9 Comparison of disturbance rejection performance |
| 图选项 |
以上2种控制器参数不变的条件下,干扰信号由0.1sin(2πt)°变为0.1sin(8πt)°时,转子系统因干扰产生的偏转角度如图 9(b)所示。由图 9(b)可知,干扰信号频率变为4 Hz时,采用交叉PID算法的转子系统产生幅值约为0.075°的往复偏转;而采用前馈解耦内模控制算法的转子系统产生幅值约为0.018°的往复偏转,偏转幅度较PID算法减少76%。
对比图 9(a)、(b)可知,当干扰信号频率发生变化时,采用交叉PID算法的转子系统偏转幅度随频率增加而变大,这主要是因为交叉PID控制器中的微分项对正弦扰动信号进行处理时,扰动信号频率越大,引入的量化噪声越大,如果改变微分系数弱化微分项的作用,系统的跟随性又将受到影响;而采用前馈解耦内模控制算法的转子系统不包含纯微分环节,且具备独立调节跟踪性和抗扰性的特点,具有较强的鲁棒性,因此偏转幅度几乎不随干扰信号频率变化。因此,前馈解耦内模控制器抗扰性优于交叉PID控制器。
结合图 8、图 9仿真结果可知,由于前馈解耦内模控制器可以同时实现跟踪性和抗扰性的独立调整,而交叉PID控制算法机动性差,难以使系统兼顾快速性和准确性,因此前馈解耦内模控制算法的响应速度和抗扰性优于交叉PID控制算法。
4 结论 1) 转子分别沿x、y轴偏转过程中,相比于采用交叉PID算法会导致转子沿y、x轴方向产生约20%的耦合性偏转跳动,基于前馈解耦的二自由度内模控制算法可以消除转子径向两偏转自由度间的耦合。
2) 基于前馈解耦的二自由度内模控制算法可兼顾系统的跟随性和抗扰性,偏转响应时间较交叉PID算法降低了57.1%,受0.1sin(2πt)°正弦信号扰动产生的偏转波动幅值较交叉PID算法减少10%,受0.1sin(2πt)°正弦信号扰动产生的偏转波动幅值较交叉PID算法减少76%。
参考文献
| [1] | YU Y, FANG J, YANG Z. Torque distribution of the integrated magnetically suspended inertia actuator for attitude maneuvers[J].Acta Astronautica, 2015, 119: 71–78. |
| [2] | ABBAS H S, ALI A, HASHEMI S M, et al. LPV state-feedback control of a control moment gyroscope[J].Control Engineering Practice, 2014, 24: 129–137.DOI:10.1016/j.conengprac.2013.05.008 |
| [3] | TANG J Q, XIANG B, ZHANG Y B. Dynamic characteristics of the rotor in a magnetically suspended control moment gyroscope with active magnetic bearing and passive magnetic bearing[J].ISA Transactions, 2014, 53(4): 1357–1365.DOI:10.1016/j.isatra.2014.03.009 |
| [4] | 崔培玲, 盖玉欢, 房建成, 等. 主被动磁悬浮转子的不平衡振动自适应控制[J].光学精密工程, 2015, 23(1): 122–131. CUI P L, GAI Y H, FANG J C, et al. Adaptive control for unbalance vibration of active-passive hybrid magnetically suspended rotor[J].Optics & Precision Engineering, 2015, 23(1): 122–131.(in Chinese) |
| [5] | CUI P L, LI S, ZHAO G Z, et al. Suppression of harmonic current in active-passive magnetically suspended CMG using improved repetitive controller[J].IEEE/ASME Transactions on Mechatronics, 2016, 21(4): 2132–2141.DOI:10.1109/TMECH.2016.2555858 |
| [6] | 任元, 王卫杰, 刘强, 等. 一种磁悬浮控制敏感陀螺: ZL201510006597. 5[P]. 2017-04-28. REN Y, WANG W J, LIU Q, et al. A kind of magnetically suspended control and sensing gyroscopic: ZL201510006597. 5[P]. 2017-04-28(in Chinese). |
| [7] | GERLACH B, EHINGER M, KNUT RAUE H, et al. Gimballing magnetic bearing reaction wheel with digital controller[C]//Proceedings of the 11th European Space Mechanisms and Tribology Symposium. Loutraki: European Space Agency, 2005: 35-40.http://adsabs.harvard.edu/abs/2005ESASP.591...35G |
| [8] | WANG C E, TANG J Q. Design and mathematical analysis of a novel reluctance force-type hybrid magnetic bearing for flywheel with gimballing capability[J].Mathematical Problems in Engineering, 2013, 2013(8): 147–160. |
| [9] | XIANG B, TANG J Q. Suspension and titling of vernier-gimballing magnetically suspended flywheel with conical magnetic bearing and Lorentz magnetic bearing[J].Mechatronics, 2015, 28: 46–54.DOI:10.1016/j.mechatronics.2015.04.008 |
| [10] | TANG J Q, XIANG B, WANG C E. Rotor's suspension for vernier-gimballing magnetically suspended flywheel with conical magnetic bearing[J].ISA Transactions, 2015, 58: 509–519.DOI:10.1016/j.isatra.2015.05.011 |
| [11] | CHEN J, LIU K, CHEN X. Modeling and low power control of active magnetic bearings system[C]//International Conference on Modelling, Identification and Control. Piscataway, NJ: IEEE Press, 2011: 319-324.http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5973724 |
| [12] | BENOMAIR A M, BASHIR F A, TOKHI M O. Optimal control based LQR-feedback linearisation for magnetic levitation using improved spiral dynamic algorithm[C]//International Conference on Methods and Models in Automation and Robotics. Piscataway, NJ: IEEE Press, 2015: 558-562.http://ieeexplore.ieee.org/document/7283936/ |
| [13] | ZHANG Y C, SUN G J, ZHANG Y J. Experimental verification for zero power control of 0. 5kWh class flywheel system using magnetic bearing with gyroscopic effect[C]//Proceedings of the First International Conference on Machine Learning and Cybernetics. Piscataway, NJ: IEEE Press, 2002: 2059-2062.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1241916 |
| [14] | 孙玉坤, 朱志莹. 三自由度混合磁轴承最小二乘向量机逆模辨识与解耦控制[J].中国电机工程学报, 2010, 30(15): 112–117. SUN Y K, ZHU Z Y. Inverse-model identification and decoupling control based on least squres support vector machine for 3-DOF hybrid magnetic bearing[J].Proceedings of the CSEE, 2010, 30(15): 112–117.(in Chinese) |
| [15] | REN Y, FANG J. High-precision and strong-robustness control for an MSCMG based on modal separation and rotation motion decoupling strategy[J].IEEE Transactions on Industrial Electronics, 2014, 61(3): 1539–1551.DOI:10.1109/TIE.2013.2257147 |
| [16] | 谢进进, 刘刚, 文通, 等. 双框架磁悬浮控制力矩陀螺磁轴承负载力矩复合补偿的控制[J].光学精密工程, 2015, 23(8): 2211–2219. XIE J J, LIU G, WEN T, et al. Composite compensation for load torque of active magnetic bearing in DGMSCMG[J].Optics and Precision Engineering, 2015, 23(8): 2211–2219.(in Chinese) |
| [17] | KANG M S, LYOU J, LEE J K. Sliding mode control for an active magnetic bearing system subject to base motion[J].Mechatronics, 2010, 20(1): 171–178.DOI:10.1016/j.mechatronics.2009.09.010 |
| [18] | PENG C, FANG J, XU X. Mismatched disturbance rejection control for voltage-controlled active magnetic bearing via state-space disturbance observer[J].IEEE Transactions on Power Electronics, 2015, 30(5): 2753–2762.DOI:10.1109/TPEL.2014.2352366 |
| [19] | ZHENG S, HAN B, GUO L. Composite hierarchical antidisturbance control for magnetic bearing system subject to multiple external disturbances[J].IEEE Transactions on Industrial Electronics, 2014, 61(12): 7004–7012.DOI:10.1109/TIE.2014.2316226 |
| [20] | 吴鹏松, 吴朝野, 周东华. 信号解耦控制系统分析[J].控制工程, 2013, 20(3): 471–474. WU P S, WU C Y, ZHOU D H. Analysis of signal decoupling control system[J].Control Engineering of China, 2013, 20(3): 471–474.(in Chinese) |
| [21] | OKAJIMA H, MATSUNAGA N, KAWAJI S. Design of dynamic quantizers for 2-DOF IMC and its application to the temperature control of a heat plate[J].SICE Journal of Control Measurement & System Integration, 2011, 4(1): 77–82. |
| [22] | OKAJIMA H, UMEMOTO T, MATSUNAGA N, et al. Analysis of dynamic quantizer in 2-DOF internal model control system with dead-time[C]//ICCAS-SICE, 2009. Piscataway, NJ: IEEE Press, 2009: 4380-4383.http://ieeexplore.ieee.org/document/5332886/ |
| [23] | 辛朝军, 蔡远文, 任元, 等. 磁悬浮敏感陀螺动力学建模与关键误差源分析[J].北京航空航天大学学报, 2016, 42(10): 2048–2058. XIN C J, CAI Y W, REN Y, et al. Dynamic modeling and key error sources analysis of magnetically suspended sensitive gyroscopes[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2048–2058.(in Chinese) |
| [24] | 房建成, 孙津济, 樊亚洪. 磁悬浮惯性动量轮技术[M].北京: 国防工业出版社, 2012: 279-280. FANG J C, SUN J J, FAN Y H. Magnetically suspended inertial momentum wheel technology[M].Beijing: National Defense Industry Press, 2012: 279-280.(in Chinese) |
| [25] | 房建成, 任元. 磁悬浮控制力矩陀螺技术[M].北京: 国防工业出版社, 2014: 107-120. FANG J C, REN Y. Magnetically suspended control momentum gyroscope technology[M].Beijing: National Defense Industry Press, 2014: 107-120.(in Chinese) |
