现代战争中，对于威胁程度较大的敌方目标，往往需要采取多弹齐射的方式进行拦截以保证毁伤概率。为了达到这种饱和攻击的战术效果，需要对多枚导弹实现一致性的攻击时间控制，各枚导弹根据指定的攻击时间，各自独立或者相互协同地完成攻击任务。
自从Kim等首次提出攻击时间控制的导引问题以来^[1]，各国****基于不同的导引理念和控制理论，已经取得不少攻击时间控制导引律(Impact Time Control Guidance，ITCG)的研究成果。文献[2]将攻击时间控制导引问题转化为标称弹目距离跟踪问题，利用动态逆理论设计了三维空间的ITCG；文献[3]继续采用文献[2]的弹目距离跟踪思想设计了一种带攻击角度约束的ITCG；文献[4]同样基于跟踪思想设计ITCG，不同的是其跟踪的变量是视线角速率而不是弹目距离；文献[1, 5]采用小前置角假设估算剩余飞行时间，利用最优控制理论求解ITCG，但这种导引律只适用于初始前置角较小的情形；文献[6-8]研究了带攻击角度约束的ITCG，基于最优控制理论将导引问题转化为能量最优的2点边值问题，但其数值解法的应用使得导引律缺乏实时性保证；文献[9]基于线性化导引方程推导了一种具有偏置项的比例导引ITCG，偏置项用于调整攻击时间；文献[10]同样设计了具有偏置结构的ITCG，不同的是采用非线性导引模型设计导引律，与文献[5]类似，在推导剩余飞行时间表达式时，其同样采用了小前置角假设；文献[11]设计了一种时变导航比的ITCG，根据不同的攻击时间在线计算所需要的导航比，但算法的实时性难以保证；文献[12-13]采用滑模控制理论设计ITCG，但其剩余时间估计表达式仍然不适用于大前置角拦截；文献[14-15]设计了基于虚拟领弹策略的ITCG，其方法是先构造出一枚可按指定时间攻击的虚拟领弹，然后设计导引律使真实导弹的轨迹跟踪虚拟导弹的轨迹完成攻击时间的控制，不需要估计剩余时间，但其制导指令往往会出现奇异或产生跳变。
综上所述，目前关于攻击时间控制的导引问题研究可大致分为2类：一类是不需要估计剩余时间的ITCG，主要是基于跟踪的思想来实现，但被跟踪的理想曲线通常不易获得；另一类是需要估计剩余时间的ITCG，但剩余时间的获取往往是通过基于小前置角假设的线性化导引方程来估算^[16]，以致导引律对大前置角拦截并不适用。针对以上问题，本文研究旨在得到一种可用于大前置角拦截的ITCG，使其不仅适用于打击固定目标，而且可以打击非机动运动目标。导引律的推导利用非线性导引方程，采取基于预测命中点(Predicting Interception Point，PIP)的剩余时间估计方法，结合等效滑模控制理论得到，通过选择合适的滑模面和控制律，使其满足大初始前置角下的拦截要求，并给出了严格的数学证明。仿真结果证明了该导引律的有效性。
1 导引模型 末制导过程的弹目相对运动是俯仰平面和偏航平面的耦合运动，本文为了研究方便，将其简化为2个通道的独立运动。考虑到俯仰平面与偏航平面运动的相似性，本文只研究二维俯仰平面的弹目相对运动，其运动模型如图 1所示。

图 1 弹目相对运动模型 Fig. 1 Missile-target relative motion model

图选项

相对运动方程如下：

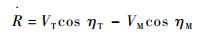(1)

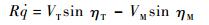(2)

(3)

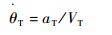(4)

式中：η_M=θ_M－q，η_T=θ_T－q分别为导弹和目标前置角；V_M和V_T分别为导弹和目标的速度；θ_M和θ_T分别为导弹和目标的弹道倾角；q和分别为弹目视线倾角和视线角速率；a_M和a_T分别为导弹和目标的法向加速度；R为弹目距离；为弹目接近速度。
对式(2)求导可得

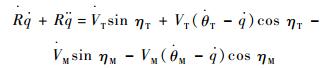(5)

整理可得

(6)

式中：A_M=a_Mcos η_M, A_T=a_Tcos η_T分别为导弹和目标加速度在视线法向上的分量。在导弹飞行过程当中，不考虑其他气动力特性，认为导弹和目标均作均速运动，即。对于非机动运动目标，另有a_T=0，则式(6)可以改写为

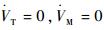
(7)

如果把攻击时间t定义为导弹发射时刻到弹目遭遇所用的总时间，则有

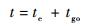(8)

式中：t_e为导弹制导时刻起已经飞行的时间；t_go为剩余飞行时间，其准确值难以获取，只能通过表达式近似估计。ITCG设计的目的就是找到一种合适的控制指令a_M，使导弹的攻击时间t与指定的期望攻击时间T_d相一致。又因弹目视线角速率收敛于零是导弹命中目标的必要条件，因此导引律设计时应对t和综合考虑。
2 导引律设计 2.1 滑模面选择依据 定义攻击时间误差

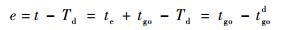(9)

式中：t_go^d为期望剩余飞行时间。考虑到导引律设计时要同时满足最小的脱靶量和最小的攻击时间误差要求，因此采用滑模控制的方法进行设计，滑模面的选择如下：

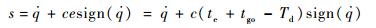(10)

式中：c=const>0，决定了攻击时间误差权重的大小。选择上述滑模面的意义在于：当=0时，导弹能以准平行接近状态高精度击中目标；当e=0时，导弹能以指定的攻击时间实现弹目交会。而且一旦导弹进入滑模运动状态，则有

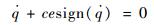(11)

即

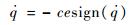(12)

如果在滑模运动的初始阶段，有：
1) 若e=0，则必有=0成立，如果接近速度，导弹就能以指定的攻击时间和较小的脱靶量命中目标，此时导引律只需要对攻击时间进行控制即可，即完成时间控制的同时也保证了制导精度。
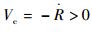
2) 若e≠0，需要对是否为零进行讨论：
① =0，按照符号函数的基本定义，此时式(12)恒成立，如果接近速度为正，则导弹能以较高的精度击中目标，但攻击时间的控制无法实现(e≠0)。为了实现攻击时间控制，应打破=0时=－cesign()的恒成立问题，即设法让=0时，sign()不再取0，因此可以对符号函数作如下新的定义:

(13)

根据重新定义的符号函数式(13)，再结合式(12)可知当=0时，=±ce，又因为=0，故此时必有e=0成立，即导弹能从e≠0的初始状态调整至能按指定时间完成攻击任务的e=0的状态，此时导引律在保证制导精度的同时也完成了攻击时间控制。
② ≠0，此时需要对e的正负情况进行讨论(e=0的情况已在①中讨论完毕)：
a) 如果e>0，由式(12)可知，当>0时，=－ce < 0，这与>0的前提相矛盾；当 < 0时，=ce>0，这与 < 0的前提也相矛盾，因此e>0时式(12)恒不成立，即无论导引律如何设计，都无法保证滑模面可达，亦无法实现攻击时间控制。
b) 如果e < 0，此时无论>0还是 < 0易知式(12)都成立，即滑模面可达，此时导引律对视线角速率和攻击时间同时控制。
综上所述，选择式(10)所示的滑模面能够完成任意e≤0，即估计攻击时间小于指定攻击时间情况下的导引控制，这也是下文t_go近似算法的选择依据。
2.2 基于等效滑模控制的导引律设计 剩余时间t_go的经典计算方法是R/V_c，V_c为接近速度，但这种计算方法只适用于导弹前置角较小的情形，对大前置角拦截并不适用。文献[17]给出了一种逆轨拦截剩余时间估计计算方法，无论打击固定目标还是非机动运动目标，都能获得良好的估计精度。其计算式为

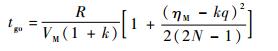(14)

式中：k=V_T/V_M为目标与导弹的速度比；N为导航比。
由式(14)可以看出，当拦截固定目标k=0且导弹前置角η_M为零或很小时，t_go=R/V_M=R/V_c，与经典计算方法相同；当导弹前置角不为零时，则通过修正项1+(η_M－kq)²/(4N－2)来修正估计误差，η_M越大，t_go越长，且式(14)所示的t_go计算方法依赖于V_M而与V_c无关，因此即使V_c < 0，即在前置角很大的情况下，也能取得较好的估计精度。同时由文献[17]可知，逆轨拦截模式下t_go的估计值要小于实际值，符合2.1节的结论。因此，将利用式(14)给出的t_go计算方法设计大前置角拦截ITCG，以保证滑模面s=0可达。
另外，采用式(14)所示的剩余时间估计计算方法能够保证时间控制和制导精度同时满足。这是因为一旦所设计的导引律使系统达到滑模面s=0，则有e=t_go－t_go^d=0成立，即t_go=t_go^d=T_d－t_e，当时间控制满足要求时，有t_e=T_d，即t_go=0成立，结合式(14)可知此时必有R=0成立；同理，R=0也必有t_e=T_d成立。
等效滑模控制算法的一般形式为

(15)

式中：a_M^eq为等效控制指令，保证系统状态到达滑模面；a_M^disc为不连续补偿控制指令，用来保证系统状态不离开滑模面。
观察式(10)可知，滑模面s包含符号函数sign()，而符号函数在原点处不可导，因此在求解制导指令时，应对s在原点以外求导，得

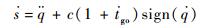(16)

对式(14)求导结合式(3)可得

(17)

将式(7)和式(17)代入式(16)得

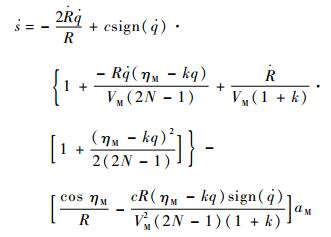(18)

令=0，解得等效控制律

(19)

a_M^disc一般采取如下形式：

(20)

式中：l为不连续控制器的增益。此时制导指令的计算式为

(21)

为了得到不连续控制器的增益l，定义Lyapunov函数为

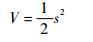(22)

对式(22)求导并将式(18)、式(21)代入可得

(23)

取

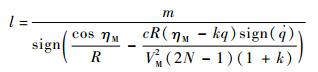(24)

式中：m=const>0。
将式(24)代入式(23)，得

(25)

注意到式(25)中，如果

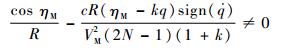(26)

成立，则在滑模到达阶段，有成立，即设计形如式(21)所示导引律，能够严格满足Lyapunov稳定条件，保证滑模状态可达，攻击时间可控。导引律的具体表达式为

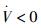
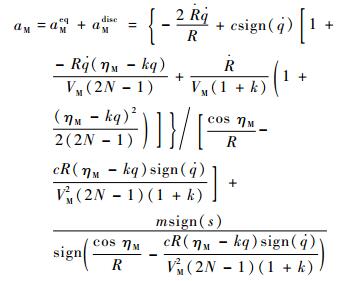(27)

记ξ=cos η_M/R－cR(η_M－kq)sign()/[V_M²(2N－1)(1+k)]，易知当ξ→0时，a_M→∞，为避免指令发散，令ξ→0时，ξ=κ=const，κ在零的邻域内取值。另外，采用双曲正切函数tanh(s)代替符号函数克服不连续控制项的影响，在保证弹道光滑的同时，也能解决滑模面s在原点处的不可导问题。
3 导引律改进方法 2.2节提到，如果式(26)成立，则所设计的导引律能够严格满足Lyapunov稳定条件，保证大前置角拦截攻击时间可控。下面证明当式(26)不成立，即Lyapunov稳定条件不能严格满足时，大前置角拦截攻击时间控制的可行性及导引律改进方法。
当式(26)不成立时，有

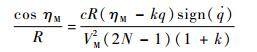(28)

对式(28)重新整理，可得

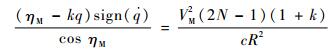(29)

因为k>0，c>0，N一般取3~6，因此式(29)的右端恒大于零。由式(2)可得

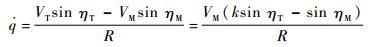(30)

不妨在式(30)中运用小角度假设近似得到≈V_M(kq－η_M)/R，因为sign()与同号，故其必然与(kq－η_M)同号，因此式(29)左端分子项(η_M－kq)sign()必然小于零。对η_M实际可能的情况进行讨论，证明任意前置角拦截的有效性：
1) 若0 < |η_M| < π/2，则cos η_M>0，此时式(29)等号左端小于零，而等号右端恒大于零，显然式(29)不成立，即所设计的导引律能够严格满足，系统稳定，攻击时间可控。
2) 若|η_M|>π/2，此时cos η_M < 0，式(29)等号左端大于零，等式可能成立，此时，Lyapunov稳定条件不能严格满足，需要对导引律式(27)作如下相应改进，取

(31)

式中：ε为大于零的常数。
将式(31)代入式(23)，得

(32)

因为ε>0，故在滑模到达阶段有恒成立，满足Lyapunov稳定条件，系统稳定，攻击时间可控。此时导引律式(27)改写为

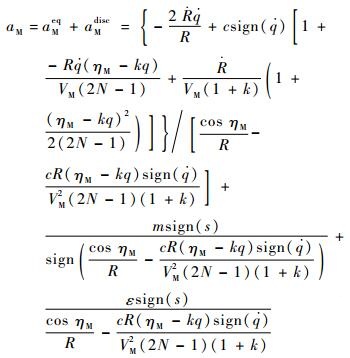(33)

此处采取与式(27)同样的方法，避免指令出现奇异，即当ξ→0时，取ξ=κ=const，κ在零的邻域内取值，其中，ξ=cos η_M/R－cR(η_M－kq)·sign()/[V_M²(2N－1)(1+k)]。
4 仿真验证 为了验证本文所设计的大前置角拦截ITCG的有效性，本节将对拦截固定目标、拦截非机动运动目标和齐射攻击3种攻击情况进行仿真验证，其中导弹和目标初始状态的选择如表 1所示，制导律参数N=3，m=200，ε=0.005，κ=0.000 1；目标静止时取c=1，目标运动时取c=0.01。自动驾驶仪等效为一阶惯性环节，时间常数取0.1 s。
表 1 仿真参数值 Table 1 Value of simulation parameters

初始参数	数值
导弹初始位置/m	(0，0)
目标初始位置/m	(10 000，0)
导弹弹道倾角θM0/(°)	60
目标弹道倾角θT0/(°)	180
导弹速度VM/(m·s-1)	300
目标速度VT/(m·s-1)	0、120
导弹最大法向加速度aMmax/(m·s-2)	250

表选项






4.1 拦截固定目标(k=0) 1) 导弹和目标的初值选取同表 1，此时前置角η_M=θ_M0=60°，指定攻击时间分别取40、50、60、70 s进行仿真，结果如图 2所示。

图 2 固定目标拦截时不同攻击时间仿真 Fig. 2 Simulation of different impact time for intercepting stationary target

图选项

从图 2(b)可以看出，4种情况下，导弹都能以指定的攻击时间命中目标，时间分别是39.99，49.99，59.99，69.99 s。而由图 2(a)可知，指定飞行时间越长，弹道弯曲程度越大，且在每一条飞行弹道的初段，导弹前置角均呈现出增大的趋势，即导弹出现偏离目标飞行的情况，此时剩余飞行时间也逐渐增大(见图 2(b))，这主要是由于调整弹道以实现指定时间攻击。而由图 2(c)可以看出，为了调整弹道以达到指定攻击时间，导弹需要以较大的法向加速度消除时间误差，随着时间误差修正完成，导弹就能以较小的前置角，较平滑的弹道命中目标，此时法向加速度逐渐减小直至维持在0.5g左右，g为重力加速度。
2) 为验证大前置角拦截时的有效性，在指定攻击时间取50 s，前置角η_M=θ_M0分别取45°、90°、135°、180°的情况下进行仿真，其余参数同表 1，仿真结果如图 3所示。

图 3 固定目标拦截时不同前置角仿真 Fig. 3 Simulation of different heading errors for intercepting stationary target

图选项

由图 3(a)和(b)可以看出，前置角的不同取值并不影响导弹的攻击时间，即使导弹在制导初始时刻速度方向背离目标，即前置角取180°时，导弹仍能以指定的时间准确命中目标。虽然此时初始时间误差较大(攻击时间大约65 s)，但随着弹目距离接近，时间误差很快消除至零，且4种情况下的拦截时间均为49.99 s，说明了所设计的导引律在大前置角拦截时的有效性。从图 3(c)可以看出，在制导初段，导弹需要以较大的法向加速度调整攻击时间，而随着弹目距离接近，法向加速度也越来越小，并在弹目交会时刻收敛到零，从而保证了弹道平滑和制导精度。
4.2 拦截非机动运动目标(k=2/5) 1) 目标速度取120 m/s，前置角η_M=θ_M0=60°，其余仿真条件同表 1，取30、40、50、60s作为不同的攻击时间进行仿真，结果如图 4所示。

图 4 运动目标拦截时不同攻击时间仿真 Fig. 4 Simulation of different impact time for intercepting moving target

图选项

由图 4(a)和(b)可以看出，针对运动目标的拦截，本文所设计的导引律同样有效，4种情况下的仿真结果显示，拦截时间分别为29.75，39.99，49.75，59.99 s，脱靶量依次为0.22、0.07、0.63、0.34 m，满足攻击时间控制和制导精度要求。对导弹剩余时间和法向加速度的变化趋势分析与4.1节拦截固定目标时的1)相同，这里不再赘述。而需要说明的是，此处运动目标的拦截与现有文献不同，现有文献在处理运动目标攻击时间控制的导引问题上采用的是PIP方法，即将运动的目标通过PIP转化为相对固定的目标，再运用针对固定目标的ITCG实施拦截，而本文所设计的ITCG可直接运用于运动目标拦截，制导指令随着目标速度的不同而不同，具体通过参数k进行相应的调整。
2) 为验证大前置角拦截时的有效性，目标速度取120 m/s，在指定攻击时间取40 s，前置角η_M=θ_M0分别取45°、90°、135°、180°的情况下进行仿真，其余参数同表 1，仿真结果如图 5所示。

图 5 运动目标拦截时不同前置角仿真 Fig. 5 Simulation of different heading errors for intercepting moving target

图选项

由仿真结果可以看出，针对运动目标的拦截问题，本文所设计的ITCG在大前置角情况下依然适用，包括初始速度指向背离目标的情形，其剩余飞行时间和法向加速度的变化趋势及分析与4.1节拦截固定目标时的2)相同，这里不再赘述。
4.3 齐射攻击(以静止目标为例) 1) 导弹和目标的初值选取同表 1，前置角η_M=θ_M0=60°，假定有4枚导弹从同一位置两两间隔2 s依次发射，从第一枚导弹发射开始计时，指定攻击时间分别取50、49、48、47 s，则相应每枚导弹的攻击时间依次为50、47、44、41 s，仿真结果如图 6所示。

图 6 相同位置齐射攻击仿真 Fig. 6 Simulation of same position for salvo attack

图选项

从仿真结果可以看出，从同一位置依次发射的各枚导弹，均能在指定的时间完成攻击任务，且时间误差均小于0.01 s。而指定的攻击时间越长，弹道弯曲程度越大，调整时间也越长，这与4.1节拦截固定目标时1)中的结论相同。
2) 目标位置取于坐标原点，4枚导弹的位置分别取(-6 000，-8 000) m、(-10 000, 0) m、(0, 10 000) m、(8 000，-6 000) m，前置角η_M=θ_M0=60°，假定导弹两两间隔1 s依次发射，从第一枚导弹发射开始50 s时同时命中目标，则相应每枚导弹的攻击时间依次为50、49、48、47 s，仿真结果如图 7所示。

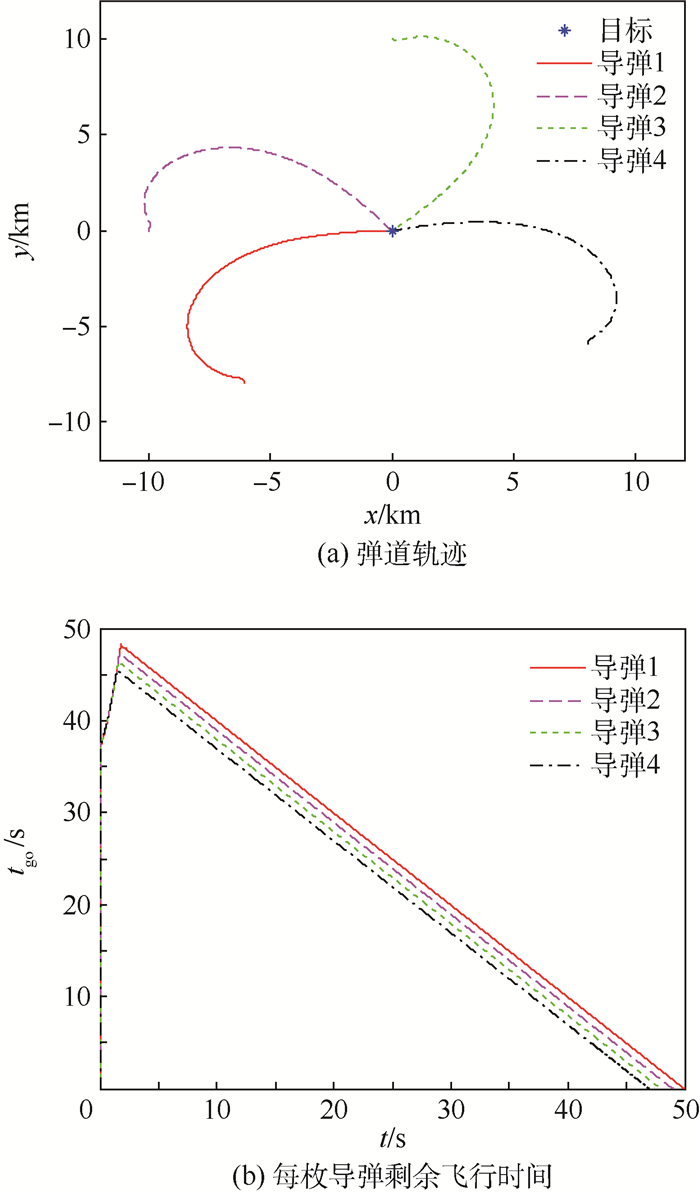图 7 不同位置齐射攻击仿真 Fig. 7 Simulation of different position for salvo attack

图选项

由图 7可知，从不同位置发射的各枚导弹也能在同一时间完成齐射攻击任务，且时间误差均小于0.01 s，进一步说明了本文所设计的ITCG运用到多弹饱和攻击上的有效性。
5 结论 1) 利用非线性导引方程，采用一种逆轨拦截剩余时间估计方法，结合等效滑模控制理论，设计了一种大前置角拦截攻击时间控制导引律(ITCG)，拓宽了导弹的初始发射条件。
2) 无论是打击固定目标，还是非机动运动目标，该导引律都能在指定时间内完成攻击任务。即使在制导初段弹目接近速度为负，即弹目距离越来越大的情况下，也能最终修正弹道以指定的时间准确命中目标。
3) 结合网络拓扑理论，研究拦截机动目标的协同导引律是下一步的工作方向。

参考文献

[1]	KIM B S, LEE J G, HAN H S. Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277–288.DOI:10.1109/7.640285
[2]	张友安, 马国欣. 攻击时间控制的动态逆三维制导律[J].哈尔滨工程大学学报, 2010, 31(2): 215–219. ZHANG Y A, MA G X. Dynamic inversion three-dimensional guidance law for impact time control[J].Journal of Harbin Engineering University, 2010, 31(2): 215–219.(in Chinese)
[3]	张友安, 张友根. 多导弹攻击时间与攻击角度两阶段制导[J].吉林大学学报(工学版), 2010, 40(5): 1442–1447. ZHANG Y A, ZHANG Y G. Two stages guidance to control impact time and impact angle for multi-missiles[J].Journal of Jilin University(Engineering and Technology Editiion), 2010, 40(5): 1442–1447.(in Chinese)
[4]	HARL N, BALAKRISHNAN S. Impact time and angle guidance with sliding mode control[J].IEEE Transactions on Control Systems Technology, 2012, 20(6): 1436–1449.DOI:10.1109/TCST.2011.2169795
[5]	LEE J I, JEON I S, TAHK M J. Guidance law to control impact time and angle[J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 301–310.DOI:10.1109/TAES.2007.357135
[6]	ARITA S, UENO S. Optimal feedback guidance for nonlinear missile model with impact time and angle constraints[C]//AIAA Guidance, Navigation, and Control(GNC)Conference. Reston: AIAA, 2013: 1-12.
[7]	ZHANG L M, SUN M W, CHEN Z Q, et al. Receding horizon trajectory optimization with terminal impact specifications[J].Mathematical Problems in Engineering, 2014, 28(6): 1–8.
[8]	YAN F, KEMAO M, YUQING C. Cooperative guidance laws with constraints on impact time and terminal angle[J].Journal of System Simulation, 2014, 26(10): 2434–2441.
[9]	马国欣, 张友安. 带有导引头视场限制的攻击时间控制导引律[J].弹道学报, 2013, 25(2): 6–11. MA G X, ZHANG Y A. Impact time control guidance law with seeker field-of-view limit[J].Journal of Ballistics, 2013, 25(2): 6–11.(in Chinese)
[10]	ZHANG Y A, MA G X, LIU A L. Guidance law with impact time and impact angle constraints[J].Chinese Journal of Aeronautics, 2013, 26(4): 960–966.DOI:10.1016/j.cja.2013.04.037
[11]	GHOSH S, GHOSE D, RAHA S. Three dimensional retro-PN based impact time control for higher speed non-maneuvering targets[C]//2013 IEEE 52nd Annual Conference on Decision and Control(CDC). Piscataway, NJ: IEEE Press, 2013: 4865-4870.
[12]	KUMAR S R, GHOSE D. Sliding mode control based guidance law with impact time constraints[C]//2013 American Control Conference(ACC). Piscataway, NJ: IEEE Press, 2013: 5760-5765.
[13]	JEON I S, LEE J I, TAHK M J. Homing guidance law for cooperative attack of multiple missiles[J].Journal of Guidance, Control, and Navigation, 2010, 33(1): 275–280.DOI:10.2514/1.40136
[14]	马国欣, 张友安, 李大鹏. 基于虚拟领弹的攻击时间和攻击角度控制[J].飞行力学, 2009, 27(5): 51–54. MA G X, ZHANG Y A, LI D P. Virtual-leader based impact time and impact angle control[J].Flight Dynamics, 2009, 27(5): 51–54.(in Chinese)
[15]	SHIYU Z, RUI Z, CHEN W, et al. Design of time-constrained guidance laws via virtual leader approach[J].Chinese Journal of Aeronautics, 2010, 23(1): 103–108.DOI:10.1016/S1000-9361(09)60193-X
[16]	KIM T H, LEE C H, JEON I S, et al. Augmented polynomial guidance with impact time and angle constraints[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2806–2817.DOI:10.1109/TAES.2013.6621856
[17]	李辕, 赵继广, 白国玉, 等. 基于预测碰撞点的剩余飞行时间估计方法[J].北京航空航天大学学报, 2016, 42(8): 1667–1674. LI Y, ZHAO J G, BAI G Y, et al. The method of time-to-go estimation based on predicted crack point[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8): 1667–1674.(in Chinese)