气体在液体中扩散系数研究常见于石油化工行业,包括其向原油及多孔介质扩散传质的报道[5-8],且研究以实验测定为主。测量气体在不同温度和压力下的扩散系数有直接和间接测量两大类方法[9]。直接测量主要是混合物成分分析法[10-11],其通过扩散过程中质谱分析原理,分析气液混合物中气体浓度变化而得到气体扩散系数值,但成分分析法存在实验花费大、分析过程繁杂、对扩散过程产生影响等问题,因此使用并不普遍;间接测量有压力降法[12-15]、恒定压力测量法[6, 16]、激光全息干涉测量法[17-19]等。相较于其他几种实验方法,压力降法由于精确度高、代价低、时间短而得到广泛应用[20]。
压力降法的基本原理是:在恒温条件下密闭容器中,气体分子扩散溶解于液体后,气相空间物质减少,气体压力降低。当气体扩散系数增大,则压力降落速率快,反之则压力降低速率慢。
扩散系数与扩散体系中物质化学组成密切相关,不能简单地采用其他液体中的扩散系数进行类比或简化,如文献[8, 10, 21-24]测量了CH4和CO2在不同油品中的扩散系数,实验结果显示,不同条件下气体扩散系数差异较大。目前国内外文献中均无法查询到CO2在国产RP-3航空燃油中的扩散系数,这对3C惰化系统的精准设计十分不利。有鉴于此,本文搭建了压力降法实验平台,测量了CO2在RP-3航空燃油溶解时气相空间压力的变化。扩散系数的大小会造成压力变化速度不同,因此可根据压力来间接得到扩散系数,一般的做法是假设满足一维扩散条件,即认为扩散的垂直方向无限大,这样在忽略高次项的条件下,可显式得到扩散系数与压力的关系[8, 10, 12, 22]。实际的容器直径总是有限的,因此无法满足一维扩散假设,上述解析解法存在一定误差,有鉴于此,本文采用数值解法,并认为扩散是二维的,但是数值解法中气体压力与扩散系数为隐式关系,需在一定数值范围内依次假设扩散系数值并根据Fick扩散方程、质量守恒和气体状态方程计算扩散过程中气体压力变化,并与实验测量压力值进行比较,定义计算与实验压力误差函数,当压力误差函数取值最小时可认为此时对应扩散系数为最优扩散系数值。数值解法减少了解析方程中的简化假设,并建立二维扩散模型求解扩散系数值,更加符合实际扩散过程,由此通过数值差分方法及误差分析法使计算结果更加精确。
1 实验材料和方法 压力降法通过测量密封不锈钢容器内与RP-3航空燃油直接接触的CO2的压力变化来计算气体扩散系数,实验装置如图 1所示。RP-3航空燃油由容器底部注入,燃油高度41.5 mm,气体由高压气瓶降压后从容器上方引入,直到达到实验开始所需压力,气相高度78.5 mm,扩散容器截面直径70 mm。工质充注结束后关闭管路阀门,实验开始,并利用压力传感器和数据采集仪记录气体压力随时间变化。为保持实验过程中温度恒定,整个实验过程在恒温水浴中进行。
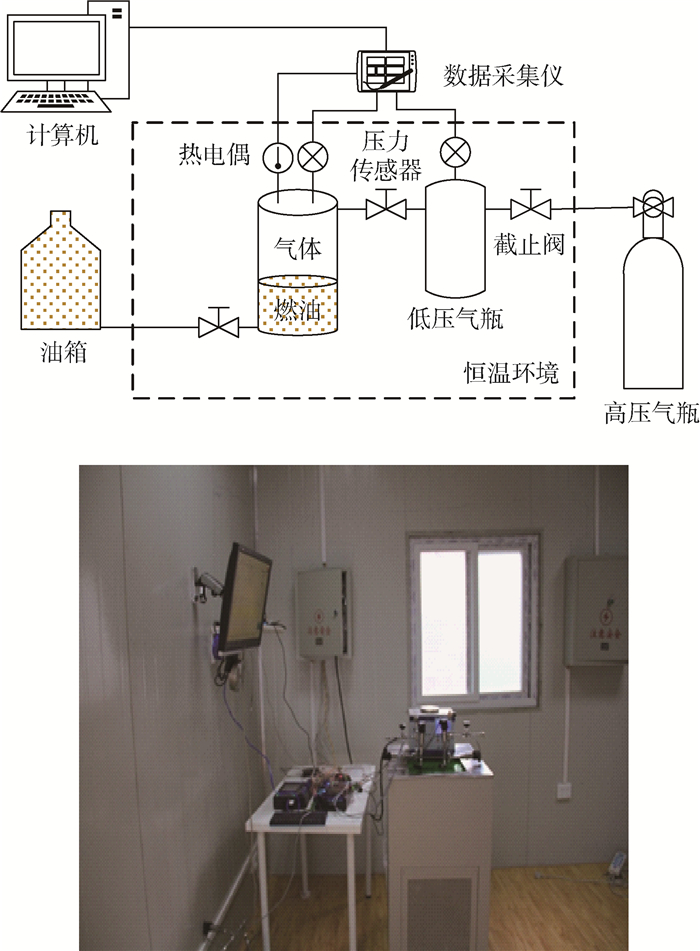 |
| 图 1 压力降法实验装置图 Fig. 1 Schematic diagram of pressure-decay experiment apparatus |
| 图选项 |
为减少实验误差,实验开始前须对实验装置进行气密性检测,防止因泄漏而导致气体压力降低,保证实验可靠性。实验中所用CO2纯度为99.99%,RP-3航空燃油由航空机电系统综合航空科技重点实验室提供。主要实验设备包含热电偶T、压力传感器(量程0~0.5 MPa)、恒温水浴DC-3030,其精度分别为±0.1℃、F.S.±0.1%、±0.1℃。
2 扩散模型 气体扩散过程如图 2所示。对气-液扩散进行数学分析须选择合适的扩散方程并对实验模型作出如下假设:
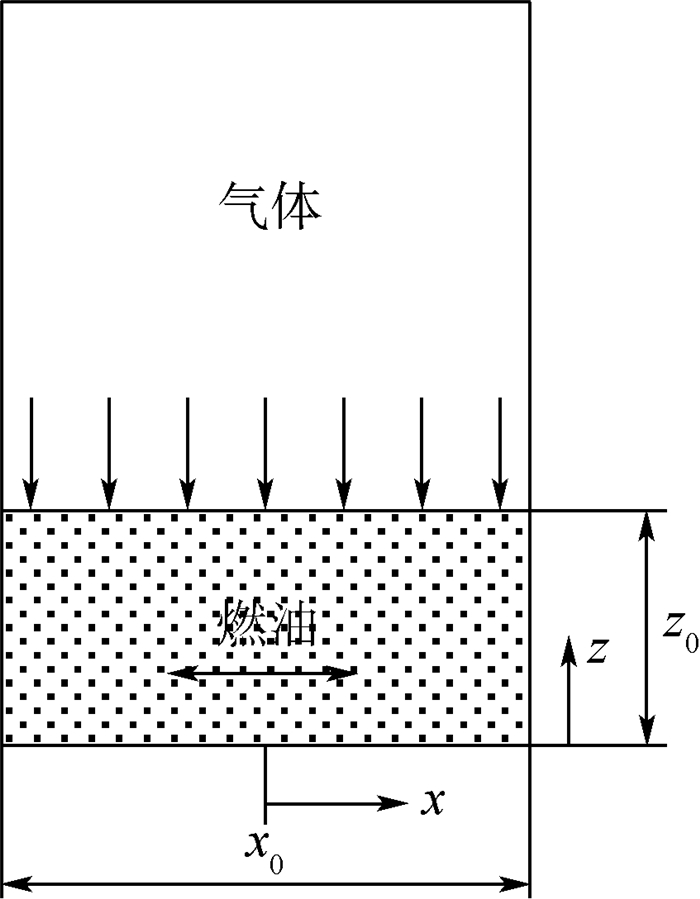 |
| 图 2 扩散模型示意图 Fig. 2 Schematic diagram of diffusion model |
| 图选项 |
1) CO2气相空间不存在浓度梯度。
2) 扩散过程为二维各向同性扩散。
3) 气-液边界处航空燃油中CO2浓度为各时刻气体压力条件下对应的饱和溶解度[7]。
4) 扩散系数为与浓度无关的常数[8]。
5) 由于在实验温度条件下扩散体系中燃油蒸气压力相对于CO2气体压力极低,且当温度恒定时燃油蒸气压力保持不变,因此实验过程中可忽略燃油蒸气压力对实验的影响[15]。
6) 扩散体系中不发生化学反应[25]。
根据Fick第一定律,二维扩散可表示为
 | (1) |
式中:c为气体在液体中浓度,mol/m3; t为时间,s; v为流体速度,m/s; z为液体高度位置,m; x为液体水平方向位置,m;D为扩散系数,m2/s。
静止条件下密闭扩散容器内燃油流速可忽略不计,则式(1)可表示为
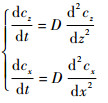 | (2) |
根据本节假设3),气-液边界扩散浓度为t时刻气体压力为p时所对应平衡溶解度,则对应扩散模型边界条件为
初始条件:
 | (3) |
边界1:
 | (4) |
边界2:
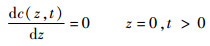 | (5) |
边界3:
 | (6) |
边界4:
 | (7) |
式中:z0为液体总高度,m; x0为液体水平方向总长度,m; p为气体压力,Pa。
气体在石油制品中溶解度可用ASTM D2780—92[4]所提供的阿斯特瓦尔德系数表示。随着扩散进行,CO2溶解于RP-3航空燃油,气体压力降低,根据阿斯特瓦尔德系数可求得在不同时刻压力变化时CO2在液相中溶解度,并以此作为式(4)在气-液界面处边界条件,运用中心差分法,假定扩散系数值求解扩散方程式(2),计算可得燃油中不同位置在不同时刻气体浓度分布,由此可知液相中气体总的物质的量。根据质量守恒定律,扩散过程中气体溶解于燃油的物质的量与气体自身减少的物质的量相等。根据实际气体状态方程,在一定温度和压力下气体物质的量可表示为
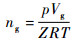 | (8) |
式中:ng为气体物质的量,mol; Vg为气体体积,m3; Z为气体压缩因子; 气体常数R=8.314 J/(mol·K);T为温度,K。
实验过程中气体初始压力为500~600 kPa, 且扩散过程中压力变化范围不大,可认为气体压缩因子为常数,则实验过程中CO2扩散导致气体压力变化为
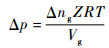 | (9) |
式中:Δp为气体压力变化,Pa; Δng为气体物质的量变化,mol。
因此,容器内气体压力可表示为
 | (10) |
式中:pi为气体初始压力,Pa。
3 数值优化 首先进行不同温度下CO2在RP-3航空燃油中压力降测量并记录。在与实验相同初始压力条件下,假定扩散系数值并结合上述扩散模型进行气相空间压力计算,与实验记录压力进行比较得到实验与理论计算气体压力平均误差函数。以扩散系数为独立变量,在一定范围内求得气体压力误差函数值,当误差函数取值最小时所对应的扩散系数即为最优解。
压力平均误差函数Δpave表示在扩散过程中时刻tj(j=0, 1, …,m)时理论计算压力与实验压力差值的平方平均数,单位为Pa。平均误差函数可表示为
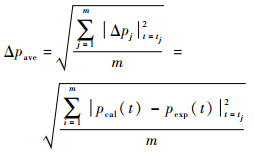 | (11) |
式中:Δpj为各时刻压力差值;pcal为计算压力,Pa; pexp为实验压力,Pa。
扩散初始条件确定后,扩散系数值为求解压力变化唯一变量。根据Husain的单一变量搜索法[26],在预设扩散系数取值范围内,可求得扩散系数最优解。由文献[23, 27]可知,气体在液体中扩散系数值取值范围一般为1×10-11~1×10-6 m2/s, 在此范围内误差函数为单峰值函数,因此存在特定扩散系数使扩散过程中理论计算压力与实验记录压力误差最小,从而达到求解目的。
4 实验结果及分析 实验测量并记录了-20、0、20、40、60℃ 5组不同温度下CO2在CO2-RP-3航空燃油体系的压力降分布。扩散过程中每隔4 s时间选取压力值进行理论与实验压力对比。选择扩散系数计算步长为0.1 m2/s进行求解,如图 3所示为压力平均误差函数Δpave随扩散系数变化关系。从图 3中可看出在扩散系数取值范围内f(D, Δpave)为一单峰函数,Δpave存在最小值,与本文设想一致。
 |
| 图 3 CO2-RP-3燃油体系不同温度下压力平均误差随扩散系数变化关系 Fig. 3 Variation of average pressure differencewith diffusion coefficient under different temperature for CO2-RP-3 jet fuel system |
| 图选项 |
从图 3中可看出在特定温度下,当Δpave取最小值Δpave,min时,对应唯一确定的扩散系数值D,如表 1所示,且扩散系数步长的选取对最优扩散系数值产生的偏差仅为0.9%~1.6%,可满足要求。表 1中所得扩散系数值即为CO2在RP-3航空燃油中的最优解。
表 1 扩散系数最优解 Table 1 Optimum solution of diffusion coefficient
| T/℃ | Δpave, min/kPa | D/(10-8m2·s-1) |
| -20 | 5.89 | 6.1 |
| 0 | 3.87 | 7.6 |
| 20 | 5.35 | 8.6 |
| 40 | 4.98 | 9.7 |
| 60 | 3.59 | 11.1 |
表选项
为验证最优扩散系数解能更准确地描述实际扩散过程,将所求扩散系数值D代入扩散方程模型,由此可计算得到扩散体系中气体压力降分布曲线。以60℃扩散为例,取3组不同扩散系数值分别进行计算,其中一组为所求最优扩散系数D,另外2组为任意大于或小于D的值,理论计算与实验记录压力变化对比如图 4所示。由图 4可知扩散系数取值不同时计算与实验压力之间平均误差发生变化,运用最优扩散系数值计算气体压力与实验记录之间误差最小,由此表明数值优化方法可以更加准确地求解CO2在RP-3航空燃油中的扩散系数。
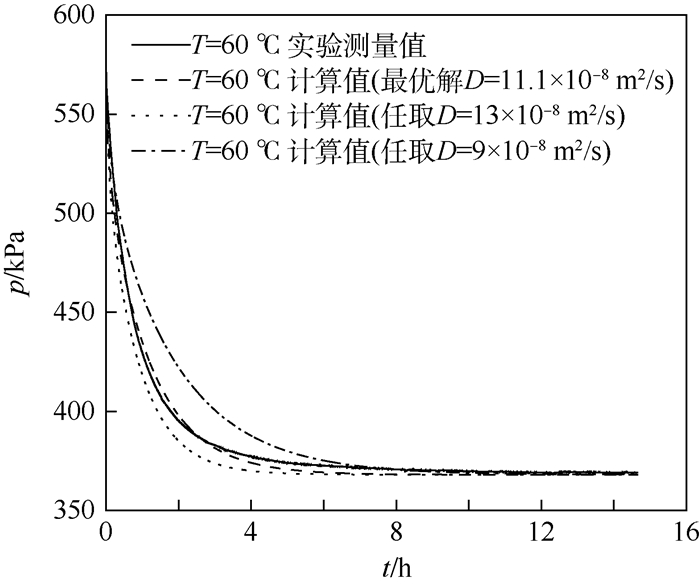 |
| 图 4 计算压力降与实验数据比较 Fig. 4 Comparison of calculated pressure decay with experimental data |
| 图选项 |
从表 1所求扩散系数值可知,CO2在RP-3航空燃油扩散体系中扩散系数随温度升高而增大,这是因为温度升高,气体分子热运动加剧,导致分子扩散速率加快。而且温度升高导致液体黏度降低,气体扩散系数增大[28]。当温度由-20℃增大到60℃时,扩散系数值增大了81.97%。在工程应用中,扩散系数随温度升高而增大,可用Arrhenius方程描述:
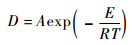 | (12) |
式中:A为数值拟合常数,m2/(s·K); E为表观活化能,J/mol。
对扩散系数与温度进行数值拟合,如图 5所示,由最小二乘法拟合结果可知,CO2在RP-3航空燃油扩散体系中A为6.8×10-7 m2/(s·K), E为5 040.2 J/mol。
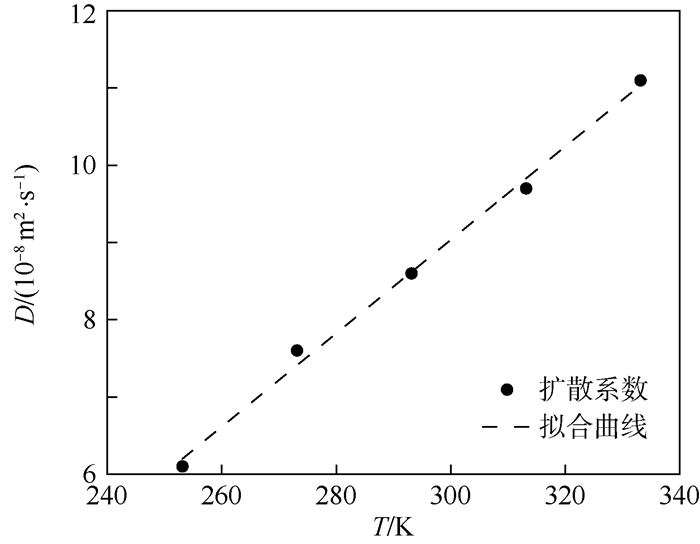 |
| 图 5 扩散系数随温度变化关系 Fig. 5 Relationship between diffusion coefficient and temperature |
| 图选项 |
对本文实验系统和实验结果进行误差分析,以60℃时CO2扩散为例,在相同实验系统和初始条件下进行3次重复性实验,记录气体压力降过程,如图 6所示。在相同条件下实验结果基本相同,运用第2、3节方法求解扩散系数方程式(2)和误差函数方程式(3),所得扩散系数分别为10.9×10-8、11.1×10-8、11.7×10-8 m2/s。本文所得扩散系数值与平均扩散系数值误差仅为1.15%,因此在实验误差允许范围内,本实验系统和实验结果具有可靠性。
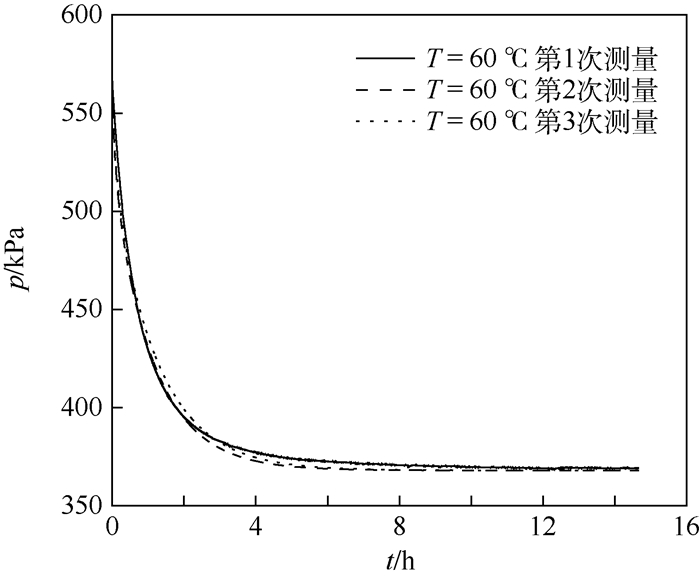 |
| 图 6 实验测量不同时刻压力变化 Fig. 6 Experimental measurement of variation of pressure versus time |
| 图选项 |
5 结论 1) 采用压力降法进行扩散系数实验测量,构建二维扩散模型,运用数值解法和误差分析能更加准确地描述实际扩散过程。
2) 气体扩散理论模型和实验测量结果之间存在一定误差,但运用数值优化方法求解扩散系数可使偏差最小。
3) 随着温度的升高,扩散系数值增大,当温度从-20℃升高到60℃时,扩散系数值增大了81.97%,在不同温度条件下CO2在RP-3航空燃油中的扩散系数可以用Arrhenius方程表示。通过对扩散系数的数值拟合,可了解更大温度范围内气体扩散系数值,为机载惰化系统的设计提供必要的数据支持。
参考文献
| [1] | JOHNSON R W, ZAKI R, YATES S F. Advanced carbon dioxide fuel tank inerting system: US 7905259B2[P]. 2011-03-15. |
| [2] | LIMAYE S, KOENIG D. Catalytic reactive component reduction system and methods for the use thereof: US 7694916B2[P]. 2010-04-13. |
| [3] | REYNOLDS T L, EKLUND T I, HAACK G A. Onboard inert gas generation system onboard oxygen gas generation system(OBIGGS/OBOGS) study: PartⅡ: Gas separation technology-state of the art: NASA/CR-2001-210950[R]. Washington, D. C. : NASA, 2001. |
| [4] | ASTM Committee. Standard test method for estimation of solubility of gases in petroleum liquids: ASTM D2780-92[S]. West Conshohocken: ASTM International, 2002. |
| [5] | 王斐, 邵晓红, 汪文川. CH4和CO2在活性炭微球内扩散系数的测定[J].化工学报, 2006, 57(8): 1891–1896. WANG F, SHAO X H, WANG W C. Measurements of diffusion coefficients for methane and carbon dioxide in activated meso-carbon microbeads[J].Journal of Chemical Industry and Engineering, 2006, 57(8): 1891–1896.(in Chinese) |
| [6] | ETMINAN S R, MAINI B B, CHEN Z X, et al. Constant-pressure technique for gas diffusivity and solubility measurements in heavy oil and bitumen[J].Energy & Fuels, 2010, 24(1): 533–549. |
| [7] | BEHZADFAR E, HATZIKIRIAKOS S G. Diffusivity of CO2 in bitumen:Pressure-decay measurements coupled with rheometry[J].Energy & Fuels, 2014, 28(2): 1304–1311. |
| [8] | ZHANG Y P, HYNDMAN C L, MAINI B B. Measurement of gas diffusivity in heavy oils[J].Journal of Petroleum Science and Engineering, 1999, 25(1-2): 37–47. |
| [9] | RIAZI M R, WHITSON C H. Estimating diffusion coefficients of dense fluids[J].Industrial & Engineering Chemistry Process Design & Development, 1993, 32(12): 3081–3088. |
| [10] | UNATRAKARN D, ASGHARI K, CONDOR J. Experimental studies of CO2 and CH4 diffusion coefficient in bulk oil and porous media[J].Energy Procedia, 2011, 4: 2170–2177.DOI:10.1016/j.egypro.2011.02.103 |
| [11] | 严小伟, 单奕彬, 王靖岱. 反相气相色谱法测定小分子溶剂在聚乙烯粒子中的无限稀释扩散系数[J].化工学报, 2007, 58(8): 1917–1925. YAN X W, SHAN Y B, WANG J D. Measurement of infinite dilution diffusion coefficients of small molecule solvents in nascent polyethylene particles by inverse gas chromatography[J].Journal of Chemical Industry and Engineering, 2007, 58(8): 1917–1925.(in Chinese) |
| [12] | CIVAN F, RASMUSSEN M L. Analysis and interpretation of gas diffusion in quiescent reservoir, drilling, and completion fluids: Equilibrium vs. non-equilibrium models[C]//SPE Annual Technical Conference and Exhibition. Richardson: SPE, 2003: 1-13. |
| [13] | SHEIKHA H, DARVISH P M, MEHROTRA A K. Development of graphical methods for estimating the diffusivity coefficient of gases in bitumen from pressure-decay data[J].Energy & Fuels, 2005, 19(5): 2041–2049. |
| [14] | JAMIALAHMADI M, EMADI M, STEINHAGEN H M. Diffusion coefficients of methane in liquid hydrocarbons at high pressure and temperature[J].Journal of Petroleum Science and Engineering, 2006, 53(1-2): 47–60.DOI:10.1016/j.petrol.2006.01.011 |
| [15] | FARAJZADEH R, ZITHA P L J, BRUINING J. Enhanced mass transfer of CO2 into water:Experiment and modeling[J].Industrial & Engineering Chemistry Process Design & Development, 2009, 48: 6423–6431. |
| [16] | DING C, FAN Y. Measurement of diffusion coefficients of air in silicone oil and in hydraulic oil[J].Chinese Journal of Chemical Engineering, 2011, 19(2): 205–211.DOI:10.1016/S1004-9541(11)60155-9 |
| [17] | BOCHNER N, PIPMAN J. A simple method of determining diffusion constants by holographic interferometry[J].Journal of Physics D:Applied Physics, 1976, 9: 1825–1830.DOI:10.1088/0022-3727/9/13/003 |
| [18] | 朱春英, 马友光, 赵长伟. 氨基酸在水溶液中的扩散系数[J].化工学报, 2005, 56(2): 243–245. ZHU C Y, MA Y G, ZHAO C W. Diffusion coefficients of amino acids in aqueous solutions[J].Journal of Chemical Industry and Engineering, 2005, 56(2): 243–245.(in Chinese) |
| [19] | COLOMBANI J, BERT J. Holographic interferometry for the study of liquids[J].Journal of Molecular Liquids, 2007, 134(1-3): 8–14.DOI:10.1016/j.molliq.2006.12.013 |
| [20] | GHOLAMI Y, AZIN R, FATEHI R, et al. Suggesting a numerical pressure-decay method for determining CO2 diffusion coefficient in water[J].Journal of Molecular Liquids, 2015, 211: 31–39.DOI:10.1016/j.molliq.2015.06.060 |
| [21] | NGUYEN T A, ALI S M F. Role of diffusion and gravity segregation in oil recovery by the immiscible carbon dioxide wag process[C]//Conference: 6. UNITAR International Conference on Heavy Crude and Tar Sands on Fueling for a Clean and Safe Environment. New York: UNITAR, 1995: 393-403. |
| [22] | THARANIVASAN A K, YANG C D, GU Y G. Comparison of three different interface mass transfer models used in the experimental measurement of solvent diffusivity in heavy oil[J].Journal of Petroleum Science and Engineering, 2004, 44(3-4): 269–282.DOI:10.1016/j.petrol.2004.03.003 |
| [23] | RONGY L, HAUGEN K B, FIROOZABADI A. Mixing from Fickian diffusion and natural convection in binary non-equilibrium fluid phases[J].AIChE Journal, 2012, 58(5): 1336–1345.DOI:10.1002/aic.v58.5 |
| [24] | SCHMIDT T, LESHCHYSHYN T H, PUTTAGUNTA V R. Diffusion of carbon dioxide into Athabasca bitumen[C]//33rd Annual Technical Meeting of the Petroleum Society of CIM. Richardson: SPE, 1982: 82-100. |
| [25] | GHOLAMI Y, AZIN R, FATEHI R, et al. Prediction of carbon dioxide dissolution in bulk water under isothermal pressure decay at different boundary conditions[J].Journal of Molecular Liquids, 2015, 202: 3–33. |
| [26] | HUSAIN A G K. Optimization techniques for chemical engineers[M].Noida: Macmillan of India, 1976: 63-65. |
| [27] | UPRETI S R, MEHROTRA A K. Diffusivity of CO2, CH4, C2H6 and N2 in Athabasca bitumen[J].The Canadian Journal of Chemical Engineering, 2002, 80(1): 116–125.DOI:10.1002/(ISSN)1939-019X |
| [28] | NAPOLEON O, UMESL R P D. Predicting diffusion coefficients in nonpolar solvents[J].Industrial & Engineering Chemistry Process Design & Development, 1981, 20(4): 662–665. |
