国内外对低温推进剂的地面停放过程开展过一系列的研究。在实验方面:Lewis研究中心[1]将4.89 m3的多层绝热液氢贮箱放在真空度为10-4 Pa环境中,研究低热流密度下液氢贮箱内压力变化和温度分布。Barsi等[2]用氟化醚(HFE-7000)作为工质研究自增压过程中贮箱内压力随热流密度变化。Seo和Jeong[3]的自增压实验用液氮为工质测量热流密度、充填率与压力上升值的关系。Das等[4]用水作为工质测量500 W/m2热流密度条件下长方体贮箱内气液温度分布。国内Wang等[5]研究液氮贮箱有排放和无排放的充填过程,并测量液氮温度分布和气枕区压力变化。聂中山等[6]利用液氢杜瓦瓶盛装液氮工质,进行液氮蒸发实验,测量了压力、充填率与蒸发率相互间的关系。王贵仁[7]采用液氮测量在不同初始充填率下杜瓦瓶内压力随时间变化。乔国发[8]采用液化天然气(LNG)为工质对密闭贮罐内压力、日蒸发气体量及蒸发率进行研究。以上实验多注重于贮箱地面停放的自增压过程,缺乏贮箱地面常压停放过程的实验数据及规律研究。数值计算方面主要有集总参数法和分布参数法,最先使用的是集总参数法,如代予东和赵红轩[9]运用数学方法来模拟箱内的增压、传热和传质过程,仅考虑气枕区向液体区传热引起的传质。Estey等[10]将气液两相各分成一个分区,并沿界面建立一个分区作为传热传质区。Panzarella和Kassemi[11]采用有限元软件FIDAP建立一个球型贮箱模型,对气枕区采用集总参数法建立能量和质量模型,并与液体不可压的Navier-Stokes方程和能量方程耦合求解。从上可以看出集总参数法不能够给出温度、速度等参数的具体分布,也影响到气液界面上的能量和热量交换的计算,本文研究的贮箱内流体传热传质过程剧烈,并且有气体的持续排放,不适合采用集总参数法。分布参数法主要是使用计算流体力学(CFD)方法对贮箱内流体物理过程求解,如刘展等[12]针对低温推进剂箱体射前停放阶段,研究了某低温液氧贮箱在地面停放阶段所经历的开口放置及高温氧气预增压过程。Chen和Liang[13]建立了包含液体推进剂和混合气体两相的流体体积法(VOF)计算流体力学模型,并引入了基于热力学平衡假设的推进剂相变模型。
本文的主要目的是研究贮箱地面常压停放过程。通过搭建可视化液氮贮箱实验系统,研究充填率和环境温度对液氮的汽化率、流体温度分布及贮箱外壁面温度的影响规律。从而进一步基于实验现象和实验确定的初边值条件,选择合理的CFD方法对液氮贮箱常压停放过程进行数值仿真,并深入分析整个流场的细节与机理,认识实验过程中无法测量的参数变化规律,为低温推进剂的常压停放过程提供合理的预测模型。
1 实验系统 依据实验的目的和性能要求,实验中建立了可视化液氮贮箱常压停放系统,实验系统由液氮供给系统、实验贮箱、测控系统和图像采集系统组成,如图 1所示。
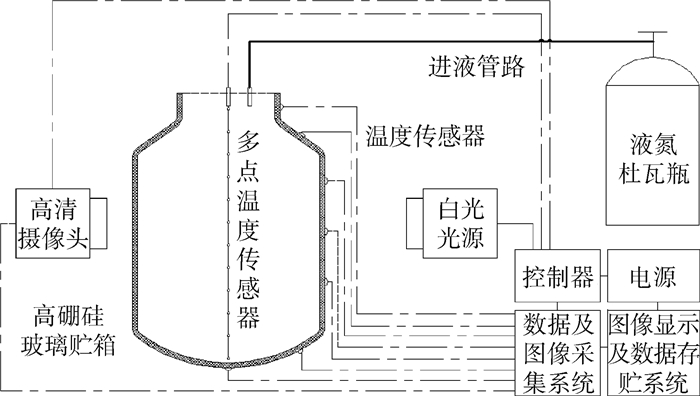 |
| 图 1 液氮贮箱常压停放实验系统原理图 Fig. 1 Schematic diagram of experimental system ofliquid nitrogen tank atmospheric ground parking |
| 图选项 |
实验贮箱的材料是高硼硅玻璃,贮箱体积21.03 L,圆柱段内径290 mm,外径300 mm,出口段内径100 mm,贮箱的总高度435 mm,平均厚度5 mm。贮箱内的液位和体积关系通过4 ℃纯净水标定,如表 1所示。
表 1 贮箱液位与体积变化关系 Table 1 Variation of volume of tank with liquid level
| 液位/cm | 体积/L | 充填率/% | 总体积/L |
| 0 | 1.607 | 7.6 | |
| 5 | 4.907 | 23.3 | |
| 10 | 8.207 | 39.0 | 21.03 |
| 15 | 11.507 | 54.7 | |
| 20 | 14.807 | 70.4 | |
| 25 | 18.107 | 86.1 |
表选项
实验通过100 L杜瓦瓶对贮箱加注液氮,加注过程需要对贮箱进行充分的预冷。多点温度传感器共12个测点,用于测量贮箱内流体的温度。壁面温度传感器共8个测点,用于测量贮箱固体外壁面的温度。实验主要对低温液体在贮箱内常压停放的物理过程进行研究。实验中记录流体的温度、固体外壁面的温度和贮箱内液体的液位,并通过图像采集设备观察贮箱内液体的运动。实验现场如图 2、图 3所示。
 |
| 图 2 液氮贮箱常压停放实验现场图 Fig. 2 Diagram of liquid nitrogen tankatmospheric ground parking on experimental site |
| 图选项 |
 |
| 图 3 液氮贮箱常压停放实验现场测控图 Fig. 3 Measurement and control diagram of liquidnitrogen tank atmospheric ground parking on experimental site |
| 图选项 |
2 实验结果与分析 2.1 液氮汽化速率与环境温度和充填率关系 实验对液氮体积充填率为39.0%、54.7%、70.4%和86.1%(即液位分别为10、15、20和25 cm)的汽化情况进行研究。图 4主要给出体积充填率对液氮汽化的影响,V为液氮体积,t为时间。在环境温度275 K时,贮箱内液氮的液位刻度每下降5 cm,记录间隔时间,环境温度285 K时每隔15 min记录贮箱内液氮的液位刻度。从图 4可以看出汽化相同液氮体积的时间间隔随时间的推移而增加;液氮初始体积充填率越大,液体的汽化速率越大,而随着时间的增加,不同充填率下液体汽化速率差值逐渐减小。这是因为充填率越大,液氮与壁面接触的面积越大,接受的热量越多,导致汽化速率越大,而相同液位刻度下初始段的汽化速率不同主要是液体充填过程中液氮初始温度高于饱和温度,充填率越大导致过热的液体越多,初始段液氮体积下降的越快。图 5给出环境温度对液氮汽化的影响。在环境温度为275 K、285 K和291 K的3种情况下,对液氮体积充填率为86.1%进行实验,实验中贮箱内液氮的液位刻度每下降5 cm记录时间数据。从图 5可以看出,汽化相同体积的液氮,环境温度291 K所需时间最少,环境温度275 K所需时间最多。这是因为充填率相同时,环境温度越高,贮箱内液氮通过贮箱壁面与外界交换的热量越多,而常压停放贮箱内的液氮饱和温度基本保持不变,液体与外界交换热量的越多,汽化的体积就越大。
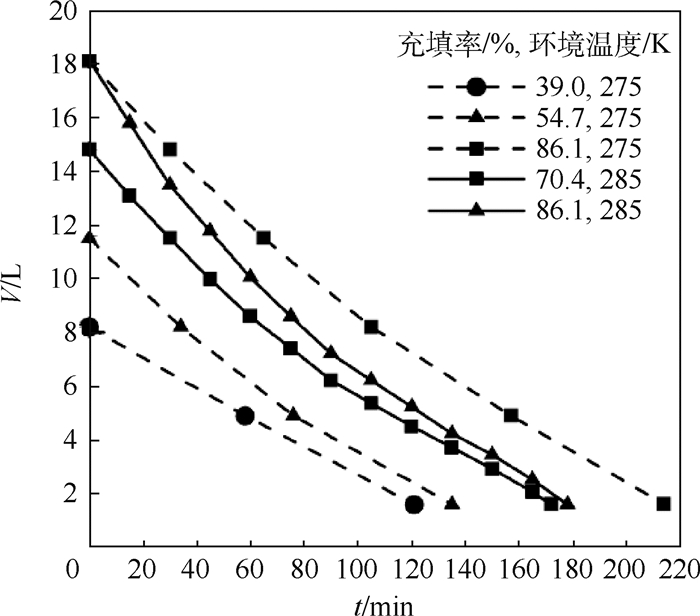 |
| 图 4 不同充填率和温度时,液氮体积随时间的变化 Fig. 4 Variation of liquid nitrogen volume with time underdifferent filling rates and temperatures |
| 图选项 |
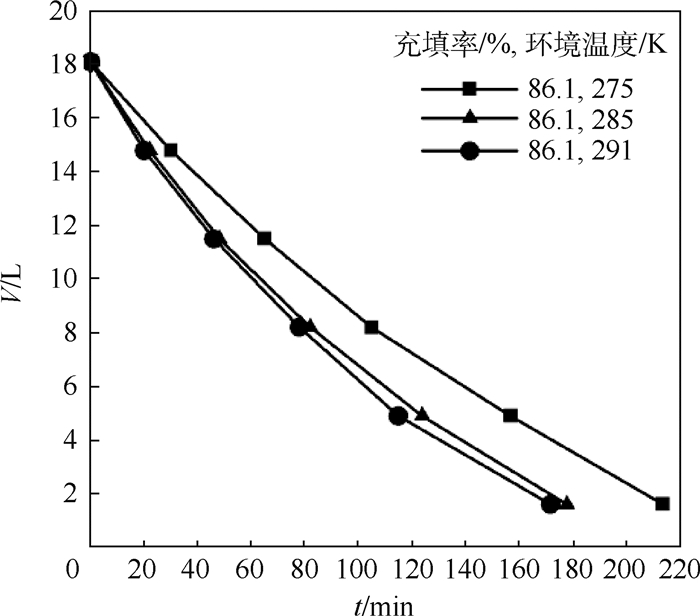 |
| 图 5 不同环境温度时,液氮体积随时间的变化 Fig. 5 Variation of liquid nitrogen volume with timeunder different ambient temperatures |
| 图选项 |
2.2 贮箱内流体温度与时间关系 流体温度测量采用12个封装在不锈钢圆管内温度传感器,其中每个测点间隔距离37 mm。图中每隔30 min取测量的温度数据绘制温度与时间、位置曲线图,具体如图 6所示,Y为轴向高度,Y=0为贮箱底部最低点,T为温度,下标f表示流体,a表示环境,虚线表示不同时刻气液界面位置。从图中可以看出气枕区的温度在轴向存在明显的温度分层,温度随时间增加而增大。液体区在远离气液界面处轴向方向上温度变化不大,且随时间的增加没有明显变化。气液界面附近液体区温度出现的偏差在于沿不锈钢圆管气枕区导热所致。液氮常压停放液体在贮箱内壁面和气液界面处汽化,汽化产生的气泡在浮力的作用下向气液界面处运动,贮箱内部液体存在剧烈运动和混合,导致液体温度趋于一致。而气枕区温度变化大是因为气体的比热和密度小,受热温度上升快。而轴向的温度分层是因为液体的温度低,生成的气体温度低,气液界面处气体向液体传热。
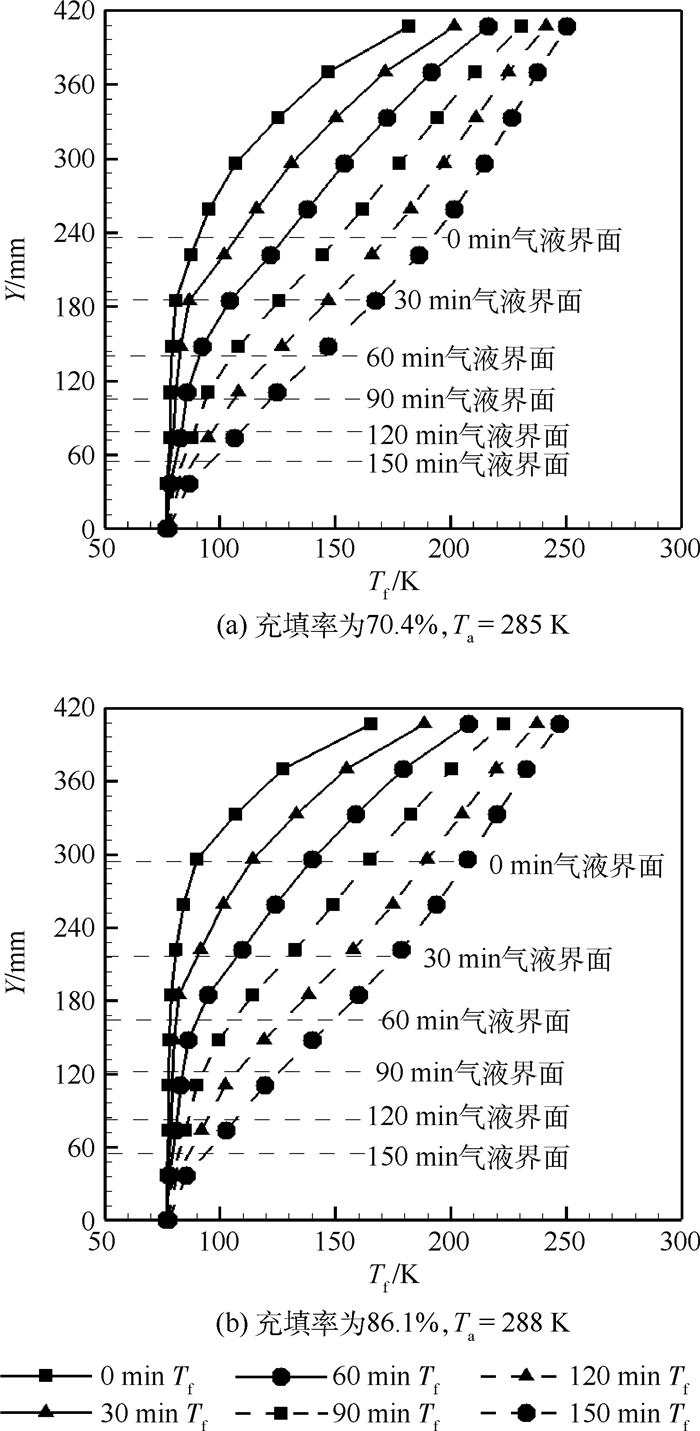 |
| 图 6 充填率为70.4%和86.1%时,流体温度与位置的关系 Fig. 6 Relationship between fluid temperature andlocation under 70.4% and 86.1% filling rate |
| 图选项 |
2.3 贮箱外壁面温度与时间的关系 实验为得到贮箱常压停放实验准确的边界条件,采用贴壁温度传感器测量贮箱外壁面的温度,每隔30 min取测量的温度数据绘制温度与时间、位置曲线图,具体如图 7所示,下标w表示固体壁面。从时间上可以看出,贮箱外壁面的温度随时间增加而增大,气枕区外壁面温度在随时间的增速显著大于液体区外壁面温度增速。从位置上可以看出,气枕区的外壁面温度在轴向方向上从出口到液面温度呈下降趋势,而液体外壁面温度在轴向方向上并没有明显的分布趋势,且液体区温度测点的变化值小于气枕区温度测点的变化值。这是因为气枕区内气体的密度小,在比热容差距不大的情况下,气体的温度上升速率快,使得外界传递的热量大部分用于固体区域的升温,导致气枕区贮箱外壁面温度高。而液体温度低,密度和比热容都比气体大,液体与贮箱壁面间的对流换热作用强,使得与贮箱接触的固体区域温度低。高充填率气液界面附近温度偏低的是因为气液界面附近液体对流运动剧烈,并且有液体的汽化,使得液体与固体区热量交换值大,外界用于固体区温度上升的热量变小。贮箱底部测点温度偏低是因为实验时贮箱底部放置在实验台上,壁面与外界的对流换热作用受到限制。
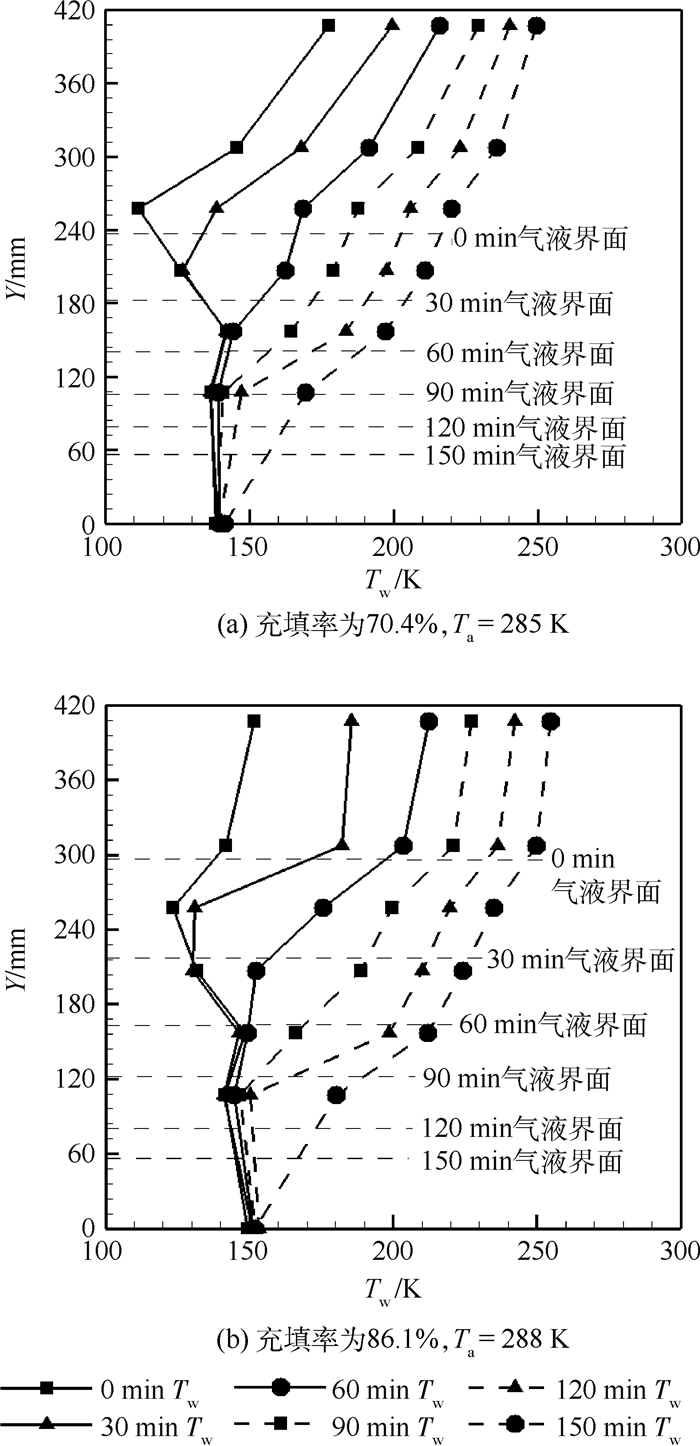 |
| 图 7 充填率为70.4%和86.1%时,壁面温度与位置关系 Fig. 7 Relationship between wall temperature andlocation under 70.4% and 86.1% filling rate |
| 图选项 |
3 数值计算与分析 3.1 流体控制方程 在贮箱内液氮的常压停放实验过程中,观测到液体(特别是液面)剧烈沸腾和翻滚,液体中有大量的气泡从贮箱内壁面产生,并在浮力的作用下向气液界面处运动,运动过程中气泡逐渐变大,并在液面处破裂。目前低温液体常压停放的数值模拟多采用文献[14-15]所用的VOF模型建模,而事实上常压停放中贮箱内部这种复杂的气液两相传热传质流动过程并不适合采用VOF模型建模(因为实验观察到只有在贮箱的自增压过程中,气液界面才是准静止的水平面),而更适合采用混合物模型。VOF模型中缺乏对气液两相间相互作用的计算,并且为获得较为准确气液界面位置付出了过高的计算代价,对计算的收敛性也有不利影响。混合物模型虽然缺乏对准确的气液界面的跟踪和处理,但对于地面常压停放阶段来说气液界面本身就是剧烈变化的,其受到液体的翻滚运动和气泡上升运动的影响。混合物模型不仅可以解决气液混合流动的问题,且能够得到贮箱中气枕和液体推进剂的气液两相分布,能够满足研究需要而且可以减少计算量,因此本文两相流模拟采用混合物模型。而混合物模型中的连续性方程、动量方程和能量方程见文献[16]。连续性方程和能量方程考虑液氮和氮气间传热传质过程中引起的质量源项Sq和能量源项Sh变化,Sq为第q相质量源项,动量方程中考虑气液两相间的滑移速度、拽力及表面张力的影响。
3.2 相变模型 数值仿真的相变模型主要有相变系数模型、假定界面温度模型、能量平衡模型和温度恢复模型。后3种模型计算时不稳定、并且需要初始化气液界面[17]。因此,文中采用相变系数模型。Knudsen和Partington[18]根据气体动力学理论推导的气液界面质量交换为
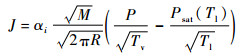 | (1) |
式中:P和Psat分别为压力和饱和压力。
运用克劳修斯-克拉珀龙方程,并转化为体积源项如下:
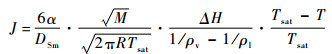 | (2) |
对式(2)进行简化得到相变系数模型
 | (3) |
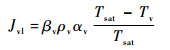 | (4) |
式中:Tl和Tv分别为液体与气体温度, K;DSm为气泡的索太尔平均直径,m;M为气体摩尔质量,kg/mol;R为摩尔气体常数,J/(mol·K);β为控制相变强弱的时间松弛系数,s-1;ai为蒸发/冷凝系数;α、al和av分别为体积分数、液体体积分数和气体体积分数;Jlv为液体汽化质量,kg/(m3·s);Jvl气体冷凝质量,kg/(m3·s);ΔH为气液的相变潜热,J/kg;ρv、ρl分别为气体和液体的密度,kg/m3;Tsat为饱和温度,K。
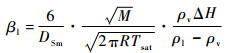 | (5) |
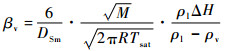 | (6) |
传质过程引起的能量交换为式(7)、式(8),Qlv为汽化热交换量,J/(m3·s);Qvl为冷凝热交换量,J/(m3·s)。
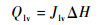 | (7) |
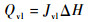 | (8) |
相变系数模型中关键是确定时间松弛系数,而过大的时间松弛系数使计算难以收敛,过小的时间松弛系数会使气液界面温度与饱和温度存在较大偏差[19-20]。Lee[21]采用时间松弛系数0.1取得很好计算结果。本文通过实验对比与试算,时间松弛系数取0.1 s-1。仿真过程中连续性方程中Sq通过式(3)、式(4)控制,能量方程中Sh通过式(7)、式(8)控制。
3.3 固体壁导热控制方程 贮箱固体壁面与内外流体间存在热交换作用。固体壁面的导热方程如下:
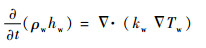 | (9) |
式中:ρw、hw、kw和Tw分别为高硼硅玻璃贮箱壁面的密度、显焓、导热系数和温度,ρw=2 230 kg/m3,kw值随温度的变化较大,其值对固体壁热量传递有十分重要的影响。温度为150 K和80 K时导热系数值分别为0.76和0.48,导热系数具体值通过文献[22]插值计算得出。
3.4 数值方法与初边值条件 贮箱的仿真模型通过Fluent建立,采用二维轴对称结构,分别对气枕区、液氮区和固体区划分结构化网格。网格在靠近贮箱内壁面、气液界面和压力出口处的区域进行适当加密,通过网格验证试算,最终采用了网格数为25 550的二维轴对称网格,其中气枕区网格数10 109,液体区网格数12 006,固体区网格数3 435,最小网格边长0.1 mm,具体如图 8所示,X和Y分别为径向方向和轴向方向。
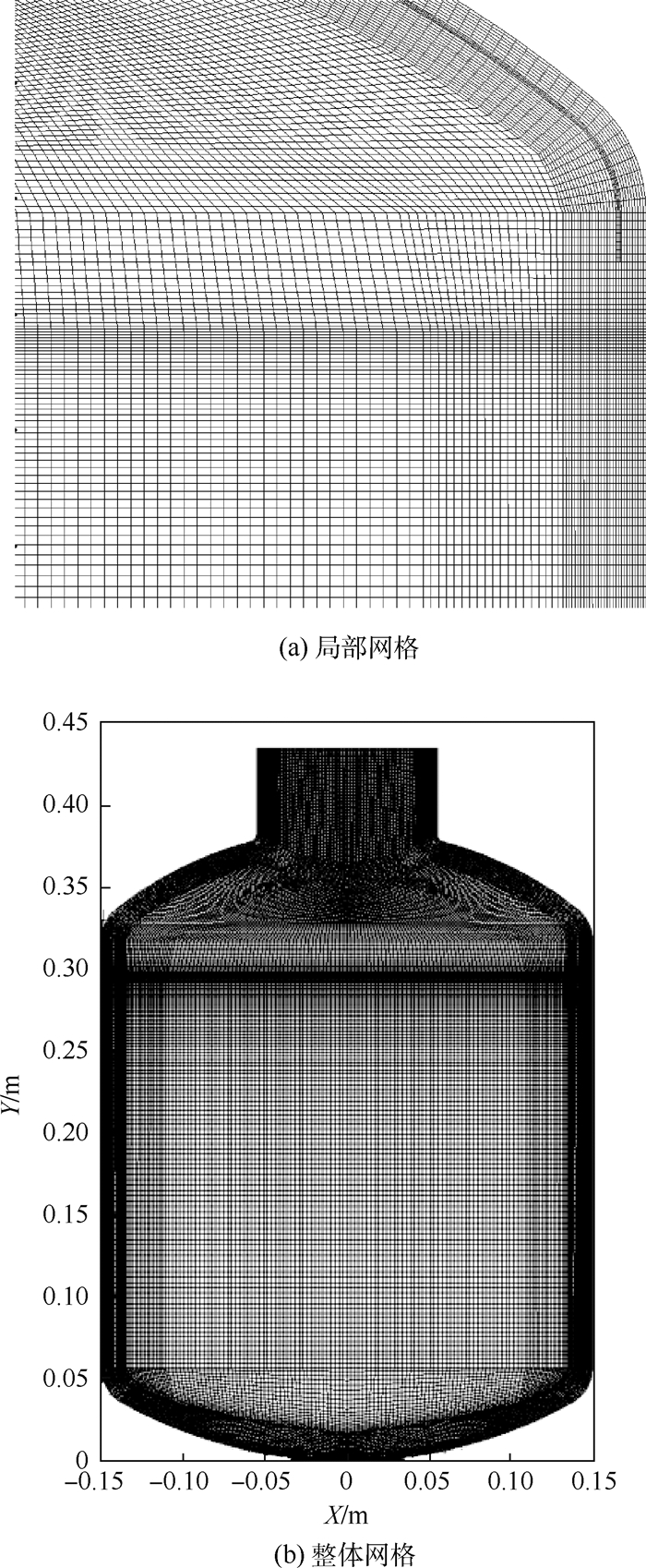 |
| 图 8 常压停放贮箱网格图 Fig. 8 Grids of tank during atmospheric ground parking |
| 图选项 |
考虑到贮箱液面高度不大,忽略重力对饱和温度的影响,而且实验发现液氮处于剧烈沸腾状态,因此近似认为贮箱常压停放过程的初始状态为气液两相饱和的准静止状态,贮箱内部流体(气体和液体两部分)的温度均为对应气体压力(101 325 Pa)下的饱和温度(77.35 K);贮箱外的环境温度为288 K,液氮的体积充填率86.1%。仿真出口条件采用恒定压力出口,其值为101 325Pa。壁面采用温度边界条件,通过UDF(User-Define Function)将实验测量的贮箱固体外壁面温度以一阶插值方式分段加入,具体值如图 9所示。仿真中通过采用4核i7计算300 h对液氮常压停放进行1 800 s数值仿真。实验中观测到贮箱内有大量气泡的上升运动,所以仿真中考虑了浮力和拽力,计算时氮气和液氮间的拽力函数选择Schiller-Naumann模型,滑移速度选择Maninnen-et-al模型,浮升力通过采用Boussinesq模型[23]。湍流模型采用适合低雷诺数RNG k-ε,壁面采用增强壁面函数(enhanced wall)。相变模型通过UDF以质量源项和能量源项加载到连续性方程和能量方程。贮箱常压停放是一个瞬态过程,仿真中选择基于压力的求解器,压力插值方式选择body-force-weight,速度压力耦合方式选择PISO,体积分数插值方式选择Quick格式,其余的选择二阶迎风格式。氮气采用理想气体模型,液氮和氮气的物性参数考虑随温度的变化,通过查找文献[24]采用一阶插值计算获得,并将获得的参数通过UDF加载到Fluent模型中。计算中连续性、动量、能量方程中残差分别为10-3、10-4、10-7。对模型多次计算时发现,时间步长在0.01~0.02 s时,计算中能够保持严格的收敛性,且计算结果基本一致,实际计算时间步长取0.02 s。
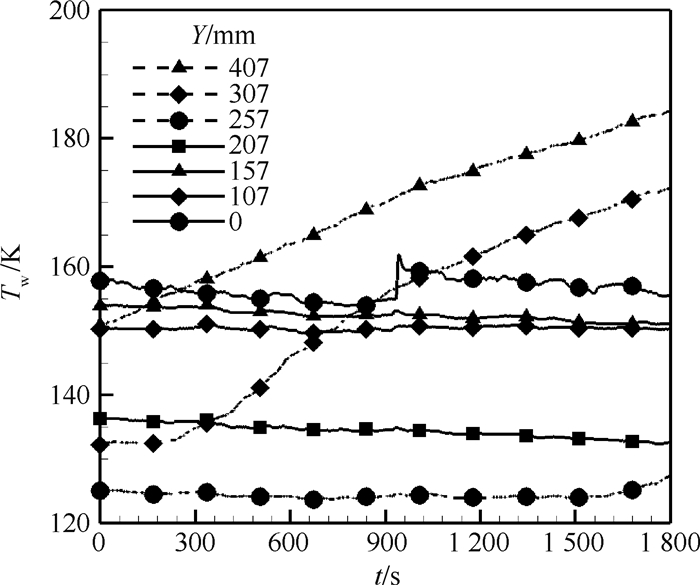 |
| 图 9 贮箱外壁面温度随时间变化 Fig. 9 Variation of tank's outer wall temperature with time |
| 图选项 |
3.5 仿真与实验结果比较 图 10给出实验和仿真得出的液氮体积随时间变化的比较。可以看出,5 min时仿真的液氮体积比实验中液氮体积多,这是实验过程中加注的液氮温度高于饱和温度,导致初始测量阶段液氮的体积变化快,5 min后在同一时刻仿真过程的液氮体积比实验过程中的液氮体积小。实验过程液氮体积的平均汽化速率为0.002 67 L/s,仿真过程液氮体积的平均汽化速率为0.002 78 L/s。图 11给出实验和仿真得出液氮温度随时间变化的比较。实验中由于温度传感器存在着轴向的热传导,为了尽量减少液体温度测量的偏差,选用液体底部温度测量值与仿真进行比较。可以看出实验中液氮温度的测量值在77.4~77.6 K之间,而仿真过程监测点液氮的温度随时间在77.35 K左右变化。从图 12看出贮箱内液氮温度基本一致,气液界面附近的液体处于饱和温度,其余液体主体区的温度略低于饱和温度,液体区等温线表明了液体处于剧烈的运动中。气枕区温度存在温度分层,距出口越近,温度越高,且气液界面附近气枕区温度梯度较小。通过比较仿真过程得出在液体区的温度与实验中测量的液体温度基本保持一致,液体区的温度基本处于饱和温度,并且液体区存在气泡运动引起的剧烈翻滚运动,可以认为贮箱内部的液体处于沸腾状态。气枕区的温度值仿真与实验存在差异,因为实际过程中气枕区的温度测点受到外界导热影响,但是仿真过程气枕区温度的分布趋势与实验基本一致。因此,可以认为仿真对低温液体常压停放过程有准确的预测性。
 |
| 图 10 实验和仿真得出的液氮体积的比较 Fig. 10 Comparison of liquid nitrogen volumebetween experiment and simulation |
| 图选项 |
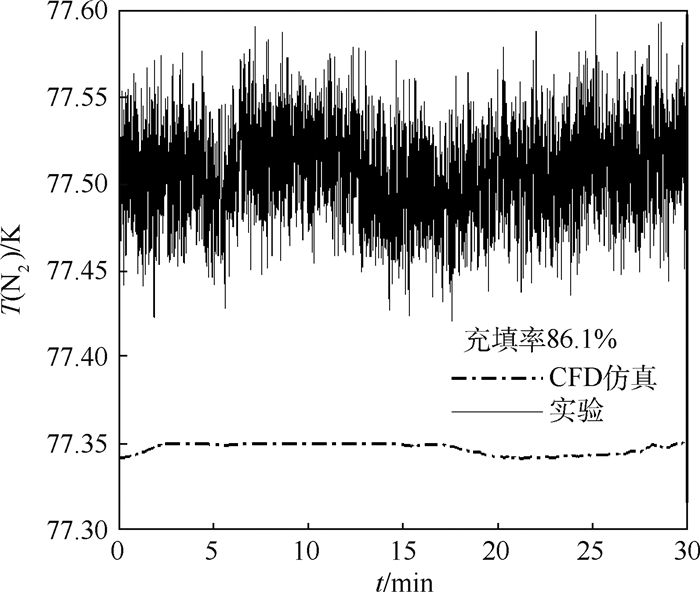 |
| 图 11 实验和仿真得出的液氮温度的比较 Fig. 11 Comparison of liquid nitrogen temperaturebetween experiment and simulation |
| 图选项 |
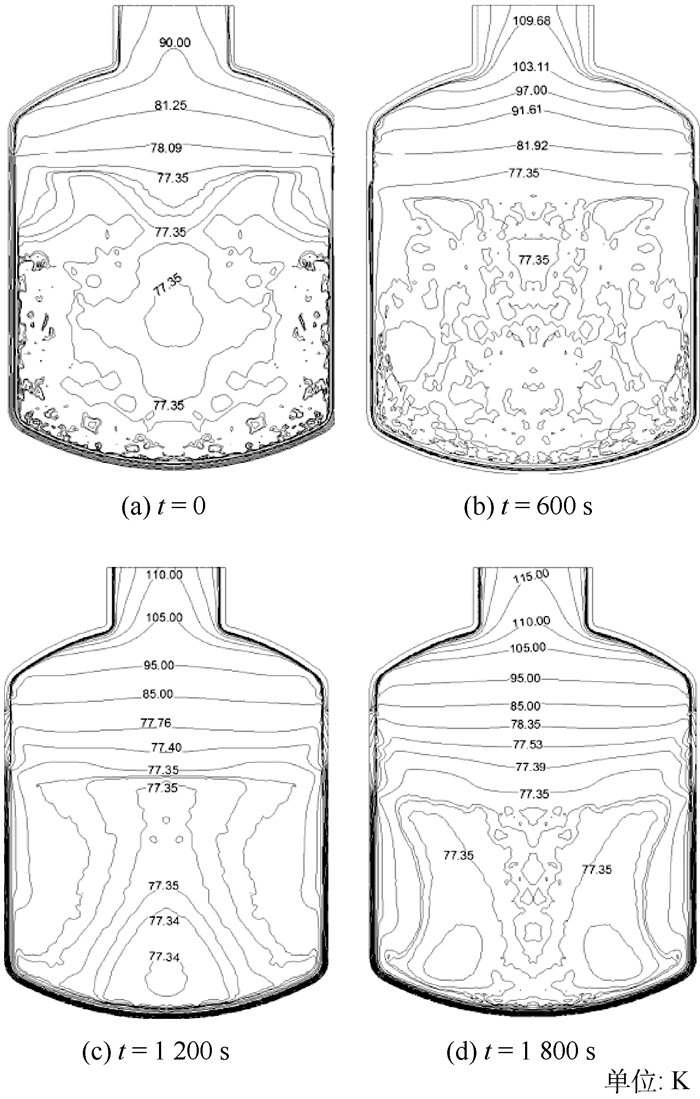 |
| 图 12 仿真得到的贮箱内流体温度分布 Fig. 12 Fluid temperature distribution simulated in tank |
| 图选项 |
由于实验没有直接测量贮箱内流体的运动及贮箱内壁面与流体间的热量交换值,本文给出仿真具体数值结果。图 13给出仿真过程贮箱内流体的速度分布。可以看出贮箱内液体由于底部受热向气液界面处运动,靠近气液界面处液体沿壁面向下运动。气枕区与液体在气液界面处存在着强烈的对流换热,壁面附近气体沿壁面向上运动。而随着时间的推移,贮箱内流体的运动趋于稳定。
 |
| 图 13 仿真得到的贮箱内流体速度分布 Fig. 13 Fluid velocity distribution simulated in tank |
| 图选项 |
图 14给出流体与固体壁面的换热量Q。可以看出:1 min前贮箱内所有的内壁面换热量呈上升趋势,1 min后贮箱底部液体内壁面和气枕区接触内壁面换热量基本保持不变,气枕内壁面换热量值在60 W左右,底部液体壁面的换热量在500 W左右,而贮箱柱状段的换热量和总的换热量随时间增加而减少,柱状段液体换热量随时间从1 164 W降至940 W,总的换热量从1 736 W降至1 520 W。贮箱柱状段内壁面换热量减少是因为液体的沸腾使气体与固体壁面接触面积变大,而气体与固体壁面的换热能力远小于液体与壁面的换热能力。结合本节液体温度和体积变化关系的分析,可以得出常压停放液体的汽化主要取决于固体壁面对液体的加热。
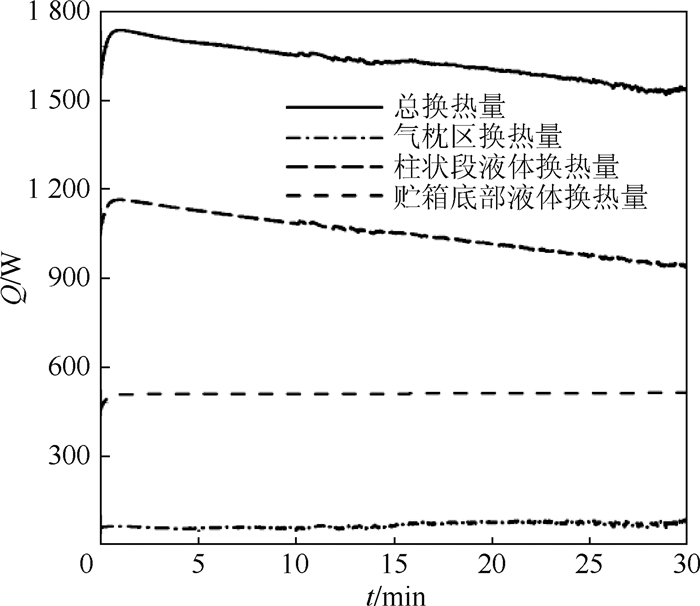 |
| 图 14 仿真得到的流体与固体壁面的换热量与时间的关系 Fig. 14 Relationship of heat transition between liquid andsolid wall simulated in tank and time |
| 图选项 |
4 结论 1) 常压停放过程,环境温度越高和贮箱的体积充填率越大,液体的汽化速率越大。
2) 常压停放过程,液体区温度基本一致,液体区处于饱和状态;气枕区温度存在沿轴向的分层,气体离贮箱压力出口越近,温度越高。
3) 常压停放过程达到稳定后,液体区与贮箱固体壁面换热量远大于气枕区与贮箱固体壁面换热量,液体区的换热量对液体汽化起决定作用。
4) 运用混合物模型,并根据相变系数模型能够准确的对低温液体常压停放过程进行预测,并能为低温液体自增压过程的仿真提供准确的初始状态。
参考文献
| [1] | STOCHL R J, KNOLL R H. Thermal performance of a liquid hydrogen tank multilayer insulation system at warm boundary temperatures of 630, 530, and 152 R[C]//AIAA, SAE, ASME, and ASEE, 27th Joint Propulsion Conference. Reston: AIAA, 1991: 1-20. |
| [2] | BARSI S, KASSEMI M, PANZARELLA C H, et al. A tank self-pressurization experiment using a model fluid in normal gravity[C]//AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2005: 1-13. |
| [3] | SEO M, JEONG S. Analysis of self-pressurization phenomenon of cryogenic fluid storage tank with thermal diffusion model[J].Cryogenics, 2010, 50(9): 549–555.DOI:10.1016/j.cryogenics.2010.02.021 |
| [4] | DAS S P, CHAKRABORTY S, DUTTA P. Studies on thermal stratification phenomenon in LH2 storage vessel[J].Heat Transfer Engineering, 2004, 25(4): 54–66.DOI:10.1080/01457630490443767 |
| [5] | WANG C L, LI Y, WANG R S. Performance comparison between no-vent and vented fills in vertical thermal-insulated cryogenic cylinders[J].Experimental Thermal and Fluid Science, 2011, 35(2): 311–318.DOI:10.1016/j.expthermflusci.2010.09.013 |
| [6] | 聂中山, 李青, 洪国同, 等. 车载液氢杜瓦蒸发率理论与试验研究[J].低温工程, 2004(4): 55–58. NIE Z S, LI Q, HONG G T, et al. Theoretical and experimental investigation of evaporation rate in vehicle liquid hydrogen dewar[J].Cryogenics, 2004(4): 55–58.(in Chinese) |
| [7] | 王贵仁. 低温容器内压力变化规律的研究[D]. 兰州: 兰州理工大学, 2008: 28-40. WANG G R. The research on variation law of pressure in cryogenic vessel[D]. Lanzhou: Lanzhou University of Technology, 2008: 28-40(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10731-2008113656.htm |
| [8] | 乔国发. 影响LNG储存容器蒸发率因素的研究[D]. 东营: 中国石油大学, 2007: 73-87. QIAO G F. The study on the influential factors of evaporation rate of the liquefied natural gas tank[D]. Dongying: China University of Petroleum, 2007: 73-87(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10425-2008199207.htm |
| [9] | 代予东, 赵红轩. 运用数学方法模拟推进剂贮箱增压[J].火箭推进, 2003, 29(3): 34–40. DAI Y D, ZHAO H X. Numerical modeling of pressurization of a propellant tank[J].Journal of Rocket Propulsion, 2003, 29(3): 34–40.(in Chinese) |
| [10] | ESTEY P N, LEWIS D H, CONNOR M. Prediction of a propellant tank pressure history using state space methods[J].Journal of Spacecraft and Rockets, 1983, 20(1): 49–54.DOI:10.2514/3.28355 |
| [11] | PANZARELLA C H, KASSEMI M. On the validity of purely thermodynamic descriptions of two-phase cryogenic fluid storage[J].Journal of Fluid Mechanics, 2003, 484: 41–68.DOI:10.1017/S0022112003004002 |
| [12] | 刘展, 孙培杰, 李鹏, 等. 地面停放低温液氧贮箱热物理过程研究[J].西安交通大学学报, 2016, 50(9): 36–42. LIU Z, SUN P J, LI P, et al. Research on the thermal physical process of cryogenic liquid oxygen tank in ground parking[J].Journal of Xi'an Jiaotong University, 2016, 50(9): 36–42.DOI:10.7652/xjtuxb201609006(in Chinese) |
| [13] | CHEN L, LIANG G Z. Simulation research of vaporization and pressure variation in a cryogenic propellant tank at the launch site[J].Microgravity Science and Technology, 2013, 25(4): 203–211.DOI:10.1007/s12217-013-9340-2 |
| [14] | FADHL B, WROBEL L C, JOUHARA H. CFD modelling of a two-phase closed thermosyphon charged with R134a and R404a[J].Applied Thermal Engineering, 2015, 78: 482–490.DOI:10.1016/j.applthermaleng.2014.12.062 |
| [15] | 陈亮, 梁国柱, 邓新宇, 等. 贮箱内低温推进剂汽化过程的CFD数值仿真[J].北京航空航天大学学报, 2013, 39(2): 264–268. CHEN L, LIANG G Z, DENG X Y, et al. CFD numerical simulation of cryogenic propellant vaporization in tank[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 264–268.(in Chinese) |
| [16] | Fluent A. ANSYS I: Fluent theory guide[EB/OL]. Canonbury: ANSYS Inc., 2010. https: //support. ansys. com/. |
| [17] | 刘泉. 纯蒸气及含不凝气蒸气冷凝的数值研究[D]. 合肥: 中国科学技术大学, 2015: 73-87. LIU Q. Numerical investigation on condensation with and without non-condensable gas[D]. Hefei: University of Science and Technology of China, 2015: 73-87(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10358-1015615597.htm |
| [18] | KNUDSEN M, PARTINGTON J R. The kinetic theory of gases:Some modern aspects[J].The Journal of Physical Chemistry, 1935, 39(2): 307. |
| [19] | DE SCHEPPER S C K, HEYNDERICKX G J, MARIN G B. Modeling the evaporation of a hydrocarbon feedstock in the convection section of a steam cracker[J].Computers and Chemical Engineering, 2009, 33(1): 122–132.DOI:10.1016/j.compchemeng.2008.07.013 |
| [20] | LIU Z, SUNDEN B, YUAN J. VOF modeling and analysis of filmwise condensation between vertical parallel plates[J].Heat Transfer Research, 2012, 43(1): 47–68.DOI:10.1615/HeatTransRes.v43.i1 |
| [21] | LEE W H. A pressure iteration scheme for two-phase flow modeling: LA-UR-79-975[R]. New Mexico: Los Alamos National Laboratory, 1979. |
| [22] | 陈国邦. 低温工程材料[M].杭州: 浙江大学出版社, 1998: 195-201. CHEN G B. Cryogenic engineering materials[M].Hangzhou: Zhejiang University Press, 1998: 195-201.(in Chinese) |
| [23] | ISHⅡ M, HIBIKI T. Thermo-fluid dynamics of two-phase flow[M].Berlin: Springer, 2011: 361-395. |
| [24] | 陈国邦, 黄永华, 包锐. 低温流体热物理性质[M].北京: 国防工业出版社, 2006: 190-200. CHEN G B, HUANG Y H, BAO R. Cryogenic fluid thermos physical properties[M].Beijing: National Defense Industry Press, 2006: 190-200.(in Chinese) |
