从上述研究可以发现,使用单一模型进行故障诊断时结果抗干扰性较差;但使用多种模型结合进行故障诊断又存在建模复杂,输出结果不直观等问题,当研究对象的故障特征发生变换时,就会严重影响故障诊断准确度。基于上述问题,本文在结合深度学习模型和决策融合算法的基础上,提出了基于深度学习的航空发动机故障融合诊断方法,把航空发动机的性能参数和故障类型样本输入到深度信念网络(DBN)模型中,提取出样本特征,从而输出故障分类数据,然后把输出数据代入到决策融合算法模型中进行决策融合,得出航空发动机故障融合诊断结果。该方法能够在结合2种模型优势的基础上,构建故障融合诊断模型, 该模型结构简单,不仅有效提高故障诊断准确度,而且能够得出更加直观的故障诊断结果,同时有一定抗干扰性。通过数据仿真实验,验证该方法具有有效性。
1 航空发动机故障诊断 航空发动机故障诊断能够在检测出系统故障时,分离故障部件、判断故障种类、评估故障严重程度,从而在第一时间展开维修工作,减少经济损失。在发动机试验故障诊断中,可利用的状态信息有:发动机振动、气动热力等过程参数、滑油参数以及试验操纵控制信息等。由于航空发动机结构复杂性,单纯依靠单一信息进行故障诊断的准确度不高,多元状态监测信息从不同角度实现了对故障的深层次认识,能够提高故障诊断的准确度。本文,首先采用基于深度学习的故障融合诊断方法对发动机主要参数[13]如:低压转子转速(N1)、高压转子转速(N2)、排气口燃气温度(EGT)、燃油量消耗量(FF)建立模型,然后进行故障融合诊断。
2 深度学习与决策融合算法 2.1 深度学习模型 深度学习是相对于浅层学习而言的,浅层学习包可以BP神经网络、支持向量机和最大熵方法等。这些模型结构只含有一层隐层或者没有隐层,理论分析难度大,同时训练方法依赖于经验和技巧,得出的样本特征也较为浅显。相对于浅层学习,深度学习模型是多隐层的人工神经网络,通过无监督学习实现网络模型的逐层学习,具有良好的特征提取和学习能力,在样本分类方面有独特的优势。深度学习模型的主要包括深度信念网络、卷积神经网络和循环神经网络等。深度信念网络模型较为灵活,与其他方法的兼容性较好,因此本文采用深度信念网络模型用于故障分类,并将分类结果输入决策融合模型得出故障融合诊断结果。
DBN模型由多个限制玻尔兹曼机(RBM)[14]层组成,一个典型的RBM结构如图 1所示。该结构包括3个部分:显层、隐层、偏置层。其中显层作为输入层,隐层作为输出层,偏置层用来控制隐层和显层节点的激活,层内单元间相互独立。
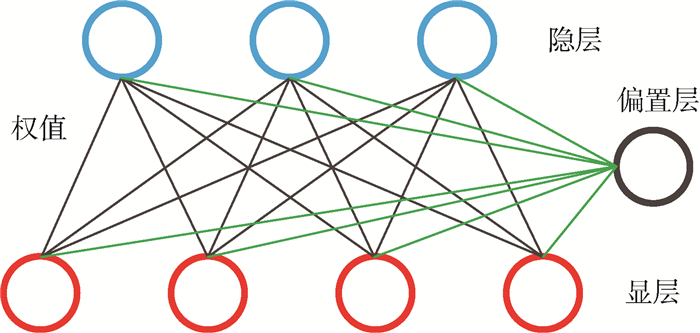 |
| 图 1 RBM结构 Fig. 1 Structure of RBM |
| 图选项 |
设显层向量为v,隐层向量为h,权值向量为w;对显层偏置为a,隐层偏置为b。对隐层和显层各单元参数定义如下:
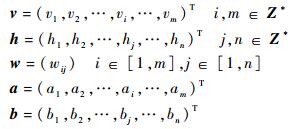 |
2.1.1 建立深度信念网络模型 DBN模型需要引入能量函数,首先用能量函数推导出显层和隐层的条件概率;然后求解偏置层,得出显层和隐层被激活的概率;最后求解能量函数,对模型参数进行更新。
1) 引入能量函数
网络的稳态对应能量函数最低值状态,针对RBM模型而言,输入v向量和隐层输出向量h之间的能量函数为
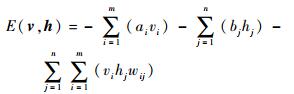 | (1) |
2) 求隐层和显层的条件概率分布
v和h的联合概率为
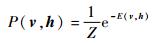 | (2) |
式中:归一化因子
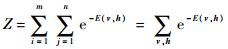
 | (3) |
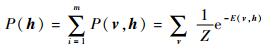 | (4) |
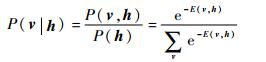 | (5) |
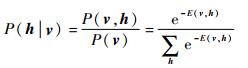 | (6) |
3) 偏置层求解
通过隐层和显层的条件概率分布和能量函数能够得到隐层和显层节点被激活(取值为1)的概率,从而得到偏置层的求解结果:
 | (7) |
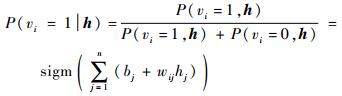 | (8) |
式中:
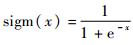
4) 能量函数求解
引入自由能量函数
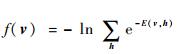
 | (9) |
从式(1)可以看出,如果要使系统(这里即指DBN网络)达到稳定,则应该是系统的能量值最小,由式(9)可知,要使能量E(v, h)最小,应该使f(v)最小,也就是要使P(v)最大。因此, 此时的损失函数可以看做是-P(v),且求导时需要是加上负号的。设θ={a, b, w},对P(v; θ)求偏导取负可得
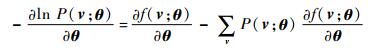 | (10) |
将式(1)中的E(v, h)代入可得
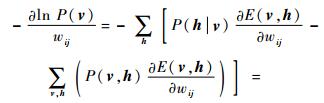 |
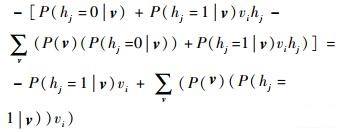 | (11) |
同理可得P(v; θ)的偏导展开有
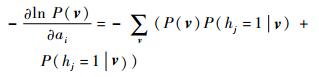 | (12) |
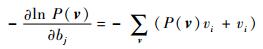 | (13) |
从偏导结果可以看出左边的减数是输入样本数据的自由能量函数期望值,v状态已知。右边的被减数是模型产生样本数据的自由能量函数期望值,v状态未知。
2.1.2 训练深度信念网络模型 1) 深度信念网络训练流程
DBN由多层RBM组成,是一种无监督学习模型,有一定的“黑箱性”。在实际应用过程中为了方便理解,更加直观得出分类结果,需要利用已知特征的样本对模型反向修正,相当于上述的RBM结构从隐层推导出显层,使故障样本的性能参数与故障类型想匹配,提高故障分类置信度。本文采用如今比较成熟的有监督算法BP神经网络来对DBN网络反向调节参数。由图 2可以看出DBN网络的训练过程,先输入样本的状态参数到多层RBM中,逐层更新参数;其后把RBM训练结果和样本特征输入到BP神经网络中反向调节完成对模型的参数优化。
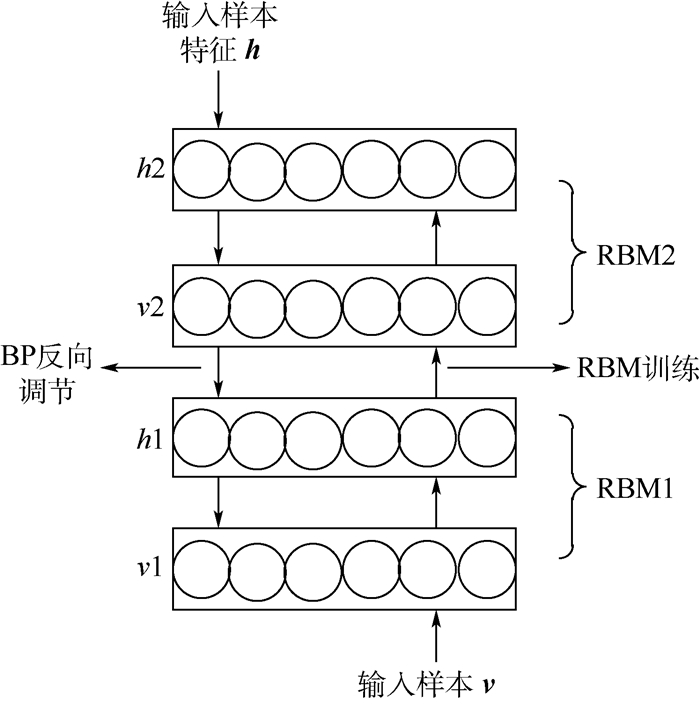 |
| 图 2 DBN训练流程图 Fig. 2 Flowchart of DBN training |
| 图选项 |
2) RBM训练过程
RBM的训练就是为了通过反复迭代得出DBN的隐藏特征。根据式(11)~式(13)可以得出参数θ的更新流程如图 3所示,k为训练次数[15]。
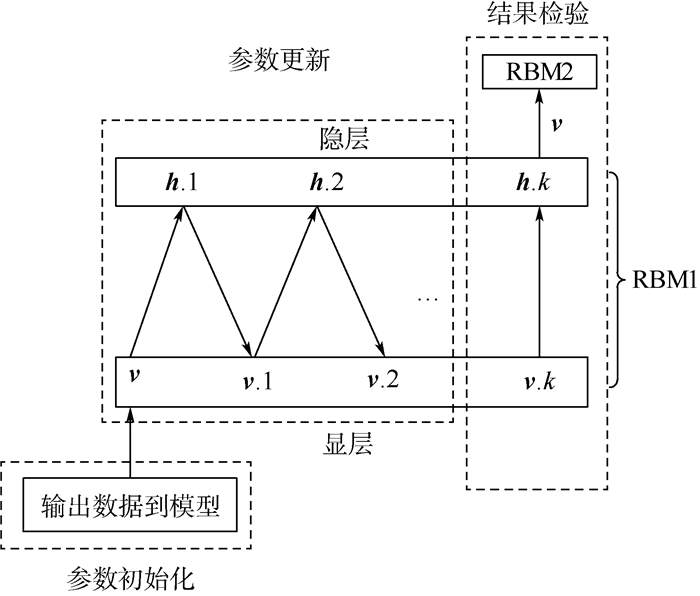 |
| 图 3 RBM训练过程 Fig. 3 RBM training process |
| 图选项 |
步骤1 ?参数初始化。初始化参数w、a、b、学习率ε,允许重构误差r、最大训练次数p,k初值赋为1。把原始的数据v输入到网络。
步骤2 ?参数更新。更新w、a、b,计算输出从显层v推导到隐层h的第1次训练结果h.1,然后又反推v.1,继续计算h.2,h.3,…,h.k。
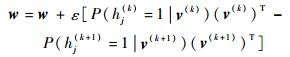 | (14) |
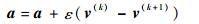 | (15) |
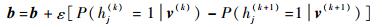 | (16) |
式中:hj(k)为第k次训练的第j个隐层节点;v(k)为第k次训练的显层。
步骤3 ?结果检验。判定循环次数和误差是否符合要求,当最后反推出的v.k和v比较其重构误差r=||v.k-v||2,当重构误差足够小时,将这个时候的h.k代入下一层RBM继续训练。如果不符合则将k赋值为k+1然后重复进行步骤2。
2.2 决策融合算法 决策融合算法以D-S证据理论[16]为基础,假设共有m个故障,其集合为{A1, A2, …, Am}, n次诊断结果{B1, B2, …, Bn}对应的函数为{F1, F2, …, Fn},结果Fi(Ak)和Fj(Ak)的相似度函数定义为
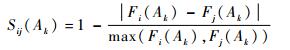 | (17) |
式中:i≠j; i, j=1, 2, …, n; k=1, 2, …, m。
可以看出2个结果之间相似度相差越小,相似度值越大。当2个结果的相似度完全相同时,相似度为最高值1。定义结果Bi(Ak)的支持度为和置信度分别为
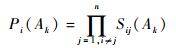 | (18) |
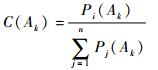 | (19) |
求出经n个结果数据融合后得出的置信度,然后取max(C(A1), C(A2), …, C(Ak))作为最终结果。
3 故障融合诊断流程 基于深度学习的航空发动机故障融合模型结合了DBN模型和决策融合模型,先通过DBN模型提取故障样本的性能参数特征,再对故障分类结果进行决策融合。具体诊断流程如图 4所示。
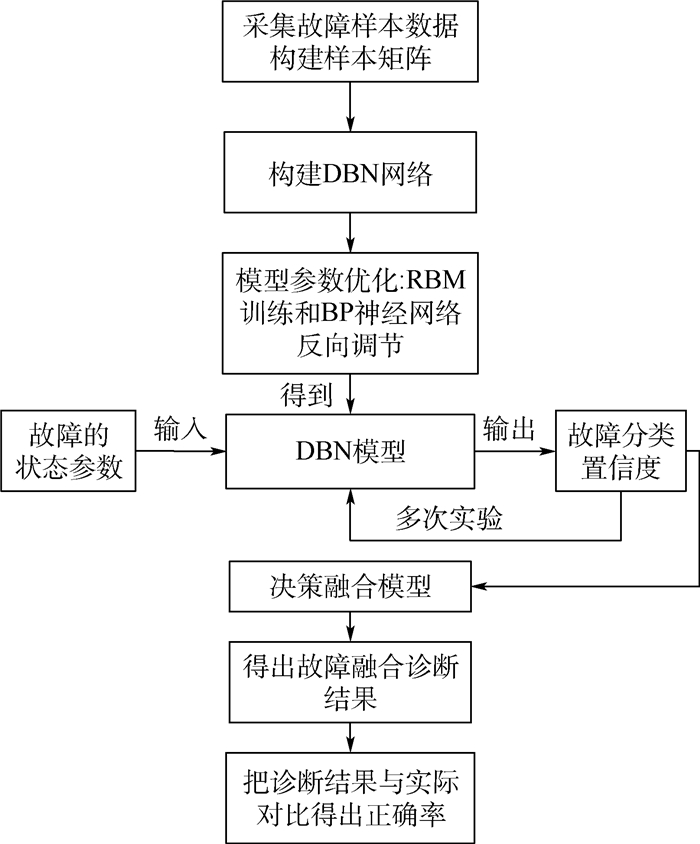 |
| 图 4 基于深度学习的航空发动机故障融合诊断流程 Fig. 4 Fault fusion diagnosis folw chart for aero-engine based on deep learning |
| 图选项 |
步骤1 ?采集故障样本数据,构建训练样本矩阵、样本标签矩阵和测试样本矩阵。样本是m×n矩阵,其中n为状态参数个数。
步骤2 ?构建DBN网络,设置网络层数和节点个数,其中节点数最大值为
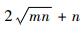
步骤3 ?模型参数优化,把训练样本输入DBN网络中,从高层到底层训练DBN中的所有RBM,得出权值w和各参数。把训练得到的参数输入到BP神经网络中进行反向优化训练,得到最终的DBN网络模型。
步骤4 ?输入测试样本的故障状态参数得出故障分类置信度。
步骤5 ?重复步骤4进行多次实验,把得出的故障分类置信度结果输入到决策融合模型中。
步骤6 ?根据决策融合结果得出故障融合诊断结果。
步骤7 ?分析故障融合诊断结果,与实际故障情况对比并统计正确率。
4 算例分析 4.1 故障样本生成 本文选用普惠公司的JT9D发动机[17]为研究对象,选择排气口燃气温度偏差(ΔEGT)、燃油消耗量偏差(ΔFF)、低压转子转速偏差(ΔN1)、高压转子转速偏差(ΔN2)作为状态参数,用表 1的发动机故障表作为原始样本进行仿真拓展,公式[14]如下:
表 1 JT9D发动机故障 Table 1 Engine failure of JT9D
| 序号 | 发动机故障类型 | 性能参数偏差 | |||
| ΔEGT/℃ | ΔFF/% | ΔN1/% | ΔN2/% | ||
| F01 | 风扇效率+1% | -1.00 | -0.25 | -0.25 | -0.05 |
| F02 | 风扇流量+1% | 4.50 | 0.80 | -0.85 | 0.05 |
| F03 | 低压压气机效率+1% | -2.00 | -0.15 | 0.10 | -0.15 |
| F04 | 低压压气机流量+1% | -2.00 | -0.40 | -2.00 | -0.05 |
| F05 | 高压压气机效率+1% | -7.00 | -0.85 | -0.10 | 0.10 |
| F06 | 高压压气机流量+1% | -0.05 | -0.10 | 0 | -0.25 |
| F07 | 高压涡轮效率+1% | -0.85 | -1.05 | -0.10 | 0.20 |
| F08 | 低压涡轮效率+1% | -4.50 | 0 | 0.45 | 0 |
| F09 | 3.0+3.5放气活门开度-20% | -11.20 | -2.40 | -0.04 | -0.24 |
| F10 | 第1级涡轮导向叶片面积+1% | 2.50 | 0.35 | 0.05 | -0.15 |
表选项
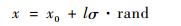 | (20) |
式中:x0为原始样本;l为噪声控制因子用来模拟噪声受到环境干扰的情况;σ为样本标准差;rand函数用来生成服从正态分布的随机数。
4.2 建立故障融合诊断模型 首先建立4维样本矩阵,每维代表各个性能参数。根据仿真建立1 000个有样本故障状态标签的训练样本,每种故障类型100个,其中故障因子设置为0.1~0.5,每隔0.1仿真20个样本。另外建立1 000个无标签的训练样本,参数设置与有标签样本相同。然后构建层数分别为2、3、4的共7个4DBN网络,代入所有训练样本求出样本的总重构误差如表 2所示,可以看出网络结构为[4, 8, 9, 10]的DBN网络,重构误差最小,说明该网络结构能够更加准确地挖掘出性能参数中的隐藏特征。因此,本文选取该网络结构做进一步的反向调节优化。
表 2 DBN网络结构与重构误差 Table 2 DBN network structure and reconstruction error
| DBN网络结构 | 重构误差 |
| [4, 6, 10] | 0.083 |
| [4, 8, 10] | 0.047 |
| [4, 6, 8, 10] | 0.076 |
| [4, 8, 12, 10] | 0.037 |
| [4, 8, 9, 10] | 0.028 |
| [4, 8, 9, 12, 10] | 0.049 |
| [4, 6, 8, 12, 10] | 0.065 |
表选项
网络结构为[4, 8, 9, 10]的DBN网络重构误差见图 5。可以看出在多次重构后,重构误差逐步下降到较小值。
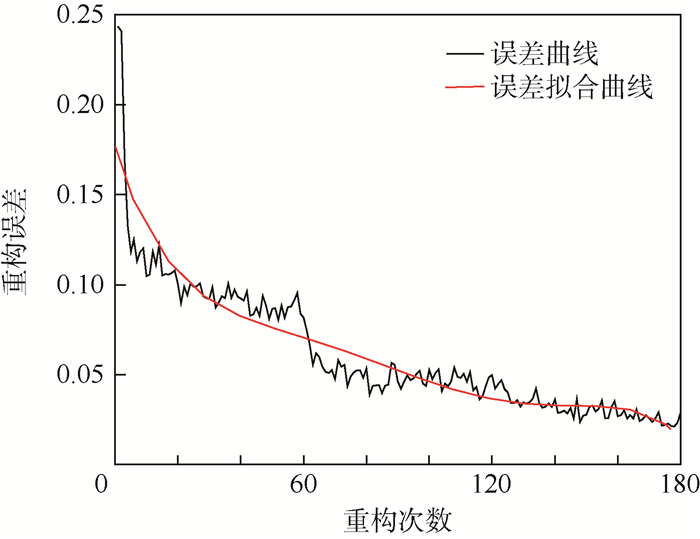 |
| 图 5 网络结构为[4, 8, 9, 10]的DBN网络重构误差图 Fig. 5 DBN reconstruction error graph with network structure of [4, 8, 9, 10] |
| 图选项 |
并对带标签样本进行反向调节,可以得到BP神经网络误差曲线如图 6所示,BP神经网络误差反映出状态参数的隐藏特征与故障类型的匹配程度,其误差为所有训练样本的特征值与故障类型的标准差总和。由于RBM训练过程为无监督训练,所以提取出的样本特征不能直接与故障类型相对应。从图 6可以看出,刚开始训练时BP神经网络误差很大,在2 500次左右样本误差已经大幅度下降。在运算30 000次后最终BP误差仅为0.41,已满足要求。
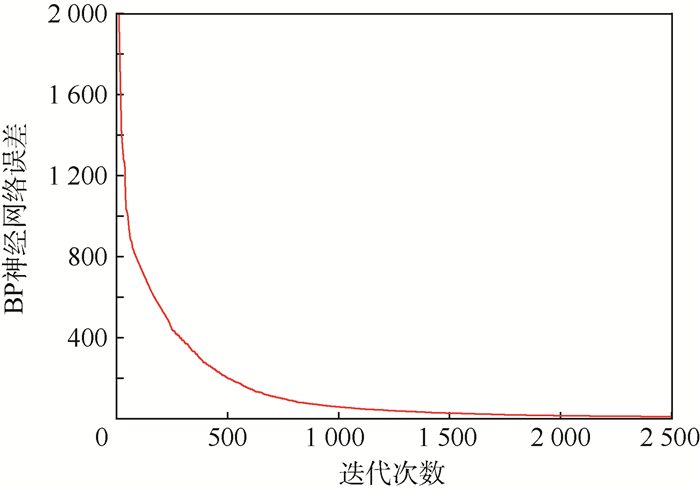 |
| 图 6 BP神经网络误差图 Fig. 6 Graph of BP neutral network error |
| 图选项 |
4.3 故障融合诊断结果 截取故障F05的5次实验结果,其置信度见表 3。从表中可以看出每次诊断得出的置信度(置信度1~置信度5)都有一定偏差,对于F05的置信度1约为0.278,同时F09的置信度1约为0.716,发生了明显的分类错误。对比故障F05和F09的状态参数可以看出由于范围较为接近,在故障仿真中的数据特征较为模糊,因此容易在单次故障诊断结果出错。为了消除个别实验结果对诊断结果的影响,需要决策融合再进行更准确的诊断。同时应当对那些特征不明显的样本,应再仿真出一些类似样本,添加到深度信念网络的训练集中,从而对深度信念网络的参数进行进一步优化。
表 3 故障分类置信度 Table 3 Confidence level of fault classification
| 故障类型 | 置信度1 | 置信度2 | 置信度3 | 置信度4 | 置信度5 |
| F01 | 9.00×10-8 | 1.08×10-6 | 6.01×10-7 | 2.35×10-6 | 4.90×10-5 |
| F02 | 2.41×10-7 | 7.09×10-7 | 5.39×10-7 | 3.77×10-7 | 6.06×10-7 |
| F03 | 5.16×10-3 | 2.60×10-3 | 3.05×10-3 | 1.40×10-3 | 6.57×10-5 |
| F04 | 6.30×10-5 | 2.35×10-4 | 1.81×10-4 | 1.15×10-4 | 2.50×10-5 |
| F05 | 2.78×10-1 | 7.97×10-1 | 6.44×10-1 | 9.47×10-1 | 9.99×10-1 |
| F06 | 1.16×10-5 | 2.05×10-6 | 3.78×10-6 | 3.17×10-7 | 1.91×10-9 |
| F07 | 1.01×10-3 | 7.27×10-4 | 1.08×10-3 | 1.88×10-4 | 1.18×10-5 |
| F08 | 1.10×10-5 | 4.65×10-5 | 2.30×10-5 | 8.12×10-5 | 4.31×10-4 |
| F09 | 7.16×10-1 | 2.01×10-1 | 3.52×10-1 | 5.14×10-2 | 5.54×10-4 |
| F10 | 4.66×10-7 | 4.68×10-7 | 4.34×10-7 | 1.40×10-7 | 3.39×10-8 |
表选项
为了消除运算结果偏差对最终故障诊断结果所造成的影响,进一步提高诊断正确率,把表 3中数据代入到决策融合算法中可得到最终结果见表 4。其中C(F)为决策融合算法得出的置信度,诊断结果0表示无故障,1表示有故障。从表中可以看出经过决策融合,故障在所属F05的置信度极高,达到了故障分类要求。
表 4 故障诊断结果 Table 4 Results of fault diagnosis
| 故障类型 | C(F) | 诊断结果 |
| F01 | 3.9×10-5 | 0 |
| F02 | 7.6×10-7 | 0 |
| F03 | 7.16×10-5 | 0 |
| F04 | 0.38×10-3 | 0 |
| F05 | 0.998 | 1 |
| F06 | 4.32×10-9 | 0 |
| F07 | 3.25×10-5 | 0 |
| F08 | 0.161×10-3 | 0 |
| F09 | 0.129 | 0 |
| F10 | 4.14×10-8 | 0 |
表选项
通过上述实验,选择网络结构为[4, 6, 8, 10]的深度信念网络模型和决策融合模型组合成故障融合诊断模型。仿真出1 000个有故障状态标签的测试样本,每种故障类型100个,为检验模型抗干扰性,故障因子设置为0.1~1.0每隔0.1仿真10个样本。把测试样本代入到故障融合诊断模型中,把得出故障融合诊断结果与故障状态标签对比可以得出故障融合诊断正确率。
下面将测试样本代入到基于深度学习的故障融合诊断模型与BP神经网络和单独深度信念网络模型进行对比,并统计正确率。从表 5中的可以看出,本文所采用的基于深度学习的故障融合诊断模型正确率为99.58%,比无决策融合模型略高,同时BP神经网络模型在多故障诊断中效果较差。说明通过决策融合有效地提高了模型抗干扰型,有更高地故障诊断正确率。
表 5 故障诊断正确率对比 Table 5 Comparison of fault diagnosis accuracy
| 模型 | 正确率/% |
| 基于深度学习的故障融合诊断模型 | 99.58 |
| 深度信念网络模型 | 95.30 |
| BP神经网络模型 | 82.13 |
表选项
5 结论 1) 本文提出的基于深度学习的故障融合诊断模型与BP神经网络和单独深度信念网络模型相比有更高的故障诊断正确率,例如对JT9D发动机进行故障诊断的正确率达到99.58%。
2) 本文模型中的深度学习方法能够充分发掘大样本特征,对多故障进行分析,提取故障样本隐含特征。
3) 本文模型结构简单,输入输出清晰直观。先把故障样本的状态参数作为输入,输出各个故障分类置信度;然后再用决策融合算法把多次故障分类结果相融合得出最终诊断结果。
4) 本文模型使用决策融合算法消除了深度信念网络故障分类结果中的偶然误差,有较好的抗干扰能力。
为了使本模型的故障诊断结果更精确、速度更快,仍需要优化相关参数和模型结构。
参考文献
| [1] | 黄强, 王建, 张桂刚. 一种航空发动机传感器故障诊断方法[J].传感技术学报, 2014, 27(10): 1315–1320. HUANG Q, WANG J, ZHANG G G. A kind of approach for aero-engine sensor fault diagnosis[J].Chinese Journal of Sensors and Actuators, 2014, 27(10): 1315–1320.DOI:10.3969/j.issn.1004-1699.2014.10.003(in Chinese) |
| [2] | 薛薇, 王涛. 基于一组卡尔曼滤波器信息融合的故障诊断[J].计算机测量与控制, 2015, 23(7): 2285–2287. XUE W, WANG T. Application of a bank of Kalman filters for aircraft engine sensor actuator fault diagnosis[J].Computer Measurement and Control, 2015, 23(7): 2285–2287.(in Chinese) |
| [3] | 俞刚, 黄金泉. 基于支持向量机和卡尔曼滤波器的航空发动机故障诊断研究[J].航空发动机, 2012, 38(1): 47–50. YU G, HUANG J Q. Aeroengine fault diagnosis based on support vector machine and Kalman filter[J].Aero-Engine, 2012, 38(1): 47–50.(in Chinese) |
| [4] | 廖洪一. 基于极限学习机的航空发动机故障诊断研究[D]. 广汉: 中国民用航空飞行学院, 2012. LIAO H Y. Research on aero-engine fault diagnosis based on extreme learning machine[D]. Guanghan: Civil Aviation Flight University of China, 2012(in Chinese). |
| [5] | 赵世荣, 黄向华. 应用神经网络信息融合诊断航空发动机故障[J].航空动力学报, 2008, 23(1): 164–168. ZHAO S R, HUANG X H. Fault diagnosis for aeroengine gas path components based on neural network multisensor data fusion[J].Journal of Aerospace Power, 2008, 23(1): 164–168.(in Chinese) |
| [6] | 徐启华, 师军, 耿帅. 应用快速多分类SVM的航空发动机故障诊断方法[J].推进技术, 2012, 33(6): 961–967. XU Q H, SHI J, GENG S. Aero-engine fault diagnosis by a new fast multi-class support vector algorithm[J].Journal of Propulsion Technology, 2012, 33(6): 961–967.(in Chinese) |
| [7] | 孙伟超, 李文海, 李文峰. 融合粗糙集与D-S证据理论的航空装备故障诊断[J].北京航空航天大学学报, 2015, 41(10): 1902–1909. SUN W C, LI W H, LI W F. Avionic devices fault diagnosis based on fusion method of rough set and D-S theory[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(10): 1902–1909.(in Chinese) |
| [8] | 于劲松, 沈琳, 唐荻音. 基于贝叶斯网络的故障诊断系统性能评价[J].北京航空航天大学学报, 2016, 42(1): 35–40. YU J S, SHEN L, TANG D Y. Performance evaluation of fault diagnosis system based on Bayesian network[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 35–40.(in Chinese) |
| [9] | TAI A H, CHING W K, CHAN L Y. Detection of machine failure:Hidden Markov model approach[J].Computers & Industrial Engineering, 2009, 57(2): 608–619. |
| [10] | GóMEZ M J, CASTEJíN C, GARCíA-PRADA J C. Automatic condition monitoring system for crack detection in rotating machinery[J].Reliability Engineering & System Safety, 2016, 152: 239–247. |
| [11] | BAJRIC R, ZUBER N, SKRIMPAS G A, et al. Feature extraction using discrete wavelet transform for gear fault diagnosis of wind turbine gearbox[J].Shock & Vibration, 2016, 2016(1): 1–10. |
| [12] | SIMANI S. Residual generator fuzzy identification for automotive diesel engine fault diagnosis[J].International Journal of Applied Mathematics & Computer Science, 2013, 23(2): 419–438. |
| [13] | 周利敏, 闫国华, 瞿红春. 一种云环境下的发动机健康管理系统及其应用[J].计算机测量与控制, 2014, 22(12): 3926–3928. ZHOU L M, YAN G H, QU H C. Engine health management system in cloud and its applications[J].Computer Measurement and Control, 2014, 22(12): 3926–3928.DOI:10.3969/j.issn.1671-4598.2014.12.026(in Chinese) |
| [14] | 单外平. 基于深度信念网络的变速器故障分类识别研究[D]. 广州: 华南理工大学, 2015. SHAN W P. Classification and recognition of transmission fault based on deep belief network[D]. Guangzhou: South China University of Technology, 2015(in Chinese). |
| [15] | 刘伟峰, 杨爱兰. 基于BIC准则和Gibbs采样的有限混合模型无监督学习算法[J].电子学报, 2011, 39(S1): 134–139. LIU W F, YANG A L. Unsupervised learning for finite mixture models based on BIC criterion and Gibbs sampling[J].Acta Electronica Sinica, 2011, 39(S1): 134–139.(in Chinese) |
| [16] | 李文立, 郭凯红. D-S证据理论合成规则及冲突问题[J].系统工程理论与实践, 2010, 30(8): 1422–1432. LI W L, GUO K H. Combination rules of D-S evidence theory and conflict problem[J].Systems Engineering Theory and Practice, 2010, 30(8): 1422–1432.DOI:10.12011/1000-6788(2010)8-1422(in Chinese) |
| [17] | 张光明. 航空发动机气路故障诊断技术研究[D]. 沈阳: 沈阳航空工业学院, 2010. ZHANG G M. Research on gas path fault diagnosis for aero-engine[D]. Shenyang: Shenyang Institute of Aeronautical Engineering, 2010(in Chinese). |
