随着人类对气候和环境变化重要性的认知, 全球性气候的监测受到了越来越广泛的关注。探测手段表现出了多样化、多功能化、便捷化、非接触等发展趋势。全球导航卫星系统反射方法(GNSS-R)是一种新型的被动非合作式遥感手段，通过协同接收、处理导航卫星直射和经地表反射信号进行地表物理参数的反演，具有低成本、低功耗、低质量等特点，已成为国内外****的研究热点之一。近年来，通过大量试验验证，该技术可用于海面有效波高^[1]、海面高度^[2]、土壤湿度^[3]、雪深^[4]等参数的探测。GNSS-R分为双天线和单天线2种探测模式。双天线模式采用直反异置的天线进行直射和反射信号的接收，需要开发和研制新型的接收设备进行信号接收和处理。相比于双天线模式，单天线模式利用GNSS定位接收机输出的信噪比(SNR)进行地球物理参数的反演，无需开发新的接收设备，可利用现有的连续运行参考站(CORS)数据，因此具有部署简单、分布广泛等特点。研究表明，该技术可用于海面测高、雪深探测以及土壤湿度反演等领域。全球导航卫星系统反射信号的干涉方法(GNSS-IR)利用干涉法(Interference Pattern Technique，IPT)对GNSS反射信号和直射信号进行分析。该方法最先由Larson等^[5]于2008年提出并用于土壤湿度的反演，并在此基础上提出了GNSS-IR的模型。随后该模型被广泛运用在土壤湿度的测量上^[6-8]。下一年，Larson等^[9]又将该模型应用到高度的测量中，自此该方法被广泛推广到雪深^[10]、海高^[11]等各种高度测量中。
本文对多径信号模型和单天线测高模型进行了详细的理论分析，并在此基础上得出解析模型。详细讨论了已有的谱分析方法以及本文提出的基于解析模型拟合的方法，通过仿真平台，估算2种方法的误差。以此为基础，分别用实测数据对2种方法的反演结果进行验证，比较反演精度；并设置不同的高度角上限，观察高度角上限对其的影响，获得最优高度角上限反演条件。
1 多径信号模型 Nievinski和Larson^[12]提出了一种近地面反射的多径信号模型：

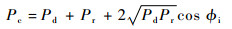(1)

式中：P_d和P_r分别为直射信号功率和反射信号功率；P_c为混合信号功率；?_i为干涉相位，定义为反射信号超出直射信号的相位：

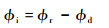(2)

其中：?_r为反射信号相位；?_d为直射信号相位。
由式(1)可以推导出信噪比SNR的表达式:

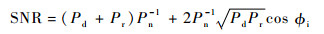(3)

式中：P_n为噪声功率。在式(3)中，等号右边第1项为直射和多径信号非相干项，称为DP；第2项为直射和多径信号干涉引起的信噪比振荡项，称为IP。
由于反射信号在传播路径中受到各种方式的削弱，包括反射介质、极化方式等，所以反射信号功率很小，可以忽略，式(3)可进一步化简为

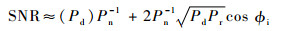(4)

Nievinski和Larson^[13]以此模型构建了多径信号信噪比的仿真平台。利用该仿真平台，分别模拟只接收直射信号和考虑多径信号时的信噪比随高度角变化的趋势，如图 1所示。实线为仅接收直射信号时信噪比的变化趋势，随着高度角的增大，信噪比单调递增；虚线为考虑了多径信号的信噪比变化趋势。从图 1中可以看出，相比于仅接收直射信号的情况，多径信号的接收对直射信号形成了干扰，产生了振荡。此外，高度角越低，多径信号与直射信号的相干成分越多，干扰效应越明显。高度测量主要利用相位信息，从式(4)可知，相位信息包含在振荡项IP中，因此，有必要去除多径信号信噪比中的非相干项DP。本文利用二阶多项式拟合非相干项DP。

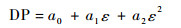(5)

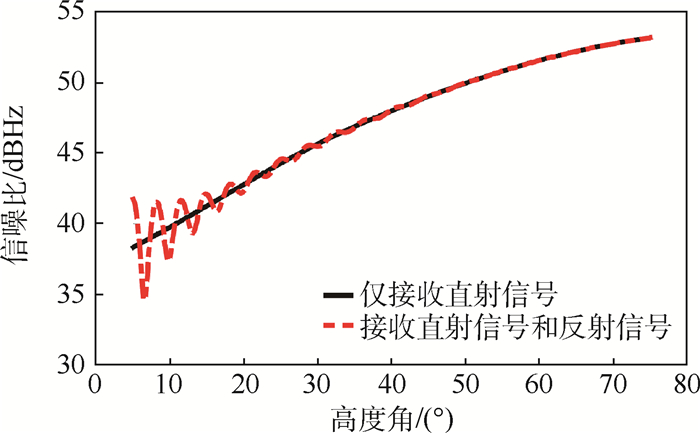图 1 输出信噪比仿真 Fig. 1 Simulation of output SNR

图选项

式中：ε为高度角；a₀、a₁、a₂为拟合参数。
因此，信噪比减去拟合后的结果便是多径信号形成的振荡部分IP，如下：

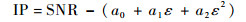(6)

自此，就提取出了多径信号对信噪比的影响，高度信息便包含其中，仿真结果如图 2中实线所示。

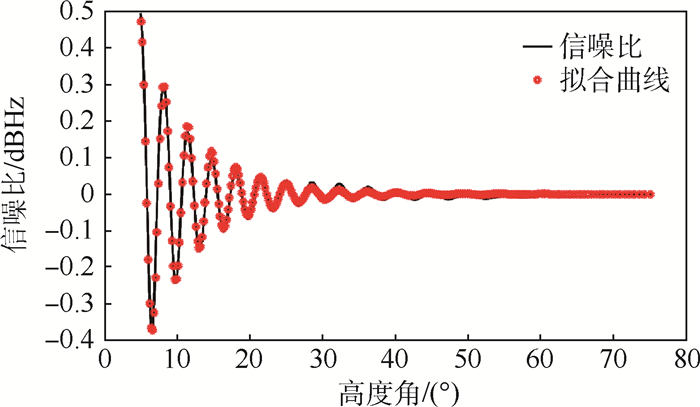图 2 信噪比仿真波形及拟合结果 Fig. 2 Simulation waveform of SNR and fitting results

图选项

由图 2实线可见，随着高度角的变化，振荡呈衰减趋势，且低高度角处振荡呈单一频率，用式(7)拟合：

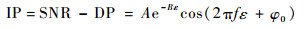(7)

式中：A、B、f和φ₀为拟合参数。本文采用非线性最小二乘法。
图 2中点号为对IP进行拟合的曲线，由此可见，该模型可以对信噪比拟合。
2 单天线测高模型 从式(4)可知，信噪比振荡是由多径信号相对于直射信号的相位差随时间变化引起的。假设接收天线高度为h，则相位差?_i可表示为^[5]

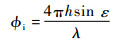(8)

式中：λ为信号波长。
由于卫星高度角随时间变化，根据频率的定义，可得信噪比振荡频率为

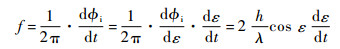(9)

从式(9)可知，信噪比的振荡频率取决于天线和反射面的垂直距离h、GPS卫星高度角ε和时间变化率dε/dt。实际上，由于高度角是随时间变化的函数，即存在：

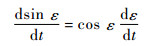(10)

将式(10)代入式(9)，则可以用sin ε替代变量t，简化式(9)，可得

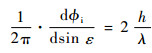(11)

定义为f_x，即信噪比对高度角正弦值的导数。从式(11)可知，f_x与h有正比关系。图 3为天线高度为2 m和4 m时，所接收信号信噪比随高度角变化的仿真波形。可以看出，4 m较2 m接收高度的信噪比具有更高的振荡频率。

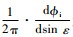
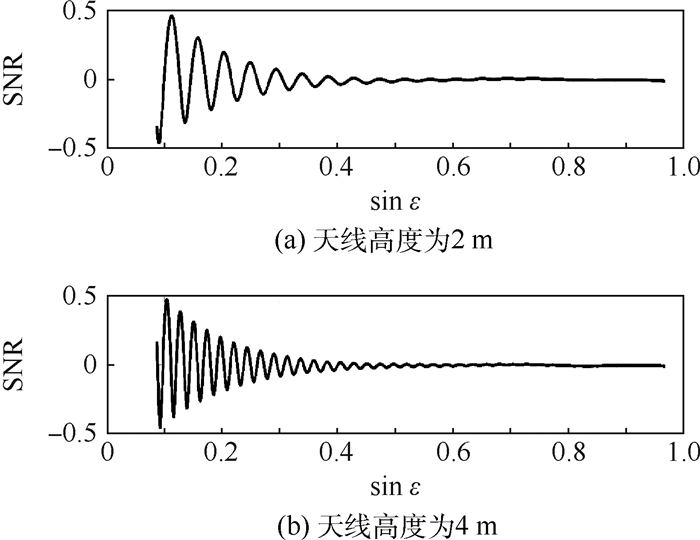图 3 不同天线高度时的信噪比仿真波形 Fig. 3 Simulation waveforms of SNR at different antenna heights

图选项

2.1 Lomb-Scargle谱分析方法 通过谱分析的方法可以从图 2所示的信噪比振荡中估计频率f_x，但是由于时域采样间隔是非均匀的，基于傅里叶变换的谱分析方法均难以解决非均匀采样的谱分析问题^[14]。Lomb-Scargle(LS)谱分析方法除了可有效获得弱周期信号的谱估计，解决非均匀采样信号的谱估计问题外，还可以克服数据缺失、序列长度不足等困难^[15]。因此，本文采用LS谱分析方法估计f_x。

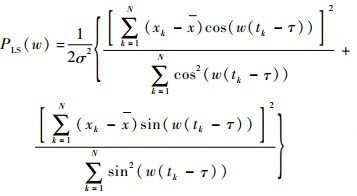(12)

式中：x_k和t_k分别为第k个采样样本值和采样点时刻；x和σ²分别为样本均值和方差；τ为时间平移不变量，其保证了所估计的功率谱为均匀采样谱。
2.2 拟合法 本文采用非线性最小二乘法得到拟合参数。非线性最小二乘法是用m个观察点来拟合有n个参数的非线性模型，m＞n。考虑一组m个数据点的数据，(x₁, y₁), (x₂, y₂), …, (x_m, y_m)，以及被拟合的函数y=f(x, β)，此函数还依赖于n个参数β=(β₁, β₂, …, β_n)，m＞n。找到一组参数β使得拟合后的曲线与原数据的最小平方和最小，即有

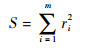(13)

式中：r_i为原始数据与拟合后曲线值之差。对S求解最小值，此时得到的β值即为所求。
由图 2可得，利用式(7)的解析函数可拟合信噪比振荡，因此，通过拟合法所得参数f即为振荡频率f_x。
利用仿真数据，对LS谱分析方法和拟合法2种方法性能进行对比分析。本文讨论了信噪比振荡频率从10 Hz到50 Hz变化，利用2种方法反演并比较两者频率的均方根误差。
仿真平台未对信噪比添加噪声，所以计算所得的误差为理论误差。LS谱分析方法的均方根误差为0.021 8 Hz，略低于拟合法的0.049 5 Hz。拟合法需要预先设置参数，而仿真时频率动态范围略大，造成拟合时的不准确，这是造成拟合法的均方根误差大于LS谱分析方法的原因之一。
3 最大测量高度 在第2节的讨论中，仅考虑了载波的相干性，但在导航信号中，还存在码的相干性。当反射信号相对于直射信号延时超过一个码片时，直射信号和反射信号相干性减弱，即存在如下关系：

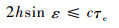(14)

式中：τ_c为码片长度；c为光速。
根据式(14)，可得天线架设高度需满足：

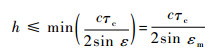(15)

式中：ε_m为高度角上限。
图 4为天线架设最大值与高度角上限之间的关系。可以看出，最大测量高度随着高度角上限的增大而减小，即天线架设高度越高，可用于测高的信噪比对应的高度角范围越小。此外，随着天线架设高度的增加，反射面粗糙度对反射信号的影响增大，反射路径延长，反射信号的功率大幅衰减，导致最终的反演结果性能下降。因此，利用干涉法进行高度测量时，天线架设高度不宜过高。所以，天线的实际架设高度小于理论计算值。

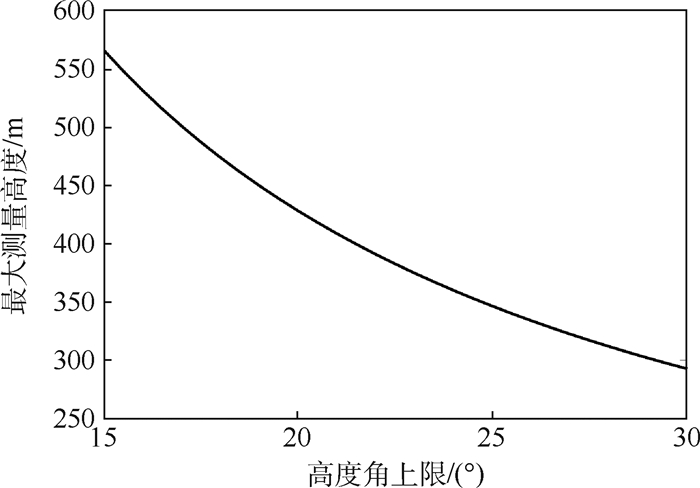图 4 最大测量高度与高度角上限关系 Fig. 4 Relationship between maximum measured height and upper limit of elevation angle

图选项

4 最小接收机输出率 根据奈奎斯特采样定理，接收机输出率应满足：

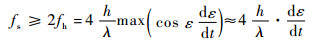(16)

式中：f_h为式(9)中的最高频率。
利用仿真平台的GPS L1 C/A码信号，根据式(16)，得到最小接收机输出率与测量高度的关系，如图 5所示。最小接收机输出率与测量高度呈正比关系。可见，接收机输出率越大，对应的可测高度范围越大。利用单天线模型测高时常用的天线架设高度不超过50 m，所以如图 5所示1 Hz的接收机输出率足以满足实际测量需要。

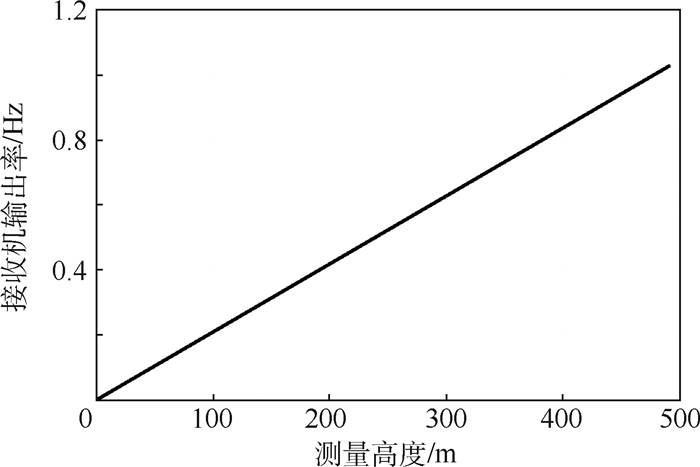图 5 最小接收机输出率与测量高度关系 Fig. 5 Relationship between minimum output rate of receiver and measured height

图选项

5 实验验证 5.1 实验场景 为了验证GNSS-IR测高方法的正确性，本文利用法国图卢兹大学CESBIO实验室在如图 6所示的法国西南部Lamasquère(43°29′14.45″N; 1°13′44.11″E)地区采集的实测数据对接收机天线高度进行反演^[16-17]。实验从2014年2月4日持续到2014年3月31日，共56天。采用Leica GR25服务器型参考站接收机，具有稳定性好、测量精度高等特点。采用Leica AR10测绘型天线，具有良好的多径抑制性能，可满足式(4)中反射功率很小的假设条件。通过测量，天线相位中心距离地面为1.7 m(本文以该值作为真实高度)。从图 6(a)可以看出，实验场地周围无明显遮挡物，一方面保证了多径信号仅来自陆地；另一方面允许接收高度角较低的信号。在实验中，卫星高度角为2°~89°的GPS L1 C/A信号被接收并处理得到输出率为1 Hz的信噪比序列。

图 6 接收设备及实验地点 Fig. 6 Receiving equipment and experimental site

图选项

5.2 实验结果
5.2.1 Lomb-Scargle谱分析方法 图 7为2014年2月12日实测的PRN2卫星信号的信噪比随高度角正弦值的变化趋势。与模型仿真相同，一方面，随着高度角增大，自由空间传播损耗的减小导致了信噪比总体上趋于变大；另一方面，多径信号的干涉效应使得信噪比出现明显振荡。首先，利用式(6)对上述信噪比进行直射信号信噪比剔除，截取信噪比，保留干涉强的低高度角部分；然后，利用LS谱分析方法对干涉部分的信噪比进行谱估计，并估计其峰值对应的高度。图 7给出了所估计信噪比的LS谱，其中，利用h=f_xλ/2将横轴频率转换为高度。峰值对应的高度为1.672 m，与实际高度的误差为0.028 m。

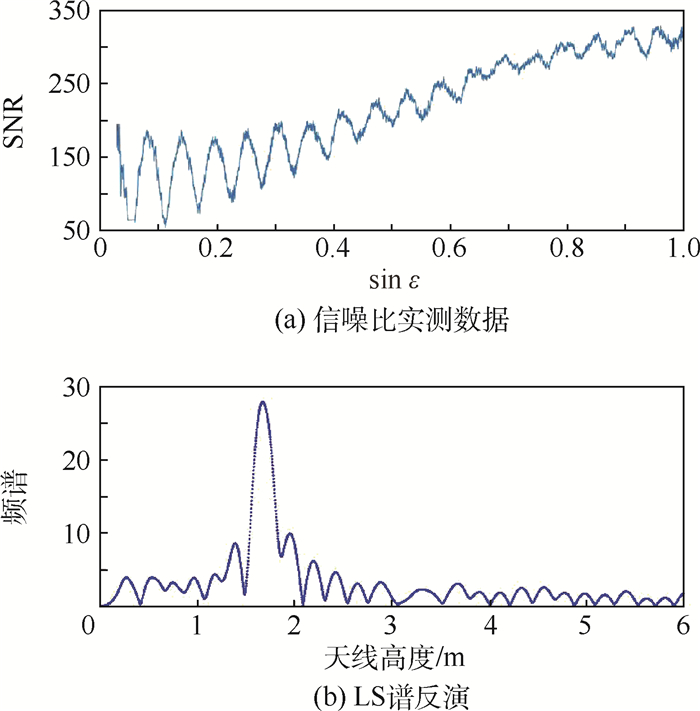图 7 信噪比实测数据和LS谱反演结果 Fig. 7 Measured SNR data and LS periodogram inversion results

图选项

5.2.2 拟合法 图 8给出了利用式(7)的解析模型拟合2014年2月12日实测的PRN2卫星信号的干涉部分信噪比的结果。可知，该解析模型可以很好地拟合实测数据，且对低高度角的数据具有更好的拟合结果。对所有实测数据进行拟合得到振荡频率估计值，并利用h=fλ/2得到反演高度。对应的高度为1.689 m，与实际高度的误差为0.011 m。

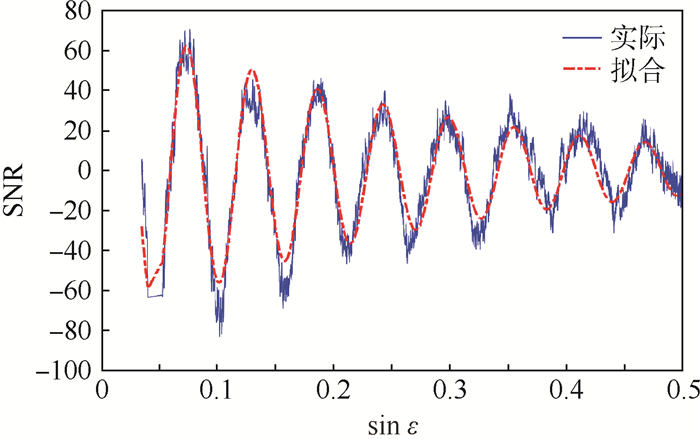图 8 信噪比实测数据及拟合结果 Fig. 8 Measured SNR data and fitting results

图选项

利用同一组数据对单天线模型的2种测高方法进行了算法操作演示，5.2.3节的实验结果是综合56天接收到的所有GPS L1 C/A信号得到的统计结果。

5.2.3 高度角上限的影响 在5.2.1节和5.2.2节的处理过程中可以看到，为了达到一定的相干性，获得更好的处理结果，需要对信噪比数据进行截取。为了获得最好反演高度结果的高度角上限，将对高度角上限为10°~50°，步长为1°的情况分别进行反演，比较其均方根误差(RMSE)的大小。综合56天的数据可以得到高度角上限和均方根误差之间的关系，如图 9所示。

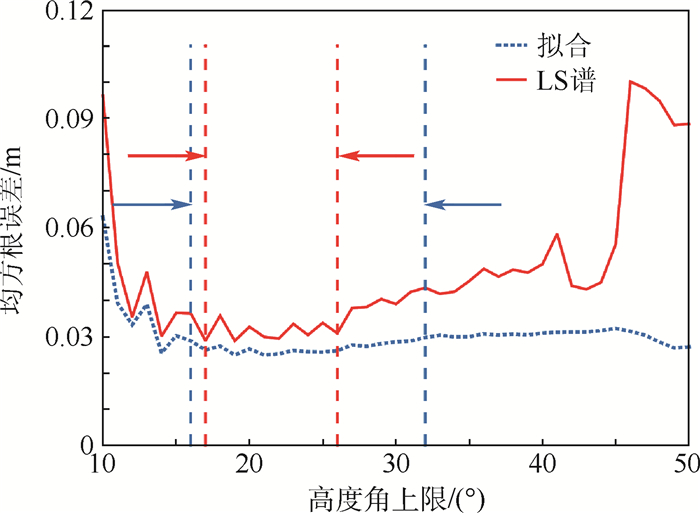图 9 均方根误差随高度角上限变化趋势 Fig. 9 Trend of RMSE variation with upper limit of elevation angle

图选项

图 9中，实线为LS谱分析方法获得的均方根误差，高度角上限为17°~26°时，均方根误差相对较小，在0.03 m上下波动，波动也较为平缓。所以，可以说高度角上限在17°~26°时获得的高度估计误差最小。其中，上限在17°时，反演高度与真值的均方根误差最小。
拟合法所获得的均方根误差随高度角上限的关系如图 9中虚线所示。高度角上限为16°~32°时，均方根误差相对较小，都在0.03 m以下，波动幅度很小。所以，高度角上限为16°~32°时获得的高度估计误差最小。其中，上限为21°时，反演高度与真值的均方根误差最小。
由图 9可以看出，拟合法反演高度的均方根误差都要小于LS谱分析方法，而且这种方法不会随着高度角上限的变化而对高度反演结果产生很大的影响。拟合开始于低高度角，低高度角处的频率决定拟合频率。同时，最优区间的估计可以在得到优化结果的同时，选择尽可能小的高度角上界，压缩数据量，获得更快的处理时间。
本次实验所用数据为法国图卢兹大学CESBIO实验室在法国南部所架设的天线相位中心距地面高度为1.7 m的数据，所以实验所反演高度的真值一直是1.7 m。该实验数据代表了土壤这类地表特征的效果，具有普适性。并且本次实验所用方法与单天线测雪深、测海面平均高度方法一致。对比3种方法均方根误差最小时的均值和误差，LS谱分析方法反演所得高度的平均误差为0.011 m，均方根误差为0.028 75 m；拟合法平均误差为0.008 m，均方根误差为0.024 85 m。可见，针对上述评价标准，拟合法的反演效果更好。综上，拟合法反演高度在一定程度上效果要优于LS谱分析方法，是一种可行的高度反演方法。
6 结论 本文对GNSS信噪比多径模型和单天线测高模型进行了理论研究，论述了GNSS信噪比多径模型并建立相应的解析模型。介绍了单天线测高模型和高度反演方法，在已有的基于LS谱估计方法的基础上，提出了基于解析模型拟合实测信噪比波形的高度反演方法。分析了GNSS-IR测高方法固有的测量限制并仿真了最大测量高度和最小接收机输出率与测量高度的关系；利用实测数据验证了2种反演方法的正确性并对比分析了二者的精度，结果表明：
1) 在高度角上限达到15°及以上时，拟合法反演精度受高度角上限影响变小，均方根误差均在0.03 m以下。
2) 无论高度角上限如何变化，拟合法得到结果的均方根误差皆小于LS谱分析方法获得的均方根误差。其中，LS谱在17°时，反演效果最好，误差均值为0.011 m，均方根误差为0.028 75 m；拟合法在21°时，其反演效果最好，误差均值为0.008 0 m，均方根误差为0.024 85 m。
3) 由于码相干中码片宽度和接收机固有输出率的影响，可测高度均会受限。这一部分将在以后的工作中进行试验验证；并且在今后的研究中还将探究反射介质以及粗糙度等因素对高度反演的影响。
致谢    
感谢法国图卢兹大学CESBIO实验室和山东农业大学杨磊的数据支持。
参考文献

[1]	CARRENOLUENGO H, CAMPS A. Empirical results of a surface-level GNSS-R experiment in a wave channel[J].Remote Sensing, 2015, 7(6): 7471–7493.DOI:10.3390/rs70607471
[2]	D'ADDIO S, MARTIN-NEIRA M, BISCEGLIE M D, et al. GNSS-R altimeter based on Doppler multi-looking[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(5): 1452–1460.
[3]	ZAVOROTNY V U, LARSON K M, BRAUN J J, et al. A physical model for GPS multipath caused by land reflections:Toward bare soil moisture retrievals[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2010, 3(1): 100–110.
[4]	VEY S, GVNTNER A, WICKERT J, et al. Monitoring snow depth by GNSS reflectometry in built-up areas:A case study for Wettzell, Germany[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(10): 4809–4816.
[5]	LARSON K M, SMALL E E, GUTMANN E, et al. Using GPS multipath to measure soil moisture fluctuations:Initial results[J].GPS Solutions, 2008, 12(3): 173–177.DOI:10.1007/s10291-007-0076-6
[6]	CHEW C C, SMALL E E, LARSON K M, et al. Effects of near-surface soil moisture on GPS SNR data:Development of a retrieval algorithm for soil moisture[J].IEEE Transactions on Geoscience & Remote Sensing, 2013, 52(1): 537–543.
[7]	VEY S, GVNTNER A, WICKERT J, et al. Long-term soil moisture dynamics derived from GNSS interferometric reflectometry:A case study for Sutherland, South Africa[J].GPS Solutions, 2016, 20(4): 641–654.DOI:10.1007/s10291-015-0474-0
[8]	敖敏思, 胡友健, 刘亚东, 等. GPS信噪比观测值的土壤湿度变化趋势反演[J].测绘科学技术学报, 2012, 29(2): 140–143. AO M S, HU Y J, LIU Y D, et al. Inversion of soil moisture fluctuation based on signal-to-noise ratio of global positioning system[J].Journal of Geomatics Science and Technology, 2012, 29(2): 140–143.(in Chinese)
[9]	LARSON K M, GUTMANN E D, ZAVOROTNY V U, et al. Can we measure snow depth with GPS receivers?[J].Geophysical Research Letters, 2009, 36(17): L17502.DOI:10.1029/2009GL039430
[10]	LARSON K M, SMALL E E. Estimation of snow depth using L1 GPS signal-to-noise ratio data[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(10): 4802–4808.
[11]	ROUSSEL N, RAMILLIEN G, FRAPPART F, et al. Sea level monitoring and sea state estimate using a single geodetic recei-ver[J].Remote Sensing of Environment, 2015, 171: 261–277.DOI:10.1016/j.rse.2015.10.011
[12]	NIEVINSKI F G, LARSON K M. Forward modeling of GPS multipath for near-surface reflectometry and positioning applications[J].GPS Solutions, 2014, 18(2): 309–322.DOI:10.1007/s10291-013-0331-y
[13]	NIEVINSKI F G, LARSON K M. An open source GPS multipath simulator in MATLAB/octave[J].GPS Solutions, 2014, 18(3): 1–9.
[14]	LOMB N R. Least-squares frequency analysis of unequally spaced data[J].Astrophysics and Space Science, 1976, 39(2): 447–462.DOI:10.1007/BF00648343
[15]	徐斌, 杨涛, 谭保华, 等. 基于Lomb-Scargle算法的周期信号探测的模拟研究[J].核电子学与探测技术, 2011, 31(6): 702–705. XU B, YANG T, TAN B H, et al. The simulate study of signal detection based on Lomb-Scargle algorithm[J].Nuclear Electronics & Detection Technology, 2011, 31(6): 702–705.(in Chinese)
[16]	ROUSSEL N, FRAPPART F, RAMILLIEN G, et al. Detection of soil moisture content changes by using a single geodetic antenna: The case of an agricultural plot[C]//Geoscience and Remote Sensing Symposium. Piscataway, NJ: IEEE Press, 2015: 2008-2011.
[17]	ROUSSEL N, FRAPPART F, RAMILLIEN G, et al. Detection of soil moisture variations using GPS and GLONASS SNR data for elevation angles ranging from 2° to 70°[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(10): 1–14.