近年来,随着航天技术的发展,大气制动在轨道建模、优化和控制等问题的研究越来越深入。大量的研究集中在大气层内飞行轨迹的优化和制导方面,如在满足热流的条件下使得探测器消耗的燃料最少[3-4],为防止热流过大对近拱点高度进行控制[5],在气动参数变化的情况下能跟踪设计轨迹等[6-7]。还有一部分研究涉及到轨道建模,如近拱点选择对大气制动过程的影响[8],大气制动期间的气动模拟方法[9-10],时间消耗与探测器、轨道参数的关系[11],以及旋转和静止大气环境下的轨道特性[12]等。但都没有涉及到气动力辅助变轨期间三体引力的影响。
众所周知,太阳系中最有科学价值的天体是木卫二、土卫六和土卫二,而土卫六是太阳系中唯一拥有浓密大气层的卫星,同地球一样富含氮气,成为当前国际深空探测的热点之一[13]。"卡西尼-惠更斯"计划的顺利进行更推动了对土卫六的探测活动。土卫六具有稠密的大气,在未来探测任务中可以在其附近实施大气制动以节约变轨的燃料消耗。
在过去火星等天体的大气制动轨道研究中,三体引力摄动比较微弱,或摄动引起的偏心率/近拱点震荡周期与大气制动的时间相比很长,三体摄动基本被忽略。然而,土卫六附近的探测器轨道受到土星周期为8 d(土卫六轨道周期的一半)的显著三体引力摄动[14],引起偏心率/近拱点的大幅震荡,会对探测器所处环境的大气密度产生显著影响,可能会加速大气制动的过程,也可能导致大气制动失败或探测器坠毁。因此,有必要对土星三体引力摄动对土卫六附近大气制动的影响进行详细研究。
本文采用基于Milankovitch参数的半解析轨道方程来研究探测器在环绕土卫六大气制动过程中土星三体引力摄动的影响。首先,考虑扁率摄动、三体引力摄动以及大气阻力,基于无奇异的Milankovitch参数建立了半解析轨道模型。然后,通过数值计算分析土星初始方位角选择对土卫六大气制动轨道运动的影响,为地外天体大气制动变轨方案提供参考。
1 轨道动力学模型及分析 1.1 轨道动力学建模 对于大气制动的轨道来说,大气阻力与三体引力摄动均为长期影响,适用于平均轨道要素建模。将长周期和短周期摄动隔离开,就得到摄动影响和轨道变化的直接关系。而Milankovitch轨道要素具有简洁的向量形式和对物理关系的显式表达,没有奇异,有利于摄动影响的讨论[15]。
大气制动过程中,探测器围绕卫星运行,将反复穿越卫星的大气层,同时卫星绕行星运动。卫星、探测器和行星的几何关系示意图如图 1所示,p为卫星自转轴方向矢量,H为探测器轨道角动量矢量,e为探测器轨道偏心率矢量,dS为行星相对于卫星的位置矢量,θ为行星相对于轨道拱线的方位角,r和v分别为探测器的位置和速度向量。
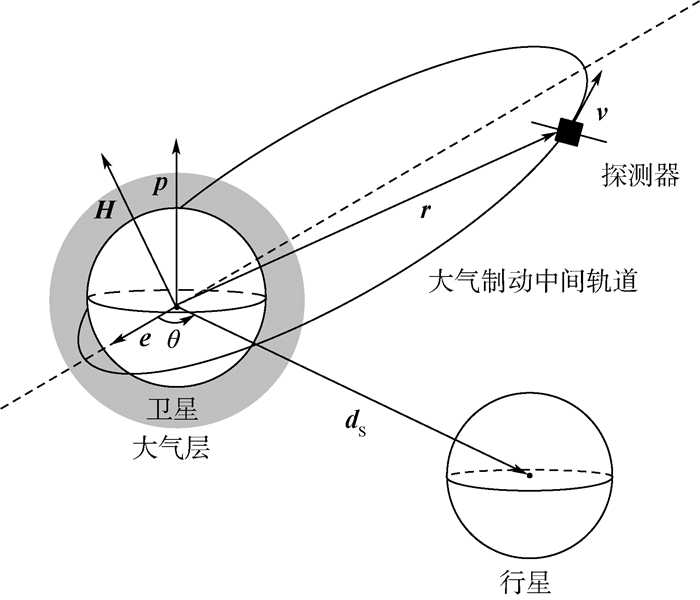 |
| 图 1 大气制动过程中卫星、探测器和行星的几何关系示意图 Fig. 1 Sketch map of geometric relation among moon, explorer and planet during aerobraking |
| 图选项 |
将角动量H和偏心率矢量e写成位置r和速度v运算的形式
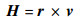 | (1) |
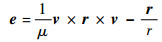 | (2) |
式中:μ为卫星的引力常数;r为探测器距卫星的距离。
对H和e建立高斯方程,并且将其平均化,有[15]
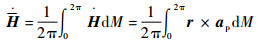 | (3) |
 | (4) |
式中:M为平近点角;ap=aJ2+aS+aatm为摄动力,包括扁率摄动力aJ2、行星三体引力摄动力aS和大气阻力aatm,定义分别为[15-16]
 | (5) |
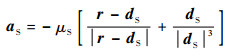 | (6) |
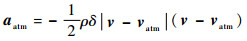 | (7) |
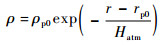 | (8) |
式中:J2为卫星扁率;RE为卫星平均半径;
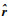
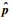
将式(5)~式(8)代入式(3)和式(4)经过运算化简后可得到与文献[15]类似的结果:
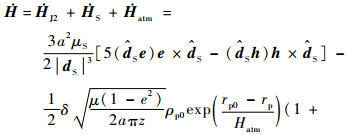 | (9) |
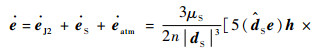 |
 | (10) |
式中:
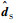


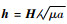
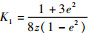
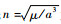

1.2 摄动力影响分析 考虑式(9)、式(10)等号右边第1项
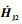
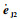
同样地,考虑式(9)、式(10)等号右边第3项
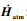
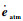
而行星三体引力摄动的分析就比较复杂。由
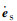
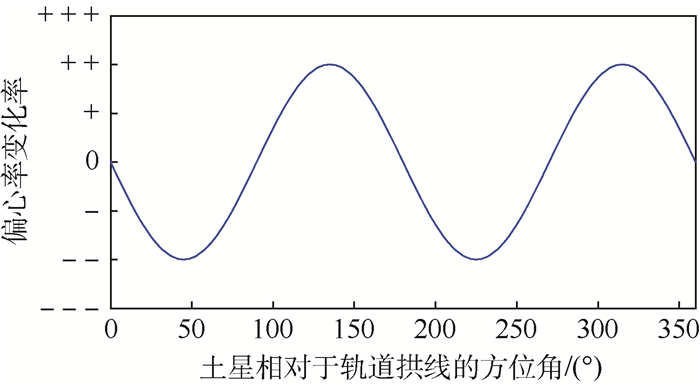 |
| 图 2 偏心率变化率与土星相对于轨道拱线的方位角近似关系 Fig. 2 Approximation of eccentricity variation with respect to azimuth between Saturn and apse line |
| 图选项 |
土星的运动导致其相对于轨道拱线的方位角不断增大,从而导致椭圆轨道的偏心率发生震荡。由图 2可知,该震荡的周期为土卫六轨道周期的一半,且震荡的初始相位由土星的初始方位角决定:若土星初始方位角为0°,则初始偏心率为震荡的最高点;而若土星初始方位角为90°,则初始偏心率为震荡的最低点。
因此土星三体引力摄动会引起轨道偏心率的震荡,从而使轨道的近拱点抬高或者降低。对于有大气的天体来说,这影响着轨道的寿命。而对于大气制动过程来说,近拱点的抬高或降低意味着探测器穿越大气层时利用大气制动效果的减弱或者加强。
2 数值仿真及分析 按照轨道模型式(9)、式(10),本文给出一组不同初始方位角情况下的土卫六探测器大气制动轨道数值仿真,并分析土星三体引力摄动对大气制动过程的影响。大气制动可以节省的燃料消耗主要与轨道的初始和结束状态相对目标轨道的关系有关,不在本文的讨论范围,因此在仿真中并未考虑。仿真参数如表 1所示,其中大气密度参数根据文献[17]数据拟合得到。
表 1 仿真参数 Table 1 Simulation parameters
| 参数 | 数值 |
| 土卫六引力系数/(km3·s-2) | 2.218 7×1010 |
| 土卫六平均半径/km | 2 575.5 |
| 扁率 | 5.044 6×10-6 |
| 土星引力系数/(km3·s-2) | 3.792 098×107 |
| 土卫六距土星距离/km | 1.221 87×106 |
| 土卫六偏心率 | 0 |
| 黄赤交角/(°) | 0 |
| 探测器面值比/(m2·kg-1) | 0.01 |
| 初始近拱点高度/km | 2 000 |
| 初始近拱点处大气密度/(kg·km-3) | 3.162 278×10-8 |
| 标高/km | 57.906 |
| 探测器阻力系数 | 2.2 |
| 初始远拱点高度/km | 20 000 |
| 初始轨道倾角/(°) | 20 |
| 初始升交点赤经/(°) | 0 |
| 近拱点幅角/(°) | 0 |
表选项
表 1中轨道根数与Milankovitch参数的转换关系可参见文献[15]。仿真时长为200 d,仿真步长为10 s,并设置偏心率和近拱点高度阈值分别为0.008和100 km,如果偏心率或轨道近拱点高度达到此值,中断仿真。
下面暂不考虑大气阻力,给出不同土星初始方位角时的轨道运动如图 3所示。
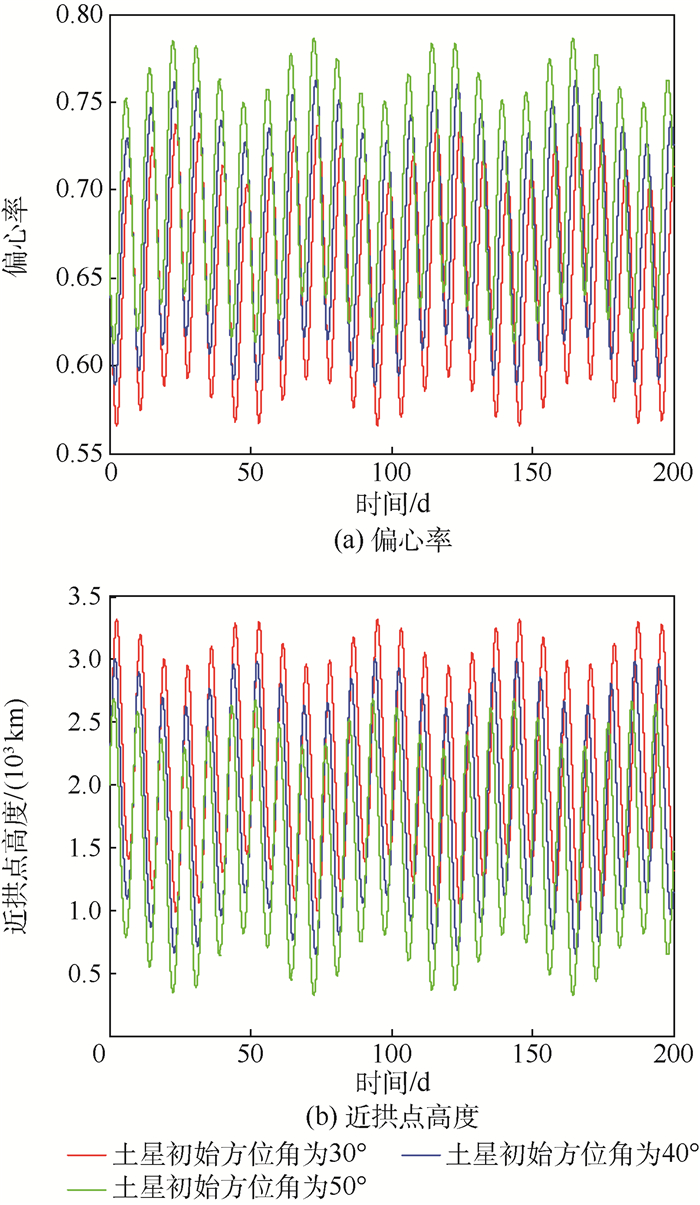 |
| 图 3 不考虑大气阻力,土星初始方位角分别为30°、40°、50°时轨道偏心率、近拱点高度曲线 Fig. 3 Curves of eccentricity and periapsis height withinitial azimuth of Saturn choices of 30°, 40° and 50°, when atmospheric drag is excluded |
| 图选项 |
从图 3可以发现,不同的土星初始方位角将导致明显不同的偏心率运动范围和近拱点高度运动范围。当土星初始方位角从30°增加到50°时,近拱点高度震荡中心明显变小。这意味着如果在有大气的情况下,初始方位角为50°的轨道将在穿越大气过程中经历更高的大气密度,减速效果更强烈。
考虑大气阻力后,不同土星初始方位角情况下的轨道运动如图 4所示。
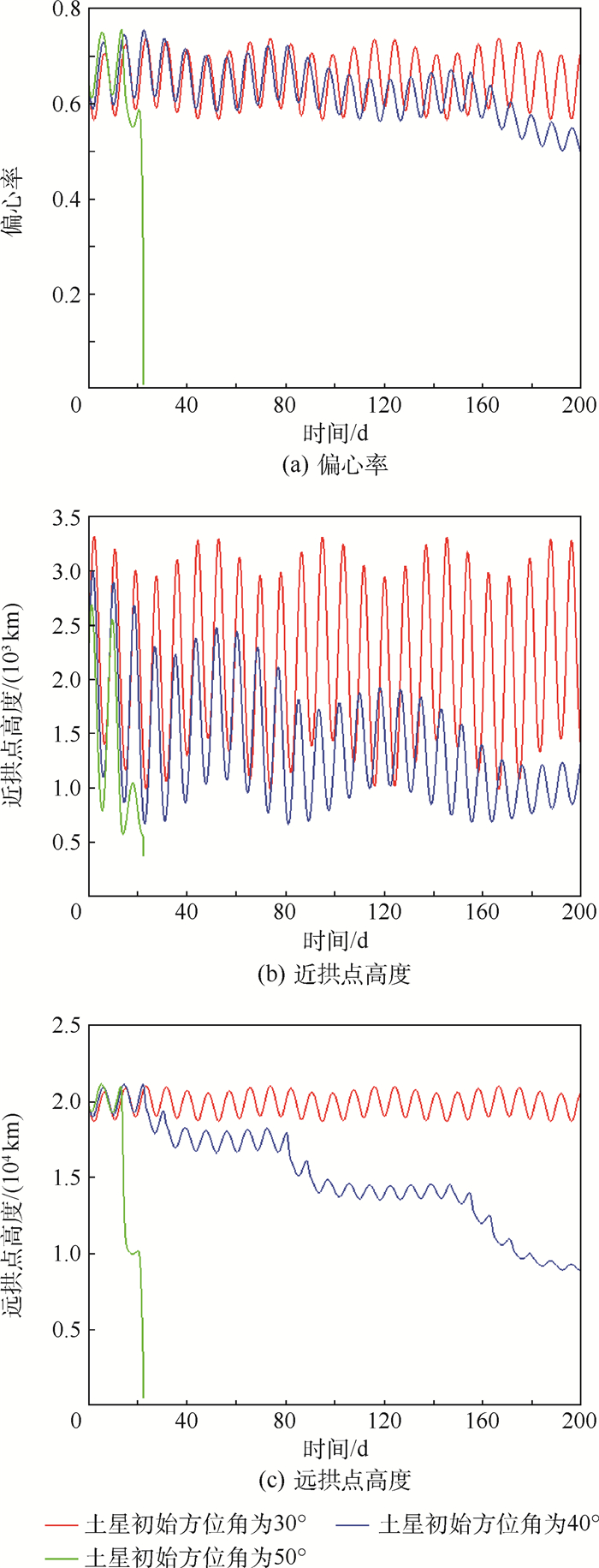 |
| 图 4 土星初始方位角分别为30°、40°、50°时大气制动过程中轨道偏心率、近拱点高度和远拱点高度曲线 Fig. 4 Curves of eccentricity, periapsis height and apoapsis height with initial azimuth of Saturn choices of 30°, 40° and 50°, during aerobraking |
| 图选项 |
从图 4可以发现,在三体引力摄动和大气阻力的双重作用下,不同土星初始方位角的轨道偏心率运动和近拱点高度运动范围和趋势明显不同。图 4(a)表明在土星初始方位角为50°时,轨道偏心率很快达到了结束阈值,而30°情况下时大气阻力作用并不明显。从图 4(b)可以看出土星初始方位角为50°时近拱点高度震荡谷值最低,气动作用最明显,同时近拱点高度震荡的峰值也降低,这是由于气动阻力的作用,轨道半长轴也在减小,相应地近拱点也会降低。图 4(c)显示随着时间的变化,大气制动作用越来越快。考虑大气制动最关注的指标热流率
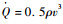
表 2 不同土星初始方位角下大气制动参数 Table 2 Aerobraking parameters at different initial azimuth of Saturn
| 土星初始方位角/(°) | 仿真结束时的半长轴/km | 最大热流率/(W·m-2) | 大气制动经历时间/d |
| 30 | 13 559 | 0.134 5 | 200 |
| 40 | 7 596.2 | 38.19 | 200 |
| 50 | 2 694.5 | 3 331.7 | 22.66 |
表选项
在大气制动过程中,如果不考虑土星三体引力摄动,相同的轨道初始条件,期间不加入远拱点机动降低近拱点高度,大气制动过程将超过数十年。
3 结论 通过轨道动力学建模和数值仿真讨论了土星三体引力对土卫六大气制动过程的影响,仿真结果表明:
1) 土星的三体引力摄动对土卫六大气制动过程的影响较大,会极大地影响大气制动过程。在土卫六大气制动设计中不能忽略土星三体引力摄动。
2) 三体引力摄动对大气制动的影响主要取决于土星的初始方位角。初始方位角的不同导致椭圆轨道的偏心率震荡范围的不同,从而引起近拱点高度震荡范围的变化,导致不同的大气制动效果。
3) 本文采用了Milankovitch参数和平均轨道要素的方法来计算大气制动过程,拓宽了大气制动的仿真手段,为未来进一步开展地外天体气动力辅助变轨技术的研究奠定了良好的基础。
参考文献
| [1] | MUNK M M, POWELL R W. Aeroassist technology planning for exploration[J].Advances in the Astronautical Sciences, 2000, 105(2): 1073–1083. |
| [2] | SPENCER D A, TOLSON R. Aerobraking cost and risk decisions[J].Journal of Spacecraft and Rockets, 2007, 44(6): 1285–1293.DOI:10.2514/1.24303 |
| [3] | RAO A V, TANG S, HALLMAN W P. Numerical optimization study of multiple-pass aeroassisted orbital transfer[J].Optimal Control Applications and Methods, 2002, 23(4): 215–238.DOI:10.1002/(ISSN)1099-1514 |
| [4] | 吴德隆, 王小军. 航天器气动力辅助变轨动力学与最优控制[M].北京: 中国宇航出版社, 2006: 10. WU D L, WANG X J. Aeroassisted orbit transfer dynamics and optimal control for spacecraft[M].Beijing: China Astronautics Publishing House, 2006: 10.(in Chinese) |
| [5] | 季英良, 朱宏玉, 杨博. 利用气动力的大气制动过程中近心点高度控制[J].北京航空航天大学学报, 2015, 41(3): 517–522. JI Y L, ZHU H Y, YANG B. Perigee altitude control using aerodynamic force during aerobraking[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 517–522.(in Chinese) |
| [6] | JITS R Y, WALBERG G D. Blended control, predictor-corrector guidance algorithm:An enabling technology for mars aerocapture[J].Acta Astronautica, 2004, 54(6): 385–398.DOI:10.1016/S0094-5765(03)00159-0 |
| [7] | LU P, CERIMELE C J, TIGGES M A, et al. Optimal aerocapture guidance[J].Journal of Guidance, Control, and Dynamics, 2015, 38(4): 553–565.DOI:10.2514/1.G000713 |
| [8] | 陈统, 徐世杰. 火星轨道大气制动策略研究[C]//全国第十四届空间及运动体控制技术学术年会论文集. 北京: 中国自动化学会空间及运动体控制专业委员会, 2010: 129-134. CHEN T, XU S J. Research on mars orbit aerobraking strategy[C]//Proceedings of the 14th National Academic Conference on Space-and Moving-body Control Technology. Beijing: Space and Moving-body Control Committee of Chinese Association of Automation, 2010: 129-134(in Chinese). |
| [9] | KUMAR M, TEWARI A. Trajectory and attitude simulation for mars aerocapture and aerobraking[J].Journal of Spacecraft and Rockets, 2006, 43(3): 585–593.DOI:10.2514/1.15458 |
| [10] | 张文普, 韩波, 张成义. 大气制动期间探测器的气动特性和轨道计算[J].应用数学和力学, 2010, 31(9): 1016–1026. ZHANG W P, HAN B, ZHANG C Y. Spacecraft aerodynamics and trajectory simulation during aerobraking[J].Applied Mathematics and Mechanics, 2010, 31(9): 1016–1026.(in Chinese) |
| [11] | 周垂红, 刘林. 利用行星大气制动形成环绕型目标轨道的耗时问题[J].飞行器测控学报, 2013, 32(5): 438–443. ZHOU C H, LIU L. Time needed to use aerobraking to insert planetary low orbiters[J].Journal of Spacecraft TT&C Technology, 2013, 32(5): 438–443.(in Chinese) |
| [12] | 吕敬, 张明明, 龚胜平. 旋转大气下火星探测器轨道捕获[J].北京航空航天大学学报, 2013, 39(3): 315–319. LV J, ZHANG M M, GONG S P. Aerocapture period under rotating atmospheric environment for mars vehicle[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(3): 315–319.(in Chinese) |
| [13] | 吴耀, 姚伟, 吕晓辰, 等. 一种用于土卫六探测的热机浮空器性能分析[J].宇航学报, 2016, 37(2): 223–228. WU Y, YAO W, LV X C, et al. Performance analysis of a heat engine aeroboat for titan exploration[J].Journal of Astronautics, 2016, 37(2): 223–228.(in Chinese) |
| [14] | VAN HOOLST T, RAMBAUX N, KARATEKIN ?, et al. The effect of gravitational and pressure torques on Titan's length-of-day variations[J].ICARUS, 2009, 200(1): 256–264.DOI:10.1016/j.icarus.2008.11.009 |
| [15] | WANG Y, GURFIL P. Dynamical modeling and lifetime analysis of geostationary transfer orbits[J].Acta Astronautica, 2016, 128: 262–276.DOI:10.1016/j.actaastro.2016.06.050 |
| [16] | ROSENGREN A J, SCHEERES D J. Long-term dynamics of high area-to-mass ratio objects in high-earth orbit[J].Advances in Space Research, 2013, 52(8): 1545–1560.DOI:10.1016/j.asr.2013.07.033 |
| [17] | WAITE J H, BELL J, LORENZ R, et al. A model of variability in Titan's atmospheric structure[J].Planetary and Space Science, 2013, 86: 45–56.DOI:10.1016/j.pss.2013.05.018 |
