本文以单向铺层的碳纤维复合材料板为对象,为了克服AE信号多模态特性以及复合材料各向异性对定位精度的影响,提出了一种基于经验小波变换(Empirical Wavelet Transform,EWT)的TDOA算法。首先,采用EWT自适应地分解AE信号并提取主频成分,通过GCC计算主频信号到达各传感器的时差;然后, 通过实验绘制波速与角度的变化曲线,并采用多项式进行拟合;最后, 结合时差信息和波速曲线完成损伤定位。
1 定位算法 1.1 EWT提取AE信号模态 EWT是由Jeromes在2013年提出的一种新的信号分解方法[9],其核心思想是自适应地划分信号频谱并建立合适的正交小波滤波器组,来提取具有紧支撑频谱的调频-调幅(Amplitude Modulated-Frequency Modulated,AM-FM)模态成分。EWT可以提取出复杂信号中的显著模态(Intrinsic Mode Function, IMF),其主要原理如下:
1) 设置模态数N,搜索信号频谱的N个局部极大值。
2) 选取连续2个局部极大值的中间频率点作为频谱划分的边界ωn(n=1, 2, …,N-1)。
3) 根据所确立的边界构造N个经验小波

4) 通过傅里叶逆变换(IFFT)得到各经验小波的时域表示。
根据经验尺度函数
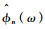

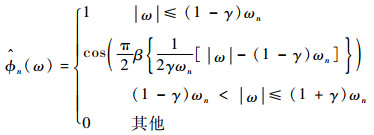 | (1) |
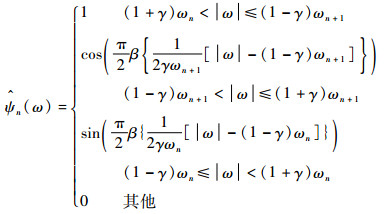 | (2) |
式中:ω为频率;γ为确保过渡带间无重合的系数,取值范围为
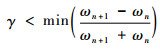 | (3) |
任意函数β(x)为
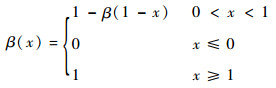 | (4) |
EWT作为一种全新的模态分解方法, 相比于应用广泛的经验模态分解[10-11]和常规的小波分解有着更完善的理论体系,具有计算复杂度更小、分解模态不含虚假模态成分等优点。目前EWT主要应用于机械故障诊断[12-14]、电晕电流降噪[15]和脑波信号分析[16]等方面。
复合材料损伤AE信号通常为成分复杂的多分量信号,伴有噪声及回波干扰。在计算各信号时差时,由于信号间的相似系数较低,常规的互相关法会产生较大误差。采用GCC法计算时差可以有效抑制噪声,但典型AE信号模态数较多,导致信号间的相关系数仍无法满足要求。同时由于不同模态导波具有不同的群速度,对定位时的波速选取也造成了困难。而通过EWT分解可以有效提取多分量损伤AE信号的主频成分同时去除多余模态,提高时差估计和波速选取的准确性,对损伤进行精确定位。
1.2 广义互相关时差定位 互相关法计算信号间时间延迟的主要原理是根据信号互相关函数峰值所对应的时刻来确定时差。信号x1(n)和x2(n)的互相关函数可以表示为
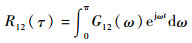 | (5) |
式中:G12(ω)为x1(n)和x2(n)的互功率谱函数;R12(τ)峰值处对应的时间即为信号间时差。
GCC法是基于互相关法的改进算法,相当于在计算信号互相关函数之前通过加权的方式对信号进行滤波[17]。令权值函数为ψv(ω),GCC函数可以表示为
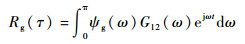 | (6) |
GCC主要原理如图 1所示,先对两信号进行快速傅里叶变换(FFT)并计算信号互功率谱;然后通过频域加权滤波处理;最后经IFFT得到GCC函数,其最大峰值处的时间即为信号间时差。在AE定位中GCC法能有效抑制噪声提高时差估计精度,其常用的权值函数表达式和特性如表 1所示。
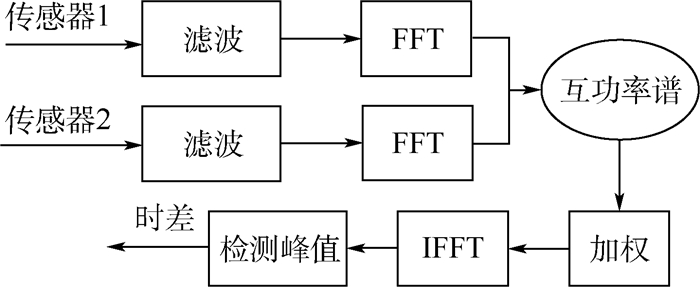 |
| 图 1 GCC原理框图 Fig. 1 Functional block diagram of GCC |
| 图选项 |
表 1 权值函数表达式及特性 Table 1 Expression and characteristics of weighted function
| 函数名称 | 表达式 | 特性 |
| CC | 1 | 相当于普通的互相关法 |
| Roth | 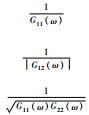 | 相当于Winener滤波,可以抑制噪声大的频带,但会展宽函数的峰 |
| PHAT | 当信号能量较小时分母趋于零,会增大误差,可在分母加入固定常数进行改进 | |
| SCOT | 与Roth类似,综合考虑两通道信号的影响 | |
| 注:G11(ω)与G22(ω)分别为通道1和2信号自功率谱密度,G12(ω)为通道1和2信号互功率谱密度。 | ||
表选项
在获取了各通道信号间的时差后即可通过TDOA法对AE源进行定位,如图 2所示。4个传感器(编号1~4)呈边长为2l的正方形布局,以正方形中心为原点设源坐标为(xs, ys)。v为波速,当材料为复合材料时信号沿不同方向传播速度不同,因此需要通过实验测得波速v与传播方向θ的关系曲线,并采用多项式进行拟合得到波速表达式v(θ)。以坐标为(l,l)的传感器2为例,可以得到信号到达时间为
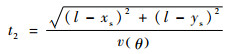 | (7) |
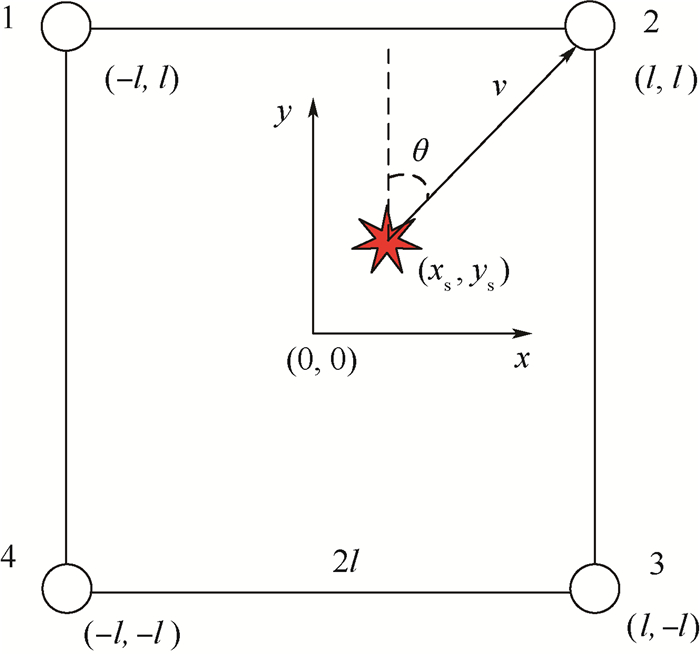 |
| 图 2 TDOA原理图 Fig. 2 Schematic of TDOA |
| 图选项 |
其中:θ可表示为
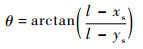 | (8) |
联立式(7)和式(8)可得
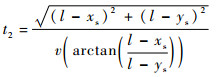 | (9) |
同理可得到信号到达传感器1、3和4的时间分别为
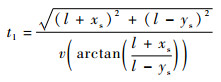 | (10) |
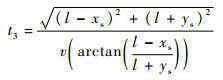 | (11) |
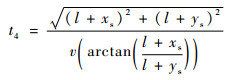 | (12) |
最后根据到达各传感器的信号时差在MATLAB中求解二元多次非线性方程组即可计算出源信号的坐标。
2 实验验证 2.1 实验方案设计 为验证本文算法在复合材料损伤定位中的有效性,设计了如图 3所示的复合材料板AE定位实验装置。实验对象为T800型碳纤维复合材料层合板,铺层方式为单向铺层,纤维方向为垂直方向,试件尺寸为300 mm×300 mm×1 mm。以复合材料板中心为原点建立坐标系,将4个R6型AE传感器布置于图中所示的位置上。在实测实验中采用0.5 mm的2H铅笔的断铅信号作为AE源,保证每次断铅角度一致。
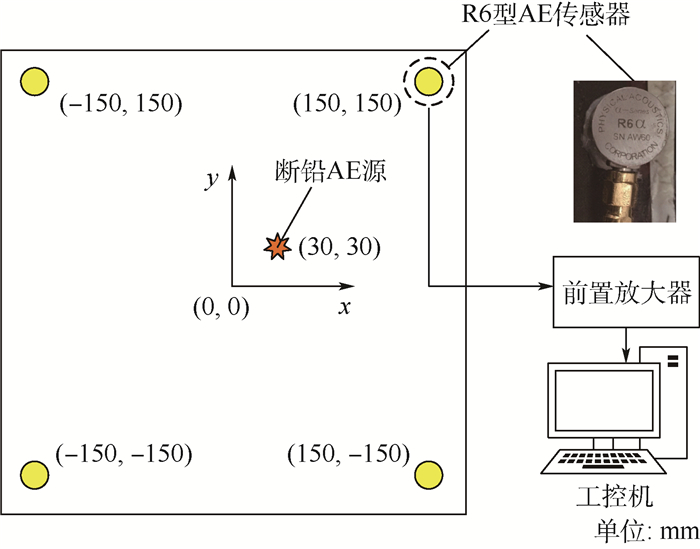 |
| 图 3 实验平台示意图 Fig. 3 Schematic of experimental platform |
| 图选项 |
2.2 声发射信号波速测量 图 4为通过断铅实验采集到的典型的断铅信号,从频谱可以看出实际的AE信号具有复杂的频率特性,其频带主要集中在35和90 kHz左右。
 |
| 图 4 实际断铅信号 Fig. 4 Actual lead break signal |
| 图选项 |
首先对其进行EWT分解,设定分解模态数为10,得到的分解结果如图 5所示。根据信号幅值确定模态5为AE信号的主频成分,模态10为高频噪声干扰,剩下的为多余模态。在定位算法中,需预先获取AE信号主频模态的波速,因此设计了如图 6所示波速测量实验。所选复合材料板为单向铺层,因此只需测出波速与纤维夹角在0°~90°范围内的关系即可,每隔15°进行测量。在90°方向上进行测量时,将传感器1和2分别布置在距离断铅信号源100和200 mm的位置上,进行5次断铅实验采集数据。采用EWT提取两传感器信号主频成分,然后通过GCC计算出时差,用两传感器间距除以时差即可求出波速。采用相同方法可得到其余方向波速,多次实验取平均得到的结果如表 2所示。
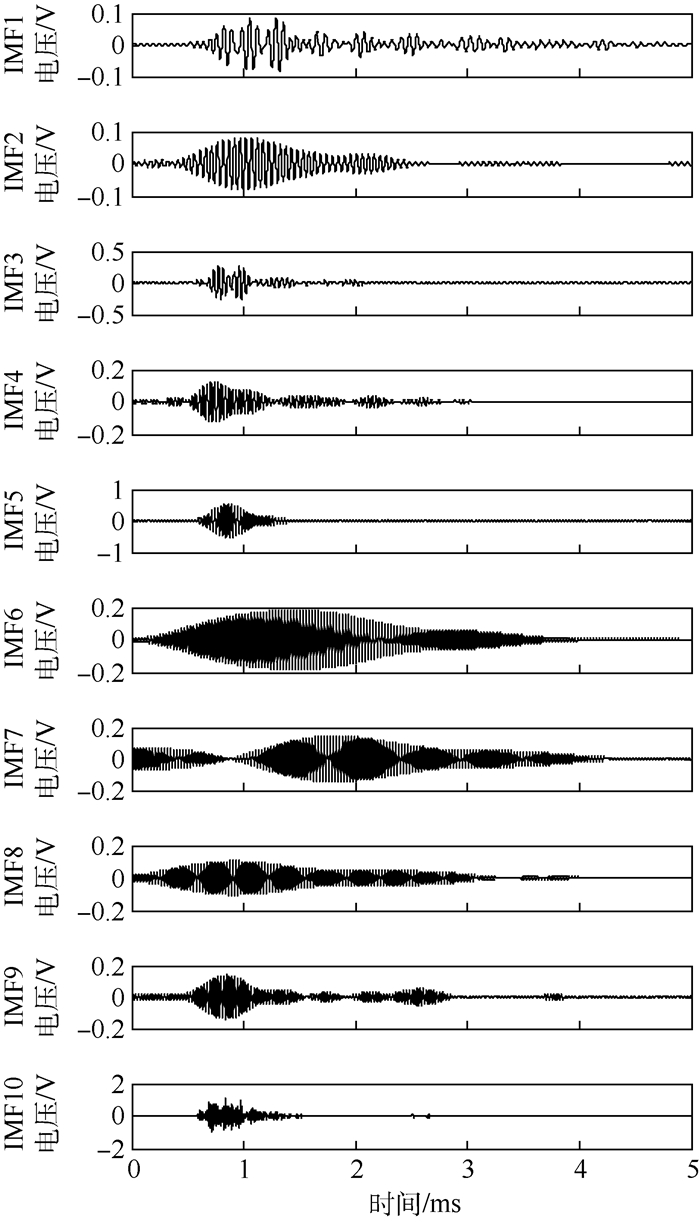 |
| 图 5 断铅信号EWT分解结果 Fig. 5 EWT decomposition results of lead break signal |
| 图选项 |
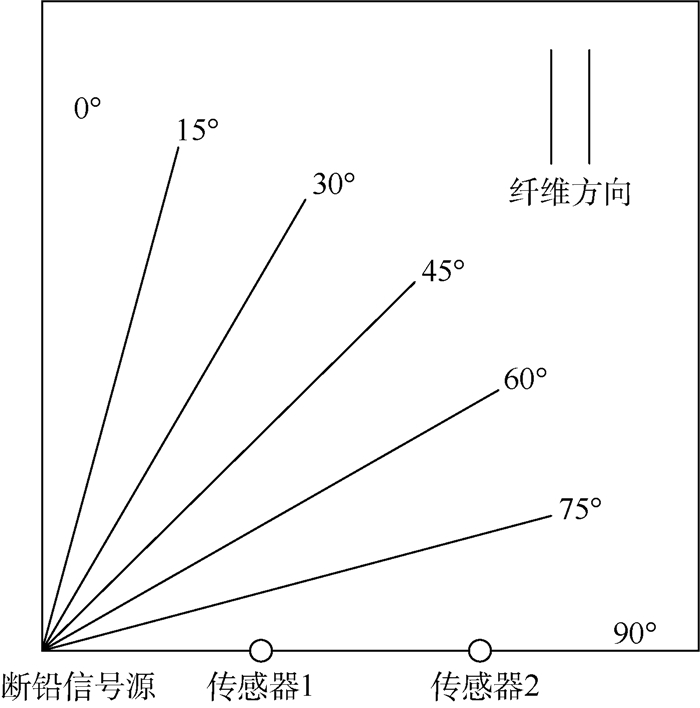 |
| 图 6 波速测量实验 Fig. 6 Experiment of wave velocity measurement |
| 图选项 |
表 2 各传播方向波速 Table 2 Wave velocities of different propagation directions
| 波速与纤维夹角/(°) | 波速/(m·s-1) |
| 0 | 2 473.3 |
| 15 | 2 421.6 |
| 30 | 2 352.1 |
| 45 | 2 264.2 |
| 60 | 2 159.1 |
| 75 | 2 066.7 |
| 90 | 1 949.8 |
表选项
根据波速与纤维方向的关系绘制的变化曲线如图 7所示。从图中可以看出主频信号波速随角度的增加而减小,当传播方向与纤维方向相同时,波速最大为2 473.3 m/s;当传播方向与纤维方向垂直时,波速最小为1 949.8 m/s。可见传播方向对波速具有较大的影响。
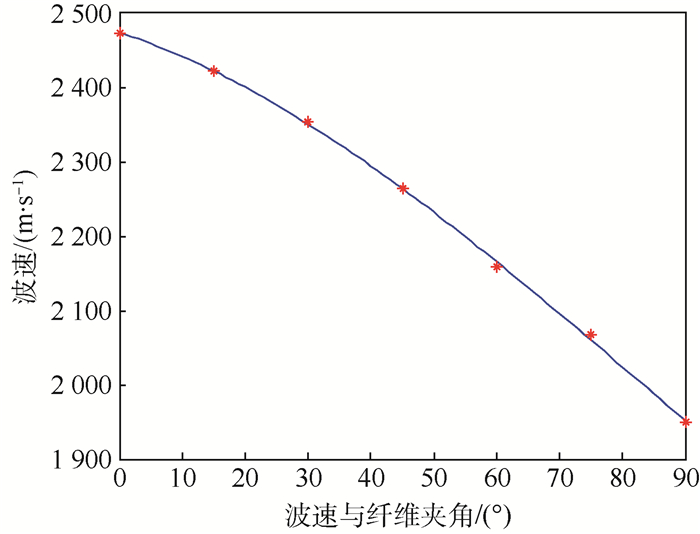 |
| 图 7 波速与传播方向关系曲线 Fig. 7 Relation curve of wave velocity and propagation direction |
| 图选项 |
对波速-角度曲线进行多项式拟合即可得到波速v与角度θ的函数关系,拟合得到的多项式
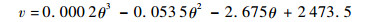 | (13) |
2.3 实验及结果分析 在平台定位实验中,设定采样率为1 MHz,在坐标为(30,30) mm的位置进行断铅,得到4路传感器观测信号如图 8所示。
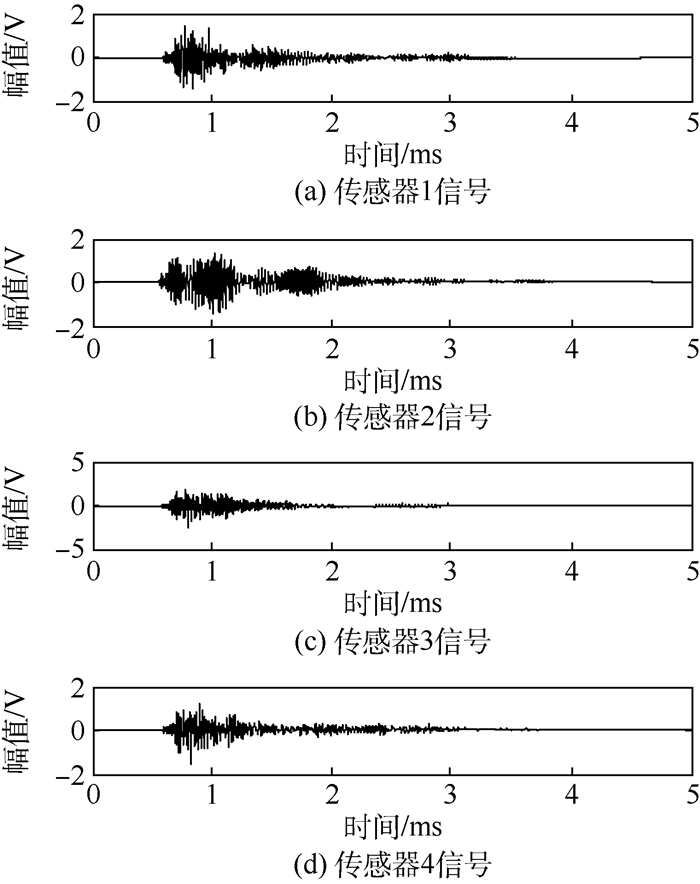 |
| 图 8 4路传感器观测信号 Fig. 8 Observed signals of four sensors |
| 图选项 |
图 9为对4路传感器观测信号进行分解重构后得到的各主频成分,中心频率均在35 kHz左右。采用PHAT加权的GCC法计算各路信号主频成分间的时差,结合拟合出的波速表达式得到定位结果,10次重复实验取平均为(25.23,27.74) mm,绝对误差D为5.28 mm,相对误差δ按式(14)计算为1.8%:
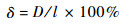 | (14) |
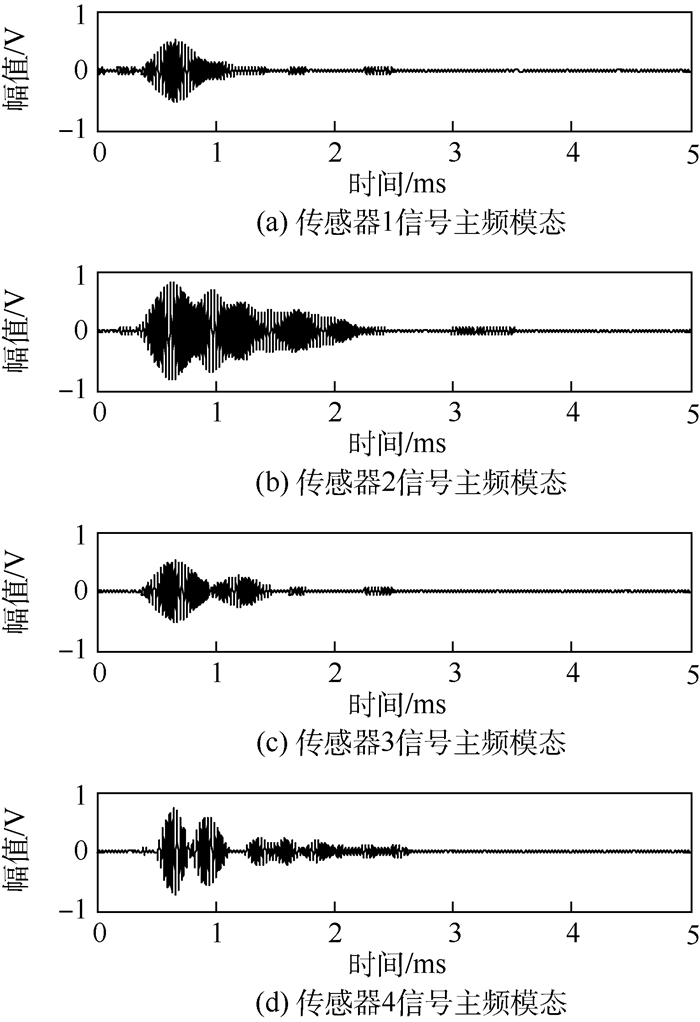 |
| 图 9 4路传感器观测信号主频模态 Fig. 9 Dominant frequency modes of observed signals of four sensors |
| 图选项 |
定位结果显示定位精度较高,误差产生的原因主要有2方面:一是对复合材料板波速进行拟合的结果不是完全准确的;二是回波干扰没有完全去除,主要是因为回波信号与主频模态频率相近,对时差估计的准确性造成了一定影响。
3 结论 本文对复合材料损伤AE定位算法进行了研究,提出了一种基于EWT的TOOA算法。以断铅信号作为AE源对所设计的定位算法有效性进行了验证。主要结论有:
1) EWT能够自适应的分解AE信号去除多分量AE信号中的噪声和多余模态,解决了由于各通道信号相关系数较低直接采用互相关法计算时差误差较大的问题。
2) 通过多项式拟合得到了波速-传播方向的函数表达式,解决了定位算法中波速的选取问题。
3) 设计了复合材料损伤AE定位的平台实验,采用所设计的算法对断铅信号进行了准确定位,绝对误差为5.28 mm,相对误差为1.8%。
参考文献
| [1] | 袁梅, 鲍鹏宇, 付重, 等. 飞机结构健康监测技术及传感器网络[J].航空制造技术, 2008, 22(13): 44–48. YUAN M, BAO P Y, FU Z, et al. Aircraft structural health monitoring technology and sensor network[J].Measurement & Control Technology in Aerospace, 2008, 22(13): 44–48.(in Chinese) |
| [2] | GUKIN R, GREEN C J, VANGRATTANACHAI S, et al. On acoustic emission for failure investigation in CFRP:Pattern recognition and peak frequency analyses[J].Mechanical Systems & Signal Processing, 2011, 25(4): 1393–1407. |
| [3] | DIRK A, ALEX C, STEVE W, et al. Acoustic emission source location on large plate-like structures using a local triangular sensor array[J].Mechanical Systems and Signal Processing, 2012, 30(7): 91–102. |
| [4] | PEARSON M R, EATON M, FEATHERSTON C, et al. Improved acoustic emission source location during fatigue and impact events in metallic and composite structures[J].Structural Health Monitoring, 2017, 16(4): 382–399.DOI:10.1177/1475921716672206 |
| [5] | 金中薇, 姜明顺, 隋青美, 等. 基于广义互相关时延估计算法的声发射定位技术[J].传感技术学报, 2013, 26(11): 1513–1518. JIN Z W, JIANG M S, SUI Q M, et al. Acoustic emission localization technique based on generalized cross-correlation time difference estimation algorithm[J].Chinese Journal of Sensors and Actuators, 2013, 26(11): 1513–1518.DOI:10.3969/j.issn.1004-1699.2013.11.009(in Chinese) |
| [6] | 袁梅, 牛奔, 董韶鹏, 等. 伪多源采样复域FastICA冲击定位算法[J].北京航空航天大学学报, 2016, 42(2): 243–250. YUAN M, NIU B, DONG S P, et al. Pseudo-multi-source-sampling complex domain FastICA for impact location[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 243–250.(in Chinese) |
| [7] | 焦敬品, 何存富, 吴斌, 等. 基于模态分析和小波变换的声发射源定位新算法研究[J].仪器仪表学报, 2005, 26(5): 482–485. JIAO J P, HE C F, WU B, et al. A new acoustic emission source location technique based on wavelet transform and mode analysis[J].Chinese Journal of Scientific Instrument, 2005, 26(5): 482–485.(in Chinese) |
| [8] | 马波, 陈健飞, 李标, 等. 玻璃纤维复合材料板声发射信号传播特性[J].无损检测, 2017, 39(1): 16–18. MA B, CHEN J F, LI B, et al. Acoustic emission signal propagation characteristics of glass fiber composite material plate[J].Non-destructive Testing, 2017, 39(1): 16–18.DOI:10.11973/wsjc201701004(in Chinese) |
| [9] | JEROMES G. Empirical wavelet transform[J].IEEE Transactions on Signal Processing, 2013, 61(16): 3999–4010.DOI:10.1109/TSP.2013.2265222 |
| [10] | KONSTANIN D, DOMINIQUE Z. Variational mode decomposition[J].IEEE Transactions on Signal Processing, 2014, 62(3): 531–544.DOI:10.1109/TSP.2013.2288675 |
| [11] | HUANG N, SHEN Z, LONG S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903–995. |
| [12] | 李志农, 朱明, 褚福磊, 等. 基于经验小波变换的机械故障诊断方法研究[J].仪器仪表学报, 2014, 35(11): 2423–2432. LI Z N, ZHU M, CHU F L, et al. Mechanical fault diagnosis method based on empirical wavelet transform[J].Chinese Journal of Scientific Instrument, 2014, 35(11): 2423–2432.(in Chinese) |
| [13] | CHEN J L, PAN J, LI Z P, et al. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals[J].Renewable Energy, 2016, 89: 80–92.DOI:10.1016/j.renene.2015.12.010 |
| [14] | JIANG Y, ZHU H, LI Z. A new compound faults detection method for rolling bearings based on empirical wavelet transform and chaotic oscillator[J].Chaos, Solitons & Fractals, 2016, 89: 8–19. |
| [15] | 王秋生, 陈璐, 袁海文, 等. 基于经验小波变换的电晕电流降噪方法[J].电网技术, 2017, 41(2): 670–676. WANG Q S, CHEN L, YUAN H W, et al. Corona current de-noising method based on empirical wavelet transform[J].Power System Technology, 2017, 41(2): 670–676.(in Chinese) |
| [16] | KUMAR R, SAINI I. Empirical wavelet transform based ECG signal compression[J].LETE Journal of Research, 2014, 60(6): 423–431. |
| [17] | WILSON K W, DARRELL T. Learning a precedence effect-like weighting function for the generalized cross-correlation framework[J].IEEE Transactions on Audio Speech & Language Processing, 2006, 14(6): 2156–2164. |
