相变材料主要分为3大类:有机类、无机类和混合类。目前研究及应用最为广泛的为有机类相变材料,其具有相变焓值大、无过冷度、无析出、性能稳定、无腐蚀性等优点,在航空航天领域具有广泛的应用,但是其导热系数小导致相变过程热量的存储/释放缓慢, 严重制约了其工程化应用,中国****研究采用金属翅片、高导热多孔金属材料、泡沫石墨[3]等方式强化相变材料导热性能。近年来,随着纳米材料科技的发展,采用高导热的金属纳米粒子、石墨烯纳米片(GnP)、单壁碳纳米管(SWCNT)强化有机类相变材料储/放热速率成为国内外的研究热点[4-5]。Li等[6-7]以硬脂酸为相变材料,通过添加多壁碳纳米管、GnP、纳米石墨片等碳材料制备了多种复合相变材料,测试结果发现同组体积组分的纳米石墨片导热强化效果最佳,添加多壁碳纳米管能够有效提高硬脂酸的导热性能,但是会降低复合相变材料熔化过程中液相的对流效应。Fang等[8]将质量分数为10%的GnP分散至正二十烷相变材料中,使得复合相变材料的导热系数提高了400%。Arici等[9]数值模拟了不同体积分数Al2O3纳米粒子对方形容器内石蜡材料熔化速率的作用效果,发现当体积分数为1%时,石蜡熔化速率最大。Harish等[10]实验研究发现在月桂酸中添加体积分数为1%的GnP能将导热系数提高230%。而且当纳米粒子导热增强体的积分数相同时,GnP的导热性能强化效果优于纳米金属粒子及SWCNT。Motahar等[11]发现将质量分数为4%的TiO2纳米粒子分散于正十八烷中能够将其凝固速率提高18%。陈杨华等[12]采用SWCNT改善石蜡导热性能,通过测试发现质量分数为5%的SWCNT能够将石蜡导热系数由0.2 W/mK高至0.28 W/mK。在基于纳米材料的物性规律研究方面,Nan等[13-14]系统建立了3种不同形式纳米复合材料等效导热系数模型并利用实验进行了验证;Santamaría-Holek和Mendoza[15]基于Maxwell-Garnett等效介质理论(EMT)模型对3种不同形式纳米复合材料黏度模型进行了研究和讨论;Das等[16]基于EMT模型和焓-多孔介质模型分析了填充不同类型纳米基复合相变材料的套管式储热系统的储能过程,还对添加GnP的复合相变材料的储能装置进行数值模拟,重点分析了换热流体工质温度和复合相变材料中GnP体积分数对装置储能速率的影响。
目前对于纳米强化有机类相变材料的研究大多集中在材料制备、物性测试、性能试验验证等方面,在数值模拟研究方面,对于其熔化/凝固过程中的传热传质、相界面变化、温度分布等问题大多采用基于焓-多孔介质模型,对于密度变化引起的对流问题采用Boussinesq假设[17-20],由于有机类相变材料固液相密度差较大,在熔化过程中体积膨胀明显,Boussinesq假设对材料体积膨胀作出线性假设,虽然能够实现相变材料相变过程液相中对流效应的刻画,但是假设具有一定局限性,而且对于体积膨胀等问题无法进行研究。夏莉等[21]尝试将流体体积(VOF)模型与焓-多孔介质模型相结合研究了储能装置中不同形式空穴的迁移情况。基于VOF模型与焓-多孔介质模型,Ye等[22]研究了具有不同体积分数空腔的储能装置中石蜡熔化过程中温度场、速度场变化及石蜡的体积膨胀。由此可见,对于相变材料熔化过程中传热传质现象的模拟严重依赖于对相变材料物性的假设。
有机类相变材料的熔化过程具有强烈的非线性特征,是一个包含多种热物理现象的复杂过程。目前对相变材料熔化过程由重力和密度变化引起的对流效应采用线性的Boussinesq假设,对整个过程中体积膨胀研究较少,本文基于EMT模型建立石蜡分别与具有代表性结构的GnP、SWCNT和金刚石纳米粒子(ND)复合后的复合相变材料物性,将VOF模型与焓-多孔介质模型耦合对这3类复合相变材料熔化过程的传热传质特性进行分析,实现对纳米复合相变材料熔化过程中固相导热、液相中自然对流和导热、相界面移动及复合相变材料在相变过程中体积变化等物理现象的较真实精细模拟。数值模拟结果为纳米复合相变材料的应用提供理论指导。
1 模型 1.1 物理模型 为了利用VOF模型与焓-多孔介质模型模拟有机纳米复合相变材料的熔化过程,建立如图 1所示的物理模型[21],为了研究石蜡材料的体积膨胀,空腔中2/3的体积填充石蜡,上界面与空气间为自由界面,底面和右侧为绝热面。左侧为定温加热面。g为重力加速度。
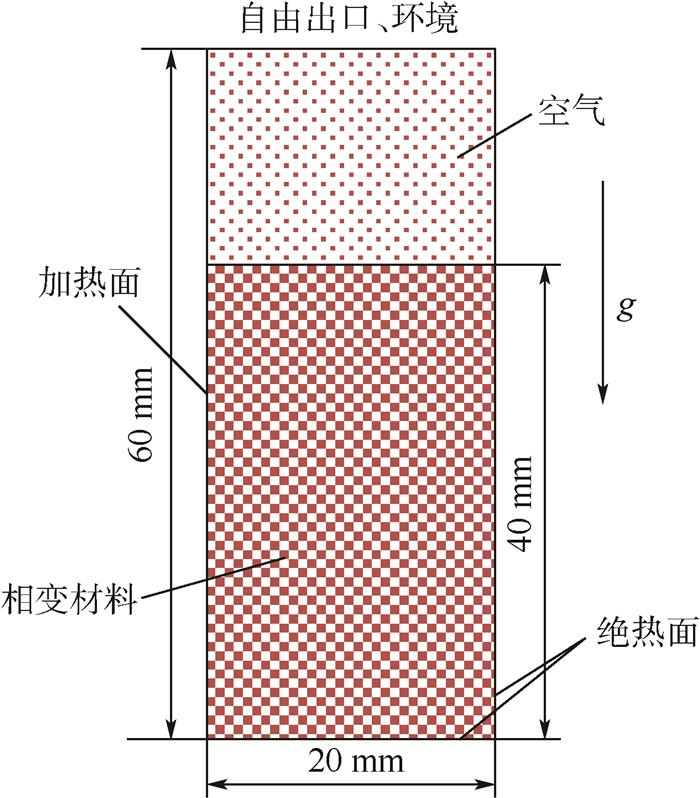 |
| 图 1 二维物理模型[21] Fig. 1 Two-dimensional physical model[21] |
| 图选项 |
1.2 数学模型 利用VOF模型和焓-多孔介质模型模拟有机纳米复合相变材料在熔化过程中固相导热、液相传热及自然对流现象、相界面移动等问题,采用EMT模型理论建立有机纳米复合相变材料的物性参数。
1.2.1 VOF模型 为了研究有机纳米复合相变材料在熔化过程中的传热传质现象,采用VOF模型求解相变材料与空气接触的自由表面的位置,求解区域包括相变材料和空气,其中空气作为第一相,相变材料作为第二相,不同相间的相界面通过求解各项体积分数的连续方程获得。
第二相的连续方程为
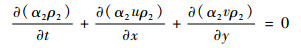 | (1) |
第一相的体积分数为
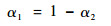 | (2) |
式中:u为x方向速度分量;v为y方向速度分量;αi为第i相的体积分数;ρi为第i相的密度。控制体中其他守恒方程的物性参数由单元中各组分的占比确定。
1.2.2 焓-多孔介质模型 能量方程为
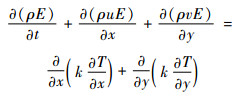 | (3) |
式中:k为控制体的导热系数;ρ为控制体的密度;T为控制体的温度;E为控制体中各相焓的质量平均值,其定义为
 | (4) |
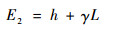 | (5) |
式中:E1为第一相的比焓;E2为第二相的比焓;h为相变材料的显热;γ为相变材料的液相体积组分;L为相变材料的潜热。
在求解区域中只求解混合相的动量方程,各相通过求解平均控制体的物性参数来影响动量方程。
动量方程为
 | (6) |
 | (7) |
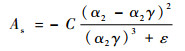 | (8) |
式中:P为压力;g为重力加速度;μpcm为相变材料动力黏度;C为相变材料固液混合区的形态常数;为了避免分母为0,ε=0.001。复合相变材料的液相组分γ的定义为
 | (9) |
式中:Tliquidus和Tsolidus分别为相变材料熔化的上限温度和下限温度。
对于有机纳米复合相变材料,其密度ρ、显热cp、潜热L、热膨胀系数β计算公式如下:
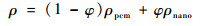 | (10) |
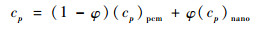 | (11) |
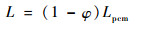 | (12) |
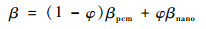 | (13) |
式中:下标nano和pcm分别表示纳米粒子和相变材料;φ为相变材料的体积组分比。
根据Krieger-Dougherty模型,动力黏度为
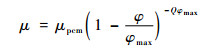 | (14) |
式中:φmax为最大填充因子;Q为材料的特性黏度。对于GnP、SWCNT和ND的最大填充因子分别为0.632、0.268和0.382,特性黏度分别为2.5、9.25和9.87[23-25]。
1.2.3 EMT模型 EMT模型被证明在考虑不同形状因素纳米粒子与周围相变材料的接触热阻情况下能够较为准确地确定有机纳米材料的等效导热系数[6, 10, 25],基于EMT模型和物性参数较为详细的石蜡材料建立GnP、SWCNT、ND与石蜡复合后的等效导热系数。
等效导热系数模型为
 | (15) |
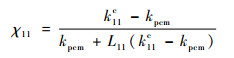 | (16) |
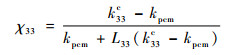 | (17) |
当as>1时,
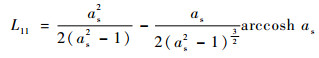 | (18) |
当as<1时,
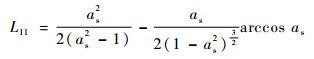 | (19) |
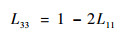 | (20) |
当as=1时,
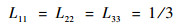 | (21) |
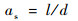 | (22) |
式中:keff为有机纳米复合相变材料的等效导热系数;kpcm为纯石蜡的导热系数;L11、L22和L33为形状因子;as为纳米粒子的长径比,对于ND,其形状为球形则长径比为1,对于SWCNT其尺度为长1 μm,直径1 nm,则长径比取1 000,而对于GnP,可看做厚度1 nm,直径1 μm,则其值为0.001;k11c和k33c分别为石蜡与纳米粒子复合后的相变微单元体轴向和径向的等效导热系数:
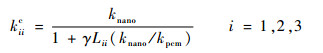 | (23) |
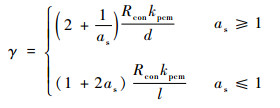 | (24) |
其中:knano为纳米粒子的导热系数;Rcon为纳米粒子与相变材料的接触热阻,文献[16]中其值为10-8 m2·K-1·W-1量级,在本文中,其值为根据文献[26]所列参数反算得出。
1.3 边界及初始条件设置 计算区域如图 1所示,相变材料中液相组分中的自然对流与空气的自然对流均由用户自定义函数(UDF)编译的材料密度随温度变化与重力同时作用引起。相变材料与空气交界面采用移动界面条件,且两相之间无相互渗透右侧边界及底面为绝热,左侧为定温边界条件,上表面为压力出口条件,计算区域中相变材料和空气的初始温度均为300 K,初始速度为0 m/s,相变材料占计算域的体积分数为2/3。
1.4 材料物性参数 为了对相变材料相变过程中传热传质现象进行更精细的模拟研究,本文选用物性参数较为明确且详细、熔化温度在306.15~308.15 K的石蜡作为相变材料。纳米材料物性参数见表 1[6, 10, 25]。根据物理和数学模型可得不同体积分数的相变材料物性见表 2。根据文献[27]中对石蜡材料的参数定义,石蜡在306.15~308.15 K温度区间内密度由850 kg/m3以线性关系递减为750 kg/m3。当T>308.15 K,定义石蜡的液相密度ρliquidus,pcm随时间变化为
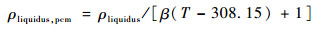 | (25) |
表 1 纳米材料物性参数[6, 10, 25] Table 1 Physical property parameters of nano materials[6, 10, 25]
| 物性参数 | ND | SWCNT | GnP |
| ρnano/(kg·m-3) | 3 300 | 1 100 | 2 200 |
| knano/(W·m-1·K-1) | 2 200 | 3 500 | 3 500 |
| (cp)nano/(kJ·kg-1·K-1) | 0.519 | 0.643 | 0.643 |
| βnano/(10-6K-1) | 1 | -0.3 | -0.7 |
表选项
表 2 相变材料物性参数 Table 2 Physical property parameters of phase change materials
| 物性参数 | 文献[27]中的相变材料 | 本文相变材料 | ||||
| GnP体积分数为1% | GnP体积分数为3% | GnP体积分数为5% | ND体积分数为3% | SWCNT体积分数为3% | ||
| ρsolidus/(kg·m-3) | 850 | 863.5 | 890.5 | 917.5 | 923.5 | 857.5 |
| ρliquidus/(kg·m-3) | 750 | 764.5 | 793.5 | 822.5 | 826.5 | 760.5 |
| ksolidus/(W·m-1·K-1) | 0.22 | 0.51 | 1.069 | 1.601 | 0.244 | 0.877 |
| kliquidus/(W·m-1·K-1) | 0.15 | 0.34 | 0.731 | 1.09 | 0.167 | 0.316 |
| cp/(kJ·kg-1·K-1) | 2 630 | 2 610 | 2 570.4 | 2 530.6 | 2 566.7 | 2 570.4 |
| β/(10-6K-1) | 1 000 | 990 | 970 | 950 | 970 | 960 |
| μ/(kg·m-1·s-1) | 0.003 184 | 0.003 52 | 0.004 33 | 0.005 4 | 0.003 4 | 0.004 27 |
| L/(kJ·kg-1) | 176 | 174.24 | 170.72 | 167.2 | 170.72 | 170.72 |
表选项
空气的密度ρair为与温度相关的函数为
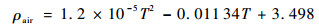 | (26) |
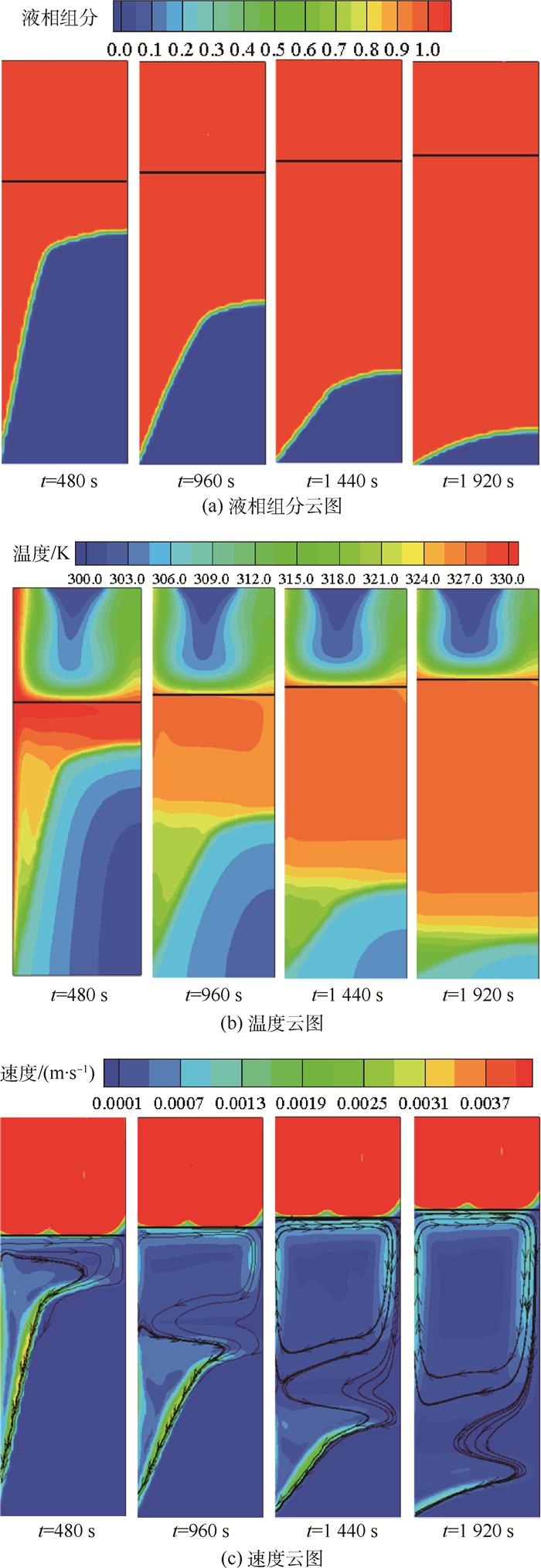
2 计算结果 2.1 纯石蜡熔化过程 图 2为纯石蜡在左侧定温333.15 K边界条件下的熔化过程中分别在480、960、1 440和1 920 s时的液相组分、温度及速度云图,各分图中黑色粗实线为纯石蜡与空气的相界面,液相组分是指相变材料熔化过程中液相状态的相变材料在整个相变材料中所占的体积分数,下同。由图 2(a)可知,在初始阶段,靠近加热壁面的石蜡首先熔化,同时随着石蜡熔化,石蜡的体积逐渐变大,而且上半部分的石蜡熔化更快;在图 2(b)中,靠近加热壁面的石蜡温度首先升高,但是随着时间的增加,石蜡内部温度场呈现出上半部分温度梯度逐渐变小;石蜡熔化过程中上半部分熔化快,上半部分温度梯度小这是由于石蜡固相密度大于液相密度,而且液相石蜡在温度升高过程中,密度逐渐变小,靠近加热壁面的石蜡首先熔化,并且在整个熔化过程中其体积膨胀速率最快,因此在重力作用下,产生的液相石蜡沿着石蜡与空气的交界面向右流动,而远离右侧加热面的石蜡温度低,其密度略大,则在重力作用下不断向位置较低的右侧流动,在液相石蜡中形成一个近似的涡如图 2(c)所示;而且速度云图还显示出,在石蜡熔化过程中,临近加热壁面和石蜡固液相交界面的石蜡流动速度相对较大,临近加热壁面的液相石蜡流动速度相对较大是由于石蜡的导热系数有限,热量无法充分在石蜡中扩散,在临近加热壁面处石蜡的温度梯度较大,导致这部分的石蜡密度梯度相应提高,进而产生较大的流速。临近石蜡固液相交界面的石蜡流动速度较大主要是由于此处临近石蜡的熔点,而石蜡在306.15~308.15 K范围内的密度变化剧烈(密度由850 kg/m3变为750 kg/m3)进而引起液相石蜡在重力作用下的较为剧烈的流动。
 |
| 图 2 石蜡熔化过程中液相组分、温度及速度云图 Fig. 2 Contours of liquid phase component, temperature and velocity of paraffin during melting process |
| 图选项 |
从图 2可以看出,在石蜡的充分熔化阶段,由重力引起的自然对流效应是石蜡内部热量传递的重要方式,在自然对流作用下,靠近加热面的高温石蜡密度小向上流动,加速了计算域中上部分石蜡的熔化和温度梯度变小,而靠近右侧绝热壁面的低温石蜡密度大不断向下流动补充进去。呈现出底部靠近加热壁面的石蜡固液相界面变化速率较小,且温度梯度大于上部分的石蜡温度梯度。
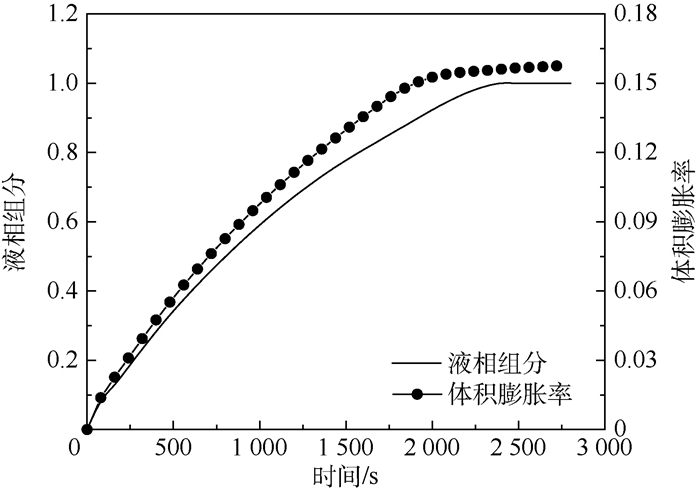
图 3为石蜡在熔化过程中的液相组分及石蜡体积膨胀率的变化。由图 3可知石蜡在初始熔化过程中,熔化速率较高,体积膨胀速率较大,随着石蜡熔化过程的发展,大约在液相组分超过0.6时,石蜡的熔化速率逐渐降低直至石蜡全部熔化。在石蜡的熔化前半部分,石蜡的体积膨胀与石蜡的熔化速率体现出相似的变化趋势,而到后期两者趋势相似但是出现一些差异,石蜡的体积膨胀较早结束,这是由于在定温边界条件下,整个石蜡液相区域由于自然对流的作用其温度梯度变小,逐渐接近333.15 K,石蜡的体积膨胀从初始的液相膨胀与固液相变化之和变成主要由固液相变产生。
 |
| 图 3 石蜡熔化过程中体积膨胀率及液相组分变化 Fig. 3 Variation of volume expansion ratio and liquid phase component of paraffin during melting process |
| 图选项 |
2.2 不同种类纳米复合相变材料的熔化过程 根据EMT模型推导出了石蜡与ND、SWCNT和GnP 3种高导热纳米材料复合后的纳米复合相变材料物性,在定温333.15 K的边界条件下,复合相变材料熔化过程中液相组分变化如图 4所示,其中添加了体积分数为3%的ND的纳米复合相变材料其熔化时间相比纯石蜡只缩短了4.05%,这是由于添加体积分数为3%的ND只将石蜡的固相和液相导热系数很有限地提升了11%,而其黏度增加了8%,黏度的增加导致复合相变材料在熔化过程中的自然对流效应减弱,因此ND材料对石蜡的熔化速率加快效果很有限;对于添加了体积分数为3%的SWCNT的纳米复合相变材料,其熔化时间缩短了40.4%;添加了体积分数为3%的GnP的纳米复合相变材料熔化时间最短,相比纯石蜡,其熔化时间缩短了69%。由此可见3种纳米材料中,GnP的导热强化效果最佳,能够实现有机相变材料对热量的快速吸收存储。
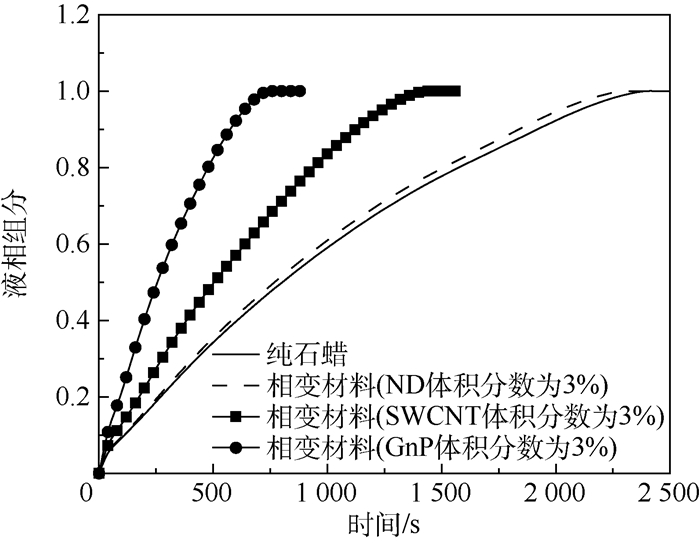 |
| 图 4 相变材料熔化过程中液相组分变化 Fig. 4 Variation of liquid phase component of phase change material during melting process |
| 图选项 |
图 5为纯石蜡和添加体积分数均为3%的ND、SWCNT、GnP的复合相变材料在熔化过程中第510 s的液相组分、温度和速度云图。纯石蜡与体积分数均为3% ND复合相变材料的液相界面、温度分布及速度分布较为相近。在第510 s,添加体积分数均为3% ND的复合相变材料的体积膨胀小于纯石蜡的体积膨胀,这是由于添加体积分数均为3%的ND以后,纳米复合相变材料的体积膨胀率相比纯石蜡缩小了2%,潜热值损失了3%,而在510 s时,其熔化进程仅比纯石蜡快了3.7%,由此可见,ND材料的相变材料导热强化作用很小;从速度云图中可知,无论是纯石蜡还是复合相变材料,其熔化过程中,液相中速度最大的3个区域为临近加热面、临近石蜡与空气交界面和临近石蜡固液交界面这3个区域。添加了体积分数均为3% GnP的复合相变材料在第510 s时,其固相体积最小,熔化速率最快,相变材料区域中温度梯度最小,而添加了体积分数均为3% SWCNT的复合相变材料的温度梯度介于两者之间。因此,3种相变材料中GnP的导热强化效果最佳、对相变材料熔化速率的促进效果最好,在相同边界条件下,GnP纳米复合相变材料中温度分布最均匀。
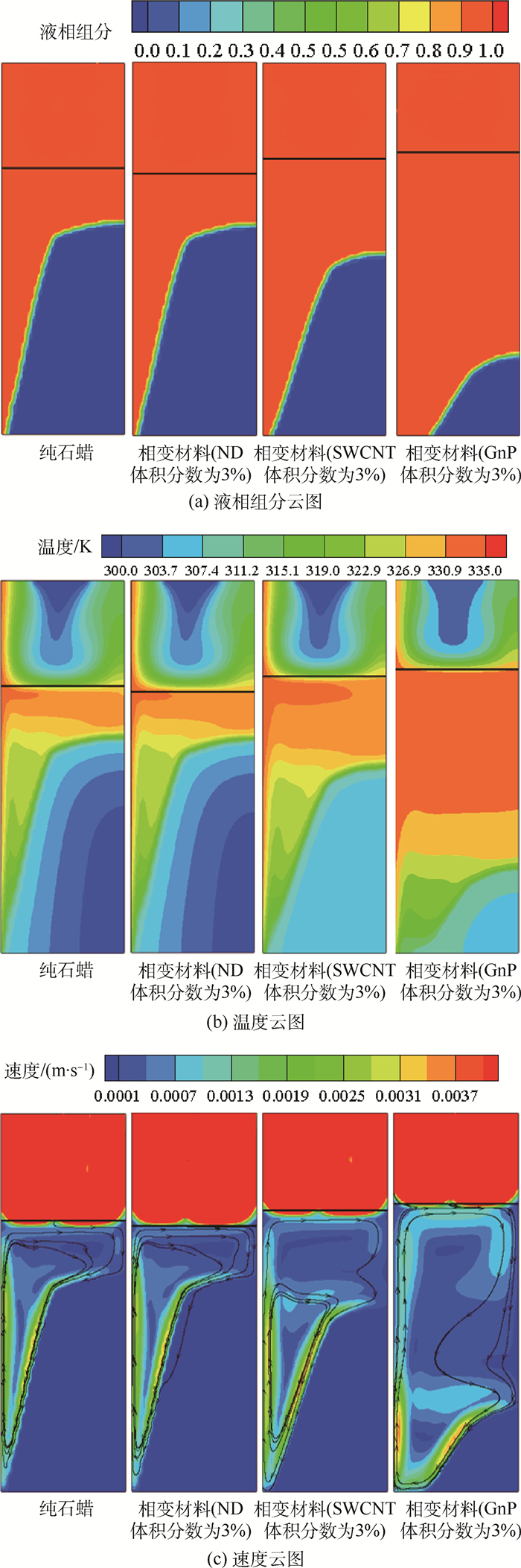 |
| 图 5 相变材料熔化过程中液相组分、温度及速度云图 Fig. 5 Contours of liquid phase component, temperature and velocity of phase change material during melting process |
| 图选项 |
2.3 GnP纳米复合相变材料熔化过程
2.3.1 不同体积分数GnP对熔化过程的影响 根据EMT模型计算得出的纳米复合相变材料物性,在添加同体积分数的纳米材料时,相比于SWCNT纳米复合相变材料与ND纳米复合相变材料,GnP纳米复合相变材料的固液两相的导热性能最佳,为了研究不同体积分数GnP材料对复合相变材料熔化速率的影响效果,图 6为添加不同体积分数GnP的复合相变材料在左侧边界定温333.15 K条件下的熔化过程液相组分变化曲线。在333.15 K温度边界条件下,添加体积分数为1%、3%和5% GnP的复合相变材料的熔化时间分别为1 301、740和553 s,相比于纯石蜡的2 393 s熔化时间,体积分数为1%、3%和5%的GnP材料能够有效缩短复合相变材料熔化时间达45.6%、69%和76.9%。在此需要指出的是当GnP材料体积组分增加时,相比于纯石蜡,复合相变材料的潜热值如表 2所示分别降低了1%、3%和5%。随着GnP材料体积组分的增加,复合相变材料的熔化速率逐渐提高,但是体积分数为3%和5%的复合相变材料熔化速率相差较小,这是由于添加纳米材料导致复合相变材料的黏度变大,同时导热性能增加引起复合相变材料中温度梯度变小,两者同时作用导致复合相变材料中由密度差引起的自由对流变弱,进而使得复合相变材料的熔化速率提高效果相对减弱。因此在GnP纳米复合相变材料应用过程中,需要综合考虑性能强化、熔化速率提升和潜热损失之间的关系,优选合适体积分数的GnP材料实现相变材料的导热性能强化。
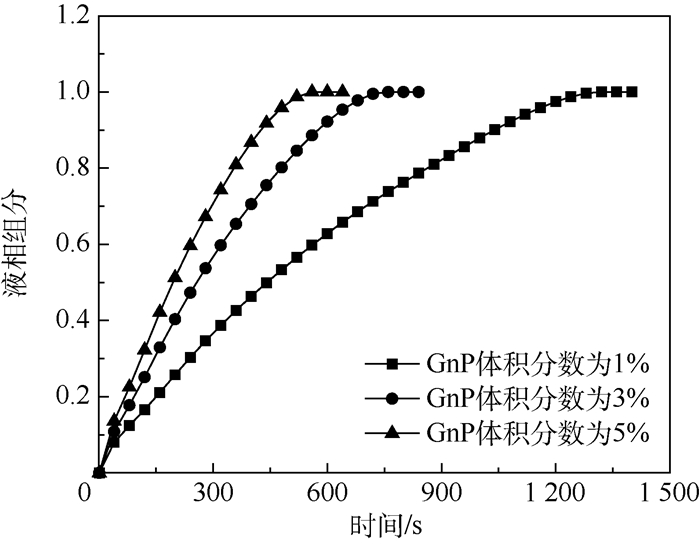 |
| 图 6 不同体积分数GnP的复合相变材料熔化过程中液相组分变化 Fig. 6 Variation of liquid phase component of composite phase change material with different volume fractions of GnP during melting process |
| 图选项 |
2.3.2 不同边界温度对复合相变材料熔化过程的影响 相变材料在熔化过程中,边界温度的升高不仅提高了换热功率,加速了相变材料的熔化速率,同时由于材料的密度与温度相关,所以内部温度梯度对熔化过程中的自然对流的强度有着重要的作用,进而影响相变材料的熔化速率。不同边界温度下GnP复合相变材料的液相组分变化如图 7所示,GnP复合相变材料中的GnP材料体积分数选用3%。相比于T=323.15 K,当T为328.15、333.15和338.15 K时,GnP复合相变材料的熔化时间分别缩短了25.3%、40.2%和49.9%。随着壁面温度的升高,GnP复合相变材料的整个熔化过程时间缩短、熔化速率变大。但是随着壁面温度的升高,GnP复合相变材料的熔化速率提升效率逐渐降低,因此在实际储能过程中需综合考虑相变材料熔点、热源温度和复合相变材料的导热性能之间的优化匹配关系。
 |
| 图 7 不同边界温度时复合相变材料熔化过程中液相组分变化 Fig. 7 Variation of liquid phase component of composite phase change material with different boundary temperature during melting process |
| 图选项 |
3 结论 本文利用EMT模型得出了具有代表性的3种纳米材料与熔点在306.15~308.15 K之间的石蜡复合后的纳米复合相变材料物性,采用VOF模型耦合焓-多孔介质模型数值模拟了相变材料的熔化过程,得到:
1) 根据EMT模型,ND、SWCNT和GnP 3种纳米材料在同体积组分情况下,GnP纳米复合相变材料的固液相导热性能最佳,添加体积分数为3% GnP的纳米复合相变材料的固相导热系数相比纯石蜡提高了486%。
2) 纯石蜡在整个熔化过程中体积膨胀了近16%,其体积膨胀变化率与液相组分变化率具有相似性;相变材料熔化过程中,在液相中由重力引起的自然对流对相变材料的熔化过程具有重要的促进作用。在临近加热面、固液相界面、气液相界面处的自然对流强度最大。
3) 在石蜡中添加GnP能够有效提高其熔化速率,当复合相变材料中GnP的体积分数为3%时,其熔化时间能够有效缩短69%。但是在实际应用中,需要综合考虑潜热损失、熔化速率和导热性能之间的关系。
4) 升高边界温度能够有效缩短GnP复合相变材料的熔化时间,但是相变材料熔点、热源温度与相变材料导热性能之间存在优化匹配关系。
参考文献
| [1] | 张寅平, 胡汉平, 孔祥冬, 等. 相变贮能:理论和应用[M].合肥: 中国科学技术大学出版社, 1996: 289-332. ZHANG Y P, HU H P, KONG X D, et al. Phase change energy storage:Theory and application[M].Hefei: Press of University of Science and Technology of China, 1996: 289-332.(in Chinese) |
| [2] | MIRó L, GASIA J, CABEZA L F. Thermal energy storage(TES) for industrial waste heat (IWH) recovery:A review[J].Applied Energy, 2016, 179: 284–301.DOI:10.1016/j.apenergy.2016.06.147 |
| [3] | WU S, LI T X, YAN T, et al. High performance form-stable expanded graphite/stearic acid composite phase change material for modular thermal energy storage[J].International Journal of Heat and Mass Transfer, 2016, 102: 733–744.DOI:10.1016/j.ijheatmasstransfer.2016.06.066 |
| [4] | BOSE P, AMIRTHAM V A. A review on thermal conductivity enhancement of paraffinwax as latent heat energy storage material[J].Renewable and Sustainable Energy Reviews, 2016, 65: 81–100.DOI:10.1016/j.rser.2016.06.071 |
| [5] | KRISHNA J, KISHORE P S, SOLOMON A B. Heat pipe with nano enhanced-PCM for electronic cooling application[J].Experimental Thermal and Fluid Science, 2017, 81: 84–92.DOI:10.1016/j.expthermflusci.2016.10.014 |
| [6] | LI T, LEE J H, WANG R, et al. Heat transfer characteristics of phase change nanocomposite materials for thermal energy storage application[J].International Journal of Heat and Mass Transfer, 2014, 75: 1–11.DOI:10.1016/j.ijheatmasstransfer.2014.03.054 |
| [7] | LI T, LEE J H, WANG R, et al. Enhancement of heat transfer for thermal energy storage application using stearic acid nanocomposite with multi-walled carbon nanotubes[J].Energy, 2013, 55: 752–761.DOI:10.1016/j.energy.2013.04.010 |
| [8] | FANG X, FAN L W, DING Q, et al. Increased thermal conductivity of eicosane-based composite phase change materials in the presence of graphene nanoplatelets[J].Energy and Fuels, 2013, 27(7): 4041–4047.DOI:10.1021/ef400702a |
| [9] | ARICI M, TVTVNCV E, KAN M, et al. Melting of nanoparticle-enhanced paraffin wax in a rectangular enclosure with partially active walls[J].International Journal of Heat and Mass Transfer, 2017, 104: 7–17.DOI:10.1016/j.ijheatmasstransfer.2016.08.017 |
| [10] | HARISH S, OREJON D, TAKATA Y, et al. Thermal conductivity enhancement of lauric acid phase change nanocomposite with graphene nanoplatelets[J].Applied Thermal Engineering, 2015, 80: 205–211.DOI:10.1016/j.applthermaleng.2015.01.056 |
| [11] | MOTAHAR S, ALEMRAJABI A A, KHODABANDEH R. Experimental investigation on heat transfer characteristics during melting of a phase change material with dispersed TiO2 nanoparticles in a rectangular enclosure[J].International Journal of Heat and Mass Transfer, 2017, 109: 134–146.DOI:10.1016/j.ijheatmasstransfer.2017.01.109 |
| [12] | 陈杨华, 李钰, 郭文帅, 等. 石蜡基碳纳米管复合相变蓄冷材料的热性能研究[J].制冷学报, 2014, 35(5): 110–113. CHEN Y H, LI Y, GUO W S, et al. Thermophysical properties of cool storage of paraffin-based composite phase change materials filled with carbon nanotubes[J].Jounal of Refrigeration, 2014, 35(5): 110–113.DOI:10.3969/j.issn.0253-4339.2014.05.020(in Chinese) |
| [13] | NAN C W. Effective-medium theory of piezoelectric composites[J].Journal of Applied Physics, 1994, 76(2): 1155–1163.DOI:10.1063/1.357839 |
| [14] | NAN C W, BIRRINGER R, CLARKE D R, et al. Effective thermal conductivity of particulate composites with interfacial thermal resistance[J].Journal of Applied Physics, 1997, 81(10): 6692–6699.DOI:10.1063/1.365209 |
| [15] | SANTAMARíA-HOLEK I, MENDOZA C I. The rheology of concentrated suspensions of arbitrarily-shaped particles[J].Journal of Colloid and Interface Science, 2010, 346(1): 118–126.DOI:10.1016/j.jcis.2010.02.033 |
| [16] | DAS N, TAKATA Y, KOHNO M, et al. Melting of graphene based phase change nanocomposites in vertical latent heat thermal energy storage unit[J].Applied Thermal Engineering, 2016, 107: 101–113.DOI:10.1016/j.applthermaleng.2016.06.166 |
| [17] | AL-ABIDI A A, BIN MAT S, SOPIAN K, et al. CFD applications for latent heat thermal energy storage:A review[J].Renewable and Sustainable Energy Reviews, 2013, 20: 353–363.DOI:10.1016/j.rser.2012.11.079 |
| [18] | NASTAC L, ZHANG L, THOMAS B G, et al.CFD modeling and simulation in materials processing[C]//Proceedings of TMS2016 Annual Meeting.Berlin: Springer, 2016: 870202. |
| [19] | SATTARI H, MOHEBBI A, AFSAHI M M, et al. CFD simulation of melting process of phase change materials (PCMs) in a spherical capsule[J].International Journal of Refrigeration, 2017, 73: 209–218.DOI:10.1016/j.ijrefrig.2016.09.007 |
| [20] | SOLOMON L, ELMOZUGHI A F, OZTEKIN A, et al. Effect of internal void placement on the heat transfer performance-Encapsulated phase change material for energy storage[J].Renewable Energy, 2015, 78: 438–447.DOI:10.1016/j.renene.2015.01.035 |
| [21] | 夏莉, 张鹏, 王如竹. 具有自由表面的固-液相变的数值模拟与实验研究[J].热能动力工程, 2010, 25(5): 505–509. XIA L, ZHANG P, WANG R Z. Numerical simulation and experimental study of the solid-liquid phase change on free surface[J].Journal of Engineering for Thermal Energy & Power, 2010, 25(5): 505–509.(in Chinese) |
| [22] | YE W B, ZHU D S, WANG N. Fluid flow and heat transfer in a latent thermal energy unit with different phase change material (PCM) cavity volume fractions[J].Applied Thermal Engineering, 2012, 42: 49–57.DOI:10.1016/j.applthermaleng.2012.03.002 |
| [23] | KRIEGER I M, DOUGHERTY T J. A mechanism for non-Newtonian flow in suspensions of rigid spheres[J].Transactions of the Society of Rheology, 1959, 3(1): 137–152.DOI:10.1122/1.548848 |
| [24] | SMITH H.Transport phenomena[M]//KUPERMAN A W.Encyclopedia of applied physics.Weinhem: Wiley, 2003: 270-272. |
| [25] | KHODADADI J M, FAN L, BABAEI H. Thermal conductivity enhancement of nanostructure-based colloidal suspensions utilized as phase change materials for thermal energy storage:A review[J].Renewable and Sustainable Energy Reviews, 2013, 24: 418–444.DOI:10.1016/j.rser.2013.03.031 |
| [26] | DAS N, KOHNO M, TAKATA Y, et al. Enhanced melting behavior of carbon based phase change nanocomposites in horizontally oriented latent heat thermal energy storage system[J].Applied Thermal Engineering, 2017, 125: 880–890.DOI:10.1016/j.applthermaleng.2017.07.084 |
| [27] | 吴淑英.纳米复合蓄热材料强化相变传热实验与数值模拟研究[D].广州: 华南理工大学, 2010. WU S Y.Enhanced heat transfer experimental and simulation research of nanocomposite phase change materials[D].Guangzhou: South China University of Technology, 2010(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10561-2010227792.htm |
