元素掺杂是一种有效的半导体改性方式。科研人员对此进行了研究,实验表明Se掺杂GeTe相变存储材料具有更优异的性质。Vinod等制备了不同Se掺杂量的(GeTe)1-xSex薄膜,指出Se掺杂能大幅提高GeTe的再结晶温度,增强其数据保持力[10];Se掺杂同时能提高GeTe非晶的光学带隙,10%的Se掺杂可大幅提高GeTe的非晶电阻,使晶相与非晶相的电阻差异增加2个数量级[11]。由于GeTe中可以存在高达8%~10%的本征Ge空位[12-13],Vinod和Sangunni推测掺入的Se原子可能占据Ge空位的位置,从而抑制了GeTe的结晶[11]。然而,这些实验研究主要针对Se掺杂后的物相组成、电学性质、光学性质和热动态性质等。Se掺杂对于体系的原子构型、成键情况等微观性质的影响以及性能增强的作用机制尚不明晰。这些微观性质需要通过第一性原理计算模拟来进一步理解,从而更好地为未来实验提供理论指导。此外,与GeTe同系列的Ge2Te2Sb5的Se掺杂实验表明,当GST1-xSex中Se含量x超过10%时,出现了奇特的相转变性质:掺杂后的GST材料在受热时直接由无定型态结晶为稳态六方,而跳过中间的亚稳面心立方相(face-centered cubic, fcc)[14]。而Wang等进行了Sb2Se掺杂Ge2Sb2Te5的研究,指出当Se原子含量超过9%时,亚稳面心立方相转变为稳定六方相的过程被抑制[15]。Se掺杂PCM对相转变过程的影响较大。对硫系化合物相变存储材料的Se掺杂进行计算研究,也可以为解释相变存储材料晶相演变机制提供线索。
本文采用第一性原理计算方法,对Se掺杂完美GeTe和含本征Ge空位的GeTe的几何构型、成键情况和电子性质进行了研究。结果表明,对于完美GeTe,Se优先取代Te原子。而对于存在本征Ge空位的GeTe晶体,Se掺杂原子不会占据Ge空位,而倾向于取代Ge空位最近邻Te原子。Se原子与Ge空位的相互吸引,形成了较强的Ge—Se键,抑制了GeTe相变存储材料的结晶,从而提高了其数据保持能力和服役温度。Se原子与本征Ge空位最近邻时,使两相的电子局域函数(Electron Localization Function, ELF)分布和体积更加接近,可能是导致奇特相转变性质的重要原因。
1 计算方法 本文计算基于维也纳大学开发的从头算模拟软件包(Vienna Ab-initio Simulation Package,VASP)[16]。体系采用了Ge(4s24p2)、Te(5s25p4)的标准PAW赝势。与先前的GeTe计算一致,本文使用了广义梯度近似GGA-PBE[17-19]来描述交换关联泛函。截断能设置为350 eV,k点设置为3×3×3的Gamma中心k点网格。截断能和k点的设置都进行了收敛性测试。自洽计算的收敛判据设置为电子步能量差小于10-5 eV,而结构弛豫收敛判据则为每个原子上的残余应力均小于0.1 eV/nm。
GeTe包含2个晶相,分别为稳态菱方相(rhombohedral)和高温亚稳面心立方相[20]。信息存储主要通过GeTe非晶态和稳态菱方相之间的快速转变来实现[21]。因此,本文主要研究Se掺杂对于菱方相的影响,并与Se掺杂的面心立方相进行了类比分析。GeTe菱方相是一种扭曲的氯化钠结构,可以看做由GeTe面心立方相中Ge原子亚结构和Te原子亚结构沿[111]方向错动一定距离形成的[22]。这种结构变形属于派尔斯变形(Peierls distortion)[23]。GeTe菱方相中形成了交替的3个Ge—Te长键和3个Ge—Te短键。从[111]方向观察,GeTe也可以被当做层状结构;其中,由Ge—Te短键连接的原子可视为处在同一层。基于GeTe菱方结构的惯用胞,构建了2×2×2的超胞,包含64个原子,结构如图 1(a)所示。对GeTe面心立方相,同样采用了2×2×2的超胞,如图 1(b)所示。所有构型均进行了结构弛豫。计算优化得到的单胞晶格数据如表 1所示。对于无缺陷的菱方相和面心立方相,计算得到晶格常数和晶胞角度分别为a0=0.608 6 nm,α= 88.14°和a0=0.601 9 nm,α=90°与实验测量值及前人的计算值吻合[20, 24]。由于GeTe中存在大量的本征Ge空位,在掺杂分析中必须考虑Ge空位的影响。对于存在本征Ge空位的GeTe体系的Se掺杂计算,分别构造了Ge31Te32(共63个原子)的菱方结构和面心立方结构,并对所有构型均进行了结构优化。
 |
| 图 1 GeTe晶体结构 Fig. 1 Crystalline structure of GeTe |
| 图选项 |
表 1 计算得到的单胞晶格数据 Table 1 Calculated crystal lattice datas of single cell
| 结构 | a0/nm | α/(°) | V/nm3 | Eg/eV |
| 菱方相GeTe | 0.608 6 | 88.14 | 0.225 05 | 0.62 |
| 菱方相Ge32Te31Se1 | 0.608 3 | 87.94 | 0.224 62 | 0.58 |
| 菱方相Ge31Te31Se1 | 0.605 8 | 87.77 | 0.221 88 | 0.58 |
| 菱方相Ge31Te32 | 0.606 2 | 87.82 | 0.222 34 | 0.59 |
| 菱方相Ge31Se1Te32 | 0.608 4 | 88.12 | 0.224 86 | — |
| 面心立方相GeTe | 0.601 9 | 90 | 0.218 08 | 0.38 |
| 面心立方相Ge32Te31Se1 | 0.600 3 | 90 | 0.216 34 | 0.40 |
| 面心立方相Ge31Te31Se1 | 0.602 4 | 90 | 0.218 52 | 0.52 |
| 面心立方相Ge31Te32 | 0.599 4 | 90 | 0.215 37 | 0.31 |
| 面心立方相Ge31Se1Te32 | 0.601 0 | 90 | 0.217 04 | — |
| ??注:晶格常数a0、晶胞角度α、惯用胞体积V以及带隙Eg。 | ||||
表选项
掺杂形成能的计算式[25-26]为
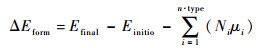 | (1) |
式中:Efinal和Einitio分别为末态体系和初始体系的总能;μi为第i种原子的化学势,通常是其最稳定单质中单个原子的能量;Ni为缺陷形成后与形成前第i种原子的数量差。
本文考虑了缺陷生长环境对于掺杂形成能的影响。当Se取代Te时,在富Te情况下,被取代的Te原子视为与体相Te单质中的一个Te原子结合;而富Ge情况下,被取代的Te原子则视为与体相Ge单质中的一个Ge原子结合,重新形成新的Ge—Te单元。故而在富Te情况下,Te原子化学势即为Te体相单质中单个原子的能量,而Ge原子化学势则为μGe=μGeTe-μTe。其中μGeTe为GeTe晶相中Ge、Te原子对的能量,μTe为Te原子化学势。反之,在富Ge情况下,Ge原子化学势为Ge体相单质中单个原子能量,而Te原子化学势为μTe=μGeTe-μGe。
2 结果与讨论 2.1 GeTe完美晶体的Se掺杂 本节研究了Se掺杂GeTe完美晶体。当掺杂Se原子时,可能的占位情况有:取代Ge原子、取代Te原子或占据间隙位置。由于Se间隙原子造成较大的晶格畸变,具有较高形成能,故不作比较。计算得到不同取代位置的形成能Ef如表 2所示。
表 2 Se掺杂完美GeTe不同取代位置的形成能 Table 2 Formation energy of Se doping at different substitution positions in ideal GeTe eV
| eV | |||||
| Se掺杂 | 菱方相 | 面心立方相 | |||
| 富Ge | 富Te | 富Ge | 富Te | ||
| 取代Ge | 1.05 | 0.88 | 0.67 | 0.50 | |
| 取代Te | -0.41 | -0.24 | -0.54 | -0.37 | |
表选项
从表 2可以看出,对于GeTe的菱方相和面心立方相,无论在富Ge或富Te的情况下,掺杂的Se原子均优先取代Te原子。Se掺杂的形成能为负,表明Se原子容易掺杂到GeTe中。从表 1中还可以看出,少量Se掺杂对于GeTe完美晶体菱方结构和面心立方结构的体积影响很小,造成体积的微量坍缩。主要由于Se的原子半径小于Te。此外,较低的形成能和较小的晶格变化,表明在GeTe中能实现高浓度的Se掺杂。这与实验观测一致,实验中Se掺杂量达到20%时,依然没有造成GeTe结构的破坏[11]。
对GeTe完美晶体的Se掺杂进行了电子局域函数分析,如图 2所示。由于Se、Te属于同主族元素,Se原子与Te原子具有十分相似的电子局域函数分布。对于GeTe菱方相,由于派尔斯形变,形成的Ge—Te短键键长RGe1-Te=0.286 nm,Ge—Te长键键长RGe2-Te=0.325 nm,与实验值十分接近[20]。当Se取代Te原子时,也呈现出长短键交替的情况,然而,其中Ge—Se短键变得更短(RGe1-Se=0.266 nm),而Ge—Se长键变得更长(RGe2-Se=0.334 nm)。这是由于Se原子具有较强的电负性,与其同层最近邻Ge原子(Ge1)形成了较强的Ge—Se键。同时Se原子较小的原子半径,使得其与邻层最近邻Ge原子(Ge2)的键合变弱。Se掺杂使得体系中原子分层排布的现象更加明显。
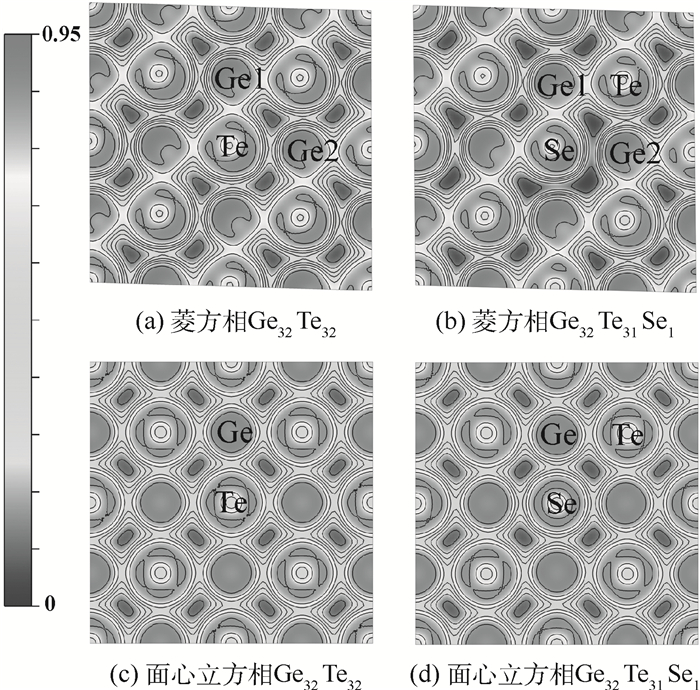 |
| 图 2 完美GeTe晶体掺杂前后在(100)面上的ELF截面图(等高线间隔为0.14) Fig. 2 ELF contour plots on (100) plane for Se doped ideal GeTe crystal (interval is 0.14) |
| 图选项 |
此外,GeTe面心立方结构则具有6个等同的Ge—Te键,RGe-Te=0.301 nm,如图 2(c)所示。Se取代Te原子之后,Se原子的电子局域函数依然呈球状分布,形成6个等同的Ge—Se键,RGe-Se=0.292 nm,键长较Ge—Te键变短。两相中,Se掺杂均形成了较强的Ge—Se键,对Ge原子的移动起到抑制作用。Ge—Se原子主要为共价键结合,详细解释见后续的电子态密度分析。
2.2 含本征Ge空位的GeTe晶体的Se掺杂 本文2.1节计算基于GeTe的完美晶体模型。然而,实际上GeTe是一种非化学计量比的半导体,GeTe中存在高浓度的本征Ge空位。对GeTe进行掺杂研究时,必须考虑其中大量存在的本征Ge空位的影响。由于Ge、Se具有相近的离子半径(分别为67 pm和64 pm),Vinod和Sangunni[11]推测Se原子可能占据Ge空位的位置。因此,本文研究了Se掺杂含Ge空位的GeTe体系(Ge31Te32,共63个原子)。对Se占据Ge空位和Se取代Te原子的情况作了重点比较。
根据掺入的Se原子与Ge空位距离的不同,构建了多种模型。计算得到的形成能如图 3所示。当Se占据Ge空位时,Se原子与Ge空位距离即为0。对于菱方相,Ge空位最近邻Te原子有2种,分别为同层最近邻和邻层最近邻,用A1和A2表示。点间连线以便于观察。从图 3可以看出,无论对于菱方相还是面心立方相,当存在Ge空位时,掺杂的Se原子依然不会占据Ge空位位置,而是倾向于取代Ge空位最近邻的Te原子。对于菱方相,则优先取代Ge空位同层最近邻的Te原子。从另一个角度来看,Se杂质原子与Ge空位具有一定互相吸引作用。这种吸引作用会抑制Ge空位的移动。
 |
| 图 3 Se掺杂Ge31Te32菱方相和Ge31Te32面心立方相的形成能随Se原子与Ge空位之间距离的变化 Fig. 3 Formation energy of Se doping in rhombohedral Ge31Te32 and fcc Ge31Te32 versus distance between doped Se atom and Ge vacancy |
| 图选项 |
图 4为菱方相中Se取代Ge空位同层最近邻Te原子时(A1构型)和邻层最近邻Te原子时(A2构型)的原子结构, 虚线环表示Ge空位,深色球、浅色球分别表示Ge、Te原子,1号原子为Se。形成能计算结果表明,Se原子更倾向于占据Ge空位同层最近邻的位置。A1与A2之间形成能差异在50 meV/supercell左右。由图 4可以发现,Ge空位使体系中形成了较强的层间Ge—Te键,部分抵消了Ge空位带来的影响。A1构型的成键情况为:3个Ge—Se键(R1-2=R1-3=0.256 nm,R1-4=0.297 nm),2个层间Ge—Te较强键(R5-6=R7-8=0.312 nm)。A2构型成键情况为:3个Ge—Se键(R1-2=0.282 nm,R1-3=R1-4=0.260 nm),3个层间Ge—Te键(R5-6=R7-8=0.312 nm,R9-10=0.309 nm)。由于Se取代同层的最近邻Te原子(A1)相较于邻层的最近邻Te原子(A2)所引起的晶格畸变更小,因此更容易形成。
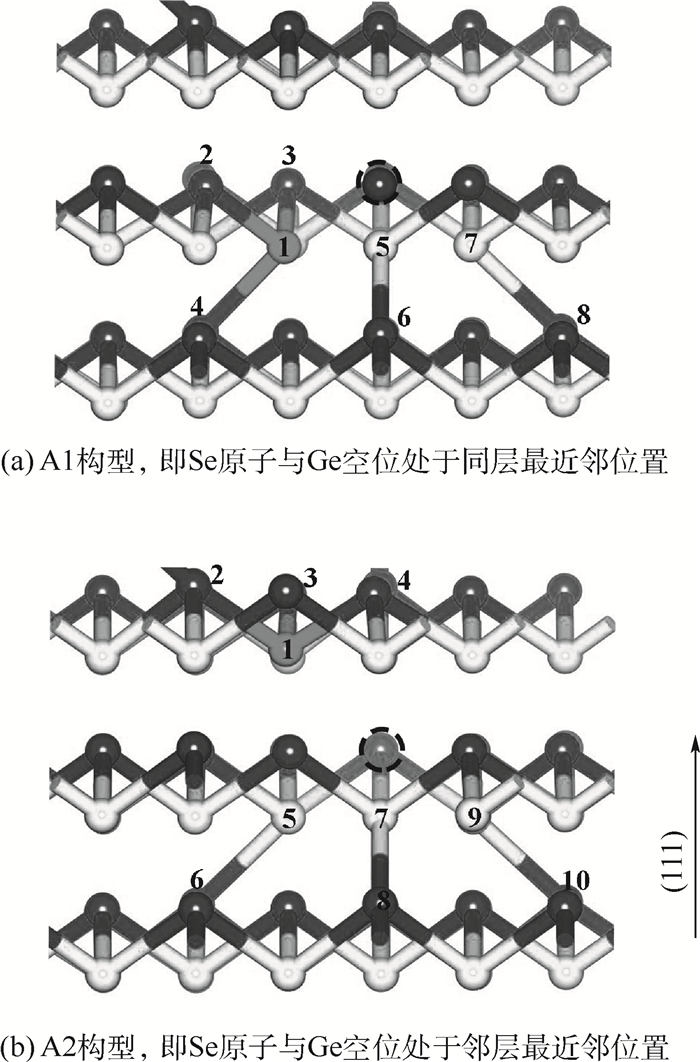 |
| 图 4 Se掺杂GeTe的2种构型 Fig. 4 Two configurations of Se doped GeTe |
| 图选项 |
进一步对含Ge空位的菱方相和面心立方相的Se掺杂进行了电子局域函数分析,如图 5所示。其中图 5(a)~(c)为菱方相,图 5(d)~(f)为面心立方相。从图 5(a)中可以看出,对于菱方相,Ge空位对ELF的影响十分局域。Ge空位同层最近邻Te原子(Te1), 与邻层的Ge原子(Ge1)形成较强的层间Ge—Te结合(RGe1-Te1=0.311 nm)。图 5(b)为Se占据Ge空位同层最近邻时的情况,ELF分布与未掺杂体系十分接近,因此Se掺杂对GeTe菱方相电子分布的作用较小。而当Se占据Ge空位时,Se原子周围的电子分布类似于球形,形成近乎等同的6个Se—Te键,(RSe-Te1=0.309 nm,RSe-Te2=0.316 nm)。此时Se杂质原子对周围Te原子的电子局域函数分布造成较大的影响,导致体系能量升高,从而具有较高的形成能。掺杂的Se原子不会占据Ge空位。
 |
| 图 5 Se掺杂含Ge空位的GeTe体系的在(100)面上的ELF截面图(等高线间隔为0.12) Fig. 5 ELF contour plots on (100) plane for Se doped GeTe systems with intrinsic Ge vacancy (interval is 0.12) |
| 图选项 |
对于GeTe面心立方相,Ge空位对电子局域函数的影响也较小。与众不同的是,当掺入的Se原子与Ge空位最近邻时,造成电子局域函数的较大变化。此时GeTe体系中的电子局域函数分布甚至接近于菱方相中的分布,部分Ge—Te键出现长短键分化,从而降低了体系的能量,形成能较低。Se掺杂模糊了GeTe面心立方相和菱方相的界线。而Se占据Ge空位时,对周围Te原子的影响较大,形成能较高,不易存在。
以上分析得出,对于GeTe实际晶体,Se掺杂元素并不会占据Ge空位的位置。掺入的Se原子更倾向于靠近Ge空位,二者具有一定吸引作用,从而限制了Ge空位的移动。GeTe相变存储材料的相转变与电场下Ge空位的定向移动关系密切[27-28]。Se掺杂对于Ge空位移动的抑制作用,是导致其再结晶温度升高的重要原因。此外,实验和计算指出,GeTe和Ge2Sb2Te5中大量存在的本征Ge空位并非以单一Ge空位的形式存在,而是形成多空位群或者小孔洞[29-30]。Se杂质原子可能聚集在空位群或孔洞处,从而对相变存储材料的动态相变过程起到更大的影响。Se掺杂含有Ge空位的GeTe体系,使得两晶相的相似度增加。这种性质也可能是实验中观察到Se掺杂PCM出现奇特相变现象的原因。
另外,从表 1晶胞数据中可以明显观察到,对于含Ge空位的菱方相,Se掺杂导致晶胞体积减小。而反常的是,Se掺杂含Ge空位的面心立方相导致晶格常数和体积增大。主要是Se掺杂后电子局域函数变化所造成的。Se掺杂后,GeTe菱方相和面心立方相将具有更相近的晶格常数和体积。这对于减小GeTe相变过程中的体积变化十分有益,有助于提高相变存储材料的稳定性。
不同体系的总态密度如图 6所示,虚线表示费米能级位置,设置为0 eV处。其带隙变化值如表 1所示。Ge空位导致费米能级向价带内移动,呈现出p型半导体的性质。对于GeTe菱方相,Se掺杂对态密度的影响较小,造成带隙的少量降低。3% Se掺杂使菱方结构Ge31Te32的带隙仅仅下降了1.7%。Se掺杂可使GeTe菱方晶体保持良好的导电性质。此外,对于含Ge空位的GeTe面心立方晶体,Se掺杂则会使导带底向能量更高处移动,显著增加其带隙。面心立方结构的Ge31Te31Se1相较于Ge31Te32,带隙增加了67.7%。这主要是由掺杂后晶格常数增大所引起的。
 |
| 图 6 菱方相和面心立方相总态密度 Fig. 6 Total density of states for rhombohedral phase and fcc |
| 图选项 |
图 7(a)、(b)分别为Ge32Te31Se1菱方相和面心立方相中,掺杂的Se原子与其最近邻Ge原子和Te原子的分波态密度图(PDOS),虚线表示费米能级位置,设置为0 eV处。可以看出,Ge 4p电子和Te 4p电子具有很强的p-p耦合,形成Ge—Te共价键。而Se原子的PDOS分布与Te原子十分相似。掺杂的Se原子与Ge原子形成类似于Ge—Te键的Ge—Se共价键。Se原子的3p电子态密度分布离价带顶较远,处在较低能量位置。Se原子与Ge原子的p电子态密度耦合更加显著,因而Ge—Se共价键较Ge—Te共价键更强。
 |
| 图 7 菱方相Ge32Te31Se1和面心立方相Ge32Te31Se1 Ge原子、Te原子和Se原子的分波态密度 Fig. 7 Partial density of states for Ge atom, Te atom and Se atom in rhombohedral Ge32Te31Se1 and fcc Ge32Te31Se1 |
| 图选项 |
3 结论 1) 对于GeTe完美晶体,Se掺杂优先取代Te原子。而对于含Ge空位的GeTe晶体,Se原子不会占据Ge空位,而更倾向于取代Ge空位最近邻的Te原子。对于菱方相,则倾向于取代Ge空位同层最近邻的Te原子。Se杂质原子与Ge空位存在一定的吸引作用,阻碍了Ge空位的移动,可以提高GeTe相变存储材料的再结晶温度,使其具有更好的数据保持力和更高的服役温度。
2) Se掺杂导致菱方相的体积收缩,而面心立方相的体积膨胀,减小了由菱方相到面心立方相转变时的体积差异,提高了相变存储材料的稳定性。
3) Se原子掺杂对GeTe菱方相的电子结构影响较小,使其带隙略微减小。故少量Se掺杂不会影响GeTe菱方相的导电性质。此外,Se掺杂使面心立方相的带隙增大。Se掺杂含Ge空位的面心立方晶体呈现类似于菱方相的电子局域函数分布,减小了两相的差异。为解释实验中Se掺杂PCM出现的奇特相转变性质提供了重要线索。
综上,Se掺杂的GeTe是一种性质优异的相变存储材料,具有较高的再结晶温度,适用于航空航天、汽车电子等较高温度的信息存储领域。对Se掺杂后的非晶态性质需要后期进一步探索。
致谢
感谢北京航空航天大学司晨老师在研究过程中给予的帮助和指导。
参考文献
| [1] | OVSHINSKY S R. Reversible electrical switching phenomena in disordered structures[J].Physical Review Letters, 1968, 21(20): 1450–1453.DOI:10.1103/PhysRevLett.21.1450 |
| [2] | RAOUX S, WELNIC W, IELMINI D. Phase change materials and their application to nonvolatile memories[J].Chemical Reviews, 2010, 110(1): 240–267.DOI:10.1021/cr900040x |
| [3] | WONG H S P, SALAHUDDIN S. Memory leads the way to better computing[J].Nature Nanotechnology, 2015, 10(3): 191–194.DOI:10.1038/nnano.2015.29 |
| [4] | LENCER D, SALINGA M, GRABOWSKI B, et al. A map for phase-change materials[J].Nature Materials, 2008, 7(12): 972–977.DOI:10.1038/nmat2330 |
| [5] | LENCER D, SALINGA M, WUTTIG M. Design rules for phase-change materials in data storage applications[J].Advanced Materials, 2011, 23(18): 2030–2058.DOI:10.1002/adma.v23.18 |
| [6] | RAOUX S. Phase change materials[J].Annual Review of Materials Research, 2009, 39(1): 25–48.DOI:10.1146/annurev-matsci-082908-145405 |
| [7] | PERNIOLA L, SOUSA V, FANTINI A, et al. Electrical behavior of phase-change memory cells based on GeTe[J].IEEE Electron Device Letters, 2010, 31(5): 488–490.DOI:10.1109/LED.2010.2044136 |
| [8] | BRUNS G, MERKELBACH P, SCHLOCKERMANN C, et al. Nanosecond switching in GeTe phase change memory cells[J].Applied Physics Letters, 2009, 95(4): 043108.DOI:10.1063/1.3191670 |
| [9] | CHONG T, SHI L, ZHAO R, et al. Phase change random access memory cell with superlattice-like structure[J].Applied Physics Letters, 2006, 88(12): 122114.DOI:10.1063/1.2181191 |
| [10] | VINOD E M, SINGH A K, GANESAN R, et al. Effect of selenium addition on the GeTe phase change memory alloys[J].Journal of Alloys and Compounds, 2012, 537(19): 127–132. |
| [11] | VINOD E M, SANGUNNI K S. The effect of Se doping on spectroscopic and electrical properties of GeTe[J].Thin Solid Films, 2014, 550(1): 569–574. |
| [12] | KOLOBOV A V, TOMINAGA J, FONS P, et al. Local structure of crystallized GeTe films[J].Applied Physics Letters, 2003, 82(3): 382–384.DOI:10.1063/1.1539926 |
| [13] | TONG F, MIAO X S, WU Y, et al. Effective method to identify the vacancies in crystalline GeTe[J].Applied Physics Letters, 2010, 97(26): 261904.DOI:10.1063/1.3531664 |
| [14] | VINOD E M, RAMESH K, SANGUNNI K S. Structural transition and enhanced phase transition properties of Se doped Ge2Sb2Te5 alloys[J].Scientific Reports, 2015, 5: 8050.DOI:10.1038/srep08050 |
| [15] | WANG M, LU Y, SHEN X, et al. Effect of Sb2Se on phase change characteristics of Ge2Sb2Te5[J].CrystEngComm, 2015, 17(26): 4871–4876.DOI:10.1039/C5CE00656B |
| [16] | HAFNER J. Ab-initio simulations of materials using VASP:Density-functional theory and beyond[J].Journal of Computational Chemistry, 2008, 29(13): 2044–2078.DOI:10.1002/jcc.v29:13 |
| [17] | BL?CHL P E. Projector augmented-wave method[J].Physical Review B, 1994, 50(24): 17953–17979.DOI:10.1103/PhysRevB.50.17953 |
| [18] | PERDEW J P, WANG Y. Pair-distribution function and its coupling-constant average for the spin-polarized electron gas[J].Physical Review B, 1992, 46(20): 12947–12954.DOI:10.1103/PhysRevB.46.12947 |
| [19] | MIAO N, SA B, ZHOU J, et al. Investigation on Ge5-xSbxTe5 phase-change materials by first-principles method[J].Applied Physics A, 2010, 99(4): 961–964.DOI:10.1007/s00339-010-5709-x |
| [20] | GOLDAK J, BARRETT C S, INNES D, et al. Structure of alpha GeTe[J].The Journal of Chemical Physics, 1966, 44(9): 3323–3325.DOI:10.1063/1.1727231 |
| [21] | LEVIN E M, BESSER M F, HANUS R. Electronic and thermal transport in GeTe:A versatile base for thermoelectric materials[J].Journal of Applied Physics, 2013, 114(8): 083713.DOI:10.1063/1.4819222 |
| [22] | CHATTOPADHYAY T, BOUCHERLE J. Neutron diffraction study on the structural phase transition in GeTe[J].Journal of Physics C:Solid State Physics, 1987, 20(10): 1431.DOI:10.1088/0022-3719/20/10/012 |
| [23] | PEIERLS R E. Quantum theory of solids[M].Oxford: Oxford University Press, 1955. |
| [24] | SUN Z, TIAN S, SA B. Investigation of the structure and properties of rhombohedral Cu-Ge-Te alloys by ab initio calculations[J].Intermetallics, 2013, 32(2): 292–296. |
| [25] | ZHANG S, WEI S H, ZUNGER A, et al. Defect physics of the CuInSe2 chalcopyrite semiconductor[J].Physical Review B, 1998, 57(16): 9642.DOI:10.1103/PhysRevB.57.9642 |
| [26] | WEI S H. Overcoming the doping bottleneck in semiconductors[J].Computational Materials Science, 2004, 30(3): 337–348. |
| [27] | NAM S W, CHUNG H S, LO Y C, et al. Electrical wind force-driven and dislocation-templated amorphization in phase-change nanowires[J].Science, 2012, 336(6088): 1561–1566.DOI:10.1126/science.1220119 |
| [28] | NUKALA P, AGARWAL R, QIAN X, et al. Direct observation of metal-insulator transition in single-crystalline germanium telluride nanowire memory devices prior to amorphization[J].Nano Letters, 2014, 14(4): 2201–2209.DOI:10.1021/nl5007036 |
| [29] | SUN Z, ZHOU J, BLOMQVIST A, et al. Formation of large voids in the amorphous phase-change memory Ge2Sb2Te5 alloy[J].Physical Review Letters, 2009, 102: 075504.DOI:10.1103/PhysRevLett.102.075504 |
| [30] | UPADHYAY M, ABHAYA S, MURUGAVEL S, et al. Experimental evidence for presence of voids in phase change memory material[J].RSC Advances, 2014, 4(8): 3659–3668.DOI:10.1039/C3RA44246B |
