全局飞行流量协同优化是一类典型的面向实际应用的工程优化问题,由于缓解空中交通拥堵与减少飞行延误在实际中往往是相互冲突的,因此该问题实质上是一个多目标优化问题。求解此类问题的难点主要是:一方面,由于扇区网络中同时运行着几千个航班,每个航班至少包括飞行路径和起飞时间2个变量,因此该问题是一个大规模优化问题;另一方面,表征扇区网络拥堵的目标函数是不可微且难分解的,传统优化算法难以处理,这将在后续详细介绍。
20世纪90年代以来,欧美等地区****就开展了空中交通流量网络运行优化问题研究,将地面等待、空中等待、空中改航、航班取消等策略覆盖到每个航班所有阶段,提出了0-1整型规划[1-3]、混合0-1整数规划、BLO等模型[4-7],马正平等提出了短期空中交通流量管理问题的整数规划模型[8],蔡开泉、管祥民、肖明明等提出了航班飞行路径与起降时隙的协同分配、飞行流量鲁棒优化等模型算法[9-11],有效解决了民用航空特别是同质化飞行活动条件下飞行流量优化问题。
军事航空飞行活动主要包括战斗飞行、任务飞行、训练飞行等,由于其在活动范围、飞行路径、管制间隔等方面有着区别于民用航空的特殊要求,特别是由于政治、军事、外交等方面因素导致延误、改航等措施对其飞行活动影响的代价也远远高于民用航空飞行活动。统筹民用航空和军事航空需求实施全局飞行流量调控,将是一种在异质化飞行活动条件下的飞行流量协同优化问题,传统的同质化飞行流量协同优化模型将在目标函数设置、条件约束等方面难以满足异质化飞行流量调控要求。同时,传统遗传算法在处理高维问题时,容易过早陷入局部最优,产生“维数诅咒”,实际应用效果往往不太理想。
本文贯彻军民融合发展思想,首先设计了全局飞行流量多目标协同优化模型——CMI模型;其次,提出了动态自适应多目标遗传算法(DA-MOGA)和基于聚集距离与种群多样性的交叉变异概率动态调整机制;最后,通过实际数据对DA-MOGA的有效性进行验证。
1 全局飞行流量协同优化模型 在飞行活动中,航空器一般沿着各自规划的航线从起飞机场飞往目的机场,管制员以空域扇区为单元实施飞行管制,保证飞行活动安全、高效、有序运行。机场、扇区构成了空域运行的基本单元。由于机场运行能力和管制员工作负荷等原因,机场和扇区的容量是有限的。空中交通流量网络优化主要是对飞行活动中的起降时间和飞行路径进行调控,以达到网络运行经济性和安全性的整体最优。
1.1 目标函数 全局飞行流量协同优化在空域扇区网络多目标优化模型基础上,考虑了军民航异质化飞行活动管制要求和差异化调配方法与代价,兼顾了军民航管制员各自工作特点,决策变量采用飞行计划的起飞时刻和飞行路径,目标函数则是扇区网络的空中交通拥堵和总体飞行延误代价。
1.1.1 空中交通拥堵 空中交通拥堵通过对负责空域扇区的管制员工作负荷进行量化,对扇区网络的所有扇区的管制员工作负荷进行累加,综合考虑各扇区的最大拥堵水平和平均拥堵水平,引用经典方法[6]得到以下目标函数:
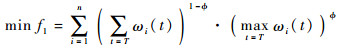 | (1) |
式中:?∈[0, 1]为最大拥堵和平均拥堵间的权重;n为空域内扇区总数;T为空域扇区网络优化时间区间;ωi(t)为扇区i在第t个时隙的管制员工作负荷。
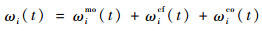 | (2) |
式中:管制员工作负荷由监视负荷ωimo(t)、冲突负荷ωicf(t)和移交负荷ωico(t) 3部分组成。
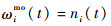 |
其中:ni(t)为扇区i在第t个时隙的飞机数。
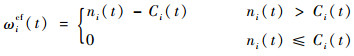 |
其中:Ci(t)为扇区i在第t个时隙的容量。
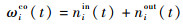 |
其中:niin(t)和niout(t)分别为在第t个时隙内飞入和飞出扇区i的飞机数。
1.1.2 总体飞行延误代价 总体飞行延误代价由起飞延误导致的地面延误代价和由空中等待、减速或飞行路径变更产生的空中延误代价组成。
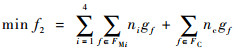 | (3) |
式中:f2为总体飞行延误代价;gf为飞行活动f的延误代价;模型中设计了ni和nc分别为相应类别军航飞行活动FMi和民航飞行FC的延误代价权重。
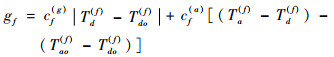 |
式中:|Td(f)-Tdo(f)|为地面等待时间;(Ta(f)-Td(f))- (Tao(f)-Tdo(f))为实际飞行时间差;cf(g)和cf(a)分别为单位时间地面和空中等待成本,由于油耗等原因,cf(a)>cf(g)。
飞行活动F包括民航飞行FC和军航飞行FM,FM主要包括了战斗飞行、专机和重要任务飞行、一般任务飞行、转场飞行、场内场外飞行等。军航本场训练飞行(含场内场外)因大都不涉及跨扇区飞行,战斗飞行因其特殊净空要求,因此不纳入扇区网络流量优化范畴。其他军航飞行计划划分为专机飞行计划FM1、重要任务飞行计划FM2、一般任务飞行计划FM3和转场飞行计划FM4。
考虑军航飞行活动在政治、军事、外交等方面有着特殊意义,延误、改航等措施对其飞行活动影响的代价与民航飞行计划有着特殊区别。按照现行飞行管制有关规定和飞行调配原则,专机和重要任务飞行调配优先级高于民航班期飞行,一般任务和转场飞行调配优先级低于民航班期飞行,即n1>n2>nc>n3>n4;为便于计算,令ni+1=ni/2,即[n1 n2 n3 n4]=n1[1 1/2 1/4 1/8]。同时,考虑军民航飞行计划协同调配问题,设计军民航飞行计划协同调配权重,即军民融合系数αcmi,令αcmi=n1/nc,可得[n1 n2 nc n3 n4]= n1[1 1/2 1/αcmi 1/4 1/8],则1/4 < 1/αcmi < 1/2,即2 < αcmi < 4。
1.2 约束条件 考虑扇区网络运行实际,还需要对模型中的空域容量、起飞时间、军航特殊间隔要求和飞行距离等进行约束。
1.2.1 空域容量约束 空域扇区网络中的各机场和扇区节点应全程满足容量要求,即
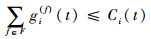 | (4) |
如飞行活动f在时隙t在扇区i,则gif(t)为1,否则为0。
1.2.2 起飞时间约束 考虑军民航飞行活动实际,民航航班、专机、重要和一般任务飞行活动由于乘客乘机原因, 一般不应提前起飞,即Td(f)-Tdo(f)≥0;民航航班和一般任务飞行起飞延误应控制在120 min以内,即Td(f)-Tdo(f)≤120 min;专机和重要任务飞行由于特殊政治和延误代价要求,起飞延误时间需严格控制在30 min以内,即Td(f)-Td0(f)≤30 min;转场飞行一般不涉及乘客原因,起飞时间较为灵活,起飞时刻可在计划时刻前120 min和计划时刻后240 min范围内,即-120 min≤Td(f)-Tdo(f)≤240 min。
 | (5) |
1.2.3 军航特殊任务约束 根据中国飞行管制有关规定,专机飞行活动由于极端安全要求须执行特殊间隔规定,即加大横向、纵向与水平飞行间隔。模型中,通过控制同一机场起飞时间间隔予以保证(即在专机起飞机场前后10 min内应无其他飞机起飞)。
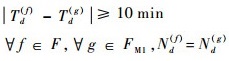 | (6) |
式中:|Td(f)-Td(g)|为专机与其在同一机场起飞的其他飞行活动的起飞时间差。
1.2.4 飞行距离约束 考虑到航空器携带燃油数量有效,航空器实际飞行距离Df应不超过最短路径Dfmin的(1+α)倍,本文取α=0.5。
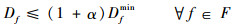 | (7) |
2 动态自适应多目标遗传算法 从第1节问题模型可知,扇区网络飞行流量协同优化问题是一个目标函数不可微、决策变量难分解的大规模优化问题,包含2个强耦合的子问题,即同时优化起飞时间和飞行路径。由于所有飞行计划均在同一时空范围内活动,同一飞行计划内起飞时间与飞行路径相互影响,不同飞行计划之间起飞时间和飞行路径也存在着相互耦合关系。
2.1 算法框架 针对以上问题,为获得最佳Pareto解集,同时避免陷入局部最优,本文提出了基于动态自适应多目标遗传算法。种群Pi由s个种子构成,每一个个体ηi均是扇区网络中一个完整的解,它由全部飞行活动的起飞时间Td(f)和飞行路径r(f)组成。Td(f)由{1, 2, …, T}中对应的离散时间值确定,r(f)由飞行计划中起降机场决定的可选飞行路径集R(f)中对应的飞行路径代号确定。
 | (8) |
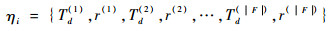 | (9) |
式中:|F|为飞行活动总数。
首先,在决策空间随机生成个体构建初始种群,个体解码后计算其目标函数并对种群个体进行排序;其次,进行“选择”操作,基于拥挤锦标赛选择法构建“交配池”;再次,进行“遗传”操作,对种群实施交叉和变异,交叉和变异概率将根据种子聚集距离和种群多样性进行动态调整,并进行约束处理;最后,计算新的种群个体目标函数后,进行种族重组、选择和更新,种群中的非支配解即构成Pareto最优解集。
2.2 动态自适应算子 在多目标遗传算法中,当存在多重同等优化时,由于选择过程中的随机错误,有限种群往往趋向于收敛到相似的一个或者几个种子,在自然界和人类的进化过程中也都能看到这种现象,被称为遗传偏差。而在种群遗传过程中,交叉操作的目的是扩大搜索范围,以增加种群多样性;变异操作的目的则是增强聚焦能力,以提高种群收敛性。为了有效解决种群在进化过程中出现的遗传偏差导致进化“不平衡不充分”问题,确保优化算法得到的非支配解能够均匀分布在Pareto前沿面上,本文通过计算种群平均聚集距离dnth和多样性Snth[12]来动态调整遗传过程中每一代的交叉和变异概率,以确保种群快速、均匀聚焦到Pareto前沿。
2.2.1 种群平均聚集距离 进化第n代种群平均聚集距离为
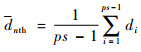 | (10) |
式中:di为种群中第i个种子与第i+1个种子间的欧氏距离。
2.2.2 种群多样性 种群多样性为
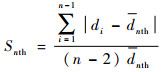 | (11) |
2.3 交叉变异概率动态调整机制 遗传过程中,交叉和变异概率决定了种群进化搜索方向。在进化之初,较高的交叉概率Pc和较低的变异概率Pv可使种群有效扩大搜索范围,增强种群多样性。
进化过程中,如种群平均聚集距离过大,意味着种子周围的搜索空间没有被充分搜索,往往不容易收敛,此时应尽快缩小搜索范围(迅速降低交叉概率Pc、增大变异概率Pv),使种群加快聚焦。如种群平均聚集距离过小,意味着种群“早熟”或陷入局部最优,则应扩大搜索范围(增大交叉概率Pc,降低变异概率Pv),避免过快聚焦。
进化过程中,如种群平均聚集距离适中,若种子间隔也适中,即多样性较好,则应保持交叉变异概率继续进化;若种子间隔有大有小,不够均匀,即多样性分布不佳,意味着种子周围空间没有被充分搜索,则应缩小搜索范围(降低交叉概率Pc、增大变异概率Pv);如多样性过差,则应尽快缩小搜索范围(迅速降低交叉概率Pc、增大变异概率Pv),以调整多样性分布。具体为
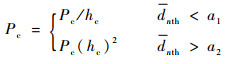 | (12) |
 | (13) |
若dnth∈[a1, a2],则
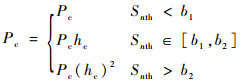 | (14) |
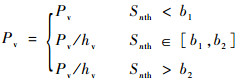 | (15) |
式中:hc和hv分别为交叉概率Pc和变异概率Pv的调节因子,需要迅速调节时系数调整为hc2。根据实验经验可得,a1=0.1、a2=0.2、b1=0.6、b2=1.4。
3 实验验证 为了评价全局飞行流量协同优化模型和动态自适应多目标遗传算法的有效性,本节利用中国扇区网络的实际数据进行对比实验。
3.1 实验数据及参数设置 实验选取的扇区网络数据是从2012年中国实际运行的扇区网络中提取出来,包括150个机场、77个扇区。飞行需求由中国民航局发布的夏秋班期时刻表和军航飞行计划实际运行统计情况获取,其中包含了计划执行航班的起飞机场、目的机场、起飞时间、飞行路径等信息。本文实验提取了一个周五早上8:00到中午12:00时间段内计划执行的2 136架次飞行活动的数据,时间间隔为5 min,共有48个时间片。此外,目标函数1中拥堵权重值?表示最大拥堵和平均拥堵间的权重,为降低部分军航演训活动导致的极端拥堵情况对扇区网络整体鲁棒性的影响,令拥堵权重值?为0.9;考虑节能减排需要和实际运行情况,飞机在空延误成本远大于地面等待成本,目标函数2中单位时间延误成本cf(g)和cf(a)分别取1和3。根据经验,交叉变异概率调节因子hc和hv均取0.7。
为了评价3种算法产生的解的收敛性、多样性等特性,本文使用多目标进化算法性能评价的3个经典指标,综合性指标、收敛性指标和多样性指标来衡量算法性能[12]。
综合性(Ih)[13]是对解集收敛性、均匀性以及广泛性的综合评价指标,可以用来反映非支配解集与Pareto最优前沿的逼近程度,综合性指标越大,越是逼近Pareto最优前沿。
收敛性(Id)[14]是指算法搜索的非支配解集对Pareto最优前沿的逼近程度,收敛性指标越小,算法逼近问题Pareto最优解集的程度越好。
多样性(Δ)[15]是评价算法求得非支配解集分布的离散程度和均匀性,多样性指标越小,非支配解集分布的越均匀分散,解的多样性越好。
本文实验选取多目标遗传算法MOGA和非支配排序遗传算法NSGA-Ⅱ 2种经典多目标遗传算法进行了对比。MOGA和NSGA-Ⅱ算法经过遍历分别取解的综合性系数最优时的交叉、变异概率取值分别为0.5、0.09和0.7、0.07。为确保算法和实验对比公平性,各算法设置相同的种群规模和适应值评价次数,并分别进行了25次独立实验。算法主要参数取值见表 1。
表 1 算法主要参数取值 Table 1 Main parameter setting of algorithms
| 算法 | 种群个数 | 进化代数 | 交叉概率 | 变异概率 |
| MOGA | 100 | 100 | 0.5 | 0.09 |
| NSGA-Ⅱ | 100 | 100 | 0.7 | 0.07 |
| DA-MOGA | 100 | 100 |
表选项
3.2 实验结果与对比分析 表 2给出了3种算法25次独立实验中得到最好的指标值。其中就综合性指标而言,DA-MOGA和MOGA均优于NSGA-Ⅱ,且DA-MOGA性能最优。这表明采用MOGA在解决异质化全局飞行流量协同优化问题上优于NSGA-Ⅱ,可以找到更优的航班飞行路径和飞行时间,使得空中交通拥堵和航班飞行延误更低。就收敛性而言,DA-MOGA明显优于其他2种算法,这表明动态自适应算子及交叉变异概率动态调整机制可以有效改善算法局部搜索能力。
表 2 主要性能评价指标对比 Table 2 Comparison of main performance evaluation indexes
| 算法 | Ih(方差) | Id(方差) | Δ(方差) |
| MOGA | 0.559 9 (0.274 8) | 0.395 8 (0.362 6) | 0.999 5 (0.001 1) |
| NSGA-Ⅱ | 0.546 4 (0.207 0) | 0.294 0 (0.215 3) | 0.998 5 (0.001 4) |
| DA-MOGA | 0.605 9 (0.228 3) | 0.241 2 (0.307 1) | 0.999 4 (0.000 8) |
表选项
表 3给出了3种算法在分别考虑效率优先和安全优先情况下,得到的Pareto最优解的目标函数值,并给出了DA-MOGA较MOGA和NSGA-Ⅱ算法在总体飞行延误代价和空中交通拥堵2个目标函数值的减少程度。
表 3 3种算法目标函数值对比 Table 3 Comparison of objective function value among three algorithms
| 优先考虑 | 目标函数值 | MOGA | NSGA-Ⅱ | DA-MOGA | DA-MOGA比MOGA减少比例/% | DA-MOGA比NSGA-Ⅱ减少比例/% |
| 效率 | 空中交通拥堵 | 2 318.44 | 2 672.48 | 2 276.39 | 1.81 | 14.82 |
| 总体飞行延误代价 | 13 457.6 | 15 728 | 11 736 | 12.79 | 25.38 | |
| 安全 | 空中交通拥堵 | 2 294.87 | 2 543.53 | 2 266.92 | 1.22 | 10.88 |
| 总体飞行延误代价 | 14 480.3 | 17 108 | 11 906 | 17.78 | 30.41 |
表选项
在效率优先情况下,DA-MOGA空中交通拥堵分别较MOGA和NSGA-Ⅱ算法减少了1.81%和14.82%,总体飞行延误代价降低了12.79%和25.38%;在安全优先情况下,DA-MOGA空中交通拥堵分别减少了1.22%和10.88%,总体飞行延误代价降低了17.78%和30.41%。这表明DA-MOGA在解决空域扇区网络飞行流量协同优化问题上,可以有效降低军民航总体飞行延误代价、减少全局空中交通拥堵,这也从另一个方面表明,动态自适应算子及交叉变异概率动态调整机制发挥了重要作用,有效印证了DA-MOGA的正确性和有效性。
DA-MOGA是基于传统MOGA改进而来的,两者最大的区别在于动态自适应算子的使用,由于其时间复杂度远小于遗传操作复杂度,因而其时间和空间复杂度与传统MOGA基本保持不变。DA-MOGA总的时间复杂度是O(N(|F|+|T|+N)),空间复杂度是O(N|T||F|)。其中,N为种群规模,|T|为全局优化时隙总数。具体各步骤时间复杂度见表 4。
表 4 DA-MOGA时间复杂度s Table 4 Time complexity of DA-MOGA
| 伪代码步骤 | 时间复杂度 |
| 选择 | O(N|F|) |
| 遗传操作 | O(N|F|) |
| 约束处理 | O(N|F|) |
| 动态自适应算子计算 | O(N) |
| 目标函数计算 | O(MN|T|) |
| 重组和保留 | O(N2) |
表选项
为了更好地对比和评价3种算法的性能,图 1给出了在目标空间下3种算法经过25次独立实验所获得Pareto前沿,从中同样可看出,DA-MOGA得到的非支配解明显优于NSGA-Ⅱ算法和MOGA。
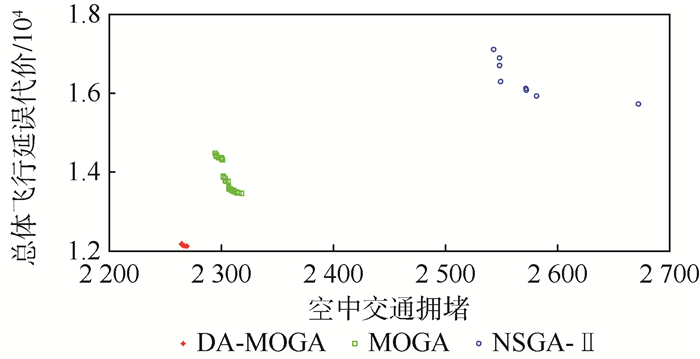 |
| 图 1 3种算法Pareto前沿对比 Fig. 1 Comparison of pareto Front among three algorithms |
| 图选项 |
图 2展示了随着进化代数的增加,交叉和变异概率逐渐趋于收敛。
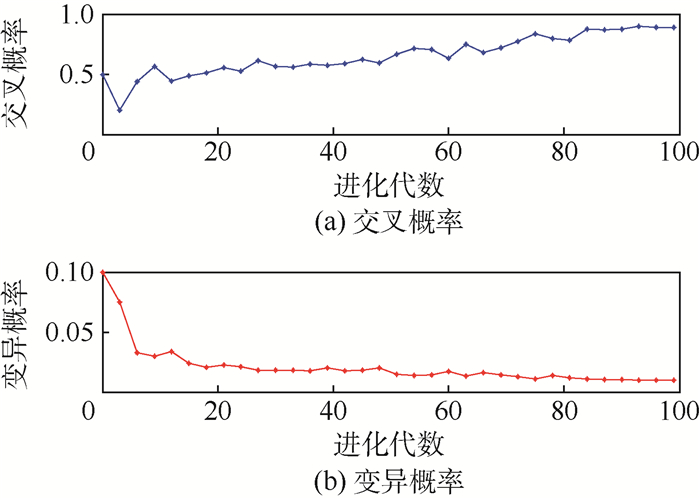 |
| 图 2 DA-MOGA交叉、变异概率进化趋势 Fig. 2 Evolutionary trend of crossover and variation probability for DA-MOGA |
| 图选项 |
图 3展示了αcmi(2<αcmi < 4)在不同取值条件下Pareto前沿面对比情况,可以看出过大或过小αcmi容易导致空中交通拥堵和总体延误代价过度增大,从而无法得到较优的Pareto面;当αcmi在取值区间向中点收敛过程中,所得Pareto面逐渐优化;αcmi=3所得Pareto面明显优于其他解。这也反映了过于侧重军航飞行活动或过于侧重民航飞行活动均无法得到全局飞行流量调控的整体最优,而适中的军民航飞行活动对比权重,即兼顾彼此的军民融合更有益于全局的协同优化,这也从一个侧面印证了军民融合、有机联动的重要性。
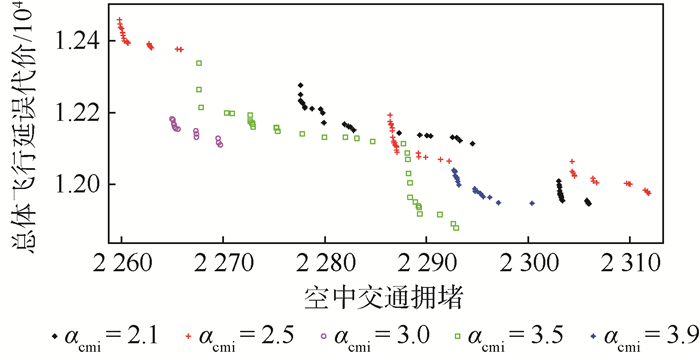 |
| 图 3 不同αcmi下的Pareto前沿对比 Fig. 3 Comparison of Pareto front at different αcmi |
| 图选项 |
4 结论 随着航空业的快速发展以及军事航空需求的不断拓展,如何在国家空域运行全局,即军民航飞行活动的共同安全与效益的全局中取得更好平衡以推进军民融合深度发展,是本文研究的出发点和落脚点,主要创新有:
1) 设计了一种基于军民航异质化飞行活动管制要求、考虑差异化调配方法与代价、兼顾军民航管制员各自工作特点、有效解决扇区网络运行安全性和经济性问题的全局飞行流量多目标协同优化模型。
2) 提出了一种动态自适应多目标遗传算法(DA-MOGA),考虑种群聚集距离及其多样性,设计了算法交叉和变异概率自适应变化机制,实验证明在Pareto前沿面和综合性、收敛性等指标方面均优于2种经典遗传算法。
考虑到军航飞行活动穿越航路航线给民航飞行带来的特定影响,基于军民融合的全局飞行流量协同优化后续研究中,将进一步深化研究军航飞行活动对民航航路航线影响,以求更加科学、有效、精细化地调配空域资源。
参考文献
| [1] | DE MATOS P A L, POWELL P L. Decision support for flight rerouting in Europe[J].Decision Support Systems, 2002, 34(4): 397–412. |
| [2] | BERTSIMAS D, LULLI G, ODONI A.The air traffic flow management problem: An integer optimization approach[C]//Proceedings of the 13th International Conference on Integer Programming and Combinatorial Optimization.Berlin: Springer, 2008: 36-46. |
| [3] | SHERALI H, STAATS R, TRANI A. An airspace planning and collaborative decision-making model:Part Ⅰ-Probabilistic conflicts, workload, and equity considerations[J].Transportation Science, 2003, 37(4): 434–456.DOI:10.1287/trsc.37.4.434.23272 |
| [4] | SHERALI H, STAATS R, TRANI A. An airspace-planning and collaborative decision-making model:Part Ⅱ-Cost model, data considerations, and computations[J].Transportation Science, 2006, 40(2): 147–164.DOI:10.1287/trsc.1050.0141 |
| [5] | DELL'OLMO P, LULLI G. A new hierarchical architecture for air traffic management:Optimization of airway capacity in a free flight scenario[J].European Journal of Operational Research, 2002, 144(1): 179–193. |
| [6] | DANIEL D, OUSSEDIK S, STEPHANE P.Airspace congestion smoothing by multi-objective genetic algorithm[C]//Proceedings of the 2005 ACM Symposiumon on Applied Computing.New York: ACM, 2005: 907-912. |
| [7] | YAOWIWAT S, LOHATEPANONT M, PUNYABUKKANA P. Multi objective micro genetic algorithm for combine and reroute problem[J].International Journal of Intelligent Systems and Technologies, 2007, 2(4): 245–255. |
| [8] | MA Z P, CUI D G, CHENG P. Dynamic network flow model for short-term air traffic flow management[J].IEEE Transactions on Systems, Man and Cybernetics-Part A:Systems and Humans, 2004, 34(3): 351–358.DOI:10.1109/TSMCA.2003.822969 |
| [9] | CAI K Q, ZHANG J, ZHOU C, et al. Using computational intelligence for large scale air route networks design[J].Applied Soft Computing, 2012, 12(9): 2790–2800.DOI:10.1016/j.asoc.2012.03.063 |
| [10] | GUAN X M, ZHANG X J, ZHU Y B, et al. An airway network flow assignment approach based on an efficient multiobjective optimization framework[J].The Scientific World Journal, 2015, 2015: 302615. |
| [11] | XIAO M M, CAI K Q, LINKE F.An evolutionary multi-objective approach for stochastic air traffic network flow optimization[C]//Proceedings of the 18th IEEE International Conference on Intelligent Transportation Systems (ITSC).Piscataway, NJ: IEEE Press, 2015: 2059-2065. |
| [12] | MEI Y, TANG K, YAO X. Decomposition-based memetic algorithm for multi-objective capacitated arc routing problem[J].IEEE Transactions on Evolutionary Computation, 2011, 15(2): 151–165.DOI:10.1109/TEVC.2010.2051446 |
| [13] | ZITZLER E, LAUMANNS M, THIELE L.SPEA2: Improving the strength Pareto evolutionary algorithm[C]//Proceedings of Evolutionary Methods for Design Optimization and Control with Applications to Industrial Problems, 2002: 95-100. |
| [14] | CZYZZAK P, JASZKIEWICZ A. Pareto simulated annealing-A metaheuristic technique for multiple-objective combinatorial optimization[J].Journal of Multi-Criteria Decision Analysis, 1998, 7(1): 34–47.DOI:10.1002/(SICI)1099-1360(199801)7:1<34::AID-MCDA161>3.0.CO;2-6 |
| [15] | DEB K, PRATAP A, AGARWAL S. A fast and elitist multi-objective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computing, 2002, 6(2): 182–197.DOI:10.1109/4235.996017 |
