为了提高算法的匹配稳定性,文献[4]提出了一种基于概率数据关联(Probabilistic Data Association Filter,PDAF)的地形匹配算法,虽然匹配稳定性得到了显著提高,但匹配精度严重下降。
针对误匹配往往发生在地形起伏不大的区域,很多研究集中于地形适配区的判定,进而筛选出适合于匹配的区域,以提高匹配的稳定性。例如,文献[5]提出了一种基于反向传播(BP)神经网络的地形适配/误配区自动识别和划分的方法;文献[6]提出了基于熵值法赋权灰色关联决策的地形辅助导航适配区选择方法;文献[7]提出了一种水下地形导航匹配区选取的模糊推理方法;文献[8]提出了一种用于景象匹配的基于信息熵的适配区选择方法。不过,这种适配区划分是基于地形特征分析进行的,只是在统计意义上适用,而且是事先离线进行的,具体到某次实时匹配结果的判定,并不一定适用。
因此,如何在线判定某次匹配结果的误匹配与否,是保证匹配结果可用性的关键。常用的地形匹配误匹配方法有M/N判据法[9-10],在一定程度上可以有效地剔除误匹配点,但该方法基于多次匹配结果,实时性差,且判断准确率不高。文献[11]提出了一种用于迭代最近等值点(Iterative Closest Contour Point,ICCP)算法的误匹配判断方法,该方法抑制了算法的发散,但需要对多次飞行优化位置概率进行累积计算,实时性不好。
本文利用TERCOM匹配相关面内若干个极小值点的联合概率分布,建立了一种基于多参照点联合概率的误匹配在线判断准则,通过设定阈值判定TERCOM算法定位点即平均平方差(Mean Square Difference, MSD)相关面内最小值点是否为正确匹配点。仿真试验结果表明, 该方法可以实时准确地对TERCOM算法进行在线误匹配判断,在保证算法匹配精度的前提下,提高了算法的匹配稳定性。
1 TERCOM算法基本原理 TERCOM算法原理如图 1所示,飞行器在飞越航线上的地形匹配区时,利用雷达高度表和气压高度表等设备测量沿航线的地形高程序列,将测得的实时高程序列和预存的基准图高程序列进行相关,按最佳相关确定飞行器的地理位置。
 |
| 图 1 TERCOM算法原理图 Fig. 1 Schematic diagram of TERCOM algorithm |
| 图选项 |
TERCOM算法的匹配准则主要有平均绝对差(Mean Absolute Difference,MAD)、MSD和互相关(Cross Correlation,CC)等3种,本文以MSD为例进行研究,其计算方法如下:
 | (1) |
式中:X=[x1, x2, …, xn]T和Y=[y1, y2, …, yn]T分别为基准高程序列和实测高程序列,n为长度。
2 参照点概率 2.1 正确匹配点概率分布 基准高程序列表示为HDEM=[hDEM1, hDEM2, …, hDEMn]T,测量高程序列表示为Hm=[hm1, hm2, …, hmn]T,当匹配正确时,二者有如下关系:
 | (2) |
式中:wi为零均值、方差为σ2的高斯量测噪声[12-13],即wi~N(0, σ2), i=1, 2, …, n。
将式(2)代入式(1)有
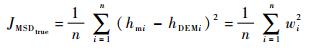 | (3) |
由wi的分布和式(3)可得
 | (4) |
即正确匹配时的MSD值JMSDtrue服从参数θ=
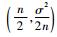
2.2 参照点概率分布 除正确匹配点外的其余待匹配点基准高程序列表示为Hr=[hr1, hr2, …, hrn]T,与测量高程序列Hm=[hm1, hm2, …, hmn]T的偏差表示为V=[v1, v2, …, vn]T,则有
 | (5) |
将这些待匹配点作为正确匹配点的参照点,则联立式(2)和式(5)可得
 | (6) |
故vi为均值为(hDEMi-hri)、与wi同方差的高斯噪声,即vi~N(hDEMi-hri, σ2)。此时有
 | (7) |
由vi的分布和式(7)可得
 | (8) |
式中:
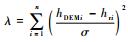
3 多参照点概率联合 在PDAF算法中,认为相关面内所有点的MSD值服从均匀分布,而由2.2节得到的相关面内各待匹配点的MSD概率分布可知,各点的MSD分布是不一样的,这也是导致PDAF算法中匹配精度下降的主要原因。
为了在提高稳定性的同时,不过多降低匹配精度,提出了一种基于多参照点联合概率的误匹配判断方法,分为点选取、联合概率计算区域确定、区域内各点为正确匹配点的概率计算、参照点概率计算、区域联合概率计算、选取区域为正确匹配区域的概率计算6个步骤,方法具体内容如下:
1) 点选取。PDAF算法以惯性导航系统(Inertial Navigation System,INS)输出位置的匹配位置为中心确定待匹配窗口,求得该窗口内各待匹配点的MSD值,构成地形轮廓匹配算法的MSD相关面,并获得其中最小的m个极小值点{p1, p2, …, pm}。
2) 联合概率计算区域确定。针对获得的m个极小值点,以每个极小值点为中心、gr个地图网格间距为半径,对应的区域即为该极小值点的联合概率计算区域。
3) 区域内各点为正确匹配点的概率计算。针对每个极小值点对应计算区域内(2gr+1)2个点{a1, a2, …, a(2gr+1)2},按式(4)分别计算每个点ai服从Γ分布[15]的概率值γai。
4) 参照点的概率计算。取ai点上下左右间隔为d个网格间距的4个网格点作为ai联合概率计算的参照点{rref1, rref2, rref3, rref4},按式(8)分别计算其服从非中心χ2分布的概率值{αref1, αref2, αref3, αref4}。
5) 区域联合概率计算。设βai为ai点联合概率,则有
 | (9) |
因此,以ai点为中心、gr个地图网格为半径的区域联合概率为
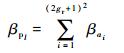 | (10) |
6) 选取区域为正确匹配区域的概率计算。第l个区域对应的极值点为正确匹配点的概率为
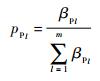 | (11) |
对选取的m个极值点分别按式(11)求其为正确匹配点的区域联合概率值,设定联合概率阈值,判断地形轮廓匹配算法直接求得的匹配点即MSD最小峰值点是否为正确匹配点。
4 仿真验证 4.1 仿真条件 仿真试验时,待匹配窗口半径为3σINS,σINS为INS的水平定位误差,设为2 000 m;极值点个数m设为10,区域半径gr设为2个网格,参照点间隔d取10个网格。
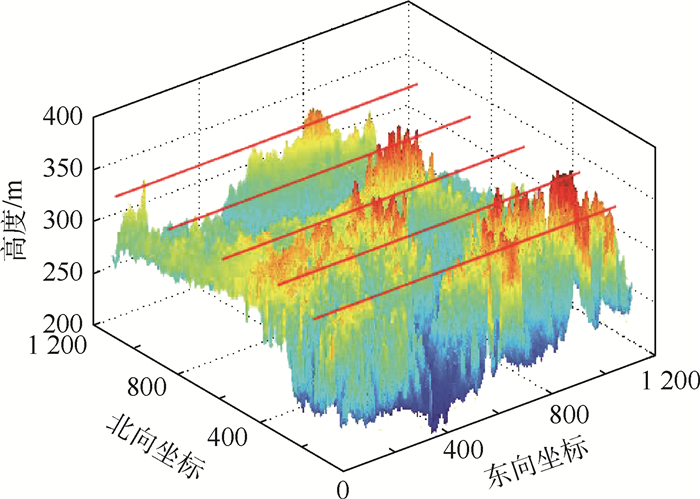
仿真所用地图数据为地理空间数据云[16]提供的地形数据,地图分辨率为1 200网格×1 200网格,网格间距为30 m,地形标准差σDEM为46 m。飞行器自西向东航行,在地图上等间隔选取飞行轨迹起点遍历。匹配序列长度分别取100、150、200个采样点,采样间隔为30 m,测量噪声方差σn设为10、17、24 m,对上述每种情况分别进行200次仿真实验。遍历轨迹在高程图和3D视图中的表示分别如图 2和图 3中的红色水平线所示。
 |
| 图 2 地形高程图 Fig. 2 Terrain elevation map |
| 图选项 |
 |
| 图 3 三维地形图 Fig. 3 Three-dimensional terrain map |
| 图选项 |
4.2 误匹配判断 图 4(a)为某次MSD算法产生误匹配时仿真结果对应的MSD相关面,实际匹配位置点坐标为(111, 112)。图 5(a)为某次MSD算法匹配正确时仿真结果对应的MSD相关面,实际匹配位置点坐标为(33, 49)。
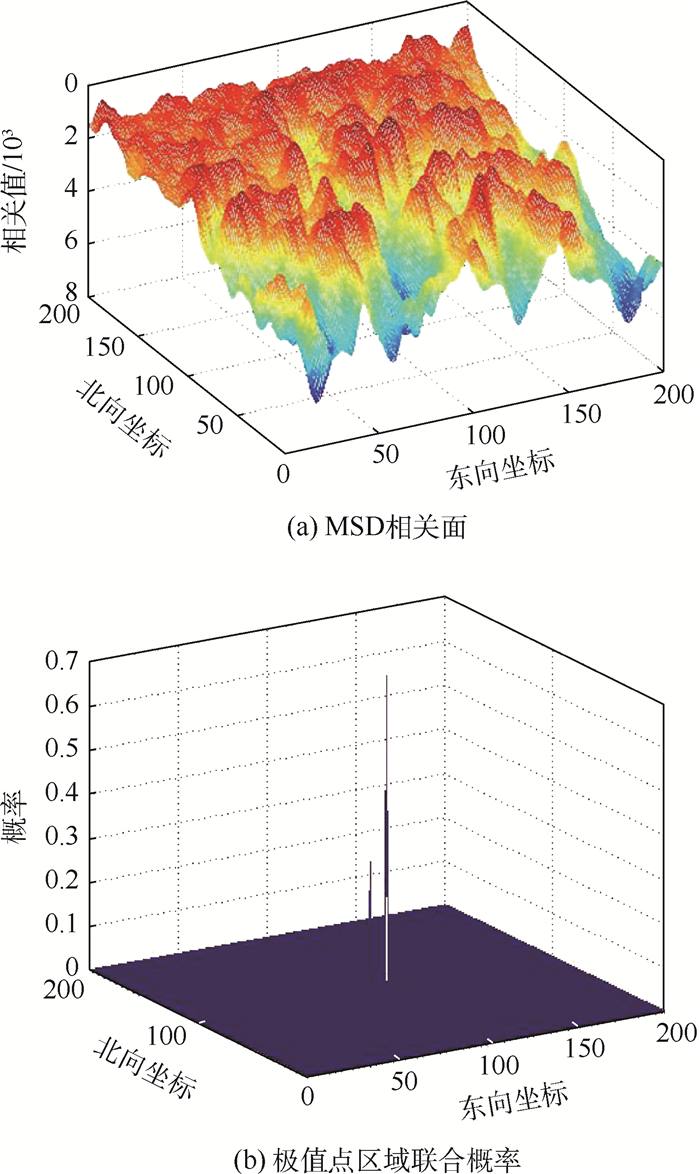 |
| 图 4 MSD相关面及其对应极值点区域联合概率示意图(误匹配) Fig. 4 Schematic diagram of MSD correlation plane and regional joint probability of corresponding extreme point (false matching) |
| 图选项 |
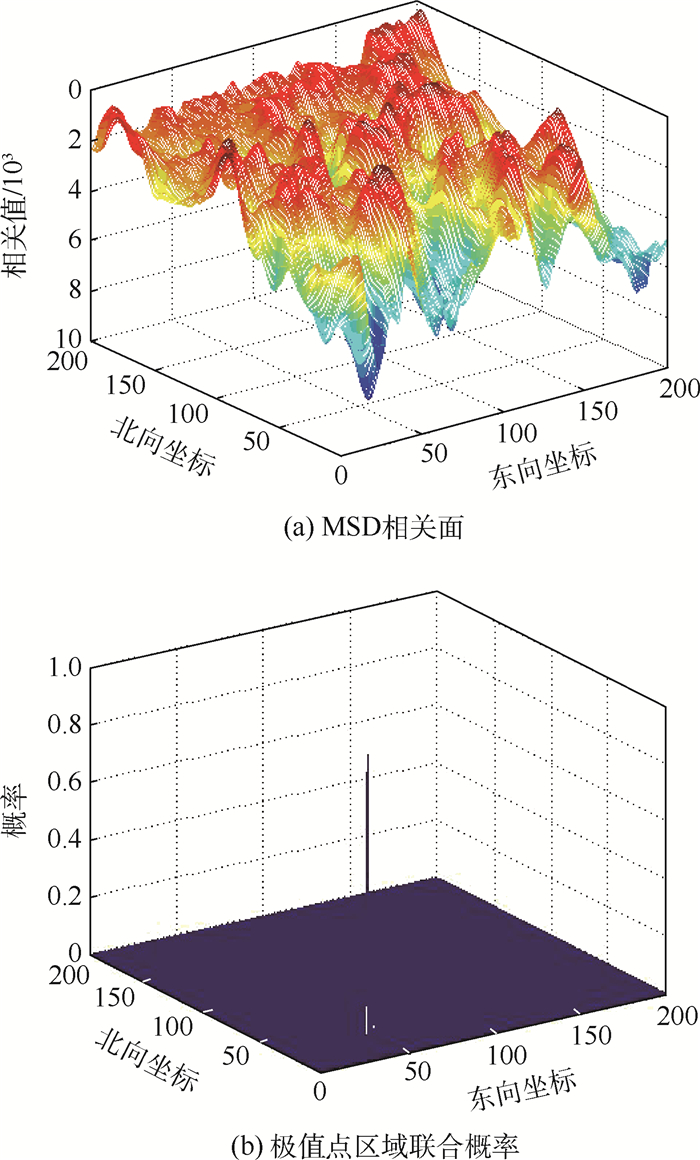 |
| 图 5 MSD相关面及其对应极值点区域联合概率示意图(匹配正确) Fig. 5 Schematic diagram of MSD correlation plane and regional joint probability of corresponding extreme point (correct matching) |
| 图选项 |
对获得的MSD相关面按第3节的计算流程得到10个极小值点的联合概率,图 4(a)、图 5(a)所示相关面内10个极小值点的坐标、MSD值和区域联合概率分别见表 1、表 2,联合概率如图 4(b)、5(b)所示。
表 1 图 4相关面对应极值点区域联合概率 Table 1 Regional joint probability of extreme points corresponding to correlation plane of Fig. 4
| 编号 | 极小值点坐标 | MSD值 | 区域联合概率 |
| 1 | (90, 90) | 347.6 | 0.31 |
| 2 | (111, 112) | 351.4 | 0.69 |
| 3 | (69, 9) | 526.8 | 0 |
| 4 | (127, 161) | 546.9 | 0 |
| 5 | (37, 142) | 595.5 | 0 |
| 6 | (147, 153) | 685.3 | 0 |
| 7 | (62, 181) | 723.6 | 0 |
| 8 | (103, 119) | 767 | 0 |
| 9 | (114, 63) | 809.5 | 0 |
| 10 | (135, 52) | 947.2 | 0 |
表选项
表 2 图 5相关面对应极值点区域联合概率 Table 2 Regional joint probability of extreme points corresponding to correlation plane of Fig. 5
| 编号 | 极小值点坐标 | MSD值 | 区域联合概率 |
| 1 | (33, 49) | 67.6 | 0.97 |
| 2 | (108, 14) | 93.5 | 0 |
| 3 | (102,107) | 130.7 | 0 |
| 4 | (93, 1) | 209.2 | 0 |
| 5 | (48,169) | 289.2 | 0 |
| 6 | (63, 109) | 303.5 | 0 |
| 7 | (113, 144) | 315.9 | 0 |
| 8 | (38, 56) | 358.7 | 0.03 |
| 9 | (199, 200) | 407.5 | 0 |
| 10 | (129, 134) | 458.9 | 0 |
表选项
图 4(a)中, MSD相关面最小值点坐标为(90, 90),其对应MSD值为347.6;次小值点坐标(111, 112),其对应MSD值为351.4。可见,最小值点对应的位置与实际匹配位置是不一样的,而次小值点才是实际位置,即TERCOM算法定位点与实际匹配位置不同,发生了误匹配。
由表 1可知, 极值点(90, 90)处2个网格区域联合概率为0.31,(111, 112)处2个网格区域联合概率为0.69,其余8个极小值点处2个网格区域联合概率均为0。如果设定联合概率大于0.9时才能判定极小值点为正确匹配点,可判定MSD最小值点(90, 90)不是正确匹配点,即判定发生了误匹配,判断正确。
图 5(a)中, MSD相关面最小值点坐标为(33, 49),其对应MSD值为67.6。最小值点对应的位置与实际匹配位置一致,即TERCOM算法定位点与实际匹配位置相同,匹配正确。
由表 2可知, 极值点(33, 49)处2个网格区域联合概率为0.97,(38, 56)处2个网格区域联合概率为0.03,其余8个极小值点处2个网格区域联合概率均为0。如果设定联合概率大于0.9时判定极小值点为正确匹配点,可判定MSD最小值点(33, 49)是正确匹配点,即判定未发生误匹配,判断正确。
4.3 阈值选取 在多参照点联合概率误匹配判定方法中,联合概率阈值的设定是关键。在图 2所示地形条件下,进行遍历仿真试验,计算其对应的MSD相关面,获得相关面内的10个最小极值点,并对这10个最小极值点计算其2个网格为半径的区域联合概率,设定不同的联合概率阈值,判断MSD最小值点是否为正确匹配点,结果如表 3所示。
表 3 遍历仿真试验结果 Table 3 Traversal simulation test results
| 序列长度 | σn/m |  | 正确点保留率/% | 匹配准确率/% | |||||
| 无阈值 | 阈值为0.6 | 阈值为0.9 | 无阈值 | 阈值为0.6 | 阈值为0.9 | ||||
| 100 | 10 | 4.6 | 100 | 97.9 | 97.9 | 94.5 | 98.9 | 99.4 | |
| 17 | 2.7 | 100 | 95.9 | 94.1 | 86 | 97 | 98.8 | ||
| 24 | 1.9 | 100 | 90.9 | 90.4 | 83.5 | 96.2 | 97.4 | ||
| 150 | 10 | 4.6 | 100 | 99 | 99 | 98 | 100 | 100 | |
| 17 | 2.7 | 100 | 98.5 | 98.5 | 97.5 | 99.5 | 99.5 | ||
| 24 | 1.9 | 100 | 96.8 | 96.2 | 92.5 | 98.4 | 98.9 | ||
| 200 | 10 | 4.6 | 100 | 99.5 | 98.9 | 98.5 | 100 | 100 | |
| 17 | 2.7 | 100 | 99 | 99 | 97.5 | 99.5 | 100 | ||
| 24 | 1.9 | 100 | 98.9 | 98.4 | 95.5 | 99.5 | 100 | ||
表选项
如表 3所示,匹配序列长度为100,测量噪声σn取10 m时,直接使用MSD最小值点作为正确点,TERCOM算法的误匹配率达到5.5%,当使用联合概率判定时,匹配准确率分别为98.9%(阈值设为0.6)和99.4%(阈值设为0.9),相较于无判断情况,匹配准确率提升,并保留了97.9%的正确点。当测量噪声σn取17 m时,TERCOM算法的误匹配率达到14%,当使用联合概率判定时,匹配准确率分别为97%(阈值设为0.6)和98.8%(阈值设为0.9),相较于无判定情况,匹配准确率大幅提升,并保留了94%以上的正确匹配结果,当测量噪声σn取24 m时,MSD误匹配率达到16.5%,当使用联合概率判定时,匹配准确率分别为96.2%(阈值设为0.6)和97.4%(阈值设为0.9),相较于无判定情况,匹配准率大幅提升,正确匹配结果保留率保持在90%上。
匹配序列长度取150个采样点,测量噪声σn分别取10、17、24 m时,直接使用MSD最小值点作为正确点,TERCOM算法的误匹配率均小于8%,但仍存在误匹配情况,使用联合概率判定,当联合概率判定阈值设定为0.6时,算法准确率可以达到98%以上,当联合概率判定阈值设定为0.9时,匹配准确率可达到98.5%以上,并保留了96%以上的正确匹配结果。
增大匹配序列长度至200,测量噪声σn分别取10、17、24 m时,直接使用MSD最小值点作为正确点算法准确率升高,TERCOM算法的误匹配率均小于4%,但仍存在误匹配情况,此时使用联合概率判定,当联合概率判定阈值设定为0.6时,算法准确率可以达到99%以上,当联合概率判定阈值设定为0.9时,匹配准确率可提升至100%,并保留了98%以上的正确匹配结果。
需要注意的是,这里判定为正确匹配结果的标准为匹配误差不大于2个网格间距,因此,匹配精度高。
5 结论 针对TERCOM算法易受高程测量误差和地形相似性等因素的影响而导致误匹配问题,提出了一种基于相关面的多参照点联合概率误匹配判断准则,经过仿真验证,得到:
1) 正确匹配判定准确率高。在不同仿真条件下,当联合概率阈值设为0.9时,判断准确率达到97%以上。
2) 正确匹配结果遗失少。选取不同的匹配序列长度和测量噪声的情况下,当概率阈值设为0.9时,依然保留了90%以上的正确匹配结果。
3) 匹配精度高。仿真中设定的正确匹配精度为不大于2个网格间距。
4) 适用于在线判定。判定结果仅基于单次匹配相关面给出,不需要额外信息。
参考文献
| [1] | WIENER T F. Terrain contour matching(TERCOM): A cruise missile guidance aid[C]//Proceedings of 24th Annual Technical Symposium. Bellingham: SPIE, 1980: 10-18.http://spie.org/Publications/Proceedings/Paper/10.1117/12.959127 |
| [2] | 徐克虎, 沈春林. 地形特征匹配辅助导航方法研究[J].东南大学学报(自然科学版), 2000, 30(3): 113–117. XU K H, SHEN C L. Study of terrain feature matching aided navigation method[J].Journal of Southeast University(Natural Science Edition), 2000, 30(3): 113–117.DOI:10.3969/j.issn.1001-0505.2000.03.025(in Chinese) |
| [3] | 李雄伟, 刘建业, 康国华. TERCOM地形高程辅助导航系统发展及应用研究[J].中国惯性技术学报, 2006, 14(1): 34–40. LI X W, LIU J Y, KANG G H. Development and application of TERCOM elevation-aided navigation system[J].Journal of Chinese Inertial Technology, 2006, 14(1): 34–40.(in Chinese) |
| [4] | FENG Q, SHEN L, CHANG W. Terrain aided navigation using PDAF[C]//IEEE International Conference on Robotics, Intelligent Systems and Signal Processing. Piscataway, NJ: IEEE Press, 2003: 1063-1068.https://ieeexplore.ieee.org/document/1285737/ |
| [5] | 张凯, 赵建虎, 施闯, 等. BP神经网络用于水下地形适配区划分的方法研究[J].武汉大学学报(信息科学版), 2013, 38(1): 56–59. ZHANG K, ZHAO J H, SHI C, et al. Study on classification of matching area of underwater topography based on BP neural network[J].Geomatics and Information Science of Wuhan University, 2013, 38(1): 56–59.(in Chinese) |
| [6] | 徐晓苏, 汤郡郡, 张涛, 等. 基于熵值法赋权灰色关联决策的地形辅助导航适配区选择[J].中国惯性技术学报, 2015, 23(2): 201–206. XU X S, TANG J J, ZHANG T, et al. Selection for matching area in terrain aided navigation based on entropy-weighted grey correlation decision-making[J].Journal of Chinese Inertial Technology, 2015, 23(2): 201–206.(in Chinese) |
| [7] | 王立辉, 乔楠, 余乐. 水下地形导航匹配区选取的模糊推理方法[J].西安电子科技大学学报(自然科学版), 2017, 44(1): 140–145. WANG L H, QIAO N, YU L. Fuzzy deduction methods of selecting the underwater terrain navigation matching area[J].Journal of Xidian University(Natural Science), 2017, 44(1): 140–145.(in Chinese) |
| [8] | ZHANG X, HE Z, LIANG Y, et al. Selection method for scene matching area based on information entropy[C]//International Symposium on Computational Intelligence & Design. Piscataway, NJ: IEEE Press, 2012: 364-368. |
| [9] | 冯庆堂. 地形匹配新方法及其环境适应性研究[D]. 长沙: 国防科学技术大学, 2004: 42-44. FENG Q T. The research on new terrain elevation matching approaches and their applicability[D]. Changsha: National University of Defense Technology, 2004: 42-44(in Chinese).http://cdmd.cnki.com.cn/article/cdmd-90002-2005144392.htm |
| [10] | 刘徐德. 地形辅助导航技术[M].北京: 电子工业出版社, 1994: 27-59. LIU X D. Terrain-aided navigation technology[M].Beijing: Electronic Industry Press, 1994: 27-59.(in Chinese) |
| [11] | 杨勇, 王可东. ICCP中单纯形优化的误匹配检测[J].北京航空航天大学学报, 2009, 35(3): 334–337. YANG Y, WANG K D. Mismatching judgement in simplex optimization for ICCP algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(3): 334–337.(in Chinese) |
| [12] | 朱华勇, 沈林成. 地形相关算法度量值的统计特性[J].国防科技大学学报, 1999, 21(4): 91–95. ZHU H Y, SHEN L C. Research on statistical properties of measures of terrain correlation algorithms[J].Journal of National University of Defense Technology, 1999, 21(4): 91–95.(in Chinese) |
| [13] | JOHNSON M W. Analytical development and test results of acquisition devices used in navigation systems[C]//10th Aerospace Sciences Meeting. Reston: AIAA, 1972: 1-9.https://arc.aiaa.org/doi/abs/10.2514/6.1972-122 |
| [14] | JOHNSON L, KORTZ S, BALAKRISHNAN N. Continuous univariate distributions-Ⅱ[M].Boston: Houghton Mifflin Harcourt, 1970: 130-146. |
| [15] | 茆诗松, 程依明, 濮晓龙. 概率论与数理统计[M].2版北京: 高等教育出版社, 2011: 252-349. MAO S S, CHENG Y M, PU X L. Probability and mathematical statistics tutorial[M].2nd edBeijing: Higher Education Press, 2011: 252-349.(in Chinese) |
| [16] | 中国科学院计算机网络信息中心地理空间数据云平台. DDEMV2数字高程数据[DB/OL]. NASA, METI, 2015[2017-03-07]. http://www.gscloud.cn. Geospatial Data Cloud Platform of Computer Network Information Center of Chinese Academy of Sciences. Digital elevation data of DDEMV2[DB/OL]. NASA, METI, 2015[2017-03-07]. http://www.gscloud.cn(in Chinese). |
