TOA测距的精度直接影响到相对位置判断的结果,在室内环境中,由于内部建筑结构复杂、障碍物遮挡等原因导致非视距(Non-Line-of-Sight,NLOS)效应,严重降低了室内测距的精度,因此需要采取措施抑制误差的影响。目前,降低NLOS误差的常用方法可以分为2类:①直接分析TOA测距值来对NLOS进行鉴别[2-4];②采用TOA与其他参量(如RSS等)进行数据融合的方法[5-7]。研究者通过分析视距(Line of Sight,LOS)和NLOS场景下的测距数据及其他能够测量的射频信号接收参数特征(如RSS、第1条到达路径的信号能量、信号的均方根时延扩展等),获得LOS/NLOS的分类依据,实现TOA测量场景的识别[8-10]。已有的研究表明,TOA测距的LOS/NLOS识别能够取得高达92%的分类准确率[7, 11]。但是,对于如何将LOS/NLOS识别结果应用于提高测距方法精度的研究仍然不够深入。
为了解决上述问题,本文提出了基于非线性规划的TOA测距值优化方法,利用TOA测距误差模型、TOA测距LOS/NLOS识别和几何约束,对TOA测距值优化进行了非线性规划问题建模,利用非线性规划算法优化了TOA测距值,提高了测距值精度。
1 室内TOA测距误差分析 TOA测距误差的来源由2个方面组成:①检测误差(εd),是由于硬件设备引入的脉冲波峰到达时间检测不准确;②信号误差,来自于实际接收信号与理想情况下接收信号之间的差异。其中,室内环境造成的信号误差在TOA测距误差中占主要成分。
LOS传输和NLOS传输是室内环境中TOA测距的2种典型信号传输场景,如图 1所示。在LOS场景中,信号发射端和信号接收端之间无障碍物遮挡,测距误差主要由多径叠加导致脉冲波峰发生偏移造成;在NLOS场景中,信号发射端和信号接收端之间存在障碍物遮挡,主要测距误差来自遮挡造成的直视路径信号无法检测(Undetectable Direct Path, UDP)的信道状况[12]。因此,信号误差可看作由多径误差和UDP误差构成:
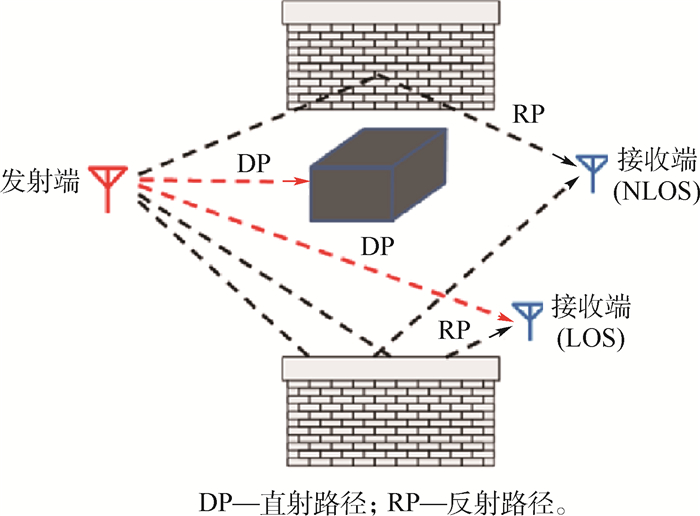 |
| 图 1 LOS和NLOS场景 Fig. 1 LOS and NLOS scenes |
| 图选项 |
1) 多径误差(εm)来自于第1个可检测路径(First Detectable Path, FDP)脉冲与邻近路径脉冲叠加导致脉冲波峰偏移所产生的测距误差。
2) UDP误差(εu)来自于UDP的状况,导致FDP不是DP所产生的测距误差。
根据上述分析,可以分为LOS和NLOS 2种情况来描述室内TOA测距误差:
 | (1) |
式中:
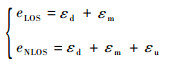 | (2) |
现有研究表明[13],εd、εm、εu均符合正态分布,eLOS和eNLOS也符合正态分布,并且均值和方差具有如下特征:
 | (3) |
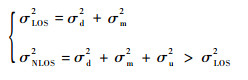 | (4) |
2 TOA测距值优化的非线性规划建模 基于非线性规划的优化过程是优化算法在约束条件的限制下,从给定的初始值出发通过迭代逐步逼近目标函数,当满足收敛条件后停止迭代输出优化结果。其中,优化算法主要影响迭代速度,对精度的影响较为有限,极大似然、序列二阶规划(Sequential Quadratic Programming,SQP)、Powell等典型算法均可以应用于测距值优化中[14]。
除了优化算法本身,非线性规划结果的关键影响因素包括初始值、约束条件和目标函数。初始值、约束条件、目标函数与优化对象密切相关,可对结果优化精度产生较大的影响。作为局部优化算法的一种,非线性规划的效果直接受到初始值设置的影响,不合理的初始值设置会导致无法得到全局最优解。约束条件的主要作用是限定优化目标的范围,因此合理的约束条件也能够提高优化结果的精度。而目标函数则决定了优化算法的迭代方向。因此,对初始值、约束条件和目标函数的定义可以看成是对非线性规划问题建模。
2.1 初始值 通过第1节的分析可知,室内TOA测距误差分布不满足高斯-马尔可夫定理的主要原因在于:TOA测距包含了LOS和NLOS 2种场景,且2种场景下的测距误差具有独立的分布特征,即
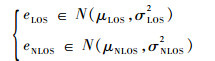 | (5) |
则随机变量eLOS-μLOS和eNLOS-μNLOS符合均值为零的高斯分布,即
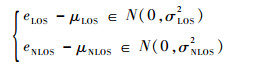 | (6) |
假设目标到基站之间的真实距离为d,目标与基站的测距值随机变量表示为
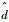
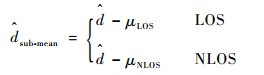 | (7) |

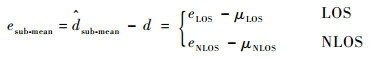 | (8) |
由式(8)可知,esub-mean也可以看成是一个均值为零的高斯分布,即
 | (9) |
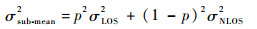 | (10) |
式中:p和1-p分别为LOS和NLOS出现的概率[15]。
通过上述分析可知,如果




上述方法需要解决μLOS与μNLOS数值获取问题、LOS/NLOS判别问题。
μLOS和μNLOS可以作为算法的输入参数,在系统运行前通过TOA待测节点在实际场景中进行大量的LOS/NLOS测距实验,统计获得;利用该方法还可以获得σLOS和σNLOS的数值,用于2.3.1节的约束条件计算。
2.2 目标函数 本文选择目标函数为非线性规划中最为常用的非线性最小二乘优化目标函数。定义优化误差为
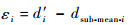 | (11) |
式中:d′i为优化后输出的第i个距离值;dsub-mean-i为初始距离集合

测距值优化的非线性最小二乘目标函数可以定义为
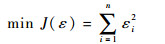 | (12) |
2.3 约束条件 本文设置的约束条件包括以下3项:测距值范围约束、Cayley-Menger行列式约束和空间四面体约束。
2.3.1 测距值范围约束 将高斯定律的3σ原则应用到设置测距值范围约束中。由高斯定律的3σ原则:正态分布在(μ+3σ, μ-3σ)以外的取值概率不到0.3%,几乎不可能发生,称为小概率事件[14-15]。
基于3σ原则,可近似认为
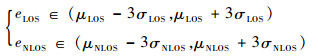 | (13) |
因此,对于测距值随机函数
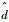
 | (14) |
进一步转换为
 | (15) |
基于式(11)中ε的定义,进一步将d的范围约束转换成ε的范围约束I(ε):
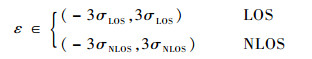 | (16) |
式(16)中的σLOS和σNLOS也可以通过节点在实际场景中的大量测量与统计获得。
2.3.2 Cayley-Menger行列式约束 距离几何理论中,Cayley-Menger行列式可以被用来处理不变空间的欧氏距离几何问题。
定义1??在m维欧氏空间中,给定2组各由n个点组成的点列,分别为{p1, p2, …, pn}和{q1, q2, …, qn},则称如下矩阵为2个点列的Cayley-Menger矩阵[16]:
 | (17) |
式中:d(pi, qj)为pi和qj两点间的欧氏距离,i, j∈(1, 2, …, n)。
定理1??当n≥m+2,则m维空间中任意一组点集{p1, p2, …, pn},都有
 | (18) |
即该m维空间中n个点之间的距离满足式(18)中所述关系, 而非相互孤立。所以,三维空间中,当节点数目n≥5(即至少4个基站以上)时,存在
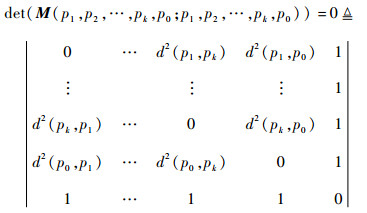 | (19) |
式中:k≥4;p1, p2, …, pk为基站;p0为待测节点。
因此,在基于TOA测距的定位中,将式(2)代入式(19)中,可以得到
 | (20) |
式中:dij(i, j≠0)为基站间距。
2.3.3 空间四面体约束 定理2??假设在三维空间中存在长度分别为a、a′、b、b′、c、c′的6条线段,则这6条线段可以组成一个四面体。
6条棱的充要条件[17]为
 | (21) |
式中:线段a与a′、b与b′、c与c′互为该四面体的一组对棱。
将上述四面体的几何约束关系应用在三维测距系统中,则目标节点(p0)与任意3个测距基站可形成空间四面体,用(p1, p2, p3)表示1、2、3号基站为例,则
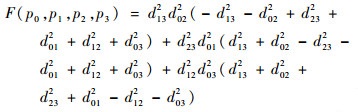 | (22) |
将式(2)代入式(22)中,可以得到四面体约束条件:
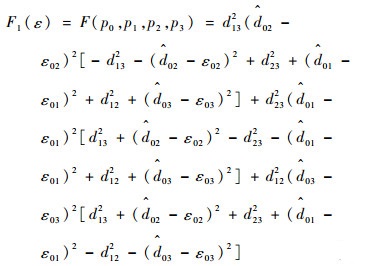 | (23) |
同理,可得到目标测距节点与其他所有基站组合构成四面体,以及各四面体的约束条件Fk(ε),其中k=1, 2, …, Cn3,n为基站总数。
3 仿真与实验验证 本节通过仿真和实验验证了本文测距值优化方法的有效性,评估了优化后的测距误差分布情况。与原始测距值、只通过几何约束(Cayley-Menger行列式约束+空间四面体约束)(简称算法1)优化后的测距值、文献[7, 14]的距离修正方法(简称算法2和算法3)优化后的测距值进行了测距误差分布对比、测距误差的均值和方差对比。
3.1 仿真验证 本文的仿真设置包括测距场景设置、算法实现和误差模型设置。算法实现中,LOS/NLOS识别算法采用文献[18]所提的基于RSS和测距值的LOS/NLOS识别算法。非线性规划算法方面采用了SQP算法[19]。
在测距误差模型方面,本文采用了文献[20]提出的测距误差模型,模型参数为500 MHz带宽下测得的参数。该模型基于在实际办公环境实测数据统计获得,与实际系统的测距误差分布具有较高的相似度。此外,由于LOS/NLOS识别算法中利用了RSS参数,本文还通过IEEE802.15.4 a标准的UWB信道模型[21-22],为每一组测距值产生了一个RSS值。图 2展示了测距误差的累积概率分布对比结果。表 1展示了5种测距误差的均值和方差统计结果。从对比结果来看,本文方法优化后的测距误差均值和方差均明显优于原始测距误差和其他3种测距值优化方法。
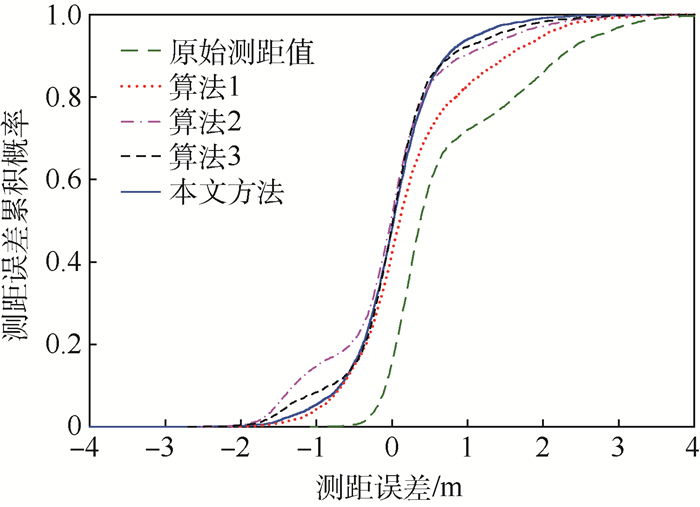 |
| 图 2 仿真实验测距误差累积概率分布曲线对比 Fig. 2 Comparison of cumulative probability distribution curves of range error in simulation experiment |
| 图选项 |
表 1 仿真实验测距误差均值和方差对比 Table 1 Comparison of mean and variance of range error in simulation experiment
| 测距方法 | 误差均值/m | 误差方差/m2 |
| 原始方法 | 0.75 | 0.87 |
| 算法1 | 0.25 | 0.72 |
| 算法2 | 0.02 | 0.54 |
| 算法3 | -0.03 | 0.76 |
| 本文方法 | 0.01 | 0.40 |
表选项
3.2 实验验证 本文以Decawave公司的DW1000硬件设备为基础搭建TOA测距实验验证系统。实验场地为10 m×17 m×4 m的办公楼一层大厅,如图 3所示。在实验中,NLOS误差主要源于测距节点间的行人和大厅障碍物。实验共获得了1 500个测距值,并进行了优化实验。
 |
| 图 3 实测实验场景 Fig. 3 Scene of actually measured experiment |
| 图选项 |
图 4显示了5种测距误差的累积概率分布的比较。表 2比较了测距误差的均值和方差。与仿真结果类似,本文提出的解决方案在现场比较中仍能达到最佳的精度。但是基于NLOS抑制的解决方案在现场测试中的性能显著低于仿真结果。这主要由于实际测距误差的分布比仿真更为复杂,使得基于NLOS检测的测距值修正算法无法准确估计测距误差。由于在非线性规划算法中合理地设置了初始值、目标函数和约束条件,本文方法在现场测试中的性能仍然接近于仿真。
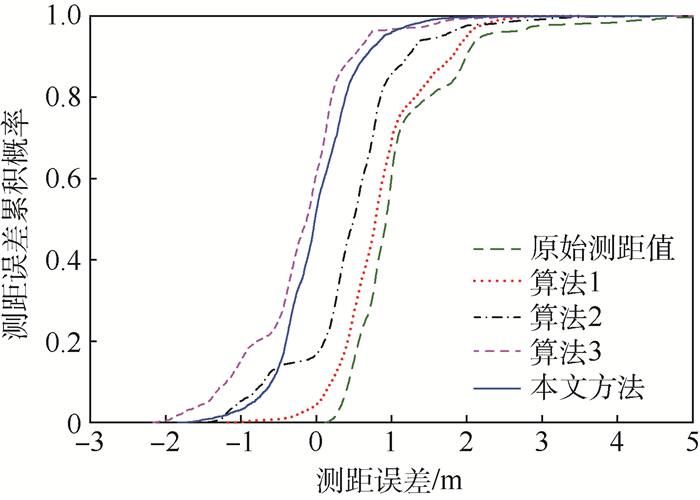 |
| 图 4 实测实验测距误差累积概率分布曲线对比 Fig. 4 Comparison of cumulative probability distribution curves of range error in actually measured experiment |
| 图选项 |
表 2 实测实验测距误差均值和方差对比 Table 2 Comparison of mean and variance of range error in actually measured experiment
| 测距方法 | 误差均值/m | 误差方差/m2 |
| 原始方法 | 1.13 | 0.67 |
| 算法1 | 0.86 | 0.37 |
| 算法2 | -0.21 | 0.50 |
| 算法3 | 0.45 | 0.58 |
| 本文方法 | 0.04 | 0.35 |
表选项
4 结论 本文对因室内环境中复杂的建筑结构和障碍物遮挡等引起的测距误差进行了优化研究,具体结论如下:
1) 分析了TOA测距误差的产生原因,进而得到测距误差分布特征,证明了其符合正态分布。
2) 将TOA测距值修正抽象为非线性规划问题,提出了基于SQP的测距值优化方法。对本文方法进行仿真,得到均值为0.01 m、方差为0.40 m2的测距误差优化结果。通过仿真结果比较,本文方法明显优于其他方法。
3) 在办公楼大厅环境中进行实测,对本文方法进行了验证。实测得到了均值为0.04 m、方差为0.35 m2的测距误差优化结果。证明通过本文方法能够显著提高测距精度,且明显优于其他方法。
参考文献
| [1] | AMUNDSON I, KOUTSOUKOS X D. A survey on localization for mobile wireless sensor networks[C]//Proceedings Mobile Entity Localization and Tracking in GPS-less Environnments. Berlin: Springer, 2009, 1: 235-254.https://www.mendeley.com/research-papers/survey-localization-mobile-wireless-sensor-networks-3/ |
| [2] | 王佳伟, 王敬东, 赵强, 等. 基于CSS的室内测距优化技术[J].指挥控制与仿真, 2016, 38(3): 131–135. WANG J W, WANG J D, ZHAO Q, et al. Optimization techniques for indoor ranging based on CSS[J].Command Control and Simulation, 2016, 38(3): 131–135.(in Chinese) |
| [3] | 李伟杰, 张霆廷, 张钦宇. 基于机器学习的超宽带NLOS鉴别方法[J].计算机工程与设计, 2014, 35(3): 750–754. LI W J, ZHANG T T, ZHANG Q Y. Identification of ultra wideband NLOS based on machine learning[J].Computer Engineering and Design, 2014, 35(3): 750–754.DOI:10.3969/j.issn.1000-7024.2014.03.003(in Chinese) |
| [4] | WANG Z, ZEKAVAT S A. Omnidirectional mobile NLOS identification and localization via multiple cooperative nodes[J].IEEE Transactions on Mobile Computing, 2012, 11(12): 47–59. |
| [5] | 徐彤阳. 基于减法聚类的TOA/AOA定位方法研究[J].电子测量技术, 2013, 36(10): 91–93. XU T Y. Research on TOA/AOA location method based on subtractive clustering[J].Electronic Measurement Technology, 2013, 36(10): 91–93.DOI:10.3969/j.issn.1002-7300.2013.10.023(in Chinese) |
| [6] | HEIDARI M, AKGUL F O, PAHLAVAN K. Neural network assisted identification of the absence of direct path in indoor localization[C]//IEEE Global Telecommunications Conference. Piscataway, NJ: IEEE Press, 2007: 387-392.https://ieeexplore.ieee.org/document/4410989/ |
| [7] | HEIDARI M, ALSINDI A N, PAHLAVAN K. UDP identification and error mitigation in TOA-based indoor localization systems using neural network architecture[J].IEEE Transactions on Wireless Communications, 2009, 8(7): 3597–3607.DOI:10.1109/TWC.2009.080415 |
| [8] | RAO N S V, XU X, SAHNI S. A computational geometry method for TDOA triangulation[C]//IEEE International Conference on Information Fusion. Piscataway, NJ: IEEE Press, 2007: 1-7.http://ieeexplore.ieee.org/document/4408050/ |
| [9] | ARIAS-DE-REYNA E. A maximum likelihood UWB localization algorithm exploiting knowledge of the service area layout[J].Wireless Personal Communications, 2013, 69(4): 1413–1426.DOI:10.1007/s11277-012-0642-2 |
| [10] | PARK C H, CHANG J H. TOA source localization based on weighted least squares estimator in LOS/NLOS mixture environments[J].International Journal of Distributed Sensor Networks, 2016, 12(12): 44–53. |
| [11] | LIANG S C, LIAO L H, LEE Y C. Localization algorithm based on improved weighted centroid in wireless sensor networks[J].Journal of Networks, 2014, 9(1): 183–189. |
| [12] | WANG Y, ZHENG F, WIEMELER M, et al. Reference selection for hybrid TOA/RSS linear least squares localization[C]//2013 IEEE 78th Vehicular Technology Conference. Piscataway, NJ: IEEE Press, 2013: 1-5.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6692388 |
| [13] | HE J, GENG Y, PAHLAVAN K. Toward accurate human tracking:Modelling time-of-arrival for wireless wearable sensors in multipath environment[J].IEEE Sensors Journal, 2014, 14(11): 122–145. |
| [14] | GHASSEMZADEH S S. The ultra-wideband indoor path loss model[J].IEEE Communication Letters, 2002, 7(2): 58–66. |
| [15] | HEIDARI M, AKGUL F O, PAHLAVAN K. Identification of the absence of direct path in ToA-based indoor localization systems[J].International Journal of Wireless Information Networks, 2008, 12(3-4): 117–127. |
| [16] | CAO M, ANDERSON B, MORSE A S. Sensor network localization with imprecise distances[J].Systems & Control Letters, 2006, 55(11): 887–893. |
| [17] | AKGUL F O. Modeling the behavior of multipath components pertinent to indoor geolocation[M].New York: Worcester Polytechnic Institute, 2010: 89-93. |
| [18] | WANN C D, CHIN H C. Hybrid TOA/RSSI wireless location with unconstrained nonlinear optimization for indoor UWB channels[C]//2007 IEEE Wireless Communications and Networking Conference. Piscataway, NJ: IEEE Press, 2007: 3940-3945.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4224965 |
| [19] | BOGGS P, TOLLE J. Sequential quadratic programming[J].Acta Numerica, 1995, 4(4): 1–51. |
| [20] | ALAVI B, PAHLAVAN K. Modeling of the TOA based distance measurement error using UWB indoor radio measurements[J].IEEE Communication Letters, 2006, 10(4): 275–277.DOI:10.1109/LCOMM.2006.1613745 |
| [21] | MARANO S, GIFFORD W M, WYMEERSCH H, et al. NLOS identification and mitigation for localization based on UWB experimental data[J].IEEE Journal on Selected Areas in Communications, 2010, 28(7): 1026–1035.DOI:10.1109/JSAC.2010.100907 |
| [22] | HATAMI A. Application of channel modeling for indoor localization using TOA and RSS[D]. New York: Worcester Polytechnic Insititute, 2006: 42-47.http://www.openthesis.org/documents/Application-channel-modeling-indoor-localization-33244.html |
