柔性铰链微动平台的结构可分为串联式和并联式。并联式中的各支链互不影响, 且共用一个动平台来实现各方向的运动, 相比于串联式的优点是其有效台面更大, 且各运动方向上的参数相同。
综上所述, 本文以柔性铰链代替传统刚性运动副为理念, 提出一种并联式微动平台的新构型, 首先, 建立了刚度模型并验证了其正确性; 然后, 分析了各结构参数对等效刚度的影响; 最后, 在此基础上对微动平台进行了结构参数优化设计[20-21], 进一步提高了微动平台的固有频率, 增强了其抗干扰能力, 达到了改善微动平台动态特性的目的。
1 二自由度微动平台的刚度分析 1.1 二自由度微动平台的结构设计 本文二自由度微动平台应该满足工作范围大、结构简单以及固有频率高的要求。为此, 设计出了一种正方形结构的微动平台, 其通过柔性铰链连接平台D和四周的柔性铰链框架, 如图 1所示。
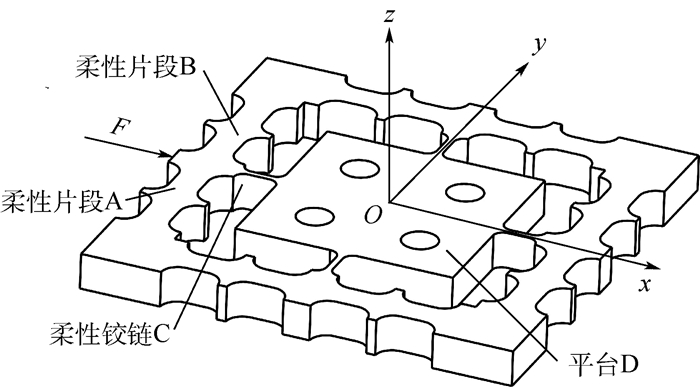 |
| 图 1 二自由度微动平台 Fig. 1 2-DOF micro-positioning stage |
| 图选项 |
该微动平台沿x和y方向的位移是解耦的:以x方向受力为例, 左右两侧对称的柔性铰链臂有效限制了y方向上的运动, 减轻了y方向上的位移问题, 提高了平台的定位精度。而二自由度微动平台的工作情况为:当x轴方向受到力F的作用时, 柔性片段A、B向内发生弯曲变形, 同时柔性铰链C起连接作用, 将位移传递给平台D。该微动平台x、y方向完全对称, 因此y方向受力运动情况相同。
1.2 倒圆角直梁型柔性铰链的刚度分析 微动平台中常见的柔性铰链为圆弧型柔性铰链和直梁型柔性铰链, 但它们分别存在运动范围小和切口处应力集中的缺陷。倒圆角直梁型柔性铰链避免了直角处严重的应力集中, 并且具有更大的运动范围, 同时兼顾两者优点, 因此本文采用倒圆角直梁型的柔性铰链结构。如图 2所示, 其由4个垂直于端面的四分之一圆柱面和2个矩形块对称切割形成倒圆角直梁型柔性铰链。设置的结构参数:直梁宽度t、直梁长度m、平台厚度h、倒圆角半径r、悬臂梁宽度c。
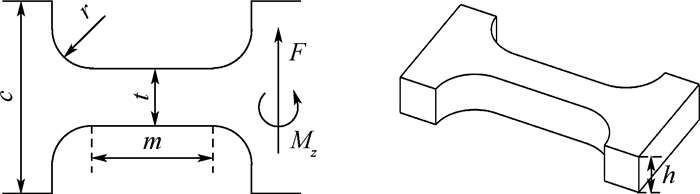 |
| 图 2 倒圆角直梁型柔性铰链 Fig. 2 Corner-filleted flexure hinge |
| 图选项 |
由于倒圆角直梁型柔性铰链的结构较为复杂, 为简化刚度的计算公式, 提出如下假设[22]:
1) 主要考虑柔性铰链的直梁和倒圆角部分的变形, 忽略其他部分。
2) 忽略柔性铰链发生变形的各部分之间的干涉。
3) 以小变形悬臂梁理论[18]为理论基础, 假定柔性铰链一端固定, 另一端承受力或力矩。
图 3中Mz表示为平台z方向所受弯矩, 首先分析运动过程中位移方向上柔性铰链所受力与力矩作用, 如图 3所示。
 |
| 图 3 倒圆角直梁型柔性铰链的受力分析 Fig. 3 Force analysis of corner-filleted flexure hinge |
| 图选项 |
当柔性铰链受力时, 其实际角位移θ非常小, 可近似等于[22]:
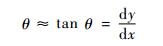 | (1) |
柔性铰链中性面的曲率半径ρ计算式为
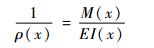 | (2) |
式中M(x)为平台所受弯矩:EI(x)为梁的弯曲刚度, E为弹性模量, I为截面惯性矩。柔性铰链切口中2r与m相比很小[10], 因此忽略柔性铰链2r长度上的弯矩变化, 即M(x)在每个微段dx上是相同的, 因此可以假设M(x)为常数Mz。式(2)可改写为
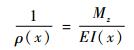 | (3) |
由图 3可知, 曲率半径和坐标x和y的关系为
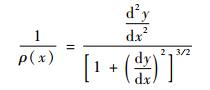 | (4) |
在柔性铰链受力发生弯曲变形时其上的任意微段dx存在:dy/dx?1, 所以式(4)可简化为
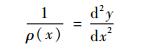 | (5) |
由式(3)和式(5)得
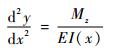 | (6) |
由式(1)和式(6)得
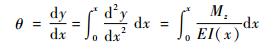 | (7) |
考虑倒圆角直梁型柔性铰链的圆弧部分, 将式(7)中直角坐标变换成极坐标, 即
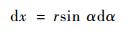 | (8) |
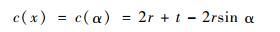 | (9) |
式中:α为极角。对于直梁部分, 式(7)仍为直角坐标, 且c(x)=t。因而, 倒圆角直梁型柔性铰链的弯曲刚度kθ的表达式为
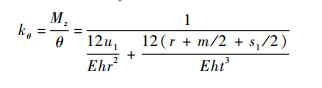 | (10) |
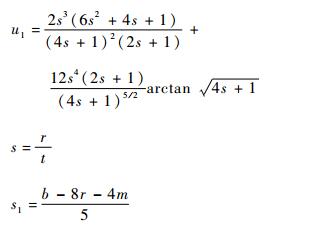 |
本文中, 确定微动平台为正方形结构。柔性铰链采用65 Mn弹簧钢, 弹性模量E=1.986×1010 Pa。
倒圆角直梁型柔性铰链的拉压刚度ks的表达式[13]为
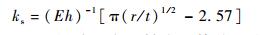 | (11) |
1.3 微动平台x轴方向等效刚度分析 如1.1节中所述, 因该微动平台关于x和y方向完全对称, 故以F沿x轴作用为例, 二自由度微动平台的受力情况如图 4所示。
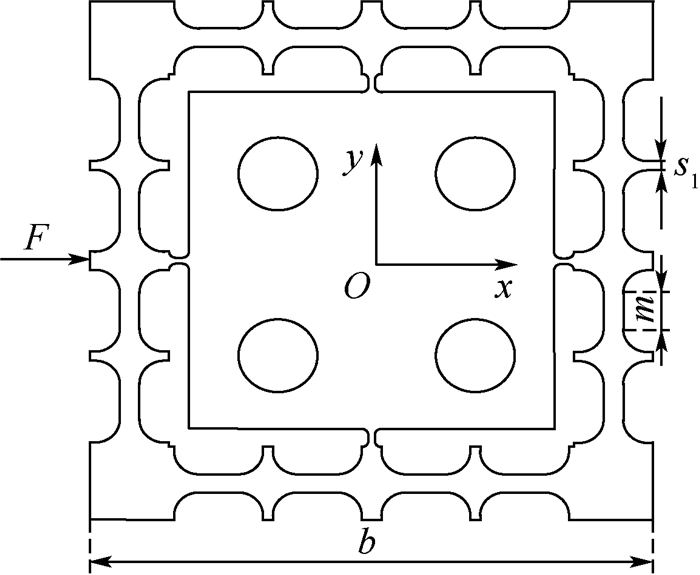 |
| 图 4 二自由度微动平台结构平面 Fig. 4 Structure plan of 2-DOF micro-positioning stage |
| 图选项 |
基于微动平台的结构, x向的柔性铰链支链可简化为如图 5所示的复合平行四杆机构, L=r+m/2+s1/2。根据其存在的几何关系可知:x向:δ=Ltanγ, γ很小, tanγ≈γ, 所以γ=δ/L。
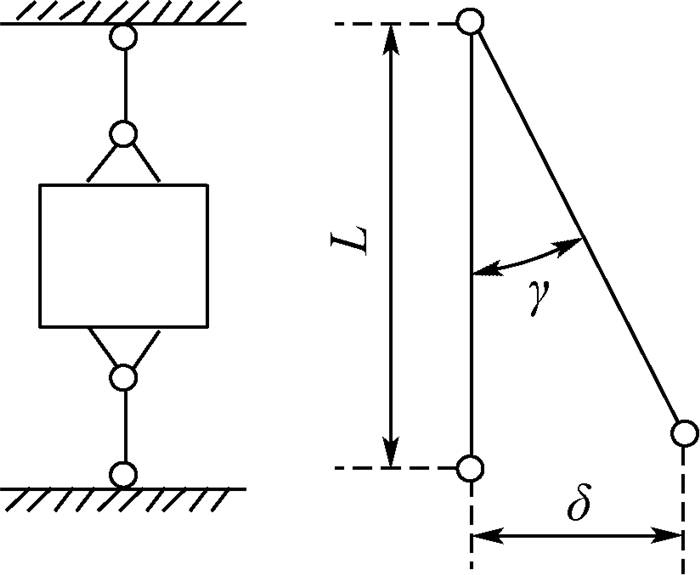 |
| 图 5 复合平行四杆机构 Fig. 5 Compound parallel four-bar mechanism |
| 图选项 |
连杆的伸长量为
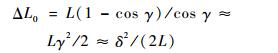 | (12) |
所以每个铰链的伸长量为
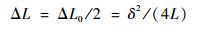 | (13) |
由于柔性铰链受力作用会发生弯曲和拉伸变形, 因此每个柔性铰链存储的弹性能为
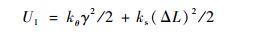 | (14) |
而驱动力所作的功为
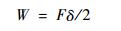 |
该微动平台每一边有4个柔性铰链, 由功能原理可得W=4U1, 即
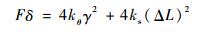 | (15) |
综合可得该微动平台在x方向上的等效刚度为
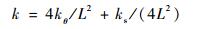 | (16) |
为实现平台在各方向上的等效刚度最大, 可优化各尺寸, 而本文中微动平台在x和y方向上的等效刚度大小相同, 均为
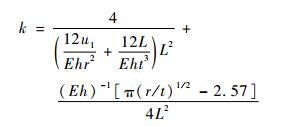 | (17) |
式中:
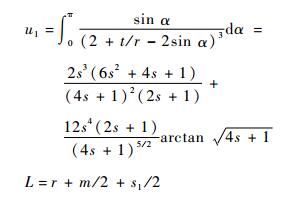 |
由以上的微动平台刚度分析过程可知, 该刚度计算模型同样适用于其他柔性铰链微动平台的刚度计算。
1.4 微动平台等效刚度的有限元仿真与验证 为验证微动平台刚度理论模型的正确性, 首先选取微动平台的材料, 65 Mn弹簧钢的弹性模量为198.6 GPa, 泊松比ν为0.31, 其为合适的微动平台材料, 同时该微动平台的结构参数如表 1所示。
表 1 二自由度微动平台结构参数 Table 1 Structural parameters of 2-DOF micro-positioning stage
| mm | ||||||
| 参数 | b | s1 | m | r | t | h |
| 数值 | 85 | 3.3 | 3.3 | 4 | 2 | 20 |
表选项
微动平台所受力F与微动平台x轴方向柔性铰链支链位移x之间的关系可描述为
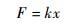 | (18) |
式中:x轴等效刚度k可以通过将表 1中的数据代入式(17)求得, 其值为1.907×107 N/m。
利用式(18)即可得到在不同大小的力作用下的微动平台位移理论值, 如表 2所示。
表 2 x轴方向位移仿真值、理论值及其相对误差 Table 2 x-axis displacement simulation value, theoretical value and its relative error
| 力/N | x轴方向位移 | ||
| 理论值/(10-7m) | 仿真值/(10-7m) | 相对误差/% | |
| 2 | 1.048 8 | 1.065 3 | 1.57 |
| 4 | 2.097 5 | 2.132 5 | 1.67 |
| 6 | 3.146 3 | 3.197 0 | 1.61 |
| 8 | 4.195 1 | 4.260 7 | 1.56 |
| 10 | 5.243 8 | 5.320 2 | 1.46 |
| 12 | 6.286 4 | 6.376 3 | 1.43 |
| 14 | 7.342 3 | 7.443 6 | 1.38 |
| 16 | 8.396 5 | 8.509 0 | 1.34 |
| 18 | 9.390 2 | 9.511 3 | 1.29 |
| 20 | 10.534 5 | 10.667 2 | 1.26 |
表选项
为验证所推导等效刚度的正确性, 在ABAQUS软件中建立如图 6所示的微动平台仿真模型, 并对其添加约束及不同大小的驱动力, 所得x轴方向位移仿真值、理论值及其相对误差如表 2所示。
 |
| 图 6 微动平台仿真模型 Fig. 6 Simulation model of micro-positioning stage |
| 图选项 |
为了更直观地表达微动平台x轴方向位移理论值与仿真值之间的关系, 根据表 2中的数据, 绘制得到微动平台力与形变的关系如图 7所示。由图 7发现, 微动平台的位移理论值与仿真值的相对误差不超过1.7%, 两者高度吻合, 且所施加的力与位移间具有良好的线性关系, 即平台x轴方向上的等效刚度较稳定。因此所推导x轴转动等效刚度计算模型的正确性得到了验证。
 |
| 图 7 x轴方向力-形变关系 Fig. 7 Relationship between x-axis force and displacement |
| 图选项 |
1.5 微动平台结构参数灵敏度分析 若要根据所推导的x轴及y轴方向的等效刚度计算模型, 设计满足性能要求的微动平台, 仍需研究各结构参数与等效刚度之间的关系, 以便有效地进行参数的修改与优化。
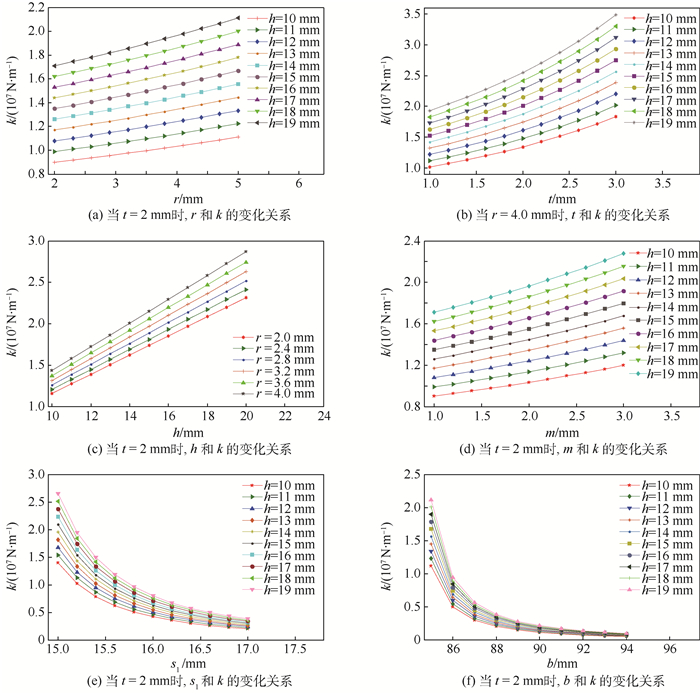
由式(4)、式(10)、式(11)及式(17)发现, 要精确定性地分析微动平台的各结构参数对等效刚度的影响比较困难。因此利用MATLAB软件定量分析各结构参数对等效刚度的影响, 基于对比和分析数据得到的各结构参数对等效刚度k的灵敏度关系, 对微动平台进行结构优化。
采用弹簧钢作为该微动平台的材料。如图 4所示, 影响该微动平台等效刚度的结构参数包括r, t, h, b, s1, m。基于式(17), 上述结构参数对该微动平台等效刚度k的灵敏度分析如图 8所示, 由图 8可知:等效刚度k与r呈曲线递增, 且增幅小幅度提升; 等效刚度k与t呈曲线递增, 且增幅趋于平稳; 等效刚度k与h呈曲线递增, 且增幅明显; 等效刚度k与m呈曲线递增, 且增幅趋于平稳; 等效刚度k与s1呈曲线递减, 且减幅较大; 等效刚度k与b呈曲线递减, 且减幅幅度较大。
 |
| 图 8 结构参数与等效刚度k的关系 Fig. 8 Relationship between structural parameters and equivalent stiffness k |
| 图选项 |
比较图 8(a)~(f)可以发现, h、s1和b对k的灵敏度影响比较大, r和t对k的灵敏度影响较小。
2 二自由度微动平台优化模型 为使平台的动态特性得到改善, 即在位移范围内, 提高平台的固有频率, 需对该微动平台进行尺寸优化。影响运动体固有频率的最主要因素是刚度, 且由于上述灵敏度分析仅局限于各单参数对等效刚度的影响, 并未考虑结构参数间相互间产生的干涉, 因此有必要对微动平台进行全局优化。
2.1 设计变量的确定 由图 6可知, 柔性结构微动平台发生弹性变形的难易程度是受微动平台尺寸影响的, 即边长b、直梁宽度t、直梁长度m、平台厚度h、倒圆角半径r、铰链连接长度s1, 于是, 平台尺寸优化的设计变量为
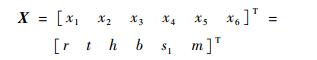 |
2.2 目标函数的建立 由于本文优化的目的为提高平台的等效刚度, 故平台尺寸优化的目标函数便通过其刚度来建立。
本文的目标是在给定的位移下, 通过尺寸优化的方式实现平台在不同方向上的刚度最大。由该微动平台的结构可知其在x和y方向上完全对称, 故x和y方向的等效刚度大小完全相等, 设为kx和ky, 由上文可知kx=ky=k。由于线性加权法在处理多目标优化问题时具有简单且易于实现的优点, 故本文采用该方法来建立统一目标函数, 该函数必须综合考虑微动平台的各方向刚度。本文微动平台在x和y方向上的刚度对弹性变形的难易程度影响相同, 所以它们的权重值取为相等, 即w1=w2=0.5, 则统一目标函数可表示为
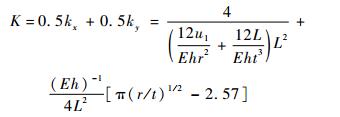 |
2.3 约束条件的给出 1) x向最大位移至少20 μm。
本文要求平台沿x(或y)向的最大位移不小于20 μm即, δ=Lγ≥20×10-6。
2) x向最大应力不超过许用应力。
平台沿x向输出最大位移时所产生的最大应力不得大于所用材料弹簧钢的许用应力570 MPa, 微动平台通过驱动输出位移时, 基于悬臂曲梁变形理论[18]计算获得沿x向的弯曲正应力σ1, 由σ=N/A+My/Iz, N为梁所受截面内力, A为梁截面面积, My为梁所受弯矩, Iz为截面惯性矩, 可得
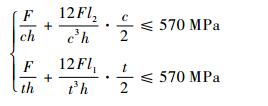 | (19) |
式中:l1=4m+3r; l2=b/2-c。
3) z向最大位移不超过1 μm。
设作用于单侧柔性铰链的重物的重力分力为F2。根据悬臂曲梁变形理论[18]计算倒圆角直梁型柔性铰链在F2作用下所产生的弯矩M2以及变形角θ2为
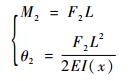 | (20) |
动平台台面承受100 N重物的情况下, 在垂直于台面方向(即z向)的最大位移δ2应在1 μm以下。基于平台z向位移很小, 采用其z向变形角θ2来代替该位移。由于δ2≤1 μm, 因此:
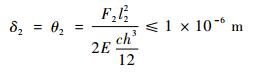 | (21) |
4) z向最大应力不超过许用应力。
动平台在承受100 N的重物时, 所产生的最大应力σ2应小于等于所用材料65Mn弹簧钢的许用应力570 MPa。I2为截面惯性矩, 根据σ2≤570 MPa, 可得
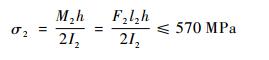 | (22) |
2.4 平台多目标尺寸优化的求解 选用的压电陶瓷驱动器其最高输出力为1 000 N, 则驱动器单方向驱动动平台时, 单个柔性铰链在驱动方向上所受的最大力为125 N。在动平台承受100 N的重物的前提下, 单侧柔性铰链所承受的垂直于台面方向上的最大力为25 N。采用MATLAB来求解该平台尺寸优化的数学模型。
和遗传算法、蚁群算法等算法相比, 自适应粒子群算法中不存在交叉和变异运算, 而是利用粒子速度进行搜索, 并且在迭代进化中通过最优的粒子传递信息, 因此其搜索速度更快; 且自适应粒子群算法能同时将粒子群体的历史最好位置传递给其他粒子; 同时自适应粒子群算法需调整的参数较少, 结构简单, 更易于实现。
基于上述优点, 本文采用自适应粒子群优化算法进行该微动平台的多目标尺寸优化, 得到优化算法适应度曲线如图 9所示, 微动平台优化后的结构参数:X=[r t h b s1 m]T=[3.94 1.94 19.86 85 3.85 3.96]T。
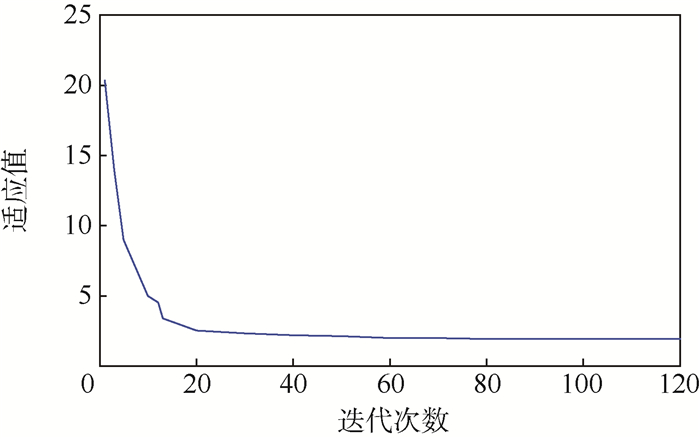 |
| 图 9 自适应粒子群优化算法适应度曲线 Fig. 9 Fitness curve of adaptive particle swarm optimization algorithm |
| 图选项 |
定义优化前的微动平台为前面所设计实例, 即该微动平台的等效刚度为1.907×107 N/m。
根据二自由度微动平台的结构参数将优化前后的等效刚度汇总于表 3。
表 3 优化前后二自由度微动平台等效刚度对比 Table 3 Comparison of equivalent stiffness of 2-DOF micro-positioning stage before and after optimization
| 等效刚度/(N·m-1) | 优化率/% | |
| 优化前 | 优化后 | |
| 1.907×107 | 2.116×107 | 10.96 |
表选项
由表 3可知, 经自适应粒子群算法优化之后, 微动平台x轴方向等效刚度k上升了10.96%, 优化结果符合预期。
3 二自由度微动平台固有频率计算 为深入研究优化后微动平台的动态特性, 需计算优化后的微动平台的固有频率。
该微动平台在其运动方向上的系统动能T为
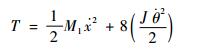 | (23) |
式中:M1为平台的质量; x为微动平台x方向上的位移; J为x方向连杆对端点的转动惯量, J=
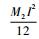
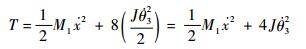 | (24) |
式中:θ3为连杆转动角度。
由1.3节可知, 微动平台机构在x方向上有8个同样的柔性铰链, 因而系统的势能为
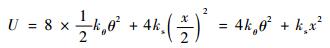 | (25) |
对于自由度数为n的系统, 在外力F作用下的运动方程满足拉格朗日方程:
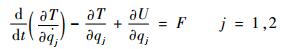 | (26) |
式中:qj和
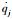
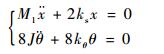 | (27) |
即
 | (28) |
主振动可设为
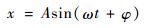 | (29) |
式中:A为振幅; ω为振动角频率; φ为初相位。
将式(29)代入式(28), 得代数齐次方程组为
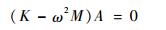 | (30) |
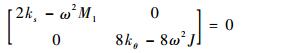 | (31) |
由式(31)可得:
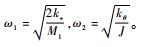
4 二自由度微动平台模态分析 分析中采用ABAQUS软件建模, 以限制运动方向平台两侧的运动为边界条件。图 6为微动平台的有限元模型。将材料的性能参数代入式(31), 计算得ω1=108.96 Hz, ω2=147.53 Hz。
基于以上模型进行微动平台的模态分析, 得到微动平台的前5阶固有频率值如表 4所示。图 10为微动平台的前5阶振型图。
表 4 二自由度微动平台前5阶固有频率仿真值 Table 4 The first five natural frequency simulation values of 2-DOF micro-positioning stage
| 阶数 | 固有频率仿真值/Hz |
| 1阶 | 116.04 |
| 2阶 | 160.94 |
| 3阶 | 232.65 |
| 4阶 | 284.39 |
| 5阶 | 358.20 |
表选项
 |
| 图 10 微动平台的各阶振型 Fig. 10 Various modes of vibration of micro-positioning stage |
| 图选项 |
模态分析得到微动平台的1阶固有频率为116.04 Hz, 由式(31)计算得到的1阶固有频率为108.96 Hz, 两者相对误差仅为6.49%。
模态分析得到微动平台的2阶固有频率为160.94 Hz, 由式(31)计算得到的2阶固有频率为147.53 Hz, 两者相对误差为8.33%。
由此可见, 公式推导进行柔性铰链及微动平台的特性分析的方法具有较好的设计精度, 是可行的。
5 结论 1) 本文选用倒圆角直梁型柔性铰链, 基于并联机构的思想, 提出了一种新型二自由度微动平台, 且实现该平台在x和y方向上位移解耦; 其次建立了x方向刚度的理论计算模型, 并利用有限元仿真分析验证了理论模型的正确性。
2) 分析了二自由度微动平台中各结构参数对等效刚度的灵敏度。
3) 以改善二自由度微动平台的动态性能为目标, 建立其优化模型, 并采用自适应粒子群优化算法对微动平台的结构参数进行了多目标优化, 提高该微动平台的刚度和固有频率。优化结果表明, 二自由度微动平台的动态性能得到了很大的提高, 优化结果符合预期。
后续将建立二自由度微动平台的物理模型, 并进行相关实验测试, 做进一步完善。
参考文献
| [1] | LIU P B, YAN P, ZHANG Z, et al. Flexure hinges guided nano-stage for precision manipultions:Design, modeling and control[J].Precision Engineering and Manufacturing, 2015, 16(11): 2245–2254.DOI:10.1007/s12541-015-0289-5 |
| [2] | 刘凯, 曹毅, 周睿, 等. 二自由度平板折展柔性铰链的分析及优化[J].航空学报, 2016, 36(1): 142–152. LIU K, CAO Y, ZHOU R, et al. Analysis and optimization of a 2-DoF flexure hinge[J].Acta Aeronautica et Astronautica Sinica, 2016, 36(1): 142–152.(in Chinese) |
| [3] | CHOI E, KWON K, DAEJOONG K, et al. Tunable reverse electrodialysis with geometrically controlled self-assembled nanoparticle network[J].Lab on A Chip, 2015, 15(1): 168–178.DOI:10.1039/C4LC01031K |
| [4] | 马立, 谢炜, 刘波, 等. 柔性铰链微定位平台的设计[J].光学精密工程, 2014, 22(2): 338–345. MA L, XIE W, LIU B, et al. Design of flexible sources positioning platform[J].Optics and Precision Engineering, 2014, 22(2): 338–345.(in Chinese) |
| [5] | 王振华, 陈立国, 孙立宁. 集成式6自由度微动并联机器人系统[J].光学精密工程, 2007, 15(9): 1391–1397. WANG Z H, CHEN L G, SUN L N. Integrated 6-DoF micro-motion parallel robot system[J].Optics and Precision Engineering, 2007, 15(9): 1391–1397.DOI:10.3321/j.issn:1004-924x.2007.09.014(in Chinese) |
| [6] | LAI L J, GU G Y, ZHU L M. Design and control of a decoupled two degree of freedom translational parallel micro-positioning stage[J].Review of Scientific Instruments, 2012, 83(4): 105–111. |
| [7] | LI Y M, WU Z G. Design, analysis and simulation of a novel 3-DoF translational micro manipulator based on the PRB model[J].Mechanism and Machine Theory, 2016, 100(3): 235–258. |
| [8] | 陶惠峰.超精密微位移系统研究[D].杭州: 浙江大学, 2003: 1-7. TAO H F.Research on ultra-precision micro displacement system[D].Hangzhou: Zhejiang University, 2003: 1-7(in Chinese). |
| [9] | 刘庆玲, 翁海珊, 邱丽芳. 新型单边直圆椭圆混合柔性铰链的柔度计算及其性能分析[J].工程力学, 2010, 27(10): 52–56. LIU Q L, WENG H S, QIU L F. Flexibility calculation and performance analysis of a new Unilateral elliptical hybrid flexure hinge[J].Engineering Mechanics, 2010, 27(10): 52–56.(in Chinese) |
| [10] | 任宁, 田国豪, 欧开良, 等. 倒圆角直梁型柔性铰链刚度研究[J].机械强度, 2012, 34(3): 366–370. REN N, TIAN G H, OU K L, et al. Study on the stiffness of inverted fillet flexible hinge[J].Mechanical Strength, 2012, 34(3): 366–370.(in Chinese) |
| [11] | BHAGAT U, SHIRINZADEH B, CLARK L, et al. Design and analysis of a novel flexure-based 3-DOF mechanism[J].Mechanism and Machine Theory, 2014, 74(2): 173–187. |
| [12] | GUO Z L Tat J T, YANG G L, et al. Integrating mechanism synthesis and topological optimization technique for stiffness-oriented design of a three degrees-of-freedom flexure-based parallel mechanism[J].Precision Engineering, 2015, 39(5): 125–133. |
| [13] | GAO P, SWEI S M, YUAN Z. A new piezodriven precision micropositioning stage utilizing flexure hinges[J].Nanoteehnology, 1999, 10(4): 394–398.DOI:10.1088/0957-4484/10/4/306 |
| [14] | 陈贵敏, 贾建援, 勾燕洁. 混合型柔性铰链研究[J].仪器仪表学报, 2004, 25(4): 110–112. CHEN G M, JIA J Y, GOU Y J. Study on hybrid flexible hinge[J].Chinese Journal of Scientific Instrument, 2004, 25(4): 110–112.(in Chinese) |
| [15] | 沈剑英, 张海军, 赵云. 压电陶瓷驱动器杠杆式柔性铰链机构放大率计算方法[J].农业机械学报, 2013, 44(9): 267–271. SHEN J Y, ZHANG H J, ZHAO Y. Calculation method of magnification of lever-type flexible hinge mechanism of piezoelectric ceramic actuator[J].Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(9): 267–271.(in Chinese) |
| [16] | LI Y M, XIAO S L, XI L Q, et al. Design, modeling, control and experiment for a 2-DOF compliant micro-motion stage[J].Precision Engineering and Manufacturing, 2014, 15(4): 735–744.DOI:10.1007/s12541-014-0394-x |
| [17] | 田延岭, 张大卫, 闫兵. 二自由度微定位平台的研制[J].光学精密工程, 2006, 14(1): 94–99. TIAN Y L, ZHANG D W, YAN B. Development of 2-DOF micro positioning platform[J].Optics and Precision Engineering, 2006, 14(1): 94–99.DOI:10.3321/j.issn:1004-924X.2006.01.017(in Chinese) |
| [18] | 崔玉国, 阮超, 马剑强, 等. 2-DoF并联柔性结构微动平台的新构型及尺寸优化[J].机器人, 2016, 38(3): 352–359. CUI Y G, RUAN C, MA J Q, et al. New configuration and dimension optimization of jogging parallel flexible structure platform[J].Robot, 2016, 38(3): 352–359.(in Chinese) |
| [19] | 李仕华, 韩雪艳, 马琦翔, 等. 新型并联柔性铰链微动精密平台的研究[J].中国机械工程, 2016, 27(7): 888–893. LI S H, HAN X Y, MA Q X, et al. Research on jogging precision platform of new type of parallel flexible hinge[J].China Mechanical Engineering, 2016, 27(7): 888–893.DOI:10.3969/j.issn.1004-132X.2016.07.007(in Chinese) |
| [20] | 徐刚, 瞿金平, 杨智韬. 一种改进的自适应粒子群优化算法[J].华南理工大学学报, 2008, 36(9): 6–10. XU G, QU J P, YANG Z T. An improved self-adaptive particle swarm optimization algorithm[J].Journal of South China University of Technology, 2008, 36(9): 6–10.DOI:10.3321/j.issn:1000-565X.2008.09.002(in Chinese) |
| [21] | 李宝磊, 施心陵, 苟常兴, 等. 多元优化算法及其收敛性分析[J].自动化学报, 2015, 41(5): 949–959. LI B L, SHI X L, GOU C X, et al. Multivariate optimization algorithm and its convergence analysis[J].Acta Automatica Sinica, 2015, 41(5): 949–959.(in Chinese) |
| [22] | 郭明陆.压电陶瓷驱动的微纳定位平台系统研究[D].沈阳: 东北大学, 2014: 21-35. GUO M L.Study on micro-nano positioning platform driven by piezoelectric ceramics[D].Shenyang: Northeastern University, 2014: 21-35(in Chinese). |
