目前多无人机编队飞行理论方面取得了丰硕成果,除了传统的领导-跟随法、虚拟结构法、人工势场法和基于行为法之外,基于一致性的编队控制方法也吸引了研究者的目光,以上方法各有优缺点[3-4],****对以上方法做了很多改进。如文献[5]提出了一种基于诱导航线的协同控制方法,实现了编队保持、避障和避碰;文献[6]提出了虚拟结构、领导-跟随及基于行为法相结合的方法,提高了机间通信的可靠性;文献[7]基于双模模型预测控制(Model Predictive Control, MPC)方法设计了领导-跟随的控制律。当前对无人机集群编队控制的研究,通常是建立理想的模型,然后进行地面仿真,也有少数进行了实验。如文献[8]将基于虚拟结构控制方法在四旋翼无人机上做了一系列实验;文献[9-10]将领导-跟随协同编队控制算法应用到固定翼无人机上进行了试验;文献[11]在四旋翼无人机上验证了基于一致性的时变编队控制理论。通过对现阶段研究现状梳理可以看出,无人机集群编队控制理论研究已经取得了丰硕的成果,但进行实验的较少[12];已经用于验证的系统多为集中式控制,采用分布式实时控制的较少。而且以上实验系统只能控制单一类型的无人机平台,而实际无人机集群通常包含不同功能、种类的无人机平台,因此这些实验系统存在对不同类型无人机平台的可移植性差、扩展性不足以及通用性不高的问题。
为了将无人机集群编队控制理论更好地应用到实践中,本文搭建了无人机集群编队控制演示验证系统。首先,采用封装和分层控制的思想,设计了无人机控制系统,将无人机控制系统分为决策层和执行层,决策层执行编队控制算法,执行层根据决策层或地面站的指令控制无人机运动,使得系统具备扩展性强,通用性好的特点。其次,为保证系统的可靠性和安全性,利用冗余设计的思想,采用两套地面站和数据链,分别用于控制算法的演示验证和应急处置,保证了系统的功能完备性和安全性。最后,以四旋翼无人机作为无人机平台,对领导-跟随协同编队控制算法进行了飞行试验,验证了系统功能的可用性和可靠性。
1 系统设计与搭建 无人机集群编队控制演示验证系统可以在户外环境下演示无人机集群运动过程,验证编队控制算法的有效性。系统可获取集群在预设控制方法下的运动状态,并可对试验过程中的飞行、通信、传感器信息进行有效监管、指挥和控制。试验过程中数据实时保存,通过分析可以得出无人机集群编队控制方法的运行效果。
1.1 系统总体架构 无人机集群编队控制演示验证系统由无人机平台、地面站和数据链共同组成。为了实现系统对异构无人机集群的控制,增强系统的扩展性和通用性,利用封装和分层控制的思想将无人机控制系统设计为决策层与执行层,执行层对无人机平台的姿态、速度、位置进行控制,决策层运行编队控制算法,用于控制无人机的行为。为了增强系统的稳定性、可靠性,利用冗余设计的思想,采用双数据链、双地面站的模式,两套数据链和地面站独立运行。为了避免编队控制算法不成熟带来的风险,地面站2直接对无人机平台执行层进行控制,且其控制指令优先级高于地面站1,起到了应急处置的作用。
系统总体架构如图 1所示,图中箭头表示信息流向,演示验证系统分为任务层、决策层和执行层。任务层的输入信息由演示任务的类型决定,可根据不同的演示验证任务需求,生成对应的任务指令发送至决策层,其功能由地面站实现。决策层根据任务指令、环境及自身和相邻个体的位置、速度等状态信息,进行分布式自主决策,生成通用的控制指令发送给执行层,其功能由无人机机载计算机实现。执行层根据决策层生成的控制指令,对无人机平台的传感器及运动行为进行控制,驱动无人机达到期望状态,并将执行结果回传给决策层,其功能由无人机底层飞行控制器实现。无人机之间以及地面站1与无人机之间通过数据链1(自组网通信)实现信息交互,通过调整地面站1发送不同的控制指令,系统可实现集中式、分布式和混合式3种控制方式,可以对集群不同的通信拓扑进行演示验证。地面站2通过数据链2直接对无人机平台执行层进行控制,用于试验开始前的状态设置、试验过程中的应急处理、试验结束后的平台回收,可以确保演示验证过程中具有较高的安全性。系统采用GPS定位模块为无人机平台提供实时定位导航服务,定位模块通过串口通信与无人机平台进行数据传输。
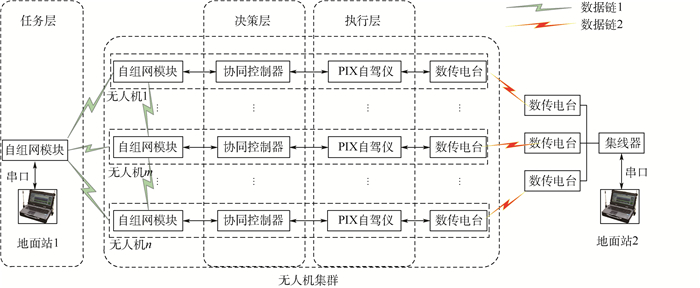 |
| 图 1 无人机集群编队控制演示验证系统结构框图 Fig. 1 Structure diagram of UAV swarm formation control demonstration and verification system |
| 图选项 |
1.2 无人机控制系统 集群系统具有良好的扩展性,能够兼容不同类型的无人机平台,同时具有分布式控制的特点,这就要求无人机控制系统具有较强的适应性,能够对不同类型的无人机进行有效控制,并实现对不同的分布式编队控制方法进行验证。本设计受智能体结构模型的启发[13],采用分层控制[14-15]和封装的思想[16],将无人机控制系统分为决策层和执行层分别进行设计和封装,如图 2所示。
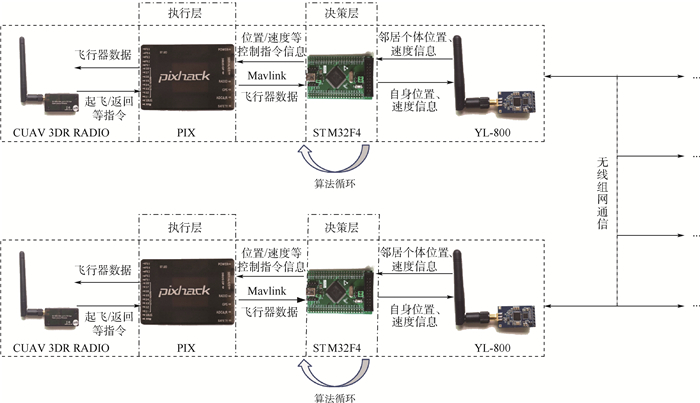 |
| 图 2 无人机控制系统结构框图 Fig. 2 Structure diagram of UAV control system |
| 图选项 |
决策层负责编队算法和无线组网通信等应用程序的处理,生成位置、速度等通用的决策信息,并通过串口发送给执行层。为保证无人机有充足的时间更新邻居个体的速度、位置等状态信息,同时节约处理器计算资源,决策层的计算频率不大于邻居无人机广播自身状态信息的频率。根据收到的决策信息,执行层负责无人机平台的姿态稳定以及驱动无人机达到期望状态,并将无人机运动参数实时存储到内置在执行层的SD卡中,以便试验后对飞行数据进行分析。执行层将飞行数据回传给决策层的同时也经数传传输给地面站2,实现对集群运动状态的实时监控。自组网模块组建Mesh网络,和执行层有双向的数据流传输。整个系统采用分布式的编队控制方法,各无人机平台并行运行程序,执行相同的软件流程,控制系统软件流程如图 3所示。
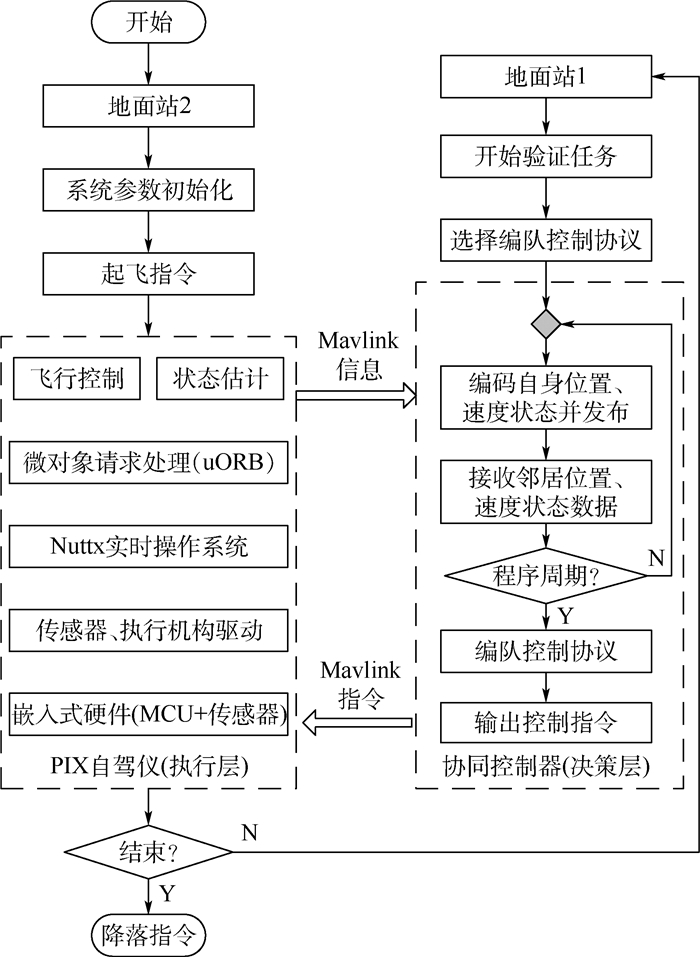 |
| 图 3 无人机控制系统软件流程图 Fig. 3 Software flowchart of UAV control system |
| 图选项 |
由于无人机控制系统的决策层需要较大的计算量和较高的实时性,对处理器的性能有较高的要求。本设计选用基于ARM Cortex-M4核心的STM32F4系列微处理器,该处理器具有功耗较低、处理能力强等优点,满足了试验要求。执行层选择开源的PIX自驾仪,PIX自驾仪是一种成熟可靠的无人载具控制器,可以控制多种类型的无人载具,如固定翼无人机、四旋翼无人机等。决策层的STM32F4和执行层的PIX通过基于Mavlink协议的串口实现信息交互。
通过分层控制,决策层可根据不同的试验需求,植入各类编队控制方法,使系统具有了较强的适应性和扩展性。执行层选择开源PIX自驾仪,搭建稳定的无人机平台,减少了程序移植工作量,提高了代码的可重用性,可以有效缩短系统的开发周期,并能够将试验重点放在决策层的编队算法开发上。通过PIX自驾仪将不同类型的无人载具封装为无人机对象,封装之后在对异构无人机进行控制时,只需调整自驾仪参数,不再需要根据不同类型的无人机特殊性能针对性的开发相应的控制策略,也就是决策层只需生成通用的位置、速度和传感器开关等控制指令,即可实现异构无人机平台的分布式协同控制。系统有效地解决了无人机平台硬件异构的差异,具备了控制异构集群的能力。
1.3 地面站 地面站是演示验证系统的指挥控制中心,可以对无人机平台各种运动数据和传感器参数进行实时监控,能够对无人机下达特定指令,如任务开始、中断、继续和结束等。地面站还需要对多无人机平台状态进行监视和控制,同时对传感器进行故障诊断和应急处理。为了增强系统的可靠性和安全性,采用冗余思想,设计了两套地面站,分别由一台笔记本电脑(CPU:i5内存:4G)和相应的数据接收和发送设备组成。
地面站1采用双串口通信,串口1负责将控制指令通过数据链1发送给指定无人机或者进行广播。根据不同试验目的,这里的控制指令既可以是中心解算生成的位置、速度指令,也可以是调用封装在协同控制器中的控制算法指令;串口2负责实时接收无人机广播的飞行数据,并实时存储,也可通过MATLAB进行实时数据处理,显示无人机的位置、速度等运动状态,观察运行的效果是否与期望的一致。
地面站2运行Mission planner 1.3.32和Qgroundcontrol 3.1.0两个无人机控制软件。Mission planner主要用来试验前无人机参数的设置,包括最大速度、加速度和低电压保护等,如图 4(a)所示。Qgroundcontrol用来控制多个无人机,同时观察数据链2传回的无人机状态信息,包括电压、电流和速度等,以对各无人机传感器参数进行实时监控。但试验过程中Qgroundcontrol只能对无人机逐一控制,当无人机增多时,可操行性将会降低。因此,对原Qgroundcontrol软件进行了二次开发,增加了一键同时动作、同时返回功能,开发后软件界面如图 4(b)所示。开发后可同时控制多个无人机动作,减少了试验人员的操作步骤,使系统操作更简单,降低了对试验人员的技能要求,使系统更实用。例如在演示验证无人机集群的控制算法时,通过Qgroundcontrol,地面站2可控制无人机集群同时起飞,试验结束后可以将无人机同时收回。
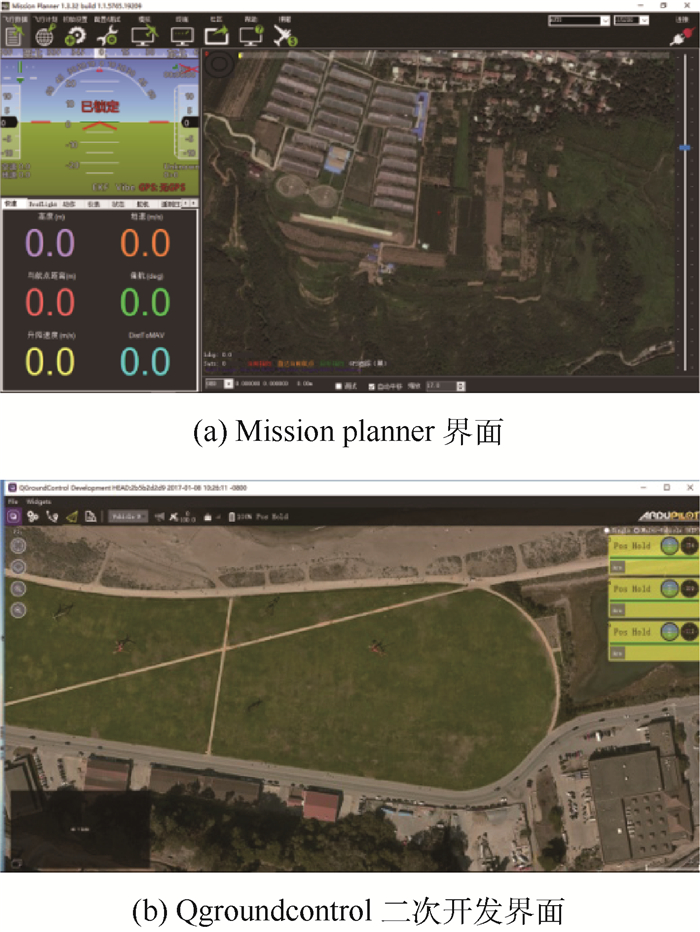 |
| 图 4 地面站软件界面 Fig. 4 Ground station software interface |
| 图选项 |
1.4 数据链 在搭建演示验证系统时,地面站与无人机以及无人机之间通信是关键。飞行试验要在户外环境中进行,无人机运动空间范围广、动态性高,为防止试验过程中无人机失控、高速、可靠的无线通信是关键;同时,在组网方式上需要建立一个去中心化的分布式对等通信网络,实现无人机平台之间双向数据通信,以交换彼此的位置和速度等状态信息,进而完成分布式解算,因此对数据链通信移动和可靠性要求很高。基于以上需求,采用双数据链的通信模式(见图 1)。
数据链1采用基于Mesh组网技术开发的YL-800模块,频率为433 MHz,如图 5(a)所示。YL-800是基于Sx1278无线方案的Mesh自组网无线模块,具有优异的网络自愈性、稳定性、扩展性和鲁棒性,同时该模块功耗低、传输距离远、移动性强等,能够实现各平台之间高速双向通信,可满足户外试验分布式组网通信的要求。由于MATLAB程序中的串口模块通信速率受到限制,无法满足地面站对无人机的高速实时控制要求,为了保证高速的传输速率,设计了指令发射机用来高速实时的向无人机集群发送控制指令。指令发射机是由STM32F4和自组网模块构成,信号发射频率设置为2 Hz。数据链2由CUAV Supter radio数传搭建,如图 5(b)所示。该数传使用工业级别USB转TTL,频率为915 MHz。该数传和PIX自驾仪配合使用,其安全性、稳定性和可靠性已经得到业界的认可,并被广泛应用于无人机通信上,因此本系统选择该数传来搭建数据链2。
 |
| 图 5 数据链模块 Fig. 5 Data link module |
| 图选项 |
2 领导-跟随协同编队控制算法 领导-跟随协同编队控制算法,是指在集群系统中设立领导者/虚拟领导者角色,通过领导者作用达到对集群系统控制的目的。设N个无人机组成的集群系统,由部分已知全局航迹信息的领导者和未知航迹信息的跟随者组成。期望的全局航迹信息表示为
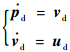 | (1) |
式中:pd、vd和ud分别为无人机的期望位置、速度和控制输入。
假设航迹信息二阶连续可微且集群中部分个体已知航迹信息,将集群中个体的动力学方程描述如下:
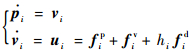 | (2) |
式中:pi∈Rn和vi∈Rn分别为第i个跟随者的位置向量和速度向量;ui∈Rn为第i个无人机的控制输入;hi为事件触发变量,当无人机i能够获取全局信息,即为集群领导者时,hi=1,否则hi=0。在式(2)的基础上采用文献[17]设计的分布式控制协议:
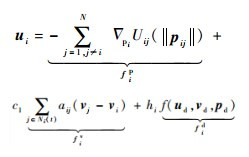 | (3) |
第1项fip为势函数梯度项,可使集群在实现位置一致性的同时避免相撞。
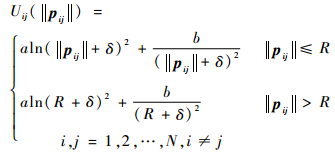 | (4) |
式中:R为无人机的通信半径;‖pij‖为无人机间的距离;a、b和δ均为常数,计算可得无人机之间的期望距离为
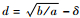
第2项fiv可使无人机i的速度与邻居个体速度实现一致。c1为正常数;当无人机i邻能够收到j的信息时,aij(t)=1,否则aij(t)=0。
第3项fid为全局航迹信息,通过航迹信息的反馈无人机可以跟踪预定航迹,有f(ud, pd, vd)=ud-c2(pi-pd)-c3(vi-vd);c2和c3为大于零的常数,反映了位置和速度一致性的权重。本文设领导者期望速度为
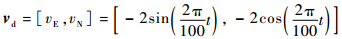 |
式中:vE和vN分别表示向东和向北的速度分量,t≥0为时间。
由于文献[17]已经给出了鲁棒性、稳定性和收敛性等证明过程,本文不再描述。
实际中每个无人机的运动速度和加速度都应在合理的范围内,本文将每个无人机的最大速度vmax设计为3 m/s,最大加速度amax设计为3 m/s2。由于GPS定位精度在2 m以内,因此无人机之间的编队间距应大于4 m。试验中其余相关参数取值如表 1所示。
表 1 试验参数取值 Table 1 Test parameter selection
| 参数 | 取值 |
| c1 | 1 |
| c2 | 2.5 |
| a | 10 |
| b | 250 |
| R/m | 100 |
| δ | 0.1 |
| d/m | 4.9 |
| c3 | 3.0 |
表选项
3 试验验证 四旋翼无人机作为一种特殊构型的飞行器,具有结构简单、成本低廉和低速巡航垂直起降等特殊的飞行性能,被认为是军事和民用中某些场合的最理想飞行器。为验证系统的有效性,本文搭建了四旋翼无人机作为无人机平台,系统实物如图 6所示。
 |
| 图 6 试验系统实物图 Fig. 6 Photo of test system |
| 图选项 |
试验采用3架四旋翼无人机,其中一架作为已知期望航迹信息的领导者,另外2架作为跟随者,图 7为3架无人机的通信拓扑图。试验的目标是利用领导-跟随协同编队控制算法实现跟随者对领导者速度、位置的跟踪。由于该算法理论研究较成熟,地面仿真后,直接将算法移植到无人机的协同控制器上。
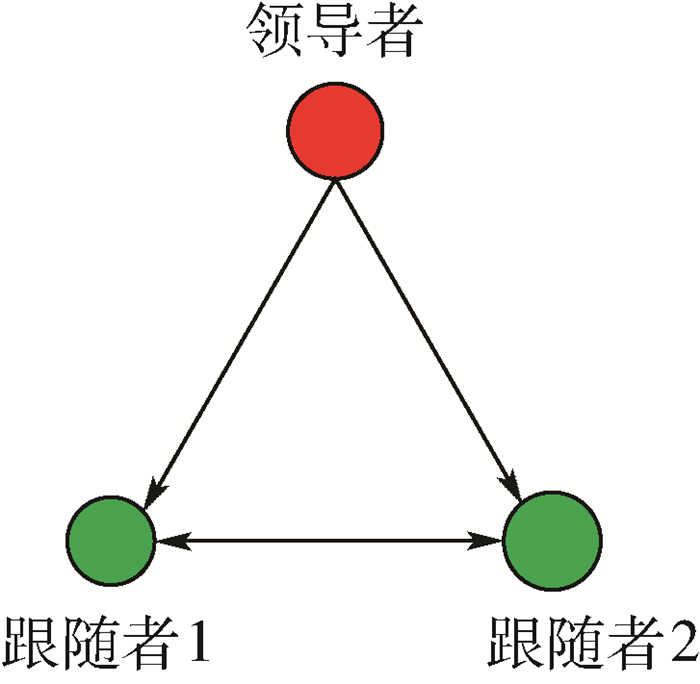 |
| 图 7 3架无人机之间通信拓扑图 Fig. 7 Topological graph of communication among three UAVs |
| 图选项 |
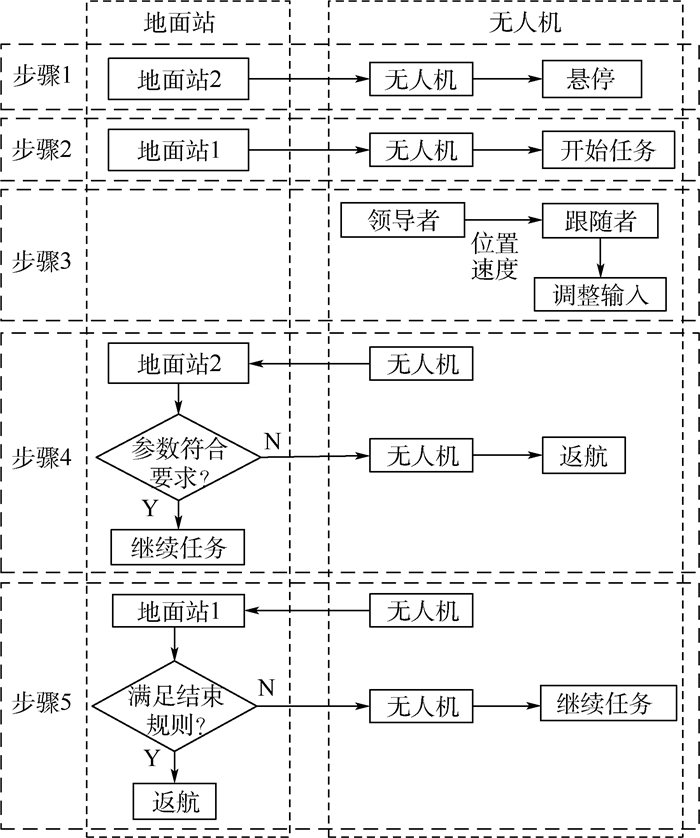
试验流程如图 8所示,具体描述如下:
 |
| 图 8 试验流程图 Fig. 8 Test flowchart |
| 图选项 |
步骤1?地面站2通过数据链2控制3架无人机起飞,高度在20 m处保持悬停。
步骤2?地面站1通过数据链1将任务指令信息发送给无人机。指定一架为领导者,作圆周运动,其余2架为跟随者。
步骤3?无人机通过数据链1以2 Hz频率广播自身位置、速度信息,跟随者在接收到其他个体的状态信息后,由协同控制器以相同频率计算出下一时刻的期望速度信息,并由执行层完成。
步骤4?地面站2观察无人机在飞行过程中传感器参数是否在合理范围内,判断是否有不符合继续演示条件的无人机,如果有则发送返回指令将无人机收回。
步骤5?地面站1将返回的无人机状态信息进行处理,判断是否满足设定的结束规则,如果不满足则继续飞行,满足将无人机收回。
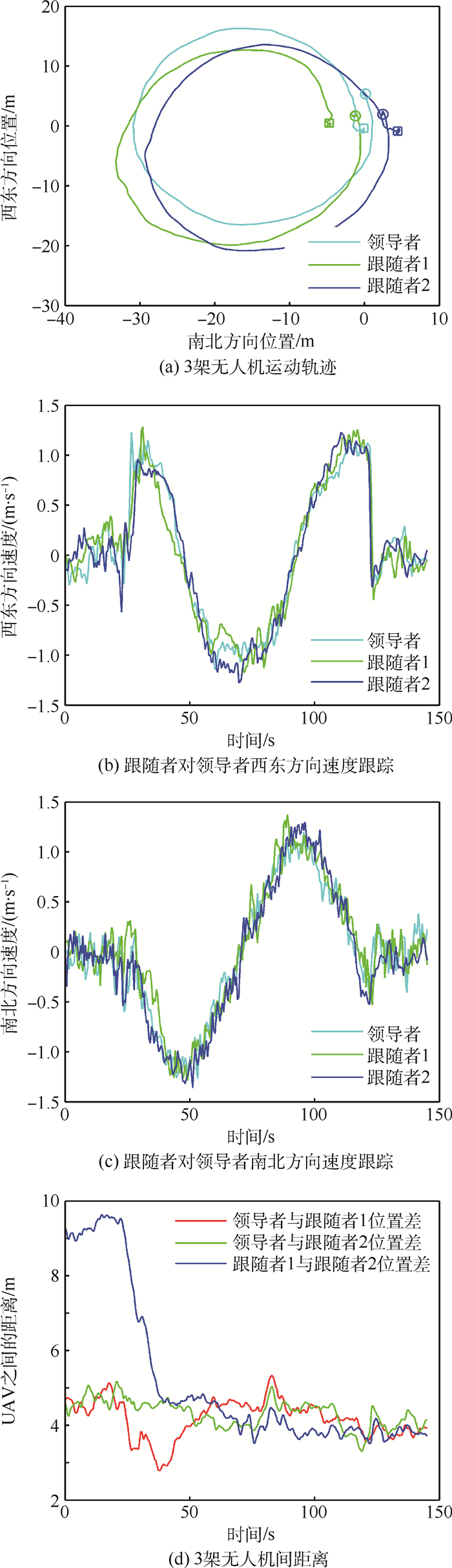
图 9为不同时刻试验视频截图。试验结束后,将PIX中的SD卡取出进行飞行数据分析,图 10为3架无人机飞行试验数据曲线。
 |
| 图 9 试验过程中地面视角的3架无人机空中位置 Fig. 9 Air position of three UAVs from view of ground in test process |
| 图选项 |
 |
| 图 10 飞行试验数据曲线 Fig. 10 Flight test data curves |
| 图选项 |
图 10(a)为跟随者对领导者的位置跟踪轨迹,图中正方形表示飞行起点,圆圈表示飞行终点。通过图 10(a)可以看到,跟随者对领导者实现了位置跟踪。图 10(b)、(c)分别为西东方向,南北方向跟随者对领导者的速度跟踪曲线。通过速度跟踪曲线发现,跟随者总体实现了对领导者的速度跟踪。通过图 10(d)跟随者相对于领导者的位置差可以看出,3架无人机逐渐稳定在期望的相对距离4.9 m。
通过飞行试验数据曲线可以认为跟随者实现了对领导者的位置和速度跟踪并形成期望的构型。但跟踪时跟随者速度存在振荡以及跟踪距离存在一定的误差,造成上述误差和速度振荡的原因可分为2类:一是系统原因,二是算法原因。系统原因包括:系统传感器本身存在误差,如GPS定位精度等;同时会存在通信时延、数据丢包、传感器更新延迟和数据处理时延的问题。算法原因包括:算法本身设计时并未考虑实际个体的动力学约束,如无人机的惯性等;同时势函数本身容易产生振荡,造成了个体在运动过程中速度振荡更加明显。针对上述问题,可以通过以下方式减小误差:系统方面可以选用差分GPS定位的方式以提高系统定位精度并提高系统采样周期;建立无人机个体模型时考虑无人机惯性、通信时延、以及一般环境噪声等实际约束。
上述试验结果表明设计的系统可满足对编队控制算法的演示验证,同时也证明了算法中势函数法本身存在振荡、不易形成稳定构型等特点。
4 结论 本文搭建了无人机集群编队控制演示验证系统,并对领导-跟随协同编队控制算法进行了验证,运行结果表明:
1) 系统运行稳定可靠,可对不同的分布式编队控制算法进行有效验证。
2) 系统存在一定误差,但在允许范围之内。
3) 系统可以缩短算法开发周期,加快算法到实际的应用。
随着任务的多种多样,异构集群协同控制将会成为未来发展趋势。同时,通信环境会异常复杂,感知约束也会随环境的复杂而增大,这就需要开展在复杂通信环境下的强鲁棒、高精度无人机集群编队控制的试验研究,这对试验系统提出了更高的要求。因此,下一步工作将是进一步提高系统的定位精度和可靠性,并利用搭建的系统对不同环境约束下异构无人机集群编队控制技术进行试验验证研究。
参考文献
| [1] | 牛轶峰, 肖湘江, 柯冠岩. 无人机集群作战概念及关键技术分析[J].国防科技, 2013, 34(5): 37–43. NIU Y F, XIAO X J, KE G Y. Operation concept and key techniques of unmanned aerial vehicle swarm[J].National Defense Science and Technology, 2013, 34(5): 37–43.(in Chinese) |
| [2] | 袁政英. 美空军未来20年小型无人机发展路线图[J].防务视点, 2016(10): 58–59. YUAN Z Y. United states air force in the next 20 years the development of a small UAV roadmap[J].Defense Point, 2016(10): 58–59.(in Chinese) |
| [3] | 宗群, 王丹丹, 邵士凯, 等. 多无人机协同编队飞行控制研究现状及发展[J].哈尔滨工业大学学报, 2017, 49(3): 1–14. ZONG Q, WANG D D, SHAO S K, et al. Research status and development of multi UAV coordinated formation flight control[J].Journal of Harbin Institute of Technology, 2017, 49(3): 1–14.(in Chinese) |
| [4] | 王祥科, 李迅, 郑志强. 多智能体系统编队控制相关问题研究综述[J].控制与决策, 2013, 28(11): 1601–1613. WANG X K, LI X, ZHENG Z Q. Survey of developments on multi-agent formation control related problems[J].Control and Decision, 2013, 28(11): 1601–1613.(in Chinese) |
| [5] | 吴俊成, 周锐, 董卓宁, 等. 基于诱导航线的多无人机编队飞行控制方法[J].北京航空航天大学学报, 2016, 42(7): 1518–1525. WU J C, ZHOU R, DONG Z N, et al. Formation flight control method of multiple UAVs based on guidance route[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7): 1518–1525.(in Chinese) |
| [6] | KOWNACKI C. Multi-UAV flight using virtual structure combined with behavioral approach[J].Acta Mechanica et Automatic, 2016, 10(2): 92–99.DOI:10.1515/ama-2016-0015 |
| [7] | DUAN H B, LIU S Q. Non-linear dual-mode receding horizon control for multiple unmanned air vehicles formation flight based on chaotic particle swarm optimization[J].IET Control Theory and Applications, 2010, 4(11): 2565–2578.DOI:10.1049/iet-cta.2009.0256 |
| [8] | ROY N, NEWMAN P, SRINIVASA S. Towards a swarm of agile micro quadrotors[J].Autonomous Robots, 2013, 35(4): 287–300.DOI:10.1007/s10514-013-9349-9 |
| [9] | YOU D I, SHIM D H. Autonomous formation flight test of multi-micro aerial vehicles[J].Journal of Intelligent and Robotic Systems, 2011, 61(1-4): 321–337.DOI:10.1007/s10846-010-9481-0 |
| [10] | 洪晔, 缪存孝, 雷旭升. 基于长机-僚机模式的无人机编队方法及飞行实验研究[J].机器人, 2010, 32(4): 505–509. HONG Y, MIAO C X, LEI X S. Formation method and flight test of multiple UAVs based on leader-follower pattern[J].Robot, 2010, 32(4): 505–509.(in Chinese) |
| [11] | DONG X W, ZHOU Y, ZHANG R, et al. Time-varying formation control for unmanned aerial vehicles with switching interaction topologies[J].Control Engineering Practice, 2016, 46: 26–36.DOI:10.1016/j.conengprac.2015.10.001 |
| [12] | 王勋, 张纪阳, 张代兵, 等. 无人机编队飞行快速试验系统设计[J].机器人, 2017, 39(2): 160–166. WANG X, ZHANG J Y, ZHANG D B, et al. Development of an experiment system for UAV formation flight[J].Robot, 2017, 39(2): 160–166.(in Chinese) |
| [13] | JIANG C M, WAN L, SUN Y S. Design of S-plane controller of autonomous underwater vehicle established on sliding mode control[J].Journal of Harbin Institute of Technology (New Series), 2017, 24(2): 58–64. |
| [14] | CUI R, LI Y, YAN W. Mutual information-based multi-AUV path planning for scalar field sampling using multidimensional RRT*[J].IEEE Transactions on Systems Man & Cybernetics Systems, 2016, 46(7): 993–1004. |
| [15] | 张少苹, 戴锋, 王成志, 等. 多Agent系统研究综述[J].复杂系统与复杂性科学, 2011, 8(4): 1–7. ZHANG S P, DAI F, WANG C Z, et al. Summary on research of multi-agent system[J].Complex System and Complex Science, 2011, 8(4): 1–7.DOI:10.3969/j.issn.1672-3813.2011.04.001(in Chinese) |
| [16] | QIN Z H, SUN H B, LIN Z. A hierarchical control strategy of autonomous unmanned surface vehicle swarm[C]//The 26th International Ocean and Polar Engineering Conference. Mountain View: International Society of Offshore and Polar Engineers, 2016: 474-479. |
| [17] | HE L L, BAI P, LIANG X L, et al. Feedback formation control of UAV swarm with multiple implicit leaders[J].Aerospace Science and Technology, 2018, 72: 327–334.DOI:10.1016/j.ast.2017.11.020 |
