目前,涡轮气动性能研究基本都采用螺旋桨/旋翼理论,由于没有考虑三维旋转效应对RAT气动特性的影响,因此不能满足高性能RAT系统涡轮气动性能计算需要[8]。刘勇[9]模拟了静止和旋转2个状态下的风力机涡轮流场,提出三维旋转效应对计算结果影响较大的结论。方祥军等[10]对RAT进行了流场数值模拟,研究了其全三维混合流场,计算结果具有一定的参考价值。目前,RAT气动性能数值仿真大都针对地面工况进行计算。然而,RAT作为飞机的应急动力装置,气动性能随载机的飞行高度而变化,这方面的研究国内文献还少见报道。虽然国外在RAT方面的研究已比较成熟,但国内基本还停留在逆向设计与计算分析阶段。本文采用正向研制方法设计RAT叶片,具有明显的先进性。
本文从目标功率出发,首先通过对不同翼型升阻比进行比较,选用升阻比较大的翼型,采用叶素-动量理论编程计算涡轮叶片沿展向的弦长分布、扭转角以及诱导因子等,生成叶片各截面参数;然后以计算流体力学(Computational Fluid Dynamics, CFD)方法分析叶片气动性能以满足设计要求,研究涡轮输出功率和风能利用系数随飞行高度和来流速度变化特性。本文为飞机应急能源系统研究奠定了基础。
1 RAT系统涡轮叶片设计 翼型是涡轮叶片的基本要素,影响叶片主体结构形式,翼型气动性能直接影响叶片和涡轮的动力特性[11]。自20世纪20年代开始,世界各主要航空发达国家建立了不同的翼型系列,如美国的NACA系列、德国的DVL系列以及英国的RAF系列等[12]。其中,NACA系列的航空翼型升阻比大,非常适用于高雷诺数流动。
通常,RAT的来流速度在100~600 km/h之间变化,以10 km为参考计算高度,依据当地环境参数可知雷诺数在2.7×105~1.7×106之间变化,属于高雷诺数流动,可选择NACA翼型设计RAT叶片。利用Profili软件计算不同翼型在迎角为-10°~15°下的升阻比,图 1为NACA系列不同翼型的升阻比Cl/Cd随叶片迎角α变化曲线。可以看出,0°~5°迎角时NACA4412翼型升阻比最大,作为本文RAT叶片设计的基本翼型。
 |
| 图 1 NACA系列不同翼型升阻比随叶片迎角变化曲线 Fig. 1 Variation curves of lift drag ratio of different NACA airfoils with attack angle of blade |
| 图选项 |
涡轮直径是RAT叶片设计时最基本的设计参数,由式(1)进行计算[13]:
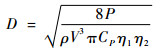 | (1) |
式中:D为涡轮直径,m;P为RAT功率,W;ρ为空气密度,kg/m3;V为来流速度,m/s;CP为风能利用系数;η1和η2分别为发电机和传动系统效率。
按照某型飞机对应急能源系统的功率需求,本文设计的RAT额定功率为15 kW。以10 km为参考计算高度,当地空气密度为0.412 7 kg/m3,取发电机和传动系统效率为0.95,风能利用系数为0.40,来流速度为450 km/h,计算可得涡轮直径为353 mm。
依据叶素-动量理论,在已知叶片迎角和该迎角下升力系数Cl、阻力系数Cd的前提下,可由式(2)和式(3)计算径向半径r处的叶素入流角和扭角:
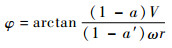 | (2) |
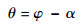 | (3) |
式中:φ为入流角,(°);a和a′分别为轴向诱导因子和切向诱导因子;ω为涡轮旋转角速度,rad/s;r为不同叶素的径向半径,mm;θ为扭角,(°)。
半径r处的法向力系数Cn和切向力系数Ct分别由式(4)和式(5)计算:
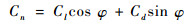 | (4) |
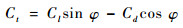 | (5) |
假设轴向诱导因子和切向诱导因子的初值为零,可由式(2)得到入流角φ,由式(4)和式(5)得到法向力系数和切向力系数,然后由式(6)和式(7)重新计算诱导因子a和a′:
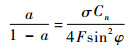 | (6) |
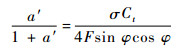 | (7) |
式中:σ为叶片在半径r处的实度;F为普朗特修正因子。
 | (8) |
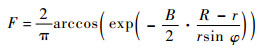 | (9) |
其中:B为涡轮叶片数目,本文取2片叶桨;c为叶片弦长,mm;R为涡轮半径。
把计算得到的诱导因子a和a′与前次计算结果进行比较,直至误差满足要求时迭代终止,本文的计算误差取0.001。通过编程计算可得不同半径r处的叶片弦长和扭角,如图 2所示。根据NACA4412翼型数据,结合计算所得的弦长和扭角,基于点的坐标变换求出各叶素截面在三维坐标系中的坐标,完成RAT的三维建模。
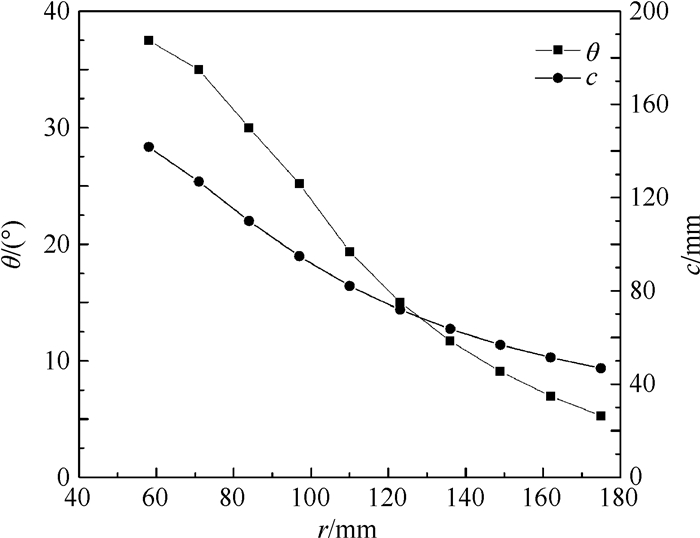 |
| 图 2 叶片弦长和扭角随径向半径变化曲线 Fig. 2 Variation curves of blade chord length and twist angle with radial radius |
| 图选项 |
2 RAT系统涡轮气动性能理论分析 RAT系统中,涡轮以迎面气流作为动力源。由空气动力学理论可知,迎面气流的冲压能量与速度的三次方成线性关系,即
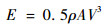 | (10) |
式中:E为迎面气流的冲压能量,W;A为空气流过的横截面积, m2。
RAT在迎面气流作用下旋转并把气流的冲压能量转换为涡轮功率而输出,涡轮输出功率可通过理论分析或数值模拟得到,由式(11)计算:
 | (11) |
式中:M为涡轮叶片气动升力沿展向的积分,N·m;n为涡轮转速,r/min。
RAT系统涡轮的功率提取系数,即风能利用系数为
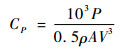 | (12) |
叶尖速比是表征RAT系统涡轮运转性能的一个重要参数,数值上等于涡轮叶片圆周速度与来流速度之比,即
 | (13) |
式中:λ为叶尖速比。
通常,飞机处于失去动力的应急状态时飞行速度很低,而RAT正常工作时涡轮转速由调节机构控制并可保持恒定,因此叶尖速比较大,有助于提升风能利用系数;而小的叶尖速比表示来流速度较高,此时虽然风能利用系数不大,但由于来流速度较大,涡轮提取的功率也能满足要求。
3 RAT系统涡轮气动性能数值模拟 3.1 计算模型 本文研究的RAT装有桨距角自动调节装置,可根据来流状态和工作转速调整桨距角到最佳迎风角度。为此,把涡轮流场划分为3个区域,分别为最外层的静止区域1、随涡轮一起旋转的旋转域2以及包围叶片的2个圆柱形区域31和32,各区域间以交界面连接,如图 3所示。其中,交界面1为旋转域和静止区域的交界,交界面2和3分别为2个叶片与旋转域的交界。这里划分的2个圆柱形区域31和32可以方便地改变叶片桨距角,且由于2个叶片各自独立,因此分别建立交界面2和3以便于数值模拟时旋转坐标系方法的运用。
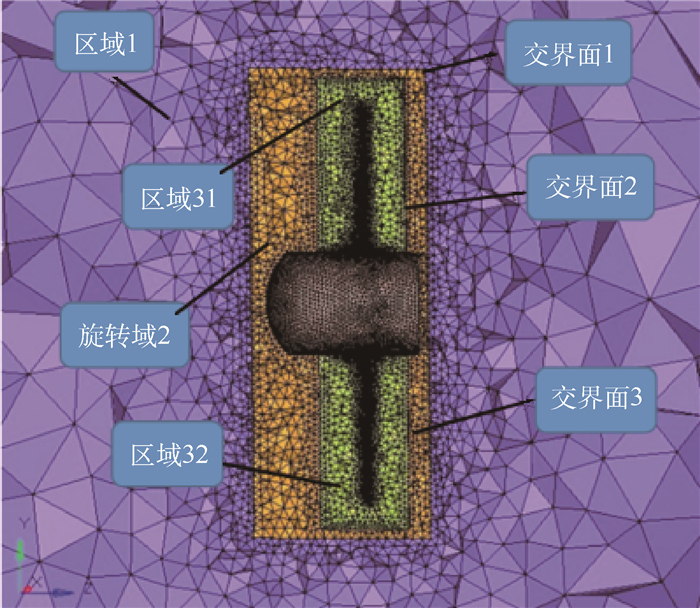 |
| 图 3 RAT涡轮流场网格 Fig. 3 Grid in turbine flow field of RAT |
| 图选项 |
RAT旋转对周围流场产生影响,为了把RAT对流场的扰动降低到最小,理论上外边界应为无限大。实际上,在数值仿真时设置合适的外边界以提高计算效率。若外边界设置太小,气体流动受到干扰,进而影响计算精度。通常,取外边界尺寸为模型尺寸的10倍或以上。考虑到本文所研究RAT直径为353 mm,计算时取外边界(区域1)直径为4400mm,入口端长度为1000mm,出口端长度为3 600 mm;旋转域2半径为210 mm,长为160 mm;区域3为2个半径为40 mm、长为155 mm的圆柱,如图 4所示。此外,区域划分时必须满足2个要求:①2个圆柱区域在靠近轮毂的端面与叶片根部相切;②2个圆柱区域和叶片共轴线,其目的是保证每次转动区域31和32时RAT具有完整性。
 |
| 图 4 流体区域划分 Fig. 4 Division of fluid region |
| 图选项 |
高质量有限元网格是高精度数值模拟的前提。考虑到黏性气流参数沿垂直于壁面方向变化剧烈,采用密集细化的网格。第1层流体网格高度为湍流边界层,可根据布拉修斯方程估算[14]:
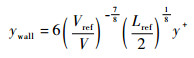 | (14) |
式中:ywall为第1层网格高度,mm;Vref为RAT入口平均速度,m/s;Lref为涡轮叶片高度,m;y+为壁面网格大小,y+=ρμτywall/μ,μ为黏性系数,μτ为摩擦速度,
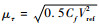
取初始值y+=30,可计算得到第1层网格高度,随来流速度而变化。为精确求解湍流边界层,在获得流场收敛解后,把求解得到的y+代入式(14)重新计算第1层网格高度,可以对网格进一步优化。
为提高模拟精度,对叶片和轮毂进行表面网格加密,并在贴近涡轮壁面处布置6层棱柱网格。流场网格总数约200万。
3.2 边界条件 1) 进出口边界条件。RAT工作条件是大雷诺数流动,理想气体并做湍流运动。进出口边界设置为速度入口、压力出口和压力远场条件。来流速度V垂直于入口边界,涡轮转速为n。
2) 壁面边界条件。壁面滑移特性与涡轮外部流动特性有关。若流体为无黏流动,则涡轮壁面具有滑移特性,视具体情况给定粗糙度和壁面滑移等。本文研究的RAT为无滑移壁面。此外,为减小边界干扰,设置静止域外围远场边界与涡轮距离为涡轮直径的10倍以上,取3 600 mm。
3.3 数值模拟 RAT处在一个可压缩有黏性的非定常流场中,采用多重旋转坐标系(MRF)模型把问题转化为稳定流动。选用CFD方法对涡轮气动性能进行数值模拟。空气设为理想气体,黏性系数随温度的变化以Sutherland公式计算,即
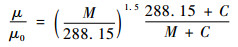 | (15) |
式中:μ0为温度等于288.15 K时空气的黏性系数,μ0=1.789 4×10-5 N·s/m2;C为常数,取值110.4。
湍流模型选用k-ω模型[15],以SIMPLEC算法进行求解,求解方式为速度与压力的耦合。设置旋转域2的转速为涡轮转速,2个圆柱形区域31和32相对于旋转域2静止,相对速度为零。
4 计算结果分析 飞机失去主动力后,RAT进入工作状态,涡轮从迎面气流获取能量并转换机械能,输出功率与涡轮叶尖速比、桨距角、气体入流角以及环境参数等有关,在飞行包线内环境参数随飞行高度而变化。输出功率和风能利用系数是评价涡轮气动性能的2个重要参数。
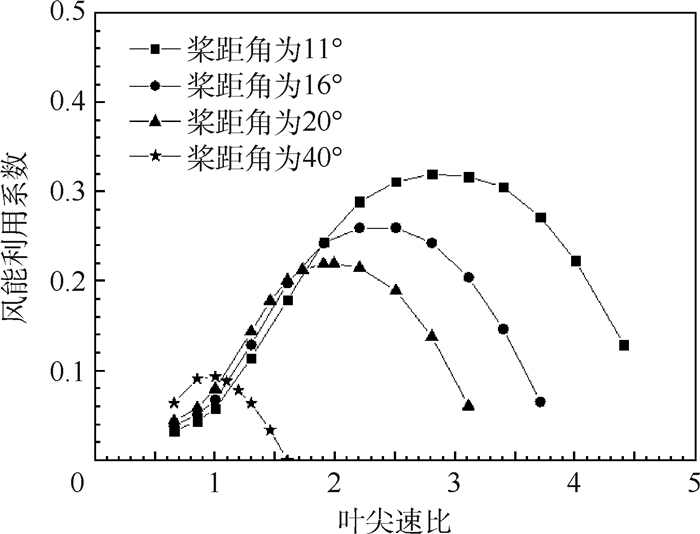
4.1 不同叶尖速比时涡轮气动性能 叶尖速比和桨距角是影响涡轮气动性能的2个重要参数。当涡轮转速恒定,来流速度变化时叶尖速比随之变化。图 5为地面性能计算时恒速工况下(n=1×104 r/min)风能利用系数随叶尖速比变化曲线。可见,同一桨距角下,随着叶尖速比的增加,风能利用系数先增大后减小,每一桨距角对应一个最大风能利用系数和最佳叶尖速比,且桨距角越小,最大风能利用系数越大,对应的叶尖速比也相应增大;桨距角为40°时,最大风能利用系数只有0.1,对应的叶尖速比只在小范围变化,已不能正常运转。因此,为提高涡轮风能利用系数,应根据来流状态适当调整桨距角。
 |
| 图 5 涡轮风能利用系数随叶尖速比变化曲线 Fig. 5 Variation curves of rotor power coefficient of turbine with tip speed ratios |
| 图选项 |
4.2 不同桨距角时涡轮气动性能 图 6为涡轮恒速(n=1×104 r/min)旋转工况下,地面性能计算时输出功率和风能利用系数随桨距角变化曲线。来流速度相同时,随着桨距角的增大,输出功率和风能利用系数都是先增大后减小,每一来流速度对应一个最佳桨距角,且来流速度越大,最大风能利用系数和涡轮输出功率越大,但当来流速度大于某一值时风能利用系数反而下降,如图 6(b)中来流速度为450 km/h时所示。由图 6(a)看出,来流速度为340 km/h时,RAT的最大输出功率为11.9 kW,小于设计功率15 kW;来流速度为450 km/h时,RAT的最大输出功率为19 kW, 大于设计功率15 kW。因此,涡轮输出功率随来流速度增加而增大,不同来流速度时可通过调节桨距角改变输出功率,以满足设计要求。当调整到最佳桨距角之前,随着桨距角的增大,涡轮输出功率缓慢上升,到达最佳桨距角之后,输出功率迅速下降。
 |
| 图 6 涡轮输出功率和风能利用系数随桨距角变化曲线 Fig. 6 Variation curves of turbine output power and rotor power coefficient with pitch angles |
| 图选项 |
4.3 不同入流角时涡轮气动性能 入流角是来流方向与涡轮旋转平面的夹角,数值模拟时可通过调节3个坐标分量改变入流角。当入流角变化时,气流作用于叶片表面的升力发生变化,涡轮输出功率和效率(风能利用系数)随之改变。为模拟不同入流角时涡轮气动性能,需要对外层静止区域1重新划分网格,本文把来流方向的外层静止区域处理为椭球形,截面为长轴7 000 m、短轴5 000 m的椭圆,而内部旋转域2和区域3由于之前的合理划分则保持不变。
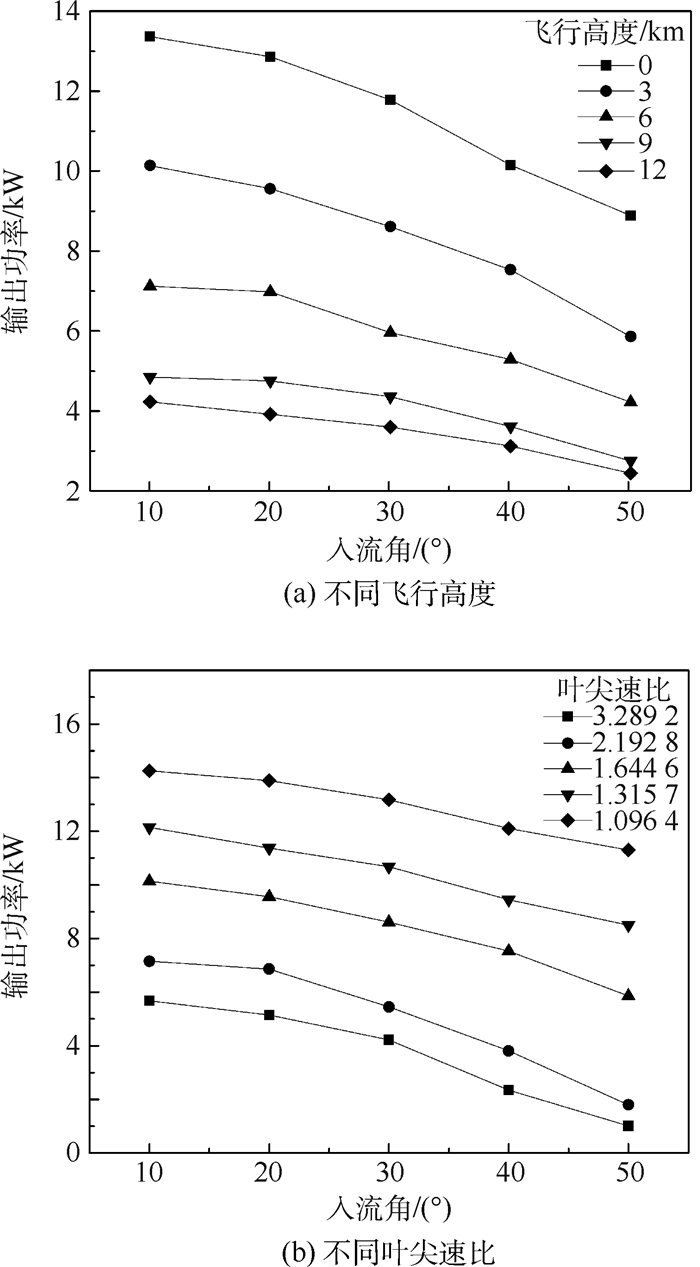
图 7(a)为不同飞行高度下涡轮输出功率随入流角变化曲线。可以看出,飞行高度一定时,随着入流角增大,输出功率逐渐减小;入流角一定时,输出功率随飞行高度增加而减小。因此,当其他条件相同时,入流角使涡轮输出功率降低。以3 km飞行高度计算结果为例,图 7(b)给出了输出功率随入流角变化曲线,叶尖速比一定时,随着入流角增大,输出功率逐渐减小,且叶尖速比越大,输出功率下降越快;当入流角一定时,叶尖速比越小,输出功率越大。因此,入流角的存在使涡轮输出功率降低,最大功率为14.2 kW, 小于额定功率15 kW。涡轮转速一定时,为获得较大输出功率,应尽可能减小叶尖速比,即提高飞行速度,同时保持较小的入流角。
 |
| 图 7 涡轮输出功率随入流角变化曲线 Fig. 7 Variation curves of turbine output power with inflow angle |
| 图选项 |
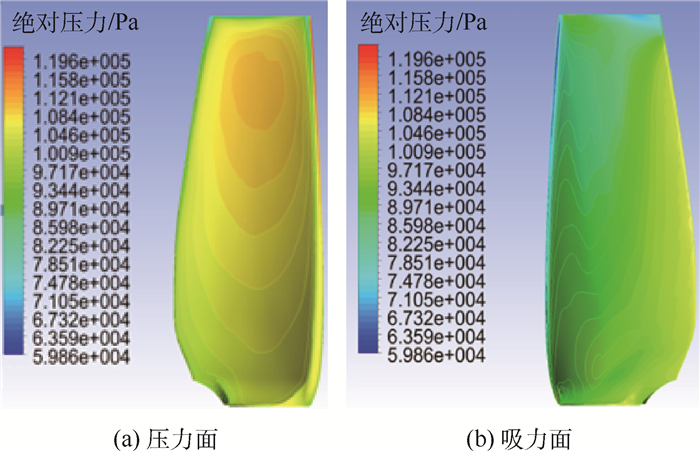
4.4 涡轮流场分析 气流沿叶片分布和流动情况直接影响涡轮输出功率和能量提取效率。图 8为地面性能计算时桨距角为8°、涡轮转速为9 700 r/min、来流速度为210 km/h时叶片表面压力云图。可以看出,叶片压力面的压力中心靠近叶尖区域,高压区域位于80%相对叶高处;在相对叶高2%~5%的叶尖区域等值线密布,静压梯度大,而叶根区域等值线比较稀疏,压力梯度小,主要原因是气流在叶片表面有一向心加速度,因此沿径向存在压力差,使得从叶根到叶尖,静压逐渐增大,即为负的逆压梯度。
 |
| 图 8 叶片压力面和吸力面压力云图 Fig. 8 Pressure contours of acting surface and suction surface |
| 图选项 |
在叶片吸力面上从叶尖到叶根,静压先降低,然后维持一段低压区域后逐渐增大,叶片根部压力较大。可见,压力面与吸力面的压差也是靠近叶尖区域较大,因此叶片主要做功区域是中部靠近叶尖部分,即相对叶高40%~95%区域。此外,吸力面叶根区域静压分布不甚合理,原因可能是受到叶根迎角和附面层影响,因此应设法减小叶根迎角,改善流动状态,并采用不等迎角设计。
涡轮转速一定时,来流速度和桨距角影响叶片周围流线分布。图 9(a)、(b)分别给出了涡轮转速为9 700 r/min、桨距角为8°时,不同来流速度时叶片截面流线分布。随着来流速度的升高,在叶片吸力面靠近后缘区域,有明显的气体流动分离现象,且吸力面上叶尖与根部区域气体流速明显增大,与压力面间的压差增大,做功能力增加;图 9(c)、(d)为来流速度为240 km/h时,不同桨距角下叶片截面流线分布。随着桨距角增大,吸力面一侧靠近叶片中间区域有明显的漩涡,导致叶片所受升力减小,进而引起输出功率下降。但从整体效应看,小桨距角和低来流速度下,本文所设计的RAT尾缘厚度小,计算结果没有粗大杂乱的尾迹,流动状况比较理想,但仍有改进的空间。
 |
| 图 9 不同来流速度和桨距角下流线图 Fig. 9 Streamlines at different inflow velocities and pitch angles |
| 图选项 |
5 结论 依据某型应急能源系统对冲压空气涡轮(RAT)的功率需求,采用正向研制方法,基于叶素-动量理论设计了RAT叶片;采用CFD方法仿真计算了不同工况下RAT气动性能,主要结论如下:
1) 涡轮转速一定时,风能利用系数随叶尖速比的增加先增大后减小,每一桨距角对应一个最大风能利用系数和最佳叶尖速比,且桨距角越小,最大风能利用系数越大。
2) 针对不同来流速度,适当调整叶片桨距角不仅可以提高涡轮风能利用系数,同时还可以实现涡轮恒功率输出,满足设计要求。
3) 从整个流场来看,叶片主要做功区域位于中部靠近叶尖部分、相对叶高40%~95%的区域,吸力面叶根区域静压分布不甚合理,仍有改进空间。
4) 采用正向研究方法,基于叶素-动量理论设计的RAT叶片能够满足某型RAT需要,研究方法具有明显的先进性。
参考文献
| [1] | KOERNER M. Recent developments in aircraft emergency power[C]//35th Intersociety Energy Conversion Engineering Conference and Exhibit (IECEC). Reston: AIAA, 2015: 12-19. |
| [2] | MANWELL J F, MCGOWAN J G, ROGERS A L. Wind enery explained: Theory, design and application[M]. New York: John Wiley & Sons Ltd., 2002. |
| [3] | BURTON T, SHARPE D, JENKINS N, et al. Wind energy handbook[M]. New York: John Wiley & Sons Ltd., 2001. |
| [4] | BETZ A. Schraubenpropeller mit geringstem energieverlust. dissertation[R]. Gottingen: Gottingen Nachrichten, 1919. |
| [5] | WILSON R E, LISSAMAN P B S. Applied aerodynamies of wind power machines[R]. Washington, D. C. : NASA STI/Recon Technical Report N, 1974. |
| [6] | GAO X, HU J. Numerical simulation to the effect of rotation on blade boundary layer of horizontal axial wind turbine[C]//2010 World Non-Grid-Connected Wind Power and Energy Conference. Piscataway, NJ: IEEE Press, 2010: 1-4. |
| [7] | 周世刚, 刘红, 王佳莉. 冲压空气涡轮验证技术研究[J].测控技术, 2016, 35(Suppl): 364–367. ZHOU S G, LIU H, WANG J L. Research on verification technology of ram air turbine[J].Measurement and Control Technology, 2016, 35(Suppl): 364–367.(in Chinese) |
| [8] | CHOI N J, SANG H N, JEONG J H, et al. Numerical study on the horizontal axis turbines arrangement in a wind farm:Effect of separation distance on the turbine aerodynamic power output[J].Journal of Wind Engineering & Industrial Aerodynamics, 2013, 117: 11–17. |
| [9] | 刘勇. 风力发电机气动性能数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2007: 33-35. LIU Y. Numerical simulation of wind turbine aerodynamic performance[D]. Harbin: Harbin Institute of Technology, 2007: 33-35(in Chinese). |
| [10] | 方祥军, 刘思永, 王屏. 可变桨距冲压空气涡轮混合型流场数值研究[J].北京航空航天大学学报, 2004, 30(2): 152–155. FANG X J, LIU S Y, WANG P. Numerical study on mixed flow field of variable pitch ram air turbine[J].Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(2): 152–155.(in Chinese) |
| [11] | 何玉林, 李海峰, 金鑫, 等. 风力机叶片翼型气动特性模型[J].机械科学与技术, 2010, 29(12): 1589–1594. HE Y L, LI H F, JIN X, et al. Airfoil aerodynamic characteristics model of wind turbine blade[J].Mechanical Science and Technology, 2010, 29(12): 1589–1594.(in Chinese) |
| [12] | 查健锐, 杨殷创, 钱燕. 基于Fluent的多翼型低速气动特性比较[J].合肥师范学院学报, 2014, 32(6): 38–42. ZHA J R, YANG Y C, QIAN Y. Comparison of aerodynamic characteristics of multi airfoils at low speed based on Fluent[J].Journal of Hefei Normal University, 2014, 32(6): 38–42.(in Chinese) |
| [13] | 勒古里雷斯D. 风力机的理论与设计[M]. 施鹏飞, 译. 北京: 机械工业出版社, 1987. LE GOURIERES D. Design and theory of wind turbine[M]. SHI P F, translated. Beijing: China Machine Press, 1987(in Chinese). |
| [14] | 王瑞. 冲压空气涡轮多工况动力性能研究[D]. 北京: 北京航空航天大学, 2017. WANG R. Study on dynamic performance of ram air turbine under different working conditions[D]. Beijing: Beihang University, 2017(in Chinese). |
| [15] | 王健, 卢岳良, 杨斐, 等. 两型冲压空气涡轮翼型气动特性分析[C]//第六届中国航空学会青年科技论坛, 2014: 5. WANG J, LU Y L, YANG F, et al. Aerodynamic characteristics analysis of two ram air turbine airfoil[C]//The Sixth China Aviation Society Youth Science and Technology Forum, 2014: 5(in Chinese). |
