在早期的研究中,分析转子动力特性时多不考虑连接结构界面接触的影响,将航空发动机作为连续结构进行分析[3-4]。近些年国内外****关于连接结构对转子动力特性的影响已经开展了大量的研究工作。李俊慧等[5]采用有限元方法研究了影响套齿连接刚度以及接触应力的主要因素,并提出了相应的套齿设计方法。闻邦椿、Arumugam、Li[6-8]等研究了在出现支承不同心时,套齿联轴器所产生的不同心激励力以及转子结构的振动响应,将不同心分为平行不同心、倾角不同心和组合不同心,结果表明不同心的典型特征为二倍频响应。在转子螺栓连接结构研究方面,姚星宇等[9-10]用薄层单元进行螺栓连接结构的模拟,并研究了螺栓载荷与结构参数对螺栓连接刚度的影响;Qin等[11-12]推导了航空发动机盘鼓混合式转子螺栓连接结构弯曲刚度,并采用非线性角弹簧模拟了弯曲刚度非线性特征;Liu等[13]通过实验表明随着工作循环数的增加,转子振动响应增大,并利用不平衡量增大进行解释;Wang等[14]研究了螺栓连接结构弯曲刚度损失的因素,并采用弹性模量修正方法进行复杂航空发动机转子结构建模分析。
上述研究中对于套齿联轴器的附加激励在柔性转子系统不同心问题中研究较为深入,而对于刚性转子系统螺栓连接结构主要是对于弯曲刚度的研究,尚缺乏连接结构界面变形(同轴度和平行度偏差)对于动力特性的影响研究。为了进一步分析文献[13]中的振动响应随循环数增加而增大的原因,本文从螺栓连接结构端面同轴度和平行度偏差出发,建立了典型航空发动机高压(HP)刚性转子考虑界面变形影响的力学模型,得出了不同界面变形形式引起的附加激振力表达式。
1 高压转子界面变形力学模型 1.1 典型高压转子系统结构特征 如图 1所示为典型航空发动机高压转子系统,支承方案为1-0-1,前伸轴颈从三级盘位置伸出,在三级盘、压气机后封严盘以及涡轮盘前后共采用四排短螺栓结构进行连接。前两级压气机盘处于悬臂结构,前伸轴颈与三级盘为一体化结构。由于压气机与高压涡轮之间的大鼓筒轴质量相对于压气机以及涡轮质量相对较小,因此在转子模型中主要考虑压气机以及涡轮处的转子盘,重点考虑三级盘、涡轮前后位置螺栓连接结构界面变形,建立转子系统分析模型如图 2所示,其中转子盘1、2、3分别为压气机前两级盘、压气机后七级盘、高压涡轮盘,轴段刚度等效保证在转子盘位置的横向等效刚度相同。A、D两处为支承位置,A、B、C为螺栓位置,Si(i=0, 1, 2, 3, 4, 5)为相邻关键位置之间的轴向距离。
 |
| 图 1 高压转子系统结构简图 Fig. 1 Sketch of HP rotor system |
| 图选项 |
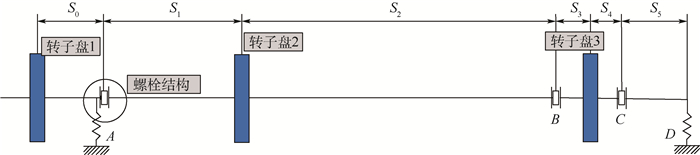 |
| 图 2 考虑螺栓连接结构的高压转子分析模型 Fig. 2 Analysis model of HP rotor considering bolted joints |
| 图选项 |
1.2 螺栓连接结构界面变形模型
1.2.1 接触端面同轴度偏差 螺栓连接结构由于接触界面变形将引起接触端面同轴度、平行度偏差。接触端面同轴度偏差是由于接触界面在复杂机械载荷作用下的滑移和磨损等的周向不均以及界面连接处周向温度分布不均导致的接触界面热变形[15]等引起,如图 3所示。
 |
| 图 3 接触界面滑移量周向分布不均示意图 Fig. 3 Schematic of skip circumferential maldistribution of contact interface |
| 图选项 |
图 3中的虚线表示无端面滑移时扇区径向位置,δi为第i个扇区接触端面径向滑移量,ζi为第i个扇区中心线与O1x1轴的夹角,则该转子的截面形心偏移量r0为
 | (1) |
式中:φ为转子截面形心偏移量r0与x1轴的夹角。
在分析中,先采用带接触非线性的实体有限元模型计算得到扇区的径向滑移量,考虑不同载荷作用下,计算不同扇区的变形后利用式(1)方法得到接触端面的同轴度偏差量。
1.2.2 接触端面平行度偏差 接触端面平行度偏差主要是由于接触端面粗糙度和装配载荷状态下螺栓拧紧力矩的分散性以及机动飞行状态下转子受到陀螺力矩载荷时,周向不同位置的螺栓拉压程度不一致导致。装配载荷作用下的界面平行度偏差可以通过界面平行度测量得到,弯矩作用下的平行度偏差可以通过计算分析确定。
图 4中,b为螺栓法兰的直径。在装配状态下,由接触端面粗糙度引起的界面平行度偏差角最大为
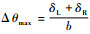
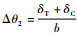
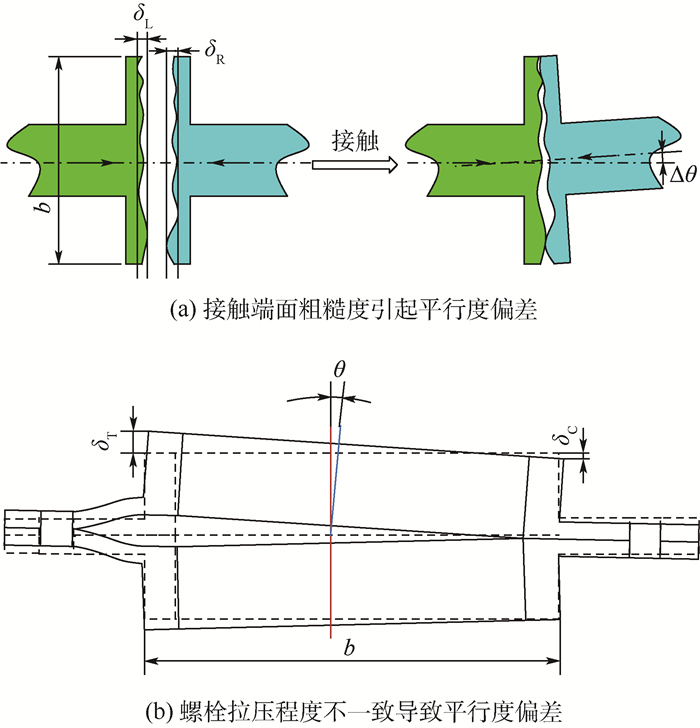 |
| 图 4 接触界面平行度偏差示意图 Fig. 4 Schematic of contact interface parallelism deviation |
| 图选项 |
1.3 界面变形对转子动力特性影响模型
1.3.1 接触端面同轴度偏差 本文主要研究接触端面同轴度以及平行度偏差,假定转子为刚性转子。如图 5所示,当转子两端均存在连接界面时,如图中的转子盘2和转子盘3,界面同轴度偏差将使得形心发生偏移,且转子盘发生倾斜;当转子仅有一侧存在连接界面时,如图 5中的转子盘1,界面同轴度偏差仅使得转子形心发生偏移。
 |
| 图 5 接触端面同轴度偏差对转子系统影响 Fig. 5 Impact of contact interface coaxial deviation on rotor system |
| 图选项 |
图 5中的δij, y为第i(i=1, 2, 3)个螺栓位置,第j侧(j=1为前侧,j=2为后侧)在yOz平面内的同轴度偏差,θk, x为第k个转子在yOz平面内的倾斜角。δij, y由1.2.1节中的接触端面形心偏移量r0在yOz平面内的投影得到,转子盘截面形心偏移量和倾斜角根据两侧接触端面的形心偏移量的大小和相位确定,如图 6所示,图中α12和α21分别为转子盘2的前后接触端面形心偏移量相位角。
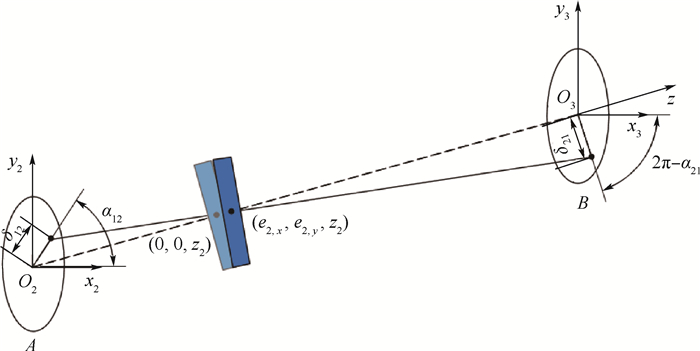 |
| 图 6 转子盘2形心偏移和倾斜示意图 Fig. 6 Schematic of centroid offset and skew of disk 2 |
| 图选项 |
设计状态下转子盘2的形心位置为(0, 0, z2),接触端面发生界面滑移后,形心位置变为(e2, x, e2, y, z2),其中
 | (2) |
式中:S1、S2分别为转子盘与左右接触端面间的距离;δ12, x=δ12cos α12;δ12, y=δ12sin α12;δ21, x=δ21cos α21;δ21, y=δ21sin α21。
由于两侧接触端面滑移引起的转子盘2的初始倾斜角为
 | (3) |
式中:θ2为转子盘2的倾斜角;θ2, x和θ2, y分别为θ2在x轴和y轴上的投影。
对于两侧均有接触界面的刚性转子,接触端面同轴度偏差通常将使得转子盘同时发生形心偏移和倾斜,如图 7(a)所示,由于端面滑移引起的转子形心偏移e使得转子盘的形心与转动中心线发生偏移,如图 7(b)所示,但并不改变无涡动时的转子自转中心,因此转子形心偏移产生的力学效果可等效于Me的附加转子不平衡量,附加不平衡量的相位与转子形心偏移的相位相同,其中:M为轮盘质量。转子盘倾斜角是转子盘法向方向与转子自转中心线的夹角,如图 7(c)所示,在采用第2类欧拉角进行动力学描述时,其改变了相应的角度位置,因而转子系统在旋转坐标系下的角速度发生变化,系统的动能方程发生变化,记该类转子盘倾斜为第1类转子初始倾斜。
 |
| 图 7 同轴度偏差导致的形心偏移和倾斜 Fig. 7 Centroid offset and skew caused by coaxial deviation |
| 图选项 |
1.3.2 接触端面平行度偏差 对高压刚性转子系统进行接触端面平行度偏差影响分析时,需要假定一个基准位置,在实际运用中,可以以装配过程中的基准面为基准位置,如图 1中的压气机三级盘端面。在该核心机转子装配过程中,首先将前两级压气机盘与三级盘热装配,然后与后六级压气机盘热装配,最后将压气机转子与涡轮转子进行连接,因此以三级盘端面为基准较为合理。与同轴度偏差引起的转子盘变形效果类似,接触端面的平行度偏差也将同时引起转子盘同时发生形心偏移与倾斜,如图 8所示。图中,Δθ21, x和Δθ22, x分别为第2排螺栓前后接触端面在yOz平面内的角度偏差,其由接触端面平行度偏差直接引起,对第1排螺栓位置采用同样的记号方式,正负号规则为相对基准侧(图 8中基准侧为三级盘位置)端面逆时针偏转为正,顺时针偏转为负;θi, x(i=1, 2, 3)为第i个转子在yOz平面内相对转动中心线的角度偏差,相对转动中心线逆时针偏转为正,顺时针偏转为负;li, y(i=1, 2, 3)为第i排螺栓位置在yOz平面内相对转动中心线的偏差,由于第一排螺栓位置为基准位置,因此l1, y=0;ri, y(i=1, 2, 3)为第i个转子盘在yOz平面内相对转动中心线的形心偏移。
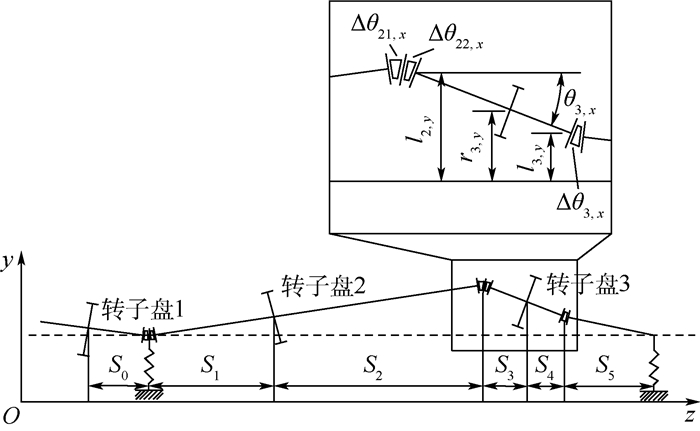 |
| 图 8 接触端面平行度偏差对转子系统影响 Fig. 8 Impact of contact interface parallelism deviation on rotor system |
| 图选项 |
通过测量或者计算可以得到接触端面的平行度偏差Δθij(i=1, 2, 3;j=1, 2),以三级盘位置为基准,可以得到各个转子的倾斜角θi
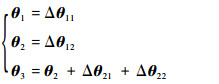 | (4) |
根据转子倾斜角可以进一步得到各个转子盘位置的形心偏移量分别为
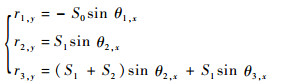 | (5) |
式中:θi, x为θi在yOz平面内的投影;r1, y表达式带负号是因为转子盘1的形心偏移与盘倾角正负相反。对式(5)进行小角度近似得
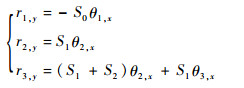 | (6) |
接触端面平行度偏差与同轴度偏差对于刚性转子动力特性影响的主要差别在于出现平行度偏差时,在螺栓连接位置角度变化连续,使得转子系统的自转中心线仍为转子的形心线,因而转子盘的形心偏移r即为自转中心线与转轴中心线的偏移,其力学效果与转子发生初始弯曲r等效,与同轴度偏差引起的力学效果不同,在动力学方程中增加一个恒定大小的附加激振力项。同时平行度偏差引起的转子盘倾斜后盘与自转中心线仍保持垂直关系,只是相对于总体坐标系的位置关系发生变换,不影响欧拉坐标系下动力学方程中的动能项,仅改变相应的势能零点位置,因此其产生附加激励的原理与同轴度偏差引起的转子盘倾斜不一致,记该类转子盘倾斜为第2类初始倾斜。
接触端面同轴度偏差和平行度偏差均会使得刚性转子盘发生形心偏移和倾斜,但其引起的力学效果相差较大。同轴度偏差带来附加不平衡量以及第1类转子初始倾斜,平行度偏差带来转子初始弯曲和第2类转子初始倾斜。在实际的航空发动机转子中,通常同时存在接触端面同轴度偏差和平行度偏差,因此以上所述的附加不平衡量、初始弯曲和2类转子初始倾斜同时存在。
2 Lagrange方法建立转子系统运动学方程 2.1 欧拉角坐标下的转子系统运动学描述 将轴承简化为各向同性弹性支承,A、D处的支承刚度分别为kA和kD,支承质量分别为mA和mD,则图 2所示的转子系统广义坐标q,共16个自由度,包括支承自由度q1=(xA, yA, xD, yD)T以及以第2类欧拉角坐标描述的3个转子盘的平动和偏摆自由度q2=(x1, θy1, y1, θx1, x2, θy2, y2, θx2, x3, θy3, y3, θx3)T,则系统动能为
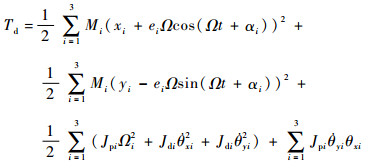 | (7) |
式中:Ω为自转角速度;ei为第i个转子盘偏心距;αi为第i个转子盘偏心距相位;Jpi和Jdi分别为极惯性矩和直径惯性矩
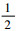
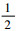
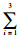
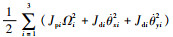
支承动能为
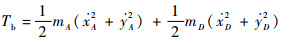 | (8) |
则系统总动能为T=Td+Tb。
在任意瞬时,xOz平面内由于弹性支承位移xA和xD引起的第i个转子盘形心位移xgi和截面转角θygi分别为
 | (9) |
式中:Φi为转换矩阵;Sgi为第i个转子盘距A支承位置的距离,其中,Sg1=S0, Sg2=S1,Sg3=S1+S2+S3;
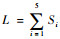
 | (10) |
式中:qx为xOz平面内所有自由度;Φ=[Φ1, Φ2, Φ3]T;
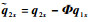
两端弹性支承的势能为
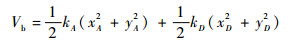 | (11) |
因此系统总势能为V=Vd+Vb。
根据第2类Lagrange方程
 | (12) |
可得系统振动微分方程为
 | (13) |
式中:Mx、My分别为xOz平面和yOz平面内的质量矩阵;Kx、Ky分别为xOz平面和yOz平面内的刚度矩阵;J为xOz平面内的陀螺矩阵;qy为yOz平面内所有自由度; Fe为初始不平衡量激振力。
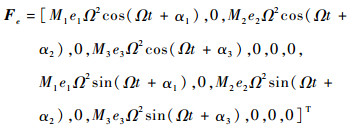 |
2.2 端面同轴度偏差对动力特性的影响 由1.3.1节分析可知,接触端面同轴度偏差将使得转子产生附加不平衡量Mea以及第1类初始倾斜角τi,附加不平衡量影响转子系统的平动动能,第1类初始倾斜影响转子的转动动能,而接触端面同轴度偏差对于转子系统势能无影响。附加不平衡量与初始不平衡量叠加后的不平衡量为
 | (14) |
式中:e′为合成后的偏心距。记第i个转子盘合成后的不平衡量相位角为γi,则第i个转子盘的平动动能为
 | (15) |
当转子存在第1类初始倾斜时,第2类欧拉角坐标描述的动力学方程中,角速度项需要叠加初始倾斜项
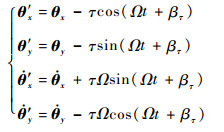 | (16) |
式中:βτ为初始倾斜的相位角;θ′x和
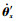
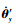
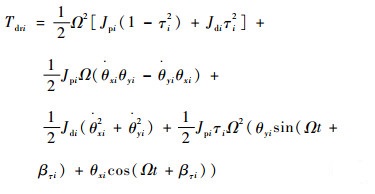 | (17) |
式(17)利用了Jpi=2Jdi的薄盘假设。
由于接触端面同轴度偏差仅影响动能,因而此时的转子轴的弹性势能和支承结构的势能与式(10)和式(11)所描述的相同,同样采用第2类拉格朗日方程得到系统的动力学方程,其质量矩阵、陀螺矩阵和刚度矩阵与式(13)中相同,改变的仅为广义力向量。考虑端面同轴度偏差后转子的广义力为
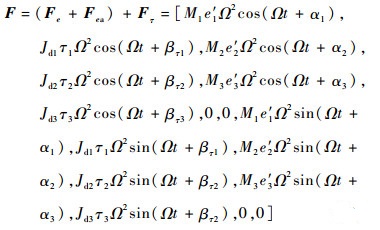 | (18) |
式中:Fea为由附加不平衡量引起的激振力;Fτ为由第1类初始倾斜引起的附加激振力。由式(18)可以看出,对于刚性转子系统,考虑接触端面同轴度偏差引起的附加不平衡量和第1类初始倾斜后,在平动自由度方向转子系统的不平衡量激振力大小以及相位发生改变,同时在偏摆自由度方向产生与转速平方和初始倾斜角成正比的附加简谐激振力,如在转子盘1的绕x轴偏摆自由度方向的附加激振力为Jd1τ1Ω2cos(Ωt+βτ1)。
2.3 端面平行度偏差对动力特性的影响 由1.3.2节分析可知,接触面平行度偏差将使得各转子盘产生类似于初始弯曲的转子形心偏移和第2类转子盘初始倾斜。具有初始弯曲的转子系统力学特性分析已经较为深入,利用同样的方法可以将其推导过程应用于第2类转子盘初始倾斜。转子初始弯曲影响的是转子平动方向的势能,第2类初始倾斜影响的是转子盘偏摆势能,其本质是改变转子盘轴的势能零点位置,对支承系统势能和转子系统动能无影响。
考虑初始弯曲量r以及第2类初始倾斜角χ,其引起的变形量在xOz平面内的分量为
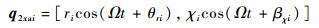 | (19) |
式中:q2xai为初始弯曲以及初始倾斜引起的变形分量在xOz平面内的投影;θri和βχi分别为第i个转子盘的形心偏移量相位角和第2类初始倾斜相位角。则此时全约束转子盘轴系统在xOz平面内的变形为
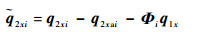 | (20) |
xOz平面内转子盘轴系统弹性势能V′dx为
 | (21) |
式中:q2xa=[q2xa1, q2xa2, q2xa3]T为3个转子盘由于形心偏移和第2类初始倾斜引起的附加变形; q′x为考虑附加变形后的变形量。同理可以得到yOz平面内的转子势能,且附加变形仅发生在转子盘的平动以及偏摆自由度方向,对支承势能没有影响。
根据Lagrange方程可以看出,该转子系统中的势能项仅对动力学方程中的刚度回复力项和激振力项产生影响。对考虑转子盘形心偏移和第2类初始倾斜的转子-支承系统,利用第2类Lagrange得到的动力学方程中质量矩阵、陀螺矩阵和刚度矩阵与2.1节中式(13)相同,激振力项变为
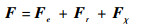 | (22) |
式中:
 |
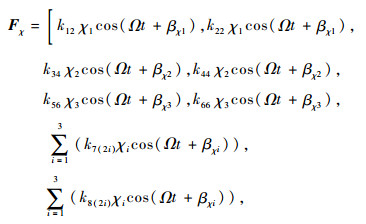 |
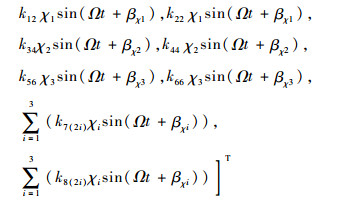 |
由式(22)可以看出,对于刚性转子系统,考虑接触端面平行度偏差引起的形心偏移和第2类转子初始倾斜将产生2个附加激振力Fr和Fχ;由于交叉刚度以及弹性支承的存在,激振力Fr和Fχ在所有自由度方向上均有分量,如Fr在x1方向存在由r1引起的激振力k11r1cos(Ωt+θr1),在θy1方向存在由r1引起的激振力k12r1cos(Ωt+θr1),在xA自由度方向上存在由形心偏移引起的附加激振力
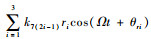
3 结论 1) 以典型航空发动机高压刚性转子为例,对界面变形模型进行分析,并对接触端面同轴度偏差以及平行度偏差的界面变形进行定量描述,建立了考虑界面变形的刚性转子系统力学模型。
2) 对典型航空发动机高压刚性转子系统采用Lagrange方法建立了考虑界面变形以及弹性支承的16自由度动力学方程,并推导了界面变形对系统动力学方程的影响。同轴度偏差将使得转子系统产生附加不平衡激振力和附加第1类初始倾斜激振力,激振力幅值均与转速平方成正比,且分别作用于平动和转动自由度,对支承自由度无影响;平行度偏差将产生附加初始弯曲激振力和第2类初始倾斜激振力,激振力幅值均与转速无关,仅与刚度和平行度偏差量有关,且该附加激振力在支承自由度方向有一定分量。
参考文献
| [1] | 付才高, 郑大平, 欧园霞. 航空发动机设计手册第19册:转子动力学及整机振动[M].北京: 航空工业出版社, 2000: 1-6. FU C G, ZHENG D P, OU Y X. Aero engine design manual 19th:Rotordynamics and whole engine vibration[M].Beijing: Aviation Industry Press, 2000: 1-6.(in Chinese) |
| [2] | 洪杰, 马艳红, 张大义. 航空燃气轮机总体结构设计与动力学分析[M].北京: 北京航空航天大学出版社, 2014: 366-369. HONG J, MA Y H, ZHANG D Y. Structure design and dynamic analysis of aero gas turbine engines[M].Beijing: Beihang University Press, 2014: 366-369.(in Chinese) |
| [3] | 陈萌, 马艳红, 刘书国, 等. 航空发动机整机有限元模型转子动力学分析[J].北京航空航天大学学报, 2007, 33(9): 1013–1016. CHEN M, MA Y H, LIU S G, et al. Rotordynamics analysis of whole aero-engine models based on finite element method[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(9): 1013–1016.(in Chinese) |
| [4] | B?SWALD M, LINK M, SCHEDLINSKI C. Computational model updating and validation of aero-engine finite element models based on vibration test data[C]//International Forum on Aeroelasticity and Structural Dynamics, 2005: 1-17. |
| [5] | 李俊慧, 马艳红, 洪杰. 转子系统套齿结构动力学设计方法研究[J].航空发动机, 2009, 35(4): 36–39. LI J H, MA Y H, HONG J. Dynamic design method of spline joint structure for rotor system[J].Aero Engine, 2009, 35(4): 36–39.(in Chinese) |
| [6] | 闻邦椿, 顾家柳. 高等转子动力学:理论、技术与应用[M].北京: 机械工业出版社, 1999: 77-82. WEN B C, GU J L. Advanced rotor dynamics-theory technology and application[M].Beijing: China Machine Press, 1999: 77-82.(in Chinese) |
| [7] | ARUMUGAM P, SWARNAMANI S, PRABHU B S. Effects of coupling misalignment on the vibration characteristics of a two stage turbine rotor[C]//ASME Design Engineering Technical Conference. New York: ASME, 1995: 1049-1054. |
| [8] | LI J, HONG J, MA Y, et al. Modelling of misaligned rotor systems in aero-engines[C]//ASME 2012 International Mechanical Engineering Congress and Exposition. New York: ASME, 2012: 535-543. |
| [9] | 姚星宇, 王建军, 翟学. 航空发动机螺栓连接薄层单元建模方法[J].北京航空航天大学学报, 2015, 41(12): 2269–2279. YAO X Y, WANG J J, ZHAI X. Modeling method of bolted joints of aero engine based on thin-layer element[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(12): 2269–2279.(in Chinese) |
| [10] | 姚星宇, 王建军. 航空发动机螺栓连接载荷与结构参数对连接刚度影响规律[J].推进技术, 2017, 38(2): 424–433. YAO X Y, WANG J J. Effects of load and structure parameters of aero engine bolted joints on joint stiffness[J].Journal of Propulsion Technology, 2017, 38(2): 424–433.(in Chinese) |
| [11] | QIN Z Y, HAN Q K, CHU F L. Analytical model of bolted disk-drum joints and its application to dynamic analysis of jointed rotor[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2014, 228(4): 646–663.DOI:10.1177/0954406213489084 |
| [12] | QIN Z, HAN Q, CHU F. Bolt loosening at rotating joint interface and its influence on rotor dynamics[J].Engineering Failure Analysis, 2016, 59: 456–466.DOI:10.1016/j.engfailanal.2015.11.002 |
| [13] | LIU S, MA Y, ZHANG D, et al. Studies on dynamic characteristics of the joint in the aero-engine rotor system[J].Mechanical Systems & Signal Processing, 2012, 29(5): 120–136. |
| [14] | WANG C, ZHANG D, ZHU X, et al. Study on the stiffness loss and the dynamic influence on rotor system of the bolted flange joint[C]//ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. New York: ASME, 2014: 1-14. |
| [15] | 杨帆. 燃气轮机螺栓连接结构热蠕动及动力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. YANG F. Gas turbine bolt connection structure thermal creep and dynamics research[D]. Harbin: Harbin Institute of Technology, 2016(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10213-1016774328.htm |
| [16] | YAMAMOTO T, ISHIDA Y. Linear and nonlinear rotordynamics:A modern treatment with applications[M].New York: John Wiley & Sons, 2001: 35-39. |
