数控机床是装备制造业的工作母机，其可靠性技术目前已成为制约行业发展的关键共性技术^[1]。现阶段检测数控机床可靠性的主要方法是“经时试验”，即使用该机床长时间切削金属坯料，使机床主轴承受切削力，以此发现机床长期运行时所发生的故障。但是，该方法耗费大量的原料和刀具，显著增加了测试成本。所以，需要研制一种可向机床主轴施加多维载荷的加载装置，以改进传统测试方法。
并联机构由于其结构紧凑、承载能力强、积累误差小和动态性能好等特点在工业领域被广泛使用^[2]。其动平台具备空间多自由度，故可以将其应用于多维力加载领域。关于并联加载装置的研究，最早可追溯到1962年Gough和Whitehall发明的6自由度并联机器人^[3], 将其应用于对轮胎的加载中，测试轮胎在不同载荷下的性能。徐彬^[4]采用Stewart平台结构的形式，对大型旋挖钻机动臂加载性能参数进行了分析。刘少欣等^[5]对6-UPS并联加载装置的动力学模型进行了简化。王博和黄其涛^[6]提出了一种正交并联机构的多轴加载试验系统，用以模拟对接机构组合体实际应用中受到的复杂载荷，是并联机构一种新的应用形式。Stokes等^[7]基于6自由度并联机构设计一种针对脊柱的加载装置，在末端安装多维力传感器，对动物脊柱进行了刚度测量。Nierenberger和Flohic等^[8-9]将Stewart平台用作多维力材料加载试验机，并对混凝土试验件进行拉力-剪力-剪切力二维加载试验。Guo等^[10-12]同样基于Stewart平台，设计多维力加载试验机，对试验机的输出载荷进行检测。但是，上述研究采用的Stewart平台的驱动电机位于运动支链中，随连杆一起运动，使机构运动部件的质量增大，对机构的动态特性产生不利影响。相比之下，6-PSS并联机构由于其驱动电机固定，可有效减小运动部件的质量，机构的动态特性好，便于在多维加载过程中实时跟随目标的空间运动。王洪瑞等^[13]建立了6-PSS并联机器人的动力学模型；孙小勇等^[14]对6-PSS并联机器人的参数进行了优化设计；Wang等^[15]基于Hexaglide型并联机构设计多维力加载装置，并对其刚度分布进行分析，但是并未对加载装置进行多维力加载试验。
本文提出一种基于6-PUS并联机构的多维力加载装置，可对目标提供多维载荷。首先根据向量叠加原理和牛顿迭代法分别介绍了6-PUS并联机构的逆、正解运算，并由旋量理论建立了机构的运动学和静力学模型；然后根据虚功原理建立了机构的动力学模型并进行仿真验证；最后对多维力加载装置进行多维力加载试验。
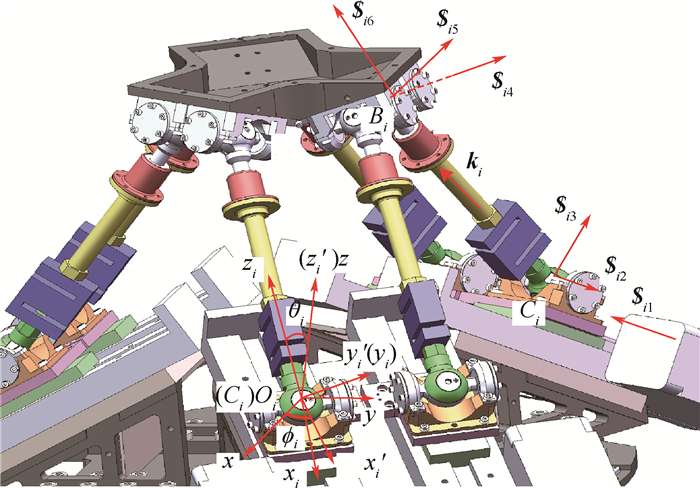
1 6-PUS并联机构的运动学建模 1.1 运动学逆解 如图 1所示，6-PUS并联机构由动平台、静平台及6根完全相同的支链组成。其中，动平台复合球铰中心B_i(i=1, 2, …, 6)的分布半径为r_p，6个球铰链分为3组，沿圆周均布，每组之间夹角为120°；6个直线驱动及静平台复合虎克铰C_i(i=1, 2, …, 6)同样分为3组在静平台上沿圆周均布，每组驱动的安装平面倾角为β。将滑块置于零位，每组两驱动的中点的分布半径为r_b，各支链中的连杆长度为L。
选任一支链, 使用向量叠加描述该运动链得

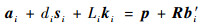(1)

图 1 多维力加载装置结构及坐标系定义示意图 Fig. 1 Schematic of structure and coordinate system definition of tested multi-dimensional loading device

图选项

式中：；d_i为各运动支链中移动副的驱动量；L_i为定长连杆的长度；s_i为静坐标系中移动副的方向向量；k_i为静坐标系中沿连杆方向的单位向量；p和R分别为动坐标系O′{x′, y′, z′}相对于静坐标系O{x, y, z}的原点位置和坐标系旋转矩阵；在动坐标系中定义
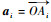
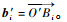
令p+Rb_i′-a_i=h_i，根据机构构型和运动的连续性求解式(1)得

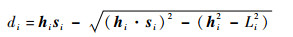(2)

1.2 运动学正解 与运动学逆解相反，多维力加载装置的运动学正解是已知6个运动支链的电机驱动量，求解机构动平台位姿的过程，即已知驱动量d_i(i=1, 2, …, 6)，求解动平台中心点O′的位置向量p=[p_x p_y p_z]^T和姿态向量Θ=[θ_x θ_y θ_z]^T，其中向量p和Θ的3个分量分别是动平台沿x、y、z轴的位移和绕其轴线的转角。
将动平台的位姿表示为Q=[p^T Θ^T]^T, 可以根据姿态向量求解出旋转矩阵R=f(Θ)，由运动学反解可知

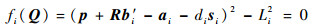(3)

式中：旋转矩阵R用四元数表示，相比欧拉角，可有效避免奇异问题。通常，可将四元数定义为A=a₀+a₁i+a₂j+a₃k, (a_i∈R, i=0, 1, 2, 3)，且

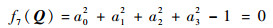(4)

则Q=[p A]^T，A=[a₀ a₁ a₂ a₃]^T。
将R代入式(3)，再与式(4)相加可得7个方程，最后利用牛顿迭代法即可求解得出位置向量Q的7个分量未知数。求解过程如图 2所示，首先确定动平台初始位姿Q₀，然后用牛顿迭代法求出迭代位姿Q_n(n为迭代次数，n≥0), 当由末端迭代位姿Q_n反解计算出的杆长与已知杆长的差值向量Δf=[f₁ f₂ … f₇]的模满足|f(Q_n)|＜ξ=10^-10 m时，即可认为此时的迭代位姿Q_n可以作为当前动平台的实际位姿向量Q，迭代结束。

图 2 机构运动学正解流程图 Fig. 2 Flowchart of forward kinematics of mechanism

图选项

2 运动学与静力学分析 2.1 速度及静力雅可比矩阵分析 任取一条运动支链作为研究对象，如图 3所示。将动平台中心点的速度旋量用Plücker坐标表示为T=[v^T ω^T]^T，其中v和ω分别表示动平台质心点相对静坐标系的平移速度和旋转角速度。
由旋量法可得

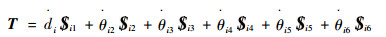(5)

图 3 支链坐标系及速度旋量分布示意图 Fig. 3 Schematic of branched-chain coordinate system and velocity screw distribution

图选项

式中：(j= 2, 3)，c_i= 和(j=2, 3，…, 6)分别为转动副旋转轴方向向量和旋转速率，且k_i6=k_i，s_i和分别为移动副的方向向量和移动速率。
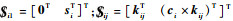
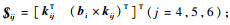
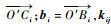
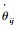
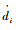
将式(5)的两端同时与单位速度旋量[k_i^T (c_i×k_i)^T]^T取互易积，且(j=2, 3, …, 6)，整理为矩阵形式可得

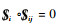
(6)

式中：动平台质心速度；滑块移动速度；速度雅可比矩阵J_v=[J_v1^T J_v2^T … J_v6^T]_6×6^T，(i=1, 2, …, 6)。
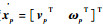
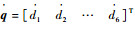
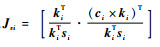
由速度和静力学对偶关系可知：

(7)

式中：F=[f^T m^T]^T为施加在动平台质心的外力载荷f为外力，m为力矩；τ=[τ₁ τ₂ … τ₆]^T为移动副滑块驱动力向量；J_f为力雅可比矩阵。
2.2 速度分析 选取任一定长连杆为研究对象，以C_i为原点, 建立如图 3所示的支链坐标系O_i{x_i, y_i, z_i}, 其初始状态x、y和z轴分别与静坐标系的3个坐标轴平行，故连杆方向向量可使用ZYZ欧拉角表示，即支链坐标系O_i先绕静坐标系z轴旋转角?_i，再绕新坐标系O_i′的y_i′轴旋转角度θ_i，此时ⁱk_i=z_i。
对式(1)的右侧求导可知：

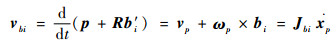(8)

式中：J_bi=[E_3×3 -b_i×]。
将v_bi通过坐标变换转换至支链坐标系得

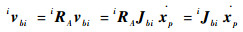(9)

式中：ⁱR_A=^AR_i^T，^AR_i为支链坐标系相对静坐标系的旋转矩阵；ⁱJ_bi=[ⁱJ_bix^{T i}J_biy^{T i}J_biz^T]^T。
对式(1)等号左侧求导且将其转化至支链坐标系中得

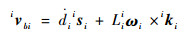(10)

对式(10)的两端同时点乘ⁱk_i，可得

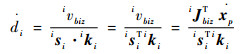将驱动量整理为矩阵形式为

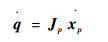(11)

式中：
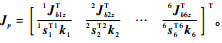
对式(10)两端同时叉乘ⁱk_i，由ⁱω_i·ⁱk_i=0可得连杆角速度在支链坐标系中的表示为

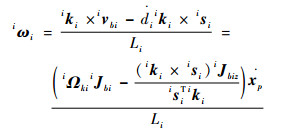式中：ⁱΩ_ki=ⁱk_i。
由滑块的质心向量r_ci=a_i+d_is_i可得其质心速度为

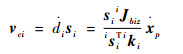(12)

同理，由连杆的质心向量r_li=a_i+d_is_i+L_ik_i/2可得连杆的质心速度，将其转换至支链坐标系：

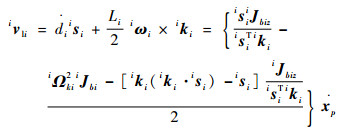(13)

使用Plucker坐标表示滑块的质心速度和连杆质心速度，

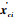
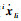
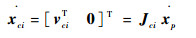(14)

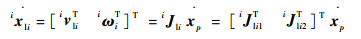(15)

式中：

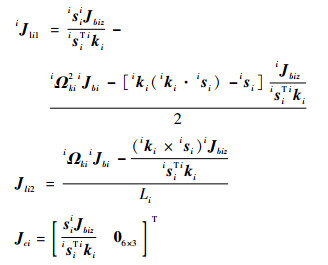2.3 加速度分析 对式(10)求导且两端同时点乘ⁱk_i可得滑块的加速度在支链坐标系中为

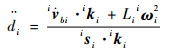(16)

对式(10)求导且两端同时叉乘ⁱk_i可得连杆角加速度在支链坐标系中为

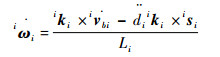(17)

对式(12)求导得滑块质心加速度向量为

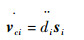(18)

对式(13)求导得连杆质心加速度向量，并将其转换至支链坐标系得

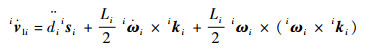(19)

3 动力学分析 3.1 动力学方程 由虚功原理可知，多维力加载装置各部件所受广义主动力及广义惯性力合力所做的功为零。
静坐标系下动平台中心点广义主动力和广义惯性力的合力(包含力f_p及力矩n_p)为

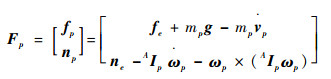式中：f_e和n_e分别为动平台中心点外力和外力矩；m_p为动平台质量；^AI_p为动平台在静坐标系下的转动惯量。
同理，静坐标系下各滑块质心点的广义主动力和广义惯性力合力(包含力f_ci及力矩n_ci)为

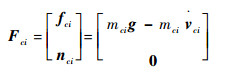式中：m_ci为滑块质量。同理，支链坐标系下各连杆质心点的广义主动力和广义惯性力的合力(包含力f_li及力矩n_li)表示为

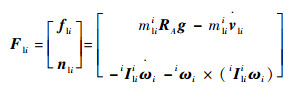式中：m_li为连杆质量；ⁱI_li为支链坐标系下连杆的转动惯量。
由虚功原理得

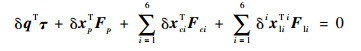(20)

当各构件运动时间相同时，δq=J_pδx_p, δx_ci=J_ciδx_p, δⁱx_li=ⁱJ_liδx_p, 将此式(3)代入式(20)得

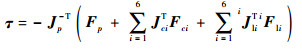(21)

3.2 动力学仿真验证 首先，建立Adams理论模型，并结合模型的质量参数在MATLAB中推导多维力加载装置的动力学方程，建立动力学方程；其次，同时设定Adams和MATLAB中的机构模型的动平台质心运动轨迹如式(22)所示：

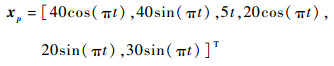(22)

则其质心速度和加速度向量也可求出；再次，同时设定Adams和MATLAB中的机构模型的动平台质心点所受外力为沿z轴负方向1 000 N；最后，在Adams中测量6个滑块的驱动力，与MATLAB计算得出的驱动力进行比较，并计算二者之间的误差，如图 4所示。由图 4可知，Adams机构理论模型与MATLAB动力学模型误差维持在2 N以内，小于驱动力的0.5%，支链2、3和5在0.04 s时误差达到4 N，但仍小于驱动力的1%，验证了本文运动学及动力学分析的正确性。

图 4 Adams与MATLAB模型所得各支链驱动力的误差 Fig. 4 Deviation of branched-chain actuation forces derived from Adams and MATLAB model

图选项

4 多维力加载试验 进行多维力加载试验时，将多维力加载装置放置在三轴联动龙门式机床试验平台上，动平台中心与机床主轴连接，主轴处于静止状态，改变动平台的位姿，其与主轴的相对运动会对应产生作用力，实现对主轴的多维力加载。具体加载过程如下：第一, 设定期望动平台输出的多维力值；第二, 由光栅尺反馈各支链的驱动量，正解得机构动平台位姿；第三, 根据动平台位姿和动力学方程求解得出施加期望多维力所需要的各支链驱动力，并由此推导得出各传感器期望力；第四, 使用模糊PID控制算法^[16]对各支链进行力闭环控制，使动平台输出期望多维力。
多维力加载试验分为2部分：六维三角波载荷和六维正弦载荷，分别代表对机床主轴匀速加载和变加速度加载2种形式。试验采用“双十指标”评估加载性能，即实际加载力与参考加载力误差小于10%，相位误差小于10°。通过比较各方向实际载荷和参考载荷间的跟随误差，分析和评估多维力加载装置的实时性和准确性。
1)六维三角波载荷加载
同时在主轴上施加幅值为200 N的三维三角波力和幅值为10 N·m三维三角波力矩，得到理论力、理论力矩及加载误差如图 5所示。

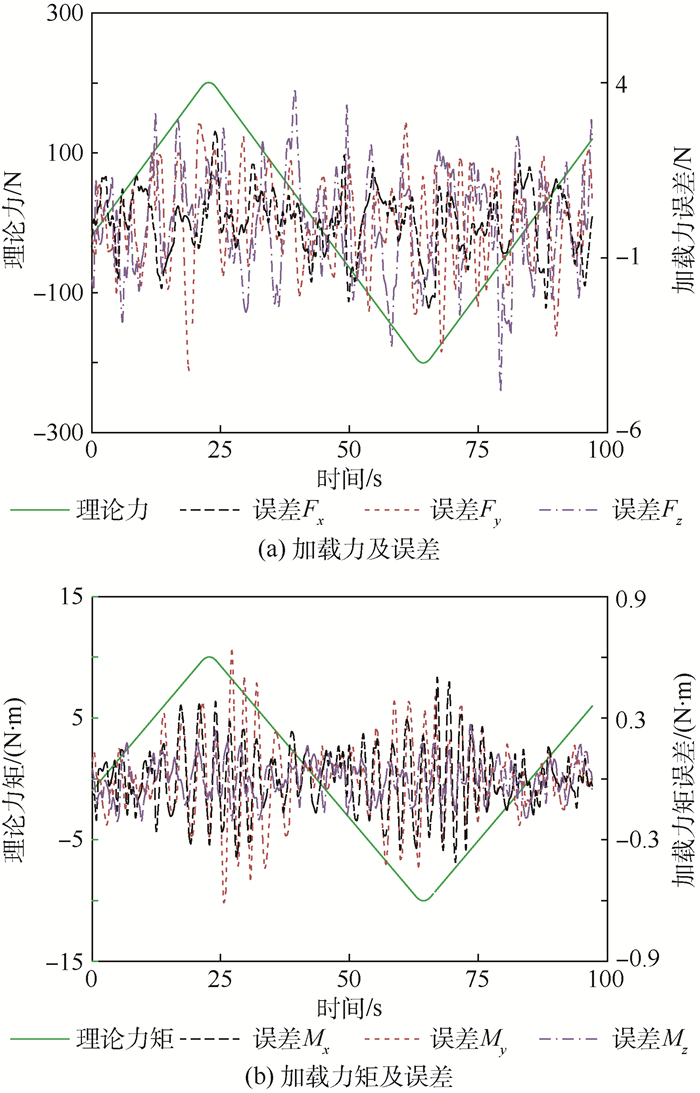图 5 六维三角波载荷加载误差 Fig. 5 Loading errors along six axes with triangular wave load

图选项

观察图 5可知，多维力加载装置对主轴施加的六维三角波载荷中，沿x、y和z轴的加载力误差最大值分别为4.680、2.636和5.264 N，基本处于参考加载力最大幅值的5%以内。另外，沿三轴加载力矩误差最大值分别为0.652、0.515和0.321 N·m，小于参考加载力矩最大幅值的10%，满足加载需要。
2) 六维正弦载荷加载
同时在主轴上施加幅值为200 N的三维正弦力和幅值为10 N·m的三维正弦力矩，得到理论力、理论力矩及加载误差如图 6所示。

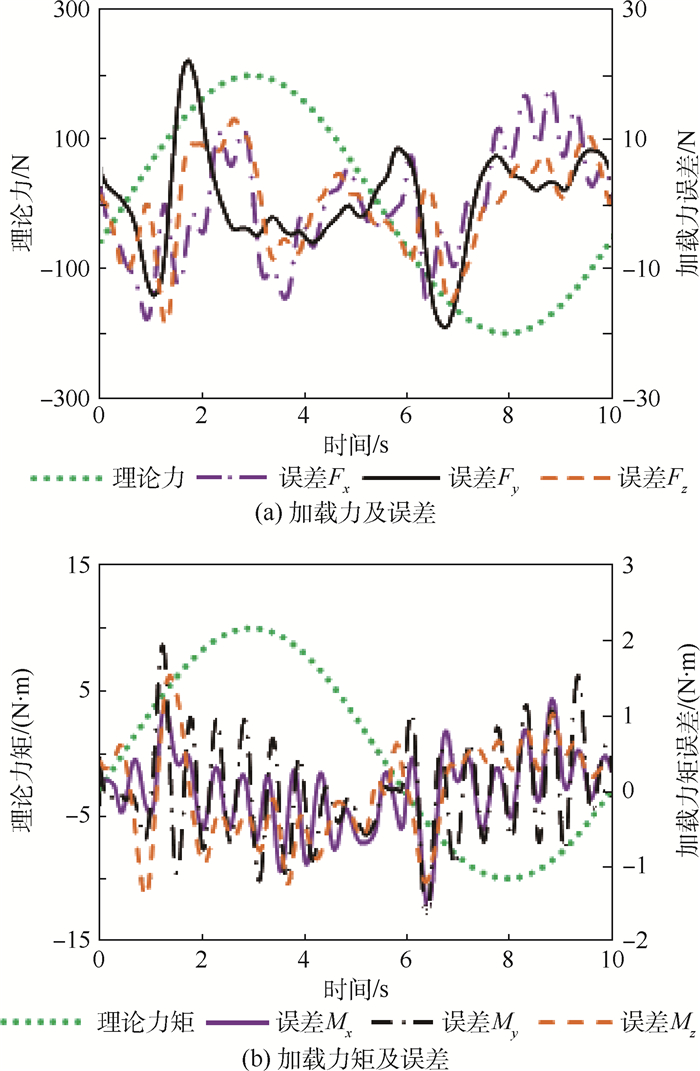图 6 六维正弦载荷加载误差 Fig. 6 Loading errors along six axes with sine load

图选项

由图 6可知，多维力加载装置对主轴施加的六维正弦载荷中，沿x、y和z轴加载力误差最大值分别为18.291、22.417和19.201 N，基本维持在参考载荷的10%以内。另外，沿三轴的加载力矩误差最大值分别为1.583、2.062和1.607 N·m，在参考加载力矩的10%以内，满足加载需要。
5 结论 本文提出一种基于6-PUS并联机构的多维力加载装置，可对机床主轴施加多维载荷。建立了加载装置的运动学、静力学以及动力学模型，并进行了动力学仿真验证和多维力加载试验，得出以下结论：
1) 采用虚功原理可对6-PUS并联机构进行准确的动力学建模。用MATLAB建立动力学模型，并在Adams中建立结构相同的虚拟样机，通过给定相同的动平台运动轨迹和外载荷，对比Adams和MATLAB仿真所得的驱动力，误差小于1%，验证了动力学建模的正确性。
2) 6-PUS并联机构具备对目标进行多维力加载的能力，加载试验结果表明，该机构可对目标施加六维三角波和正弦载荷信号，最大跟随误差均小于10%，证明其可以对目标进行匀速和变加速多维力加载，为数控机床加载试验提供新的加载手段和理论基础。

参考文献

[1]	杨兆军, 陈传海, 陈菲, 等. 数控机床可靠性技术的研究进展[J].机械工程学报, 2013, 49(20): 130–139. YANF Z J, CHEN C H, CHEN F, et al. NC machine tool reliability technology database applications[J].Journal of Mechanical Engineering, 2013, 49(20): 130–139.(in Chinese)
[2]	郭江真, 王丹, 樊锐, 等. 3PRS/UPS冗余驱动并联机器人刚度特性分布[J].北京航空航天大学学报, 2014, 40(4): 500–506. GUO J Z, WANG D, FAN R, et al. Stiffness characteristics distribution of 3PRS/UPS parallel manipulator with actuation redundancy[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(4): 500–506.(in Chinese)
[3]	GOUGH V E, WHITEHALL S G. Universal tyre test machine[C]//Proceedings of the FISITA Ninth International Technical Congress. London: Institution of Mechanical Engineers, 1962: 117-137.
[4]	徐彬. 基于并联机构的多维力加载试验系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 10-40. XU B. Research on multi-DOF loading system based on parallel mechanism[D]. Harbin: Harbin Institute of Technology, 2013: 10-40(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10213-1014003564.htm
[5]	刘少欣, 王丹, 陈五一. 6-UPS并联多维力加载装置的动力学建模及简化[J].机床与液压, 2014, 42(19): 5–8. LIU S X, WANG D, CHEN W Y. Dynamics modeling and simplification of a 6-UPS parallel multi-dimensional loading device[J].Machine Tool and Hydraulics, 2014, 42(19): 5–8.DOI:10.3969/j.issn.1001-3881.2014.19.002(in Chinese)
[6]	王博, 黄其涛. 正交并联多自由度加载试验系统研究[J].机电工程, 2016, 33(11): 1334–1338. WANG B, HUANG Q T. Loading test system of orthogonal parallel multi degree of freedom[J].Mechanical and Electrical Engineering, 2016, 33(11): 1334–1338.(in Chinese)
[7]	STOKES I A, GARDMEMORSE M, CHURCHILL D, et al. Measurement of a spinal motion segment stiffness matrix[J].Journal of Biomechanics, 2002, 35(4): 517–521.DOI:10.1016/S0021-9290(01)00221-4
[8]	NIERENBERGER M, PONCELET M, PATTOFATTO S, et al. Multiaxial testing of materials using a stewart platform:Case study of the Nooru-Mohamed test[J].Experimental Techniques, 2012, 38(2): 74–83.
[9]	FLOHIC J L, PARPOIL V, BOUISSOU S, et al. A 3D displacement control by digital image correlation for the multiaxial testing of materials with a Stewart platform[J].Experimental Mechanics, 2014, 54(5): 817–828.
[10]	GUO J Z, WANG D, FAN R, et al. Development of a material testing machine with multi-dimensional loading capability[J].Journal of Advanced Mechanical Design Systems & Manufacturing, 2016, 10(2): JAMDSM0017.
[11]	GUO J Z, FAN R, WANG D, et al. Development of multidimensional loading material testing machine[J].Materials Science Forum, 2013, 770: 164–169.DOI:10.4028/www.scientific.net/MSF.770
[12]	樊锐, 李茜, 王丹. 6PUS并联机构的运动学整机标定[J].北京航空航天大学学报, 2016, 42(5): 871–877. FAN R, LI X, WANG D. Integral kinematics calibration of 6PUS parallel mechanism[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(5): 871–877.(in Chinese)
[13]	王洪瑞, 马丽, 肖金壮. 一种6-PSS并联机器人动力学模型的建立[J].中国高新技术企业, 2010(10): 19–21. WANG H R, MA L, XIAO J Z. A 6-PSS parallel robot dynamic model[J].China High-Tech Enterprises, 2010(10): 19–21.(in Chinese)
[14]	孙小勇, 郑彬, 鲍捷, 等. 高速6-PSS并联机器人参数优化设计[J].农业机械学报, 2015, 46(5): 372–378. SUN X Y, ZHENG B, BAO J, et al. Parameter optimization design of high speed 6-PSS parallel robot[J].Transactions of the Chinese Society of Agricultural Machinery, 2015, 46(5): 372–378.DOI:10.6041/j.issn.1000-1298.2015.05.052(in Chinese)
[15]	WANG D, FAN R, CHEN W. Stiffness analysis of a Hexaglide parallel loading mechanism[J].Mechanism & Machine Theory, 2013, 70(6): 454–473.
[16]	樊锐, 刘力军, 王丹, 等. 6-PUS并联加载机构模糊PID力控制系统设计[J].航空制造技术, 2016, 513(18): 34–39. FAN R, LIU L J, WANG D, et al. Design of fuzzy PID force control system based on 6-PUS parallel machine[J].Aeronautical Manufacturing Technology, 2016, 513(18): 34–39.(in Chinese)