为结合3、5轴机床经济、技术优势,韩国Suh等提出了3+2轴的加工方式[8-9]。该加工方式采用3个线性联动轴和2个旋转半联动轴组成运动机构,2个半联动轴在加工中不参与运动。在加工前将主轴姿态或工件姿态调整到合适位置,并锁死2个旋转半联动轴,然后使用3个线性轴联动加工零件表面。此方法由于存在可旋转的半联动轴,在保持3轴加工的高刚性优势的同时,可根据加工需要调整刀轴方向[10-11]。
然而由于刀轴与工件之间的干涉,3+2轴机床无法高效加工叶轮等回转类零件。为了加工这类零件,在4轴机床上通常只能采用球头刀进行精加工,或使用玉米铣刀进行开粗。相比5轴机床可使用高效加工刀具精加工叶轮,4轴机床的加工效率较低。现在国内叶轮制造厂拥有大量4轴机床,为了高效地使用4轴机床加工这类零件,扩展4轴机床的加工能力,将2个半联动轴分配给4轴联动机床,组成4+2轴机床。相比3+2轴机床,该机床多一个旋转联动轴,更适合整体叶轮等回转零件的加工;在优化刀轴姿态时增加了1个可优化参数,可使用高性能刀具加工,如圆环面刀、鼓形刀等;通过半联动轴改变主轴方向或零件安装姿态,增大了叶轮在加工时的刀矢可行域,减少了刀杆伸出的长度,为解决刀具干涉和提高加工效率、质量提供了基础;经济性上,4轴联动机床成本相比5轴联动机床大大降低[12]。所以4+2轴机床可以兼得4轴和5轴机床的经济和技术优势。
4+2轴机床的2个半联动轴可以以多种形式分配到4轴联动机床上:① 两半联动轴同时分配到刀具主轴上,例如将万向头安装在主轴上,在调整好主轴姿态后,锁死主轴方向,实现4+2轴加工;② 两半联动轴同时分配在转台上,例如在旋转联动轴上安装角度分度转台,将旋转联动轴固定在空间某方向后,实现4+2轴加工;③ 2个半联动轴分别安装在主轴和转台上。
本文以第1种4+2轴机床结构作为研究对象,研究4+2轴叶轮加工的相关问题。首先从机构学角度建立机床运动模型,得到机床运动链和运动变化关系,推导出机床运动的求解公式。并在此基础上,研究半联动轴参数对于刀轴姿态的影响,给出半联动轴参数的优选方法。然后根据切触点轨迹,干涉约束条件优化刀轴姿态[13],最终生成4+2轴加工刀轨。通过对某一叶轮的仿真与加工,验证本文提出的基于4+2轴机床的叶轮加工方法及相应算法。
1 4+2轴机床机构运动学建模 为研究4+2轴加工过程中,半联动轴、联动轴运动参数和刀具姿态参数之间的运动变换关系,以及为选择半联动轴、优化刀轴矢量与生成刀具轨迹提供理论模型,需构建机床的运动学模型,即建立机床各运动部件对应的坐标系及其组成的运动链。根据模型求得半联动轴参数与刀具姿态的关系,并推导机床4个联动轴的运动参数求解公式。
1.1 机床运动链建模 本文在XYZ+A式4轴机床模型的基础上,配合带B、C两旋转轴的万向铣头[14]实现4+2轴加工,如图 1所示。机床运动链由刀具、半联动B轴、半联动C轴、Z轴、床身、XY平动工作台、A轴回转工作台和工件组成。
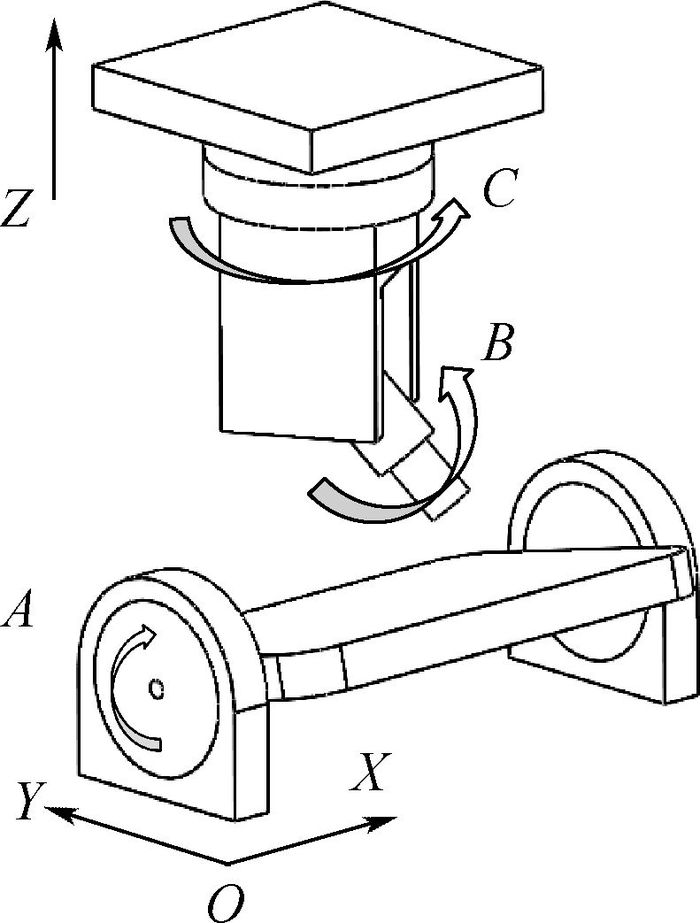 |
| 图 1 4+2轴机床模型 Fig. 1 4+2-axis machine tool model |
| 图选项 |
为描述机床各轴之间运动,建立图 2所示机床坐标各部件的坐标系。其中OMXMYMZM为机床坐标系(MCS);OWXWYWZW为与工件固连的工件坐标系(WCS);OTXTYTZT为与刀具固连的刀具坐标系(TCS),原点OT在万向铣头B、C轴交点处。初始时,工件坐标系(WCS)、刀具坐标系(TCS)与机床坐标系(MCS)的对应轴相互平行。假设刀具摆长为l,则在刀具坐标系(TCS)下,刀心点的位置矢量tc和刀轴的方向矢量ta分别为[00-l]T[0 0 1]T。
 |
| 图 2 4+2轴机床坐标系 Fig. 2 Coordinate systems of 4+2-axis machine tool |
| 图选项 |
1.2 机床运动求解 通过坐标变换关系,将不同坐标系下描述的刀轴矢量、刀心坐标变换到同一坐标系下,以确定各运动构件的相对运动。本文通过建立“刀具坐标系(TCS)—机床坐标系(MCS)—工件坐标系(WCS)”和“局部坐标系(LCS)—工件坐标系(WCS)”的坐标变换关系,将刀轴矢量和刀心坐标转换到工件坐标系(WCS)内进行比较,从而在工件坐标系(WCS)下建立机床运动坐标与刀具姿态参数的方程。
1.2.1 TCS到WCS的坐标变换关系 从刀具坐标系(TCS)经机床坐标系(MCS)到工件坐标系(WCS),刀具先通过B、C轴固定方向,再沿Z、Y、X轴做平移运动,最后绕A轴进行旋转运动。对应的运动变换矩阵为TWT=R(A)·T(X)T(Y)T(Z)R(C)R(B),TWT的上下角标对应变换前后的坐标系,R(A)、R(B)、R(C)、T(X)、T(Y)、T(Z)对应绕A、B、C轴的旋转变换矩阵和沿X、Y、Z轴的平移变换矩阵。由式(1)、式(2) 求得工件坐标系(WCS)下,机床坐标表示的ta和tc表达式为
 | (1) |
 | (2) |
式中:a、b、c对应A、B、C轴旋转坐标;x、y、z对应X、Y、Z轴移动坐标;[x0?y0?z0]为工件坐标系原点在机床坐标系中的位置。
1.2.2 LCS到WCS的坐标变换关系 在切触点Pcc上建立图 3所示局部坐标系(LCS,进给坐标系)。
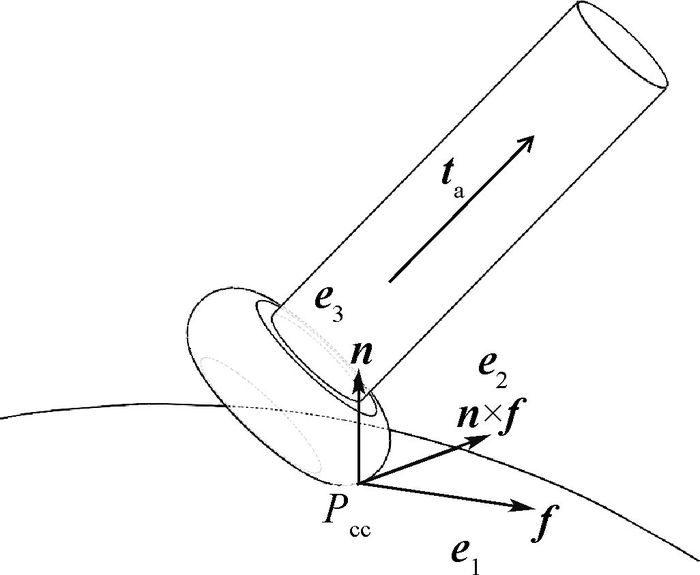 |
| 图 3 局部坐标系 Fig. 3 Local coordinate system |
| 图选项 |
设e1、e2、e3为局部坐标系(LCS)坐标轴的单位方向向量,e1、e2、e3分别平行于切触点Pcc的进给方向f、法矢方向n和n×f。在局部坐标系(LCS)中,满足相应切触条件的刀具姿态由前倾角λ和侧偏角θ来表示。局部坐标系(LCS)下刀轴矢量ta由式(3) 求得
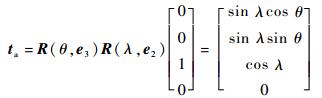 | (3) |
局部坐标系(LCS)下刀心矢径rc由刀具与曲面的切触位置和姿态决定。
为了在工件坐标系中(WCS)表达满足切触条件的刀心矢径tc和刀轴矢量ta,建立“局部坐标系(LCS)—工件坐标系(WCS)”的坐标变换关系。设在工件坐标系(WCS)内,局部坐标系(LCS)的坐标轴方向向量e1=[ix jx kx]T、e2=[iy jy ky]T、e3=[iz jz kz]T。根据空间解析几何,从局部坐标系(LCS)到工件坐标系(WCS)的坐标变换矩阵为
 |
TWL的上下角标对应变换前后的坐标系。故得到在工件坐标系(WCS)中,由刀具姿态参数表示的刀轴矢量ta和刀心矢径tc的表达形式:
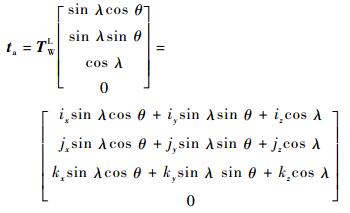 | (4) |
 | (5) |
式(5) 中TWL和rc对于确定的刀具轮廓、切触点和切触条件已知,为前倾角λ和侧偏角θ的函数,为方便描述,记
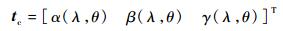 |
1.2.3 半联动轴与刀具姿态的关系 根据刀轴矢量ta在工件坐标系(WCS)中的2种表达形式(式(1) 和式(4)),求解机床运动轴参数与刀具姿态角之间的运动关系。联立式(1) 和(4) 的第1分量,得到sin bcos c=(ixcos θ+iysin θ)sin λ+izcos λ,求解可得
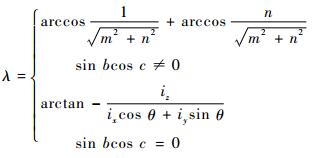 | (6) |
式中:
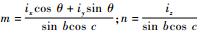
式(6) 得到两半联动轴的运动参数(b、c)和刀具姿态参数(前倾角λ、侧偏角θ)的函数关系,即已知B、C和侧偏角θ,可求解前倾角λ,λ=f(b, c, θ)。故得到结论,4+2轴加工在设定好半联动轴参数后(b、c),可以对侧偏角θ进行优化。
1.2.4 联动轴运动参数求解 根据已知的刀具姿态(刀心矢径tc、刀轴矢量ta)和半联动轴参数(b、c),求解机床的4个联动轴运动参数(a、x、y、z)。联立式(1) 和式(4) 的第2、第3分量推导出式(7)。式(7) 在已知半联动轴参数和刀轴姿态的情况下,可求解切触点处机床A轴的运动参数。
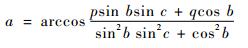 | (7) |
式中:p=jxsin λcos θ+jysin λsin θ+jzcos λ;q=kxsin λ cos θ+kysin λsin θ+kzcos λ。联立式(2) 和式(5) 推导出式(8)。式(8) 用于求解机床平移轴(X、Y、Z)的运动参数
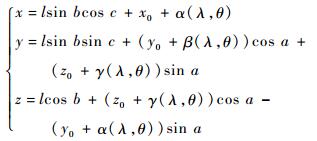 | (8) |
至此,由式(6)~式(8) 得出在选定半联动轴参数和给定优化切触条件的情况下,任意切触点对应的机床运动坐标求解方法。
2 半联动轴参数选择 2.1 刀轴矢量的可达锥面 刀轴矢量的可达方向是指初始主轴经机床旋转运动变换后可以达到的刀轴方向。
在机床坐标系(MCS)下,4+2轴机床的Z轴方向固定不变,如图 1所示。由于加工时旋转联动轴(A轴)的运动,使得在工件坐标系(WCS)下,刀轴矢量可以到达以A轴为轴线的锥面上的任意母线方向,即刀轴矢量的可达方向,该锥面称为刀轴矢量的可达锥面。设半联动轴(B、C)参数分别为b、c,求出可达锥面的半锥角Ψ与b、c关系为
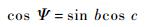 | (9) |
由式(9) 可知,一组b、c对应一个可达锥面。对于一个确定的可达锥面,所有满足式(9) 的b、c皆可使刀轴矢量平行于该可达锥面。图 4所示为一组b、c对应的可达锥面,设锥面半锥角为Ψ,刀具可达方向为(I, J, K),则各参数间满足式(10)。
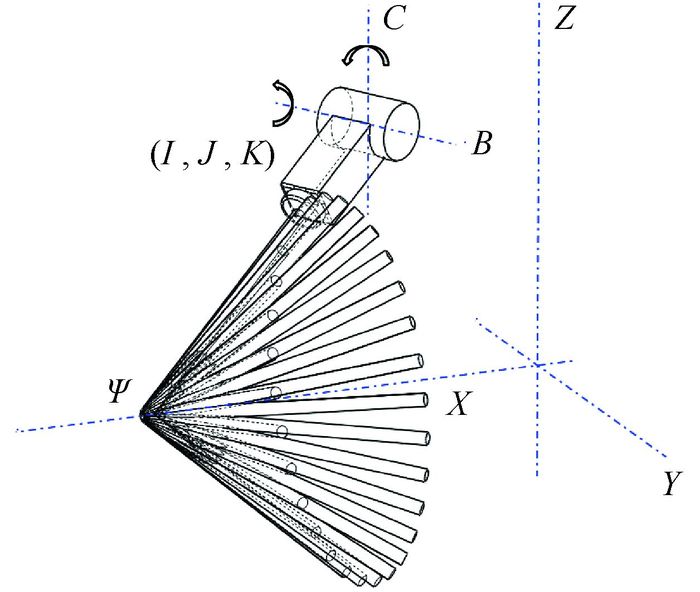 |
| 图 4 刀轴矢量的可达锥面 Fig. 4 An accessible cone of tool axis vector |
| 图选项 |
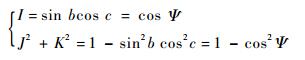 | (10) |
2.2 求解半联动轴参数 为避免干涉并减少机床各轴的运动,需对两个半联动轴的姿态进行优化。尤其对整体叶轮来说,其扭曲度大、叶展长,叶片间的通道深而窄、开敞性很差,刀杆与相邻或待加工叶片间易发生干涉,更应选择合适的主轴方向。
2.2.1 刀具可达锥面的选择 本文采用鼓形刀侧铣加工叶轮叶片。设切触点Pm(m=1, 2, …, n)的最小主曲率方向为tm=[im?jm?km]T,因为最小主曲率方向反映了曲面切触点附近的局部特性。对于切触点Pm,沿此方向曲率最小,使用鼓形刀侧铣加工时,易避免局部干涉的发生。本文初步选取此方向作为半联动轴参数的几何依据。将tm代入式(10) 求解对应的Ψm,由式(10) 知,只要刀轴矢量的可达锥面的半锥角为Ψm,即可满足目标刀轴方向tm。图 5为主轴方向t绕机床A轴旋转Δa后与目标刀轴矢量(i?j?k)重合的重合过程。
 |
| 图 5 锥面上的任意主轴方向经A轴运动皆可目标刀轴方向重合 Fig. 5 Every tool axis direction in a cone coinciding with target tool axis direction by rotating around A axis |
| 图选项 |
由于一组半联动轴参数(b、c)对应唯一刀轴矢量的可达锥面,不能与所有切触点的理想刀轴方向平行,故根据通过tm,应用最小二乘法初选可达锥面的半锥角ψ,使ψ靠近所有点的Ψm:
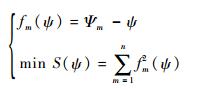 | (11) |
2.2.2 半联动轴参数初选 由可达锥面的性质(见图 5)可知:同一个的可达锥面,选取A轴相差转角为Δa的两条母线分别作为主轴固定方向,对于同一模型的同一个切触点的相同刀轴矢量方向,为达到目标刀轴方向,A轴旋转运动将会相差相同转角Δa。若分别以两主轴方向生成各自的加工刀轨,A轴旋转坐标将会整体相差A轴转角Δa。实际加工过程中,由于夹具、工件等干涉体,机床A轴实际行程无法达到360°,且万向铣头的行程范围(B轴±90°,C轴0°~360°,最小分度1°)进一步限制了A轴的实际行程范围。
为使最终生成的刀轨能满足A轴实际行程范围,设切触点Pm(m=1, 2, …, n)的最小主曲率方向为tm=[im?jm?km]T,在2.2.1节中求解的可达锥面的半锥角为ψ。将tm投影到YOZ平面上,如图 5所示,计算使得Δa=max1≤s, t≤n(∠ps, pt), s, t∈Z,成立的ps, pt。根据ps, pt求平均,得向量pst。若Δa>180°,将pst反向;若Δa≤180°,pst不变。以此时pst作为实际主轴方向在YOZ平面的投影,设pst=[0?J?K]T。由式(10) 求得,机床坐标系(MCS)下的实际主轴方向为[cos ψ?J?K]T。该主轴方向可以使得最大A轴运动距离最小。
然后由式(9) 和几何关系,求解半联动轴参数(b,c):
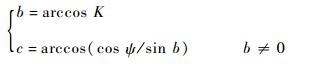 | (12) |
b=0时,4+2轴加工等同于4轴加工的情况。
至此,由式(11) 和式(12) 求得4+2轴加工叶轮的初选半联动轴参数。
2.2.3 半联动轴参数优选及加工刀轨生成 在生成刀轨的过程中,对初选的半联动轴参数(b、c)进行干涉检查,并光顺A轴运动。流程(如图 6所示)如下:
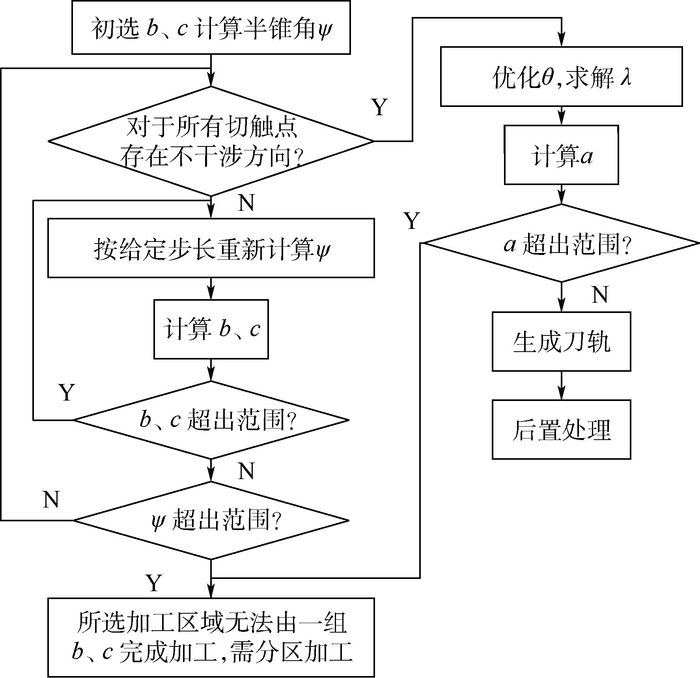 |
| 图 6 刀轨生成算法流程图 Fig. 6 Flowchart of tool path generation algorithm |
| 图选项 |
1) 将初选b、c代入式(9) 反解半锥角ψ,得到刀轴矢量的可达锥面。
2) 判断对于所有切触点Pm(m=1, 2, …, n)的可达方向上是否存在不干涉方向。若?Pm的所有刀轴可达方向均干涉,转到步骤3)。若对于?Pm均存在不干涉方向,则转到步骤4)。
3) 在给定的B、C轴搜索范围内,以初选半锥角ψ为中心搜索使所有Pm均存在不干涉方向的半锥角ψ,并重新计算b、c。若b、c未超出范围,则重复步骤1)、2),直到步骤2) 判断成功;若超出,则算法结束,返回该曲面无法只使用一组半联动轴参数(b、c)完成加工,需分区加工。
4) 遵循切触条件及行宽最大化原则[15-17],优化θ。并根据式(7) 计算A轴运动角度范围,根据机床碰撞判断其是否超出A轴实际运动范围。若未超出,则转步骤5);若超出,则算法结束,返回该加工曲面无法使用4+2轴一次成型加工,需多次分区加工。
5) 生成刀轨,得到半联动轴参数。根据式(8),完成机床运动坐标的计算。
6) 根据实际加工摆长,对4+2轴刀轨进行后置处理,完成实际加工。
3 实验验证与分析 本文提出的4+2轴加工方法已经在UG二次开发模块[18]下进行了较完善的开发。本节通过试算、加工某一叶轮叶片来验证本文算法的可行性。
实验叶轮半径98 mm,叶片长45 mm,叶片个数10片,流道间最小宽度20 mm,最大宽度28 mm,如图 7所示。使用半对称鼓形刀生成刀轨,半对称鼓形刀的鼓型半径50 mm,圆心偏离轴线44.5 mm,距端面17.0 mm,刃长10 mm,刀杆直径10 mm,如图 8所示。
 |
| 图 7 叶轮模型 Fig. 7 Impeller model |
| 图选项 |
 |
| 图 8 半对称鼓形刀刃口母线尺寸 Fig. 8 Generatrix dimensions of semi-symmetric drum-like cutting edge |
| 图选项 |
设置叶盆、叶背每行各离散80个采样点,残留高度0.02 mm,以等参数的方式进行刀轨规划。算法求得半联动轴B、C角度分别为-20°和57°,刀轨行数共17行。其中叶背加工刀轨的刀轴矢量端点的空间分布如图 9所示,从图中可看出所有的刀轴矢量端点落在与X轴垂直的平面上,该矢量范围证明了所有的刀轴矢量皆在同一个锥面上。
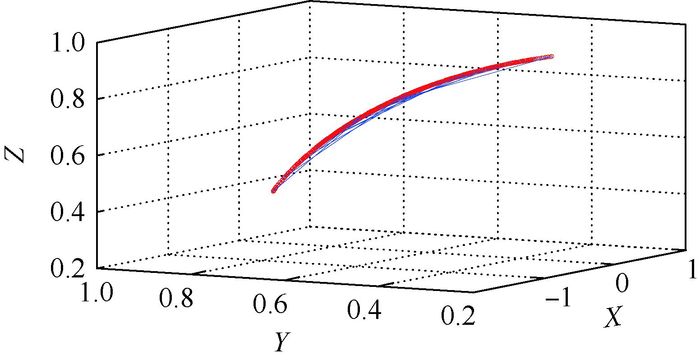 |
| 图 9 叶背刀轴矢量端点分布 Fig. 9 Distribution of tool axis vector endpoints on suction surface |
| 图选项 |
使用VERICUT软件进行仿真验证,图 10为使用VERICUT软件的仿真结果。仿真后发现无过切现象、无干涉发生,欠切量全部在公差范围以内,图 11为局部欠切仿真放大视图。
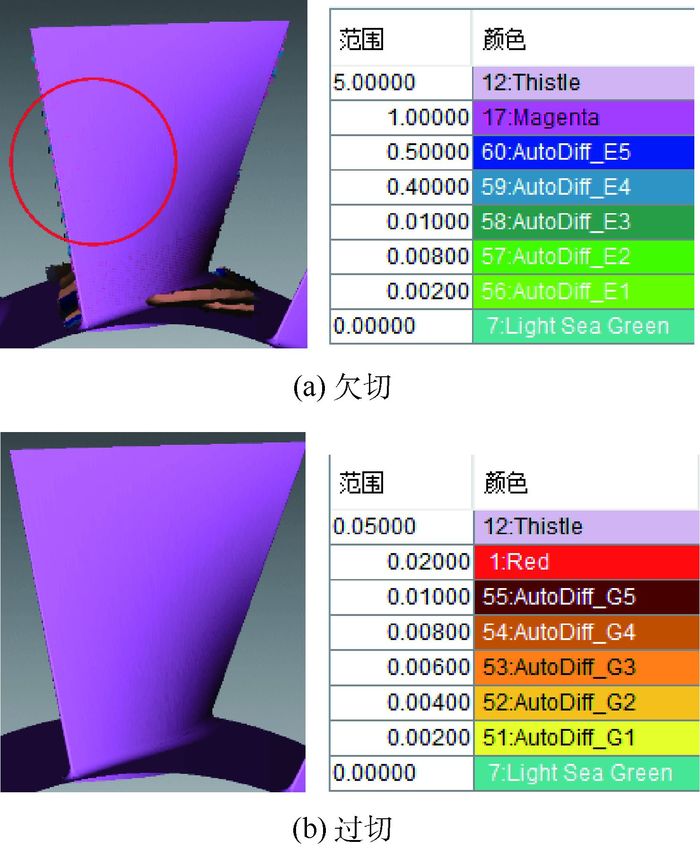 |
| 图 10 VERICUT切削仿真结果 Fig. 10 Cutting simulation result with VERICUT |
| 图选项 |
 |
| 图 11 欠切仿真局部放大视图 Fig. 11 Partial enlarged view of undercut simulation |
| 图选项 |
实际加工实验中,将万向铣头安装在4轴机床上,测得实际刀具摆长,将万向铣头按计算出的B、C参数进行调整,最后用4+2轴后置处理算法对刀轨进行后置处理。叶轮的实际加工过程和结果照片如图 12所示。仿真和加工结果说明,4+2轴加工刀轨正确、可用,使用4+2轴加工方法加工叶轮叶片的方案是可行的。
 |
| 图 12 加工过程和实验结果 Fig. 12 Machining process and experimental results |
| 图选项 |
目前本文的重点在于实现4+2轴加工方法,论证其可行性。在未来的研究中,须对4+2轴加工中的A轴光顺问题和分区加工问题进行优化和研究。通过可行域分析的方法可对A轴运动进行光顺处理。通过优化加工参数和刀轨生成策略,未来零件的加工质量和效率可以有更好的提升。
4 结论 1) 提出一种新的多轴数控加工方法。该方法通过在4轴机床的基础上添加2个半联动轴实现,并根据实际机床模型构建了机床的理论结构,并分析了其运动模型,推导出了机床运动求解公式。
2) 提出2个半联动轴姿态的确定方法,并使用4+2轴加工方法对某叶轮进行加工。仿真及实际加工结果表明,由4+2轴加工方法生成的刀轨正确可用,使用4+2轴加工方法加工叶轮叶片的方案是可行的。
3) 本文的刀轴矢量有一定的局限性,未来可求每一个切触点处的刀轴矢量可行域,并根据可行域进行半联动轴参数的优化寻找。另外对于4+2轴加工的刀轨光顺、4+2轴分区加工方法、4+2轴加工叶轮工艺参数优化等问题,尚有待进一步的研究。
参考文献
| [1] | 宋春华. 数控技术的现状及发展趋势[J].装备制造技术, 2011(3): 114–117. SONG C H. Status and developing trend of NC technology[J].Equipment Manufacturing Technology, 2011(3): 114–117.(in Chinese) |
| [2] | 程奎. 四轴数控机床运动分析及加工应用研究[D]. 西安: 西安理工大学, 2010. CHENG K.Motion analysis and processing application research of four-axis numerical control machine tool[D].Xi'an:Xi'an University of Technology, 2010(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10700-2010141110.htm |
| [3] | 曾志迎. 复杂曲面的五坐标数控加工关键技术研究[D]. 太原: 太原科技大学, 2012. ZENG Z Y.The key research on five-axis NC machining technology of complex curved surface[D].Taiyuan:Taiyuan University of Science & Technology, 2012(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10109-1012427015.htm |
| [4] | 王晶, 张定华, 罗明, 等. 复杂曲面零件五轴加工刀轴整体优化方法[J].航空学报, 2013, 34(6): 1452–1462. WANG J, ZHANG D H, LUO M, et al. A global tool orientation optimization method for five-axis CNC machining of sculptured surfaces[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1452–1462.(in Chinese) |
| [5] | 修春松, 安鲁陵, 戚家亮. 整体叶轮鼓形刀五坐标数控加工刀位轨迹生成[J].机械制造与自动化, 2011, 40(4): 165–168. XIU C S, AN L L, QI J L. Tool path strategy for integrated impeller using barrel cutter in 5-axis NC system[J].Machine Building & Automation, 2011, 40(4): 165–168.(in Chinese) |
| [6] | 金曼, 张俐, 陈志同. 圆环面刀具五坐标加工端点误差控制刀位优化[J].北京航空航天大学学报, 2006, 32(9): 1125–1128. JIN M, ZHANG L, CHEN Z T. End-points error controlling method for torus tool position optimization in five-axis NC machining[J].Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(9): 1125–1128.(in Chinese) |
| [7] | 石巍, 宁涛, 陈志同. 环面工具加工叶根过渡曲面的刀位可行域[J].航空学报, 2014, 35(12): 3470–3479. SHI W, NING T, CHEN Z T. Research on feasible area of torus tool position in machining of blade root area and its application[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3470–3479.(in Chinese) |
| [8] | SUH H S, LEE J. Five-axis part machining with three-axis CNC machine and indexing table[J].Journal of Manufacturing Science and Engineering, 1998, 120(1): 120–128.DOI:10.1115/1.2830087 |
| [9] | SUH S H, LEE J J, KIM S K. Multiaxis machining with additional-axis NC system:Theory and development[J].The International Journal of Advanced Manufacturing Technology, 1998, 14(12): 865–875.DOI:10.1007/BF01179075 |
| [10] | 朱燏, 宁涛, 陈志同. 圆柱坐标数控机床加工整体叶轮的运动学分析[J].航空学报, 2014, 35(8): 2364–2374. ZHU Y, NING T, CHEN Z T. Kinematic analysis of cylindrical coordinate CNC machine in integral impeller machining[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2364–2374.(in Chinese) |
| [11] | 韩飞燕, 张定华, 吴宝海, 等. 高缠绕叶轮流道4+1轴高效分段开槽方法[J].航空学报, 2015, 36(5): 1684–1694. HAN F Y, ZHANG D H, WU B H, et al. High-efficiency section-by-section method for 4+1-axis NC machining of high-wrap impeller channel[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1684–1694.(in Chinese) |
| [12] | 吴宝海, 王尚锦. 自由曲面叶轮的四坐标数控加工研究[J].航空学报, 2007, 28(4): 993–998. WU B H, WANG S J. Research on 4-axis numerical control machining of free form surface impellers[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(4): 993–998.(in Chinese) |
| [13] | ZHU Y, CHEN Z T, NING T, et al. Tool orientation optimization for 3+2-axis CNC machining of sculptured surface[J].Computer-Aided Design, 2016, 77. |
| [14] | 陈东祥, 肖延萍, 沈兆光, 等. 万向转头机构的旋转定位算法[J].机械设计, 2004, 21(11): 55–56. CHEN D X, XIAO Y P, SHEN Z G, et al. Rotating positioning algorithm of universal head mechanism[J].Machine Design, 2004, 21(11): 55–56.DOI:10.3969/j.issn.1001-2354.2004.11.021(in Chinese) |
| [15] | 李正强, 陈志同, 肖俊. 鼓形刀宽行刀位优化纬线分割算法[J].北京航空航天大学学报, 2007, 33(6): 731–735. LI Z Q, CHEN Z T, XIAO J. Latitude distribution algorithm of cutter position optimization on drum-like cutter for strip-maximization[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(6): 731–735.(in Chinese) |
| [16] | 孟凡军, 陈志同, 宁涛, 等. 基于纬线法的鼓形刀具刀位误差分布计算[J].航空学报, 2015, 36(12): 4014–4024. MENG F J, CHEN Z T, NING T, et al. Calculation of tool position error distribution of barrel cutter based on latitude approach[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 4014–4024.(in Chinese) |
| [17] | 陈果, 陈志同. 复杂母线鼓形刀具宽行侧铣加工算法[J].航空精密制造技术, 2010, 46(5): 34–38. CHEN G, CHEN Z T. Flank milling with complex generatrix barrel cutter[J].Aviation Precision Manufacturing Technology, 2010, 46(5): 34–38.(in Chinese) |
| [18] | 杨志强. 基于UG二次开发的数控加工刀具轨迹生成系统的研究[D]. 沈阳: 沈阳工业大学, 2007. YANG Z Q.Tool-path programming research based on UG redevelopment in NC machining[D].Shenyang:Shenyang University of Technology, 2007(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10142-2008204182.htm |
