目前,国内外许多****都对其进行了分析。徐颖[2]提出了含初始冲击损伤层合板疲劳逐渐累积损伤的寿命预测方法,试验结果表明,该方法能够较好地预测含初始冲击损伤层合板在疲劳载荷作用下的损伤累积扩展以及疲劳寿命。李伟占[3]、施志凯[4]和鲁国富[5]利用有限元软件对复合材料层合板进行损伤渐进失效模拟分析。近年来,由于神经网络应用领域的不断扩大,Schulz等[6]将其引入到复合材料层合板损伤状态监测领域。利用传感器来模拟“细胞”,构建结构损伤状态监测,并通过试验及研究,实现了通过神经网络来诊断冲击损伤的发生。Kirikera等[7]通过对复合材料进行多次试验,并利用传感器网络获取的数据建立了一个预测剩余强度及疲劳寿命的经验公式,为复合材料损伤预测的发展起到了积极的作用。
针对含冲击损伤的飞机复合材料机翼盒段,本文采用布置在机翼盒段上的光纤光栅应变传感器网络所获取的应变信息作为原始信息,对应变信息采用基于多元经验模态分解(Multivariate Empirical Mode Decomposition,MEMD)的能量熵方法进行特征提取。由于飞机复合材料机翼盒段出现损伤的位置无法预知,因此采用动态主元分析法(Dynamic Principal Component Analysis,DPCA)对特征信息进行降维融合,对提取的特征信息即融合后的能量熵采用极限学习机(Extreme Learning Machine,ELM)进行线性回归建模,实现飞机复合材料机翼盒段健康状态预测研究。
1 特征提取原理 1.1 多元经验模态分解 经验模态分解(Empirical Mode Decomposition,EMD)存在明显的模态混叠及尺度对齐问题,MEMD不仅克服了以上问题,而且具备了更好的自适应性与时频局部化能力[8-10]。其分解过程如下:
原始信号为z(t)=[z1(t), z2(t), …, zM(t)],M为同一时刻原始信号的维度,即信号采集的个数,vn=[v1n, v2n, …, vnM]为原始信号z(t)的第n个向量。
步骤1?求取方向向量集V。
步骤2?求取获取的原始信号即z(t)在每一个方向向量vk(k=1, 2, …, l)上的投影集,即Pk(t)(k=1, 2, …, l),l为方向向量个数。
步骤3?查找并记录每个投影集Pk(t)(k=1, 2, …, l)中的投影极大值与之相对应的时间刻度{tik}。
步骤4?对所有的{tik, z(tik)}数据进行拟合,求其包络线{Ek(t)}。
步骤5?计算所有包络线的均值C(t)=
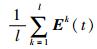
步骤6?获取低频信号D(t)=Z(t)-C(t),对D(t)进行判断,是否满足多本征模态函数(Multivariate Intrinsic Mode Function,MIMF)条件。如果满足,则D(t)为第1个MIMF分量,记为mimf1;若不满足,将D(t)作为原始信号重复步骤1~步骤5,直至D(t)满足MIMF条件为止。
求其剩余向量r(t)=Z(t)-D(t),并将剩余向量作为原始信号重复步骤1~步骤6,得到mimf2,多次重复直至满足MIMF停止条件,最终获得MIMF分量。
1.2 能量熵特征提取 当飞机结构出现不同损伤时,光纤传感器采集的应变信息的能量分布会发生变化,不同状态下所产生的应变信号的能量频率分布不同,这就需要一种评判能量大小的标准,为此引入能量熵概念。在MEMD分解的基础上,计算各个MIMF的能量分布,然后通过MIMF分量求其能量分布,最后求其能量熵。具体步骤如下[11]:
步骤1?MEMD自适应分解。采用MEMD算法对传感器获取信号进行自适应分解,将得到的各阶MIMF分量和残余分量由高到低排列。
步骤2?能量分布求解。由于原始信号的总能量与经过MEMD分解后获得MIMF各频段的能量之和相同,由高到低排列的不同频段包含的能量不相同,因此原始信号的能量分布可以根据不同频段能量进行划分。求解公式如下:
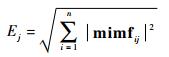 | (1) |
式中:j为原始数据MEMD分解后MIMF分量的个数; n为第j个MIMF分量的数据长度。如果原始信号经MEMD分解过后得到m个MIMF分量,则其能量分布可表示为T=[E1, E2, …, Em]。
步骤3?能量熵求解。基于能量分布的求解,采用更加有效的能量熵作为不同损伤状态的特征表征量,求解公式如下:
 | (2) |
式中:pi=Ei/E(i=1, 2, …, m)表示第i个MIMF分量的能量在总能量E中的比重,总能量E=

1.3 基于DPCA的特征融合 传统的主元分析法(Principal Component Analysis,PCA)认为变量之间都是没有相互关系的,然而复合材料试验件疲劳加载过程中传感器获取的特征信息之间存在着时间的延续性。为了高效获取损伤状态特征信息[12-14],本文采用DPCA对4个传感器获取的特征信息进行特征层降维融合。
DPCA核心思想为:采用前S时刻的每一个变量使之变成增广矩阵变量,为了消除变量之间的相关性,用PCA对其进行降维。DPCA计算流程如下[15]。
步骤1?增广矩阵构造。试验件在进行冲击后疲劳加载,传感器网络获取特征信息后,由此特征信息组成的原始矩阵记为X,表达式如下:
 | (3) |
式中:m为监测变量个数即传感器个数;n为每个监测变量中观测值的个数,即每个传感器获取特征信息的个数;xti∈Rm(i=1, 2, …, n)为m维的观测向量。
由于DPCA理论知识中变量当前值与过去值相关,因此用过去时刻的观测向量对现在时刻的观测向量进行扩充构建增广矩阵,式(4) 对时间t前的h个观测向量进行扩充构建增广矩阵。
 | (4) |
式中:xTt与式(3) 中的xti相同,即t时刻m维的观测向量;h为滞后长度。
步骤2?滞后长度的确定。在进行DPCA分析过程中,滞后长度起着关键性作用,本文采用平行分析方法对滞后长度进行计算,其具体步骤如下:
1) 计算静态情况,即令h=0。此情况下,静态关系数为变量数减去主元个数差的绝对值。
2) 计算动态关系数,即令h=1,此情况下,动态关系数为变量数与主元个数和1) 中计算的静态关系数之差。
3) 计算动态关系数,即当h从1开始不断递增时,动态关系数满足以下递推关系:
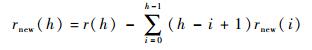 | (5) |
直至rnew(h)≤0,即静态和动态关系不再变化为止。
步骤3?对式(4) 中获得的增广矩阵X(h)进行标准化处理,即均值为0、方差为1的标准化处理,最终得到矩阵
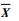
步骤4?计算矩阵
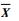
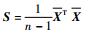
步骤5?通过协方差矩阵S计算其特征值[λ1, λ2, …, λm]T及特征向量[q1, q2, …, qm]。
步骤6?主元个数确定的计算公式为CPV=
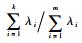
步骤7降维融合后的特征信息为前k个特征值对应的特征向量。
2 极限学习机预测模型 极限学习法的输入层节点数是由单隐含层前馈神经网络(Single-hidden Layer Feedforward Neural Network,SLFN)算法计算得到,建模过程中不需要对其进行设置,只需要对隐含层的神经元个数进行设置即可,且能够找到唯一的最优解。SLFN与传统的前馈神经网络相比,不仅泛化性能好且学习效率高。以下为基于ELM的预测模型表达式[16]:
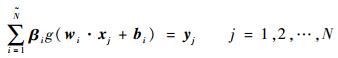 | (6) |
式中:bi=[bi1, bi2, …, bim]T为第i个隐含层的阈值;βi=[βi1, βi2, …, βim]T为第i个隐含层与输出层之间的权值;wi=[wi1, wi2, …, win]T为第i个输入层与隐含层之间的权值;wi·xj为内积;g(x)为激活函数;

图 1为SLFN的结构图。
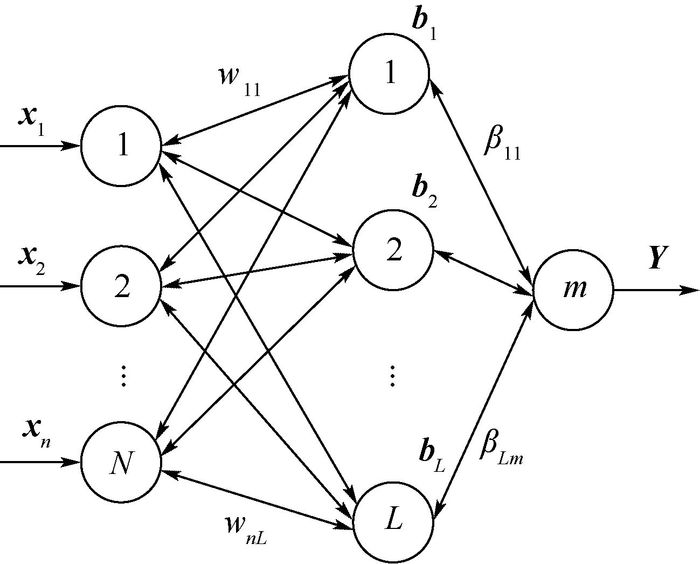 |
| 图 1 SLFN结构图 Fig. 1 Structure chart of SLFN |
| 图选项 |
基于ELM的预测模型的求解过程如下。
假设给定的样本集为N,其表达式如下[17-18]:
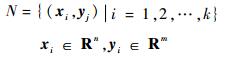 | (7) |
式中:xi=[xi1, xi2, …, xin]T为输入样本向量,xi∈Rn中的n为输入样本向量的个数;yi=[yi1, yi2, …, yim]T为输出样本向量,yi∈Rm中的m为输出样本向量个数。具有
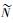
 | (8) |
式中:

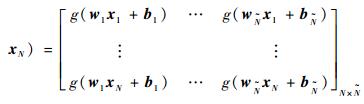
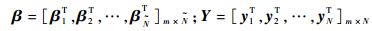
H矩阵的第i列对应第i个隐含层节点的输出。
为了构建性能优良的SLFN模型,
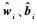
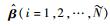
 | (9) |
从中可知,当

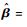
若训练集、激活函数、隐含层个数给定,则根据以上理论可归纳出ELM预测模型的3个求解步骤:对权值及阈值进行随机赋值;计算H矩阵;计算β,由Hβ=Y进行预测。
3 健康状态预测 在复合材料结构损伤预测过程中,采用MEMD方法对募集到的应变信号进行分解,并提取能量熵,将融合后能量熵作为特征量,采用ELM预测模型,实现飞机健康状态预测。具体步骤如下:
步骤1?结构状态原始信息获取。利用光纤传感器网络获取应变值。本文采用表面贴式元件网络,在飞机复合材料机翼盒段表面激发主动监测信号,并在同一表面的其他4个地方接收结构响应信号。
步骤2?特征提取。结合高效的信息处理方法,对健康状态信息进行特征提取。本文采用的特征提取方法为基于MEMD分解的能量熵的特征提取。
步骤3?构建预测模型并预测。创建基于ELM的、以融合后的能量熵作为建模数据的健康状态预测模型,然后输入数据进行健康状态预测。
步骤4?计算预测精度并修正模型。分别采用均方根误差σMSE及平均相对误差σARE作为评判标准计算预测精度,如果结果满足工程标准即误差小于20%,则输出预测结果,否则,更正模型参数以修正模型,再次进行预测直到达到工程标准。
具体结构损伤预测方案如图 2所示。
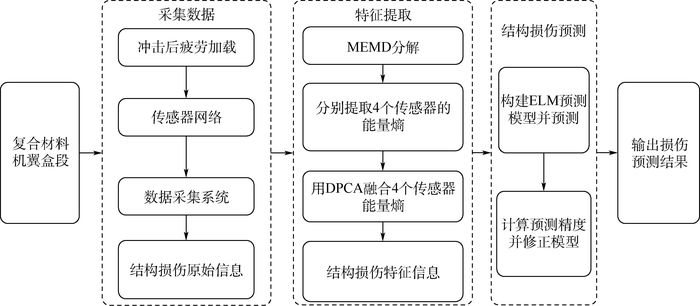 |
| 图 2 结构损伤预测方案 Fig. 2 Prediction scheme of structural damage |
| 图选项 |
4 试验验证 以某型飞机复合材料机翼盒段为具体研究对象,在试验条件下进行结构损伤预测试验验证。机翼盒段复合材料层合板铺层角度为[45/-45/0/-45/0/45/0/90/0/45/-45/0]s,共24层,单层厚度0.18 mm,共4.32 mm。对试验件进行冲击后的疲劳加载试验,即对试验件A面蒙皮及梁上共进行5处冲击,在试验件B面蒙皮加载疲劳载荷,如图 3所示。最大疲劳载荷4 kN,加载频率2 Hz,传感器采样频率20 Hz。共进行120万次疲劳加载循环,每隔2万次进行无损检测,并用由4个光纤传感器组成的传感器网络采集应变值。因位于梁上的冲击损伤扩展最快,故以此为例进行详细说明。梁上冲击损伤位置及传感器布置如图 4所示。
 |
| 图 3 疲劳加载试验 Fig. 3 Test of fatigue loading |
| 图选项 |
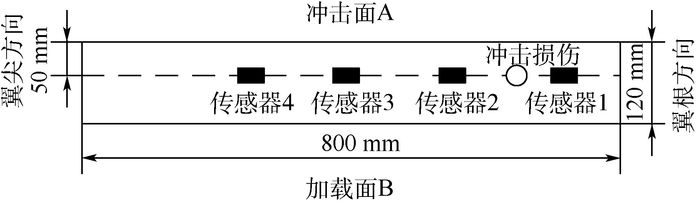 |
| 图 4 机翼盒段梁上冲击损伤位置及传感器布置 Fig. 4 Impact damage location and sensor placement on beam of aircraft wing box section |
| 图选项 |
4.1 飞机机翼特征提取
4.1.1 飞机机翼原始信息MEMD分解 试验每隔2万次疲劳加载,进行一次无损检测并记录损伤形式,每次无损检测记录24次疲劳加载的应变值,每次疲劳加载传感器采集10个应变值,即取每次无损检测后每个传感器采集的240个应变值作为一次损伤状态量进行MEMD分解。
因第42万次(即第21次无损检测)疲劳加载后,复合材料有明显分层损伤出现,故以第42万次疲劳加载后,传感器1获取的240个应变值进行MEMD分解为例,绘制图 5。
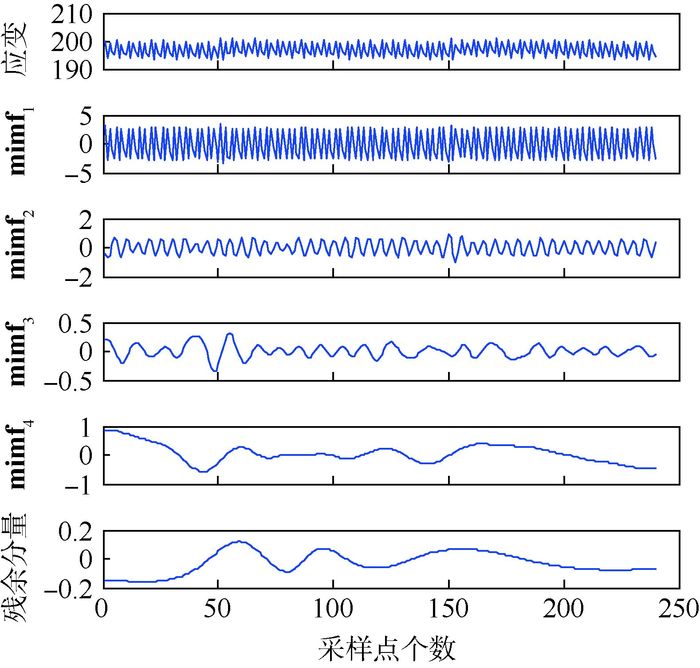 |
| 图 5 第42万次疲劳循环加载后传感器1数据MEMD分解 Fig. 5 Decomposition of data from Sensor 1 with MEMD after 420 000 times of cyclic fatigue loading |
| 图选项 |
如图 5所示,第42万次疲劳加载后传感器所获取的原始信号被分解为多个MIMF分量,由上至下按照从高频到低频排列,且不同损伤状态的MIMF分量不同。
4.1.2 飞机机翼状态信息能量熵特征提取 以每次无损检测后4个传感器分别采集的240个应变值为一组,试验件从好到坏共测得的60组应变数据,进行MEMD分解,求其各阶MIMF分量。由于每组数据共采集24次疲劳加载循环,对于整体的疲劳加载循环来说微乎其微,且每组数据只能求得一个能量熵值,因此将每组求得的能量熵值与这组数据的第1个循环次数相对应。图 6为4个传感器获取原始应变数据从初始损伤、损伤扩展到损伤失效提取的能量熵特征。
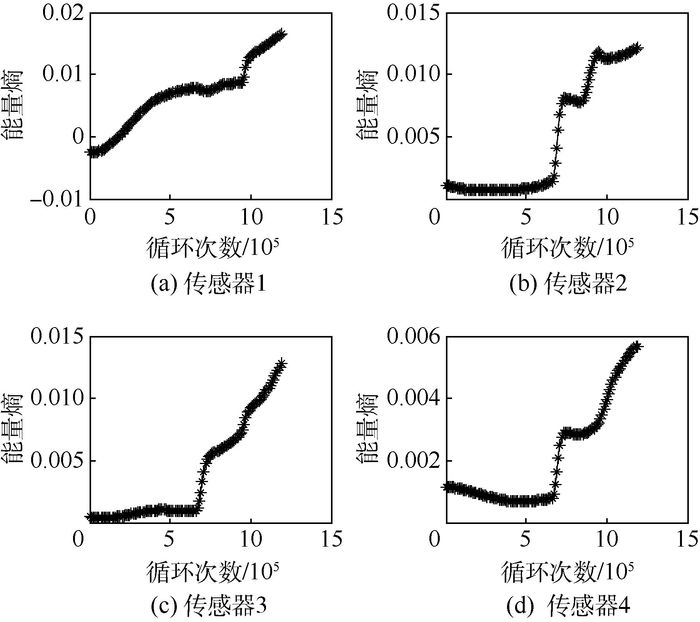 |
| 图 6 4个传感器对应能量熵特征趋势分析 Fig. 6 Energy entropy feature trend analysis corresponding to four sensors |
| 图选项 |
4.1.3 能量熵特征融合 从图 6中可以看出,随着损伤的不断扩展直至失效,4个传感器获取的能量熵特征信息趋势均能很好地表现损伤过程,然而疲劳加载过程中损伤位置无法预测,因此不能人为判断采用哪个传感器采集的特征信息作为后期的预测数据。为了更加有效地提取能够表征飞机复合材料机翼盒段损伤状态特征量,对4个传感器采用的信息进行降维融合。将降维融合后获得的特征信息作为最终表征飞机复合材料机翼盒段损伤状态特征量。图 7为4个传感器采集的原始应变数据的能量熵特征信息降维融合。
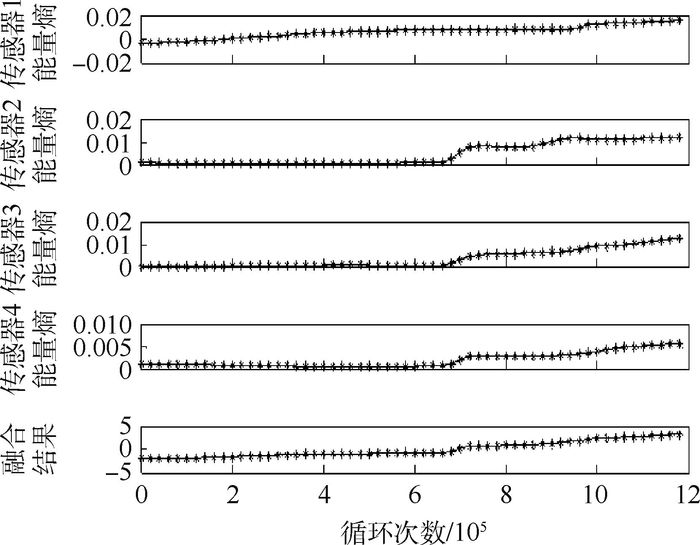 |
| 图 7 能量熵特征融合结果 Fig. 7 Results of energy entropy feature fusion |
| 图选项 |
4.2 飞机机翼健康状态预测 根据提取的特征信息即融合后的能量熵可以看出,随着疲劳循环次数的增加,损伤在不断扩展,且特征提取的能量熵也呈现不断增大的趋势,能够很好地表征健康状态变化情况。
采用ELM方法对能量熵进行预测建模时,根据专家经验及建模试验效果,选取重构个数为5,构建预测模型输入样本集,即
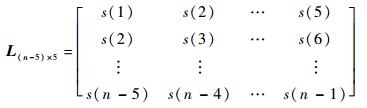 |
预测模型的输出样本集为
 |
根据建模试验效果,动态建模过程中每次建模数据选取51组(含输入和输出数据),每组数据包含输入模型的5个数据,以及对应模型输出的1个数据,即以第1~51组数据建模时模型输入为
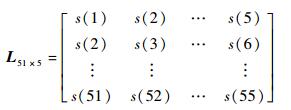 |
模型输出为
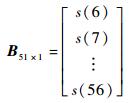 |
其中, 矩阵L的每一行数据为模型的一组输入数据,矩阵B的每一行数据为模型对应的输出数据,由矩阵L与B便可构建预测模型。用所构建的预测模型进行测试时,以第52、53组数据作为预测模型的输入数据,即XL2×5=
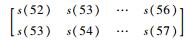
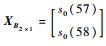

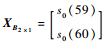
 |
| 图 8 基于融合能量熵的机翼盒段健康状态预测 Fig. 8 Health state prediction of aircraft wing box section based on fused energy entropy |
| 图选项 |
试验件在疲劳加载进行到第120万次时,梁上复合材料11~14层,层间分层损伤长度急剧增加,对应此时提取的能量熵为3.283 0,依据试验确定其为失效阈值,高于该阈值则认为损伤失效。图 8为基于能量熵的飞机复合材料机翼盒段健康状态预测结果。
从图 8中可知,在疲劳加载至116万次循环时,预测得到的118万次疲劳加载循环时的特征值为3.385 0,已经非常接近于3.283 0损伤失效阈值线,可认定为疲劳加载118万次时损伤失效,而真实的损伤失效是在疲劳循环加载到120万次损伤失效,为了验证其预测效果的优异程度,本文采用均方根误差σMSE及平均相对误差σARE来作为评判标准,表达式如下:
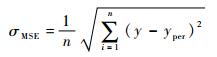 | (10) |
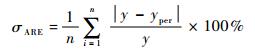 | (11) |
式中:y为真实能量熵值;yper为预测得到的能量熵值;n为预测数据的个数。
经计算,基于能量熵的预测误差σMSE=0.015 8,σARE=1.832 9%,满足预测误差小于20%的工程需求。
5 结论 本文提出了一种基于MEMD和ELM的飞机机翼健康状态预测方法。
1) 对传感器采集的原始应变数据采用MEMD方法,并提取能量熵。提取的特征信息能够很好地表征飞机复合材料机翼盒段损伤不断扩展信息,证明了其有效性与可行性。
2) 采用DPCA方法对4个传感器获取的特征信息进行降维融合,将降维融合后的特征信息作为飞机复合材料机翼盒段损伤状态特征量用于预测。试验表明,采用DPCA方法融合后的特征信息更能高效地表征飞机复合材料机翼盒段损伤状态。
3) 采用ELM方法对提取融合后的能量熵值进行建模预测。将预测得到的特征值与失效阈值相对比,越接近失效值,损伤越严重甚至失效。试验表明,ELM所创建的模型均能很好地对飞机复合材料机翼盒段健康状态进行预测。
参考文献
| [1] | 郑锡涛, 李泽江, 李光亮. 含损伤复合材料层合板剩余压缩强度研究进展[J].宇航材料工艺, 2011, 41(3): 20–26. ZHENG X T, LI Z J, LI G L. Advance of study on residual compressive strength of damaged composite laminates[J].Aerospace Material & Technology, 2011, 41(3): 20–26.(in Chinese) |
| [2] | 徐颖. 复合材料层合板冲击损伤及冲击后疲劳寿命研究[D]. 南京: 南京航空航天大学, 2007: 108-123. XU Y.Research on impact damage of laminates and fatigue life of impacted laminates[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2007:108-123(in Chinese). |
| [3] | 李伟占. 复合材料层合板损伤失效模拟分析[D]. 哈尔滨: 哈尔滨工程大学, 2012: 29-55. LI W Z.Progressive damage analysis of composite laminates[D].Harbin:Harbin Engineering University, 2012:29-55(in Chinese). |
| [4] | 施志凯. 热力耦合下复合材料层合板渐进性损伤分析[D]. 大连: 大连理工大学, 2013: 43-60. SHI Z K.Progressive damage analysis of laminated composite under thermal-mechanical coupling load[D].Dalian:Dalian University of Technology, 2013:43-60(in Chinese). |
| [5] | 鲁国富. 直升机复合材料桨叶疲劳研究[D]. 南京: 南京航空航天大学, 2010: 59-71. LU G F.Research on fatigue progressive damage analysis method for composite of helicopter blade[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2010:59-71(in Chinese). |
| [6] | SUNDARESAN M J, SCHULZ M J, GHOSHAL A, et al.A neural system for structural health monitoring[C]//Proceedings of SPIE, Smart Structures and Materials.Bellingham, WA:SPIE, 2001, 4328:130-141. |
| [7] | KIRIKERA G, DATTA S, SCHULZ M J, et al.Recent advances in an artificial neural system for structural health monitoring[C]//Proceedings of the SPIE, NDE and Health Monitoring of Aerospace materials and Composites Ⅱ.Bellingham, WA:SPIE, 2003:152-163. |
| [8] | 刘源. 基于多元EMD的BCI信号处理研究[D]. 秦皇岛: 燕山大学, 2013: 22-39. LIU Y.Study on signal processing of BCI based on multivariate empirical mode decomposition[D].Qinhuangdao:Yanshan University, 2013:22-39(in Chinese). |
| [9] | 张毅, 周春雨, 罗元. 基于MEMD的运动想象脑电信号的特征提取与分析[J].重庆邮电大学学报(自然科学版), 2015, 27(3): 386–391. ZHANG Y, ZHOU C Y, LUO Y. Feature extraction and analysis of imaginary movements in EEG based on MEMD[J].Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2015, 27(3): 386–391.DOI:10.3979/j.issn.1673-825X.2015.03.016(in Chinese) |
| [10] | 武哲, 杨绍普, 刘永强. 基于多元经验模态分解的旋转机械早期故障诊断方法[J].仪器仪表学报, 2016, 37(2): 241–248. WU Z, YANG S P, LIU Y Q. Rotating machinery early fault diagnosis method based on multivariate empirical mode decomposition[J].Chinese Journal of Scientific Instrument, 2016, 37(2): 241–248.(in Chinese) |
| [11] | 张超. 基于自适应振动信号处理的旋转机械故障诊断研究[D]. 西安: 西安电子科技大学, 2012: 26-43. ZHANG C.Fault diagnosis research of rotating machinery based on adaptive processing of vibration signal[D].Xi'an:Xidian University, 2012:26-43(in Chinese). |
| [12] | 张超, 陈建军, 郭迅. 基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击, 2010, 29(10): 216–220. ZHANG C, CHEN J J, GUO X. A gear fault diagnosis method based on EMD energy entropy and SVM[J].Journal of Vibration and Shock, 2010, 29(10): 216–220.DOI:10.3969/j.issn.1000-3835.2010.10.045(in Chinese) |
| [13] | 张超, 陈建军, 郭迅. 基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J].中南大学学报(自然科学版), 2012, 43(3): 932–939. ZHANG C, CHEN J J, GUO X. Gear fault diagnosis method based on ensemble empirical mode decomposition energy entropy and support vector machine[J].Journal of Central South University (Science and Technology), 2012, 43(3): 932–939.(in Chinese) |
| [14] | 石怀涛, 刘建昌, 丁晓迪, 等. 基于混合动态主元分析的故障检测方法[J].控制工程, 2012, 19(1): 148–151. SHI H T, LIU J C, DING X D, et al. Fault detection based on hybrid dynamic principal component analysis[J].Control Engineering of China, 2012, 19(1): 148–151.(in Chinese) |
| [15] | 钟丽丽. 基于动态主元分析的故障诊断研究[D]. 青岛: 青岛科技大学, 2013: 18-21. ZHONG L L.Research on fault dlagnosis of dynamic principle component analysis[D].Qingdao:Qingdao University of Science & Technology, 2013:18-21(in Chinese). |
| [16] | 李磊. 基于极限学习机的风机机械传动部件剩余寿命预测研究[D]. 秦皇岛: 燕山大学, 2015: 20-36. LI L.Residual life prediction research for mechanical drive components of wind turbing based on extreme learning machine[D].Qinhuangdao:Yanshan University, 2015:20-36(in Chinese). |
| [17] | 李培. 基于PCA-ELM的预测模型在煤矿突水预测中的应用[D]. 徐州: 中国矿业大学, 2014: 18-26. LI P.The application of forecasting model based on PCA-ELM in coal mine water burst prediction[D].Xuzhou:China University of Mining & Technology, 2014:18-26(in Chinese). |
| [18] | 潘华贤, 程国建, 蔡磊. 极限学习机与支持向量机在储层渗透率预测中的对比研究[J].计算机工程与科学, 2010, 30(2): 131–134. PAN H X, CHENG G J, CAI L. Comparison of the extreme learning machine with the support vector machine for reservoir permeability prediction[J].Computer Engineering & Science, 2010, 30(2): 131–134.(in Chinese) |
