近些年来,国内外研究者对这种与颤振相关的非定常流动现象做过大量的参数化研究,包括叶片间相位角(Inter Blade Phase Angle,IBPA)、折合频率、振动模态、叶尖间隙、激波等。Lane[2]根据行波理论定义的叶片间相位角,描述振动的叶片间存在的相互气动干涉,是叶盘振动节径的表征量。Carta和St Hilaire[3-4]通过实验研究了叶片间相位角、迎角、折合频率等参数对发动机叶片气动弹性稳定性的影响。另外,叶片振动模态对颤振边界的影响很大,张小伟等[5]采用能量法发现振动模态通过影响叶片表面的非定常气动力使气动弹性稳定性发生改变。Bell和He[6]进行了三维涡轮叶栅弯曲振动下的非定常气动响应实验,首次研究了叶尖间隙对叶表非定常压力的影响,结果表明非定常压力幅值随间隙的变化规律一致。Isomura和Giles[7]指出通道激波对压力面有失稳作用,对吸力面有稳定作用;激波是否处于脱体位置是诱发颤振的重要条件。综上所述,大多数的叶片颤振研究都局限在单转子模型基础上。
随着对叶片颤振问题认识的加深,研究发现由于没有考虑上下游叶排对转子叶片非定常流动的影响,仅对单转子进行叶片颤振特性分析,有时会对叶片气弹失稳的算例得出气弹稳定的相反结论[8],所以叶排干涉与颤振之间关联性研究也逐渐兴起。Culver和Liu[9]研究结果表明加入导叶(Inlet Guide Vanes, IGV)之后跨声速压气机叶片扭转振型的气动弹性稳定性下降。而Huang等[10]对低压涡轮叶片扭转振型的颤振研究表明,上游静子叶排对转子气动弹性稳定性在不同节径下影响规律不一致。杨慧和李振鹏[11]用流固耦合法研究了转静干涉对三维压气机气动弹性稳定性的影响,结果表明导叶引起的非定常压力波反射使得弯曲振型的稳定性增强。上述结果表明上下游叶排对叶片气动弹性稳定性有着显著的影响,从而轴向间距成为****研究上下游叶排影响的关键因素。Li和He[12]使用单通道模型研究了跨音压气机气动弹性稳定性受转静叶排轴向间距的影响规律,结果表明转静叶排存在一个最优间距值,静子引起的干涉效应使得转子的稳定性最佳。杨慧和沈真[13]用能量法研究了上下游叶排对二维压气机转子弯曲颤振特性的影响,结果表明压气机转子上下游叶排在小的轴向间距下,使转子气动弹性稳定性降低。上述方法模型虽然给出了上下游叶排及对转子叶片颤振特性的影响以及最佳轴向间距的存在,但没有分析出转子叶片气动阻尼主要来源以及转子叶片表面非定常气动功变化的规律。影响系数法[14]是一种基于小振幅振动线性叠加的方法,量化每个叶片对叶栅整体非定常气动响应的贡献。北京航空航天大学杨慧等[15]采用影响系数法考虑叶尖间隙变化对压气机线性叶栅进行了气动弹性实验。实验结果表明:随着叶尖间隙的增加,间隙流对振动叶片有失稳影响,间隙流在叶栅稳定性最差时影响最显著。
本文使用影响系数法,考虑上游叶排轴向间距变化,分析弯曲振动的涡轮转子的气动弹性稳定性。首先,对转子叶片表面非定常压力进行傅里叶变换,分析轴向间距影响气动阻尼的规律;其次,对影响系数法在多排算例中的适用性进行了分析;最后,分析叶片表面非定常压力幅值和相位影响因素,进一步解释轴向间距影响转子叶片最小气动阻尼系数的机理,加深对叶片颤振问题的认识。
1 数值方法 1.1 控制方程 流场的数值模拟采用了自行开发程序HGAE,求解动边界和动态变形网格下的守恒型积分形式的三维非定常可压缩雷诺平均Navier-Stokes方程,其形式为
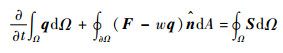 | (1) |
式中:?Ω、Ω和
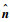
1.2 影响系数法 影响系数法是通过振动中间一个叶片来获得振动叶栅所有叶片间相位角下非定常气动响应数据的方法,简单高效,但不适用于非线性大分离流,有其局限性。其基本原理为:
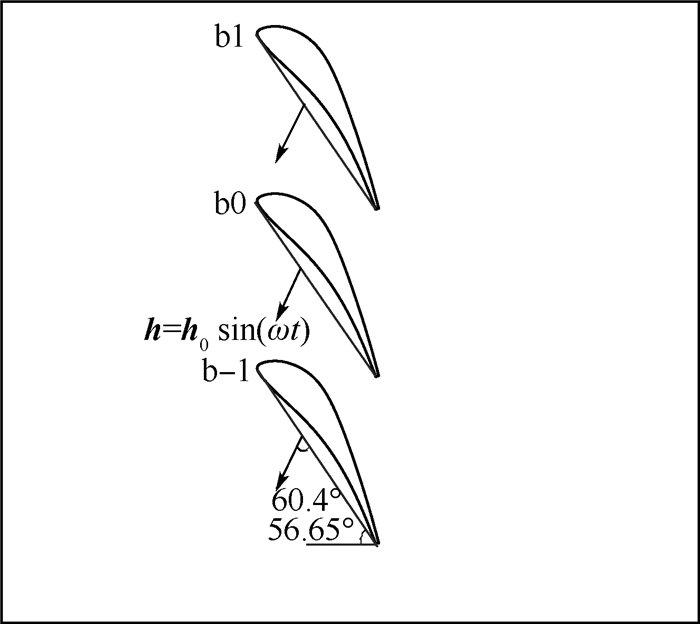
1) 协调叶栅所有叶片都是振动的,当不考虑叶片间相位角影响时,所有叶片都是一样的,某个叶片表面的非定常气动力相当于所有振动叶片对其影响的线性叠加;图 1是由2m+1个叶片组成的涡轮单转子叶片排(图 1中m=1),当所有叶片都振动时,参考叶片0(表示为b0)上无量纲非定常影响系数记为Cf0(此处以压力
 | (2) |
 |
| 图 1 转子叶栅几何示意图 Fig. 1 Geometric sketch map of rotor cascade |
| 图选项 |
因此获得叶片b0上由2m+1个振动叶片耦合后的非定常影响系数
 | (3) |
2) 只有叶片b0振动时,参考叶片b0的振动对叶片bn的影响系数,记为Cf(n, 0),系数可以通过实验或计算得出
 | (4) |
进一步得到
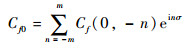 | (5) |
此方法的要点如下:非定常压力影响系数Cf(n, 0)称为"直接项",其通过量化每个叶片对整个叶栅非定常气动响应的贡献,来体现每个叶片的相对重要性。而影响系数Cf0称为"耦合项",为各个叶片气动阻尼之和。分解的"直接项"可以认识每个叶片的相对重要性,而"耦合项"能判断颤振起点,可以得到强迫响应中的阻尼项。由于叶片间相位角仅仅出现在后处理中不是计算参数,大大地缩减了获得所有叶片间相位角下振动叶栅气动阻尼的工作量。对影响系数法具体介绍参见文献[17]。
2 算例说明及定常验证 本文使用影响系数法进行气动弹性稳定性分析,转子叶栅共21个叶片(即m=10),其几何叶型选自气动弹性标准算例4[18],中间叶片b0的振动参数选自其二维亚声速工况[19]。标准算例4是三维的跨声速高负荷涡轮叶栅,叶片具有较大的厚度和弯角,容易产生气流分离,是现代典型的涡轮叶片造型,具有完整的实验数据,便于数值验证。实验采用了所有叶片全部振动的行波法,转子叶栅为协调叶栅,振动方向如图 1所示,其基本实验参数见表 1。
表 1 叶片几何和实验参数 Table 1 Blade geometry and experimental parameters
| 参数 | 数值 |
| 弦长/mm | 72 |
| 栅距/mm | 56.25 |
| 安装角/(°) | 56.65 |
| 振幅/(10-4m) | 3 |
| 振动方向/(°) | 60.4 |
| 振动频率/Hz | 149 |
| 折合频率 | 0.118 7 |
表选项
为了研究轴向间距对转子气动弹性稳定性的影响,在转子上游加入了类似薄平板的导叶。图 2为导叶-转子叶片单通道网格示意图,为了满足程序的计算要求,计算网格为边界层加密的非结构网格,保证第1层网格的y+在1.5以下,周期性边界采用了对接型网格设置。在转静交界面处,定常、非定常计算分别采用掺混面模型和滑移面模型。
 |
| 图 2 导叶-转子叶片单通道网格 Fig. 2 IGV-rotor blade single-passage grids |
| 图选项 |
本文选取了7个不同的轴向间距Δx以弦长c无量纲化(即Δx/c),分别为10%、15%、30%、50%、70%、90%、150%,轴向间距改变时转子通道的网格保持不变,针对不同间距生成导叶通道的网格。表 2为算例的边界条件,在计算时为了保证不同轴向间距下转子叶片表面的定常气动载荷基本一致,对转子出口的静压进行了微调。
表 2 边界条件 Table 2 Boundary conditions
| 参数 | 数值 |
| 进口总压/kPa | 160.9 |
| 进口总温/K | 317.8 |
| 出口静压/kPa | 101.3 |
| 出口气流角/(°) | -71.5 |
| 出口等熵马赫数 | 0.85 |
表选项
在非定常颤振计算之前,进行了定常验证。图 3为转子叶片表面定常压力系数Cp计算值和实验值的对比图,x为网格坐标。计算结果与实验数据基本符合,仅在压力面尾缘和吸力面0.3倍弦长处存在细微差异。
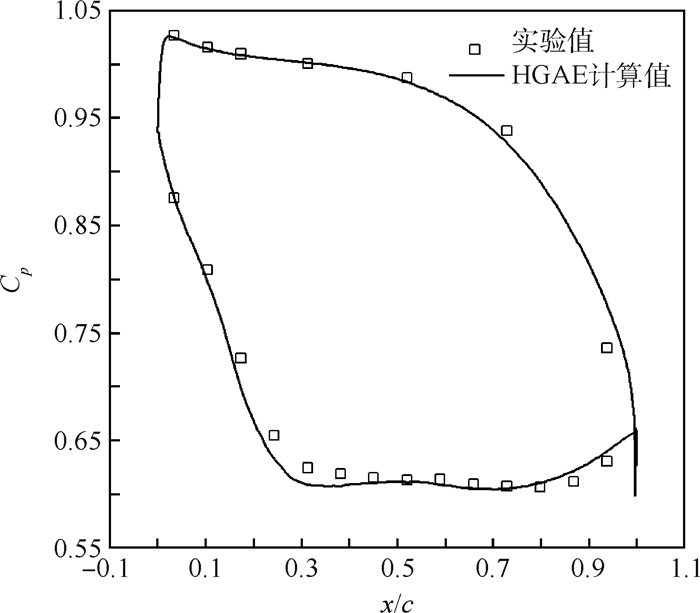 |
| 图 3 叶片表面定常压力系数分布 Fig. 3 Distribution of steady pressure coefficient on blade surface |
| 图选项 |
3 计算结果 非定常颤振分析以收敛的定常计算结果作为初场。取转子叶片振动周期为1个周期,每周期包含200个时间步,时间步长为3.355 704 698×10-5 s。
3.1 不同轴向间距对气动阻尼的影响 为了研究轴向间距对转子气动弹性稳定性的影响,首先进行了单转子颤振计算。图 4为不同轴向间距下转子叶片气动阻尼系数D随叶片间相位角σ的变化,从图中可以看出:单转子的最小气动阻尼值与实验值基本一致,说明影响系数法能准确预测最小气动阻尼系数以及其对应的叶片间相位角;轴向间距对气动阻尼系数的影响范围主要在气动弹性最不稳定状态对应的叶片间相位角附近;随着轴向间距的减小,最小气动阻尼系数对应的叶片间相位角明显左移(见图 4中红色箭头),即导叶使得气动弹性最不稳定点的节径增大;在最佳轴向间距下,导叶的影响可以使转子气动弹性稳定性提高32.04%,在工程应用中轴向间距对气动弹性稳定性的影响不可忽略。
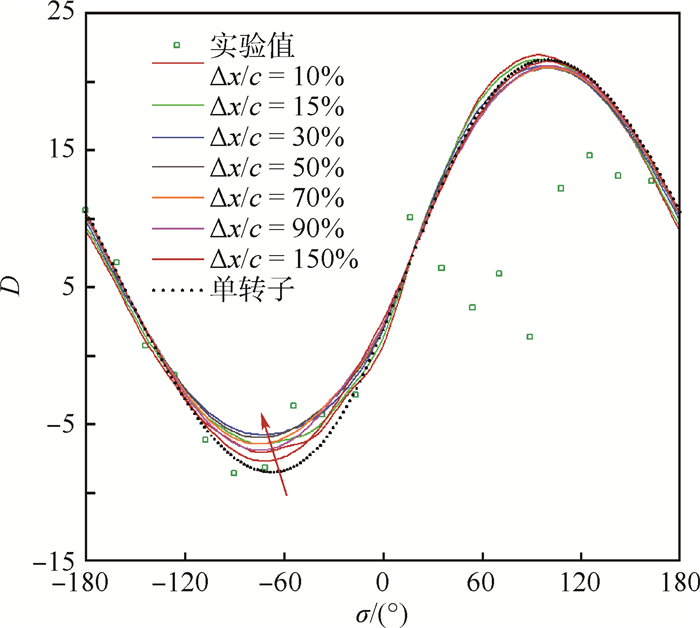 |
| 图 4 不同轴向间距下的气动阻尼系数 Fig. 4 Aerodynamic damping coefficient with different axial spacing |
| 图选项 |
3.2 确定影响转子叶片气动阻尼的关键叶片 通常研究人员最关注气动阻尼系数最小值处对应的叶片间相位角。图 5给出了单转子叶排在叶片间相位角为-72°时各叶片非定常气动阻尼系数分量,各分量之和为影响系数耦合项Cf0(见1.2节),图中b-1和b0气动阻尼系数分量最大,是转子叶片气动阻尼系数贡献最大的部分。可以看出,气动阻尼系数分量的数值随着与振动叶片周向距离的增加指数级的减小,比如b-2的气动阻尼系数大小只有b0的4.27%。
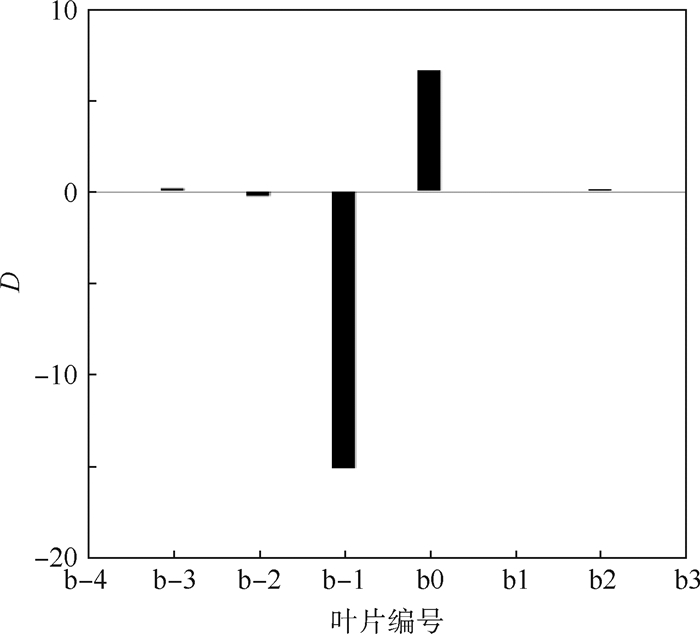 |
| 图 5 叶片间相位角为-72°时,单转子各叶片气动阻尼系数分量 Fig. 5 Each blade's aerodynamic damping coefficient component of single-rotor at inter blade phase angle equals to -72° |
| 图选项 |
图 6为有导叶时b-2~b2气动阻尼系数分量随Δx变化情况(孤立转子是以Δx/c=180%来表示)。从图 6可以看出:添加导叶之后,b-1和b0仍是构成气动阻尼系数的主要部分;影响系数Cf(0, -1)(表示在影响系数法中,叶片b0的振动对b-1气动阻尼系数的影响,见1.2节)的绝对值明显大于Cf(0, 0),并且影响系数Cf(0, -1)使得转子气动阻尼系数由正变为负,直接改变了转子气动弹性稳定性。上述结果表明:系数Cf(1, 0)(表示在协调叶栅中,叶片b1的振动对b0气动阻尼系数的影响,见1.2节)对转子气动阻尼系数的大小起决定性作用,其影响甚至超过振动叶片b0本身的影响Cf(0, 0)。
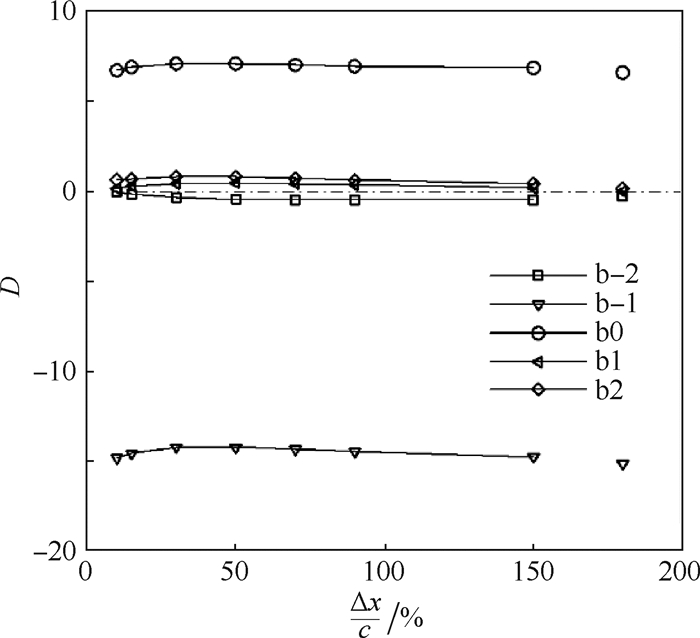 |
| 图 6 不同轴向间距下气动阻尼系数分量 Fig. 6 Aerodynamic damping coefficient component with different axial spacing |
| 图选项 |
由于b0叶片振动产生的非定常扰动沿周向的快速衰减,使用影响系数法时,只需选取有限的叶片数目。为了检验影响系数法在多排算例中的适用性,图 7给出了不同叶片数下转子在叶片间相位角为-72°时气动阻尼系数随Δx的变化规律(孤立转子是以Δx/c=180%来表示),b-1~b1表示b-1、b0、b1 3个叶片气动阻尼系数叠加。由图 7可知:随着轴向间距的减小,气动阻尼系数先增加后减小,转子叶排在Δx/c=30%时气动弹性稳定性最好,说明导叶-转子之间存在一个最佳的轴向间距,这和文献[12]中的结论一致,上游导叶对转子叶片表面非定常压力波的反射,导致转子叶片的气动阻尼系数随轴向间距改变发生变化;b-1和b0气动阻尼系数分量的叠加已经能基本预测导叶对转子气动阻尼系数的影响趋势,更多的叶片数只是使得转子气动阻尼系数误差更小。
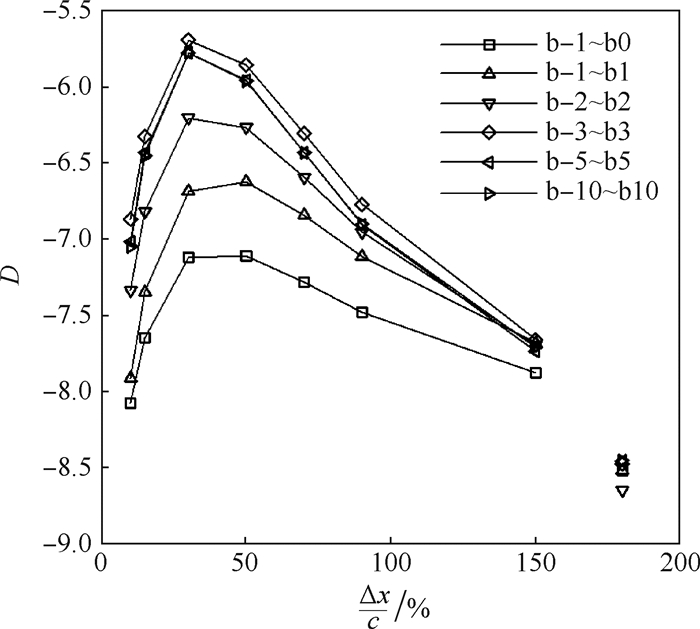 |
| 图 7 不同叶片数下气动阻尼系数 Fig. 7 Aerodynamic damping coefficient with different blade numbers |
| 图选项 |
表 3为在叶片间相位角为-72°时不同叶片数下转子气动阻尼系数相对误差。从表 3可以看出:在Δx/c≥90%时,b0及其相邻叶片就可以较为准确得出转子叶排气动阻尼系数;随着Δx的减小,导叶在转子叶片上引起的非定常气动响应增强,b-1和b0气动阻尼系数分量相对于转子叶排气动阻尼系数所占的比重有所下降,表明导叶对非定常压力波的反射作用减弱了非定常压力波的周向衰减;在Δx/c < 90%时,b0及其相邻叶片得出转子气动阻尼系数相对误差明显增大,需要测量更多的叶片才能得到较为准确的气动阻尼系数。为了进一步弄清楚轴向间距影响转子气动阻尼系数的机理,需要对b0和b-1叶片表面非定常气动力及其做功情况进行分析。
表 3 不同叶片数下气动阻尼系数相对误差 Table 3 Relative error of aerodynamic damping coefficients with different blade numbers
| % | ||||||||
| 叶片编号 | Δx/c=10% | Δx/c=15% | Δx/c=30% | Δx/c=50% | Δx/c=70% | Δx/c=90% | Δx/c=150% | 单转子 |
| b-1~b0 | 14.58 | 18.50 | 23.31 | 19.25 | 13.24 | 8.40 | 2.21 | 0.77 |
| b-1~b1 | 12.27 | 13.84 | 15.77 | 11.08 | 6.39 | 3.09 | 0.37 | 0.76 |
| b-2~b2 | 4.08 | 5.64 | 7.42 | 5.10 | 2.51 | 0.81 | 0.13 | 2.30 |
| b-3~b3 | 2.57 | 1.99 | 1.44 | 1.76 | 1.97 | 1.84 | 0.63 | 0.24 |
| b-5~b5 | 0.44 | 0.34 | 0.03 | 0.09 | 0.01 | 0.11 | 0.34 | 0.02 |
表选项
3.3 b0与b-1非定常压力和气动功分布 对b0与b-1来说,叶片表面非定常压力响应来源主要有两部分:一部分是由于b0振动引起的非定常压力响应,另一部分来源于上游导叶对转子叶片表面非定常压力波的反射。
图 8(a)为b0表面无量纲非定常气动功W的分布图,可以看出:振动叶片本身的吸力面(SS)前部和压力面(PS)做负功,吸力面后半部分做正功;做功最大位置发生在吸力面前缘;受导叶的影响,随Δx的减小,做功变化主要发生在吸力面前部和压力面。由于转子叶片表面气动功的大小是由叶片表面非定常气动力的一阶幅值和相位决定的[13],需要进一步分析b0表面非定常压力响应一阶幅值和相位变化情况。
 |
| 图 8 b0表面无量纲非定常气动功、压力幅值和相位 Fig. 8 Non-dimensional unsteady aerodynamic work, pressure amplitude and phase on b0 surface |
| 图选项 |
图 8(b)、(c)为b0表面非定常压力响应一阶幅值H和相位Φ分布图,可以看出:b0一阶幅值在吸力面前部和吸力面后半部分较大,原因是在图 1中b0振动必然导致b0与b-1、b1之间部分流道宽度发生周期性改变,通过计算发现b0的振动主要影响b-1、b0吸力面前半部分与b0、b1压力面后半部;幅值最大位置位于吸力面前部,原因是这里不仅为图 3中压力梯度最大的区域而且是b0振动直接影响区域;随轴向间距的变化,导叶使b0压力面幅值和相位都有改变,改变主要集中在图 2中转子受导叶影响区域(吸力面前部和压力面)。同时这些幅值和相位改变说明转子表面压力波在上游导叶发生反射,反射波与转子叶片表面压力波叠加,从而导致图 8中b0表面气动功变化。
图 9(a)为b-1表面无量纲非定常气动功分布图,可以看出:气动力做功主要集中在吸力面前部;在b-1吸力面前部,轴向间距引起叶片表面气动功的变化只占叶片表面气动功很小的一部分,说明振动引起的通道周期性变化对转子气动阻尼系数的影响远大于导叶对其的影响。结合图 8(a)和图 9(a)可以看出:b-1吸力面做的正功明显大于b0做的负功,从而使转子气动阻尼系数为负,并与图 6相对应。
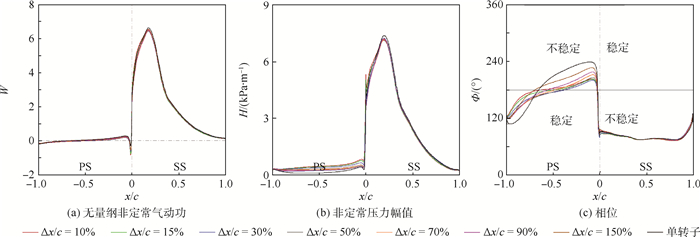 |
| 图 9 b-1表面无量纲非定常气动功、压力幅值和相位 Fig. 9 Non-dimensional unsteady aerodynamic work, pressure amplitude and phase on b-1 surface |
| 图选项 |
图 9(b)、(c)为b-1表面非定常压力响应一阶幅值和相位分布图,可以看出:幅值较大区域集中在吸力面前部,原因是这部分不仅为压力梯度最大的区域而且是b0振动引起的通道周期性变化区域;随轴向间距的变化,导叶对压力面幅值和相位都有影响,而压力面由于不受叶片振动直接影响变化较大,说明相邻叶片振动引起的通道变化抑制了导叶对非定常压力波的反射作用。
对比图 8(b)和图 9(b)不难发现:b0与b-1吸力面幅值基本一致,但它们在图 6气动阻尼系数分量却相差甚远,从相位图中不难发现是由于b0与b-1吸力面相位角的不同导致的。
4 结论 本文使用影响系数法研究了不同轴向间距下上游叶排对转子气动弹性稳定性的影响,得到以下结论:
1) 导叶轴向间距对每个节径下的转子叶片气动阻尼的影响程度不同,主要影响范围在气动弹性最不稳定状态对应的节径附近,气动阻尼系数最小值处影响最大。随着轴向间距的减小,转子叶片气动阻尼系数最小值先增加后减小,并使得气动弹性最不稳定点对应的节径增大。
2) 在协调叶栅中,叶片b1振动对b0影响Cf(1, 0),对转子气动阻尼的大小起决定性作用,其影响甚至超过振动叶片b0本身的影响Cf(0, 0)。研究发现两叶片吸力面上的相位差异是造成这种影响结果的直接原因。
3) 随着轴向间距的减小,导叶对非定常压力波的反射作用减弱了非定常压力波的周向衰减,这说明导叶的存在使得转子叶片振动的非定常影响范围明显增大。为了获得较为准确的转子叶片气动阻尼值,使用影响系数法时需要包括更多的叶片数。
4) 在协调叶栅中,相邻叶片振动引起的通道变化对气动阻尼的影响抑制了导叶对非定常压力波的反射作用。
参考文献
| [1] | 陈懋章. 风扇/压气机技术发展和对今后工作的建议[J].航空动力学报, 2002, 17(1): 1–15. CHEN M Z. Development of fan/compressor techniques and suggestions on further researches[J].Journal of Aerospace Power, 2002, 17(1): 1–15.(in Chinese) |
| [2] | LANE F. System mode shapes in the flutter of compressor blade rows[J].Journal of the Aeronautical Sciences, 1956, 23(1): 54–66.DOI:10.2514/8.3502 |
| [3] | CARTA F O, ST HILAIRE A O. Experimentally determined stability parameters of a subsonic cascade oscillating near stall[J].Journal of Engineering for Power, 1978, 100(1): 111–120.DOI:10.1115/1.3446301 |
| [4] | CARTA F O, ST HILAIRE A O. Effect of inter-blade phase angle and incidence angle on cascade pitching stability[J].Journal of Engineering for Power, 1980, 102(2): 391–396.DOI:10.1115/1.3230268 |
| [5] | 张小伟, 王延荣, 徐可宁. 叶轮机械叶片颤振的影响参数[J].航空动力学报, 2011, 26(7): 1558–1562. ZHANG X W, WANG Y R, XU K N. Effects of parameters on blade flutter in turbomachinery[J].Journal of Aerospace Power, 2011, 26(7): 1558–1562.(in Chinese) |
| [6] | BELL D L, HE L. Three dimensional unstea-dy flow for an oscillating turbine blade and the influence of tip leakage[C]//ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition. New York: ASME, 1998: V005T14A049. |
| [7] | ISOMURA K, GILES M B. A numerical study of flutter in a transonic fan[J].Journal of Turbomachinery, 1998, 120(3): 500–507.DOI:10.1115/1.2841746 |
| [8] | HSU K, HOYNIAK D, ANAND M S. Full annulus multi-row flutter analyses[C]//ASME Turbo Expo 2012: Turbine Technical Conference and Exposition. New York: ASME, 2012: 1453-1462. |
| [9] | CULVER R, LIU F. Mixing-plane method for flutter computation in multi-stage turbomachines: AIAA-2009-862[R]. Reston: AIAA, 2009. |
| [10] | HUANG X Q, HE L, BELL D L. Influence of upstream stator on rotor flutter stability in a low pressure steam turbine stage[J].Proceedings of the Institution of Mechanical Engineers, Part A:Journal of Power and Energy, 2006, 220(1): 25–35.DOI:10.1243/095765005X69170 |
| [11] | 杨慧, 李振鹏. 转静干涉对转子叶片颤振特性的影响[J].北京航空航天大学学报, 2016, 42(2): 258–264. YANG H, LI Z P. Influence of rotor-stator interaction on rotor blade flutter characteristics[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 258–264.(in Chinese) |
| [12] | LI H D, HE L. Blade aerodynamic damping variation with rotor-stator gap:A computational study using single-passage approach[J].Journal of Turbomachinery, 2005, 127(3): 573–579.DOI:10.1115/1.1928932 |
| [13] | 杨慧, 沈真. 上下游干涉对转子叶片颤振特性的影响[J].航空动力学报, 2016, 31(5): 1170–1177. YANG H, SHEN Z. Influence of up-and downstream blade rows on the rotor blade flutter characteristics[J].Journal of Aerospace Power, 2016, 31(5): 1170–1177.(in Chinese) |
| [14] | HANAMURA Y, TANAKA H, YAMAGUCHI K. A simplified method to measure unsteady forces acting on the vibrating blades in cascade[J].Bulletin of the JSME, 1980, 23(180): 880–887.DOI:10.1299/jsme1958.23.880 |
| [15] | 杨慧, 何力, 王延荣. 压气机线性振荡叶栅气弹试验研究(二):叶尖间隙的影响[J].航空学报, 2008, 24(4): 804–810. YANG H, HE L, WANG Y R. Experimental study on aeroelasticity in linear oscillating compressor cascade.PartⅡ:Tip-clearance effect[J].Journal of Turbomachinery, 2008, 24(4): 804–810.(in Chinese) |
| [16] | 郑赟. 基于非结构网格的气动弹性数值方法研究[J].航空动力学报, 2009, 24(9): 2069–2077. ZHENG Y. Computationalaeroelasticity with an unstructured grid method[J].Journal of Turbomachinery, 2009, 24(9): 2069–2077.(in Chinese) |
| [17] | 杨慧, 郑赟. 测量叶轮机振动叶片表面非定常气动响应的实验技术-影响系数法[J].实验流体力学, 2011, 25(3): 71–77. YANG H, ZHENG Y. Experimental technique for measuring unsteady aerodynamics of vibrating blade in turbomachinery influence coefficient method[J].Journal of Experiments in Fluid Mechanics, 2011, 25(3): 71–77.(in Chinese) |
| [18] | BLCS A, FRANSSON T H. Aeroelasticity in turbomachines: Comparison of theoretical and experimental cascade results: LTT-CONF-1986-001[R]. Lausanne: éole Polytechnique Fédérale de Lausanne, 1986. |
| [19] | FRANSSON T H, VERDON J M. Updated report on standard configurations for unsteady flow through vibrating axial flow turbomachine cascades: LTT-CONF-1991-005[R]. Lausanne: éole Polytechnique Fédérale de Lausanne, 1991. |
