皮纳卫星具有质量轻、体积小、研制周期短及成本低廉等特点，能够通过组成分布式星座完成大卫星难以完成的工作^[1]。其整个星群可以构成“虚拟卫星”，利用协同控制的方法完成通信、遥感、科学实验等任务^[2]。因此，皮纳卫星的发展将对未来军民两用有着重要而广阔的应用前景。皮纳卫星姿态控制时主要研究的问题是角度机动时的快速性和指向稳定时的精确性。
目前，皮纳卫星大多使用PID和改进PID控制方法，而结合皮纳卫星本身成本低廉、体积小的特性研究高精度的控制算法依旧是****们需要努力的方向。从不同角度研究解决小卫星控制精度问题的方法有：Yang和Sun^[3]针对小卫星姿态控制的鲁棒性和精度，采用线性矩阵不等式求解混合H₂/H_∞状态反馈控制器的数值解，其控制效果兼具H₂与H_∞的特点；文献[4]针对小卫星的非线性耦合模型，利用滑模变结构控制响应快、对外界干扰和系统参数不敏感的强鲁棒性^[5-7]设计了滑模控制律，并用饱和函数抑制抖振现象；Qiao和Guo^[8]针对小卫星的输入延迟、扰动误差以及模型等不确定问题，设计了兼有故障观测器和扰动观测器的复合容错控制器；Bellar等^[9]针对低轨喷气小卫星的机动最短时间和最少燃料消耗问题，设计了模糊脉冲宽度及频率控制器。
卫星姿态控制使用的执行机构主要有磁力矩器、反作用飞轮、喷气、电推等，可以单独或组合使用，而对于皮纳卫星采用多种执行机构联合姿态控制问题近年来也有过一些研究和应用。如Grassi和Pastena^[10]针对SMART-1卫星反作用飞轮故障时，提出了采用磁力矩器辅助姿态控制的方案，并结合以控制精度和能耗最优为目标的姿态控制算法；Queen和Silverberg^[11]提出了采用飞轮和推力器联合执行的控制方案，其结合以燃料消耗和电源功耗最优为目标的联合姿态控制算法；Hall等^[12]针对姿态跟踪的快速性和精度问题，提出了采用飞轮和喷气推力器联合控制方案；孙兆伟等^[13-14]采用飞轮和磁力矩器联合控制解决小卫星大角度机动过程中的飞轮易饱和问题。尽管上述提出的控制执行方案解决了一些小卫星系统控制过程中的问题，但就应用的执行机构的精度限制是难以实现皮纳卫星低成本下的高精度控制的。
MEMS固体微推力器(SPM)阵列是基于MEMS技术的固体推进剂为推进系统，通过MEMS技术在一块芯片上集成若干个微推力器单元，具有集成度高、体积小、功耗低等优点。推力器单元可单独工作，也可以多个同时工作，能够为皮纳卫星的高精度轨道修正和姿态调整提供所需的微小冲量和冲量矩，现在主流的微推力器能够在一个“脉冲节”内产生10^-4～10^-6 N·s冲量的脉冲，微小的“脉冲节”在对皮纳卫星姿态控制时可以看作连续控制。但其每个推力单元只能单次使用，同时装配在卫星上的MEMS芯片总数有限，故推力器消耗问题是必须考虑的。当前各国也都在大力发展微推力芯片工艺，美国Honeywell中心和Princeton大学利用红外景象仪中的相关技术，研究了拥有512×512个推力单元的MEMS兆单元推力器阵列^[15]。随着集成工艺技术的发展，推力单元的集成数量将会不断增加，使得低成本的皮纳卫星实现高精度的控制成为可能。
MEMS固体微推力器阵列由于可以产生很小的冲量，故在卫星控制时可以提供高精度的控制力及控制力矩，而对于转动惯量很小的皮纳卫星，利用微推力器阵列即可以完成高精度姿态定向稳定任务，以此减少对飞轮和磁力矩器的精度及成本要求，拓展皮纳卫星的应用领域。
综上分析，本文提出了将飞轮与MEMS固体微推力器阵列联合执行姿态控制的方案，并结合全局快速终端滑模控制律，同时采用粗、细2种控制模态，即在进行姿态控制初期由飞轮输出较大力矩进行大角度控制粗调，而当指向偏差到达一定精度后，则利用固体微推力器实现高精度的控制和稳定。根据飞轮和MEMS固体微推力器的固有特性，研究建立了飞轮与固体微推力器2种执行器切换的“能量最优切换模型”，有效提高了微推力器的使用率，大大减少了其总消耗量。
1 皮纳卫星姿态运动模型 1.1 姿态误差动力学模型 对于本体转动惯量很小的皮纳卫星，不可忽略飞轮产生的角动量，故有皮纳卫星姿态动力学方程建立如下^[16]：

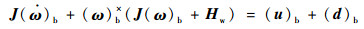(1)

式中：J∈R^3×3为皮纳卫星本体系下的转动惯量矩阵；(ω)_b∈R³为皮纳卫星本体系相对于惯性系的绝对角速度矢量在本体系下的分量列阵；(ω)_b^×为向量(ω)_b=[ω_bx?ω_by?ω_bz]^T的叉乘反对称矩阵，；H_w∈R³为飞轮角动量矩阵；(u)_b∈R³为控制力矩在本体系下的分量列阵；(d)_b∈R³为干扰力矩在本体系下的分量列阵。
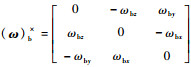
假设航天器要相对于某动参考系保持稳定，此参考系相对于惯性系的期望角速度矢量在参考系下的分量列阵表示为(ω_d)_o∈R³，因此本体系相对于参考系的误差角速度在本体系下的分量列阵表示为

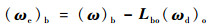(2)

式中：L_bo为从参考系到本体系的坐标转换矩阵。
将式(2)代入式(1)中，得到皮纳卫星的姿态误差动力学方程^[17]为

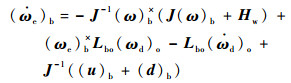(3)

1.2 姿态误差运动学模型 为避免大角度机动产生奇异现象，采用误差四元数来描述皮纳卫星本体系到参考系的姿态，，和分别为误差四元数的标量和向量部分。
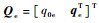
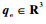
根据文献[18]，基于误差四元数的皮纳卫星姿态误差运动学方程为

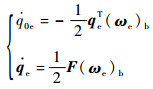(4)

式中：，E₃为3×3的单位矩阵。
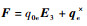
2 全局快速终端滑模控制律 终端滑模控制律已经广泛应用于非线性系统的控制，具有良好的鲁棒性，能够抵抗外界干扰，并能使系统在有限时间内收敛。考虑皮纳卫星执行定向任务时，姿态角通常需要快速机动，以及空间中会受到摄动力矩的影响，因此设计了全局快速终端滑模控制律。
2.1 控制律设计 结合线性与非线性滑模面各自的特点，设计了如下全局快速终端滑模面：

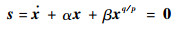(5)

式中：α, β>0且p，q(q < p)为奇数。
对于二阶非线性系统：

(6)

递归结构的快速滑动模态可表示为

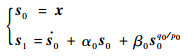(7)

式中：α₀, β₀>0且p₀，q₀(q₀ < p₀)为奇数。
设计全局快速终端滑模控制律为

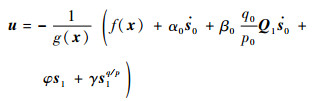(8)

式中：φ、γ为控制律参数。

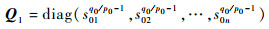对式(4)求导得

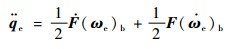(9)

将式(3)代入式(9)，不考虑干扰力矩时得

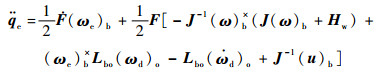(10)

取s₀=q_e，将式(10)代入式(6)得

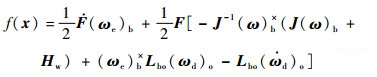(11)

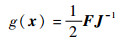(12)

将式(11)、式(12)代入式(8)，得到皮纳卫星的全局快速终端滑模控制律为

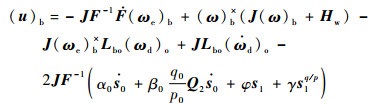(13)

式中：。

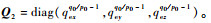
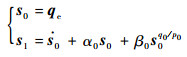(14)

定理1??对于系统式(3)，选用全局快速终端滑模面式(14)和控制律式(13)，可以使得系统达到稳定。
证明??选取Lyapunov函数：

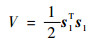(15)

对式(15)求导得

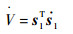(16)

由式(14)得

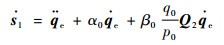(17)

将式(10)代入式(17)得

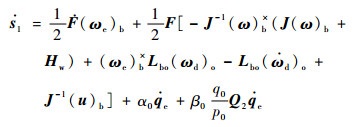(18)

将式(13)代入式(18)得

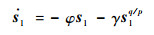(19)

将式(19)代入式(16)得

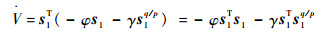(20)

因为(q+p)为偶数，所以≤0，因此系统稳定。??????证毕
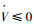
2.2 有限时间收敛 由于终端滑模具有有限时间稳定的特点，因此可以满足皮纳卫星快速机动的任务。由式(19)得

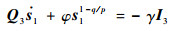(21)

式中：。
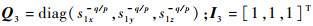
令y=s₁^1－q/p，则，式(21)写为

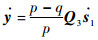
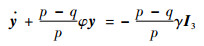(22)

解此一阶非线性微分方程得

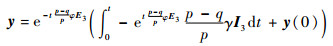(23)

化简得

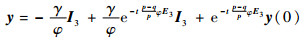(24)

当s₁=[0, 0, 0]^T时，y=[0,0, 0]^T, t=t_s，则

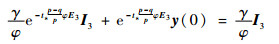(25)

即

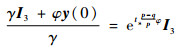(26)

将y(0)=s₁(0)^1－q/p代入式(26)得到在滑动模态上，系统从任何初始状态沿到达滑模面的时间为

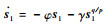
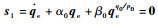
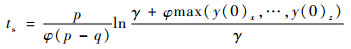(27)

通过设计φ、γ、p、q，可使系统在有限时间t_s内到达稳定状态。
3 双模式分配策略 本节把第2节中控制律提供的总控制力矩根据能量最优切换模型分配给飞轮与固体微推力器，再将固体微推力器的力矩分配给每个芯片执行点火。
3.1 能量最优切换模型 低成本的皮纳卫星的转动惯量很小，采用飞轮做执行机构时，在力矩接近0附近时近似服从如图 1所示的力矩输入输出关系。图中：u_c为控制律给出的指令控制力矩；u_w为飞轮输出的实际控制力矩；M为飞轮精度允许情况下的最小输出力矩。

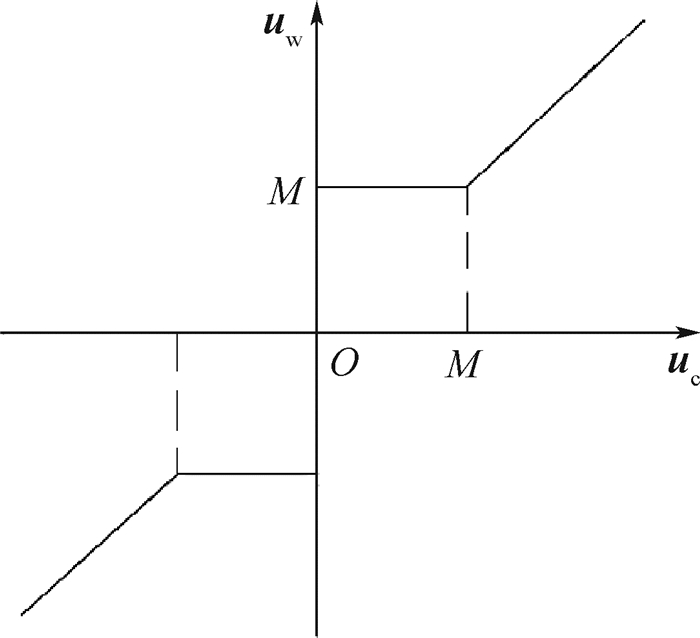图 1 飞轮力矩输出示意图 Fig. 1 Schematic of torque output of flywheel

图选项

图 1给出了飞轮最小力矩输出限制，使得皮纳卫星的姿态控制精度受M所限制。当皮纳卫星需求更高精度控制时，可由微推力器辅助作用。固体微推力器阵列与飞轮双模式的切换是基于固体微推力器的总消耗量最少，即全局能量最优原则进行设计，同时按照固体微推力器输出的总冲量矩最少建立全局最优分界点。
全局能量最优切换模型的数学表达式如下：

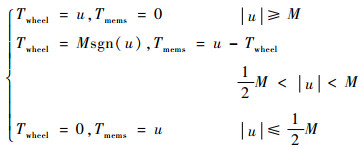(28)

式中：u为控制律给出的指令控制力矩在3个轴上的分量；T_wheel为分配后的飞轮指令控制力矩；T_mems为分配后的微推力器指令控制力矩。
定理2??对于使用飞轮与MEMS固体微推力器阵列联合姿态控制的皮纳卫星，利用式(28)进行控制力矩分配时，固体微推力器燃料的总消耗量最少，达到全局能量最优。
证明??令h(t)为指令控制力矩绝对值随时间的函数，0≤h(t)≤M，只需证明h(t)≤M时固体微推力器指令控制力矩的总冲量矩最小。初始力矩h(t₀)=M，控制状态收敛后h(t_2n)=0，h(t_i)=K，i=1, 2, …, n－1，h(t)在t_i处连续可导。根据式(28)，当h(t) < K时，固体微推力器控制力矩为h(t)，当K < h(t) < M时，则为M－h(t)。因此，总冲量矩可由式(29)表示：

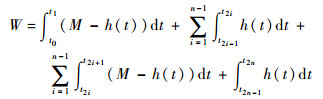(29)

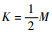
只需证明当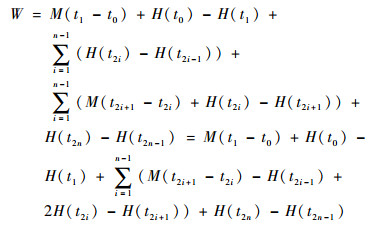时，总冲量矩W取最小值即可。设H(t)是h(t)的原函数，则

取为h_j(t)的反函数，则t_j=h_j^－1(K)，且H′(h_j^－1(K))=，则

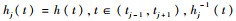
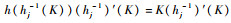
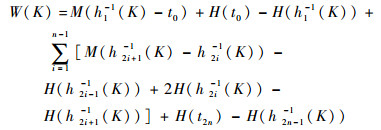求导得

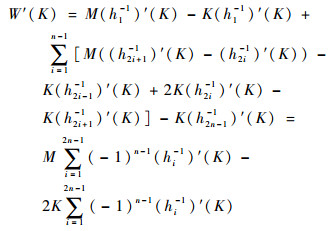当W′(K)=0时，，W(K)取最小值。
故式(28)为能量最优切换模型，即按式(28)分配飞轮和固体微推力器2种执行机构时，在达到同样控制效果下，固体微推力器产生的总冲量矩最小，也即全局燃料消耗量最少。???证毕
3.2 固体微推力器执行分配方案 以笔者团队前期研制的规格为10×10个推力单元的MEMS固体微推力器芯片(见图 2)为例，将其装配在皮纳卫星4个侧表面的4个角点处，利用每次点火产生的推力对质心造成的力矩来进行皮纳卫星姿态控制。由于芯片面积小，可将每个芯片看作一个点，其点火一次可提供的推力即可唯一确定，如图 3所示，每个箭头代表每个固体微推力器芯片所造成的推力。

图 2 10×10固体微推力器阵列 Fig. 2 10×10 solid propellant microthruster array

图选项

图 3 固体微推力器推力示意图 Fig. 3 Schematic of thrust of solid propellant microthruster

图选项

固体微推力器在执行时存在冗余，需要将固体微推力器指令控制力矩经过执行分配算法转化为每个芯片的点火个数。同时，为避免对质心造成力的作用而改变轨道，要求两侧对称提供推力，以保证固体微推力器只对质心产生力矩。建立每个芯片点火个数与提供的总力矩之间的关系方程：

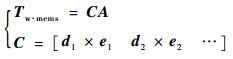(30)

式中：T_w·mems∈R³为固体微推力器实际作用的力矩；C为所有固体微推力器的单位推力矢量对皮纳卫星的力矩矩阵，d_i∈R³为第i个固体微推力器芯片在本体系中的位置矢量，e_i∈R³为第i个固体微推力器点火一次的推力在本体系中的推力矢量；A∈Z⁸中每个元素对应各芯片使用推力单元的个数。
根据图 3中固体微推力器芯片的安装位置及序号顺序，可计算C，T₀∈R为每个推力单元点火一次时对本体轴造成的力矩。

(31)

固体微推力器执行分配时的目标是求解分配矩阵A，此问题经验证不能使用飞轮力矩分配时所用的伪逆法，而是求解整数规划问题，并且要求A中元素尽可能小，这样才能准确控制每个固体微推力器的点火个数，并且保证总消耗量最小。
为使实际控制力矩尽可能接近其指令控制力矩，本文利用蒙特卡罗方法搜索实际力矩与指令力矩最接近的分配矩阵，同时考虑固体微推力器消耗量最小的条件。具体操作流程如下：
步骤1??已知固体微推力器指令控制力矩T_mems，k=1。
步骤2??在(0, 1, …, [K/T₀])中随机产生一个8×1的整数分配矩阵A_k，[·]为取整符号。
步骤3??将A_k代入式(30)，得到A_k对应的实际控制力矩(T_w·mems)_k，并计算

(32)

式中：||·||₂表示2-范数。
步骤4??循环步骤2、步骤3，留下J₁中取值最小时的A_k1, A_k2, …, A_km。
步骤5??计算

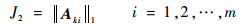(33)

式中：||·||₁表示1-范数。
步骤6??取J₂最小时的A_ki作为最终的分配矩阵A。
式(32)的目标是寻找力矩最接近期望的分配矩阵，再利用式(33)寻找这些矩阵中点火个数最少的作为最终结果，以达到能量最优的目的。
4 仿真算例 皮纳卫星采用第3节双模式分配策略实现高精度姿态控制的过程是：由控制律给出指令控制力矩，再根据式(28)所示的切换策略将指令控制力矩分解为飞轮和固体微推力器的指令控制力矩，固体微推力器指令力矩再分配到各个芯片执行输出。飞轮输出力矩限制如图 1所示，初始条件和控制参数如表 1所示，仿真时间为40 s。
表 1 参数取值 Table 1 Parameter value

参数	数值
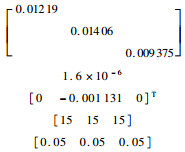α0	0.8
β0	0.04
p0	7
q0	5
φ	0.8
γ	0.04
p	7
q	5
M/(N·m)	0.0001
T0/(N·m)	1.4×10－5
注：Jwheel为飞轮的转动惯量；[φ0 θ0 ψ0]为初始姿态角。

表选项






400 km高度轨道处，气动干扰力矩可建模为

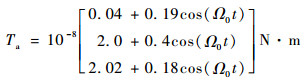磁干扰力矩可建模为

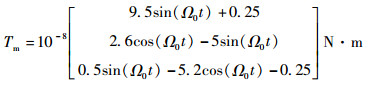式中：轨道角速率Ω₀=0.001 131 rad/s。
4.1 仅用飞轮控制 当仅用服从图 1所示的输入输出关系的飞轮做执行机构时，仿真结果如图 4所示。

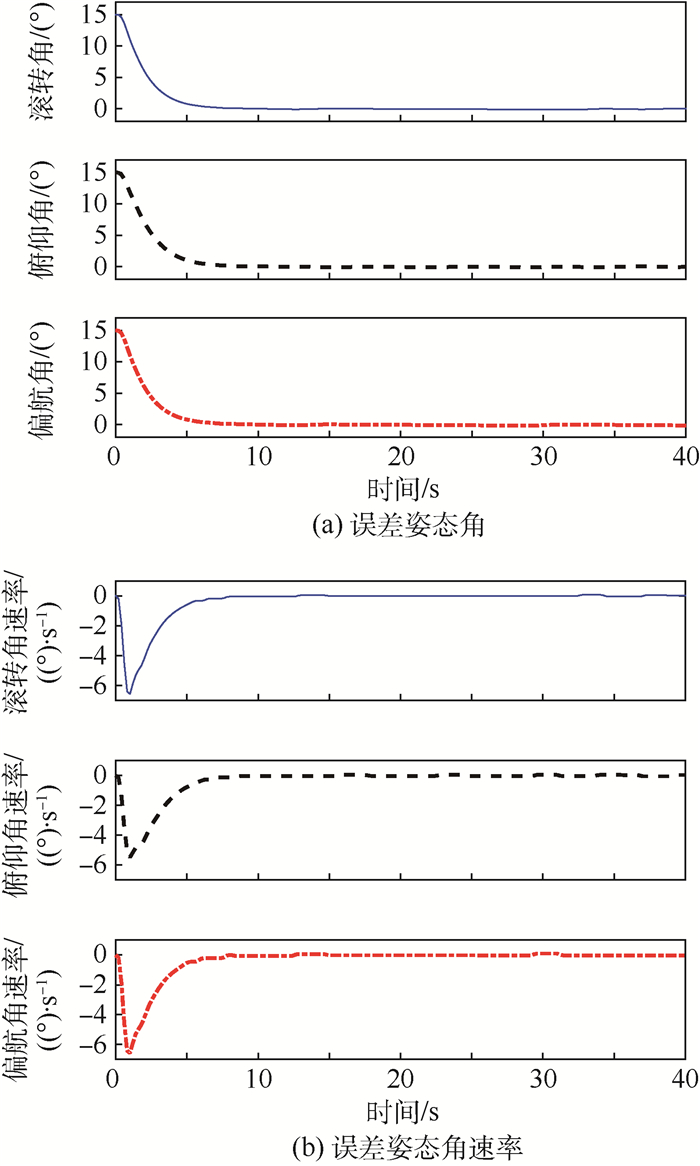图 4 飞轮力矩限制时的误差姿态角和误差姿态角速率示意图 Fig. 4 Error attitude angle and error attitude angular rate when flywheel's torque is limited

图选项

由图 4可以看出，由于飞轮的最小输出力矩限制，使得皮纳卫星在稳定阶段中，控制力矩的超调造成姿态角和姿态角速率存在较大波动，经统计得到姿态角精度为0.146 4°，姿态角速率精度为0.113 3(°)/s，只用飞轮作为执行机构难以满足皮纳卫星高精度指向任务要求。
4.2 固体微推力器阵列与飞轮联合控制 利用固体微推力器的微小冲量矩弥补飞轮的最小输出力矩限制，以提高皮纳卫星的姿态控制精度，根据第3节所述的固体微推力器阵列与飞轮实现联合控制的双模式分配策略，结合式(28)能量最优切换模型，以及式(30)固体微推力器分配方案，仿真结果如图 5所示。

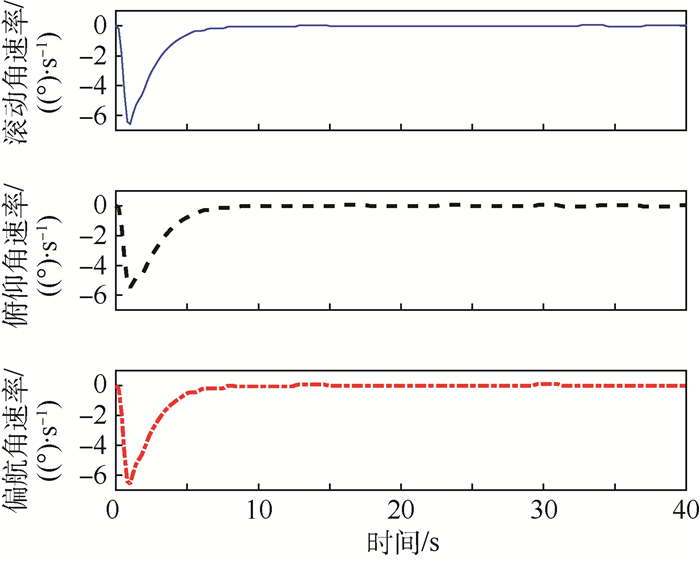图 5 加入固体微推力器后的误差姿态角和误差姿态角速率示意图 Fig. 5 Error attitude angle and error attitude angular rate after adding solid propellant microthruster

图选项

从图 5可以看出，在全局快速终端滑模控制律作用下，误差姿态角和误差姿态角速率都快速收敛到0，并且始终保持稳定。将表 1的参数代入式(29)，可求得t_s=10.897 3 s，与图 5中所显示的收敛时间基本符合，说明控制器的控制有效，能使系统在大约10 s的有限时间内达到稳定，满足皮纳卫星快速姿态机动的任务要求。
由图 5与图 4对比明显看出，加入固体微推力器后的控制精度有所提高，曲线波动大大降低，仿真计算得到姿态角精度为0.045 7°，姿态角速率精度为0.006 2(°)/s，与仅用飞轮控制时相比精度提高了一个数量级，证明采用固体微推力器可以实现皮纳卫星高精度姿态控制的目的。
4.3 固体微推力器阵列与飞轮的切换策略分析 从图 6可以看出，控制任务进行的后期阶段中，飞轮与固体微推力器交替使用，并且遵循了能量最优切换模型式(28)，即先由飞轮作用，再由两者共同作用，最后由固体微推力器阵列单独作用的3个阶段，达到了高控制精度。并经统计，此过程中固体微推力器共消耗了158个。

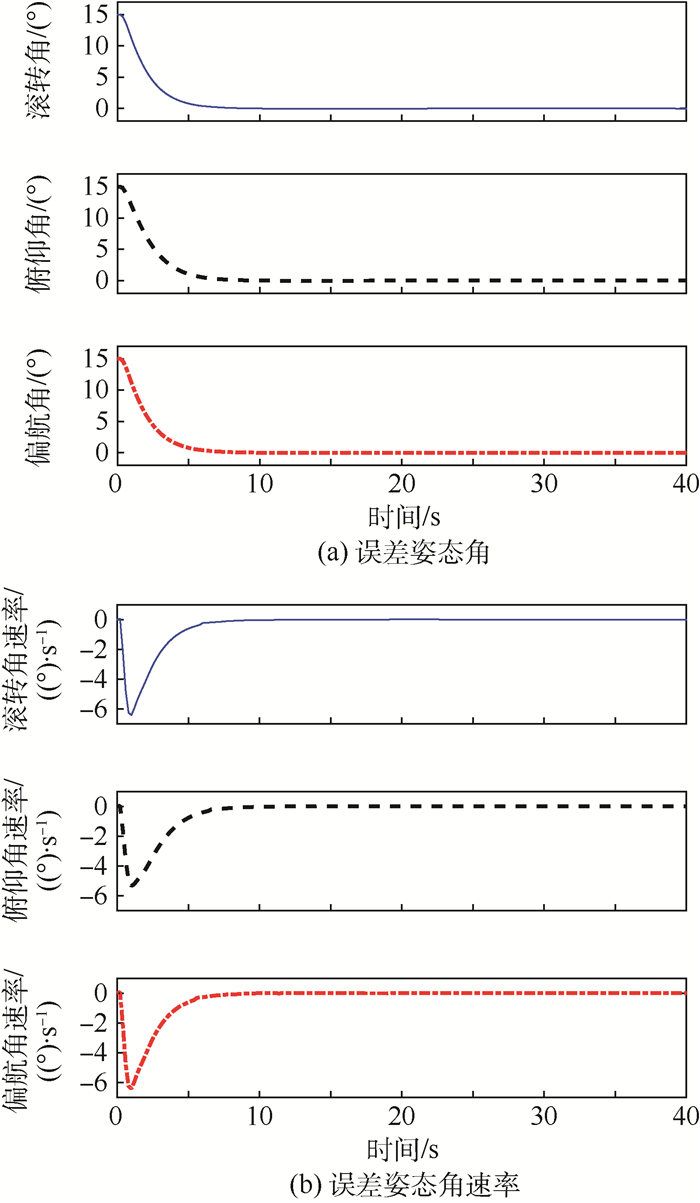图 6 加入固体微推力器后的实际控制力矩示意图 Fig. 6 Actual control torque after adding solid propellant microthruster

图选项

如果不按照式(28)进行分配，而是当控制力矩低于飞轮最小输出力矩后飞轮停用，直接开启固体微推力器提供全部控制力矩，此过程相当于使K=M，则此时的控制力矩示意图如图 7所示。

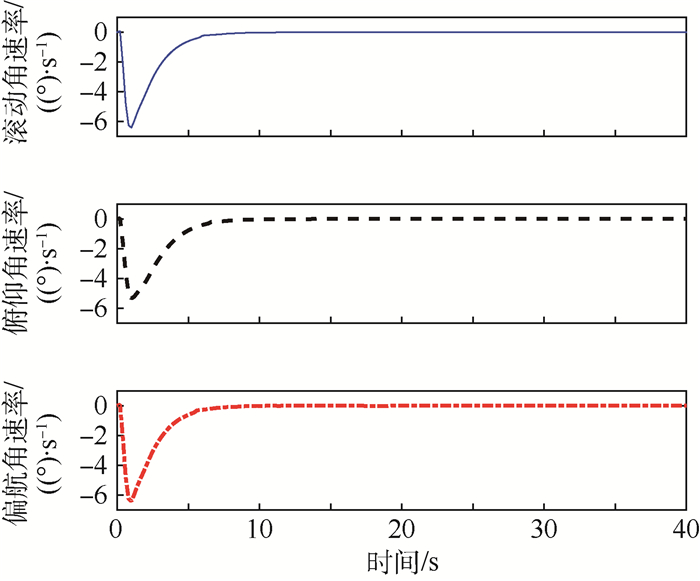图 7 K=M时的实际控制力矩示意图 Fig. 7 Actual control torque when K=M

图选项

从图 7中看出，在开始使用固体微推力器的前半段区间内，没有飞轮的力矩输出配合，需要固体微推力器输出较大的力矩，而后半阶段与图 6差别不大，统计固体微推器消耗量增大到了308个。此时姿态角精度为0.041 3°，姿态角速率精度为0.004 7(°)/s。比较看出，本文提出的双模式分配策略可以在保证高控制精度的同时，节约固体微推力器消耗量48.7%。
如果取不同组控制器参数(见表 2)，同时改变K/M比值，分别进行仿真并统计固体微推力器的消耗量，结果如表 3所示，并绘制不同参数取值下固体微推力器消耗量与K/M取值的关系，如图 8所示。
表 2 多组控制参数取值 Table 2 Values of multiple groups of control parameter

参数	第1组	第2组	第3组	第4组	第5组
α0	0.8	0.8	1	1	1
β0	0.04	0.04	0.02	0.02	0.02
p0	7	9	9	9	9
q0	5	7	7	7	7
φ	0.8	0.8	0.8	0.8	1
γ	0.04	0.04	0.04	0.04	0.02
p	7	7	7	9	9
q	5	5	5	7	7

表选项






表 3 各组参数下取不同K/M值时的固体微推力器消耗量 Table 3 Consumption of solid propellant microthruster with different groups of parameter and different K/M

K/M	第1组	第2组	第3组	第4组	第5组
0.2	230	226	203	208	197
0.4	164	156	148	154	130
0.5	158	148	134	146	126
0.6	168	158	166	154	134
0.8	248	238	224	224	212
1.0	308	322	310	326	296

表选项

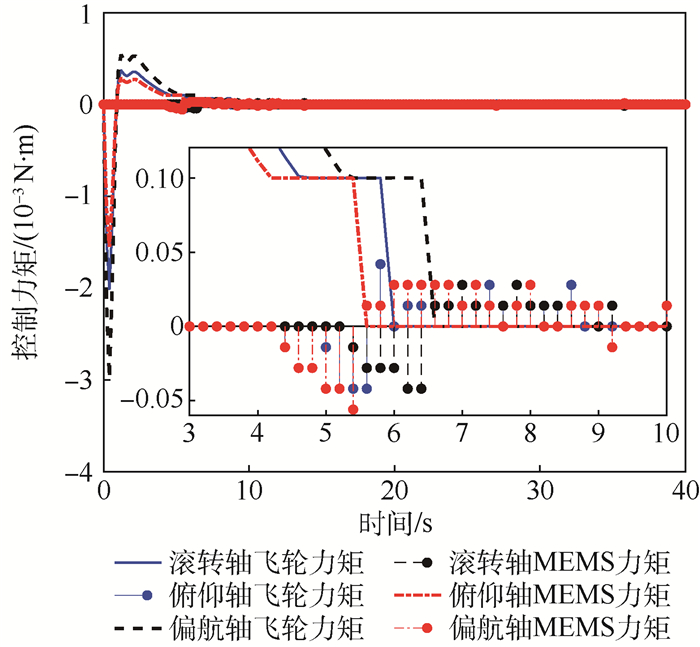图 8 不同控制参数与K/M时固体微推力器消耗量示意图 Fig. 8 Consumption of thruster with different control parameters and K/M

图选项

从图 8中可以看出，在取不同控制参数组合时，对应的推力单元消耗量都不尽相同，但对于每一组参数中，当且仅当K/M=0.5时推力单元消耗量最少。因此，通过仿真也进一步证明了第3节的分配策略中能量最优切换点是在K/M取0.5时，即此时固体微推力器消耗量最低。
5 结论 通过对本文提出的飞轮与固体微推力器阵列联合执行机构实现皮纳卫星高精度姿态控制方法的深入研究，得到了以下几点结论：
1) 用飞轮与固体微推力器阵列联合执行机构提高皮纳卫星姿态控制精度是可行的。
2) 采用全局快速终端滑模控制律能够很好地解决小转动惯量皮纳卫星易受扰的快速收敛问题，并通过了Lyapunov稳定性证明。
3) 飞轮与固体微推力器阵列的双模式分配策略是基于能量最优切换模型进行的，其飞轮与固体微推器共同作用的过渡段对减少固体微推力器的力矩输出、节约固体微推力器的消耗有重要作用。
4) 通过计算机仿真验证了本文方法使皮纳卫星的控制精度提高，并且K/M=0.5时能量消耗最省，可节约固体微推力器消耗48.7%。

参考文献

[1]	赵炜渝, 白保存, 金仲和. 皮纳卫星应用与特点分析[J].国际太空, 2013(8): 36–40. ZHAO W Y, BAI B C, JIN Z H. Analysis on application and characteristics of pico-and nano-satellite[J].Space International, 2013(8): 36–40.(in Chinese)
[2]	林来兴. 小卫星技术的发展和应用前景[J].中国航天, 2006(11): 43–47. LIN L X. Development and application prospect of moonlet technology[J].Aerospace China, 2006(11): 43–47.DOI:10.3969/j.issn.1672-9463.2006.11.017(in Chinese)
[3]	YANG C D, SUN Y P. Mixed H2/H∞, state-feedback design for microsatellite attitude control[J].Control Engineering Practice, 2002, 10(9): 951–970.DOI:10.1016/S0967-0661(02)00049-7
[4]	NEMATI H R, BAHRAMI M, EBRAHIMI B. Sliding mode control of a microsatellite attitude[C]//International Symposium on Systems and Control in Aeronautics and Astronautics. Pisca-taway, NJ: IEEE Press, 2010: 561-565.
[5]	MCDUFFIE J H, SHTESSEL Y B. A de-coupled sliding mode controller and observer for satellite attitude control[C]//Proceedings of the American Control Conference, 1997. Pisca-taway, NJ: IEEE Press, 1997: 564-565.
[6]	BANG H, LHO Y. Sliding mode control for spacecraft contain-ing rotating wheels[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2001: 1-8.
[7]	CHEON Y J. Sliding mode control for attitude tracking of thruster-controlled spacecraft[J].Transaction on Control Automation & Systems Engineering, 2002, 3(3): 257–261.
[8]	QIAO J, GUO L. Antidisturbance fault tolerant control of attitude control systems for microsatellite with unknown input delay[J].Mathematical Problems in Engineering, 2013, 2013: 804754.
[9]	BELLAR A, FELLAH M K, MOHAMMED M A S. A cold gas thruster microsatellite attitude control[J].Revue Roumaine des Sciences Techniques-Serie électrotechnique et énergétique, 2013, 58(4): 395–404.
[10]	GRASSI M, PASTENA M. Minimum power optimum control of microsatellite attitude dynamics[J].Journal of Guidance, Control, and Dynamics, 2015, 23(5): 798–804.
[11]	QUEEN E M, SILVERBERG L. Optimal control of a rigid body with dissimilar actuators[J].Journal of Guidance, Control, and Dynamics, 1971, 19(3): 738–740.
[12]	HALL C, TSIOTRAS P, SHEN H. Tracking rigid body motion using thrusters and momentum wheels[J].Journal of the Astronautical Sciences, 2002, 50(3): 311–323.
[13]	SUN Z W, GENG Y, XU G, et al. The combined control algorithm for large-angle maneuver of HITSAT-1 small satellite[J].Acta Astronautica, 2004, 54(7): 463–469.DOI:10.1016/S0094-5765(03)00223-6
[14]	孙兆伟, 杨旭, 杨涤. 小卫星磁力矩器与反作用飞轮联合控制算法研究[J].控制理论与应用, 2002, 19(2): 173–177. SUN Z W, YANG X, YANG D. The combined control algorithm for magnetorquer and reaction wheel of small satellite[J].Control Theory and Application, 2002, 19(2): 173–177.(in Chinese)
[15]	杨灵芝, 魏延明, 刘旭辉. MEMS固体微推力器阵列发展研究[J].空间控制技术与应用, 2016, 42(1): 13–19. YANG L Z, WEI Y M, LIU X H. Development of MEMS solid micro thruster array[J].Aerospace Control and Application, 2016, 42(1): 13–19.(in Chinese)
[16]	CHENG Y, JIANG B, ZHANG X. A micro-satellite attitude system using sliding mode observer and sliding mode controller with perturbation estimation[C]//International Symposium on Systems and Control in Aerospace and Astronautics. Pisca-taway, NJ: IEEE Press, 2008: 1-4.
[17]	AHMED J, COPPOLA V T, BERNSTEIN D S. Adaptive asymptotic tracking of spacecraft attitude motion with inertia matrix identification[C]//IEEE Conference on Decision and Control, 1997. Piscatway, NJ: IEEE Press, 1998: 2471-2476.
[18]	ZOU A M, KUMAR K D. Adaptive fuzzy fault-tolerant attitude control of spacecraft[J].Control Engineering Practice, 2011, 19(1): 10–21.DOI:10.1016/j.conengprac.2010.08.005