当相变材料与发热部件的接触界面温度高于相变材料的熔点时,相变材料融化并吸收发热部件释放的热量,使界面温度保持在相变点附近;当接触界面温度低于相变材料的熔点时,相变材料凝固并释放潜热,维持界面温度基本不变[3]。Leimkuehler等[4-5]选择纯水作为相变材料,针对在低月轨道的航天器和月球车所处的工作环境分别设计了相变温控单元以及相变热沉。Ye等[6-7]研究了金属肋片强化传热的相变热沉内部传热与流动过程。Ismail等[8]和Abduljalil等[9]研究肋片对环状相变材料传热性能的影响。Assis等[10-11]研究了球状相变材料融化与凝固过程,通过量纲分析研究液相质量分数和热流密度随时间的关系。
但是,大部分研究人员没有对微重力环境中相变过程进行数值模拟或实验研究。基于此,本文通过数值模拟方法探究微重力环境下相变过程中的传热与流动特性,并对比重力作用下相变过程,为航天器相变热控技术提供参考依据。
1 物理模型与数值方法 1.1 物理模型 数值模拟的物理模型如图 1所示。相变储能单元由基座、肋片、相变材料以及具有一定真空度的空气组成。气体和相变材料的体积比为1:4。空气的压力为相变材料在此温度下的饱和蒸汽压(约为100Pa),预留空气以便观察相变材料融化后体积膨胀过程。选用铝作为基座与肋片材料,增加肋片以强化相变材料与加热面之间的传热,相变材料选用十八烷。计算单元左右两侧设定为对称面,顶部设为绝热壁面,底部为温度加热面。
 |
| 图 1 计算单元 Fig. 1 Computational unit |
| 图选项 |
计算单元尺寸如图 1(b)所示。肋片与相变材料的宽度比为1:1,肋片高度hfin为22mm,相变材料腔体高度hPCM为20mm,气体高度hair为4mm,气体宽度wair为3mm。十八烷没有严格的相变温度,定义其相变温度区间为27~29℃。相对于一个固定的相变点,相变温度区间更加符合真实的物理现象。十八烷的密度随温度变化,当温度T低于27℃时,密度ρ=814kg/m3,当温度高于27℃时,密度表达式为
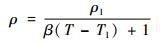 | (1) |
式中:ρl为温度处于Tl时相变材料的密度;β为相变材料的热膨胀系数。
当27℃ < T < 29℃时,相变材料处于多孔介质状态,取β =0.025,在这个过程中,相变材料密度近乎线性地从814kg/m3变化到775.2kg/m3。当T>29℃时,取β=0.001[12]。铝、空气以及相变材料的其他物性参数如表 1所示。
表 1 各物质物性参数 Table 1 Physical parameters of various materials
| 物质 | 导热系数/ (W·m-1·K-1) | 密度/ (kg·m-3) | 比热/(J·kg-1·K-1) | 动力黏度/ (kg·m-1·s-1) | 相变温度/℃ | 相变潜热/ (kJ·kg-1) |
| 十八烷 | 0.1507 | 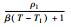 | 2160 | 0.00346 | 27~29 | 244 |
| 铝 | 202.4 | 2719 | 871 | |||
| 空气 | 2.42×10-5 | 1.2×10-8T2-1.134×10-5+3.498×10-3 | 1.006 |
表选项
计算单元初始温度为25℃,相变材料处于过冷状态。加热面处给定的恒定温度边界条件T=48℃,边界温度与相变材料平均相变温度温差ΔT=20℃。
1.2 控制方程 采用焓-多孔介质模型求解相变材料的相变过程,多孔介质区域的每个单元内设置相同的流动阻力。对于全凝固区域和全融化区域,多孔性分别为0和1。Bertrand等[13]将多种数值模拟方法运用于相变过程的数值模拟中,相变过程中考虑自然对流对融化的影响,并且覆盖2个系列的Prandtl准则数,这2个系列的准则数分别对应金属和有机材料。结果表明,焓-多孔介质模型能够很好地应用在具有移动界面的固-液相变问题中。
控制方程如下:
连续方程
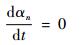 | (2) |
式中:αn为计算单元中第n种流体的体积分数; t为时间。
动量方程
 | (3a) |
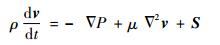 | (3b) |
式(3a)为受重力作用时动量方程;式(3b)为不受重力作用时动量方程;v为速度,P为压力,μ为动力黏度,g为重力加速度,S为动量源项。
能量方程
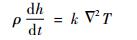 | (4) |
式中:k为热传导系数,h为比焓,其是显热焓
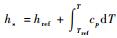
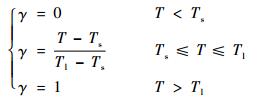 | (5) |
动量方程中的源项S=-A(γ)v,其中A(γ)为Brent等[14]定义的“多孔函数”。定义A(γ)使得动量方程能够模拟多孔介质中流动的Carman-Kozeny(卡尔曼-科泽尼)方程。定义如下:
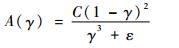 | (6) |
式中:ε为恒等于0.001的计算小量,用来消除分母为0时产生的振荡;C为反映融化前沿形态的模糊区常数,一般取104~107,本文取C=105[15]。
采用Fluent14.5进行求解,使用双精度求解器和SIMPLE算法进行压力-速度的耦合。选取3种不同网格数量进行网格独立性验证,分别是2700、4500和6200。图 2(a)显示3种不同的网格数量下,相变材料液相质量分数随时间变化情况,从图 2(a)可以看出,不同网格数对相变过程的影响差别很小,本文选取网格数为2700进行数值模拟,具体网格划分见图 2(b)。非稳态时间步长等于比特征长度除以比特征时间,本文取时间步长Δt=0.005s。每个时间步长内,确保连续性方程和动量方程残差小于10-6,能量方程残差小于10-10。
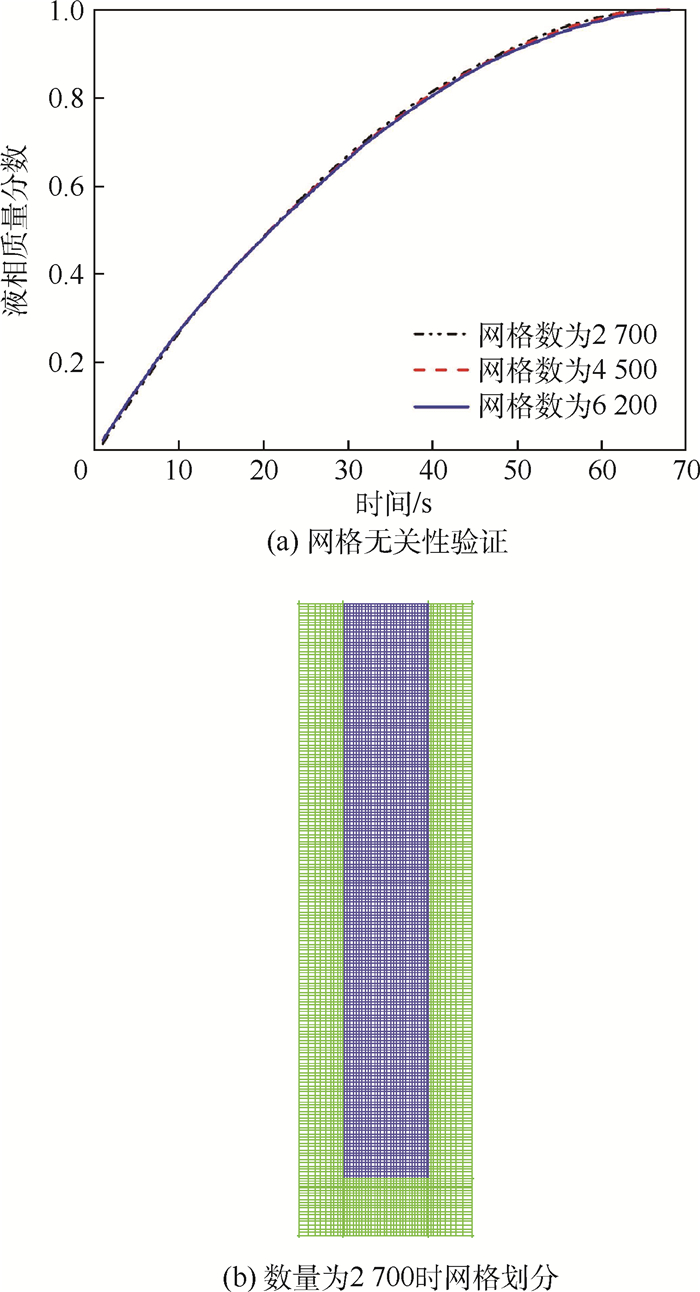 |
| 图 2 网格无关性验证和网格划分 Fig. 2 Grid independence verification and grid partition |
| 图选项 |
1.3 实验验证 因为实验条件限制,无法搭建微重力条件下的实验台。搭建地面实验台,观察受重力影响时相变储能单元相变过程。实验装置如图 3所示。实验开始前,先对实验件进行抽真空处理,抽完真空后,往实验件中填充体积分数为80%的相变材料。待实验件充装完毕后,将其放置在水箱中。接着,打开泵和阀门,从恒温水槽内通入48℃热水,从而达到恒定温度边界条件。通过相机拍摄实验结果。
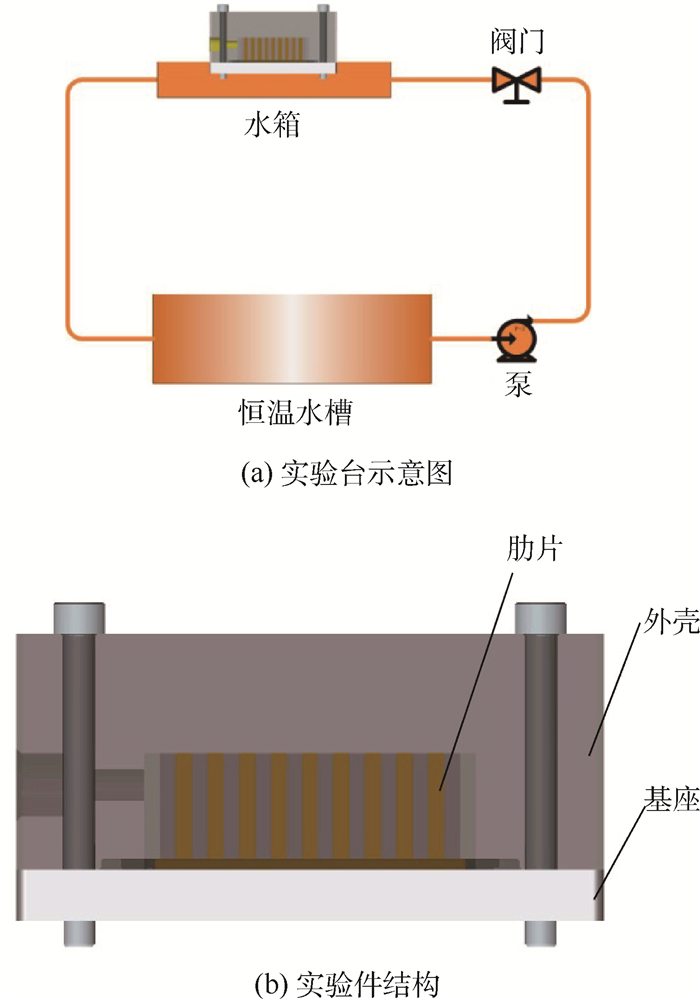 |
| 图 3 实验装置 Fig. 3 Experimental setup |
| 图选项 |
恒温水槽采用DC-1030低温恒温槽,温度范围为-10~90℃,相机为佳能EOS70D单反相机。
选取相变过程中8个时间节点作对比,分别是0、Δtmelt/7、2Δtmelt/7、3Δtmelt/7、4Δtmelt/7、5Δtmelt/7、6Δtmelt/7、Δtmelt,Δtmelt为相变材料完全融化的时间。实验与数值模拟如图 4所示,其中白色区域是固态相变材料,黑色部分是液态相变材料,由于部分固态相变材料存在于液态相变材料后面,影响观察结果,导致部分固-液相变界面比较模糊,不过仍可以从图 4看出,数值模拟结果与实验结果相吻合,数值模拟结果具有参考价值。
 |
| 图 4 相变材料融化过程数值模拟与实验结果对比 Fig. 4 Comparison of numerical simulation and experimental results for melting process of phase change material |
| 图选项 |
2 结果分析与讨论 为了更加深入了解微重力环境下,相变材料融化过程中各时刻状态变化,将同一计算单元进行受重力影响和受微重力影响2种情况的数值模拟,对比分析2种情况下相变材料融化过程的异同。给定恒定的温度边界条件T=48℃,初始温度T0=25℃。
2.1 融化速率与热流密度 图 5和图 6是2种情况下,相变材料液相质量分数和边界热流密度对比情况,边界热流密度为加热壁面传递给相变储能单元的热流密度。
 |
| 图 5 液相质量分数随时间变化 Fig. 5 Liquid fraction versus time |
| 图选项 |
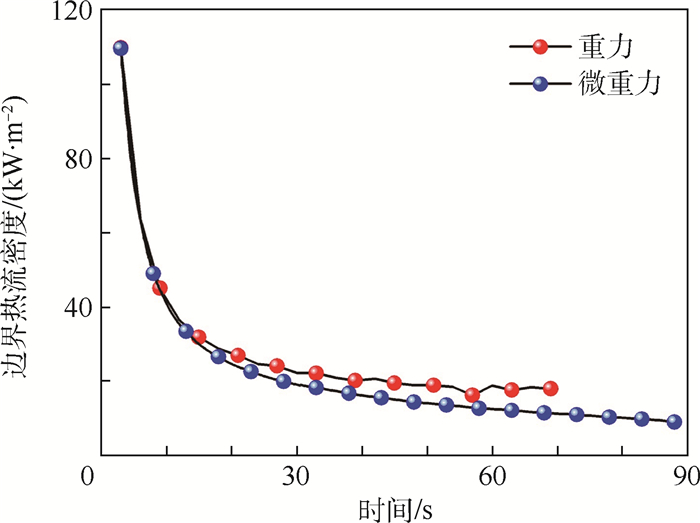 |
| 图 6 边界热流密度随时间变化 Fig. 6 Heat flux density versus time |
| 图选项 |
从图 5可以看出,当相变储能单元受重力作用时,其完全融化耗时70s;当相变储能单元受微重力作用时,其完全融化耗时90s。相对于受重力作用,当相变储能单元受微重力作用时,相变材料融化速率明显下降。融化速率受边界热流密度影响,当相变储能单元受微重力作用时,其边界热流密度明显小于相变储能单元受重力作用时的热流密度。
当时间t < 15s时,2种情况下液相质量分数和边界热流密度没有明显的区别;当时间t>15s且t < 20s时,2种情况下液相质量分数没有明显的差异,但是受重力作用的相变储能单元边界热流密度明显大于受微重力作用的相变储能单元边界热流密度,说明此阶段中,受重力影响的相变储能单元内相变材料吸收更多的热量,并将这部分热量转化为相变材料的显热。
2.2 速度分布 图 7为2种情况下相变储能单元内相变材料的速度分布,取液相质量分数?=0.2、0.4、0.6、0.8和1.0等5个时刻表示整个融化过程。
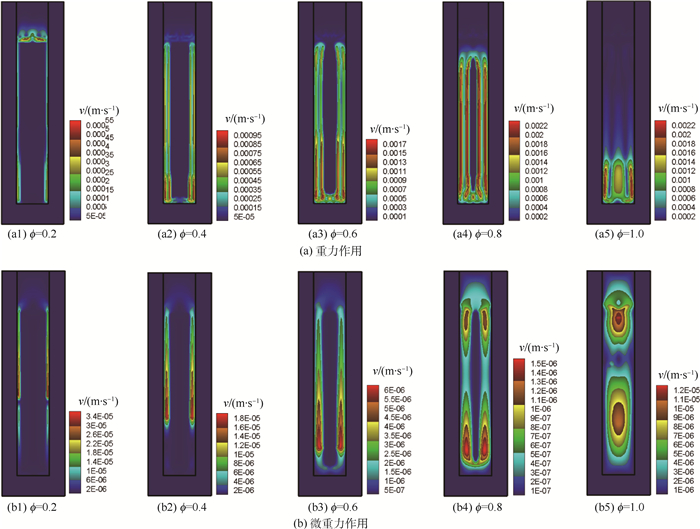 |
| 图 7 相变材料融化过程中速度分布 Fig. 7 Velocity distribution for melting process of phase change material |
| 图选项 |
从图 7可以看出,有无重力作用对相变储能单元内部速度分布起决定性作用。当相变储能单元受重力作用时,肋片处液相相变材料内部产生自然对流,并且对流换热是主要的换热形式[6]。当相变储能单元受微重力影响时,液态相变材料速度由相变材料膨胀产生,其数量级大概为1.0×10-5m/s,无对流换热,热量主要通过热传导传递。
2.3 温度分布 图 8为2种情况下相变储能单元内相变材料的温度分布图,同样取液相质量分数?=0.2、0.4、0.6、0.8和1.0等5个时刻表示整个融化过程。
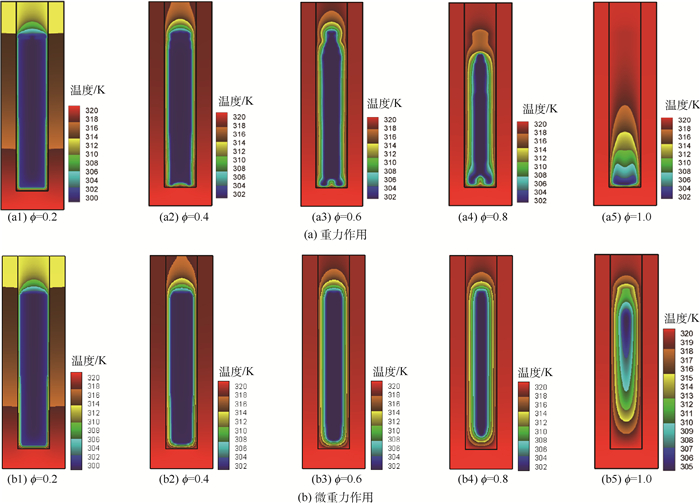 |
| 图 8 相变材料融化过程中温度分布 Fig. 8 Temperature distribution for melting process of phase change material |
| 图选项 |
相变过程初始阶段,相变储能单元内部温度分布并没有明显的区别。当融化进行到一定阶段,二者开始出现差异。当相变储能单元受重力影响时,内部自然对流使得温度较低、密度较大的相变材料进入底部,底部出现局部低温区域。当相变储能单元受微重力影响时,内部温度分布无自然对流影响,局部低温区域出现在相变材料顶端,由于相变储能单元顶部预留部分气体,此部分气体比热容很小,温度上升快,所以相变材料低温区域出现在相变储能单元中上部区域。
2.4 固-液两相分布 2种情况下相变储能单元固-液两相分布如图 9所示,当相变储能单元受重力影响时,融化的相变材料膨胀从顶端溢出,受重力作用后,液相相变材料覆盖于顶部;当相变储能单元受微重力影响时,融化的相变材料从顶端膨胀溢出,无重力作用时,向空间扩散。受重力作用时,未融化的相变材料下沉;无重力作用时,未融化相变材料悬浮于已融化相变材料中间,不出现下沉。
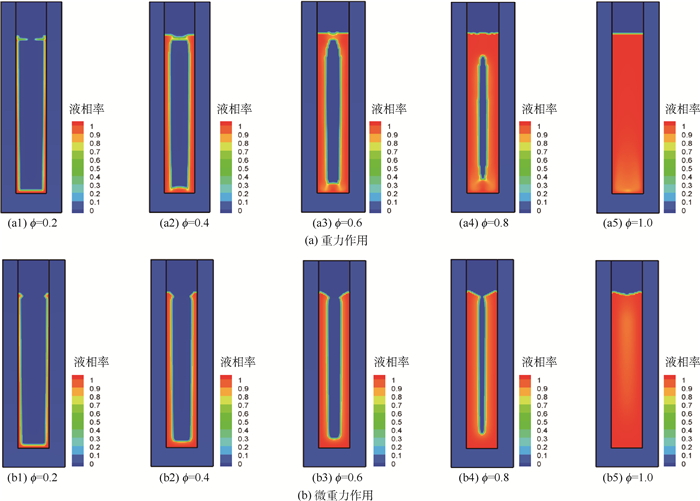 |
| 图 9 相变材料融化过程中固-液两相分布 Fig. 9 Solid-liquid distribution for melting process of phase change material |
| 图选项 |
3 结论 通过数值模拟方法对相变过程在重力和微重力作用的2种情况进行研究,并对受重力作用的相变过程数值模拟结果进行实验验证。数值模拟结果表明:
1) 相对于受重力作用,当相变储能单元无重力作用时,相变材料融化速率明显下降。融化速率受边界热流密度影响,当相变储能单元受微重力作用时,其边界热流密度明显小于相变储能单元受重力作用时的热流密度。
2) 当相变储能单元受重力作用时,肋片附近液相相变材料内部产生自然对流,并且对流换热是主要的换热形式。当相变储能单元受微重力影响时,液态相变材料速度是由于相变材料膨胀产生,无对流换热,热量主要通过热传导传递。
3) 当相变储能单元受重力影响时,内部自然对流使得温度较低、密度较大的相变材料进入底部,底部出现局部低温区域;当相变储能单元受微重力影响时,内部温度分布无自然对流影响,局部低温区域在相变储能单元中上部。
4) 当相变储能单元受重力影响时,融化的相变材料膨胀从顶端溢出,受重力作用后,液相相变材料覆盖于顶部;当相变储能单元受微重力影响时,融化的相变材料从顶端膨胀溢出,微重力作用时,向空间扩散。受重力作用时,未融化的相变材料下沉;无重力作用时,未融化相变材料悬浮于已融化相变材料中间,不下沉。
参考文献
| [1] | 闵桂荣, 郭舜. 航天器热控制[M]. 北京: 科学出版社, 1998: 320-357. MIN G R, GUO S. Thermal control technology of spacecraft[M]. Beijing: Science Press, 1998: 320-357. (in Chinese) |
| [2] | 王磊, 菅鲁京. 相变材料在航天器上的应用[J]. 航天器环境工程, 2013, 30(5): 522-528. WANG L, JIAN L J. Application of phase change materials in spacecraft[J]. Spacecraft Environment Engineering, 2013, 30(5): 522-528. DOI:10.3969/j.issn.1673-1379.2013.05.013 (in Chinese) |
| [3] | 侯增祺, 胡金刚. 航天器热控制技术原理及其应用[M]. 北京: 中国科学技术出版社, 2007: 177-188. HOU Z Q, HU J G. Principle and application of thermal control technology of spacecraft[M]. Beijing: China Science and Technology Press, 2007: 177-188. (in Chinese) |
| [4] | LEIMKUEHLER T O, STEPHAN R A, HANSEN S.Development, testing, and failure mechanisms of a replicative ice phase change material heat exchanger[C]//40th International Conference on Enviromental Systems.Reston: AIAA, 2010: 1-14. |
| [5] | LEE S A, LEIMKUEHLER T O, STEPHAN R A, et al.Thermal vacuum test of ice as a phase change material integrated with a radiator[C]//40th International Conference on Enviromental Systems.Reston: AIAA, 2010: 1-10. |
| [6] | YE W B, ZHU D S, WANG N. Numerical simulation on phase-change thermal storage/release in a plate-fin unit[J]. Applied Thermal Engineering, 2011, 31(1): 3871-3884. |
| [7] | YE W B, ZHU D S, WANG N. Fluid flow and heat transfer in a latent thermal energy unit with different phase change material (PCM) cavity volume fractions[J]. Applied Thermal Engineering, 2012, 42(3): 49-57. |
| [8] | ISMAIL K A R, ALVES C L F, MODESTO M S. Numerical and experimental study on the solidification of PCM around a vertical axially finned isothermal cylinder[J]. Applied Thermal Engineering, 2001, 21(1): 53-77. DOI:10.1016/S1359-4311(00)00002-8 |
| [9] | ABDULJALIL A A, MAT S, SOPIAN K, et al. Numerical study of PCM solidification in a triplex tube heat exchanger with internal and external fins[J]. International Journal of Heat and Mass Transfer, 2013, 61(1): 684-695. |
| [10] | ASSIS E, KATSMAN L, ZISKIND G, et al. Numerical and experimental study of melting in a spherical shell[J]. International Journal of Heat and Mass Transfer, 2007, 50(9-10): 1790-1804. DOI:10.1016/j.ijheatmasstransfer.2006.10.007 |
| [11] | ASSIS E, ZISKIND G, LETAN R. Numerical and experimental study of solidification in a spherical shell[J]. Journal of Heat Transfer, 2009, 131(2): 273-289. |
| [12] | HUMPHRIES W R, GRIGGS E I. A design handbook for phase change thermal control and energy storage devices[M]. New York: NASA Scientific and Technical Information Office, 1977: 155-160. |
| [13] | BERTRAND O, BINET B, COMBEAU H, et al. Melting driven by natural convection.A comparison exercise:First results[J]. International Journal of Thermal Science, 1999, 38(1): 5-26. DOI:10.1016/S0035-3159(99)80013-0 |
| [14] | BRENT A D, VOLLER V R, REID K J. Enthalpy-porosity technique for modeling convection-diffusion phase change:Application to the melting of a pure metal[J]. Numerical Heat Transfer, 1988, 13(3): 297-318. DOI:10.1080/10407788808913615 |
| [15] | SHATIKIAN V, ZISKIND G, LETAN R. Numerical investigation of a PCM-based heat sink with internal fins[J]. International Journal of Heat and Mass Transfer, 2005, 48(17): 3689-3706. DOI:10.1016/j.ijheatmasstransfer.2004.10.042 |
