为解决非合作目标的捕获难题,需发展一种新型的捕获方式。针对这一需求,科研人员通过近几年研究发现,壁虎脚掌表面微小的刚毛阵列在接触物体时可依靠范德华力效应,黏附在物体表面,无需目标物提供特殊接口[2],因此可将这种黏附方式运用到非合作目标物的捕获中,弥补传统捕获方式的局限性。国内外研究人员相继开展了基于这种仿壁虎黏附机理的捕获装置研究(仿生附着装置)[3]。美国斯坦福大学Hawkes等于2013年研制了基于范德瓦尔斯力效应的仿生附着装置[4-5],该装置通过腱加载方式控制黏附脚掌实现对平面目标物的附着和脱附,但未考虑目标物的运动特性对捕获过程的影响。来自同一实验室的Estrada等在2017年研制了一种基于同样机理的曲面目标抓取器[6],带有3自由度柔顺腕关节,可捕获运动中的曲面物体,并将运动参数对捕获过程的影响进行定量分析,利用穷举方法确定关节柔顺单元参数。同年,斯坦福大学Jiang等将上述平面和曲面抓取方法结合[7],研制了带有2自由度腕关节的整合附着装置,可捕获平面或曲面运动目标物,腕关节包含4根形状记忆合金,其目的是利用柔顺性耗散目标物能量并提供操作时的过载保护,但其局限是关节位移小且缺乏对关节柔顺参数的优化设计。在国内,北京航空航天大学和北京工业大学的研究人员也开展了仿生附着装置的研究,于2017年设计了基于恒力弹簧和串联滑轮组进行黏附力加载的附着装置[8-10],通过负载均担机制将阵列化扩展的仿生黏附单元黏附效果最大化,并建立静力学模型,分析和优化了附着装置对目标不同表面特性的适应能力。但空间中非合作目标的运动、姿态特性各异,上述装置并未考虑对不同运动目标的适应性,没有制定捕获不同运动目标的针对性方案,捕获运动目标物的能力有限,难以实现真正的在轨捕获。
考虑到以上问题,本文在实验室研制的附着装置基础上[8-10],利用多自由度柔顺关节辅助附着机构适应运动目标物,首先完成了柔顺关节构型设计,并提出在捕获中利用柔顺单元能量耗散原理降低目标物动能以提高附着装置对于目标运动参数适应性的方法。基于ADAMS/View建立了集成柔顺关节的仿生附着装置参数化模型,针对运动中的平面目标物捕获过程进行仿真,分析了关节运动规律,并通过ADAMS-iSIGHT联合仿真完成对关节柔顺单元弹簧刚度系数、黏滞阻尼系数等参数优化,进一步提高了装置对运动目标物的捕获能力,其结果可为样机制作提供参考。
1 仿生附着装置柔顺关节构型设计 该仿生附着装置整体由2部分组成:上部的多自由度柔顺关节和下部的附着机构,如图 1所示。
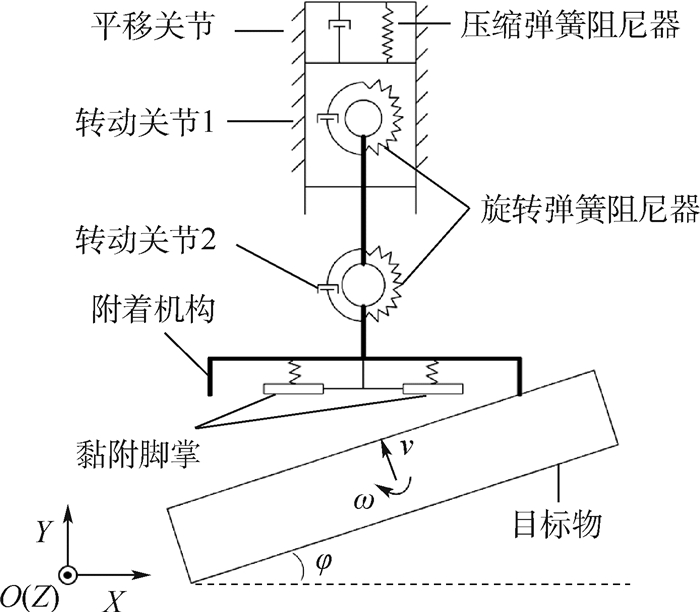 |
| 图 1 仿生附着装置组成原理图 Fig. 1 Schematic diagram of bionic adhesive device composition |
| 图选项 |
附着机构部分用于黏附力的加载与卸载控制[8-10],其位姿的改变由上部连接的多自由度柔顺关节运动配合完成。柔顺关节由1个平移关节和2个转动关节串联组成,其中平移关节一端连接基座,使用压缩弹簧及直线阻尼器作为柔顺单元;另一端使用铰链依次连接2个连杆,形成转动关节1和转动关节2,各使用一组旋转弹簧及旋转阻尼器作为柔顺单元,转动关节2下部连杆通过机械接口刚接在附着机构框架上。在捕获运动目标物时,机构工作过程可分为碰撞、对齐、实施捕获3个阶段:
1) 碰撞:空间微重力环境下待捕获目标物处于自由漂浮状态,各关节均处于弹簧未发生形变的起始位置。运动目标物以一定相对速度和偏航角逐渐贴近附着机构,直到与附着机构刚性外伸支撑架碰撞(见图 1),目标物及附着机构受碰撞力和摩擦力的影响后相对姿态发生改变。
2) 对齐:受到冲击力后附着机构姿态发生改变,其中转动关节1与转动关节2以相反方向发生转动,扭转弹簧扭转,旋转阻尼器根据关节转速输出力矩,同时平移关节产生Y向位移,弹簧压缩,直线阻尼器根据关节移速输出阻尼力。通过3个关节自适应运动,使附着机构姿态逐渐适应目标物偏航角,最终附着机构底部黏附脚掌与目标物表面实现对齐(见图 2),这是仿壁虎黏附脚掌进行黏附力加载的特殊前提条件[11]。在此过程中目标物因柔顺单元持续产生的弹簧阻尼力作用,其动能逐渐被耗散。
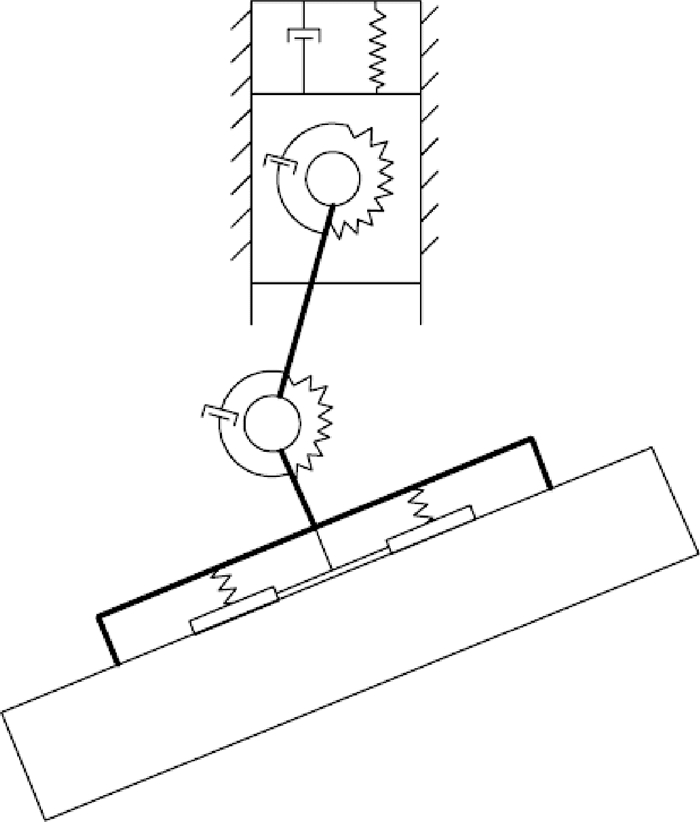 |
| 图 2 对齐示意图 Fig. 2 Schematic diagram of alignment |
| 图选项 |
3) 实施捕获:在被动对齐完成后,通过附着机构内部控制模块和加载模块进行黏附力加载,保证黏附脚掌与目标物稳定锁合[8-10],完成捕获。
根据以上3部分机构工作原理,可实现装置对运动目标的适应,以上部分作为运动学与动力学建模的基础。
2 仿生附着装置柔顺关节建模 2.1 运动学和动力学建模 为验证柔顺关节有效性,利用虚拟样机分析软件ADAMS(Automatic Dynamic Analysis of Mechanical Systems),建立基于柔顺关节的附着装置捕获运动目标物的运动学和动力学模型[12],相比于纯数学建模方式可节省大量的建模时间和成本,模型整体组成如图 3所示。
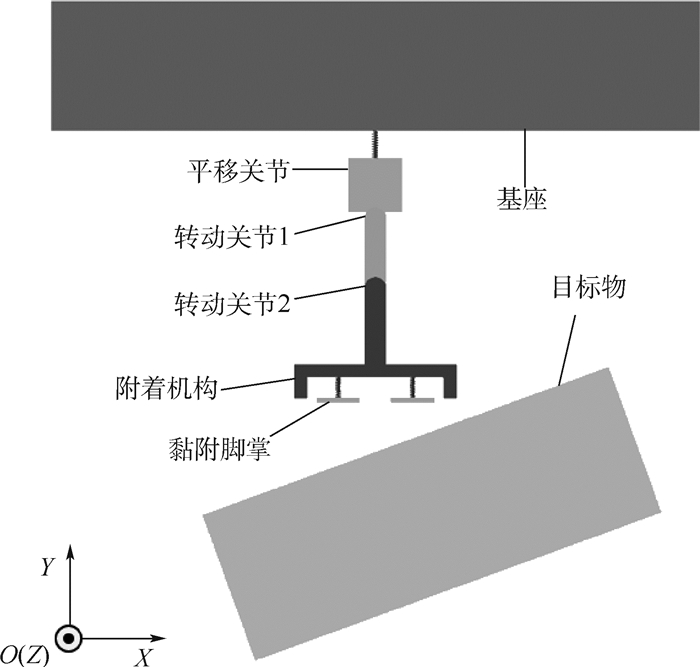 |
| 图 3 ADAMS模型整体组成 Fig. 3 Overall composition of ADAMS model |
| 图选项 |
ADAMS模型中,使用大质量漂浮基作为连接基座。平移关节用滑块表示,一端使用弹簧连接在基座上并添加移动副约束,另一端依次用转动副连接两连杆,形成2个转动关节。附着机构框架模型与连杆2刚性连接,底部黏附脚掌使用一对通过弹簧连接在框架上的刚体替代,模拟机构进行腱加载的柔性脚掌阵列[8-10]。此外,添加漂浮状态的长方体作为待捕获的目标物,以便进行下一步的仿真。以上模型运动约束目前只考虑在XY平面内的运动,零件关键物理参数如表 1所示。
表 1 零件关键物理参数 Table 1 Parts' key physical parameters
| 零件 | 质量/kg | 绕质心转动惯量/(kg·mm2) |
| 基座 | 224.67 | 3.27×106 |
| 平移滑块 | 1.80×10-2 | 2.37 |
| 连杆1 | 0.29 | 0.28 |
| 连杆2+附着机构框架 | 0.562 | 13.65 |
| 目标物 | 31.37 | 1.58×105 |
表选项
通过在模型中添加载荷,建立动力学模型。目标物与附着机构框架和黏附脚掌间碰撞力在ADAMS/View中根据Hertz接触理论,由IMPACT函数提供的非线性等效弹簧阻尼模型计算,如式(1)所示:
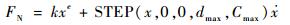 | (1) |
式中:FN为构件碰撞产生的正压力;k为材料等效刚度;x为碰撞物体挤压变形量; e为力的非线性指数;STEP为阶跃函数;dmax为构件最大变形深度;Cmax为材料最大等效阻尼系数。
构件间摩擦力使用Coulomb干摩擦模型表征,摩擦力计算式为
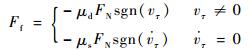 | (2) |
式中:μd和μs分别为物体间动摩擦系数和静摩擦系数;vτ和
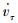
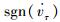
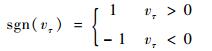 | (3) |
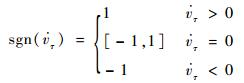 | (4) |
根据以上接触和摩擦模型,在ADAMS中将必要参数做相应设置,如表 2所示。
表 2 接触和摩擦模型参数 Table 2 Contact and friction model parameters
| 参数 | 数值 |
| 材料等效刚度k/(N·mm-1) | 100 000 |
| 非线性指数e | 2.2 |
| 材料最大等效阻尼系数Cmax /(N·s·mm-1) | 10 |
| 构件最大变形深度dmax/mm | 0.1 |
| 静摩擦系数μs | 0.3 |
| 动摩擦系数μd | 0.1 |
| 静摩擦临界速度vs/(mm·s-1) | 100 |
| 动摩擦临界速度vd/(mm·s-1) | 1 000 |
表选项
关节柔顺性通过在ADAMS中对各关节施加柔性连接力实现,平移关节处添加一对压缩弹簧阻尼器,作用力计算式为
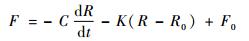 | (5) |
式中:R为弹簧两端相对位移;t为时间;C为黏滞阻尼系数;K为弹簧刚度系数;R0为初始相对位移;F0为弹簧预紧力。2个转动关节处各添加一对旋转弹簧阻尼器,作用力矩计算式为
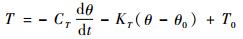 | (6) |
式中:θ为弹簧扭转角;CT为旋转弹簧阻尼系数;KT为旋转弹簧刚度系数;θ0为初始相对角位移;T0为弹簧预紧力矩。3个关节处的初始位移与预紧都设置为零值,因此影响关节柔顺性的参数为3个关节各自的柔顺单元弹簧刚度和阻尼系数。
2.2 捕获条件和状态分析 捕获模型建立后,考虑到不同的运动情况,捕获过程可能发生如下3种结果:
1) 通过柔顺关节带动附着机构自适应运动,底面仿壁虎黏附脚掌完成与目标物表面的充分对齐,可成功通过黏附力加载实施捕获。
2) 关节在运动中达到自身极限位移,未能在有效行程内辅助附着机构与目标物对齐,不满足黏附力加载条件,无法实施捕获。
3) 关节柔顺性差,目标物与附着机构发生初始碰撞后受到过度冲击,造成目标逃逸,捕获失败。
将以上3种可能发生的结果均作为ADAMS中捕获仿真结束条件,在软件中设置捕获工况如表 3和表 4所示,通过仿真,对关节运动状态进行分析。
表 3 柔顺单元相关参数 Table 3 Related parameters of compliant units
| 参数 | 数值 |
| 平移关节压缩弹簧刚度系数/(N·mm-1) | 0.1 |
| 平移关节黏滞阻尼系数/(N·s·mm-1) | 0.1 |
| 转动关节1旋转弹簧刚度系数/(N·mm·(°)-1) | 0.1 |
| 转动关节1黏滞阻尼系数/(N·mm·s·(°)-1) | 0.1 |
| 转动关节2旋转弹簧刚度系数/(N·mm·(°)-1) | 0.1 |
| 转动关节2黏滞阻尼系数/(N·mm·s·(°)-1) | 0.1 |
表选项
表 4 目标物运动参数 Table 4 Target motion parameters
| 参数 | 数值 |
| 线速度/(m·s-1) | 0.1 |
| 角速度/((°)·s-1) | 0.1 |
| 偏航角/(°) | 20 |
表选项
目标物在0.22 s与附着机构外伸框架发生碰撞后,多自由度柔顺关节开始配合目标物运动,平移关节压缩,2个转动关节以相反方向扭转,位移变化趋势如图 4所示,最终在0.53 s实现黏附脚掌与目标物的对齐,仿真停止,模型状态如图 5所示。
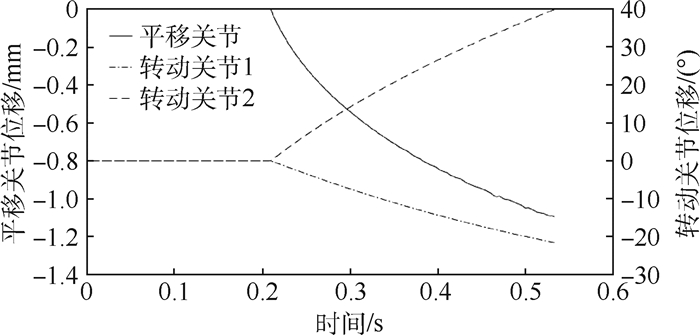 |
| 图 4 柔顺关节位移曲线 Fig. 4 Curves of compliant joint displacement |
| 图选项 |
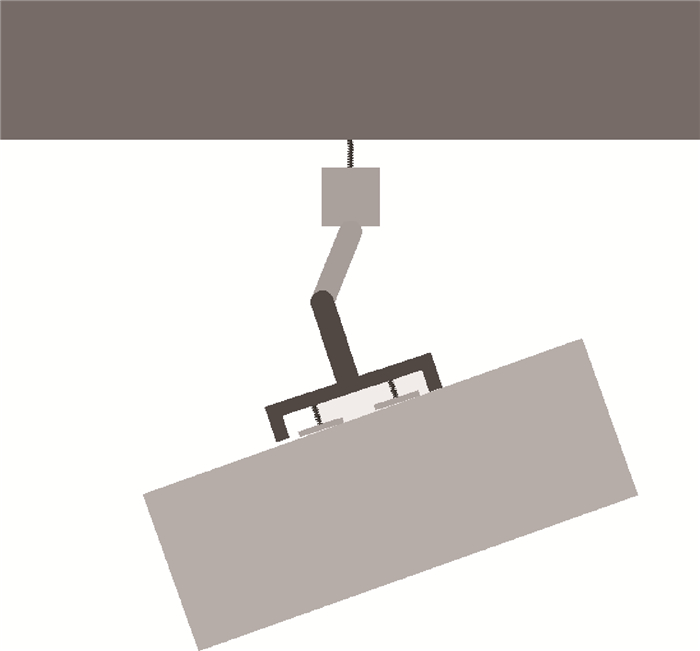 |
| 图 5 对齐完成时刻模型状态 Fig. 5 Model state at alignment completion moment |
| 图选项 |
由于柔顺关节的能量耗散作用,目标物动能由156.85 mJ降低到139.51 mJ,且经观察得知由于初始偏航角的存在,目标物在被动对齐过程中角速度变化呈上升趋势,结果如图 6所示。
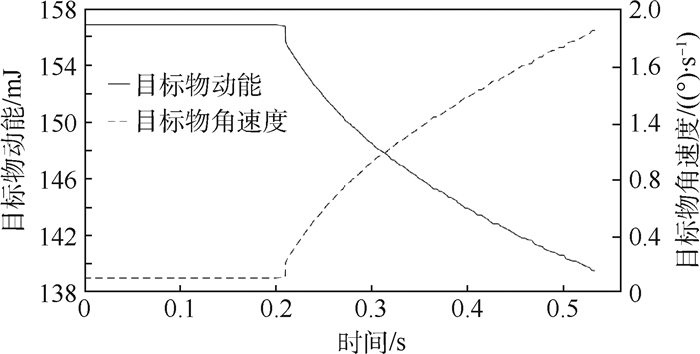 |
| 图 6 目标物状态参数变化 Fig. 6 Change of target state parameters |
| 图选项 |
在上述工况下,柔顺关节可以辅助机构完成对齐过程,但随着柔顺单元参数组合的改变,对齐时刻的目标物角速度和残余动能各有差异。若目标物角速度超出黏附脚掌材料能承受的极限[13],则对应的柔顺单元参数不可取,并且按照设计预期,目标物残余动能应尽量小,才能尽可能减少捕获后目标物扰动,为捕获后的目标物操控提供便利。此外,不同的参数组合还会导致第2、3种捕获失败的结果,例如若平移关节柔顺单元系数取值过小,则会在捕获中过早达到位移极限,使对齐无法完成;又或当转动关节柔顺单元取值过大,关节柔顺性差,碰撞后未配合目标物初始偏航角实现被动姿态适应,使目标物所受反作用力过大,经过度撞击后发生逃逸。综上,受限于黏附脚掌与目标物需完成对齐这一捕获前提,以及对齐时的目标物角速度,为达到最优的能量耗散效果,提高附着装置捕获运动目标物的能力,须对关节柔顺单元参数进行优化。
3 仿生附着装置柔顺关节参数优化 3.1 优化模型建立 为提高附着装置对目标运动参数的适应性,应能通过对柔顺关节的参数优化,使其可捕获的目标物运动参数达到一定包络范围,本次优化中规定该范围:线速度v≤0.1 m/s,角速度ω≤0.1(°)/s,偏航角φ≤20°。即对于运动参数在上述范围以内的目标,都能通过柔顺关节的被动姿态调整与黏附脚掌完成被动对齐,并保证目标对齐时刻角速度在黏附脚掌动态模型允许范围内,且被耗散动能尽可能大,详细模型的数学表述如下[14]。
优化函数目标:使柔顺关节的能量耗散效果最优,即经过能量耗散后目标物残余动能E(由线动能和角动能之和表示)最小:
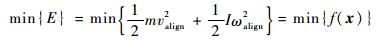 | (7) |
式中:valign和ωalign分别为对齐时刻目标物质心线速度和角速度;m和I分别为目标物的质量和转动惯量;向量x为设计变量。
设计变量:影响关节柔顺性的变量为各关节的弹簧刚度系数和黏滞阻尼系数,写成向量形式为
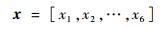 | (8) |
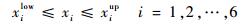 | (9) |
式中:xi为每个关节的弹簧刚度或黏滞阻尼系数。本次优化中,根据满足实际关节尺寸、可供选择的弹簧阻尼器设定变量范围如表 5所示。
表 5 设计变量范围 Table 5 Design variable range
| 变量 | 变化区间 |
| 平移关节压缩弹簧刚度系数x1/(N·mm-1) | [0, 1] |
| 平移关节黏滞阻尼系数x2/(N·s ·mm-1) | [0, 1] |
| 转动关节1旋转弹簧刚度系数x3/(N·mm·(°)-1) | [0, 1.5] |
| 转动关节1黏滞阻尼系数x4/(N·mm·s·(°)-1) | [0, 1.5] |
| 转动关节2旋转弹簧刚度系数x5/(N·mm·(°)-1) | [0, 1.5] |
| 转动关节2黏滞阻尼系数x6/(N·mm·s·(°)-1) | [0, 1.5] |
表选项
约束条件:以目标物平面分别与左、右黏附脚掌的距离lleft、lright同时为0表征被动对齐时刻:
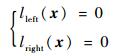 | (10) |
ωalign为对齐时刻的目标物角速度:
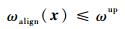 | (11) |
本次优化中假定黏附脚掌可允许最大对齐角速度即ωup=5(°)/s。
3.2 优化方法 由于ADAMS自身参数优化功能有限,且仅提供广义梯度下降法和序列二次规划法,经试验发现运用这2种算法对于本优化模型求解均会产生早熟现象,无法找到真正全局最优解,且ADAMS进行优化求解占用资源大,优化周期较长。因此,本文借助多学科优化软件iSIGHT集成ADAMS/View的方式进行参数优化[14],可大量减少优化时间,并且iSIGHT优化器中可供选择的优化算法更为丰富,运行流程如图 7所示。首先,利用simcode方式编写输入文件,与ADAMS模型中的变量建立映射关系;然后,调用ADAMS模型脚本进行仿真,将每次仿真输出的文件送入iSIGHT优化器进行分析完成一次优化求解。
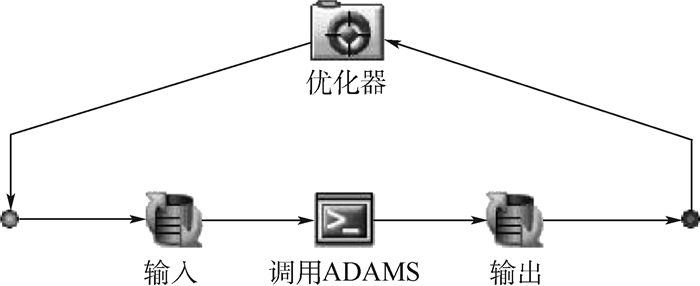 |
| 图 7 iSIGHT集成ADAMS优化流程 Fig. 7 Flowchart of iSIGHT integrated ADAMS optimization |
| 图选项 |
为避免早熟现象,选择iSIGHT中的多岛遗传算法(multi-island genetic algorithm)作为本次参数优化算法,该算法本质上是Kaneko、Miki和Hiroyasu等对并行分布遗传算法(Parallel Distributed Genetic Algorithms, PDGAs)的改进[15],优点是对初值不敏感,鲁棒性强,相比传统遗传算法,在全局求解能力和计算效率上更具优势[16],且不容易陷入局部极值状态[17]。
3.3 优化结果分析 优化后得到126组目标函数即目标物残余动能迭代过程,结果如图 8所示。图中:违约解表示目标物无法完成对齐或者对齐角速度超出极限,其余点为可行解,其中使目标函数达到最小值的参数组合即最终优化结果。优化前后参数对比如表 6所示。
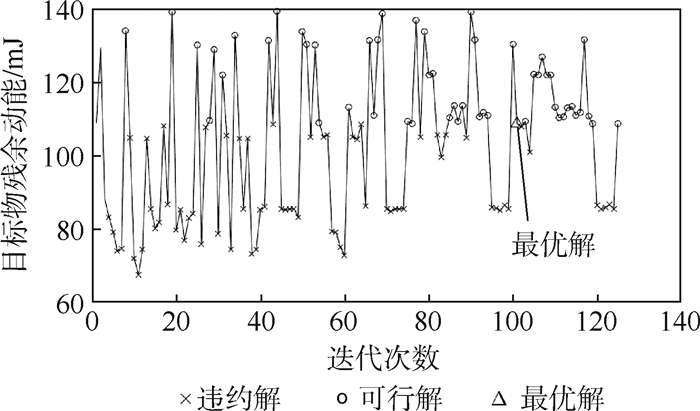 |
| 图 8 目标函数迭代过程 Fig. 8 Objective function iterative process |
| 图选项 |
表 6 优化变量对比 Table 6 Optimized variable comparison
| 变量 | 初始值 | 优化值 |
| x1/(N·mm-1) | 0.1 | 0.103 66 |
| x2/(N·s ·mm-1) | 0.1 | 0.897 07 |
| x3/(N·mm·(°)-1) | 0.1 | 0.176 26 |
| x4/(N·mm·s·(°)-1) | 0.1 | 0.211 61 |
| x5/(N·mm·(°)-1) | 0.1 | 0.117 29 |
| x6/(N·mm·s·(°)-1) | 0.1 | 0.397 71 |
表选项
取目标物运动参数处于极端工况时(线速度v=0.1 m/s,角速度ω=0.1(°)/s,偏航角φ=20°观察优化效果,装置通过柔顺关节的自适应运动,完成黏附脚掌与目标物表面的对齐,其动能由自由漂浮状态下的156.85 mJ耗散至108.58 mJ,柔顺单元的能量耗散效果在参数优化后得到显著提升,优化前后目标物动能的变化趋势如图 9所示,详细参数如表 7所示。
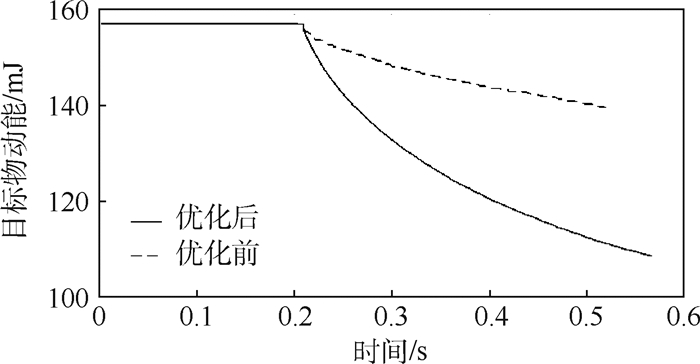 |
| 图 9 优化前后目标物动能变化对比 Fig. 9 Comparison of target kinetic energy before and after optimization |
| 图选项 |
表 7 优化目标对比 Table 7 Optimization target comparison
| 参数 | 优化前 | 优化后 |
| 目标物初始动能/mJ | 156.85 | 156.85 |
| 目标物残余动能/mJ | 139.51 | 108.58 |
| 动能耗散量/mJ | 17.34 | 48.27 |
| 对齐角速度/((°)·s-1) | 1.8 | 4.9 |
表选项
因此,通过参数优化,附着装置对目标运动参数的适应性得到提升,能够捕获运动参数在规定包络范围内变化的目标物,并且多自由度柔顺关节对目标物的能量耗散效果显著提高。
4 结论 1) 通过多自由度柔顺关节构型设计,提高了实验室研制的仿生附着装置对运动目标物的适应能力,根据设计构型,在ADAMS软件中建立了运动学与动力学模型,并进行了捕获仿真,通过附着装置及目标物相关参数变化趋势,对附着装置柔顺关节运动规律进行了分析。
2) 通过多学科优化软件iSIGHT集成ADAMS的方式,采用多岛遗传算法对多自由度柔顺关节参数进行优化设计,优化后附着装置能够捕获运动参数在线速度v≤0.1 m/s,角速度ω≤0.1(°)/s,偏航角φ≤20°的包络范围内变化的平面目标物,且能量耗散效果显著提高,优化结果可为样机制作提供参考。
参考文献
| [1] | 王超, 董正宏, 尹航, 等. 空间目标在轨捕获技术研究综述[J]. 装备学院学报, 2013, 24(4): 63-66. WANG C, DONG Z H, YIN H, et al. Research summarizing of on-orbit oapture technology for space target[J]. Journal of Academy of Equipment, 2013, 24(4): 63-66. DOI:10.3783/j.issn.2095-3828.2013.04.016 (in Chinese) |
| [2] | 陈罗婧, 傅丹膺, 袁春柱, 等. 仿生壁虎微纳米黏附阵列的空间应用[J]. 航天器环境工程, 2013, 30(6): 616-622. CHEN L J, FU D Y, YUAN C Z, et al. Biomimetic gecko micro/nano-structure adhesive array in space application[J]. Spacecraft Environment Engineering, 2013, 30(6): 616-622. DOI:10.3969/j.issn.1673-1379.2013.06.010 (in Chinese) |
| [3] | 张昊.大壁虎运动行为研究及仿壁虎机器人研制[D].南京: 南京航空航天大学, 2010: 7-11. ZHANG H.Research on gecko's moving behavior and developing gecko-like robot[D].Nanjing: Nanjing University of Aeronautic and Astronautics, 2010: 7-11(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291444.htm |
| [4] | HAWKES E W, EASON E V, ASBECK A T, et al. The gecko's toe:Scaling directional adhesives for climbing applications[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(2): 518-526. DOI:10.1109/TMECH.2012.2209672 |
| [5] | HAWKES E W, CHRISTENSEN D L, EASON E V, et al.Dynamic surface grasping with directional adhesion[C]//IEEE International Conference on Intelligent Robots and Systems.Piscataway, NJ: IEEE Press, 2013, 8215(2): 5487-5493. https://www.researchgate.net/publication/261353633_Dynamic_surface_grasping_with_directional_adhesion |
| [6] | ESTRADA M A, JIANG H, NOLL B, et al.Force and moment constraints of a curved surface gripper and wrist for assistive free flyers[C]//IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 2017: 2824-2830. http://www.researchgate.net/publication/318688860_Force_and_moment_constraints_of_a_curved_surface_gripper_and_wrist_for_assistive_free_flyers |
| [7] | JIANG H, HAWKES E W, FULLER C, et al. A robotic device using gecko-inspired adhesives can grasp and manipulate large objects in microgravity[J]. Science Robotics, 2017, 2(7): n4545. DOI:10.1126/scirobotics.aan4545 |
| [8] | 叶家宇.空间仿生附着机构的设计与实现[D].北京: 北京工业大学, 2017: 25-41. YE J Y.Design and implementation of spatial biomimetic adhesive device[D].Beijing: Beijing University of Technology, 2017: 25-41(in Chinese). |
| [9] | 崔晶, 楚中毅, 叶家宇, 等.一种基于复合恒力弹簧加载的仿生干黏附机构: 2016108360112[P].2017-03-15. CUI J, CHU Z Y, YE J Y, et al.A biomimetic dry adhesion mechanism based on composite constant force spring loading: 2016108360112[P].2017-03-15(in Chinese). |
| [10] | YE J Y, CHU Z Y, CUI J.Optimization design of microstroke table for gecko adhesives actuating[C]//IEEE International Conference on Nanotechnology.Piscataway, NJ: IEEE Press, 2017: 330-333. |
| [11] | HAWKES E W.Applying dry adhesives to the real world[D].Palo Alto: Stanford University, 2015: 7-9. |
| [12] | 刘坤明, 徐国艳, 余贵珍. 驾驶机器人机械腿动力学建模与仿真分析[J]. 北京航空航天大学学报, 2016, 42(8): 1709-1714. LIU K M, XU G Y, YU G Z. Dynamic modeling and simulation analysis of robot driver's mechanical legs[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8): 1709-1714. (in Chinese) |
| [13] | KATO H.Anisotropic adhesion model for translational and rotational motion[C]//IEEE/SICE International Symposium on System Integration.Piscataway, NJ: IEEE Press, 2013: 385-391. |
| [14] | 吴建云, 王春洁, 汪翰. 月球着陆器模型参数修正[J]. 北京航空航天大学学报, 2013, 39(10): 1366-1369. WU J Y, WANG C J, WANG H. Model parameters updating of lunar lander[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(10): 1366-1369. (in Chinese) |
| [15] | 赖宇阳, 姜欣. Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012: 139-140. LAI Y Y, JIANG X. Isight parameter optimization theory and example explanation[M]. Beijing: Beihang University Press, 2012: 139-140. (in Chinese) |
| [16] | 赵德建, 王延奎, 周平, 等. 基于多岛遗传算法的二维翼型吸气减阻优化[J]. 北京航空航天大学学报, 2015, 41(5): 941-946. ZHAO D J, WANG Y K, ZHOU P, et al. Optimization of drag-reduction by suction using multi-island genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 941-946. (in Chinese) |
| [17] | 张鼎逆, 刘毅. 基于改进遗传算法和序列二次规划的再入轨迹优化[J]. 浙江大学学报(工学版), 2014, 48(1): 161-167. ZHANG D N, LIU Y. Reentry trajectory optimization based on improved genetic algorithm and sequential quadratic programming[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(1): 161-167. (in Chinese) |
