基于模型的机械臂运动学标定方法主要包括运动学建模、末端位姿测量、运动学参数辨识和运动学参数补偿4个步骤[1-3]。用于机械臂运动学标定的运动学模型有3个评价原则:完整性、连续性和极小性[4]。完整性是指机械臂运动学模型必须有足够多的参数去辨识实际结构参数与名义结构参数之间的所有偏差。连续性是指机械臂结构参数的任意微小连续变动会伴随着运动学参数的连续改变。极小性是指运动学误差模型不包含冗余参数。
针对机械臂运动学标定问题,国内外****开展了大量的研究工作。传统的机械臂运动学标定方法大多基于DH模型,此方法的缺点是当相邻关节接近平行时,机械臂会出现奇异性问题。Hayati[5]在DH模型的基础上,通过引入绕Y轴转动的参数β描述相邻平行关节轴线的偏差,消除了基于DH模型进行运动学标定时出现的奇异性问题。Stone[6]提出了6个参数的S模型,并应用到机械臂运动学标定。Zhuang等[7-8]提出了6参数的CPC(Complete and Parametrically Continuous)模型和4参数的MCPC (Modified Complete and Parametrically Continuous)模型,在此基础上建立了运动学标定模型进行机械臂运动学标定。Chen和Yang[9]提出了一种基于指数积(Product of Exponentials, POE)公式的机械臂运动学标定方法,该方法建立的运动学误差模型包含了关节角度误差。何锐波等[10-11]基于指数积公式提出了一种通用的串联机械臂运动学标定方法(该方法包含3种实用的运动学误差模型),并分析了各种运动学参数的可辨识性。陈根良等[12]基于指数积公式提出了一种系统性的串联机械臂运动学标定方法,该方法建立的运动学误差模型满足完整性、极小性和连续性原则。
由于在轨环境的特殊性,无法借助外部精密测量设备测量机械臂末端实际位姿。在空间机械臂运动学标定过程中,需要使用空间机械臂自带的视觉系统测量机械臂末端实际位姿,进行运动学自标定。针对机械臂运动学自标定问题,国内外****开展了一定的研究工作。Angulo和Torras[13]提出了一种基于神经网络的空间机械臂自标定方法,并将运动学标定系统应用到戴姆勒奔驰宇航中心的空间站模型。Liang等[14]提出了一种基于视觉反馈的手眼系统自适应标定方法,并使用卡尔曼滤波技术论证了其有效性。Gong等[15]使用安装在机械臂末端执行器上的混合非接触式光学传感器实现了基于距离误差的6自由度机械臂运动学自标定。刘宇等[16]提出了一种基于手眼视觉的空间机械臂自标定方法, 该方法建立了空间机械臂相对位姿误差模型,并使用粒子群算法对运动学参数进行辨识。Du和Zhang[17]利用安装在机械臂末端的相机和安装在固定位置的标定板测量机械臂末端位姿,实现了机械臂运动学自标定。Zhang等[18]利用安装在固定位置相机和安装在机械臂末端的平面标识测量机械臂末端位姿,实现了基于局部指数积公式的机械臂运动学标定。
上述机械臂运动学标定方法能在一定条件下解决机械臂的运动学标定问题。然而7自由度大臂展空间机械臂结构尺寸较大且材料特殊,导致其臂杆容易发生较大变形;此外在轨环境存在一定的特殊性,导致无法借助外部精密设备测量空间机械臂末端位姿。这对空间机械臂末端位姿测量和运动学标定模型的建立提出了更高的要求。因此传统的机械臂运动学标定方法无法应用于7自由度大臂展空间机械臂运动学在轨标定问题。
针对7自由度大臂展空间机械臂运动学在轨标定存在的问题,提出了一种基于指数积公式的空间机械臂运动学在轨自标定方法。首先, 建立了空间机械臂运动学在轨自标定系统,标定系统在不使用外部测量设备的前提下,实现了空间机械臂末端位姿自动测量;然后, 通过误差分析建立了空间机械臂实际运动学模型,在此基础上推导了空间机械臂运动学误差模型和运动学标定模型;最后, 进行了7自由度大臂展空间机械臂运动学自标定仿真,结果表明本文提出的运动学自标定方法能有效提高空间机械臂末端位姿精度。
1 空间机械臂运动学在轨标定系统 不同于地面上的机械臂运动学标定,在轨运行期间,7自由度大臂展空间机械臂末端位姿测量存在2方面问题:一方面是由于自身较大的结构尺寸和在轨极端的温度环境,无法使用外部精密测量设备测量末端位姿;另一方面是由于空间环境存在一定的特殊性,对末端位姿测量的自动化程度提出了更高的要求。针对上述问题,利用空间机械臂自带的视觉系统和棋盘式标定板测量空间机械臂末端位姿,建立了一种新的空间机械臂运动学在轨自标定系统。
空间机械臂运动学自标定系统如图 1所示。空间机械臂为7自由度大臂展空间机械臂,安装在空间站舱体外侧,其末端安装有双目空间相机, 7自由度大臂展空间机械臂如图 2所示。标定板为棋盘式,安装在空间站舱体外侧,利用棋盘格上的角点可以构建标定板坐标系,棋盘式标定板通常用于空间相机内外参数标定,在标定系统中作为空间相机测量的靶标。假设标定板坐标系{c}相对于空间机械臂基座坐标系{s}的位姿变换矩阵sTc已知,使用空间相机测量标定板,可得到空间机械臂末端坐标系{t}相对于标定板坐标系{c}的位姿变换矩阵cTt,进一步可计算得到空间机械臂末端坐标系{t}相对于空间机械臂基座坐标系{s}的位姿变换矩阵sTt = sTccTt,即空间机械臂末端位姿实际值。因此,运动学标定系统充分利用空间站现有设备实现了空间机械臂末端位姿自动化测量。
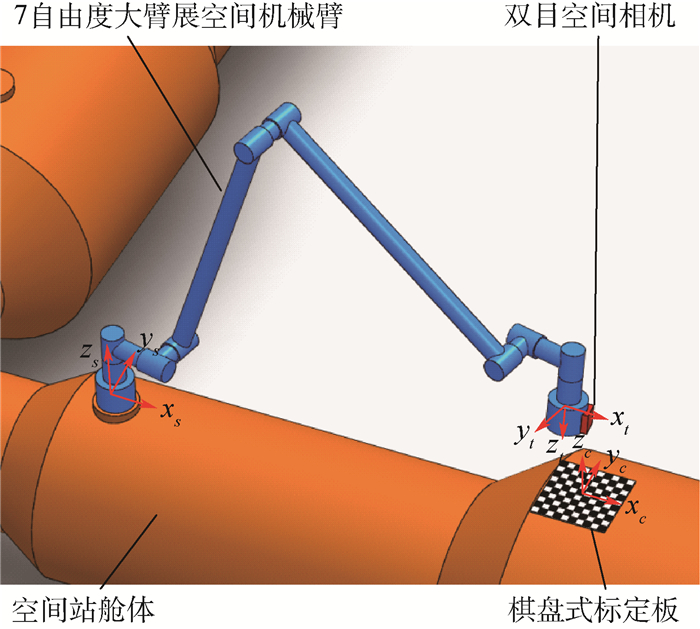 |
| 图 1 空间机械臂运动学自标定系统 Fig. 1 Kinematics self-calibration system for space manipulator |
| 图选项 |
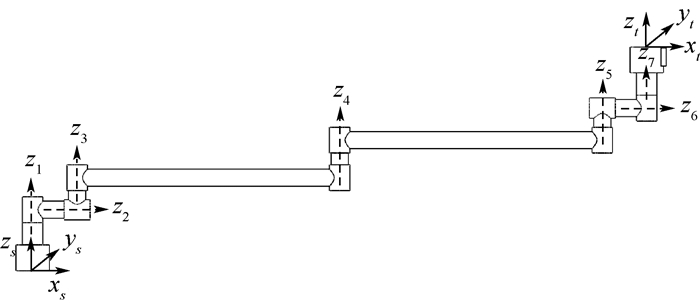 |
| 图 2 7自由度空间机械臂 Fig. 2 A 7-DOF space manipulator |
| 图选项 |
测量足够多的末端位姿,利用下文推导的空间机械臂运动学标定模型,可以实现空间机械臂运动学在轨自标定。
2 空间机械臂运动学模型 2.1 理论运动学模型 不同于传统的运动学建模方法,基于指数积公式的空间机械臂运动学模型仅需要建立2个坐标系:空间机械臂基座坐标系{s}和空间机械臂末端坐标系{t},如图 2所示。n自由度空间机械臂运动学模型的表达式为
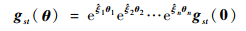 | (1) |
式中:θ为空间机械臂关节角度向量;θi为第i号关节的关节角度;
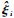
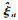
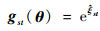 | (2) |
式中:
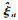
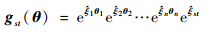 | (3) |
2.2 误差分析 对空间机械臂运动学模型取微分,可以得到空间机械臂运动学误差模型:
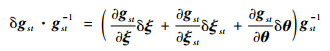 | (4) |
式中:ξ=[ξ1T, ξ2T, …, ξnT]T∈R6n;θ=[θ1, θ2, …, θn]T∈Rn。
由空间机械臂运动学误差模型式(4)可知,空间机械臂的末端位姿误差是由关节旋量误差δξ、关节零位误差δθ和初始位姿变换旋量误差δξst造成的。文献[20]证明了空间机械臂关节零位误差δθ可归结到关节旋量误差δξ,不需要单独辨识。因此,空间机械臂运动学标定只需要辨识和补偿关节旋量误差δξ和初始位姿变换旋量误差δξst。空间机械臂运动学误差模型式(4)可化简为
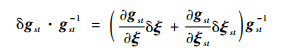 | (5) |
假设空间机械臂末端位姿实际值为gsta,理论值为gstn,则δgst·gst-1可写为[21]
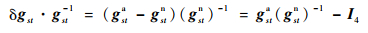 | (6) |
如果末端位姿误差足够小,gsta(gstn)-1近似于单位矩阵,可得[9]
 | (7) |
取一阶近似,式(6)可写为
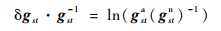 | (8) |
因此,空间机械臂运动学参数辨识也就是求解如式(9)所示的最小二乘问题:
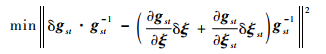 | (9) |
2.3 实际运动学模型 由误差分析可知,空间机械臂的运动学参数误差是由空间机械臂的关节旋量误差δξ和初始位姿变换旋量误差δξst造成的。关节旋量误差δξ可以使用某个旋量指数
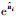
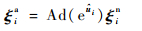 | (10) |
式中:旋量指数
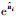
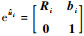
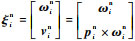
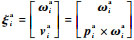
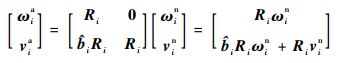 | (11) |
可以证明,经过伴随变换得到的关节旋量实际值ξia仍满足关节约束条件:
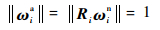 | (12) |
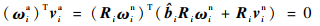 | (13) |
根据式(10)中空间机械臂关节旋量理论值和实际值的伴随变换关系,可以建立空间机械臂实际运动学模型:
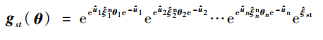 | (14) |
3 空间机械臂运动学标定模型 3.1 运动学误差模型 将式(14)代入式(5),得到空间机械臂运动学误差模型的表达式为
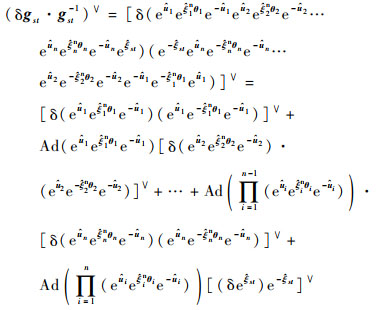 | (15) |
式中:
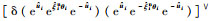
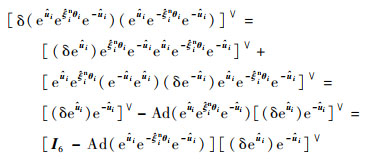 | (16) |
其中:
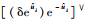
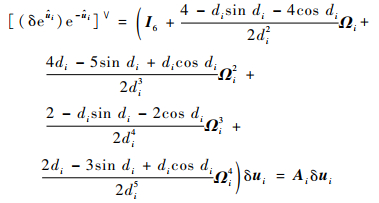 | (17) |
式中:
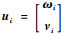
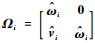
同理,式(15)中
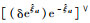
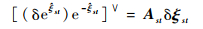 | (18) |
将式(16)~式(18)代入式(15),空间机械臂运动学误差模型可化简为
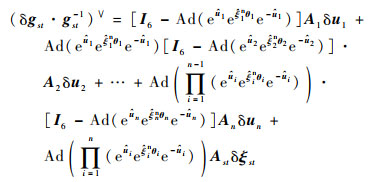 | (19) |
空间机械臂运动学误差模型式(19)可以整理为
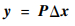 | (20) |
式中:
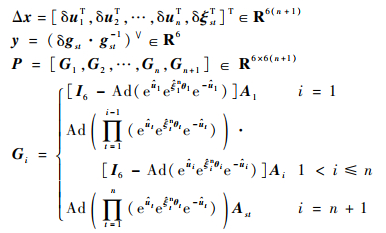 |
3.2 运动学标定方程 由空间机械臂运动学误差模型可知,利用每个末端测量位姿可以建立1组运动学误差方程。设置m个空间机械臂末端测量位姿,可以建立m组运动学误差方程,联立这些运动学误差方程可以得到空间机械臂运动学标定模型:
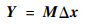 | (21) |
式中:Y=[y1T, y2T, …, ymT]T;M=[P1T, P2T, …, PmT]T。
使用最小二乘法求解空间机械臂运动学标定模型,可以得到空间机械臂运动学参数误差:
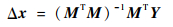 | (22) |
4 空间机械臂运动学自标定仿真 通过对7自由度大臂展空间机械臂进行运动学自标定仿真验证本文提出的基于指数积公式的空间机械臂运动学在轨自标定方法的有效性。空间机械臂运动学参数理论值和实际值(预设值)如表 1所示。空间机械臂总共有48个运动学参数需要辨识,为了辨识这些运动学参数至少需要在8个独立构型下测量空间机械臂末端位姿。在运动学自标定仿真过程中,总共生成了120个空间机械臂末端位姿,其中60个为测量位姿,测量位姿均位于标定板上方区域,用于空间机械臂的运动学自标定,另外60个为测试位姿,测试位姿在空间机械臂关节空间内随机生成,用于验证运动学自标定方法的有效性。
表 1 空间机械臂运动学参数理论值和实际值 Table 1 Theoretical values and actual values of kinematics parameters of the space manipulator
| 参数 | 理论值 | 实际值(预设值) |
| ξ1 | [0??0??1??0??0??0]T | [0.005 3??-0.005 2??1.000 0??0.100 5??-0.099 5??-0.001 0]T |
| ξ2 | [1??0??0??0??1 500??0]T | [1.000 0??0.007 0??-0.006 9??-10.401 3??1 500.128 8??10.237 0]T |
| ξ3 | [0??0??1??0??-1 000??0]T | [0.008 8??-0.008 7??0.999 9??8.851 8??-1 000.122 7??-8.729 7]T |
| ξ4 | [0??0??1??0??-5 000??0]T | [0.010 6??-0.010 4??0.999 9??52.616 0??-5 000.248 9??-52.372 8]T |
| ξ5 | [0??0??1??0??-9 000??0]T | [0.012 4??-0.012 1??0.999 9??110.220 7??-9 000.253 1??-109.983 9]T |
| ξ6 | [1??0??0??0??4 500??0]T | [0.999 8??0.015 7??-0.015 7??-69.617 5??4 500.653 5??69.001 3]T |
| ξ7 | [0??0??1??0??-10 000??0]T | [0.017 8??-0.017 1??0.099 7??173.282 4??-9 998.774 8??-174.560 3]T |
| ξst | [0??0??0??10 000??0??6 000]T | [0.114 4??0.129 3??0.114 4??9 603.673 9??-199.070 3??6 652.637 1]T |
表选项
空间机械臂运动学标定模型只是考虑了空间机械臂自身的运动学参数误差,忽略了双目空间相机的测量误差。实际上双目空间相机的测量精度比较低,会影响到空间机械臂运动学自标定的结果。因此,在空间机械臂运动学自标定仿真过程中,需要考虑双目空间相机的测量误差,以提高空间机械臂运动学自标定仿真的真实性和有效性。假设双目空间相机随机测量噪声的位置量和姿态量分别服从范围为[-2.4 mm, 2.4 mm]和[-0.3°,0.3°]的均匀分布。为了减小双目空间相机随机测量噪声对标定仿真结果的影响,一方面针对每个测量位姿,使用双目空间相机重复测量多次,并求取平均值作为末端位姿实际值;另一方面增加了部分冗余测量位姿进一步降低随机测量噪声的不良影响。
空间机械臂运动学自标定仿真流程如下:在标定板上方生成60个末端测量位姿,并加入双目空间相机随机测量噪声,作为末端位姿测量值,生成空间机械臂运动学参数理论值和运动学参数实际值;利用运动学参数实际值和60个末端位姿测量值,计算60组关节角度;利用运动学参数理论值和60组关节角度,计算60个末端位姿理论值;利用式(22)计算运动学参数误差Δx;对运动学参数进行更新;重复之前2个步骤,直到达到预先设定的最大迭代次数k,完成运动学自标定仿真。空间机械臂运动学自标定仿真流程如图 3所示。
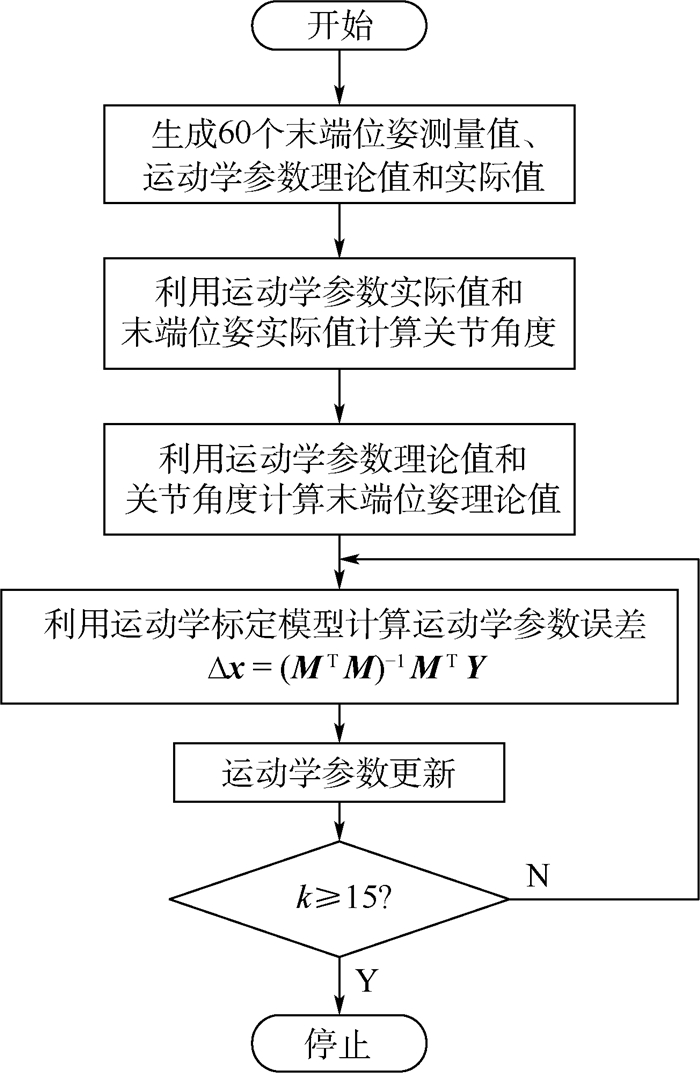 |
| 图 3 空间机械臂运动学自标定仿真流程 Fig. 3 Kinematics self-calibration simulation process for the space manipulator |
| 图选项 |
在运动学自标定仿真每次迭代计算过程中,空间机械臂的运动学参数会进行更新。运动学参数x(关节旋量ξ和初始位姿旋量ξst)的更新方法如下:
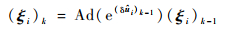 | (23) |
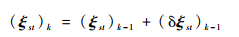 | (24) |
按照图 3所示的仿真流程完成空间机械臂运动学自标定。在每次迭代计算后,利用更新后的运动学参数计算60个测量位姿处的最大末端位置误差和姿态误差。如图 4所示,在运动学自标定仿真过程中,空间机械臂末端的最大位置误差和姿态误差快速收敛到稳定值,即空间机械臂的运动学参数快速收敛到稳定值。
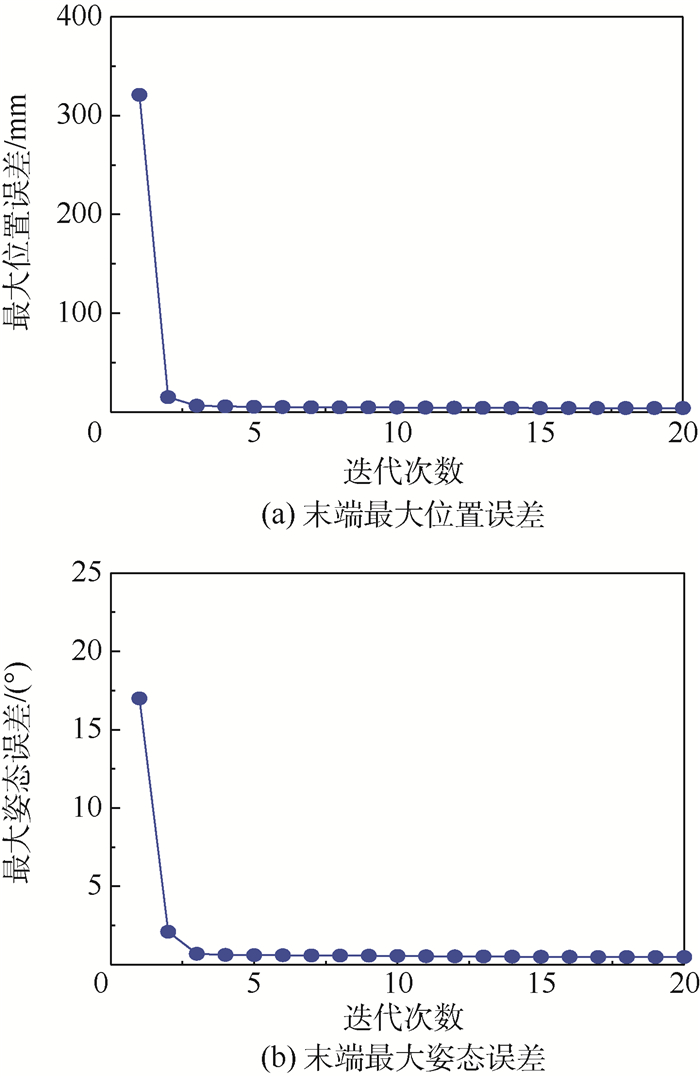 |
| 图 4 迭代过程中末端位姿误差 Fig. 4 Pose errors of the end-effector during iterative procedure |
| 图选项 |
为了验证运动学自标定方法的有效性,在60个测试位姿处分别计算标定前和标定后空间机械臂的末端位置误差和姿态误差。如图 5所示,经过运动自学标定,空间机械臂末端的位置和姿态误差平均值分别由223.153 mm和12.049°降低到5.312 mm和0.467 1°。这说明本文方法能有效提高空间机械臂末端位姿精度。
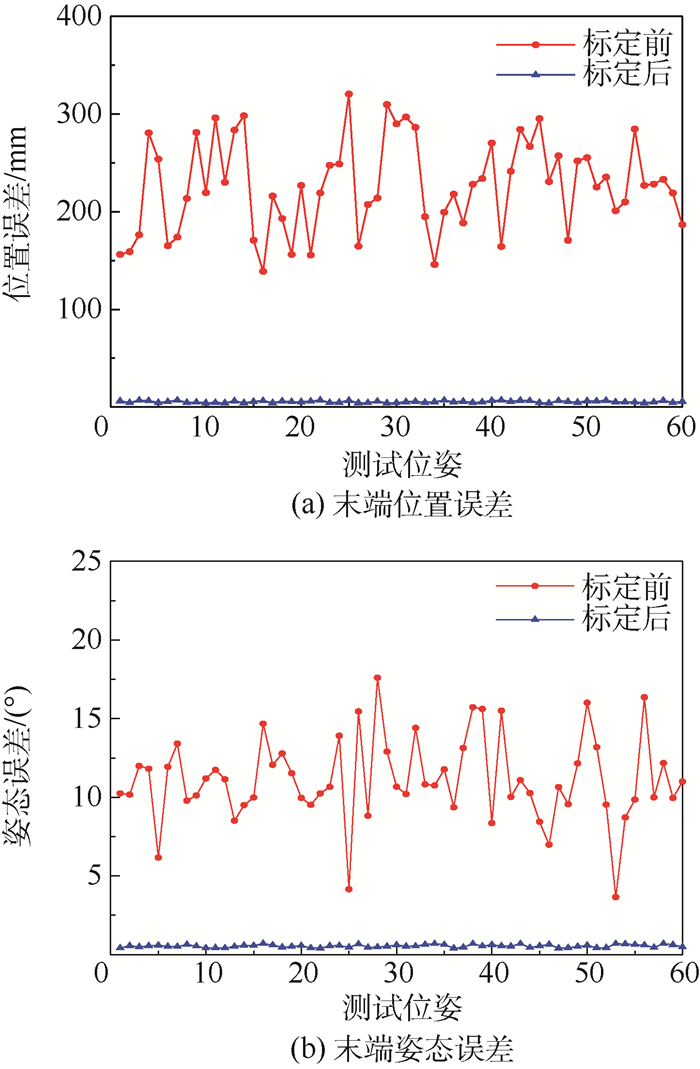 |
| 图 5 末端位姿误差 Fig. 5 Pose errors of the end-effector |
| 图选项 |
5 结论 本文提出了一种基于指数积公式的空间机械臂运动学在轨自标定方法,并通过运动学自标定仿真验证了运行学标定方法的有效性。
1) 在空间机械臂基座坐标系和标定板坐标系位姿变换关系已知的前提下,运动学标定系统能充分利用空间站现有的双目空间相机和棋盘式标定板实现空间机械臂末端位姿测量,无需借助外部精密测量设备;同时运动学标定系统能够实现空间机械臂末端位姿测量过程的自动化,测量过程不需要人的干预。
2) 使用指数积公式建立空间机械臂的运动学模型克服了使用DH等建模方法的不足之处:相邻关节接近平行时的奇异性、坐标系不能任意设置和建模过程复杂等问题。
3) 本文方法在每次迭代计算过程中,关节旋量通过伴随变换的方式进行更新,更新后的关节旋量依然满足关节旋量的约束条件,克服了使用传统的基于指数积公式的运动学自标定方法进行运动学自标定时每次迭代计算过程中都需要对更新后关节旋量进行归一化处理的缺点。
4) 经过运动学自标定仿真,在60个测试位姿处,空间机械臂末端位姿精度有了显著提高, 验证了本文方法的有效性。
参考文献
| [1] | BAI Y, WANG D L. Improve the robot calibration accuracy using a dynamic online fuzzy error mapping system[J]. IEEE Transactionson Systems, Man and Cybernetics, 2004, 34(2): 1155-1160. DOI:10.1109/TSMCB.2003.821453 |
| [2] | CHEN G, LI T, CHU M, et al. Review on kinematics calibration technology of serial robots[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(8): 1759-1774. DOI:10.1007/s12541-014-0528-1 |
| [3] | ROTH Z S, MOORING B W, RAVANI B. An overview of robot calibration[J]. IEEE Journal of Robotics and Automation, 1987, 3(5): 377-385. DOI:10.1109/JRA.1987.1087124 |
| [4] | SCHROER K, ALBRIGHT S L, GRETHLEIN M. Complete, minimal and model-continuous kinematic models for robot calibration[J]. Robotics and Computer-integrated Manufacturing, 1997, 13(1): 73-85. DOI:10.1016/S0736-5845(96)00025-7 |
| [5] | HAYATI S.Robot arm geometric link parameter estimation[C]//22nd IEEE Conference on Decision and Control.Piscataway, NJ: IEEE Press, 1983, 22: 1477-1483. https://ieeexplore.ieee.org/document/4047808 |
| [6] | STONE H W. Kinematic modeling, identification, and control of robotic manipulators[M]. New York: Kluwer Academic Publisher, 1987. |
| [7] | ZHUANG H Q, ROTH Z S, HAMANO F. A complete and parametrically continuous kinematic model for robot manipulators[J]. IEEE Transactions on Robotics & Automation, 1992, 8(4): 451-463. |
| [8] | ZHUANG H Q, WANG L K, ROTH Z S. Error-model-based robot calibration using a modified CPC model[J]. Robotics and Computer-Integrated Manufacturing, 1993, 10(4): 287-299. DOI:10.1016/0736-5845(93)90042-I |
| [9] | CHEN I M, YANG G L. Kinematic calibration of modular reconfigurable robots using product-of-exponentials formula[J]. Journal of Robotic Systems, 1997, 14(11): 807-821. DOI:10.1002/(ISSN)1097-4563 |
| [10] | HE R B, ZHAO Y J, YANG S N, et al. Kinematic-parameter identification for serial-robot calibration based on POE formula[J]. IEEE Transactions on Robotics, 2010, 26(3): 411-423. DOI:10.1109/TRO.2010.2047529 |
| [11] | HE R B, LI X W, SHI T L, et al. A kinematic calibration method based on the product of exponentials formula for serial robot using position measurements[J]. Robotica, 2015, 33(6): 1295-1313. DOI:10.1017/S026357471400071X |
| [12] | CHEN G L, WANG H, LIN Z Q. Determination of the identifiable parameters in robot calibration based on the POE formula[J]. IEEE Transactions on Robotics, 2014, 30(5): 1066-1077. DOI:10.1109/TRO.2014.2319560 |
| [13] | ANGULO V R D, TORRAS C. Self-calibration of a space robot[J]. IEEE Transactions on Neural Networks, 1997, 8(4): 951-963. DOI:10.1109/72.595895 |
| [14] | LIANG P, CHANG Y L, HACKWOOD S. Adaptive self-calibration of vision-based robot systems[J]. IEEE Transactions on Systems Man & Cybernetics, 1989, 19(4): 811-824. |
| [15] | GONG C, YUAN J, NI J. Nongeometric error identification and compensation for robotic system by inverse calibration[J]. International Journal of Machine Tools & Manufacture, 2000, 40(14): 2119-2137. |
| [16] | LIU Y, LIU H, NI F L, et al. New self-calibration approach to space robots based on hand-eye vision[J]. Journal of Central South University of Technology, 2011, 18(4): 1087-1096. DOI:10.1007/s11771-011-0808-1 |
| [17] | DU G L, ZHANG P. Online robot calibration based on vision measurement[J]. Robotics and Computer-integrated Manufacturing, 2013, 29(6): 484-492. DOI:10.1016/j.rcim.2013.05.003 |
| [18] | ZHANG X C, SONG Y T, YANG Y, et al. Stereo vision based autonomous robot calibration[J]. Robotics and Autonomous Systems, 2017, 93: 43-51. DOI:10.1016/j.robot.2017.04.001 |
| [19] | 高文斌, 王洪光, 姜勇. 一种基于指数积的串联机器人标定方法[J]. 机器人, 2013, 35(2): 156-161. GAO W B, WANG H G, JIANG Y. A calibration method for serial robots based on POE formula[J]. Robot, 2013, 35(2): 156-161. (in Chinese) |
| [20] | LOU Y J, CHEN T N, WU Y Q, et al.Improved and modified geometric formulation of POE based kinematic calibration of serial robots[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ: IEEE Press, 2009: 5261-5266. https://www.researchgate.net/publication/221067020_Improved_and_Modified_Geometric_Formulation_of_POE_Based_Kinematic_Calibration_of_Serial_Robots |
| [21] | PARK F C, OKAMURA K. Kinematic calibration and the product of exponentials formula[M]. Cambridge: MIT Press, 1994: 119-128. |
