从本质上讲,陀螺仪的标定技术其实是一种误差补偿技术[2-4],其目的是建立IMU输入输出关系的精确数学模型,惯性组件的标定精度会直接影响后续的导航精度。捷联惯导系统标定的方法有很多,常见的分立标定方法主要是依靠速率试验和位置试验来确定IMU中陀螺的标度因数误差、安装误差角和常值误差[5-10]。目前,随着陀螺仪技术的不断发展,且传统的速率试验和位置试验标定法会引入较大的转台速率误差和标定参数的耦合误差等,故该种标定方法已不能满足对高精度陀螺组件的标定要求。为了避免参数耦合误差所带来的影响,孙枫和孙伟[11]提出了基于双轴转位机构的陀螺标定方法,该方法利用了双轴转位机构的定位精度高的特点,设计了一种陀螺组件静态6位置标定方法,该方法能够很好地激励出陀螺组件误差模型的12个误差参数,而且还可以独立求解出陀螺的各项误差参数,避免了误差参数相互耦合作用对标定结果带来的影响。目前,按照敏感轴与转台转轴重合的方式进行转位时,转轴每转一次,IMU中仅有2个敏感轴位置发生变化,为了建立12个独立的误差方程,需要进行至少6次转位,故该静态6位置分立式标定法是标定出陀螺组件12个主要误差源所需位置数最少的方法。
无论上述哪种分立标定模式,限制分立标定快速性的主要因素是标定方法中所需要的转位位置数。由于在标定过程中,每一标定位置处都需要花费大量的时间和精力进行数据采集,故标定所需位置数越多,采集数据所花费的时间越长,从而会限制标定的快速性和高效性。所以,为了进一步提高惯性组件标定的快速性,研究在保持原有标定精度不变的前提下进一步减少标定所需的位置数成为缩短标定时间的关键。
总结现有捷联惯导系统相关技术研究文献发现,无论是IMU的标定技术、快速寻北技术还是多位置对准技术等,IMU的转位模式都是转台转轴与惯性器件敏感轴重合的方式进行转动的[12-16]。根据文献[17]中所引入的偏矢轴和偏矢角的概念,设计了一种IMU的偏轴安装和转位方式。在此基础上,以偏轴转位为核心思想,设计了一种新的快速分立标定方法——偏轴4位置标定方法。相较于传统的静态6位置标定方法,偏轴4位置标定方法在所需转台的转轴数不增加的情况下,仅需4次转位便可标定出陀螺组件的标度因数误差、安装误差和常值误差共12个主要误差源,且标定精度与6位置方法的标定精度基本相同(或略优于6位置标定方法)。即偏轴4位置标定方法在保持标定精度不变和硬件条件相同的情况下,进一步缩短了标定时间,提高了标定的快速性和标定效率。
1 传统分立标定方法 目前常见的分立标定方法类型主要有“速率+位置”分立标定法和静态位置标定法两大类。这里主要对“速率+24位置”分立式标定法和静态6位置标定方法进行简要介绍。
1.1 “速率+24位置”分立式标定法 “速率+24位置”分立式标定法需要以3轴惯导试验转台为基础,依次通过速率实验和24个位置实验来确定陀螺各个误差模型的系数[5, 9]。IMU陀螺组件在3轴转台上的具体安装方式为:x轴陀螺与转台内框架的转轴重合,y轴陀螺与转台中框架的转轴重合,z轴陀螺与转台外框架的转轴重合。
1.1.1 标度因数与安装误差的确定 首先,依次将IMU的x轴、y轴和z轴陀螺的轴向处于天向。然后,绕着此时的天向轴使转台以一定的转动速率ω按顺时针和逆时针方向进行转动,与此同时,记录下转动整数圈内陀螺的输出数据。为减少篇幅,这里列出最终结果。
“速率+24位置”分立式标定法对陀螺组件标定出的标度因数为
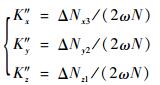 | (1) |
式中:N为陀螺旋转一周时一共进行数据记录的组数;ω为IMU绕天向轴顺时针和逆时针旋转的角速率值;ΔNxi、ΔNyi和ΔNzi定义如下:
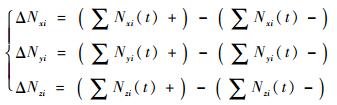 |
其中:Nxi(t)+、Nyi(t)+和Nzi(t)+(i=1, 2, 3)分别为当IMU中x轴指向天向、y轴指向天向和z轴指向天向时陀螺的正向转动中任意时刻t下陀螺组件的输出值,而Nxi(t)-、Nyi(t)-和Nzi(t)-(i=1, 2, 3)为对应情况下陀螺逆向转动中任意时刻t下陀螺组件的输出值。
标定出的安装误差为
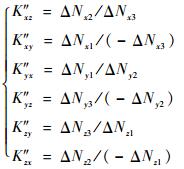 | (2) |
1.1.2 陀螺常值误差的确定 当x轴、y轴和z轴陀螺的轴向依次指北时,依次绕着该指北陀螺按逆时针方向进行转位,每次转位角度为45°,转位一周共有7个位置,总共有24个独立的标定位置,记录每个位置处各陀螺的输出值,便可求取陀螺组件的常值误差为
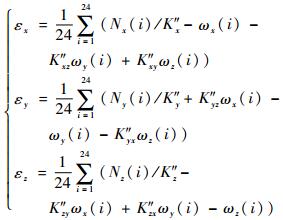 | (3) |
式中:Nx(i)、Ny(i)和Nz(i)为各轴向陀螺在24个位置处的实际输出值;ωx(i)、ωy(i)和ωz(i)为在各个位置处陀螺组件的理想输入值,此处i=1, 2,…, 24;K″x、K″y和K″z为“速率+24位置”分立式标定法标定出的陀螺组件的标度因数。
从式(3)可看出,陀螺组件常值误差的解析算法中含有陀螺组件的标度因数误差和安装误差,故其常值误差的标定精度会受到标度因数误差和安装误差的标定精度影响。
速率实验的目的主要是确定3个陀螺的标度因数和安装误差角,而24位置实验的主要目的是确定陀螺的常值误差。在使用“速率+24位置”分立式标定法进行标定时,由于方法本身的特点,陀螺的常值误差会与陀螺的标度因数误差和安装误差产生关联,因此只有在用该方法所标定出的标度因数误差和安装误差足够可信的情况下,才能够对陀螺的常值误差进行精确计算。
1.2 静态6位置标定法 由于“速率+24位置”分立式标定法在进行陀螺组件标定时会有误差参数相互耦合作用的影响,这对于目前迅速发展的捷联惯导技术来说,已无法满足捷联惯导系统对高精度陀螺组件的要求,所以从实际的工程应用角度出发,有必要利用双轴捷联惯导系统中的转位机构进行惯性器件的高精度自标定[11]。
由于求解陀螺12个误差参数时需要建立至少12个独立方程才能求解,且传统转位方案具有每一次转位仅有2个陀螺敏感轴位置发生变化的特点,所以只有当转台给IMU提供至少6个相对独立的位置时才可以建立12个独立的未知方程。根据IMU在当地地理坐标系下的6个固定方位,将地球自转角速度的北向和天向分量作为已知量对陀螺仪的误差参数进行求解,从而完成对陀螺仪各项误差的标定工作。
静态6位置标定法的转位方案如图 1所示。初始位置时IMU坐标系(s系)与载体系(b系)重合,且载体系与东北天地理坐标系(n系)重合,然后依次绕着敏感轴旋转相应角度到达其余位置。然后通过3个轴向上陀螺的实际敏感值进行分立标定,分别标定出3个陀螺的标度因数误差,安装误差和常值误差。具体转位位置见图 1。
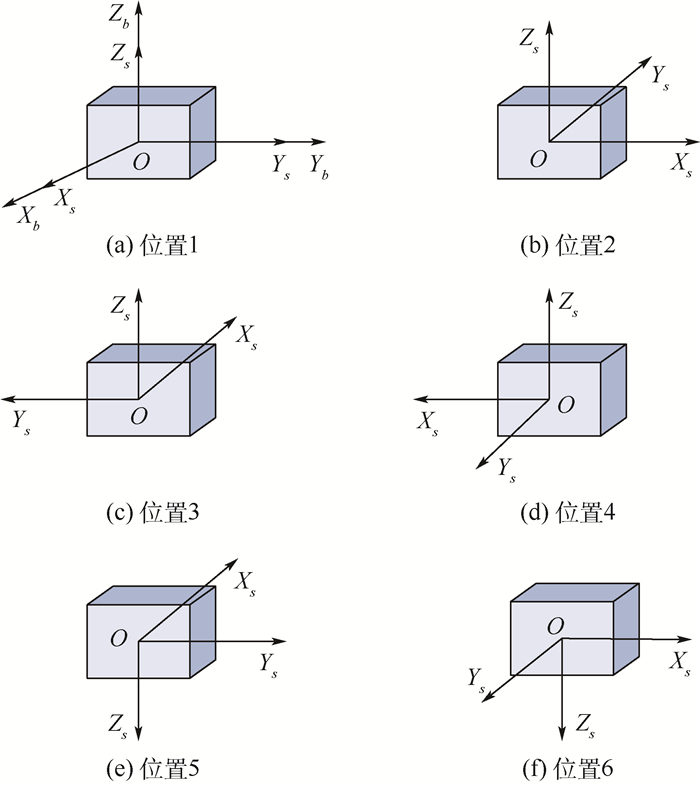 |
| 图 1 静态6位置标定转位方案示意图 Fig. 1 Schematic diagram of static six-position calibration transposition scheme |
| 图选项 |
将IMU在位置1~位置6时陀螺组件的输出分别用6组符号表示为
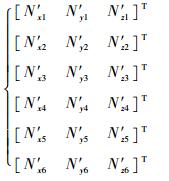 | (4) |
通过使用式(4)的6组陀螺的输出数据,经过静态6位置分立标定方法进行解算,便可得出陀螺组件的12个误差参数。为减少篇幅,这里只列写出标定的最终结果。
通过使用静态6位置标定方法,得出IMU的3个轴向上陀螺的标度因数分别为
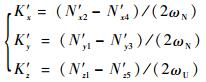 | (5) |
式中:ωN和ωU分别为地球角速度在东北天地理坐标系中北向和天向的分量,ωN=ωiecos L,ωU=ωiesin L,ωie为地球角速度,L为地理纬度。
IMU的3个轴向上陀螺的常值误差分别为
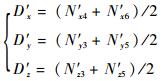 | (6) |
IMU中陀螺组件的6个安装误差参数分别为
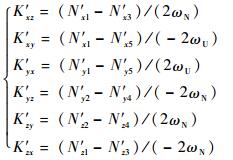 | (7) |
2 基于偏轴转位的4位置分立标定法 在进行分立标定时,随着转位次数的增加,会在标定过程中引入多次转位机构的定位误差以及其他因素造成的不稳定误差等,从而造成误差的累积,且转位次数越多,所需要标定的时间越长。为提高标定速度,设计一种IMU在转台上的偏轴安装方式,研究一种位置数更少的分立标定方法。
2.1 IMU偏轴转位安装方式 在具体设计IMU偏轴转位安装方式之前,先简要介绍一种新的坐标变换理论——三元角两位置坐标旋转变换方法。该方法的核心内容是:空间中,任意2个共原点的直角坐标系可以仅通过2次转位便可重合。该转位的具体过程描述如下:首先,使共空间原点的2个直角坐标系的Z轴重合,从而使得2个坐标系的XY平面重合;然后,绕着其中任意一个坐标系的Z轴旋转,从而使得2个空间直角坐标系完全重合。此过程可以用3个参数进行描述[17]。
受此过程的启发,设计一种IMU偏轴转位的安装方式,其具体内容描述如下:将IMU坐标系(s系)的Zs轴与双轴转台的外框轴(Zb轴)重合,而IMU坐标系的Xb轴和转台的内框轴偏移一个固定角度进行安装。为了保证对称性,通常偏移的角度为45°。其中,按照文献[15]中的相关定义,这里将双轴转台的内框轴定义为偏矢轴(Ps轴)。其具体的安装结构图如图 2所示。
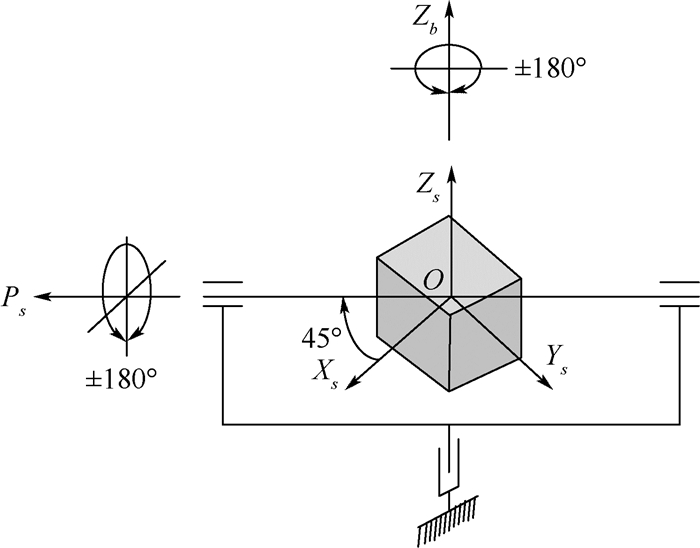 |
| 图 2 IMU偏轴安装方式结构示意图 Fig. 2 Structure diagram of partial axis installation for IMU |
| 图选项 |
相较于传统的安装方式而言,该种偏轴安装方式可以使得转台在转动过程中,实现IMU 3个敏感轴的位置同时发生变化,进而可以最大限度地激励出陀螺组件的误差参数。此外,按照该设计的偏轴转位安装方式,根据三元角坐标变换理论,可以很方便的用3个参数表示出其任意时刻的旋转矩阵,为分析所设计的偏轴4位置分立标定方法的效果提供了有利的数学手段。
2.2 偏轴4位置分立标定路径设计 采用双轴旋转调制型捷联惯导系统中的旋转调制机构控制IMU进行转位,假定惯导系统所在的地理位置精确已知,由于地球自转角速度在固定位置是定值,通过利用旋转调制机构精确定位特性,便可设计一组能精确得到确定输入的偏轴4位置静态标定方法。
具体标定路径如图 3所示:位置1中IMU的坐标系(s系)与东北天坐标系(n系)重合,在位置1的基础上,依次绕着偏矢轴(Ps轴)逆时针旋转调制180°到位置2,在位置2的基础上,绕着方位轴(Z轴)顺时针旋转调制180°到位置3,在位置3的基础上,绕着偏矢轴(Ps轴)逆时针旋转调制180°到位置4。
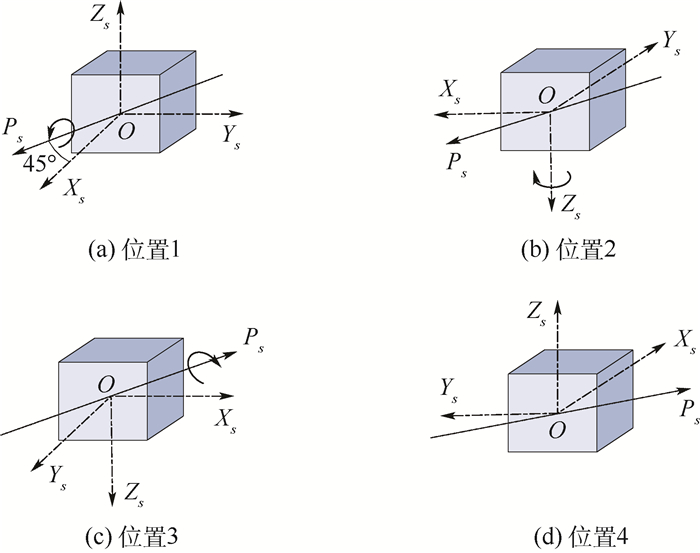 |
| 图 3 偏轴4位置标定方法转位路径 Fig. 3 Transposition path of partial axis four-position calibration method |
| 图选项 |
由于传统的“速率+24位置”分立标定法在标度因数误差和安装误差足够可信的基础上才能求得较为精确的常值误差,故这里的偏轴4位置标定方法考虑到了标定参数之间耦合误差的影响,设计的4个位置不但能够激励出12个误差参数,而且各个误差参数的计算互相独立,互不干扰。同时,和静态6位置分立标定方法相比,标定所需的位置数减少2个,采集数据所用的时间减少了33%,从而可提高标定的快速性。
2.3 陀螺仪误差参数标定理论公式推导 由于地球自转角速度和当地纬度已知,可以精确算出陀螺在偏轴4位置标定方法中各个位置处的理想输入。
陀螺在位置1处的理想输入为[0 ωN ωU]T,在位置2处的理想输入为[-ωN 0 -ωU]T,在位置3处的理想输入为[ωN 0 -ωU]T,在位置4处的理想输入为[0 -ωN ωU]T。
其中ωN=ωiecos L,ωU=ωiesin L。将陀螺组件在4个位置处的实际输出分别设为
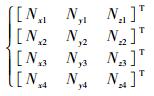 | (8) |
陀螺的误差源主要包括常值误差、安装误差和标度因数误差,将以上3种陀螺的误差项综合考虑在内列写的具体误差模型[8]如下:
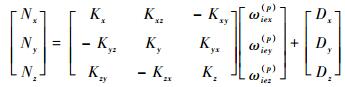 | (9) |
式中:Nx、Ny和Nz为IMU 3个轴向上陀螺的最终输出;ωiex(p)、ωiey(p)和ωiez(p)为地球角速度在各个位置处的理论角速度分量;Kx、Ky和Kz为3个轴向上陀螺的标度因数;Kxz、Kxy、Kyx、Kyz、Kzy和Kzx为陀螺的安装误差;Dx、Dy和Dz为3个轴向上陀螺的常值误差。
将各个位置处的理想输入角速度分别代入陀螺误差模型中,从而可求得各个陀螺仪的实际输出,4个位置处各个陀螺敏感轴的实际输出为
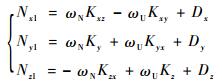 | (10) |
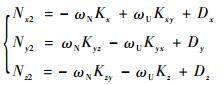 | (11) |
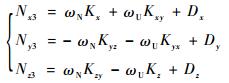 | (12) |
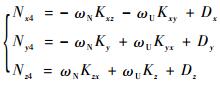 | (13) |
通过进一步分析整理,由式(10)-式(13)可得
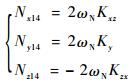 | (14) |
式(12)-式(11)可得
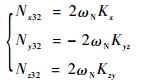 | (15) |
式(10)~式(13)各式相加可得
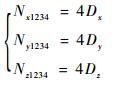 | (16) |
[式(10)+式(13)]-[式(11)+式(12)]可得
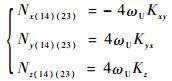 | (17) |
利用式(14)~式(17)便可得到IMU中12个陀螺误差的标定结果,最终标定出的3个陀螺仪标度因数为
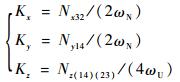 | (18) |
标定出的6个陀螺仪安装误差为
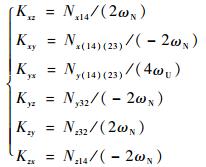 | (19) |
标定出的3个陀螺仪常值误差为
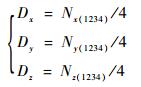 | (20) |
其中:
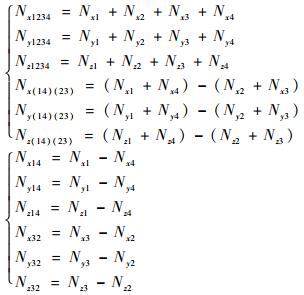 |
至此,陀螺的12个误差系数全部经过计算求出。
3 转位机构定位误差对标定精度的影响 旋转调制机构所存在旋转调制定位误差将会对惯性陀螺组件各个误差参数的标定结果产生影响。下面具体分析IMU位于4个位置的情况下,旋转调制机构的定位误差对偏轴4位置标定结果的影响。假设旋转调制机构在4个位置时的定位误差角分别为θxi、θyi、θzi,其中i=1, 2, 3, 4。由于定位误差角是小角度,因此旋转调制机构的定位误差矩阵可表示为
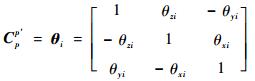 | (21) |
式中:误差角θi为理想坐标系到实际坐标系时所转过的角度,p系为理想坐标系,p′系为误差坐标系,也就是IMU坐标系(s系)在转位机构控制下实际转到位置。
旋转调制机构在各位置处定位误差角的存在导致IMU陀螺组件在4个位置处的真实输入为
 |
式中:
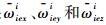
将陀螺在4个位置的真实输入角速度分别代入陀螺误差模型式(1)中,对不同位置的陀螺仪输出角速度作加减运算,并忽略二阶小量后可得
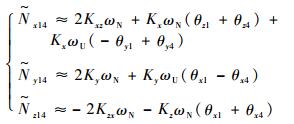 | (22) |
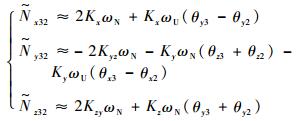 | (23) |
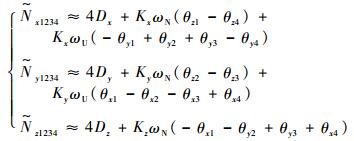 | (24) |
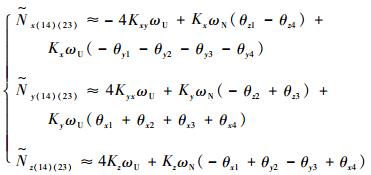 | (25) |
式中:
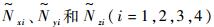
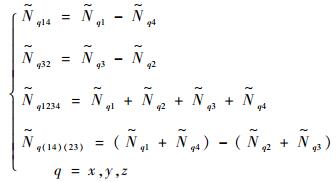 |
将式(14)~式(17)与式(22)~式(25)各式分别对应比较,可以得到旋转调制机构旋转定位误差产生的标定偏差为
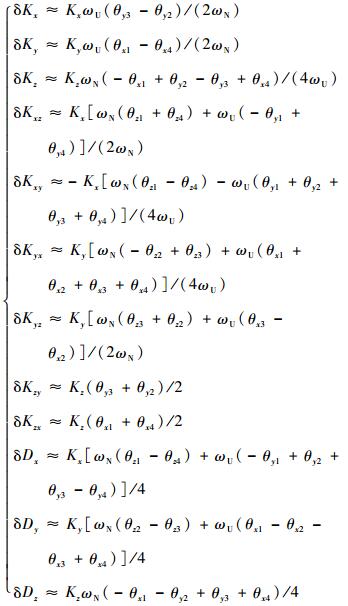 |
为与静态6位置分立标定进行比对,下面给出由转位机构定位误差引起的静态6位置分立标定误差,其标定误差为
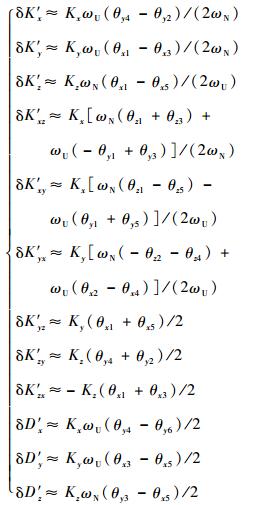 |
式中:δK′x、δK′y和δK′z为在存在转位机构定位误差时,静态6位置方法标定出的陀螺标度因数误差的偏差;δK′xz、δK′xy、δK′yx、δK′yz、δK′zy和δK′zx为陀螺安装误差的偏差;δD′x、δD′y和δD′z为陀螺常值误差的偏差。
通过比较分析发现,二者有区别的地方为δKxy、δKyx、δKyz、δKz、δDx、δDy和δDz,在某些情况下,因转位机构定位误差而造成的标定误差中,偏轴4位置标定方法比静态6位置标定方法标定误差小或大,甚至相同的可能性均存在。假定转位机构在各个位置处的定位误差角均相同,该定位误差角度值用θ表示,则2种标定方法有11个误差项的标定误差值均相同,只有δKyx有区别。偏轴4位置标定方法因转位机构定位误差引起的δKyx=Kyθ,而静态6位置标定方法的为
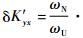
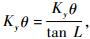
综合以上分析可得出,在转位机构定位误差的影响下,偏轴4位置标定方法与静态6位置标定方法的标定效果几乎相同,即在标定精度相同的情况下,偏轴4位置标定方法要比静态6位置标定方法所用时间更短。
此外,除了转位机构定位误差会对偏轴4位置分立标定法的标定精度产生影响外,还有许多其他误差源会对最终标定结果产生影响。比如转台的非正交度以及不水平度同样会引起标定过程中陀螺组件的实际输入与理想输入之间存在偏差,进而采用所提方法对陀螺组件进行标定时会产生标定偏差,其分析过程与转台定位误差对其影响的分析过程基本相同,这里不再过多阐述。同时,陀螺组件自身的噪声水平也会对最终标定结果产生影响,如果在偏轴4位置分立标定解算过程中考虑陀螺随机误差的影响,则陀螺组件标度因数、安装误差和常值误差的最终标定结果分别为
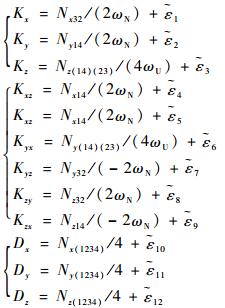 |
式中:
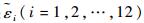
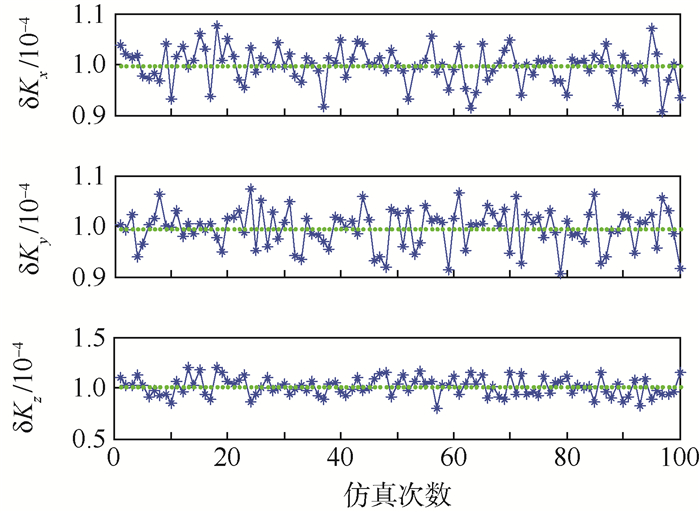
4 两种标定方法效果仿真验证 参照式(9)建立的IMU中陀螺仪的误差模型,同时综合考虑陀螺仪实际标度因数误差的取值范围,设定3个陀螺标度因数误差均为1×10-4,其6个安装误差都为2.145×10-5 rad,3个陀螺的常值误差分别为2.041 736 93(°)/h、3.01844241(°)/h、2.095 457 51(°)/h;北京地理纬度采用34°,系统的采样频率为100 Hz。在静态6位置标定和偏轴4位置标定中,假定转位机构在各个位置处的定位误差范围均为±3″。
对上述2种标定方法分别进行100次仿真,将每种标定方法标定出的陀螺误差项取平均值作为最终标定值。2种方法的标定误差曲线如图 4~图 9所示。
 |
| 图 4 静态6位置标定方法陀螺仪标度因数误差 Fig. 4 Gyro scale factor error of static six-position calibration method |
| 图选项 |
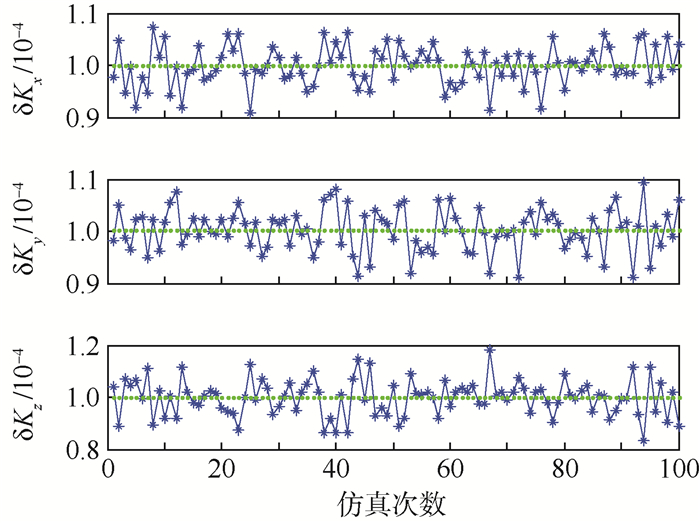
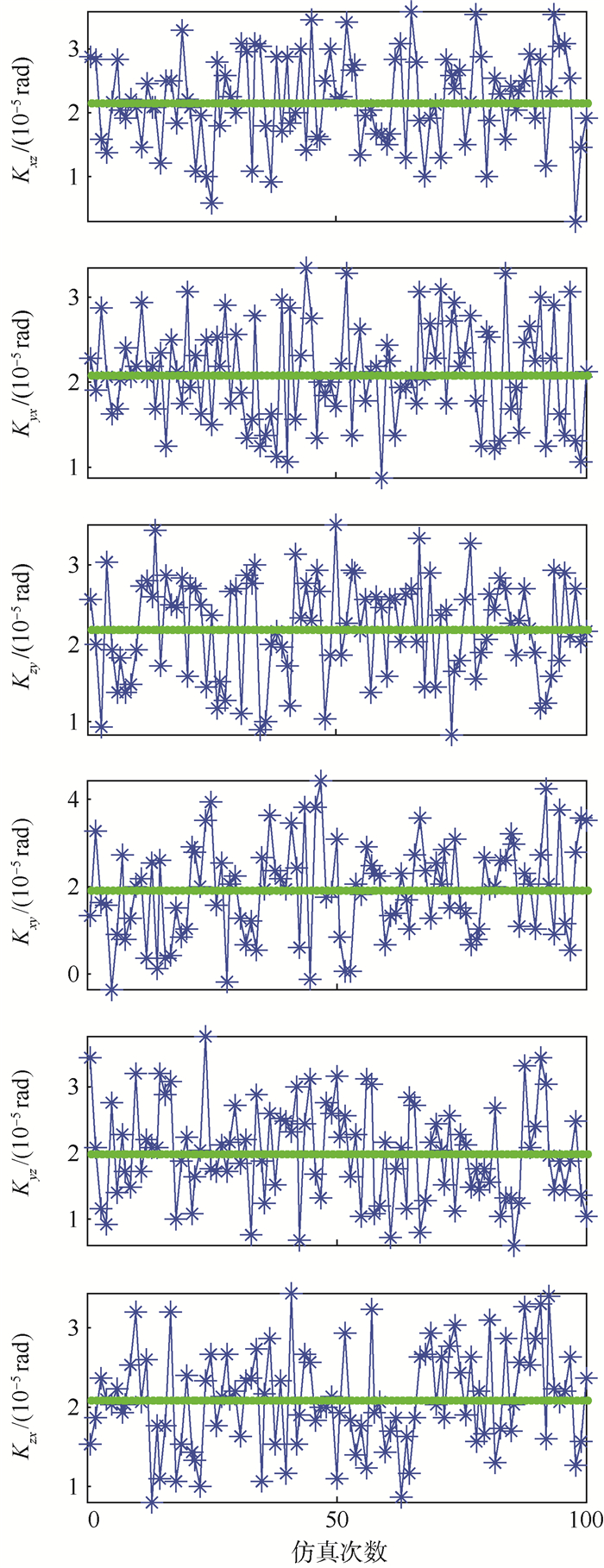 |
| 图 5 静态6位置标定方法陀螺仪安装误差 Fig. 5 Gyro installation error of static six-position calibration scheme |
| 图选项 |
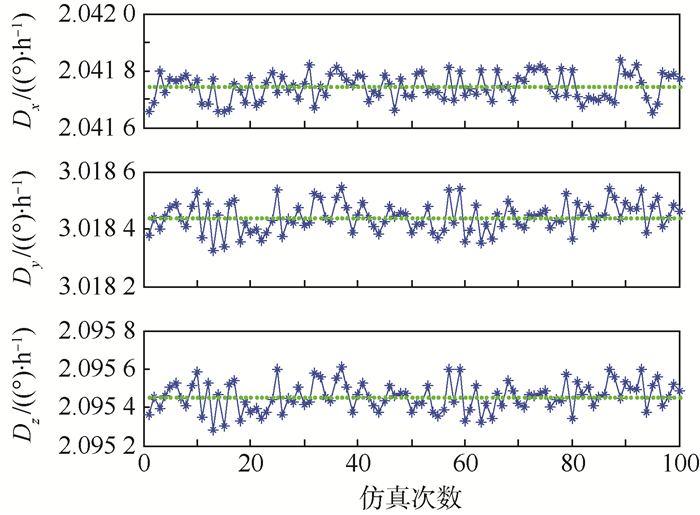 |
| 图 6 静态6位置标定方法陀螺仪常值误差 Fig. 6 Constant value error of gyroscope in static six-position calibration method |
| 图选项 |
 |
| 图 7 偏轴4位置标定方法陀螺仪标度因数误差 Fig. 7 Scale factor error of gyroscope in four-position calibration method of partial axis |
| 图选项 |
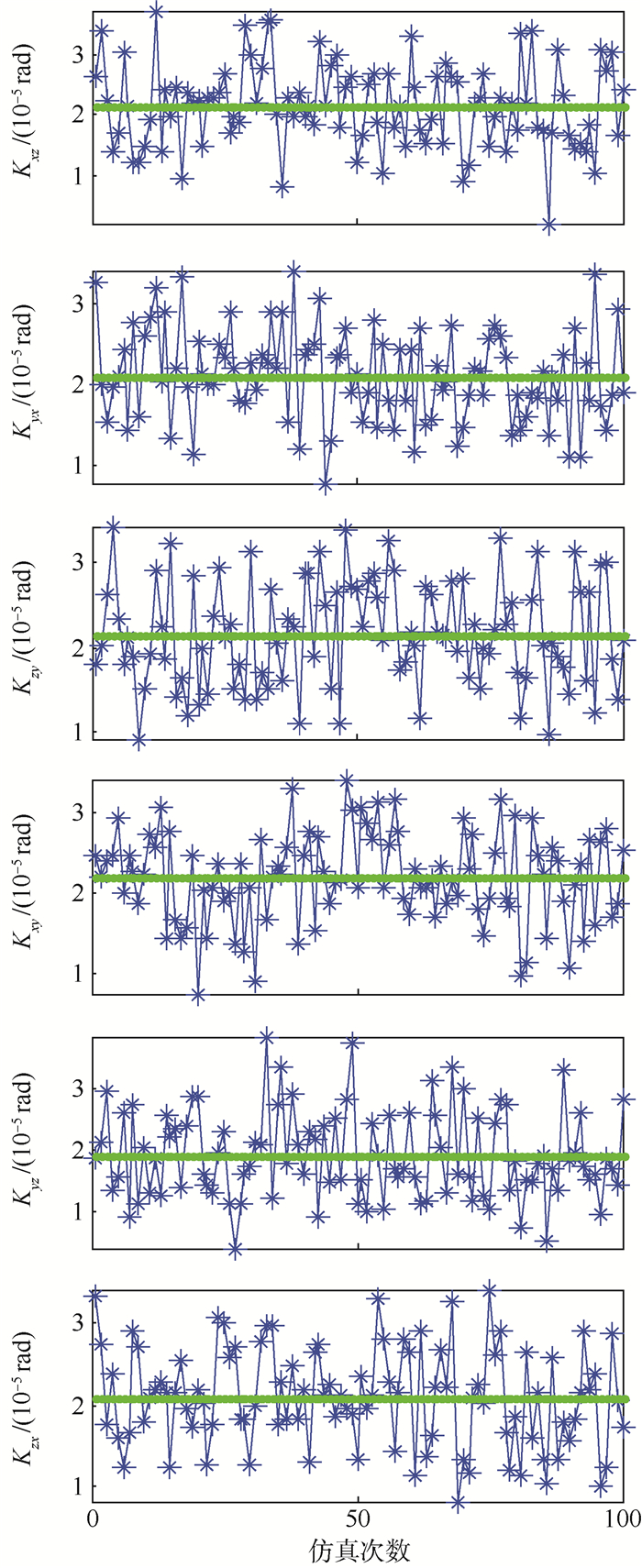 |
| 图 8 偏轴4位置标定方法陀螺仪安装误差 Fig. 8 Installation error of gyroscope in four-position calibration method of partial axis |
| 图选项 |
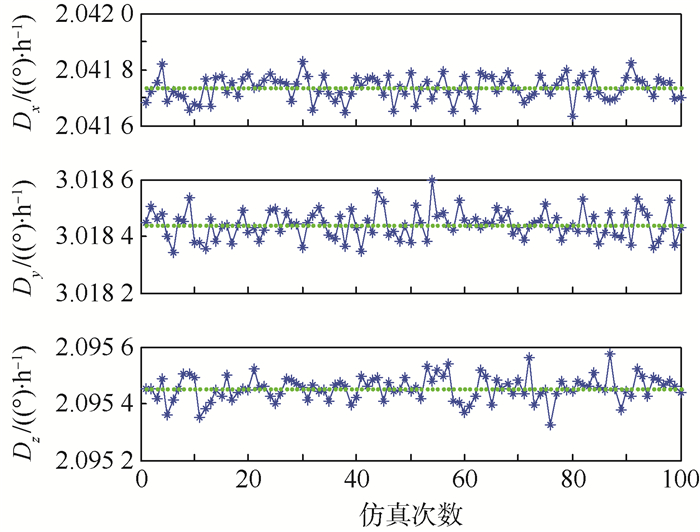 |
| 图 9 偏轴4位置标定方法陀螺仪常值误差 Fig. 9 Constant value error of gyroscope in four-position calibration method of partial axis |
| 图选项 |
2种标定方法标定的最终结果如表 1所示。
表 1 不同标定方法下的陀螺仪误差参数比较 Table 1 Comparison of gyroscope error parameters under different calibration methods
| 误差项 | 静态6位置标定 | 偏轴4位置标定 |
| δKx/10-4 | 0.996 871 | 0.999 207 |
| δKy/10-4 | 0.995 594 | 0.100 265 |
| δKz/10-4 | 1.011 19 | 0.997 956 |
| Kxz/(10-5rad) | 2.197 14 | 2.151 31 |
| Kxy/(10-5rad) | 1.958 93 | 2.194 24 |
| Kyx/(10-5rad) | 2.100 79 | 2.110 21 |
| Kyz/(10-5rad) | 2.000 29 | 1.910 05 |
| Kzy/(10-5rad) | 2.198 92 | 2.161 23 |
| Kzx/(10-5rad) | 2.090 67 | 2.098 70 |
| Dx/((°)·h-1) | 2.041 742 49 | 2.041 734 15 |
| Dy/((°)·h-1) | 3.018 441 56 | 3.018 441 43 |
| Dz/((°)·h-1) | 2.095 456 24 | 2.095 454 32 |
表选项
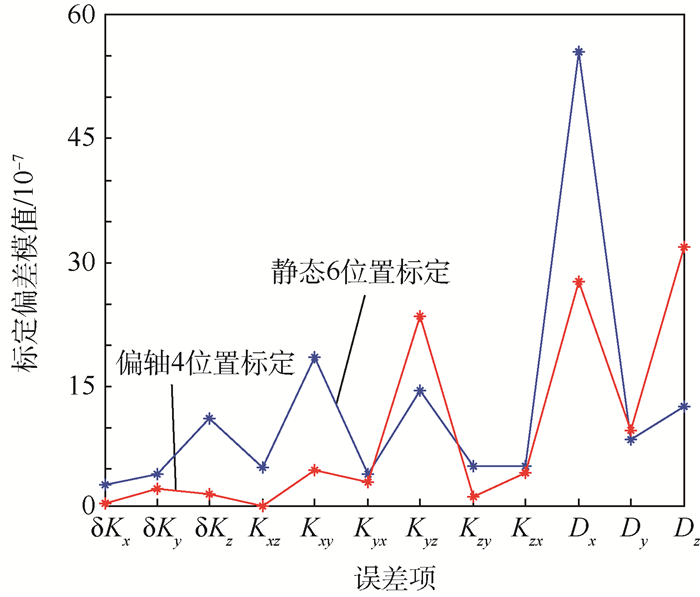
为直观反映2种标定方法的标定效果,以每种方法标定出的各个误差项的误差模值为纵坐标,以各个误差项的种类为横坐标作图,如图 10所示。
 |
| 图 10 2种标定方法所标定出的各个误差项的偏差模值 Fig. 10 Deviation mode values of each error calibrated by two calibration methods |
| 图选项 |
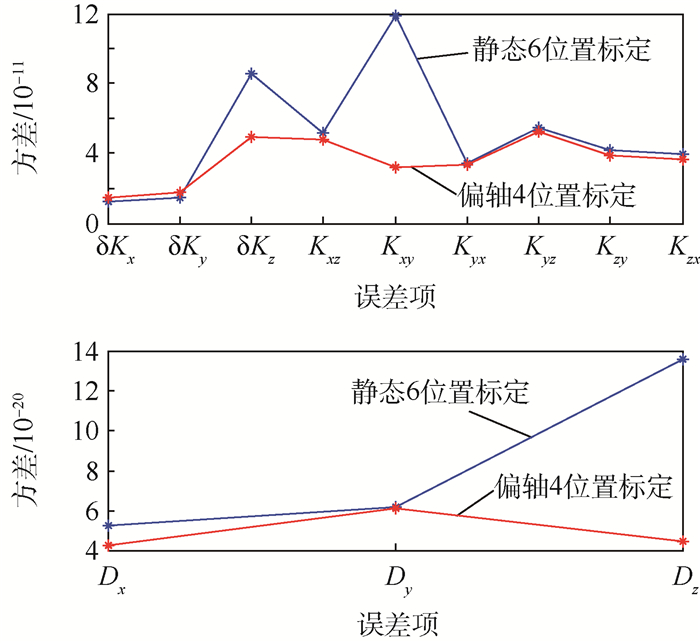
为了直观反映2种方法对各个误差项标定的稳定性,以每种方法对各个误差项进行标定时的方差为纵坐标,以各个误差项的种类为横坐标作图,如图 11所示。
 |
| 图 11 2种标定方法标定各个误差项时的方差 Fig. 11 Variance of each error calibrated by two calibration methods |
| 图选项 |
由图 10可以看出,由偏轴4位置标定方法所标定出的12个陀螺误差中,仅有3个误差项的标定偏差值大于静态6位置标定方法的标定结果,同时由于2种方法的标定偏差结果都在10-7量级,说明2种标定方法的标定精度都比较高,但偏轴4位置标方法标定结果整体上要优于静态6位置标定方法;此外,由图 11可以看出,偏轴4位置标定方法对各个误差项标定的稳定性整体上也要优于静态6位置方法。因此,通过实际标定效果仿真,验证了偏轴4位置标定方法在求取陀螺仪标度因数误差、安装误差和常值误差中的可行性以及优越性。
5 结论 1) 偏轴4位置标定方法能够实现对IMU中陀螺组件的3个标度因数误差、6个安装误差和3个常值误差项的标定,且标定精度不低于传统的“速率+24位置”分立式标定法和静态6位置分立标定方法的标定精度。
2) 在对IMU中陀螺组件12个确定性误差项的标定精度不低于传统标定方法的情况下,偏轴4位置标定方法比目前标定位置数最少的静态6位置标定方法的位置数还要少2个,且标定速度与其相比提高约33%。
3) “速率+24位置”分立式标定法需要在3轴转台上进行,而偏轴4位置标定方法只需借助双轴转台便可完成对陀螺12个确定性误差项的标定,故偏轴4位置标定方法与传统标定方法相比,所需硬件条件也更为宽松;同时,“速率+24位置”分立式标定法标定的误差项之间存在耦合关系,而偏轴4位置标定方法对各个误差项的标定相互独立,对各个误差项标定时,标定精度不受限于其他误差项的标定精度。
4) 就IMU的转位方式而言,本文所提的偏轴转位方法在每次转位时会有3个敏感轴位置同时发生变化,故相较于传统的转轴与敏感轴重合的转位方式来说,能够更大限度的激励相关误差参数,从而提高标定效率。
同样,通过分析IMU偏轴转位方案的特点,以偏轴转位思想为基础,可进一步研究基于偏轴转位的捷联惯导系统快速寻北和高效的旋转调制等其他惯导技术。
参考文献
| [1] | 张华强, 赵剡, 陈雨. 捷联惯性导航系统整体标定新方法[J]. 北京航空航天大学学报, 2012, 38(4): 459-463. ZHANG H Q, ZHAO Y, CHEN Y. New system calibration method for strapdown inertial navigation system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 459-463. (in Chinese) |
| [2] | 丁继成, 李冠男, 班镜超. 基于双轴位置转台的捷联惯导系统级标定技术[J]. 舰船科学技术, 2015, 37(4): 76-83. DING J C, LI G N, BAN J C. Research on SINS systematic calibration technique based on dual-axis turntable[J]. Ship Science and Technology, 2015, 37(4): 76-83. DOI:10.3404/j.issn.1672-7649.2015.04.015 (in Chinese) |
| [3] | SUN F, SUN W, GAO W, et al.Research on the technology of rotational motion for FOG strapdown inertial navigation system[C]//Processing of the 2009 IEEE International Conference on Mechatronics and Automation.Piscataway, NJ: IEEE Press, 2009: 4913-4918. |
| [4] | GAO W, ZHANG Y, WANG J G. Research on initial alignment and self-calibration of rotary strapdown inertial navigation systems[J]. Sensors, 2015, 15(2): 3154-3171. DOI:10.3390/s150203154 |
| [5] | 王昆明, 谢建, 周召发, 等. 双轴旋转捷联惯导的误差参数标定方法[J]. 西安交通大学学报, 2016, 50(10): 153-160. WANG K M, XIE J, ZHOU Z F, et al. A calibration method of error parameters for dual-axial rotary strapdown inertial navigation systems[J]. Journal of Xi'an Jiaotong University, 2016, 50(10): 153-160. DOI:10.7652/xjtuxb201610023 (in Chinese) |
| [6] | EDUARDO N, HUGH D W. Initial calibration and alignment of low-cost inertial navigation units for land vehicle applications[J]. Journal of Robotic Systems, 1999, 16(2): 81-92. DOI:10.1002/(ISSN)1097-4563 |
| [7] | LIU Q, LIU L, QI Z K. Error analysis and compensation of strapdown inertial navigation system[J]. Journal of Beijing Institute of Technology:English Edition, 2002, 11(2): 117-120. |
| [8] | YUN C S, GOOK P C. A calibration technique for a redundant IMU containing low-grade inertial sensors[J]. Electronics and Telecommunications Research Institute Journal, 2005, 27(4): 418-425. |
| [9] | 孙伟. 旋转调制型捷联惯性导航系统[M]. 北京: 测绘出版社, 2014: 84-87. SUN W. Rotary modulation strapdown inertial navigation system[M]. Beijing: Surveying and Mapping Press, 2014: 84-87. (in Chinese) |
| [10] | 董春梅, 陈希军, 任顺青. 捷联惯导系统的一种系统级标定方法[J]. 导航定位与授时, 2016, 3(4): 74-80. DONG C M, CHEN X J, REN S Q. Systematic calibration method for strapdown inertial navigation system[J]. Navigation Positioning & Timing, 2016, 3(4): 74-80. (in Chinese) |
| [11] | 孙枫, 孙伟. 基于双轴转位机构的光纤陀螺标定方法[J]. 控制与决策, 2011, 26(3): 346-350. SUN F, SUN W. Research on calibration of IFOG based on two-axis indexing[J]. Control and Decision, 2011, 26(3): 346-350. (in Chinese) |
| [12] | 包为民, 申功勋, 李华滨. 惯性平台在系统中多位置翻滚自标定方法[J]. 北京航空航天大学学报, 2011, 37(4): 462-465. BAO W M, SHEN G X, LI H B. Investigation on inertial platform multi-position rolling self-calibration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(4): 462-465. (in Chinese) |
| [13] | 牟玉涛, 周振威, 方海涛. SINS外场系统级标定方法的优化——最佳六位置[J]. 北京航空航天大学学报, 2011, 37(7): 855-860. MOU Y T, ZHOU Z W, FAGN H T. Optimization of systematic calibration method for SINS in outer field-optimal six-position[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(7): 855-860. (in Chinese) |
| [14] | 杨国梁, 王玮. 基于双轴旋转的惯导系统误差自补偿技术[J]. 北京航空航天大学学报, 2012, 38(4): 519-524. YANG G L, WANG W. Error auto-compensation technology of inertial navigation system based on double-axis rotation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 519-524. (in Chinese) |
| [15] | 谭彩铭, 王宇, 苏岩, 等. 捷联惯导系统最简多位置解析对准[J]. 北京航空航天大学学报, 2015, 41(9): 1645-1650. TAN C M, WANG Y, SU Y, et al. The simplest multi-position analytic alignment for SINS[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(9): 1645-1650. (in Chinese) |
| [16] | 张小跃, 杨功流, 张春熹. 三轴一体光纤陀螺高精度标定方法[J]. 北京航空航天大学学报, 2012, 38(4): 478-486. ZHANG X Y, YANG G L, ZHANG C X. High precision calibration method for three-cluster FOG[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 478-486. (in Chinese) |
| [17] | 苗继松, 邵琼玲, 任元. 基于三元角的坐标旋转变换方法[J]. 北京航空航天大学学报, 2017, 43(12): 2539-2546. MIAO J S, SHAO Q L, REN Y. Coordinate rotation transformation method based on ternary angle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(12): 2539-2546. (in Chinese) |
