甲板环境下的舰载机路径规划是甲板作业自动化的关键技术之一。近几年, 随着人工智能技术的发展和航母甲板运作对自动化和智能化的需求,针对舰载机在飞行甲板上,面对紧迫的任务和相对密集的任务环境,研究路径规划问题,已经有些文献开展了相关的研究。分析对该问题研究的文献,可以概括为2个主要方面:一方面是舰载机路径规划的建模问题[5-8];另一方面是针对模型的算法设计问题[5, 8-11]。在算法设计方面,较多的采用了智能算法,如改进的蚁群算法[8]、混沌蜂群算法、混沌捕食-食饵算法[9-10]和聚类粒子群算法[11]。这些规划方法为该问题的研究奠定了理论基础。但是,舰载机在飞行甲板上有2种运动方式[12]:一种是舰载机自主运动,其主要适用于舰载机起飞之前从初始位置到弹射器的滑行过程;另一种是由牵引车牵引运动,除起飞之前的滑行外,舰载机在甲板上的保障、回收等调运一般由牵引车牵引运动。相对于舰载机自主运动,牵引运动方式的优势主要有2点:其一,降低在甲板滑行的能耗,以提高舰载机的续航能力;其二,可避免航空发动机频繁处于低速工况,以提高发动机使用寿命。现有的文献主要针对舰载机自主运动,而由牵引车牵引的舰载机运动系统路径规划问题鲜有研究。
本文针对由牵引车牵引舰载机运动的路径规划问题,基于牵引系统的运动特征,考虑飞行甲板环境,建立路径规划的模型,并利用几何理论和Dijkstra算法求解该模型。
1 问题描述 航母飞行甲板环境如图 1所示。飞行甲板上布置有舰岛、升降机、弹射器等装置,同时飞行甲板上停放着一些等待起飞、回收或补给维修的舰载机。
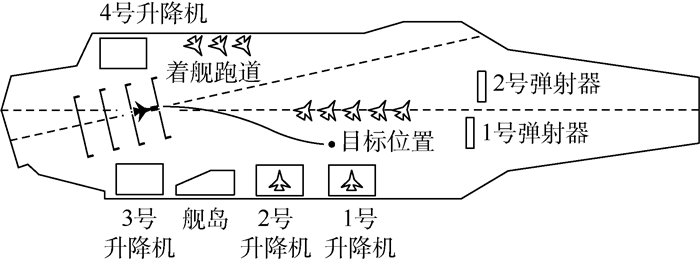 |
| 图 1 航母飞行甲板示意图 Fig. 1 Schematic diagram of aircraft carrier flight deck |
| 图选项 |
着舰跑道上有一个由舰载机和牵引车组成的牵引系统,其构型如图 2所示。
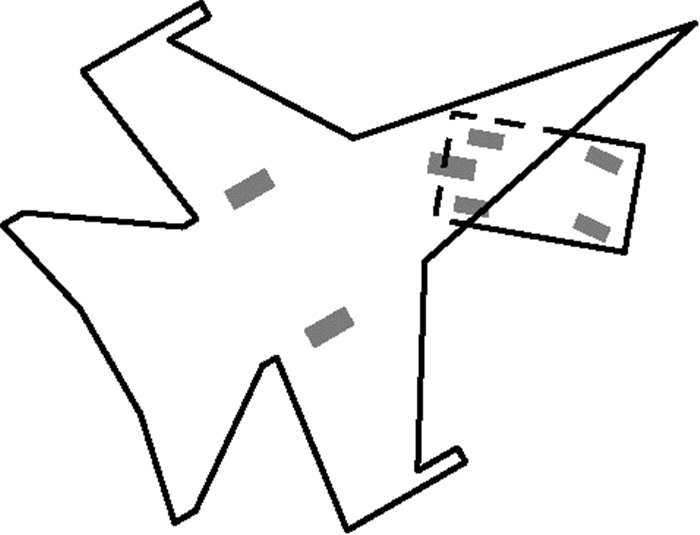 |
| 图 2 牵引系统示意图 Fig. 2 Schematic diagram of a traction system |
| 图选项 |
该牵引车需要将该舰载机从初始位置牵引至目标位置,并在规避所有的障碍物的同时使出行路径尽可能短。图 1给出了一条可能的出行路径。针对牵引系统在飞行甲板上的高效出行问题,本文建立了数学模型并设计了最优路径搜索方法。
2 数学模型 首先需要建立牵引系统、出行任务和障碍物规避的模型。
2.1 牵引系统模型 牵引系统由牵引车和舰载机组成。其中,牵引车通过舰载机的前起落架牵引舰载机。牵引系统模型包括牵引系统运动学模型和机动能力约束。
牵引系统运动学模型的建立,用到了以下假设条件:
1) 牵引系统为二刚体系统。
2) 牵引车与舰载机前起落架固连,牵引车方向即为舰载机前起落架方向。
3) 以舰载机几何中心为参考点进行路径规划。
4) 牵引车的后轮用于驱动,前轮用于转向。
图 3为牵引系统的几何模型,矩形代表牵引车,三角形代表舰载机,MN为牵引车的对称轴线,NK为舰载机的对称轴线。
根据假设条件1)和2),牵引系统有4个运动自由度。根据假设条件3),点G为舰载机的几何中心,在甲板坐标系上的坐标为(x, y)。?为NK与X轴正方向的夹角,用于表示舰载机在甲板坐标系中的方向,逆时针为正。α为MN与NK之间的夹角,即舰载机前起落架转向角,左偏为正。本文选择[x, y, ?, α]作为描述牵引系统运动的4个独立状态参数。
根据假设条件4),选择牵引车的后轮驱动速度v1和前轮转向角θ作为牵引系统的控制参数。其中,θ左偏为正。
则牵引系统的运动特征可用式(1)进行描述:
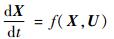 | (1) |
式中:X=[x, y, ?, α]T和U=[v1, θ]T分别为牵引系统的状态量和控制量。
利用瞬心法建立牵引系统的运动学模型。如图 3所示,I1和I2分别表示牵引车和舰载机的速度瞬心,v2和γ分别为点G速度的大小和方向。则牵引系统的运动模型为
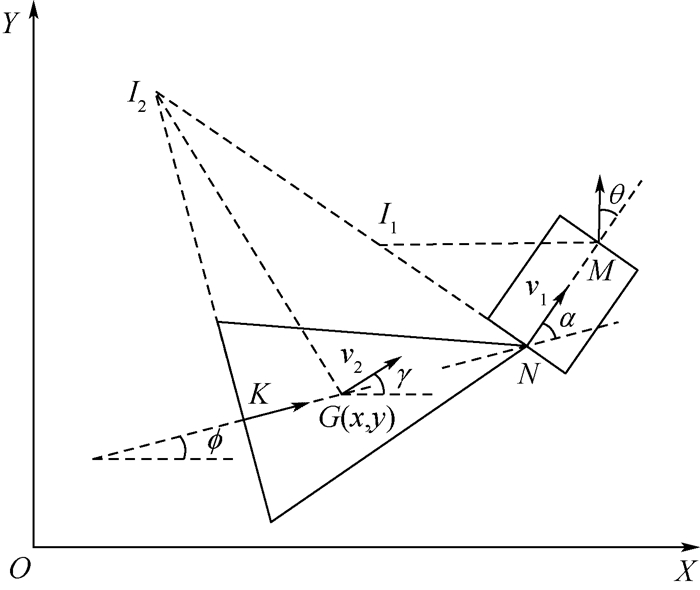 |
| 图 3 牵引系统的几何模型 Fig. 3 Geometric model of a traction system |
| 图选项 |
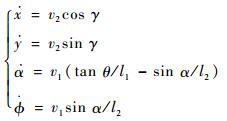 | (2) |
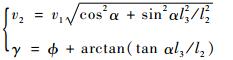 | (3) |
式中:l1、l2和l3分别为MN、NK和KG的长度。
牵引系统的机动能力约束为牵引车转向角和舰载机前起落架转向角的约束范围。
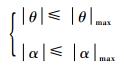 | (4) |
由式(4)可分别得到牵引车和舰载机几何中心处的最小转弯半径Rt和Ra:
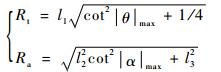 | (5) |
式(4)和式(5)为牵引系统的机动能力约束。
2.2 出行任务模型 航母飞行甲板出行任务要求牵引系统从初始位置到目标位置的路径尽可能短。出行任务模型包括任务目标函数和任务约束。
目标函数表示为
 | (6) |
式中:l为长度。牵引系统的初始状态均为已知,即
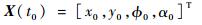 | (7) |
式中:t0为出行任务的初始时刻。
任务约束为牵引系统末端位置和方向约束。其中,牵引系统的位置为其参考点的位置,方向为该系统中舰载机的方向。即
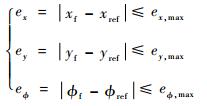 | (8) |
式中:[xf, yf, ?f]表示牵引系统的末端状态;[xref, yref, ?ref]表示牵引系统的末端参考状态。
2.3 障碍物规避模型 飞行甲板上除了需要完成出行任务的牵引系统外,还有停放的舰载机。考虑到出行任务的安全性,需要建立障碍物的规避模型。
利用特征图形来描述牵引系统和障碍物。单个舰载机可以简化为一个包含自身的最小圆[6]。由于牵引车相对于舰载机较小,当牵引舰载机移动时,牵引车始终位于舰载机的特征圆之内,则牵引系统也可以简化为一个特征圆。
当单架舰载机被视为障碍物时,为了避免牵引系统与单舰载机之间的碰撞,其关系应满足:
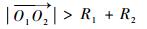 | (9) |
式中:O1和O2分别为牵引系统和单舰载机对应特征圆的圆心;R1和R2分别为圆O1和圆O2的半径。
如图 4所示,以O2为圆形,R1+R2为半径,可得到该舰载机的威胁区域。当O1位于该威胁区域之外时,牵引系统和舰载机之间可避免碰撞。
 |
| 图 4 单舰载机的避障模型 Fig. 4 Obstacle avoidance model of single carrier aircraft |
| 图选项 |
为了合理地使用甲板空间,停放在飞行甲板上的舰载机通常被并排摆放,可以简化为一个包含所有舰载机特征圆的凸包,如图 5所示。其对应的威胁区域也可以用扩展的方法得到[6, 13]。
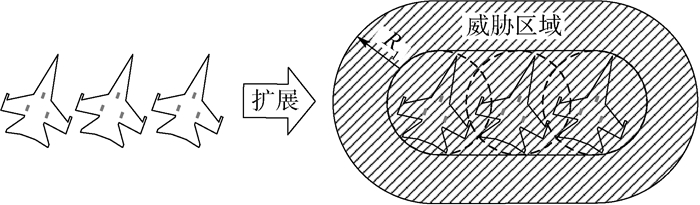 |
| 图 5 多舰载机的避障模型 Fig. 5 Obstacle avoidance model of multiple carrier aircraft |
| 图选项 |
由图 5易知当执行出行任务的牵引系统的特征圆圆心位于该威胁区域之外时,则可以避免碰撞。
3 最优路径搜索方法 基于第2节数学模型,根据几何理论设计最优路径的搜索域,在搜索域中得到所有备选路径,采用Dijkstra算法分步描述最优路径的求解过程。
3.1 基于几何理论的路径搜索域 路径规划需要考虑牵引系统的运动学模型和机动能力约束、任务目标函数和任务约束,以及障碍物规避。其中,任务约束包括牵引系统的位置约束和方向约束。
当只考虑任务目标函数和位置约束时,最优路径即为初始位置到目标位置的直线段。
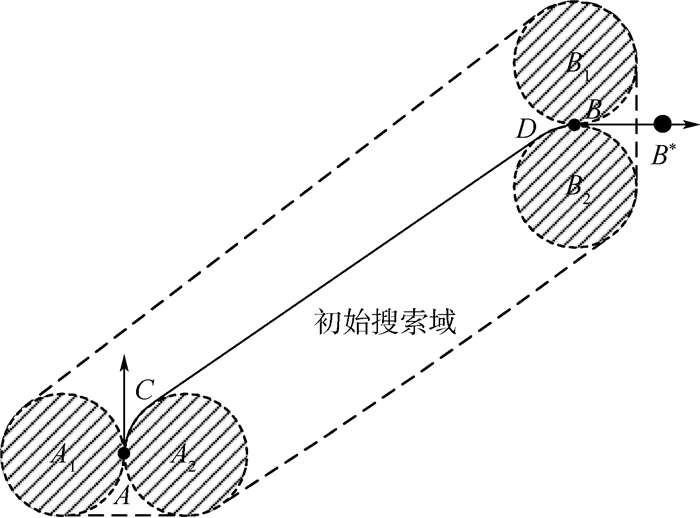
如图 6所示,点A和点B*分别为初始位置和目标位置,且两点处的箭头表示牵引系统的初始方向和目标方向。
 |
| 图 6 初始搜索域示意图 Fig. 6 Schematic diagram of initial search zone |
| 图选项 |
由牵引系统的运动学模型可知,当牵引系统转弯时,其速度方向与轴线方向不一致。因此为了满足方向约束,规划路径的最后一段应为直线段。如图 6所示,本文选择沿B*处箭头相反方向的一点B作为最优路径的一点,则BB*为最优路径的最后一段。则问题转化为规划点A到点B的最优路径。
点A处箭头所在直线为圆A1和圆A2的内公切线,且这2个圆的半径均等于牵引系统的最小转弯半径。基于牵引系统的机动能力约束,当牵引系统从点A处出发时,其不可能进入圆A1和圆A2。同理可得到圆B1和圆B2。由几何理论可知,点A到点B的最短路径由一段公切线和2段圆弧组成,例如A—C—D—B即为一条备选路径。
图 6中虚线为包含圆A1、圆A2、圆B1和圆B2的凸包,则所有的备选路径均在该凸包内。该凸包被称为最优路径的初始搜索域。
当有障碍物与搜索域边界重叠时,则需要对搜索域进行扩展。
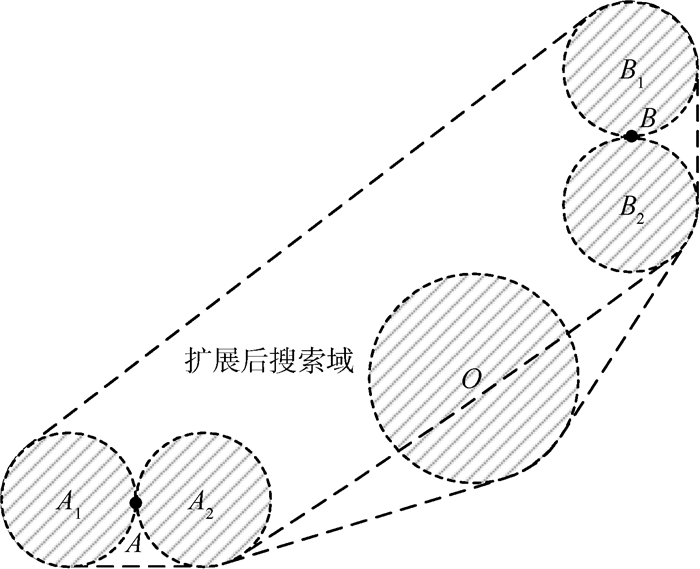
如图 7所示,圆O表示一个障碍物的威胁区域,且其与初始搜索域的边界重叠,这必将会导致一些备选路径失效。因此,选择包含这5个圆的凸包作为新的搜索域。同样的,如果还有其他威胁区域与新的搜索域边界重叠,则需要重新建立搜索域直到其边界不再与任何威胁区域重叠。
 |
| 图 7 搜索域扩展示意图 Fig. 7 Schematic diagram of search zone expansion |
| 图选项 |
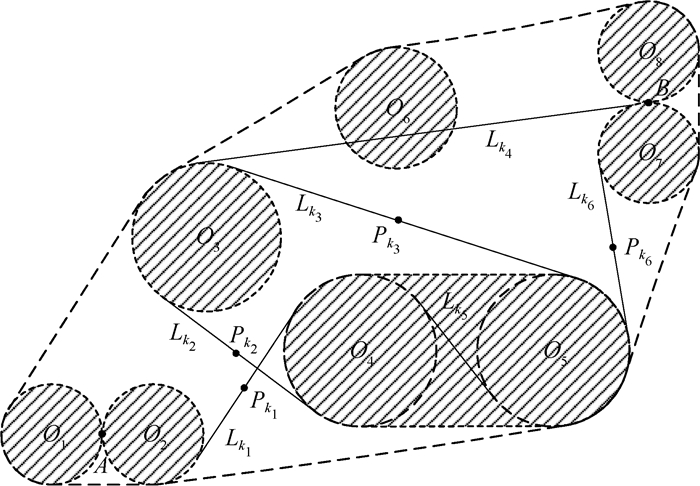
3.2 备选路径 最终搜索域如图 8所示。最终搜索域内有3个威胁区域,其中最大的一个为多舰载机的威胁区域。为了方便描述,所有圆均被依次标号。
 |
| 图 8 最终搜索域和备选路径 Fig. 8 Final search zone and alternative path |
| 图选项 |
节可知,所有的备选路径均由公切线以及连接公切线的圆弧组成。因此,找到搜索域内所有的公切线,并用式(10)进行描述:
 | (10) |
式中:Lj为最终搜索域中圆Oi1和圆Oi2的一条公切线。Di1j和Di2j表示该公切线与2个圆之间的方向关系,如果Di1j=1表示当牵引系统沿着Lj移动至圆Oi1时,其将绕圆Oi1逆时针转动;反之Di1j=-1表示将顺时针转动。Qi1j和Qi2j为Lj的2个端点。lj为Lj的长度。例如,图 8中的Lk1可以表示为
 | (11) |
若一些公切线与威胁区域相交,则认为这些公切线的长度为无限大。例如,lk4=lk5=Inf。
3.3 Dijkstra算法描述 Dijkstra算法是一种全局最优算法,可求解带权图中任意2个路径点之间的最短路径[14-15]。Dijkstra算法又称双标号法,对带权图中的路径点赋予2个标号(l(Pi), ki),其中l(Pi)为从起点P1到路径点Pi最短路径的长度,ki为该最短路径上Pi前一个路径点的下标,由此可从终点到起点进行反向追踪,找到最短路径上的所有路径点。
令带权图中任意2个路径点之间的初始代价为Cost(Pi, Pj)≥0。若路径点Pi和Pj不相邻,则有Cost(Pi, Pj)=Inf;若相邻,则Cost(Pi, Pj)即为该2个路径点之间的路径长度。在求解最短路径之前,先给出如下定义:
1) 设li(m)*为起点P1到路径点Pi最短路径的权,若路径点Pi获得了标号li(m)*,则称路径点Pi在第m步获得了永久标号li(m)*。
2) 设lj(m)为起点P1到路径点Pj最短路径权的上界,若路径点Pj获得了标号lj(m),则称路径点Pj在第m步获得了临时标号lj(m)。
3) 设Fm={Pi|Pi获得永久标号}为第m步通过集。
4) 设Em=P-Fm为第m步未通过集。
Dijkstra算法流程如下:
步骤1??算法初始化:令m=0,P1获永久标号l1(0)*=0,Pj(j≠1)获临时标号lj(0)=Cost(P1, Pj),F0={P1},E0=P-{P1}。
步骤2??求解下一个永久标号路径点:
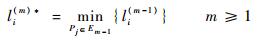 | (12) |
进而有Fm=Fm-1∪{Pi},Em=Em-1-{Pi}。检查Em,若Em=?则算法结束,否则跳转至步骤3。
步骤3??修改Em中各路径点的临时标号:
 | (13) |
令m=m+1,并跳转至步骤2。
3.4 基于Dijkstra算法的路径搜索 由Dijkstra算法可知,首先需要在备选路径中找到所有路径点,并计算得到所有路径点之间的初始代价。
选择各个公切线的中点作为路径点。点A和点B可视为2个圆的内公切线中点,则点A和点B也是路径点。接下来,将分步描述任意2个路径点之间长度的计算过程。
步骤1??找出所有的公切线,并命名为Lk(k=1, 2, …, n)。找到公切线中点,并命名为Pk(k=1, 2, …, n)。令P1=A,Pn=B。令i=1,j=1,并跳转至步骤2。
步骤2??判断Li和Lj是否与同一个圆相切。如果是,找到该公切圆Ocom,则跳转至步骤3。如果不是,令Pi和Pj之间的初始代价Cost(Pi, Pj)=Inf,令j=j+1,如果j=n+1则跳转至步骤6,否则跳转至步骤2。例如,Cost(Pk1, Pk6)=Inf。
步骤3??判断牵引系统是否能沿着Li移动至Ocom并继续移动至Lj。如果是,则有Dcomi·Dcomj=-1,找到牵引系统沿Ocom移动的圆弧Arccom,并跳转至步骤4。如果不是,则有Dcomi·Dcomj=1,令Cost(Pi, Pj)=Inf、j=j+1,如果j=n+1则跳转至步骤6,否则跳转至步骤2。例如,D5k3=-1表示牵引系统从Lk3移动至O5后将绕O5顺时针转动,D5k6=-1表示只有当牵引系统绕O5逆时针转动时才能从O5移动至Lk6,则Pk3和Pk6之间的初始代价Cost(Pk3, Pk6)=Inf。
步骤4??判断Arccom是否与威胁区域重叠。如果不是,则跳转至步骤5。如果是,令Cost(Pi, Pj)=Inf、j=j+1,如果j=n+1则跳转至步骤6,否则跳转至步骤2。例如,Cost(Pk1, Pk2)=Inf。
步骤5??首先计算牵引系统从Pi移动至Pj需要绕Ocom转动的角度。
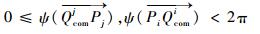 | (14) |
式中:
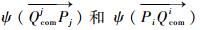
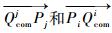
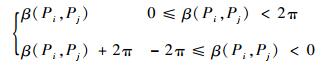 | (15) |
式中:
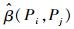
 | (16) |
式中:Rcom为圆Ocom的半径。令j=j+1,如果j=n+1则跳转至步骤6,否则跳转至步骤2。
步骤6??令i=i+1。如果i < n,则令j=i+1并跳转至步骤2。如果i=n,则停止循环,并得到了所有路径点之间的初始代价。
根据上述步骤以及Dijkstra算法,给出了最优路径的计算流程图,如图 9所示。
 |
| 图 9 最优路径计算流程图 Fig. 9 Calculation flowchart of optimal path |
| 图选项 |
4 仿真及分析 为了验证本文规划方法的合理性和有效性,本节对牵引系统在航母飞行甲板上的出行任务进行了路径规划,并利用模型预测控制方法(Model Predictive Control,MPC[16-18])对路径进行了跟踪控制。
4.1 仿真算例描述 从任务环境、任务要求和牵引系统3个方面描述仿真算例。
任务环境即为航母飞行甲板,如图 10所示。图中的5架舰载机均停放在飞行甲板上,其位置和方向信息如表 1所示。
 |
| 图 10 航母飞行甲板布局 Fig. 10 Layout of aircraft carrier flight deck |
| 图选项 |
表 1 停放在飞行甲板上的舰载机位置及方向 Table 1 Positions and directions of carrier aircraft parked on flight deck
| 位置/m | 方向/(°) |
| (82, 23) | -90 |
| (120, 12) | 60 |
| (134, 12) | 60 |
| (148, 12) | 60 |
| (162, 12) | 60 |
表选项
出行任务要求牵引系统从其初始位置运动至目标位置,满足末端方向约束并规避所有停放在飞行甲板上的舰载机。牵引系统在甲板坐标系下的初始位置和方向以及目标位置和方向均标注在图 10中,末端位置和末端方向的误差允许范围为
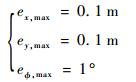 | (17) |
牵引系统的具体参数如表 2所示。
表 2 牵引系统参数 Table 2 Parameters of traction system
| 参数 | 数值 |
| |θ|max/(°) | 60 |
| |α|max/(°) | 60 |
| l1/m | 3 |
| l2/m | 8 |
| l3/m | 4 |
| 舰载机特征圆半径/m | 8 |
| 舰载机后起落架间距/m | 6 |
| 牵引车特征圆半径/m | 2.5 |
| v1/(m·s-1) | 3 |
表选项
4.2 仿真结果 仿真结果给出了牵引系统最优路径、跟踪最优路径的状态响应和控制指令响应。
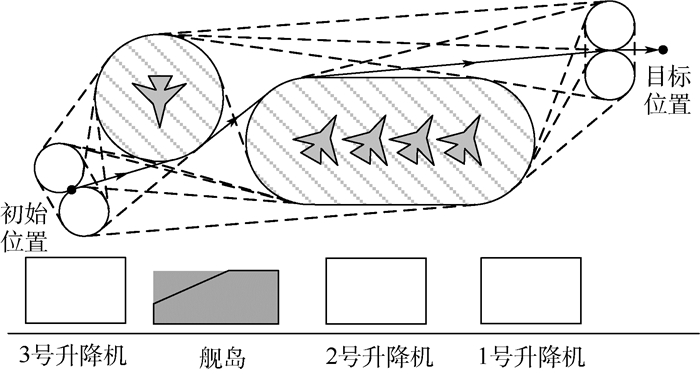
图 11为牵引系统从初始位置到目标位置的路径。其中,虚线表示备选路径段,实线为最优路径。规划路径最后一段(即图 6 BB*段)的长度为12 m。
 |
| 图 11 路径规划结果 Fig. 11 Results of path planning |
| 图选项 |
由图 11可以看出牵引系统的最优路径由4段圆弧与4段直线段组成,体现了规避障碍和最短路径的任务要求。
牵引系统跟踪最优路径的状态响应如图 12~图 14所示。
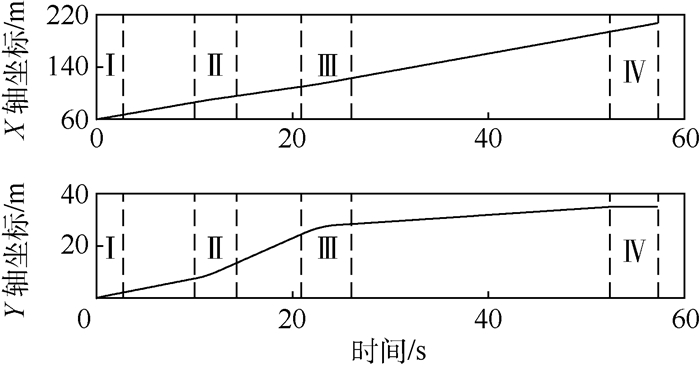 |
| 图 12 牵引系统位置 Fig. 12 Position of traction system |
| 图选项 |
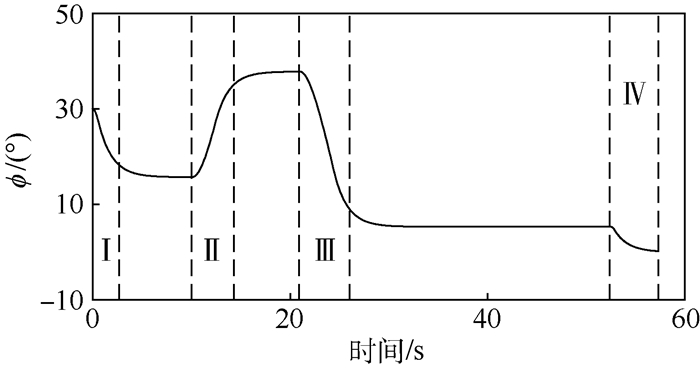 |
| 图 13 牵引系统方向角 Fig. 13 Direction angle of traction system |
| 图选项 |
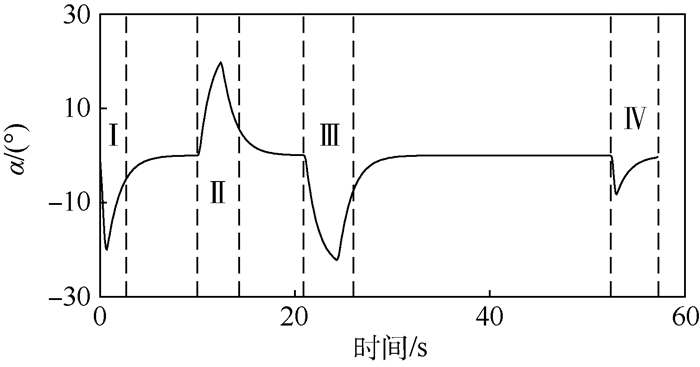 |
| 图 14 舰载机前起落架转向角 Fig. 14 Steering angle of carrier aircraft nose gear |
| 图选项 |
牵引系统跟踪最优路径的控制指令响应如图 15所示。
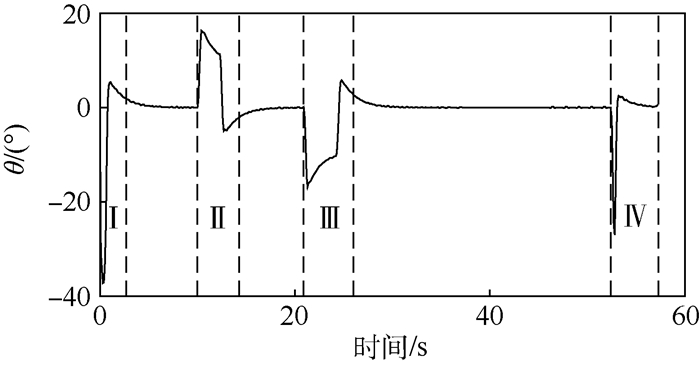 |
| 图 15 控制指令(牵引车转向角) Fig. 15 Control command (steering angle of tractor) |
| 图选项 |
4.3 结果分析 本文通过分析牵引系统状态响应和控制指令响应,来验证模型的合理性,通过分析出行任务的完成效果,说明方法的有效性。
牵引系统状态响应和控制指令响应的仿真结果中(见图 12~图 15)标注了4个阶段,在这4个阶段中,牵引车转向角、舰载机前起落架转向角以及牵引系统方向发生了明显的变化。这是由于牵引系统在这4个阶段中作转弯运动,其中阶段Ⅰ、Ⅲ、Ⅳ对应右转弯,阶段Ⅱ对应左转弯。表 3描述了各个运动阶段,可以看出,仿真结果体现了各阶段对应的牵引系统运动特征和任务要求。
表 3 仿真结果描述 Table 3 Description of simulation results
| 阶段 | 牵引系统运动 |
| Ⅰ | 调整初始方向 |
| Ⅰ | 规避单体障碍 |
| Ⅲ | 规避多体障碍 |
| Ⅳ | 调整末端方向 |
表选项
以阶段Ⅰ为例,牵引系统作右转弯运动(见图 11),因此其方位角逐渐变小(见图 13)。为了使牵引系统右转弯,其前起落架转向角需要右偏(见图 14),对应的牵引车转向角也需要右偏(见图 15)。当牵引系统结束右转弯运动进入直线运动时,牵引车转向角会小幅左偏并最终收敛至零(见图 15)。这是因为相对于牵引车转向角,舰载机前起落架转向角和牵引系统方向具有滞后性。综上所述,牵引系统跟踪最优路径的状态响应和控制指令响应验证了模型的合理性。
从出行任务的完成效果来看,牵引系统的末端位置为(xf, yf)=(206.92, 35.00) m,末端方向为?f=0.20°,满足末端位置和方向的任务要求。整个路径跟踪过程中牵引系统的最大跟踪误差为7.16×10-4 m,表明牵引系统能有效规避所有障碍物。另外,由图 14和图 15可以看出牵引系统在出行过程中满足其机动能力约束。由此,验证了方法的有效性。
5 结论 针对舰载机在飞行甲板上由牵引车牵引的运动特征,提出了甲板环境下舰载机牵引系统的路径规划方法。
1) 建立了舰载机牵引系统的路径规划模型,该模型体现了牵引系统的运动学特性和机动能力约束、任务要求和任务约束、以及障碍物特征。
2) 针对该模型,基于几何理论和Dijkstra算法设计了规划方法。仿真结果表明牵引系统能够对规划路径进行准确的跟踪,能有效规避所有障碍物,并满足任务要求和机动能力约束。
参考文献
| [1] | 刘相春, 卢晶, 黄祥钊. 国外航母舰载机出动回收能力指标体系分析[J]. 中国舰船研究, 2011, 6(4): 1-7. LIU X C, LU J, HUANG X Z. Analysis on the index system of sortie generation capacity of embarked aircrafts[J]. Chinese Journal of Ship Research, 2011, 6(4): 1-7. DOI:10.3969/j.issn.1673-3185.2011.04.001 (in Chinese) |
| [2] | MICHINI B, HOW J P.A human-interactive course of action planner for aircraft carrier deck operations[C]//Proceedings of AIAA Information Technology.Reston: AIAA, 2011: 1515. http://arc.aiaa.org/doi/pdf/10.2514/6.2011-1515 |
| [3] | ZHANG Z, LIN S L, DONG R, et al.Designing a human-computer cooperation decision planning system for aircraft carrier deck scheduling[C]//Proceedings of AIAA Information Technology.Reston: AIAA, 2015: 1111. http://arc.aiaa.org/doi/abs/10.2514/6.2015-1111 |
| [4] | WU Y, SUN L G, QU X J. A sequencing model for a team of aircraft landing on the carrier[J]. Aerospace Science and Technology, 2016, 54(1): 72-87. |
| [5] | WU Y, QU X J. Path planning for taxi of carrier aircraft launching[J]. Science China Technological Sciences, 2013, 56(6): 1561-1570. DOI:10.1007/s11431-013-5222-5 |
| [6] | WU Y, QU X J. Obstacle avoidance and path planning for carrier aircraft launching[J]. Chinese Journal of Aeronautics, 2015, 28(3): 1-10. |
| [7] | ZHENG Y, ZHANG Z, XIA G H.Complex-shaped object path planning algorithm with kinematics and terminal pose constraints[C]//27th Chinese Control and Decision Conference.Piscataway, NJ: IEEE Press, 2015: 3408-3412. http://ieeexplore.ieee.org/document/7162511/ |
| [8] | 刘洋, 章卫国, 李广文, 等. 动态环境中的无人机路径规划方法[J]. 北京航空航天大学学报, 2014, 40(2): 252-256. LIU Y, ZHANG W G, LI G W, et al. Path planning of UAV in dynamic environment[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 252-256. (in Chinese) |
| [9] | ZHU W R, DUAN H B. Chaotic predator-prey biogeography-based optimization approach for UCAV path planning[J]. Aerospace Science and Technology, 2014, 32(1): 153-161. DOI:10.1016/j.ast.2013.11.003 |
| [10] | XU C F, DUAN H B, LIU F. Chaotic artificial bee colony approach to uninhabited combat air vehicle(UCAV) path planning[J]. Aerospace Science and Technology, 2010, 14(8): 535-541. DOI:10.1016/j.ast.2010.04.008 |
| [11] | 韩维, 司维超, 丁大春, 等. 基于聚类PSO算法的舰载机舰面多路径动态规划[J]. 北京航空航天大学学报, 2013, 39(5): 610-614. HAN W, SI W C, DING D C, et al. Multi-routes dynamic planning on deck of carrier plane based on clustering PSO[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 610-614. (in Chinese) |
| [12] | 林圣琳.舰载机甲板作业辅助规划系统设计与实现[D].哈尔滨: 哈尔滨工程大学, 2014: 12-31. LIN S L.Designing and Realizing an auxiliary planning system for aircraft scheduling on deck[D].Harbin: Harbin Engineering University, 2014: 12-31(in Chinese). |
| [13] | BLACKMORE L, ONO M, WILLIAMS B C. Chance-constrained optimal path planning with obstacles[J]. IEEE Transactions on Robotics, 2011, 27(6): 1080-1094. DOI:10.1109/TRO.2011.2161160 |
| [14] | MUROTA K, SHIOURA A. Dijkstra's algorithm and L-concave function maximization[J]. Mathematical Programming, 2014, 145(1-2): 163-177. DOI:10.1007/s10107-013-0643-2 |
| [15] | GUNKEL C, STEPPER A, MULLER A C, et al. Micro crack detection with Dijkstra's shortest path algorithm[J]. Machine Vision and Applications, 2012, 23(3): 589-601. DOI:10.1007/s00138-011-0324-1 |
| [16] | QIN S J, BADGWELL T A. A survey of industrial model predictive control technology[J]. Control Engineering Practice, 2003, 11(7): 733-764. DOI:10.1016/S0967-0661(02)00186-7 |
| [17] | MAYNE D Q, RAWLINGS J B, RAO C V, et al. Constrained model predictive control:Stability and optimality[J]. Automatica, 2000, 36(6): 789-814. DOI:10.1016/S0005-1098(99)00214-9 |
| [18] | KOURO S, CORTES P, VARGAS R, et al. Model predictive control-A simple and powerful method to control power converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1826-1838. DOI:10.1109/TIE.2008.2008349 |
