对于单个航天器的姿态控制问题,国内外****采用自适应控制[7]、鲁棒控制[8]、滑模控制[9]等多种方法进行了研究,取得了丰富的研究成果。在上述方法中,航天器的姿态大多采用的是欧拉角、四元数[10]或罗格里德参数模型[11],在姿态运动范围较小时可以取得良好效果,但仍存在一定的局限性。欧拉角模型在姿态角全局范围变化时会出现奇异,导致基于这种方法设计的控制器也只适用于某个范围内;采用四元数进行姿态表示的方法能够避免奇异,但其与旋转矩阵的映射不具有唯一性,用于控制时可能导致姿态散开,引起系统性能下降[12];罗格里德参数模型同样存在非全局与不唯一性。为了解决这些问题,文献[13-14]提出了基于特殊正交群(Special Orthogonal Group,SO(3))的姿态建模与控制方法。SO(3)与旋转矩阵是一一对应的,满足姿态描述的全局性,相比传统区分通道分别设计的方法更为统一,且不存在奇异问题。针对个体控制问题,SO(3)方法已经取得了一定的研究和应用成果。文献[14-15]采用旋转矩阵对航天器姿态进行建模,克服了姿态展开现象。文献[16]详细讨论了单刚体的SO(3)姿态跟踪控制问题,保证了系统的全局指数稳定性。
另外,在实际复杂的环境中,航天器系统不可避免地会受到干扰,而干扰会造成系统的稳定性能和协同效果下降。文献[17-18]分别考虑了存在执行器安装偏差和不确定性情形,提出了航天器鲁棒控制方法,属于对干扰的被动抑制。针对干扰的主动抑制控制,以扩张状态观测器(Extended State Observer, ESO)为核心的自抗扰控制方法近年来得到越来越多的关注。ESO将系统的不确定性和干扰等效为总干扰,以其作为扩张状态进行实时估计,进而在控制器设计中可以针对系统的总干扰进行补偿,提高系统的抗干扰能力。ESO的稳定性分析相对复杂,目前主要基于Lyapunov理论开展。文献[19]证明了可以通过严格构造Lyapunov函数完成对常值增益的线性ESO的收敛性分析。而对于非线性ESO则需要假设Lyapunov函数存在[20],不便于控制器设计和稳定性分析。因此在后续研究中,线性ESO已经得到了一定的实际应用[21-23]。但需要注意的是,线性常值增益ESO在初值和系统初值不一致时,经常会出现峰化现象(peaking phenomenon)[24-25],对系统造成不利影响。
相比单个航天器,多航天器控制系统更为复杂[26]。而对于多航天器系统的SO(3)建模、ESO设计以及协同控制问题,目前研究还比较有限。除了个体动力学外,航天器之间的通信拓扑也会对系统的整体行为产生影响。在多航天器SO(3)控制中,需要根据拓扑结构设计恰当的SO(3)形式的协同指令。同时,由于SO(3)模型中姿态采用矩阵而非向量表示,因此针对SO(3)模型的ESO也需要重新设计和分析。
考虑到上述问题,本文将SO(3)姿态描述引入到多航天器系统,结合航天器之间的有向通信拓扑建立其协同控制模型。在此SO(3)模型上设计了一种时变增益ESO对系统的总干扰进行估计,在保证观测误差收敛的同时,削弱常值ESO的峰化现象。进一步,利用相邻航天器的信息构造了SO(3)形式的协同控制指令,并设计了对应的协同控制器,从理论上证明了闭环系统的稳定性,所提出的方法能够实现干扰情形下多航天器系统的有效协同。以5个包含不同干扰和不确定性的航天器系统进行了仿真,验证了理论分析结果。
1 多航天器姿态模型建立 1.1 航天器姿态SO(3)模型 在三维空间中,姿态代表了航天器本体坐标系与惯性坐标系之间的旋转关系,而坐标系之间的旋转变换可以用一个正交变换矩阵R来表示,所有的正交变换矩阵构成了SO(3)群:
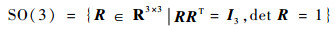 | (1) |
任意姿态都与特定矩阵R∈SO(3)一一对应。因此,可以考虑采用SO(3)中对应的元素R来表示航天器的姿态。令Ω=[ω1??ω2??ω3]T,定义运算
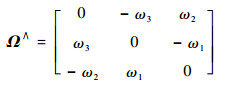 | (2) |
为hat映射。hat映射的逆运算∨称为vee映射,其将任意三维反对称阵映射为三维向量,即
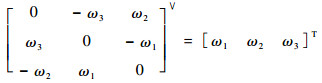 | (3) |
在本文中,对于一般矩阵X=(xij)∈R3×3,其vee映射定义为X∨=
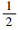
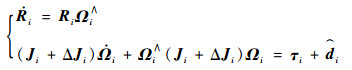 | (4) |
式中:Ωi∈R3为航天器的角速度;τi∈R3为航天器的控制力矩;Ji为转动惯量;ΔJi为转动惯量不确定性;
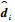
对式(4)进行展开后处理可得
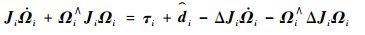 | (5) |
记
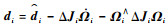
 | (6) |
对于干扰di,有如下假设[19-20]。
假设1??存在常数Md > 0,使得||di|| < Md,
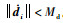
1.2 多航天器通信拓扑描述 在多航天器控制系统中,除了每个航天器自身的动力学外,航天器之间的通信关系也会对协同控制性能产生重要影响。本文的设计方法避免了对系统全局信息的使用,同时考虑了通信传递的方向性。本文采用图论相关理论对通信拓扑进行描述,设

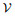
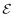
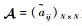
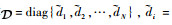
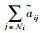
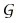
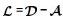
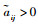
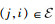
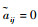
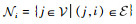
本文研究的姿态协同控制目标可以表述为:在存在干扰的情况下,考虑多航天器之间的有向通信拓扑,设计ESO对干扰进行观测和补偿,进而设计合适的协同指令与控制器,使得
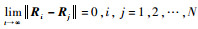
2 线性时变增益ESO设计 针对第i个航天器展开ESO设计及收敛性分析。考虑系统式(4),令X1i=Ri,X2i=RiΩi∧,则有
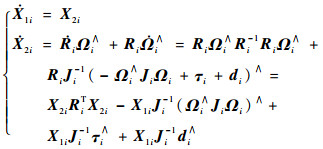 | (7) |
选取扩张状态X3i=Di=X1iJi-1di∧,系统式(7)就可以表示为
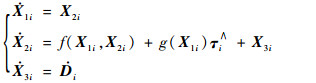 | (8) |
式中:X1i, X2i, X3i∈R3×3;g(X1i)=X1iJi-1;f(X1i, X2i)=X2iX1iTX2i-X1iJi-1(X1iTX2iJi(X1iTX2i)∨)∧。
对于式(8)所示系统,考虑设计以下形式的ESO:
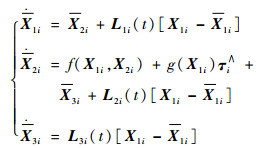 | (9) |
式中:Lki(t)=diag{lki(t), lki(t), lki(t)},lki(t)为时变增益系数,k=1, 2, 3。
根据SO(3)的性质,有||X1i||=1。
假设2??存在常数M > 0,使得||X2i||≤M,
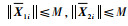
定义观测误差
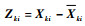
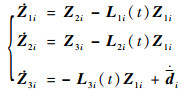 | (10) |
系统式(10)对于Zki的每一个行向量而言是解耦的,记zki(j)为Zki的第j个行向量,则有
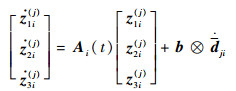 | (11) |
式中:
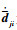
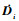
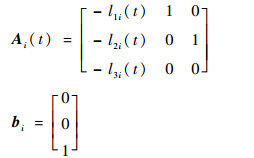 |
为了分析系统式(11)的稳定性,将其转换为标准型:
 | (12) |
式中:
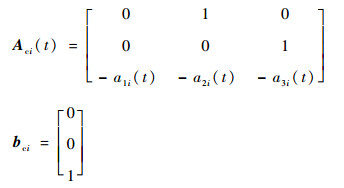 |
其中:aki(t)为与lki(t)有关的函数,且满足以下假设。
假设3??aki(t)有界且三阶连续可导,k=1, 2, 3。
系统式(11)的可控性矩阵记为Ui(t)=[p1i(t)??p2i(t)??p3i(t)],p1i(t)=bi,p2i(t)=
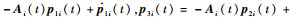
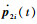
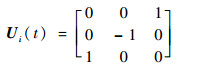 | (13) |
同理,与系统式(12)对应的可控性矩阵为
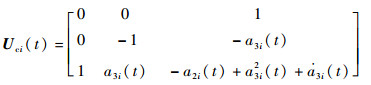 | (14) |
则系统式(11)到系统式(12)的坐标变换矩阵为
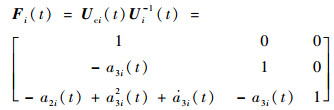 | (15) |
根据假设3,Fi-1(t)存在且有界,可以求出:
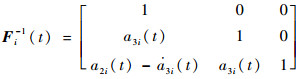 | (16) |
进一步,在系统式(11)中令Zji=[(z1i(j))T??(z2i(j))T??(z3i(j))T]T。根据ζji=Fi(t)Zji可得
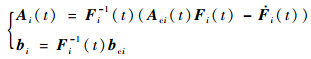 | (17) |
由Fi(t)、bi和bci的表达式以及式(17)中的第1个式子可以得出:
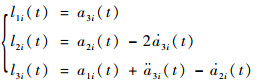 | (18) |
由式(18)可知,lki(t)能够表示为aki(t)的函数,即可以通过设计aki(t)来保证系统式(12)稳定,进而保证ESO的稳定性。在确定合适的aki(t)后,ESO的参数也随之确定。于是,考虑与系统式(12)对应的PD特征值和SD特征值分别为ρki(t)和μki(t)[25, 27],定义:
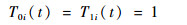 | (19) |
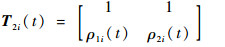 | (20) |
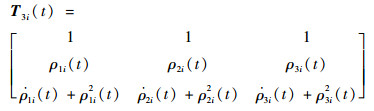 | (21) |
则有如下关系成立:
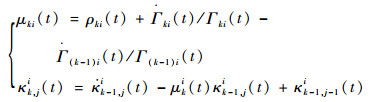 | (22) |
式中:k, j=1, 2, 3;κn, 0(t)=0, κn, n+1(t)=0, n=0, 1, 2;Γ2i(t)和Γ3i(t)分别为T2i(t)和T3i(t)对应的行列式。根据式(22)可以递推计算出a1i(t)=κ3, 1(i)(t), a2i(t)= κ3, 2i(t), a3i(t)=κ3, 1i(t)。因此,对于观测器参数lki(t)的选择可以转化为对ρki(t)的设计。
引理1??设ρki(t)为实数且满足如下条件:
1) ρki(t)有界且三阶连续可导;
2) 由式(19)~式(22)得到的aki(t)满足假设3;
3) 存在常数c > 0,使得ρki(t)≤-c < 0。
则系统
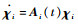
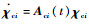
证明??根据条件1)~3)可知,T3i(t)非奇异且连续可导,记χzi=T3i-1(t)χci,则有
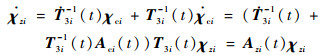 | (23) |
式中:Azi(t)=diag{ρ1i(t), ρ2i(t), ρ3i(t)}。根据条件3),选取Lyapunov函数V1(χzi)=χziTχzi,对其求导数可得
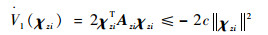 | (24) |
即证明了χzi是指数稳定的。设
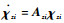
考虑χci和χi系统的状态转移矩阵分别为Φχci(t, t0)和Φχi(t, t0),同理可得
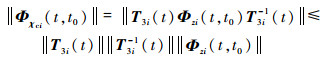 | (25) |
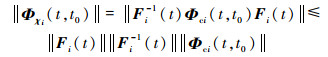 | (26) |
由于T3i(t)、T3i-1(t)、Fi(t)、Fi-1(t)均存在且连续有界,因此存在常数k3 > 0和k4 > 0, 使得:
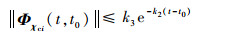 | (27) |
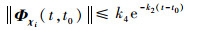 | (28) |
从而证明了χi和χci是指数稳定的。????证毕
在此基础上,关于观测误差的稳定性有如下定理成立。
定理1??若
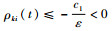
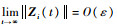
证明??考虑对称正定矩阵Pzi(t)=(T3i-1(t)·Fi(t))T (T3i-1(t)Fi(t)),结合引理1中的条件,Pzi(t)有界连续可导。定义变量χzi=T3i-1(t)χci=T3i-1(t)Fi(t)χi,对其求导数得到关系式:
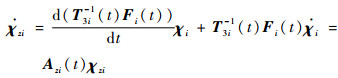 | (29) |
式中:
 | (30) |
由此可知:
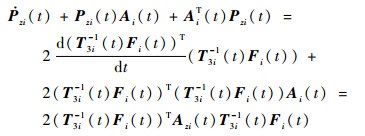 | (31) |
令
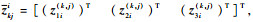
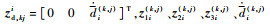
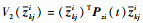
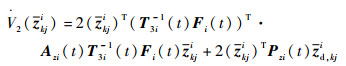 | (32) |
易知存在常数c2 > 0,使得
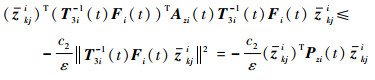 | (33) |
再根据Pzi(t)的性质可知,存在正常数c3、c4和c5使得:
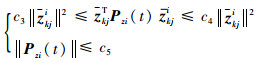 | (34) |
从而有
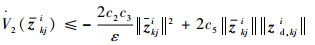 | (35) |
进一步,由于Zi为矩阵,因此考虑将Zi拉直后重新排列。记
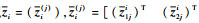
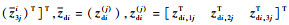
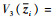
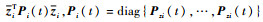
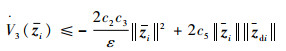 | (36) |
根据hat变换的性质,有
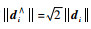
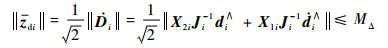 | (37) |
式中:
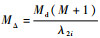
将式(37)代入式(36),则有
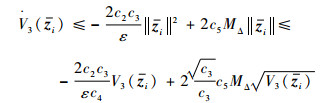 | (38) |
同时,根据
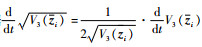
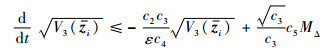 | (39) |
最终得到
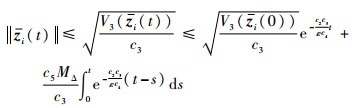 | (40) |
根据式(40)易知,当t→∞时,||zi(t)||→O(ε),即||Zi(t)||→O(ε)。????证毕
注1??定理1在引理1的基础上分析了时变增益ESO的收敛性。若ρki(t)取1/ε的同阶量,则观测误差有界且趋于ε的同阶量。同时,在ρki(t)确定后,通过式(18)和式(22)可以计算得到ESO增益lki(t)。
3 SO(3)协同控制器设计 本节首先对SO(3)中姿态误差定义以及协同指令进行推导。在基于SO(3)的控制方法中,姿态由R∈SO(3)来表示,对于每个航天器i,设协同指令Rdi=[bdi(1)??bdi(2)??bdi(3)]。由于Rdi是正交矩阵,在[bdi(1)??bdi(2)??bdi(3)]中给定其中2个变量后,可以由正交性计算出第3个变量。因此,Rdi的设计包含2个自由度。由于在协同控制系统中,每个航天器只能获得其相邻航天器的状态信息,所以在协同指令设计时也需要考虑通信拓扑结构。为此,本文设计的协同指令bdi(1)、bdi(2)和bdi(3)如下:
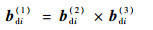 | (41) |
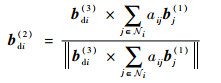 | (42) |
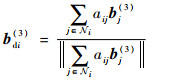 | (43) |
在姿态指令信号Rdi的基础上,定义SO(3)中的相对姿态误差和角速度误差分别为
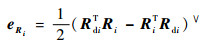 | (44) |
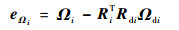 | (45) |
同时,根据Rdi的性质有RdiTRdi=I3,等式两边同时对t求导可得
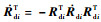
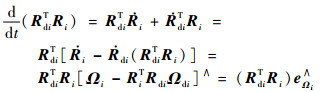 | (46) |
根据式(45)和式(46),航天器i的误差方程可以表示为
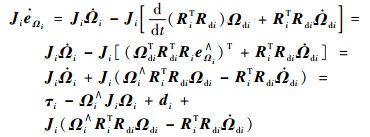 | (47) |
得到SO(3)姿态指令和姿态误差模型后,进一步设计航天器协同控制器以完成对指令的跟踪,同时实现姿态一致。同时,考虑ESO输出的扩张状态X3i,由于X3i=X1iJi-1di,则可以得到干扰观测值
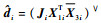
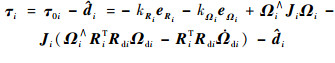 | (48) |
4 闭环系统协同控制稳定性分析 定理2??在时变增益ESO式(9)和控制律式(48)的作用下,多航天器系统能够实现有效的姿态协同,闭环系统一致最终有界稳定,且稳定的界为
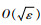
证明??选取闭环系统的Lyapunov函数为
 | (49) |
式中:
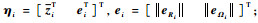
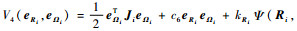
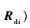
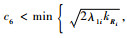
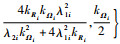
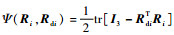
首先证明V4的正定性。易知
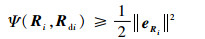 | (50) |
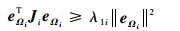 | (51) |
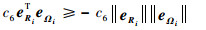 | (52) |
根据条件
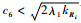
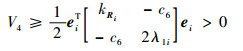 | (53) |
进一步,考虑式(49)中Ψ(Ri, Rdi)对时间t的导数:
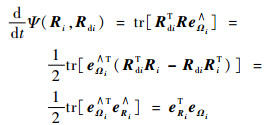 | (54) |
而V5(ηi)中c6eRiTeΩi沿时间t的导数为
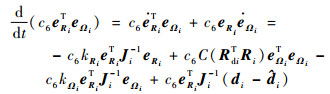 | (55) |
式中:
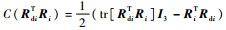
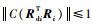
结合式(54)、式(55)对V5(ηi)求导可得
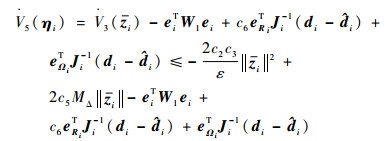 | (56) |
式中:
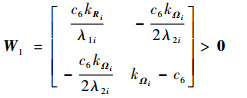 | (57) |
同时,根据前述的分析可知:
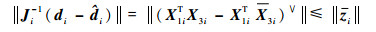 | (58) |
进一步,根据Young不等式,有
 | (59) |
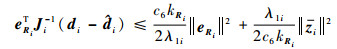 | (60) |
将上述结果代入式(56)中可得
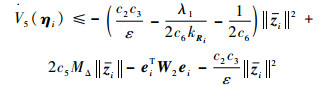 | (61) |
式中:
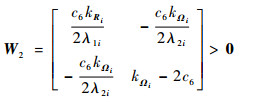 | (62) |
取
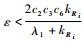
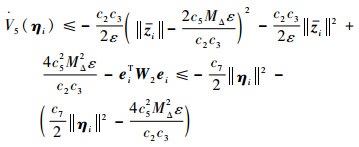 | (63) |
式中:
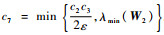
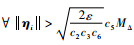
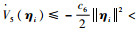
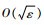
进一步,需要证明多航天器在所设计的协同控制器作用下形成姿态协同,即证明在t→∞时,

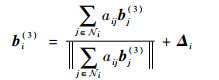 | (64) |
式中:
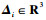
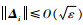
记
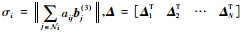
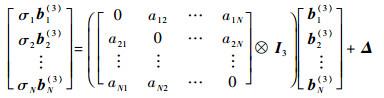 | (65) |
下面要证明
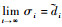
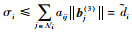
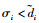
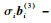
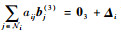
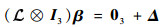 | (66) |
若航天器之间的拓扑包含生成树,则
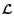
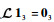
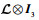
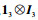
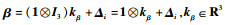
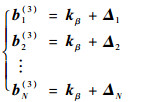 | (67) |
所以,
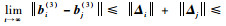
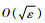
注2??通过航天器模型式(4)和控制器式(48)设计过程可以看出,本文提出的SO(3)协同控制方法允许各航天器具有不同的总体和控制参数,即适用于航天器异构的情况,有利于本文方法在工程中的应用。
5 仿真验证 为了验证本文所提出的ESO设计方法和SO(3)协同控制方法的有效性,本节采用包含5个个体的多航天器系统进行仿真。各航天器的转动惯量标称值为Ji=diag{20, 10, 10} kg·m2,其不确定性ΔJi参数和初始条件在表 1中给出。外部干扰设置为
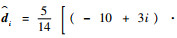
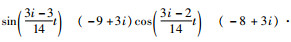
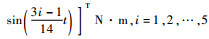
表 1 航天器初始条件和参数 Table 1 Initial conditions and parameters of spacecraft
| 航天器 | 不确定性 ΔJi/(kg·m2) | 俯仰角/ (°) | 偏航角/ (°) | 滚转角/ (°) |
| 1 | 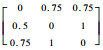 | 50 | 30 | 10 |
| 2 |  | 15 | 10 | 20 |
| 3 |  | 0 | -10 | 40 |
| 4 |  | 5 | -8 | 20 |
| 5 |  | -10 | 0 | 10 |
表选项
航天器之间的通信拓扑由图 1给出。相应的边的权重为
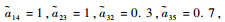
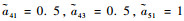
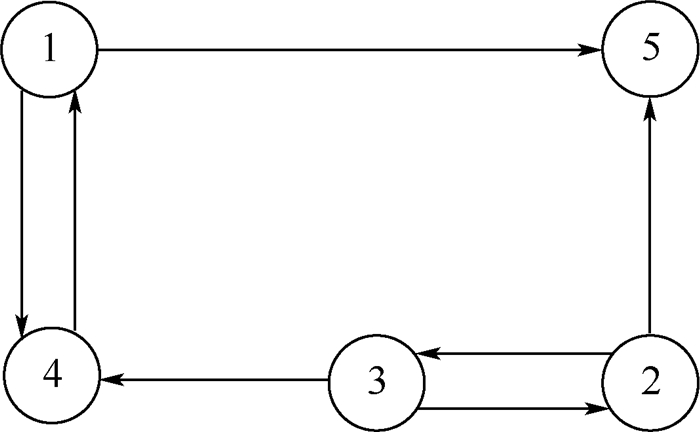 |
| 图 1 航天器通信拓扑 Fig. 1 Communication topology of spacecraft |
| 图选项 |
在仿真算例中,选取各航天器的ESO采用相同的参数。根据引理1与定理1的相关分析,对于时变ESO参数可以取为
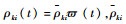
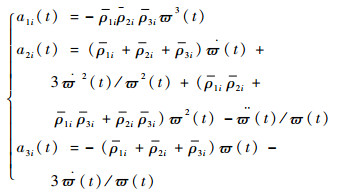 |
lki(t)的表达式可以进一步通过式(18)得到。再根据定理1取ε=0.01,
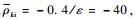
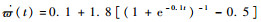
在协同控制器设计与仿真中,均采用R矩阵对航天器姿态进行描述,并基于SO(3)方法完成上述过程。为了便于结果呈现,本文在仿真结果图中将R转换为姿态角度进行表示。图 2给出了多个航天器的俯仰、偏航、滚转角度随时间变化曲线。可以看出,在存在干扰的情况下,多航天器系统能够以较快的速度实现稳定的协同,控制效果良好。
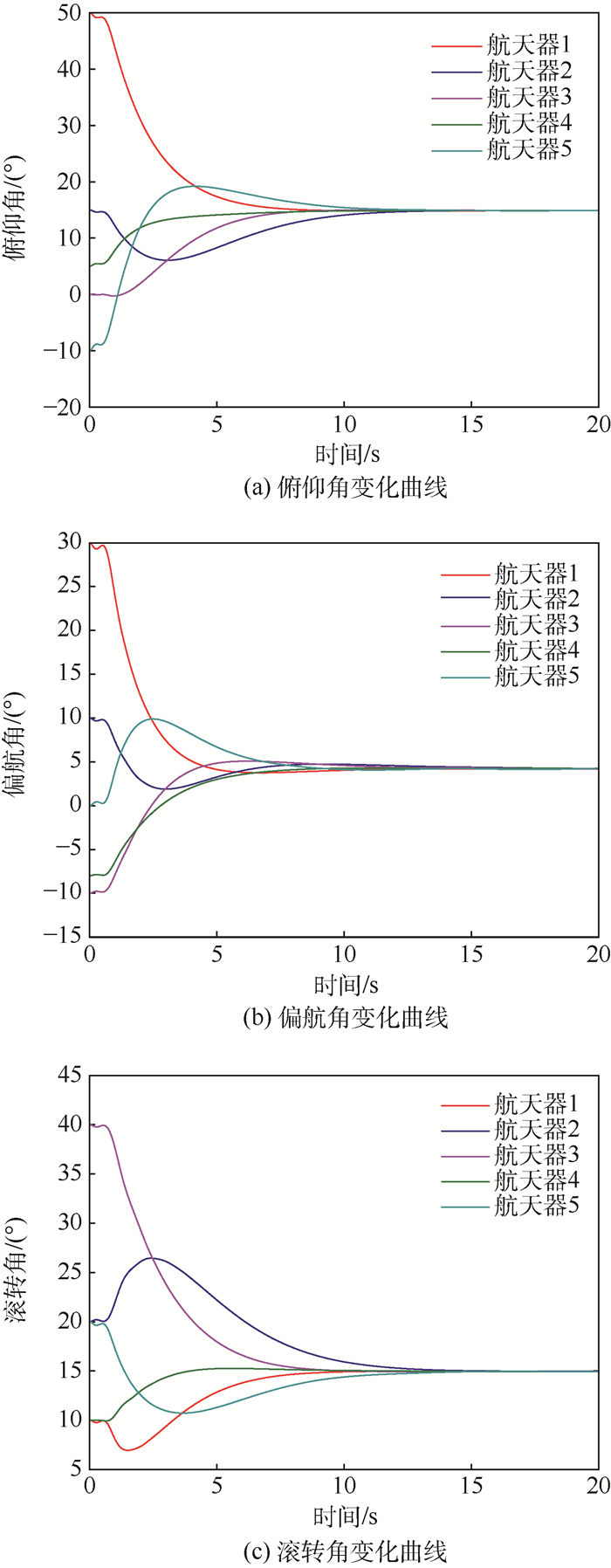 |
| 图 2 多航天器姿态角变化曲线 Fig. 2 Variation curves of attitude angles of multiple spacecraft |
| 图选项 |
为了说明控制输入与ESO干扰观测情况,选取
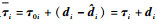
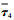

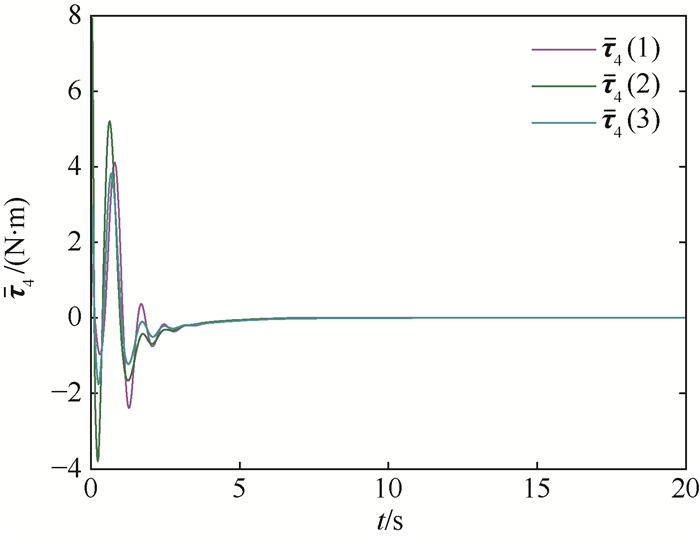 |
| 图 3 考虑干扰补偿的控制力矩(航天器4) Fig. 3 Control moment with disturbance compensation (Spacecraft 4) |
| 图选项 |
定义控制力矩范数为
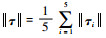
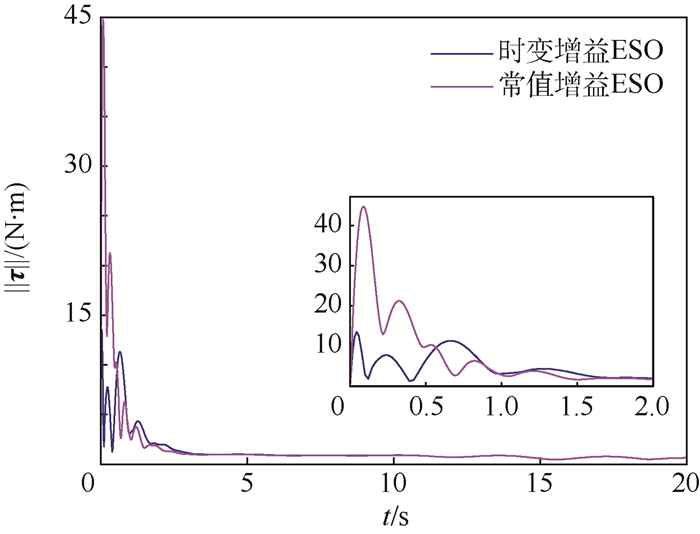 |
| 图 4 控制力矩范数对比曲线 Fig. 4 Comparative curves of norms of control moment |
| 图选项 |
进一步,为了定量描述各航天器姿态协同收敛情况,对比说明本文基于SO(3)方法的控制效果,定义:
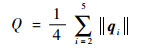 | (68) |
式中:qi=ri-r1,ri=[φi??ψi??γi]T,φi、ψi和γi分别为航天器的俯仰角、偏航角和滚转角。
根据Q的定义可知,若Q趋于0,则表示多航天器实现了姿态协同。在相同初始条件与ESO参数的情况下,文献[10]采用四元数模型,文献[11]使用罗格里德参数。从图 5可以看出,文献[10]方法和文献[11]方法的Q值收敛到1°的时刻分别为10.87 s和7.26 s,而本文方法为5.88 s,验证了本文方法的有效性和快速性。
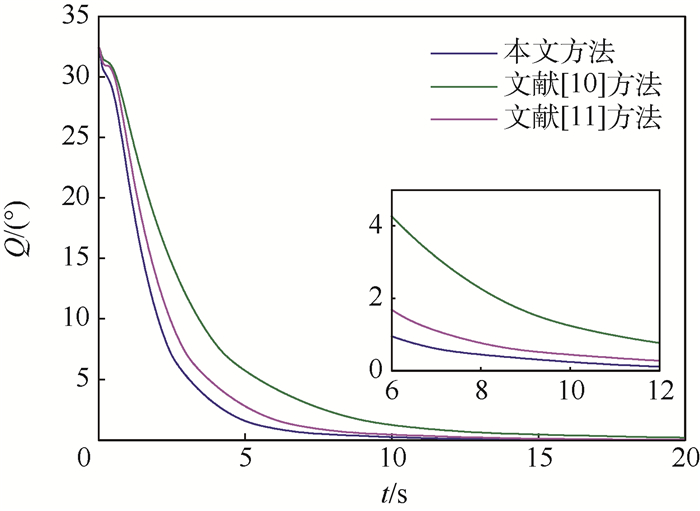 |
| 图 5 不同方法Q值变化对比曲线 Fig. 5 Comparative curves of Q with different methods |
| 图选项 |
6 结论 本文针对存在干扰情形下的多航天器系统,对其协同控制问题进行了研究。
1) SO(3)能够从整体的角度对姿态进行描述,结合有向通信拓扑建立了多航天器SO(3)控制模型,并以此提出了相应的控制策略。基于SO(3)方法的协同控制是可行的。
2) 模型不确定性和外部干扰可以等效为系统的总干扰。在此情形下,设计了适用于SO(3)模型的线性时变增益ESO,所提出的时变增益ESO能够完成对干扰的有效估计。相比常值增益ESO,时变增益ESO可以削弱峰化现象,降低了对控制力矩大小的需求。
3) 设计了SO(3)形式的协同指令,结合ESO可以对干扰进行观测并在控制器中补偿,保证干扰情形下多航天器的协同控制效果。本文给出了稳定性证明过程。
4) 仿真算例结果表明,多航天器系统能够实现稳定协同,验证了本文方法的有效性和快速性。
参考文献
| [1] | 张保群, 宋申民, 陈兴林. 考虑控制饱和的编队飞行卫星姿态协同控制[J].宇航学报, 2011, 32(5): 1060–1069. ZHANG B Q, SONG S M, CHEN X L. Attitude coordination control of formation flying satellites under control saturation[J].Journal of Astronautics, 2011, 32(5): 1060–1069.DOI:10.3873/j.issn.1000-1328.2011.05.015(in Chinese) |
| [2] | 胡勇, 徐李佳, 解永春. 针对失控翻滚目标航天器的交会对接控制[J].宇航学报, 2015, 36(1): 47–57. HU Y, XU L J, XIE Y C. Control for rendezvous and docking with a tumbling target spacecraft[J].Journal of Astronautics, 2015, 36(1): 47–57.DOI:10.3873/j.issn.1000-1328.2015.01.007(in Chinese) |
| [3] | 王有亮, 李明涛, 郑建华, 等. 编队卫星法向机动的切向耦合效应补偿方法[J].北京航空航天大学学报, 2017, 43(6): 1165–1172. WANG Y L, LI M T, ZHENG J H, et al. Compensation method of in-track coupling effect of cross-track maneuver for formation-flying satellites[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(6): 1165–1172.(in Chinese) |
| [4] | ZHANG K W, DEMETRIOU M A. Adaptation and optimization of the synchronization gains in the adaptive spacecraft attitude synchronization[J].Aerospace Science and Technology, 2015, 46: 116–123.DOI:10.1016/j.ast.2015.06.002 |
| [5] | RAN D C, CHEN X Q, MISRA A K, et al. Relative position coordinated control for spacecraft formation flying with communication delays[J].Acta Astronautica, 2017, 137: 302–311.DOI:10.1016/j.actaastro.2017.04.011 |
| [6] | 连克非, 董云峰. 电磁航天器编队位置跟踪自适应协同控制[J].北京航空航天大学学报, 2017, 43(10): 2154–2162. LIAN K F, DONG Y F. Adaptive cooperative control for electromagnetic spacecraft formation flight position tracking[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(10): 2154–2162.(in Chinese) |
| [7] | THAKUR D, SRIKANT S, AKELLA M R. Adaptive attitude-tracking control of spacecraft with uncertain time-varying inertia parameters[J].Journal of Guidance, Control, and Dynamics, 2014, 38(1): 41–52. |
| [8] | ZHANG H, FANG J. Robust backstepping control for agile sa-tellite using double-gimbal variable-speed control moment gyroscope[J].Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1356–1363.DOI:10.2514/1.59327 |
| [9] | LU K F, XIA Y Q, ZHU Z, et al. Sliding mode attitude tracking of rigid spacecraft with disturbances[J].Journal of the Franklin Institute, 2012, 349(2): 413–440.DOI:10.1016/j.jfranklin.2011.07.019 |
| [10] | HUANG D, WANG Q, DUAN Z. Distributed attitude control for multiple flexible spacecraft under actuator failures and saturation[J].Nonlinear Dynamics, 2017, 88(1): 529–546.DOI:10.1007/s11071-016-3258-3 |
| [11] | 王青, 龚立纲, 董朝阳. 基于时变增益ESO的航天器无源姿态跟踪控制[J].控制与决策, 2018, 33(2): 193–202. WANG Q, GONG L G, DONG C Y. Passive attitude tracking control of spacecraft based on time-varying gain ESO[J].Control and Decision, 2018, 33(2): 193–202.(in Chinese) |
| [12] | 何朕, 王广雄. 姿态控制中的散开现象[J].机电与控制学报, 2015, 19(7): 101–105. HE Z, WANG G X. Unwinding phenomenon in attitude control[J].Electric Machines and Control, 2015, 19(7): 101–105.(in Chinese) |
| [13] | SANYAL A, FOSBURY A, CHATURVEDI N, et al. In-ertia-free spacecraft attitude tracking with disturbance rejection and almost global stabilization[J].Journal of Guidance, Control, and Dynamics, 2009, 32(4): 1167–1178.DOI:10.2514/1.41565 |
| [14] | LEE T. Exponential stability of an attitude tracking control system on SO(3) for large-angle rotational maneuvers[J].Systems and Control Letters, 2012, 61(1): 231–237.DOI:10.1016/j.sysconle.2011.10.017 |
| [15] | 郑重, 宋申民. 基于旋转矩阵描述的航天器无角速度测量姿态跟踪无源控制[J].控制与决策, 2014, 29(9): 1628–1632. ZHENG Z, SONG S M. Rotation matrix based passive attitude tracking control of spacecraft without angular velocity measurements[J].Control and Decision, 2014, 29(9): 1628–1632.(in Chinese) |
| [16] | LEE T. Global exponential attitude tracking controls on SO(3)[J].IEEE Transactions on Automatic Control, 2015, 60(10): 2837–2842.DOI:10.1109/TAC.2015.2407452 |
| [17] | 董晓光, 曹喜滨, 张锦绣, 等. 卫星编队飞行的鲁棒自适应控制方法[J].自动化学报, 2013, 39(2): 132–141. DONG X G, CAO X B, ZHANG J X, et al. A robust adaptive control law for satellite formation flying[J].Acta Automatica Sinica, 2013, 39(2): 132–141.(in Chinese) |
| [18] | 李冬柏, 解延浩, 吴宝林. 考虑执行器安装偏差的航天器姿态跟踪控制[J].宇航学报, 2017, 38(6): 598–604. LI D B, XIE Y H, WU B L. Robust spacecraft attitude tracking control with actuator misalignments[J].Journal of Astronautics, 2017, 38(6): 598–604.(in Chinese) |
| [19] | GUO B Z, ZHAO Z L. On convergence of non-linear extended state observer for multi-input multi-output systems with uncertainty[J].IET Control Theory & Applications, 2012, 6(15): 2375–2386. |
| [20] | GUO B Z, WU Z H, ZHOU H C. Active disturbance rejection control approach to output-feedback stabilization of a class of uncertain nonlinear systems subject to stochastic disturbance[J].IEEE Transactions on Automatic Control, 2016, 61(6): 1613–1618.DOI:10.1109/TAC.2015.2471815 |
| [21] | TAN W, FU C. Linear active disturbance-rejection control:Analysis and tuning via IMC[J].IEEE Transactions on Industrial Electronics, 2016, 63(4): 2350–2359. |
| [22] | 杨明, 董晨, 王松艳, 等. 基于有限时间输出反馈的线性扩张状态观测器[J].自动化学报, 2015, 41(1): 59–66. YANG M, DONG C, WANG S Y, et al. Linear extended state observer based on finite-time output feedback[J].Acta Automatica Sinica, 2015, 41(1): 59–66.(in Chinese) |
| [23] | CHANG X, LI Y, ZHANG W, et al. Active disturbance rejection control for a flywheel energy storage system[J].IEEE Transactions on Industrial Electronics, 2015, 62(2): 991–1001.DOI:10.1109/TIE.2014.2336607 |
| [24] | KHALIL H K, PRALY L. High-gain observers in nonlinear feedback control[J].International Journal of Robust and Nonlinear Control, 2014, 24(6): 993–1015.DOI:10.1002/rnc.v24.6 |
| [25] | PU Z Q, YUAN R Y, YI J Q, et al. A class of adaptive extended state observers for nonlinear disturbed systems[J].IEEE Transa-ctions on Industrial Electronics, 2015, 62(9): 5858–5869.DOI:10.1109/TIE.2015.2448060 |
| [26] | 邵龙飞, 师鹏, 赵育善. 电磁航天器编队动力学建模与运动规划方法[J].北京航空航天大学学报, 2015, 41(4): 738–743. SHAO L F, SHI P, ZHAO Y S. Dynamics modeling and motion programming for electromagnetic formation flight[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 738–743.(in Chinese) |
| [27] | LEE H C, CHOI J W. Linear time-varying eigenstructure assignment with flight control application[J].IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(1): 145–157.DOI:10.1109/TAES.2004.1292149 |
