具有力觉感知的主从双边遥操作机械手系统在水下排雷、排爆及水下样本采集中的应用具有重要意义，其避免了操作者直接处于危险区域，减少了操作人员心理压力，并具有精细化操作的特点。从机械手位于工作区域直接与操作对象交互，跟踪主机械手的运动信号并将与环境交互力信号传送至本地主机械手，使操作者在操作本地主机械手的同时能够感知从机械手传送至本地的力信息。整体遥操作系统融合了人的高级智能及机器人的可扩展性，提高了作业效率及人机交互性能^[1]。然而主从机械手具有非线性特征，存在参数不确定性、关节摩擦问题，使得机器人数学模型无法真实获知^[2-4]，水下机械手受到水阻力及水密度影响，水下洋流以及附连水对数学模型带来干扰，主从手之间数据通信带来的时延问题。因此不确定遥操作控制在保证整体系统稳定性前提下，提高透明性及鲁棒性，将位置、力信号能够同步地在从机械手、主机械手上再次复现，依然是整体控制目标^[5]。
为了解决遥操作控制中存在的模型不确定及外部干扰等问题，国内外很多****提出了不同的控制方法^[6-7]。刘霞和Tavakoli^[8]针对遥操作机器人中动力学参数和运动学参数不确定性和外部干扰的问题，设计了一种基于PEB(Position Error Based)的自适应控制器，并利用李雅普诺夫函数证明了系统的稳定性和位置跟踪误差的收敛性。Chopra等^[9]针对常数时延的遥操作系统，面向机器人的动力学参数的不确定性提出了基于无源性的自适应控制方法，确保自由空间上主从机器人位置速度同步。Nu?o等^[10]针对柔性关节遥操作中模型不确定问题提出了阻尼注入的P+D控制策略，并通过自适应律补偿机器人模型的不确定性，通过Barbalat定理证明了整体系统力-位置跟踪误差趋于零。Hua等^[11]针对主从机械手通信时延下将主从手跟踪误差作为不确定部分，通过设计径向基函数(RBF)神经网络自适应控制器实现了自由空间下主从机械手的位置速度同步。文献[12]针对网络化机器人系统的模型参数及运动参数不确定问题提出了无源性控制算法，并通过自适应控制实现了位置跟踪同步。
在遥操作系统中，主手可以看作一个实现标准力信号再现以及给从手提供位置跟踪信号的力反馈机器人，从手可以看作与外界环境接触、运动约束受限条件下的位置跟踪机器人。本文针对水下机械手遥操作过程中主从机械手运动模型不确定及外部干扰问题提出了自适应双边控制策略。对主机械手模型参数与运动参数不确定性，设计了基于名义模型的参考自适应阻抗控制，利用自适应控制律补偿模型不确定性，实现主手上操作者施加力与从手和环境交互力信号的跟踪匹配。针对从手的不确定性通过RBF神经网络逼近模型的不确定部分，通过滑模变结构控制器与自适应控制器消除逼近误差，满足了从机械手对主机械手位置跟踪误差一致稳定有界。并通过李雅普诺夫函数证明了主从机械手控制稳定性。
1 数学模型及基本属性 主从机械手在关节空间非线性动力学模型可描述为^[13]

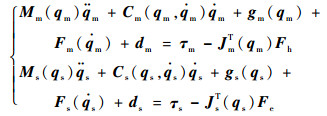(1)

式中：下标m、s分别表示主、从机械手；q_i、和分别为主从机械手运动关节的位置、速度和加速度，i=m或s；和J_i(q_i)分别为机械手的惯性量、离心力与哥氏力的和、重力项、摩擦力矩以及雅可比矩阵；d_m、d_s分别为主机械手、从机械手的干扰转矩。设主从机械手的干扰主要来自于内部关节摩擦，可表示为和N_i分别为黏滞系数和库伦摩擦系数；τ_m和τ_s为控制输入转矩，即给机械手关节转动的驱动力；F_h为操作者施加力；F_e为水下机械手与环境的接触力。
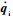
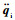
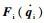
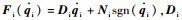
主从手操作空间与关节空间的换算有

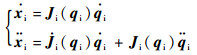(2)

设x_i为机械手笛卡儿坐标系下位置，且机械手为非冗余，即x_i与q_i同维，J_i为非奇异矩阵。将式(2)代入式(1)，可得机械手在笛卡儿空间的动力学模型：

(3)

由式(1)与式(3)对比可得

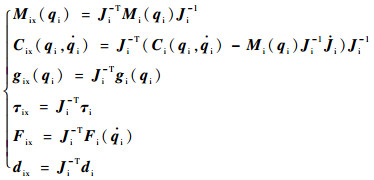(4)

主从机械手系统具有以下属性^[14]：
属性1??机械手惯性矩阵M_i及M_xi正定。
属性2??及是负对称矩阵。
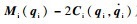
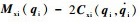
属性3??机械手动力学模型根据未知参数不同，可以线性化表示为

(5)

式中：φ₁和φ₂为任意已知向量；回归矩阵为包含关节空间信息的参数已知的矩阵函数；α_i为包含机械手数学模型未知的参数项。
从机械手跟踪主机械手运动过程中，可以分为自由空间运动以及与环境接触受限运动。只考虑运动位置对F_e的影响，从机械手在与环境接触时，环境受力可以看成无源的线性弹簧，接触力F_e可以表示为

(6)

式中：x_e表示从机械手由自由空间到约束空间的临界距离；k_e为抓取目标的刚度系数。当x_s < x_e时，主手、从手的运动处于自由空间状态；当x_s≥ x_e时可以看成从机械手与环境接触，产生触觉力。
2 整体控制策略 遥操作机械手整体示意图如图 1所示，以平面二连杆旋转机器人作为遥操作机械手研究对象，设主从机械手有相同的模型。操作者在主手上施加作用力，主手根据施加力产生运动，主手控制器将主手位置通过通信网络传送给从手，从手控制器获取主手位置信息作为从手位置跟踪目标，从手完成位置跟踪并将从手与外部环境力传送给主手，主手上实现操作者施加力与从手作用力的一致匹配，满足主从机械手上力-位置的一致性，实现操作者真实感知从手触觉力的目的。

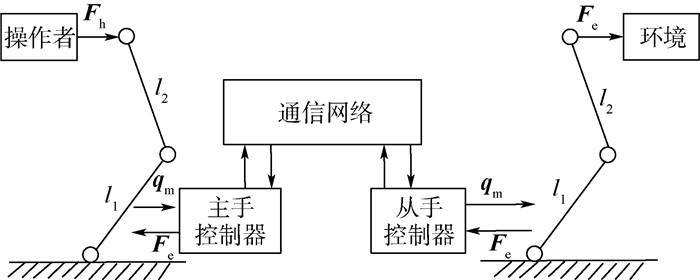图 1 遥操作机械手整体示意图 Fig. 1 Overall schematic diagram of manipulator in teleoperation

图选项

针对机械手动力学模型参数不确定及外界干扰问题，分别设计针对主手力跟踪的自适应阻抗控制器与针对从机械手位置跟踪的自适应滑模神经网络控制器，来实现模型不精确及外部干扰条件下的力-位移跟踪渐进收敛性能。
2.1 主手自适应力跟踪控制 阻抗控制通过调节由用户设定的目标阻抗模型，使机械手终端达到柔顺性运动的目的，将阻抗控制加入自适应特征，使在外界不确定条件下主机械手触觉力跟踪从手触觉力信号具有鲁棒性能^[15]。操作者施加主手作用力、从手触觉力、末端速度、加速度之间可以建立一个二阶线性数学模型，这个控制模型称为目标阻抗模型。为了实现操作者施加力对环境接触力的跟踪，在笛卡儿坐标系下采用的阻抗控制模型为^[16]

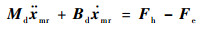(7)

式中：矩阵M_d和B_d为目标阻抗参数，分别为机械手期望的惯性、阻尼矩阵，都为正定对角矩阵；x_mr为笛卡儿坐标系下目标阻抗模型的动态响应，为主手期望参考位置。在目标阻抗二阶模型中，通过操作者施加力与环境力之间的差值获取参考位置x_mr作为主机械手位置跟踪目标，通过调整机械手位置实现抓取力与环境力之间的匹配。当系统处于稳态时，F_h= F_e，此时和为零，满足阻抗关系式(7)平衡。主手模型参考自适应阻抗控制结构如图 2所示。

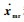
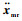
图 2 主手模型参考自适应阻抗控制结构 Fig. 2 Structure of master manipulator model reference adaptive impedance control

图选项

由于主机械手动态方程是一个非线性二阶系统，为了实现主手操作空间位置x_m对主手期望参考位置x_mr跟踪，设计滑模面为

(8)

式中：λ₁为正定对角矩阵，定义，即为主手末端位置x_m与期望参考位置x_mr的差。定义参考速度向量为

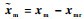
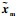
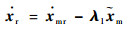(9)

由式(8)和式(9)可得。在笛卡儿坐标系下，设计主机械手的控制律为

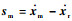
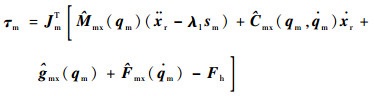(10)

由于无法获取主机械手的真实模型参数，和分别为主机械手参数的相应估计值。设计角度关节坐标系下的控制律，则式(10)在关节坐标系下的控制律对应为

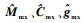
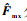
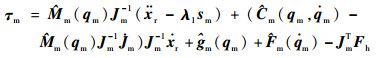(11)

式(11)可以表示为

(12)

机械手运动关节角度、长度已知，即雅可比矩阵J_m为已知量。式(12)中γ₁和γ₂为已知向量，其表达式为

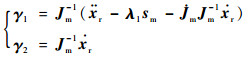(13)

参考机器人属性3，控制律式(12)可以表示为

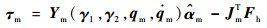(14)

式中：Y_m为机器人方程线性化推导的回归矩阵；为不确定参数的估计值，设计自适应律为

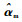
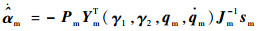(15)

其中：P_m为正定对角矩阵。将控制律式(14)代入主机器人动力学模型式(1)，并根据机器人模型属性3，利用自适应控制律的闭环控制系统可以表示为

(16)

式中：，表示不确定项估计值与真实值之间的误差。α_m为常数向量，可得。主机械手可以看作一个实现力反馈功能的机器人，在自适应控制器中应保证主机械手的稳定性。为了证明主机械手的稳定性以及力跟踪误差趋于零，设计李雅普诺夫函数V₁为

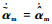
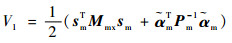(17)

由M_mx和P_m^-1的正定性，易得V₁>0。对V₁求关于时间的一阶导数，由及式(15)和式(16)结合机器人属性2可得

(18)

由式(18)知，根据李雅普诺夫稳定性定理可知，控制器保证了主机械手系统全局稳定以及t→∞时，s_m→0，从而实现，故使主机械手在目标阻抗模型条件下主机械手位置x_m渐进收敛于阻抗模型的参考位置x_mr。
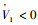
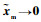
2.2 从手自适应位置跟踪控制 主手一般位于船上或者水下作业潜器内，从手一般固定在带缆水下机器人或者自主水下机器人等水下运载器上，这里忽略通信时延对系统影响。即直接将主手关节位置信号作为从手关节位置跟踪目标。针对从手的外部不确定条件下的位置跟踪，设计自适应控制器，包括RBF神经网络补偿器，滑模控制与自适应控制律。其中利用RBF神经网络^[17]在线学习算法具有较强的自学习和自组织能力，可以有效学习外界复杂环境干扰，准确逼近复杂模型并降低干扰对水下机械手系统的运动影响。
从手控制目标是当t→∞时，通过自适应控制器实现从手在任意初始位置，实现q_m(t)－q_s(t)∈ 0的目的。设从机械手触觉力可测，利用计算转矩法设计控制器，定义从机械手跟踪主手位置误差为，其中q_r(t)为角位移跟踪参考变量，λ₂为正定对角矩阵。定义滑模变量为

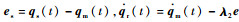
(19)

由式(1)和式(19)，可得

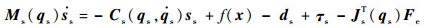(20)

式中：。利用RBF神经网络逼近f(x)的精确函数，根据RBF神经网络特征^[18]，f(x)可表示为f(x)= W^Tφ(x)+ ε^*。W为神经网络权值矩阵，φ(x)为基函数，ε^*为准确模型的逼近误差。f(x)的估计值可以表示为。式(20)可以写成

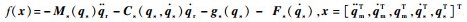
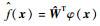
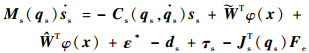(21)

其中：，表示权值误差。根据式(21)，设计从机械手控制律为τ_s= u_s+ u_nn+ u_a+ J_s^T(q_s)· F_e，J_s^T(q_s) F_e为从手与环境接触作用力在从机械手上施加的转矩。u_s为滑模变结构控制规律，取u_s=－k₁ s_s－ k₂sgn(s_s)，k₁和k₂为正定对角矩阵；u_nn为神经网络控制规律，取，其中的自适应律为为正定矩阵；u_a为鲁棒自适应控制律，用于克服神经网络逼近误差和系统不确定性，提高鲁棒性能。取，且自适应律为, t为时间。整体控制如图 3所示。

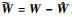
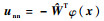
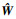
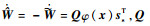
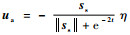
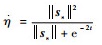
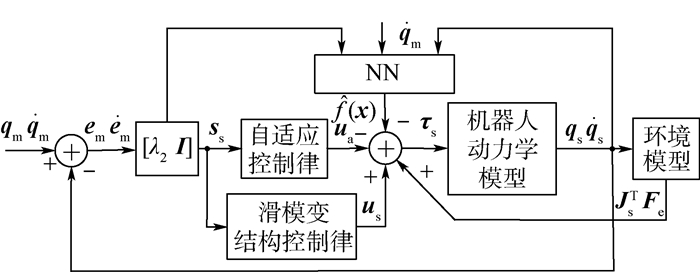图 3 从机械手控制结构 Fig. 3 Control structure of slave manipulator

图选项

将控制律τ_s代入从机械手方程，可得闭环方程为

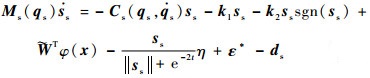(22)

利用李雅普诺夫函数证明从手在自适应控制律条件下跟踪主机械手角关节位置稳定性。设从机械手系统李雅普诺夫函数V₂为

(23)

式中：tr(·)为矩阵的迹；η₀为||ε^*－ d_s||的上界。由M_s、Q^-1为正定矩阵，易得V₂>0。求V₂关于时间导数，根据从手闭环系统式(22)可得

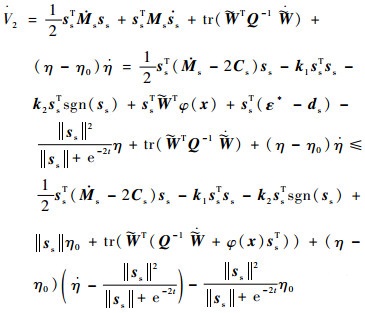(24)

式(24)由机器人属性2，及η和的自适应律可得

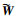
(25)

将式(25)两边由0至T时刻积分，可得

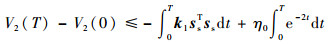(26)

式(26)可化为

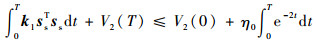(27)

由于，则有

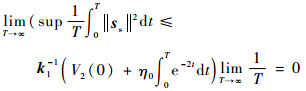(28)

由式(28)可知，T→∞时，s_s→ 0，位置跟踪误差e_s及误差变化率渐进收敛于0。从手控制器根据参数不确定性、外部干扰引起的跟踪误差通过RBF神经网络得到了补偿，并且通过滑模控制与自适应律使控制器具有鲁棒性特征。
3 仿真与验证 根据主从机械手的系统模型以及控制要求，在MATLAB/Simulink下进行仿真验证。不考虑机械手运动学参数不确定性，只考虑机械手动力学模型不确定及外部干扰问题，不考虑水下机械手中运载体对姿态影响，设主从机械手在竖直平面运动。参考文献[5, 19-20]的数学模型，阻抗模型参数：M_d=diag(1, 1)，B_d=diag(10, 10)，λ₁=diag(30, 30)，P_m=diag(1, 1, 1)；主机械手质量m₁=0.1 kg, m₂=0.1 kg, 长度l₁=0.1 m, l₂=0.1 m。主机械手初始位置：q₁=π/3 rad，q₂=π/6 rad。
从机械手系统，RBF神经网络参数选择高斯基函数中心c =[-3-2-1 0 1 2 3]，宽度b=3, 滑模系数λ₂=diag(0.5, 0.5)，Q =diag(2, 2)，控制器输入增益k₁=diag(20, 20)，k₂=diag(30, 30)，不确定上界估计初始值η₀=1.2。从手质量m₁=0.1 kg, m₂=0.1 kg, 长度l₁=0.1 m, l₂=0.1 m。从手初始位置：q₁=π/3 rad，q₂=π/6 rad。
设环境刚度系数为：k_e=diag(100, 100)，从机械手在x轴方向0.1 m处与抓取目标接触。设主从手内部关节摩擦干扰：。设主机械手、从机械手外部不确定干扰分别为。
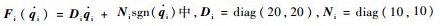
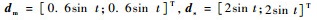
仿真时间设为30 s, 前10 s在主机械手上施加10 N的作用力，然后将作用力为0 N。即在机械手上施加10 N作用力持续10 s，然后不再施加力，持续20 s，观察机械手的力-位移跟踪状态。
由图 4~图 6可知，在自由空间运动以及与环境触碰后的运动过程中，从机械手能够保证对主机械手的位置跟踪，主手力满足对从手力的跟踪。主机械手目标阻抗模型实现参考位置x_mr输出，通过设计的自适应控制器主机械手末端位置与参考位置跟踪误差渐进趋于零。从手初始位于自由运动的位置，在从机械手运动到0.1 m时，约3 s与抓取对象触碰产生触觉力信号。从手依然实现对主机械手的位置跟踪，跟踪位置的同时实现主手力对从手力跟踪，满足主手、从手上的力信号协调一致相等。从而实现了在主手和从手上的位置、力信息的完全一致相等。并且从手力对主手力的跟踪静态误差≤1%，无超调量。

图 4 遥操作机械手力跟踪曲线 Fig. 4 Force tracking curves of manipulator in teleoperation

图选项

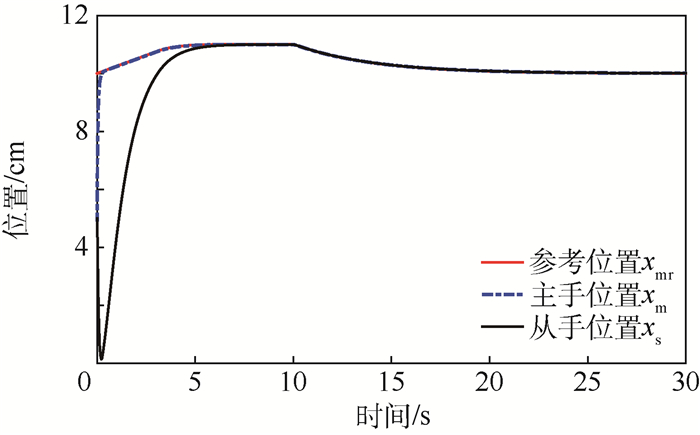图 5 遥操作参考位置、主手、从手位置跟踪曲线 Fig. 5 Tracking curves of reference position and position of master and slave manipulator in teleoperation

图选项

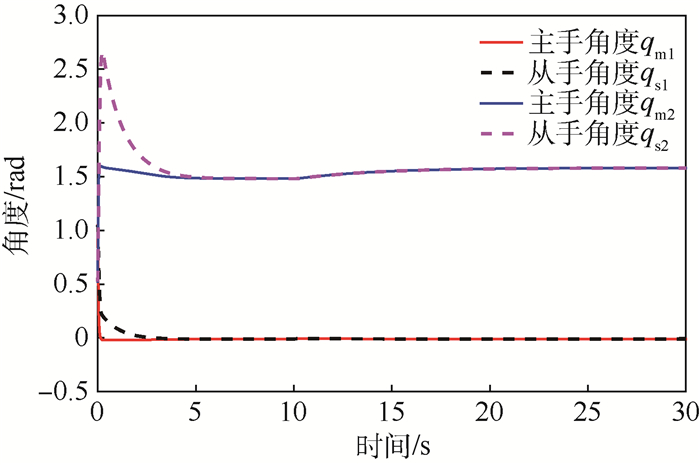图 6 遥操作主从手角度跟踪曲线 Fig. 6 Angle tracking curves of master and slave manipulator in teleoperation

图选项

由图 4~图 6可知，从手位置对主手位置的跟踪静态误差≤1%，整体跟踪无超调量。主手上力释放后，从手、主手最终静止在与环境临界接触的0.1 m处，依然从手保证对主手位置跟踪，主手实现对从手力跟踪。由图 7和图 8可知，主从机械手自适应律输出参数有界，保证了估计值有效性能，实现系统控制稳定。

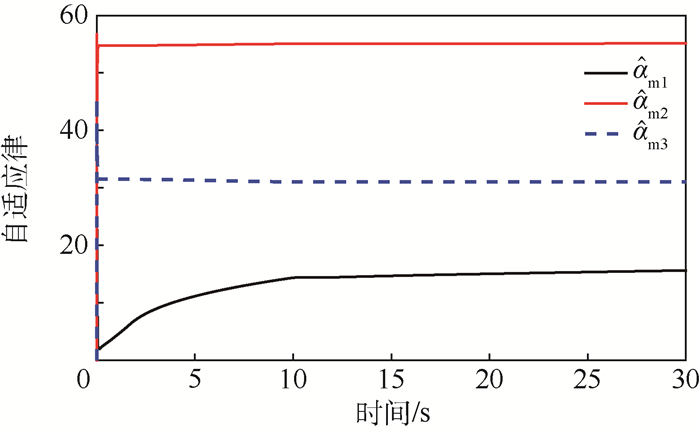图 7 主手自适应律曲线 Fig. 7 Curves of master manipulator adaptive law

图选项

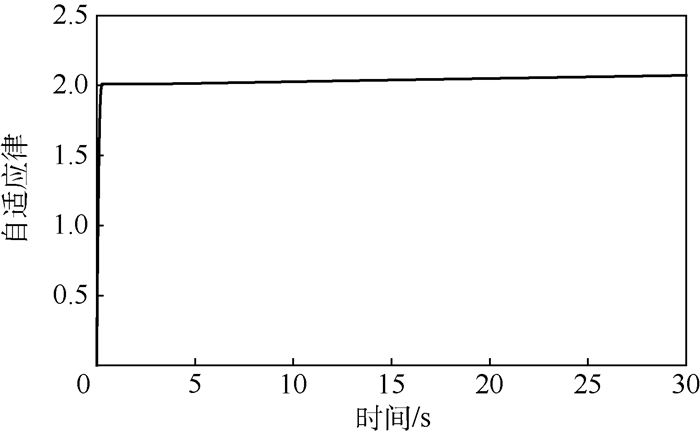图 8 从手自适应律曲线 Fig. 8 Curve of slave manipulator adaptive law

图选项

由图 4~图 7可知，在系统模型不确定以及外部干扰条件下，整体系统仍然保证从手对主手的力跟踪以及从手对主手的位置跟踪。主手自适应控制以及从手RBF神经网络实现了对外部干扰以及自身模型不定性的补偿。
4 结论 1) 对主机械手摩擦干扰与外部不确定干扰引起的不确定性以及非线性特性，设计了基于名义模型的参考自适应阻抗控制，利用自适应控制律补偿不确定性，通过从手力与操作者施加的主手力误差调节期望轨迹，并实现主手力对从手力的跟踪。
2) 通过RBF神经网络进行自适应补偿从手的不确定性，通过滑模变结构控制器与自适应控制器消除逼近误差，满足了从机械手位置对主机械手位置跟踪，提高了跟踪效果。
3) 利用李雅普诺夫函数证明了跟踪的渐进收敛性能与全局稳定性，保证遥操作过程控制力-位置跟踪的协调一致能力。
4) 整体控制在内部干扰及外部不确定干扰条件下具有很好的力-位置跟踪能力，整体系统具有稳定性和自适应性。

参考文献

[1]	LI Y, JOHANSSON R, LIU K, et al. Guaranteed cost control design for delayed teleoperation systems[J].Journal of the Franklin Institute, 2015, 352(11): 5085–5105.DOI:10.1016/j.jfranklin.2015.08.011
[2]	贾鹤鸣, 张利军, 齐雪, 等. 基于神经网络的水下机器人三维航迹跟踪控制[J].控制理论与应用, 2012, 29(7): 56–62. JIA H M, ZHANG L J, QI X, et al. Three-dimensional path tracking control for autonomous underwater vehicle based on neural network[J].Control Theory & Applications, 2012, 29(7): 56–62.(in Chinese)
[3]	WANG H, XIE Y. Adaptive inverse dynamics control of robots with uncertain kinematics and dynamics[J].Automatica, 2009, 45(9): 2114–2119.DOI:10.1016/j.automatica.2009.05.011
[4]	张文辉, 齐乃明, 尹洪亮. 基于滑模变结构的空间机器人神经网络跟踪控制[J].控制理论与应用, 2011, 28(9): 1141–1144. ZHANG W H, QI N M, YIN H L. Neural-network tracking control of space robot based on sliding-mode variable structure[J].Control Theory & Applications, 2011, 28(9): 1141–1144.(in Chinese)
[5]	GANJEFAR S, REZAEI S, HASHEMZADEH F. Position and force tracking in nonlinear teleoperation systems with sandwich linearity in actuators and time-varying delay[J].Mechanical Systems and Signal Processing, 2017, 86: 308–324.DOI:10.1016/j.ymssp.2016.09.023
[6]	LIU Y C, KHONG M H. Adaptive control for nonlinear teleoperators with uncertain kinematics and dynamics[J].IEEE/ASME Transactions on Mechatronics, 2015, 20(5): 2550–2562.DOI:10.1109/TMECH.2015.2388555
[7]	HOSSEINI S K, MOMENI H, JANABI S F, et al. A modified adaptive controller design for teleoperation systems[J].Robotics and Autonomous Systems, 2010, 58(5): 676–683.DOI:10.1016/j.robot.2009.11.006
[8]	LIU X, TAVAKOLI M. Adaptive control of teleoperation systems with linearly and nonlinearly parameterized dynamic uncertainties[J].Journal of Dynamic Systems Measurement & Control, 2012, 134(2): 194–203.
[9]	CHOPRA N, SPONG M W, LOZANO R. Synchronization of bilateral teleoperators with time delay[J].Automatica, 2008, 44(8): 2142–2148.DOI:10.1016/j.automatica.2007.12.002
[10]	NUN~O E, SARRAS I, BASAN~EZ L, et al. Control of teleoperators with joint flexibility, uncertain parameters and time-delays[J].Robotics and Autonomous Systems, 2014, 62(12): 1691–1701.DOI:10.1016/j.robot.2014.08.003
[11]	HUA C C, YANG Y, GUAN X. Neural network-based adaptive position tracking control for bilateral teleoperation under constant time delay[J].Neuro Computing, 2013, 113(7): 204–212.
[12]	WANG H. Passivity based synchronization for networked robotic systems with uncertain kinematics and dynamics[J].Automatica, 2013, 49(3): 755–761.DOI:10.1016/j.automatica.2012.11.003
[13]	KIM B Y, AHN H S. A design of bilateral teleoperation systems using composite adaptive controller[J].Control Engineering Practice, 2013, 21(12): 1641–1652.DOI:10.1016/j.conengprac.2013.08.013
[14]	SHARIFI M, BEHZADIPOUR S, VOSSOUGHI G. Nonlinear model reference adaptive impedance control for human-robot interactions[J].Control Engineering Practice, 2014, 32: 9–27.DOI:10.1016/j.conengprac.2014.07.001
[15]	MENDOZA M, BONILLA I, GONZáLEZ-GALVáN E, et al. Impedance control in a wave-based teleoperator for rehabilitation motor therapies assisted by robots[J].Computer Methods & Programs in Biomedicine, 2016, 123(C): 54–67.
[16]	SHARIFI M, BEHZADIPOUR S, VOSSOUGHI G R.Model reference adaptive impedance control of rehabilitation robots in operational space[C]//IEEE Ras & Embs International Conference on Biomedical Robotics and Biomechatronics.Piscataway, NJ: IEEE Press, 2012: 1698-1703.
[17]	HSU C F, LIN C M, YEH R G. Supervisory adaptive dynamic RBF-based neural-fuzzy control system design for unknown nonlinear systems[J].Applied Soft Computing Journal, 2013, 13(4): 1620–1626.DOI:10.1016/j.asoc.2012.12.028
[18]	PAN Y, YU H, ER M J. Adaptive neural PD control with semiglobal asymptotic stabilization guarantee[J].IEEE Transactions on Neural Networks & Learning Systems, 2014, 25(12): 2264–2274.
[19]	LONDHE P S, MOHAN S, PATRE B M, et al. Robust task-space control of an autonomous underwater vehicle-manipulator system by PID-like fuzzy control scheme with disturbance estimator[J].Ocean Engineering, 2017, 139: 1–13.DOI:10.1016/j.oceaneng.2017.04.030
[20]	张文辉, 齐乃明, 尹洪亮. 自适应神经变结构的机器人轨迹跟踪控制[J].控制与决策, 2011, 26(4): 597–600. ZHANG W H, QI N M, YIN H L. Neural-variable structure-based adaptive trajectory tracking control of robot manipulators[J].Control and Decision, 2011, 26(4): 597–600.(in Chinese)