相比于其他卫星,LEO卫星轨道高度更低,因此具有传输延迟低的特点;又因其在自由空间传输衰减小,所以所需的发射功率更低[2]。因此,相比于其他卫星通信系统,LEO卫星更适合于提供语音和数据等用户服务[3]。而在LEO卫星通信系统中,随着业务需求的增大,传统的L频段资源已经不足以满足要求;与L频段相比,Ka频段具有更丰富的频谱资源。因此,利用Ka频段资源就成了LEO通信系统的发展趋势。由于在自由空间中信号的衰减与信号波长的大小成反比,在实际通信中,Ka天线往往比L频段天线具有更高的极化增益,更窄的半功率宽度,Ka波束相比L频段具有更小的覆盖范围。因此在星座设计中,将Ka频段与L频段相结合,既可以利用L波束的广覆盖提供信令支持,降低星座密度;又可以利用Ka波束的大带宽,提供用户服务,实现宽窄带结合的LEO卫星全球宽带通信。
然而,由于GEO卫星系统的用户链路与馈电链路均有Ka频段的占用。国际电信联盟(ITU)的《无线电规则》中明确规定在17.8~19.3/28.6~ 29.1 GHz频段的频率协商工作应本着先到先得的原则;而在其他Ka频段,协商工作则应以该文献[4]中的Article 22所提出的等效功率流量密度(EPFD)限制条件作为参考指标。因此,基于Ka频段的LEO星座设计就可能对现有GEO卫星系统存在潜在干扰。
文献[5]的LEO-GEO系统中,干扰场景可分为LEO卫星下行信号对GEO地面站(ES)接收的干扰与LEO地面站上行信号对GEO卫星接收的干扰。
针对LEO与GEO卫星之间由于频率共享所引起的干扰,文献[6-7]根据LEO卫星、GEO卫星与地面站的位置关系调,通过功率控制的方式达到减小干扰的目的。文献[8-9]则通过划分频谱信道或认知无线电的方式来进行频谱的重复利用。文献[10]采用卫星隔离、地面站隔离等空间隔离方法,通过设置规避区域与规避角来避免干扰的发生。
在现阶段已有的研究文献中,大多是采用功率控制的方法来对已有NGEO卫星进行干扰分析,或是采用认知无线电的方式侦测空闲频谱以实现频谱资源的重复利用。而对于通过空间隔离来消除干扰,相关文献大多只是简要阐述了判定方法与规避方式,缺乏详细论证。比如文献[11-13]中,提出了地面站隔离角与干扰规避区域的概念,却并没有对如何确定相关角度与区域做进一步论述。
同时,文献[11-13]指出,当卫星与地面在之间满足空间隔离条件后,将采取波束切换来避免干扰。在OneWeb低轨星座系统中,采用一种被称之为“渐进俯仰”(progressive pitch)的专利技术[14],通过对邻近赤道面的卫星的Ku/Ka主波束采取南北向偏转的方式来达到干扰消除的目的。不难看出在采用波束切换技术的星座中,当卫星波束为避免干扰而发生偏转,地面站如果想要继续保持通信不中断,则通信链路必须切换至相邻卫星。因此,在LEO星座设计中,就需要将星座密度问题列入考虑。对此,相关分析研究很少在文献中出现,也无明确的结论。
另外需要指出,尽管ITU建议书提到由于轨道摄动,在GEO卫星在运行期间会出一定角度的轨道倾斜,但并未在干规避区域的选取中考虑这一因素。本文也将在研究过程中会将其纳入考虑。
本文研究分析LEO-GEO共存系统中空间隔离角的确定方法;通过引入GEO带的概念,提出了一种基于空间隔离角的LEO-GEO干扰规避区域确定方法,并分析了GEO轨道倾斜对该区域带来的影响;在考虑到保证星座通信业务不中断的前提下,研究并分析了空间隔离角、干扰规避区域对LEO星座密度带来的影响,最终通过仿真给出干扰限制条件下的星座所需卫星数目的最小值。
最后,在LEO星座设计中,由于采用宽窄带结合的系统设计,单颗卫星在保证比较大的覆盖范围的情况下,仅用少量Ka点波束即可实现对特定热点区域宽带服务的支持,这在客观上降低了LEO星座密度与系统的复杂度,因此本文将采用这种模型对LEO星座密度进行研究分析。
1 场景模型 由于轨道摄动,GEO卫星会在运行中产生轨道倾斜,因此在考虑GEO卫星空间分布时,为方便做一般化处理,可将其看成是沿GEO的连续分布。如图 1所示,GEO卫星分布可以被看成是一条以GEO为中轴,南北偏移地心角为θ的环状带,即GEO带。
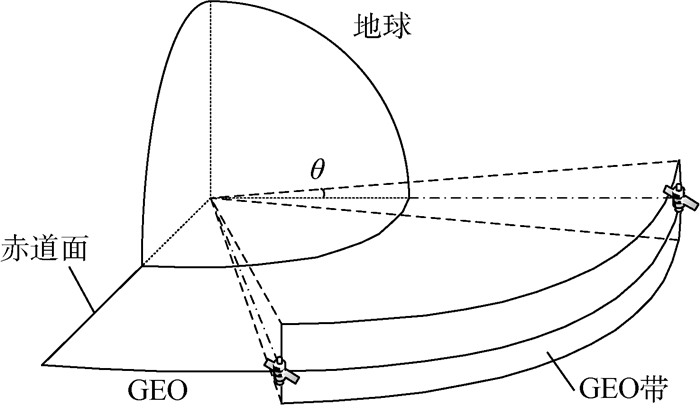 |
| 图 1 GEO带示意图 Fig. 1 Schematic of GEO band |
| 图选项 |
在LEO-GEO卫星系统中,干扰场景可分为2种,分别如图 2和图 3所示。
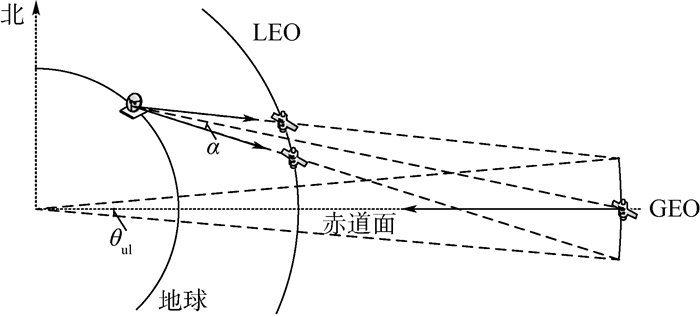 |
| 图 2 LEO-GEO上行干扰场景 Fig. 2 LEO-GEO uplink interference scenario |
| 图选项 |
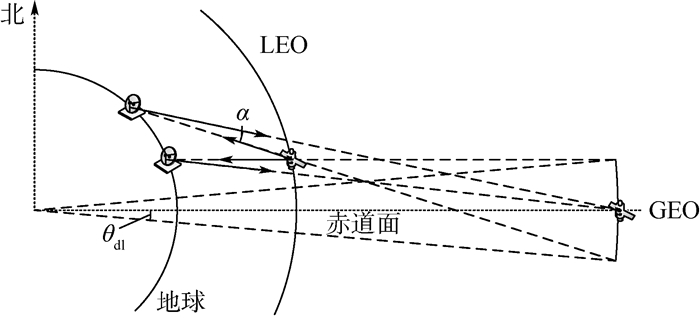 |
| 图 3 LEO-GEO下行干扰场景 Fig. 3 LEO-GEO downlink interference scenario |
| 图选项 |
在图 2的上行干扰场景中,LEO地面站随着LEO卫星的运行而改变上行信号发射天线指向,当其指向邻近GEO轨道时,会对GEO卫星产生干扰,且干扰随地面站夹角α的减小而增加。因此在上行场景中,必然存在满足条件的最小α,使得LEO地面站上行信号对GEO卫星的干扰符合干扰门限。此时,如果将LEO地面站与卫星的连线反向延长至GEO轨道球面,则会在轨道球面上截取一段地心角为θul的GEO带。
在图 3的下行干扰场景中,当LEO卫星、GEO卫星与GEO地面站处于共线关系时,地面站收到的来自LEO卫星的同频干扰达到最大[15]。因此若想降低干扰,则GEO地面站、LEO卫星与GEO卫星不可共线,而是彼此需要满足一定的角度关系。同理,其与LEO卫星连线的延长线与GEO轨道天球所截取的GEO带的地心角为θdl。
不难看出,无论上下行干扰场景,地面站与卫星之间的空间隔离关系都可以通过几何方法转化成一定角度的GEO带来表示,这也给在确定干扰规避区域时考虑轨道摄动因素带来了可行性。
2 分析与推导 根据文献[4]规定,在GEO-NGEO系统中干扰级别的评判应该以EPFD值为参考。EPFD是指在GEO系统接收端收到的有NGEO系统内所有发送端产生的功率通量密度的总和,其公式定义为
 | (1) |
式中:N为发送端个数;Pi为个发送端发送功率;di为个发送端到接收端的距离,;Gt(θi)为发射天线增益;Gr(φi)为接收天线增益,在此做了归一化处理;θi与φi分别为发射天线与接收天线的天线指向与发射到接受端连线的夹角。从式(1)可以看出,天线的发射与接收增益都跟其指向与信号传播路径的夹角有关,具体关系可参考文献[16]。
2.1 上下行干扰规避区域分析 如图 2与图 3所示,文献[11]中指出,当地面站夹角α小于某一预设值时,LEO系统即可进行波束关闭或切换操作,以此达到避免同频干扰的目的。图 2中,LEO地面站在夹角αul小于预设值时选择波束切换卫星;图 3中,GEO地面站夹角αdl小于预设值时,LEO卫星的Ka波束必须关闭或做偏移处理。因此在上下行规避区域选择的问题上,可以简化为隔离角α的选取,综合考虑上下行干扰场景,不难得出:
 | (2) |
地面站夹角α、GEO带地心角θ与地面站和GEO卫星的星下点经度差Δφlon的几何关系如图 4所示。
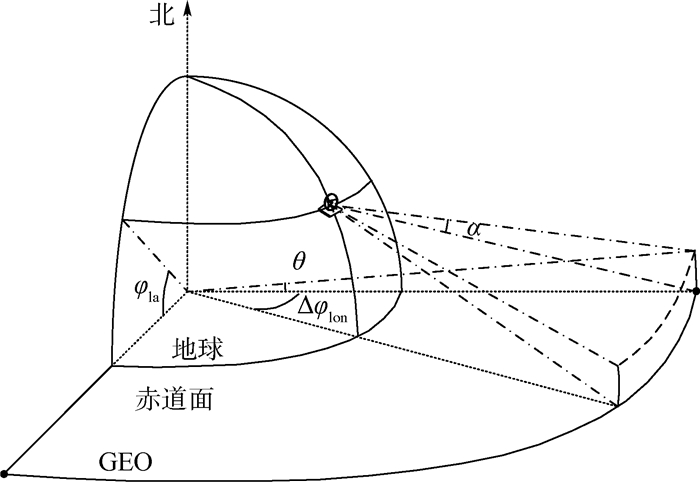 |
| 图 4 α与θ和地面站位置关系示意图 Fig. 4 Schematic of relationship amongα, θand ES location |
| 图选项 |
从图 4可以看出,在同一纬度φla下,保持α不变,θ随Δφlon的变大而变大。因此,可以在θ角的选取上做一次放大。在地面站仰角允许范围内,假设隔离角门限值α=αthreshold,在满足最小仰角的地面站的可视区域边界处,即Δφlon最大时的θ选做GEO带的地心角,即
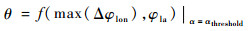 | (3) |
2.1.1 下行干扰场景αdl的选取分析 文献[15]指出,在下行场景中,GEO地面站、LEO卫星和GEO卫星三者共线时,LEO卫星对地面站的下行干扰达到最大。同时,如图 4所示,地面站与卫星星下点存在经度差;不难得出,当经度差Δφlon=0时,即地面站与卫星共存于同一经度平面,此时LEO卫星到地面站距离最短,根据式(1)可得,GEO地面站收到的LEO卫星下行EPFD将达到最大。
对于αthreshold的选取,可以进行第二次放大,即针对Δφlon=0时不同纬度的地面站变换仰角φele时所取得的满足EPFD门限标准的最大α定为αthreshold,如图 5所示。
 |
| 图 5 下行场景α与θ和地面站天线仰角关系示意图 Fig. 5 Schematic of relationship among α, θ and elevation angle of ES antenna in downlink scenario |
| 图选项 |
当GEO地面站纬度φla不变时,LEO卫星沿轨道运行,其对GEO地面站造成的干扰可以通过地面站与2个卫星的夹角α决定。通过对该场景GEO地面站接收端EPFD的计算与ITU给出的下行EPFD限制条件,不难找出下行隔离角门限αdl。
需要注意的是,LEO卫星的下行Ka波束宽度较窄,且天线指向可以调节,因此可以假设在LEO星座系统的统一调配下,不会出现Ka下行波束的同频混叠现象。对于GEO地面站,同一时刻不存在来自LEO星座系统下行多个Ka波束干扰叠加的现象。
2.1.2 上行多用户干扰场景αul的选取分析 在上行场景中,由于存在多地面用户同时进行上行信号传输的情况,因而其对GEO卫星造成的干扰为多个LEO地面站用户的累加值。由于每个地面站用户与GEO卫星相对位置的不同,地面站上行天线所指向的NGEO卫星位置也不确定,因而造成了对上行多用户干扰场景分析的复杂性。
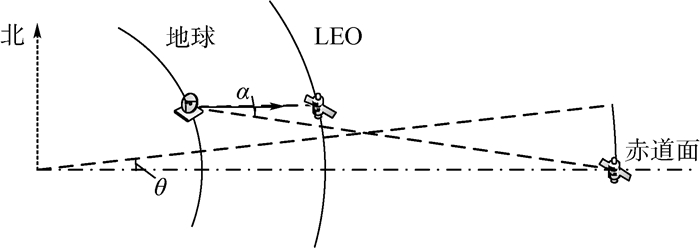
如图 6所示,LEO地面站天线对准LEO卫星,其上行波束会对GEO卫星造成干扰;同时,该LEO卫星波束覆盖区域可能存在多个地面站用户,假设在该区域内满足α门限值的地面站都与该LEO卫星进行上行通信,则在GEO接收端造成的干扰为多个地面站干扰信号的叠加。
 |
| 图 6 上行场景α与θ和地面站天线仰角关系示意图 Fig. 6 Schematic of relationship among α, θand elevation angle of ES antenna in uplink scenario |
| 图选项 |
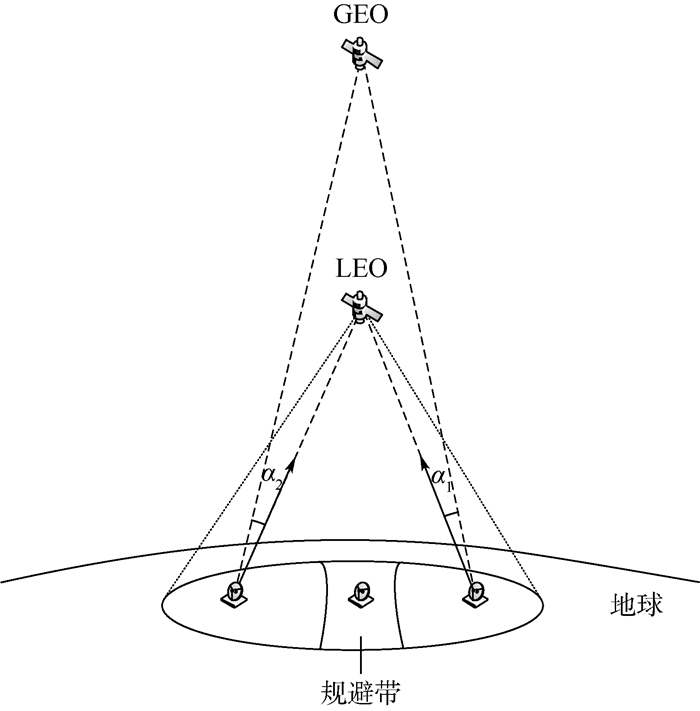
由图 7可知,在上行多用户场景中,假设当地面站夹角α小于αthreshold时,地面站不发送上行信号,则GEO卫星收到的上行干扰为其余地面站上行信号干扰的叠加;且考虑GEO卫星在轨道上连续分布的情况,在某颗LEO卫星波束覆盖区域内,地面站夹角α小于αul的区域为带状,具体形状与LEO星下点纬度和αul都有关系。
 |
| 图 7 多用户上行干扰场景 Fig. 7 Multi-user uplink interference scenario |
| 图选项 |
假设在LEO卫星波束覆盖区域内,地面站用户是均匀分布的,通过设定不同的αul值确定规避区域形状,再由式(1)可得GEO卫星接收端收到的EPFD值。由此不难得出α,LEO星下点纬度和上行多用户EPFD的关系,从而根据限制条件确定αul。
需要注意的是,这里计算的是单颗LEO卫星覆盖范围内的多用户上行干扰。考虑到GEO卫星收到的上行集总干扰可能是来自多颗LEO卫星的星下用户,因此在选择αul时需留出一定余量。
2.2 引入连续GEO带的分析 确定满足EPFD门限的α值,根据式(3)可求得相应的GEO带地心角,在这里设为θepfd。根据分析,当不存在轨道摄动时,LEO地面站上行天线指向地心角为θepfd的GEO带以外的区域,则其对GEO卫星产生的干扰满足ITU约束;同时,LEO卫星与GEO地面站连线的反向延长线与GEO轨道天球的相交于该GEO带以外区域,则LEO下行波束对GEO地面站产生的干扰满足约束条件。
如图 1所示,由于轨道摄动的存在,在GEO卫星运行期间会产生轨道面的倾斜,在这里将倾斜角设为θshift。相比于理想运行场景,这种偏移可被视作地面站与GEO卫星之间纬度差的变化。显然,这种变化并未影响αthreshold的选取,因此,最终的GEO带地心角θ可以简单的视为两者相加,即
 | (4) |
2.3 带有规避带的LEO星座密度分析 由于存在干扰规避区域,当LEO卫星运行至规避区时,地面站需要做避让处理;因此,针对测定的规避区域,单个地面站就会在LEO轨道天球上产生连续的规避带,如图 8所示。
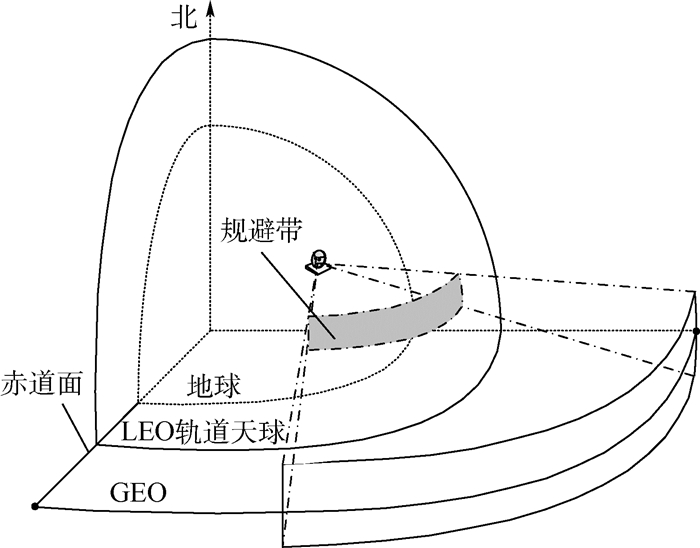 |
| 图 8 LEO天球规避区域示意图 Fig. 8 Schematic of avoidance area on LEO celestial sphere |
| 图选项 |
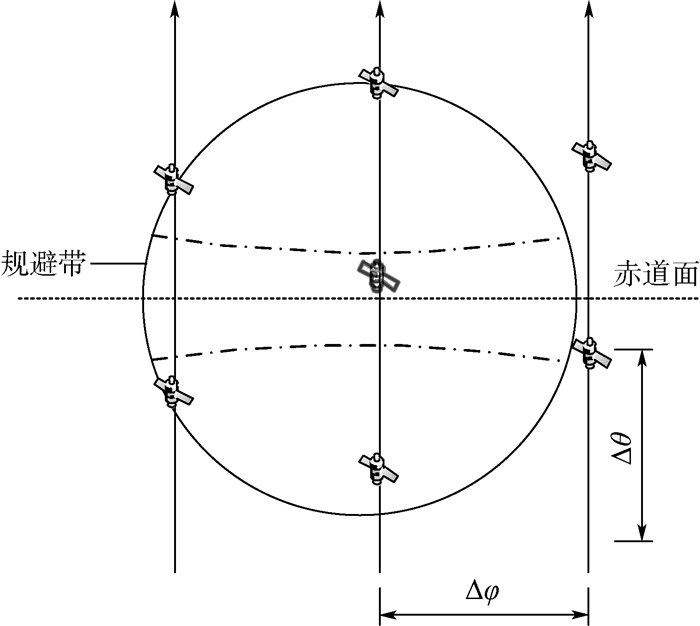
地面站在给定最小仰角的情况下在低轨天球上的可视区域如图 9所示(假设地面站纬度为0°)。
 |
| 图 9 地面站可视区域规避带示意图 Fig. 9 Schematic of avoidance band in visible area of ES |
| 图选项 |
如图 9所示,圆形区域为地面站可视区域,虚线部分则为地面站对GEO带的规避区域在低轨天球上的截取部分。
星座密度由轨道之间经度差Δφ和同一轨道内邻星之间的相位差Δθ决定。考虑到当地面站处于高纬度地区,可视区域内星座不同轨道间的距离会缩短,因此在分析中可以采用赤道地面站作为对象,此时轨道间距最大。且出于系统复杂度考虑,在满足波束切换的条件下,星座密度应该越小越好。
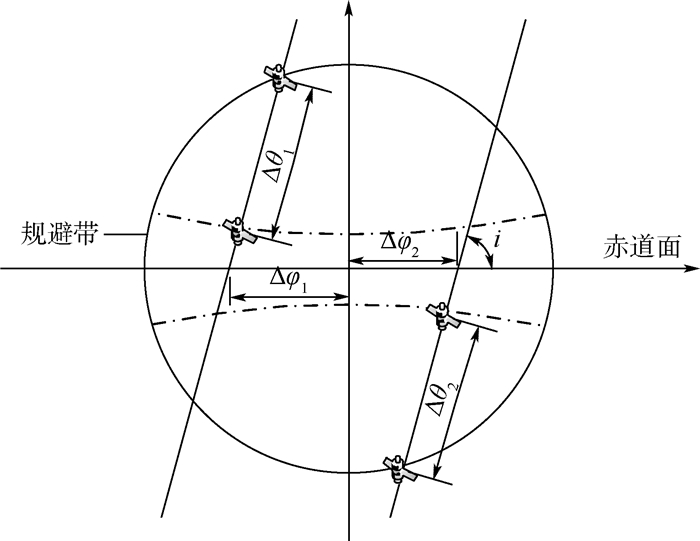
当卫星进入规避区域后,地面站需要在可视区域内的非规避区选择另外一个卫星进行波束切换,因此,星座的密度分析模型如图 10所示。
 |
| 图 10 星座密度参数示意图 Fig. 10 Schematic of constellation density parameters |
| 图选项 |
在图 10中,所有变量的单位均为度(°)。轨道倾角为i。在地面站可视范围内囊括了2条卫星轨道。轨道之间的经度差Δφ=Δφ1+Δφ2。研究规避带对星座密度的影响,分析思路如下:
1) 当轨道间经度差固定且轨道在可视区域内相对位置固定(确定Δφ1与Δφ2)时,星座密度需保证在除去规避带的可视区域内至少有一颗卫星存在。同时,假设异轨卫星之间的相位差可以随意设置,为满足条件,当图 10中,当左侧轨道卫星1-1运行至可视区上边缘时,需保证右侧邻轨有卫星2-1从可视区域下边缘进入该区域;并且当2-1运行至规避带下边缘时,卫星1-1的同轨邻星1-2需要运行至规避带上边缘,由此即可保证地面站在两条轨道间进行切换而中断通信。因此,同一轨道内的邻星相位差为Δθ=Δθ1+Δθ2。
2) 保持轨道间经度差Δφ不变,改变轨道在区域内相对位置(即Δφ1、Δφ2可变),重复思路1),找到相应的Δθ。
3) 变动轨道间经度差Δφ,重复思路1)与2),得到一系列(Δφ,Δθ)配对组合,这些组合即可视为星座密度设计方案。
当对上述思路做进一步简化,分析可得:保持Δφ不变的情况下,当轨道在可视区域内相对位置发生变化时,通过简单的数学推导不难得出:只有当Δφ1=Δφ2的时候,Δθ才可以取到最大值,即
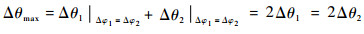 | (5) |
由此可推得
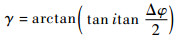 | (6) |
式中:γ为LEO轨道面与地面站在LEO轨道天球上的可视区域的横截平面的交线与赤道面的夹角。把该可视区横截面视为坐标系,可视区域中心为坐标原点,则LEO轨道面与该可视区域的上半部的交点坐标(x,y)可表示为
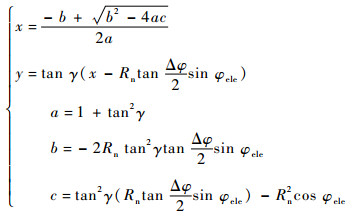 | (7) |
式中:φele为地面站最小仰角;Rn为LEO轨道天球的半径。设此时的GEO带的地心角为θ,则有同轨邻星相位差:
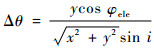 | (8) |
针对不同的(Δφ,Δθ),可以得出在考虑GEO带的情况下该星座所需的卫星数量。在此设计下,地面站的可视区域内,当其波束追踪的LEO卫星进入规避区域,则至少保证有一个同轨或异轨的邻星可见,因而可以进行波束切换,可以达到避免干扰的同时通信不中断的目的。
3 仿真与验证 表 1为仿真所需相关参数。
表 1 仿真参数 Table 1 Simulation parameters
| 参数 | 数值 |
| LEO轨道高度/km | 850 |
| GEO轨道高度/km | 35 786 |
| 地球半径/km | 6 371 |
| 地面站最小仰角/(°) | 10 |
| 轨道倾角/(°) | 87 |
| 发射功率/dBw | 0 |
| 载波带宽/MHz | 54 |
| 上行频率/GHz | 28 |
| 下行频率/GHz | 18.2 |
| LEO地面站天线口径/m | 1.2 |
| GEO地面站天线口径/m | 1 |
| LEO卫星天线口径/m | 0.4 |
| GEO卫星天线口径/m | 3a |
| 地面站天线增益 | 见文献[17] |
| LEO卫星天线增益 | 见文献[18] |
| GEO卫星天线增益 | 见文献[16] |
| 地面站密度/(°) | 1b |
| 注:a.上行EPFD值对2~4区间的变化不敏感; b.设沿纬度线均匀分布,在赤道线上地面站间隔经度值为1°。 | |
表选项
表 2为文献[4]中明确列出的EPFD门限(上、下行场景门限的载波带宽均为40 kHz)。
表 2 干扰门限[4] Table 2 Interference threshold [4]
| 干扰场景 | 载波频率/GHz | EPFD门限/(dB(W·m-2)) |
| 上行场景 | 27.5~28.6 | -162 |
| 下行场景 | 17.8~18.6 | -164 |
表选项
3.1 EPFD与α和地面站纬度之间的关系仿真 图 11为上行多用户干扰场景的EPFD值随隔离角α与LEO星下点纬度的变化图。由图中仿真结果不难看出,随着LEO卫星纬度的升高,其星下波束覆盖范围内的地面站上行信号对GEO卫星的集总EPFD值随着纬度的升高而逐渐降低;而当引入隔离角α后,集总EPFD值会出现显著下降。
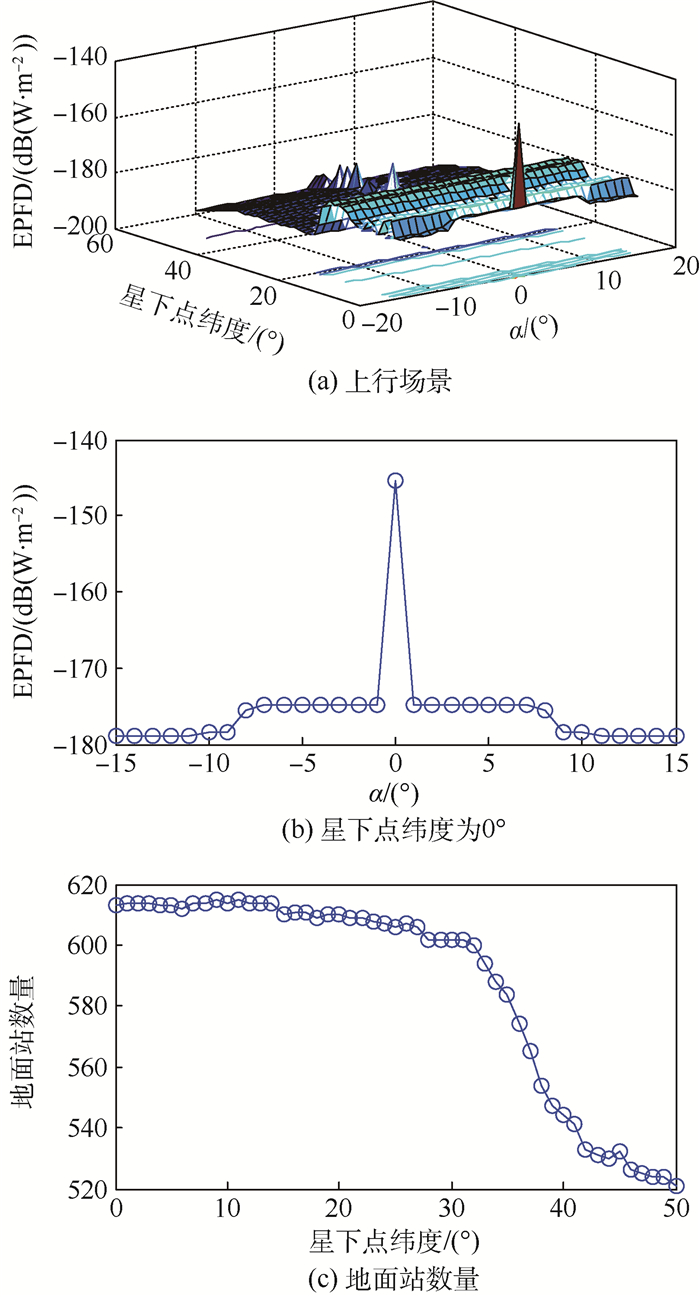 |
| 图 11 上行多用户干扰场景EPFD值 Fig. 11 EPFD values of multi-user uplink interference scenario |
| 图选项 |
由图 12(a)的仿真结果不难看出,随着地面站纬度的升高,GEO系统所接收端收到来自LEO系统的EPFD值是呈下降的趋势,因而两图右侧列出了干扰最大时(纬度φla=0°)EPFD随夹角α的变化曲线。
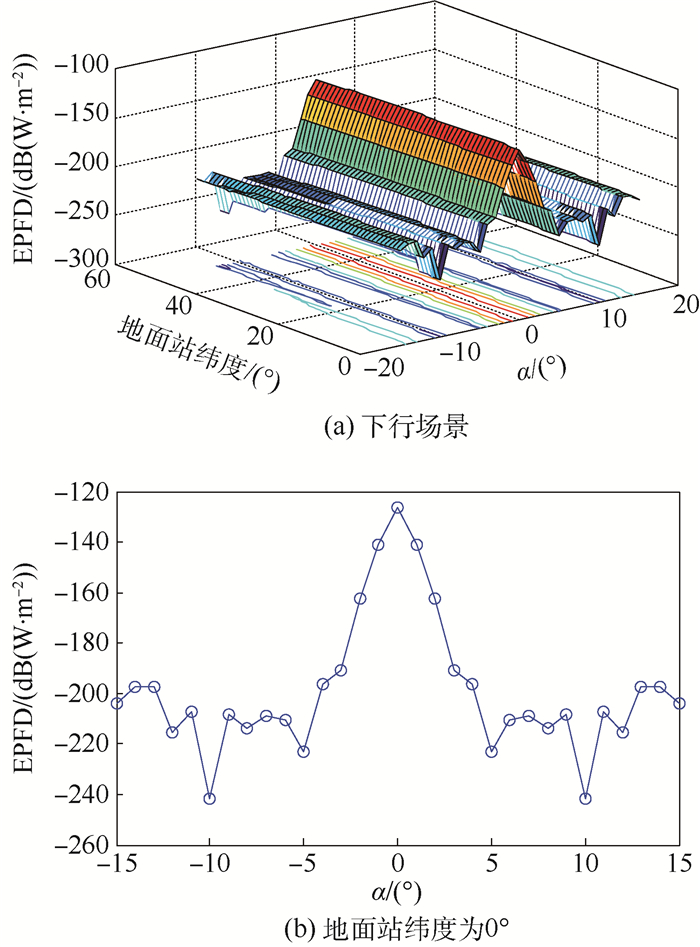 |
| 图 12 下行干扰场景EPFD值 Fig. 12 EPFD values of downlink interference scenario |
| 图选项 |
由表 2与图 11可知,当LEO卫星星下点位于赤道时,有其波束覆盖范围内地面站上行集总EPFD值最大,且当引入隔离角α后,EPFD值会出现急剧下降。由于上行EPFD门限值为-162 dB(W/m2),当α>1°时,上行集总EPFD值就会降至-175 dB(W/m2)以下,从而带来13 dB(W/m2)以上的余量。考虑到单颗GEO卫星可能同时面对多颗LEO卫星波束所覆盖的地面站的上行集总干扰,该余量意味着即使当LEO星下地面站的上行集总EPFD值取得最大时,为满足GEO接收到的上行EPFD门限,这样同时存在的会对GEO产生上行干扰的LEO卫星数目上限可以达到20颗。
而在下行场景中,结合表 2与图 12,可以看到,当α取到3°即可,GEO地面站收到来自LEO卫星的下行干扰EPFD值即可满足要求。
综上所述,根据式(2)不难得出,结合上下行干扰场景,为使GEO系统接收端收到的来自该LEO系统的EPFD值满足要求,地面站分别与LEO卫星与GEO卫星连线夹角的门限值αthreshold=3°。
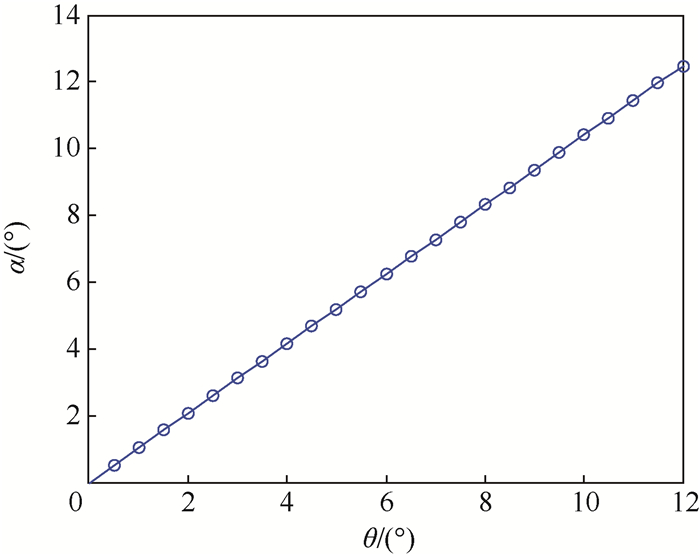
3.2 GEO带地心角θ与α关系仿真 由式(3)可知,在已经确定αthreshold的情况下,GEO带地心角θepfd与地面站所在纬度φla和该地面站在最小仰角约束条件下和可见GEO卫星的最大经度差Δφlon有关;因此,对于每一个给定的α,需要通过遍历φla找到最大θepfd。经过仿真,可得θepfd最大值与α关系仿真结果如图 13所示。
 |
| 图 13 α与θ关系仿真结果 Fig. 13 Relationship between α and θ in simulation |
| 图选项 |
由图 13不难得出,当αthreshold=3°时,可以取此时的GEO带地心角θepfd=3°。因此,根据式(4),在考虑GEO卫星轨道偏移的情况后(θshift < 15°),可得最终的GEO带地心角θ∈(3°,18°)。
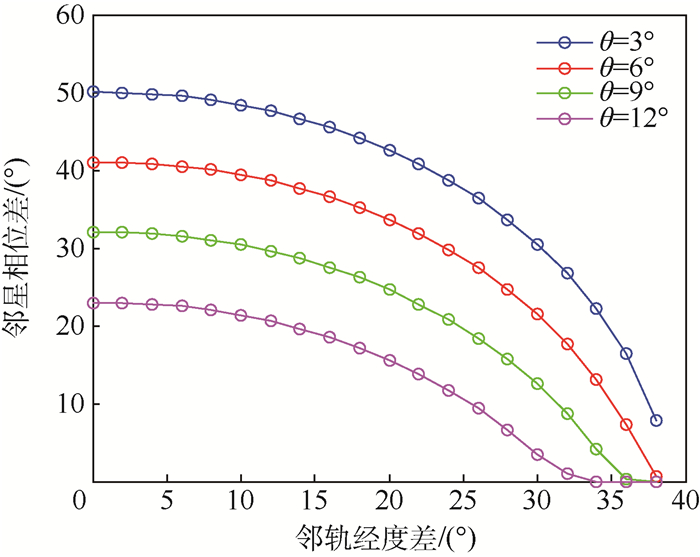
3.3 星座密度仿真 在引入规避区域后,决定星座密度的同轨邻星相位差和轨道之间的经度差与所需规避的GEO带地心角θ的关系如图 14所示。
 |
| 图 14 不同θ值时星座密度参数仿真结果 Fig. 14 Simulation result of constellation density parameter at different θ |
| 图选项 |
由图 14易得,在保持θ不变的情况下,邻星相位差与轨道经度差呈现负相关的关系,这就为在同等规避条件下寻找该LEO星座所需最低卫星数目提供了可能。同时,当θ变大时,星座密度也逐步变大,体现在保证轨道相位差相同的情况下,同轨星间相位差缩小,反之亦然。
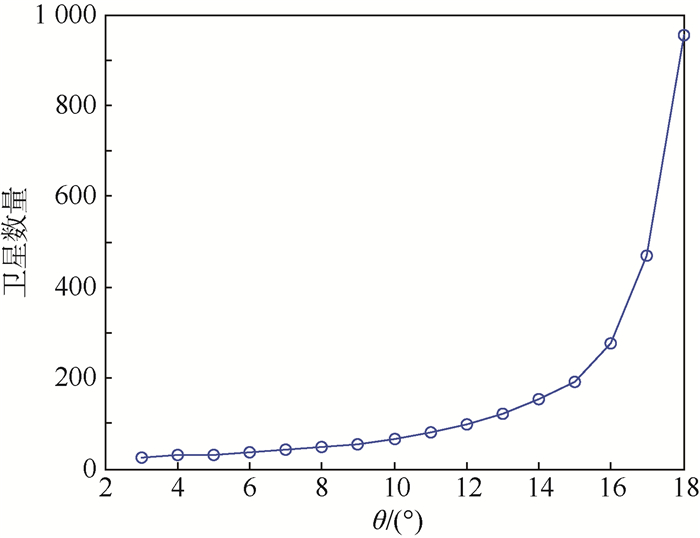
图 15则展示了GEO带地心角θ与LEO星座所需最低卫星数目的关系。不难看出,随着LEO地面站所需规避的GEO带不断拓宽,星座所需最低卫星数目也在不断增加;当GEO带地心角为3°时,系统大约需要50~70颗卫星即能保证在其对GEO系统干扰满足约束条件的情况下实现无间断服务。
 |
| 图 15 θ与星座卫星数量关系 Fig. 15 Satellite amount in constellation versus θ |
| 图选项 |
4 结论 本文主要通过引入GEO环状带与ITU建议书给出的干扰限制,结合上下行干扰场景,提出了一种基于空间隔离的LEO与GEO卫星在Ka频段频谱共享的方法,并对该方法的干扰避让原理给出了详细的论证过程。通过仿真验证,得出如下结果:
1) 通过仿真地面站隔离角、地面站纬度与上下行场景中干扰EPFD值的关系,基于ITU给出的限制条件,得到了该仿真参数下满足干扰门限的地面站隔离角阈值。
2) 仿真给出规避带地心角与地面站隔离角的关系,找出符合干扰门限的GEO带宽度。
3) 通过确定的GEO带找出LEO星座系统对GEO卫星的干扰规避区域,并通过仿真结果展示该方法对LEO星座密度的影响。
参考文献
| [1] | VATALARO F, CORAZZA G, CAINI C, et al. Analysis of LEO, MEO, and GEO global mobile satellite systems in the presence of interference and fading[J].IEEE Journal on Selected Areas in Communication, 1995, 13(2): 291–300.DOI:10.1109/49.345873 |
| [2] | SHARMA S K, CHATZINOTAS S, OTTERSTEN B. In-line interference mitigation techniques for spectral coexistence of GEO and NGEO satellites[J].International Journal of Satellite Communications and Networking, 2016, 34(1): 11–39.DOI:10.1002/sat.1090 |
| [3] | PRATT S R, RAINES R A, FOSSA C E., et al. An operational and performance overview of the IRIDIUM low earth orbit satellite system[J].IEEE Communications Surveys, Second Quarter, 1999, 2(2): 2–10. |
| [4] | ITU Radiocommunication (ITU-R).Radio Regulations Articles Edition of 2012[S].Geneva: ITU, 2012: 271-289. |
| [5] | ITU Radiocommunication (ITU-R).Analytical method for estimating interference between non-geostationary mobile-satellite feeder links and geostationary fixed-satellite networks operating co-frequency and codirectionally[S].Geneva: ITU, 1997: 2-3. |
| [6] | SHARMA S K, CHATZINOTAS S, OTTERSTEN B.Transmit beamforming for spectral coexistence of satellite and terrestrial networks[C]//20138th International Conference on Cognitive Radio Oriented Wireless Networks.Piscataway, NJ: IEEE Press, 2013: 275-281. |
| [7] | ZHENG Y, SUN S, BO R, et al.Traffic aware power allocation and frequency reuse for green LTE-A heterogeneous networks[C]//2015 IEEE International Conference on Communications (ICC). Piscataway, NJ: IEEE Press, 2015: 3167-3172. |
| [8] | SHARMA S K, CHATZINOTAS S, OTTERSTEN B.Cognitive radio techniques for satellite communication systems[C]//2013 IEEE 78th Vehicular Technology Conference(VTC Fall). Piscataway, NJ: IEEE Press, 2013: 1-5. |
| [9] | REED A G, POSEN M C J.Interference in the fixed satellite service bands between the feeder-links of networks using non-geostationary satellites and network using geostationary satellites[C]//3rd European Conference on Satellite Communications ECSC3, 1993. Manchester: IET, 1993: 251-256. |
| [10] | WANG A W.Method and apparatus for providing wideband services using medium and low earth orbit satellites: US6678520[P].2014-01-23. |
| [11] | ITU Radiocommunication(ITU-R).Simulation methodologies for determining statistics of short-term interference between co-frequency, codirectional non-geostationary-satellite orbit fixed-satellite service systems in circular orbits and other non-geostationary fixed-satellite service systems in circular orbits or geostationary-satellite orbit fixed-satellite service networks[S].Geneva: ITU, 2003: 3-5. |
| [12] | ITU Radiocommunication(ITU-R).Interference mitigation techniques to facilitate coordination between non-geostationary-satellite orbit mobile-satellite service feeder links and geostationary-satellite orbit fixed-satellite service networks in the bands 19.3-19.7 GHz and 29.1-29.5 GHz[S].Geneva: ITU, 1999: 2. |
| [13] | ITU Radiocommunication(ITU-R).Analytical method to calculate short-term visibility and interference statistics for non-geostationary satellite orbit satellites as seen from a point on the earth's surface[S].Geneva: ITU, 2002: 2-3. |
| [14] | 晓春. OneWeb太空互联网低轨星座的新进展[J].卫星应用, 2016(6): 75–77. XIAO C. New Progress of OneWeb LEO satellite constellation in space internet[J].Satellite Application, 2016(6): 75–77.(in Chinese) |
| [15] | ITU Radiocommunication(ITU-R).Static methodology for calculating epfd↓ to facilitate coordination of very large antennas under Nos. 9.7A and 9.7B of the radio regulations[S].Geneva: ITU, 2005: 2-4. |
| [16] | ITU Radiocommunication(ITU-R).Satellite antenna radiation pattern for use as a design objective in the fixed-satellite service employing geostationary satellites[S].Geneva: ITU, 1997: 2-5. |
| [17] | 国际电联无线电通信全会.用于在10.7 GHz和30 GHz之间的频段内涉及非GSO卫星的平共处干扰评估的参考FSS地球站的辐射方向图[S].日内瓦: 国际电联无线电通信全会, 2001: 2-3. ITU Radiocommunication(ITU-R).Reference FSS earth-station radiation patterns for use in interference assessment involving non-GSO satellites in frequency bands between 10.7 GHz and 30 GHz[S].Geneva: ITU, 2001: 2-3(in Chinese). |
| [18] | ITU Radiocommunication(ITU-R).Satellite antenna radiation patterns for non-geostationary orbit satellite antennas operating in the fixed-satellite service below 30 GHz[S].Geneva: ITU, 2001: 2-4. |
