现代雷达所面临的电磁环境日益恶劣, 针对雷达的电磁干扰技术迅速发展, 特别是有源压制干扰的大量使用, 极大制约了雷达作战效能的发挥^[1]。面对有源压制干扰, 对干扰信号的分类识别成为抗干扰工作的关键, 根据分类识别结果, 抗干扰系统才能有针对性地采取不同的抗干扰措施, 以达到较为理想的抗干扰效果。因此, 对有源压制干扰的分类识别是当前抗干扰领域亟须解决的关键问题。
目前, 国内外****在雷达压制干扰分类识别方面做了大量研究。文献[2]提出了一种基于随机投影和稀疏分类的雷达波形识别算法; 文献[3-4]分别提取不同的时域特征参数对有源压制干扰进行分类识别; 文献[5]提取信号的一阶矩和二阶矩作为特征参数, 并通过分类器实现有源压制干扰的分类识别; 文献[6]将回波信号转换为时频图像, 并利用前馈神经网络实现压制干扰的分类识别; 文献[7]提取信号在FRFT域的信息维度和盒维数作为特征参数, 通过门限判决法完成干扰类型的分类识别。
上述文献通过提取不同的特征参数完成了有源压制干扰的分类识别, 但是当干信比相对较低时, 上述文献的分类识别正确率均出现较明显的下降, 从而导致在干信比未知的情况下, 压制干扰分类识别结果可信度较低。
针对此问题, 本文充分分析目标回波信号和压制干扰信号的特性差异, 综合考虑有源压制干扰的存在性检测以及分类识别, 提出了一种基于FRFT域特征差异的压制干扰检测与分类算法。
1 模型的建立与分析 1.1 模型建立 线性调频(Linear Frequency Modulation, LFM)信号作为一种重要的信号体制, 具有较大的时宽带宽积, 能够同时满足作用距离和距离分辨率的要求^[8-9], 从而被广泛应用于现代雷达系统中, 因此, 本文选取LFM信号作为雷达发射信号进行研究。
假设在一段观测时间内目标的运动速度不变, 则有源压制干扰环境下的回波信号r(t)表示为

(1)

式中:s_r(t)=s(t-τ)e^jω_d(t-τ)为目标回波信号, ω_d为多普勒角频率, τ为回波时延; J(t)为射频噪声干扰、噪声调幅干扰和噪声调频干扰3种有源压制干扰中的1种; n(t)为过程噪声, 并假设n(t)服从高斯分布, 且与J(t)相互独立。
雷达发射的LFM信号s(t)表示为^[10]

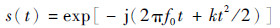(2)

式中:f₀为LFM信号的载频; k为调制斜率。
1.2 模型分析 通过式(1)可以看出, 在干扰距离远、干扰方向未对准或干扰机功率不足等情况下, 压制干扰J(t)功率较小, 此时回波信号r(t)的干扰特征不明显, 从而导致压制干扰分类识别正确率较低, 所以在分类识别之前进行压制干扰的存在性检测是有必要的, 通过检测, 从而保证在干信比较高、回波信号干扰特征较明显时再进行压制干扰的分类识别。
在检测到压制干扰存在后, 根据不同压制干扰类型之间的特性差异, 提取多个特征参数分别进行压制干扰的分类识别。同时, 为避免硬判决造成的分类识别错误, 本文采用模糊判决的方法, 并通过判决结果融合得到最终的分类识别结果。基于以上分析, 本文算法流程如图 1所示。

图 1 本文算法流程图 Fig. 1 Flowchart of proposed algorithm

图选项

2 压制干扰的检测与分类 2.1 压制干扰的存在性检测
2.1.1 算法分析 由于压制干扰存在性检测的主要目的是解决干信比未知情况下分类识别结果可信度不高的问题, 所以结合分类识别正确率曲线对检测算法进行分析。
图 2中:JSR为回波信号干信比; p为分类识别正确率; 点Q表示检测到压制干扰存在的干信比临界点。由图 2可以看出, 对于点Q而言, 其取值越大, 则在此之后进行压制干扰分类识别的正确率越高, 分类识别结果的可信度也越高, 但同时, 点Q取值越大, 也意味着在此之前无法判定压制干扰的存在, 这对于雷达抗干扰而言是不利的。

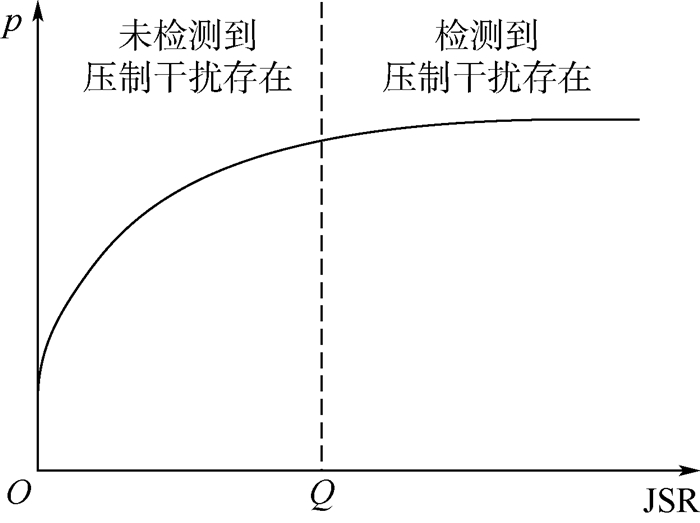图 2 压制干扰的分类识别正确率曲线 Fig. 2 Classification recognition correct rate curve of suppression interference

图选项

为解决这一矛盾, 本文借鉴文献[11-12]中基于FRFT域峰值搜索的目标检测算法, 通过提取FRFT域峰值作为特征参数, 将压制干扰存在性检测与目标检测相结合:一方面, 当压制干扰不存在或者干扰功率较低时, 能够根据文献[11-12]算法进行目标检测; 另一方面, 因为FRFT对LFM信号的增益达10 dB以上, 所以当判断压制干扰存在时, 能够保证回波信号的干信比大于10 dB, 此时分类识别正确率较高。

2.1.2 FRFT域峰值特性分析 1) LFM信号峰值特性分析
时域函数x(t)的p阶FRFT变换^[13]X_p(u)表示为

(3)

式中:K_p(u, t)为FRFT核函数, 表示为

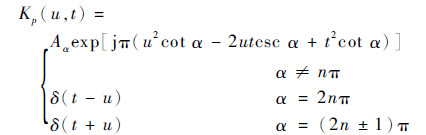(4)

其中: 。当变换角度α与LFM信号的调制斜率k正交, 即α=-arctan(1/(2πk))时, LFM信号的FRFT表示为

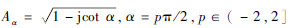
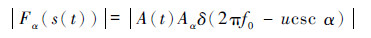(5)

由式(5)可以看出, 此时LFM信号在u域表现为冲激函数, 具有明显的能量聚集特性。能量聚集点所在变换阶次p_z, 即LFM信号最佳变换阶次可以通过式(6)求得:

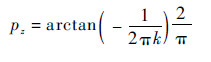(6)

同时, 由式(6)可以看出, 由于LFM信号的调制斜率k满足k>0, 所以p_z>1。
2) 压制干扰信号峰值特性分析
通过仿真实验得到不同压制干扰类型在FRFT域的峰值特性。图 3~图 5分别表示射频噪声干扰、噪声调幅干扰和噪声调频干扰在FRFT域的谱分布以及峰值点所在变换阶次情况。图中:A为幅值。

图 3 射频噪声干扰在FRFT域的谱分布以及峰值变换阶次 Fig. 3 RF noise jamming spectrum distribution in FRFT domain and its order of peak

图选项

图 4 噪声调幅干扰在FRFT域的谱分布以及峰值变换阶次 Fig. 4 Noise AM jamming spectrum distribution in FRFT domain and its order of peak

图选项

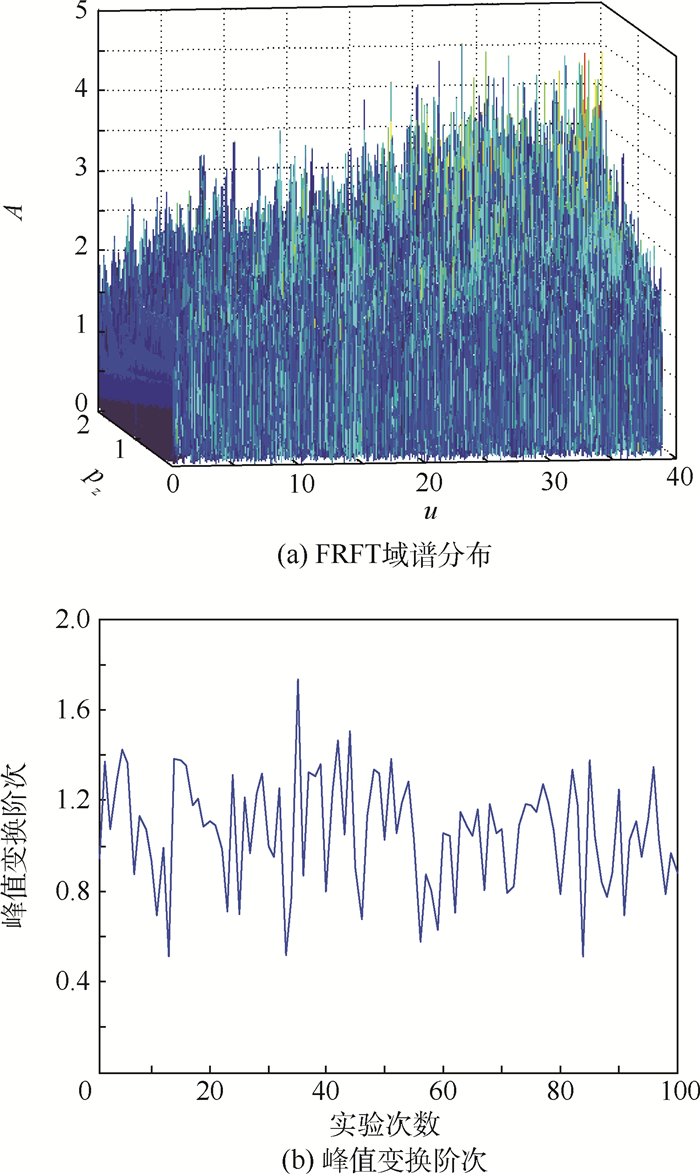图 5 噪声调频干扰在FRFT域的谱分布以及峰值变换阶次 Fig. 5 Noise FM jamming spectrum distribution in FRFT domain and its order of peak

图选项

由图 3~图 5可以看出, 射频噪声干扰在FRFT域能量均匀分布, 其在FRFT域的峰值随机出现在任意变换阶次; 噪声调幅干扰在FRFT域具有较强的能量聚集特性, 其在FRFT域的峰值稳定出现在变换阶次p=1的位置; 噪声调频干扰在FRFT域具有局部能量聚集的特性, 其在FRFT域的峰值出现在一定变换阶次范围内。
结合LFM信号的峰值特性可以看出, LFM信号与压制干扰信号在FRFT域的峰值阶次具有明显差异, 所以根据回波信号在FRFT域的峰值阶次进行压制干扰的存在性检测是可行的。

2.1.3 算法流程 本文采用序贯判决算法^[14-15]进行压制干扰的存在性检测。根据式(6)得到LFM信号在FRFT域的最佳变换阶次p_z, 取以p_z为中心的一小段区间为δ(p_z)。将一定观测时间内的回波信号分成N段, 通过峰值搜索算法得到其在FRFT域的峰值阶次分别为p_j(j=1, 2, …, N), 若p_j中, 取值落在δ(p_z)区间内的个数D小于门限值T, 则判断压制干扰存在, 否则判定压制干扰不存在。压制干扰存在性检测算法如图 6所示。

图 6 压制干扰存在性检测算法示意图 Fig. 6 Schematic of suppression interference existence detection algorithm

图选项

2.2 压制干扰的分类识别 在检测到压制干扰存在后, 进一步根据不同压制干扰类型之间的特性差异进行压制干扰的分类识别。

2.2.1 FRFT域特征参数提取 由图 3(b)、图 4(b)和图 5(b)的对比可以看出, 不同压制干扰类型在FRFT域的峰值阶次也表现出较明显差异, 可以作为压制干扰分类识别的依据, 并且峰值具有唯一性, 在判断压制干扰存在后, 峰值特性不受目标回波信号的影响。
同时, 由图 3(a)、图 4(a)和图 5(a)可以看出, 3种压制干扰类型在FRFT域的能量聚集程度差异较大, 所以导致不同干扰类型在FRFT域的极值阶次离散程度差异明显, 据此, 通过提取压制干扰在FRFT域的极值阶次作为特征参数, 对3种压制干扰类型进行区分。
根据不同压制干扰类型在峰值阶次以及极值阶次上表现出来的差异, 分别提取单时段极值阶次标准差和多时段峰值阶次标准差作为特征量进行压制干扰的分类识别。
1) 单时段极值阶次标准差
取c倍的FRFT域峰值幅度f作为门限, c < 1, 对大于门限的极值点进行搜索。当极值点个数大于M时, 求取前M个极值点所在阶次标准差作为特征量; 当极值点个数小于M时, 求取全部极值点所在阶次标准差作为特征量。
2) 多时段峰值阶次标准差
将一定观测时间内的回波信号分成G份, 通过峰值搜索得到G段信号在FRFT域的峰值所在阶次, 并求取G个变换阶次的标准差作为特征量。

2.2.2 算法流程 在判断压制干扰存在后, 根据不同干扰类型的特性差异, 分别以单时段极值阶次标准差和多时段峰值阶次标准差为特征量进行压制干扰的模糊判决。
1) 基于单时段极值阶次标准差的模糊判决
根据式(7)求取极值阶次标准差σ_e:

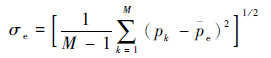(7)

式中:M为极值点个数; p_k为第k个极值点所在变换阶次; p_e为所有极值阶次的平均值。
对极值阶次标准差σ_e的模糊判决如图 7所示。

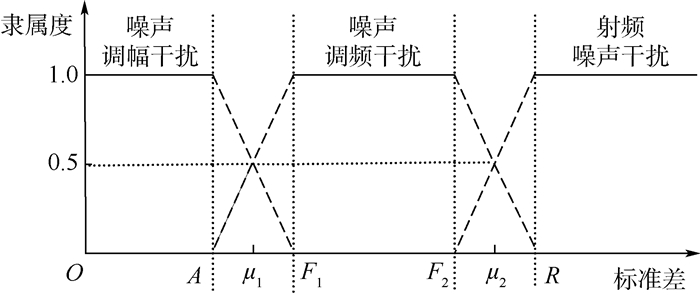图 7 极值阶次标准差模糊判决示意图 Fig. 7 Schematic of fuzzy decision of extreme order standard deviation

图选项

图 7中:A、F₁、F₂和R分别表示标准差σ_e的判决门限值, 区间[A, F₁]为噪声调幅干扰和噪声调频干扰的判决置信区间, 区间[F₂, R]为噪声调频干扰和射频噪声干扰的判决置信区间, μ₁和μ₂为置信区间中隶属度为0.5时所对应的标准差取值。当标准差σ_e落在判决置信区间以外时, 判别压制干扰属于某一种干扰类型; 当标准差σ_e落在判决置信区间之内时, 根据图 7虚线得到压制干扰属于不同干扰类型的可能性。
2) 基于多时段峰值阶次标准差的模糊判决
根据式(8)求取峰值阶次标准差σ_p:

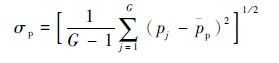(8)

式中:G为峰值阶次个数; p_j为峰值所在变换阶次; p_p为所有峰值阶次的平均值。
采用与极值阶次标准差相同的模糊判决算法, 得到压制干扰属于不同干扰类型的可能性。
3) 判决结果融合算法
为提高分类识别正确率, 将基于不同特征参数的判决结果按一定准则进行融合。根据极值阶次标准差、峰值阶次标准差以及融合后所得到的分类识别结果分别用向量P=(p₁, p₂, p₃)、T=(t₁, t₂, t₃)、K=(k₁, k₂, k₃)表示, 其中, p₁、k₁、t₁表示干扰信号属于射频噪声干扰的可能性, p₂、k₂、t₂表示干扰信号属于噪声调幅干扰的可能性, p₃、k₃、t₃表示干扰信号属于噪声调频干扰的可能性。针对可能出现的情况, 提出以下融合准则:
① 一种方法得到的干扰信号属于某种干扰类型的可能性为1, 若另一种方法得到的干扰信号属于该种干扰的可能性不为0, 则最终判断干扰来自于该种压制干扰类型, 即max(P)=p_j=1, 若k_j≠0, 则取T = P。
② 若一种方法得到的干扰信号属于某种干扰类型的可能性为1, 另一种方法得到的干扰信号属于该种干扰的可能性为0, 则认定判决无效, 进行下一次判决。
③ 除上述情况外, 最终判决结果向量T均为P和K的平均值。
在完成融合之后, 取向量T中可能性最大的压制干扰类型作为最终的判决结果。
完整的压制干扰检测与分类算法流程如图 8所示。

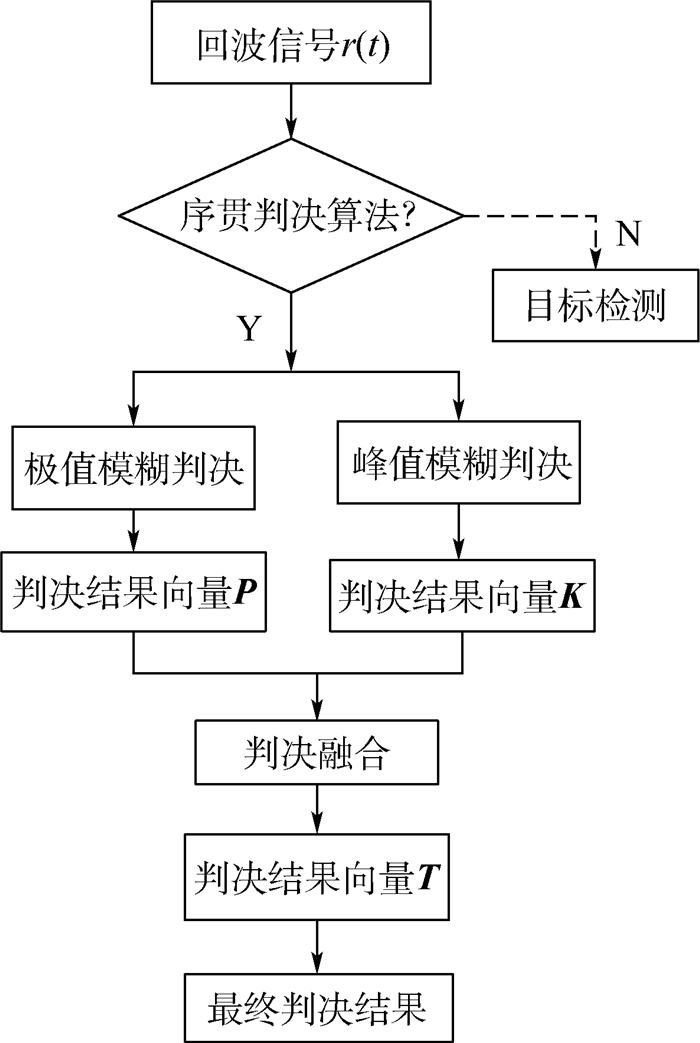图 8 压制干扰检测与分类算法流程图 Fig. 8 Flowchart of detection and classification algorithm of suppression interference

图选项

3 仿真实验验证 3.1 仿真参数设置 采用与文献[4]相同的参数设置, 如表 1所示。
表 1 干扰信号仿真参数 Table 1 Interference signal simulation parameters

参数	射频噪声干扰	噪声调幅干扰	噪声调频干扰
中心频率/MHz	4	4	4
调制噪声		白噪声	白噪声
调制系数		0.5	100
时间宽度/μs	50	50	50
采样频率/MHz	20	20	20

表选项






LFM信号调制斜率k=4×10¹⁰ Hz/s, 时宽为50 μs, 载频为4 MHz; 过程噪声为高斯白噪声, 其方差σ_n²=1。
算法参数设置如下:取观测时间为50 μs, FRFT的变换阶次p的取值范围为[0, 2];变换阶次的步长取为0.001;压制干扰存在性检测中, 信号段数N取值为6, 序贯判决算法门限值为3;单时段极值阶次标准差模糊判决中, 倍数c取值为0.5, 极值点个数M取值为50, 多时段峰值阶次标准差模糊判决中, 信号段数G取值为6;干信比取值范围为0~20 dB, 在每个节点进行100次蒙特卡罗实验来获得概率值。
3.2 仿真验证
3.2.1 特征参数的仿真实验 仿真参数条件下, 在干信比为15 dB时, 对射频噪声干扰、噪声调幅干扰和噪声调频干扰在FRFT域的单时段极值阶次标准差进行仿真实验, 实验结果如图 9所示。

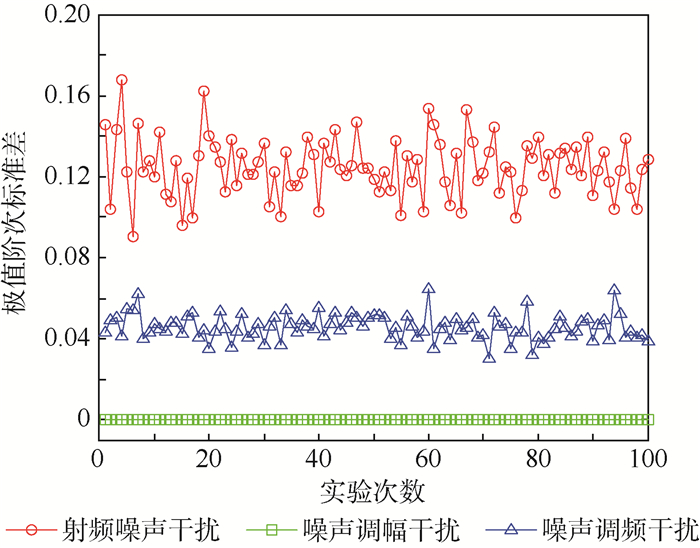图 9 极值阶次标准差 Fig. 9 Standard deviation of extreme value order

图选项

由图 9可以看出, 3种压制干扰的极值阶次标准差之间差异明显, 可以作为压制干扰分类识别的依据。
仿真条件下, 在干信比为15 dB时对射频噪声干扰、噪声调幅干扰和噪声调频干扰在FRFT域的多时段峰值阶次标准差进行仿真实验, 实验结果如图 10所示。

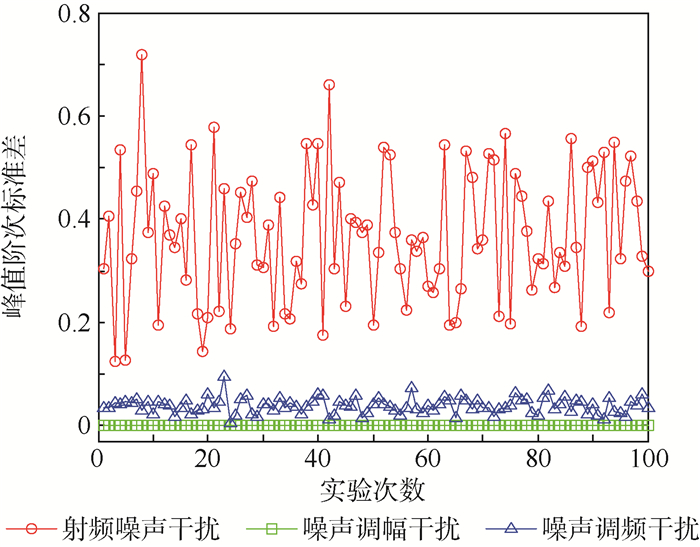图 10 峰值阶次标准差 Fig. 10 Standard deviation of peak order

图选项

由图 10可以看出, 3种压制干扰的峰值阶次标准差之间差异明显, 可以作为压制干扰分类识别的依据。

3.2.2 仿真结果与分析 1) 射频噪声干扰环境下的干扰检测与分类识别结果如图 11所示。图 11(a)表示射频噪声干扰的检测结果, 可以看出, 当干信比大于12.3 dB后, 射频噪声干扰被检测到, 在此之前可以直接进行目标检测; 图 11(b)表示在检测到干扰存在后, 对干扰进行识别的结果, 可以看出, 在检测到射频噪声干扰存在后, 射频噪声干扰的分类识别正确率在98%以上。
1) 射频噪声干扰环境下的干扰检测与分类识别结果如图 11所示。图 11(a)表示射频噪声干扰的检测结果, 可以看出, 当干信比大于12.3 dB后, 射频噪声干扰被检测到, 在此之前可以直接进行目标检测; 图 11(b)表示在检测到干扰存在后, 对干扰进行识别的结果, 可以看出, 在检测到射频噪声干扰存在后, 射频噪声干扰的分类识别正确率在98%以上。

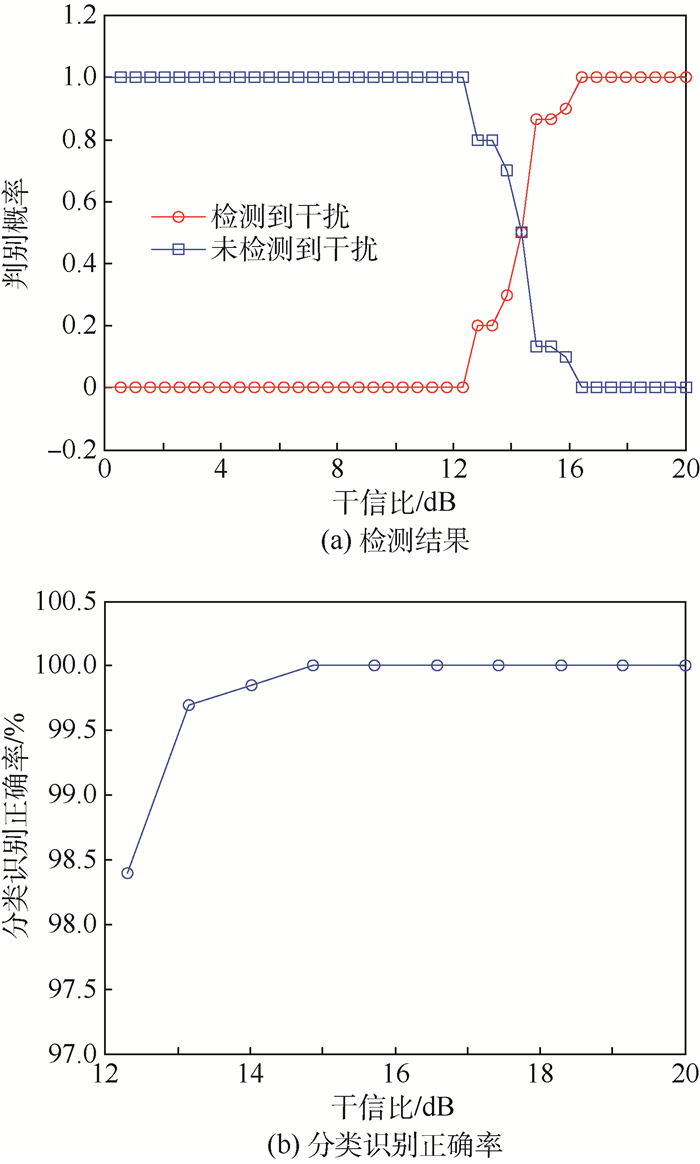图 11 射频噪声干扰检测结果及分类识别正确率 Fig. 11 Detection results and classification recognition accuracy rate of RF noise jamming

图选项

2) 噪声调幅干扰环境下的干扰检测与识别结果如图 12所示。图 12(a)表示噪声调幅干扰的检测结果, 可以看出, 当干信比大于9.7 dB后, 噪声调幅干扰被检测到, 在此之前可以直接进行目标检测; 图 12(b)表示在检测到干扰存在后, 对干扰进行识别的结果, 可以看出, 在检测到噪声调幅干扰存在后, 噪声调幅干扰的分类正确识别率在99%以上。

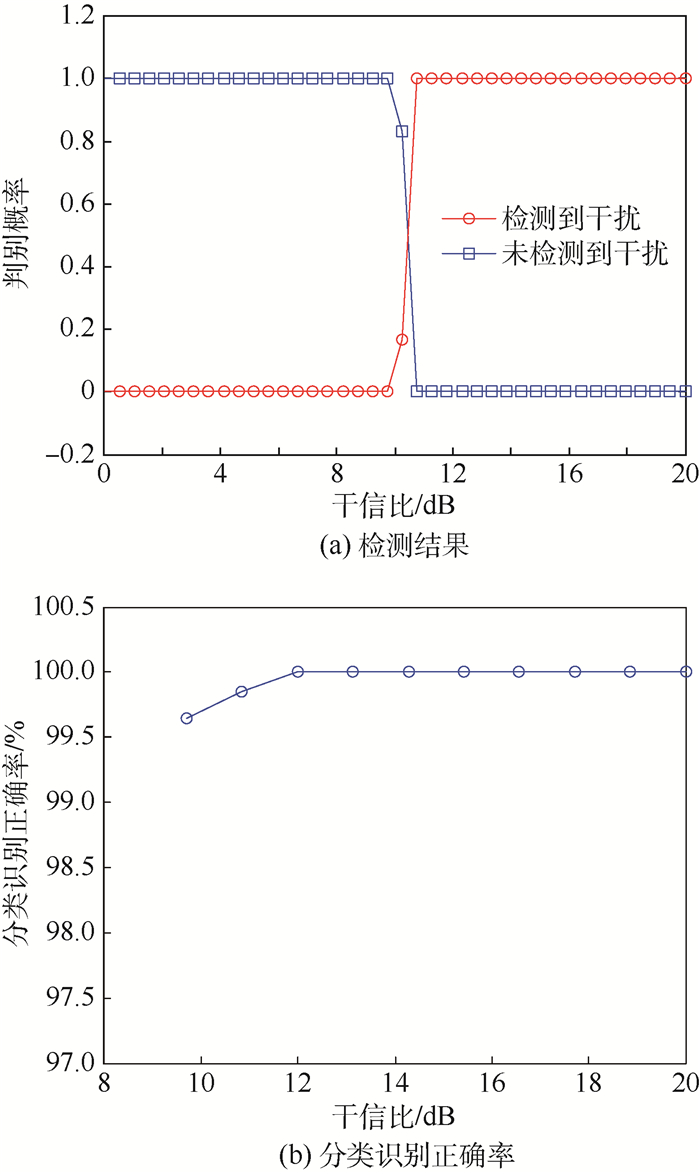图 12 噪声调幅干扰检测结果及分类识别正确率 Fig. 12 Detection results and classification recognition accuracy rate of noise AM jamming

图选项

3) 噪声调频干扰环境下的干扰检测与识别结果如图 13所示。图 13(a)表示噪声调频干扰的检测结果, 可以看出, 当干信比大于9.2 dB后, 噪声调频干扰被检测到, 在此之前可以直接进行目标检测; 图 13(b)表示在检测到干扰存在后, 对干扰进行识别的结果, 可以看出, 在检测到噪声调频干扰存在后, 噪声调频干扰的分类正确识别率在96%以上。

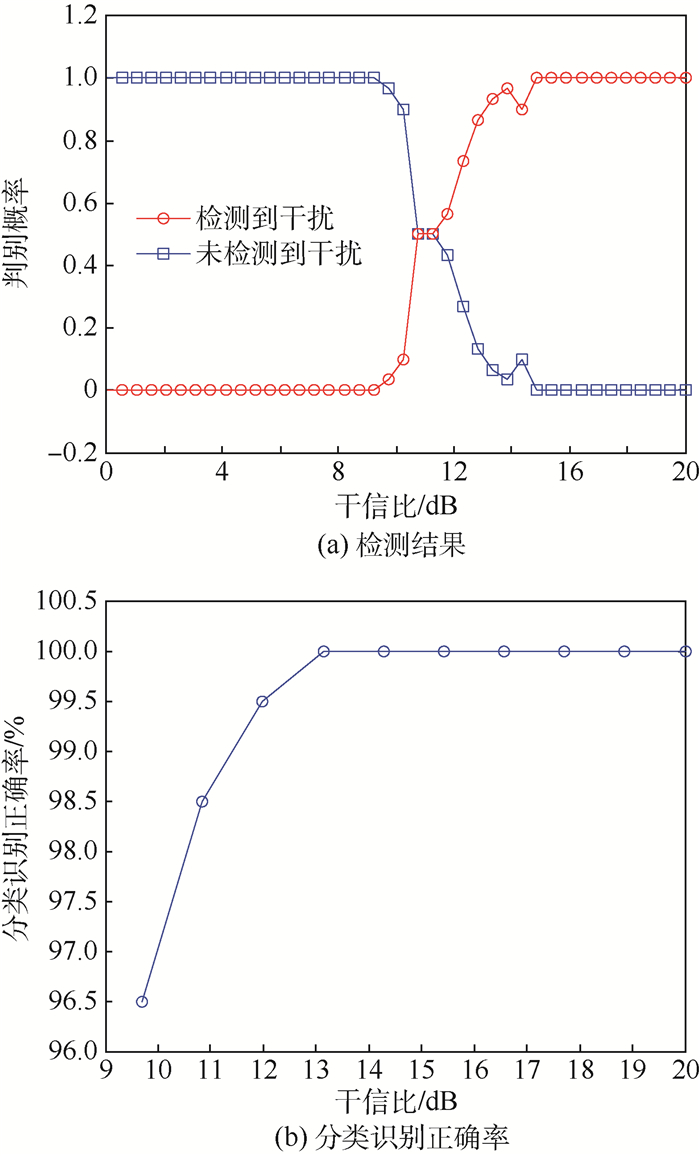图 13 噪声调频干扰检测结果及分类识别正确率 Fig. 13 Detection results and classification recognition accuracy rate of noise FM jamming

图选项

3.2.3 与现有算法比较 由于目前将压制干扰存在性检测与分类识别相结合的文献较少, 所以主要将本文算法与文献[4]算法进行比较。图 14为文献[4]算法分类识别结果, 图 15(a)、(b)、(c)分别表示射频噪声干扰、噪声调幅干扰和噪声调频干扰环境下本文算法与文献[4]算法分类识别结果的比较。

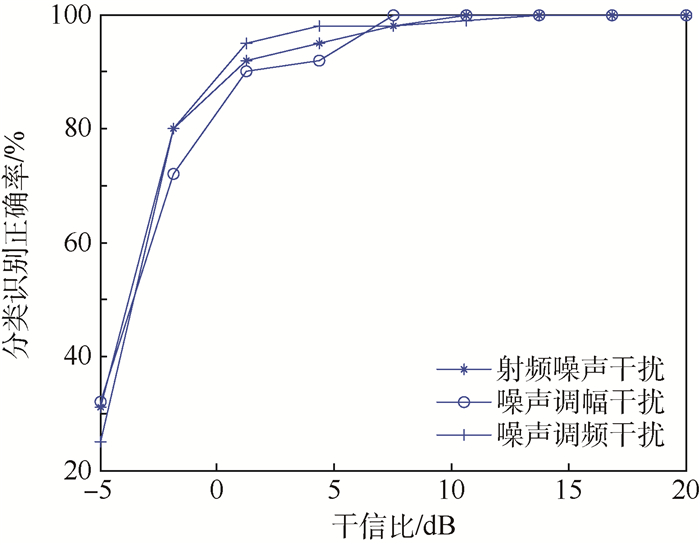图 14 文献[4]算法分类识别结果 Fig. 14 Classification recognition results of Ref.4 algorithm

图选项

通过图 15的比较可以看出, 在检测到压制干扰存在后, 本文对压制干扰的分类识别正确率高于文献[4]算法。同时, 在回波信号干信比未知情况下, 本文算法所得到的射频噪声干扰、噪声调幅干扰和噪声调频干扰识别结果可信度分别在98%、99%和96%以上, 而文献[4]算法未进行压制干扰检测, 从而导致干信比未知情况下分类识别结果可信度较低。

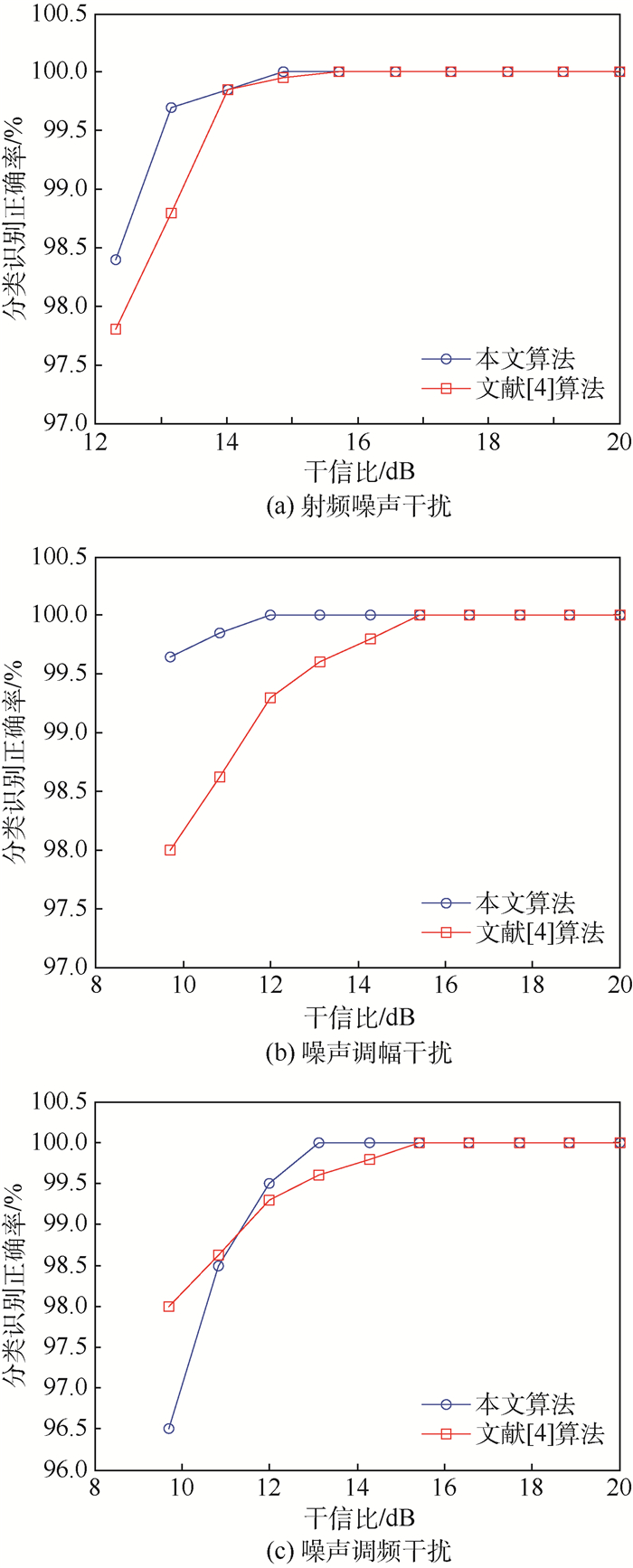图 15 不同压制干扰下本文算法与文献[4]算法分类识别结果对比 Fig. 15 Comparison of classification and recognition results under different kinds of jamming with proposed algorithm and Ref.4 algorithm

图选项

4 结论 本文通过在压制干扰分类识别之前进行压制干扰的存在性检测, 有效解决了回波信号干信比未知情况下, 压制干扰分类识别结果可信度较低的问题。
1) 对于射频噪声干扰而言, 当干信比大于12.3 dB时能够被检测出来, 而后进行分类识别, 结果可信度大于99%。
2) 对于噪声调幅干扰而言, 当干信比大于9.7 dB时能够被检测出来, 而后进行分类识别, 结果可信度大于98%。
3) 对于噪声调频干扰而言, 当干信比大于9.2 dB时能够被检测出来, 而后进行分类识别, 结果可信度大于96%。

参考文献

[1]	赵国庆. 雷达对抗原理[M].西安: 西安电子科技大学出版社, 2012: 122-123. ZHAO G Q. Principle of rdar countermeasure[M].Xi'an: Xidian University Press, 2012: 122-123.(in Chinese)
[2]	MA J, HUANG G, ZUO W, et al. Robust radar waveform recognition algorithm based on random projections and sparse classification[J].Radar Sonar & Navigation IET, 2014, 8(4): 290–296.
[3]	TANG Z, ZHANG B, LI G Q. Radar active blanket jamming sorting based on resemblance coefficient cluster[C]//IEEE International Conference on Signal Processing. Piscataway, NJ: IEEE Press, 2013: 1-6.
[4]	杜东平. 雷达压制式干扰抑制算法研究[D]. 成都: 电子科技大学, 2008: 11-21. DU D P. Research on radar suppress interference suppression algorithm[D]. Chengdu: University of Electronic Science and Technology, 2008: 11-21(in Chinese).
[5]	LU L, YANG J, WANG H, et al. The analysis and feature extraction of nonstationary random characteristics of radar jammer signal[C]//International Symposium on Electromagnetic Compatibility. Piscataway, NJ: IEEE Press, 2002: 660-663.
[6]	HAYKIN S, BHATTACHARYA T K. Modular learning strategy for signal detection in a nonstationary environment[C]//MILCOM 97-Proceedings. Piscataway, NJ: IEEE Press, 1997, 3: 1113-1116.
[7]	ZHU H, JIANG G, ZHANG H. Existence detection of blanket jamming based on fractal characteristics in FRFT domain[J].High Power Laser and Particle Beams, 2016, 28(5): 1–7.
[8]	WANG J H, XIE F, WANG Y C, et al. LFM radar signal processing based on multi-model Kalman filter[C]//International Conference on Intelligent Computation Technology and Automation. Piscataway, NJ: IEEE Press, 2011: 592-595.
[9]	QIAN R, GAO Y, JIANG D, et al. Implementation of wideband digital transmitting beamformer based on LFM waveforms[J].IET Signal Processing, 2016, 11(2): 11–14.
[10]	WU H, ZHAO H Z. Modeling and simulation of a full coherent LFM pulse radar system based on Simulink[C]//International Conference on Measurement, Information and Control. Pisca-taway, NJ: IEEE Press, 2013: 95-99.
[11]	LIU D, LIU Y, CAI H, et al. Linear frequency-modulated continuous wave active sonar signal processing[C]//Oceans Conference. Piscataway, NJ: IEEE Press, 2014: 1-5.
[12]	陈小龙, 关键, 刘宁波, 等. 基于FRFT的LFM信号自适应滤波算法及分析[J].现代雷达, 2010, 32(12): 48–53. CHEN X L, GUAN J, LIU N B, et al. Adaptive filtering algorithm for LFM signal and performance analysis based on FRFT[J].Modern Radar, 2010, 32(12): 48–53.DOI:10.3969/j.issn.1004-7859.2010.12.011(in Chinese)
[13]	陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M].北京: 清华大学出版社, 2004: 55-57. TAO R, DENG B, WANG Y. Fractional Fourier transform and its applications[M].Beijing: Tsinghua University Press, 2004: 55-57.(in Chinese)
[14]	YANG Y, WU Y, ZHANG H, et al. Improved sequential extraction method for determination of alkali and alkaline earth metals in Zhundong coals[J].Fuel, 2016, 181: 951–957.DOI:10.1016/j.fuel.2016.05.014
[15]	LINN C, WERTH D. Sequential anomaly detection techniques in business processes[M]//ABRAMOWICZ W, ALT R, BOGDAN F. Business information systems workshops. Berlin: Springer, 2016: 196-208.