目前关于浮空器热特性的研究主要集中在平台方面[2-3],对载荷舱的研究相对较少,特别是处于临近空间环境下的载荷舱。这些研究主要分为2类:第1类以研究封闭方腔换热机理为主,而不考虑实际的应用背景,所使用的模型多为简化的二维模型,边界条件比较简单;第2类考虑实际的应用背景,研究载荷舱在具体环境下的不同结果,但条件较为简化,无法兼顾舱内对流、导热和辐射的影响。第1类研究如Choi和Kim[4]分析不同Reynolds应力及热通量处理方法对矩形腔内自然对流模拟结果的稳定性和精确性的影响;Xamán等[5]研究分别忽略导热或辐射对存在太阳辐射的二维腔内耦合换热结果的影响;Kuznetsov和Sheremet等[6-8]分析瑞利数、表面发射率和导热系数等参数变化对存在恒温热源的封闭方腔内耦合换热结果的影响。第2类研究如许玉等[9]分析分别处于20 km高空和地面时载荷舱内温度场分布的区别,但其只考虑了自然对流与辐射换热,而忽略了导热的影响;邓丽君[10]研究临近空间浮空器载荷舱的热控技术,所使用的模型也没有考虑导热的影响。这2类研究都无法准确反映临近空间环境下载荷舱内的耦合换热特性。实际情况下载荷舱外受到对流换热、长波辐射以及太阳辐射等多种因素的影响,而舱内同时存在自然对流、热辐射和热传导3种热量传递方式,研究时需要综合考虑舱内外的影响。
本文以临近空间浮空器载荷舱为应用背景,建立封闭方腔热分析模型。以方腔外壁面的对流换热系数和辐射热流作为浮动边界条件,把方腔内外耦合传热分割为2个相对独立的传热过程,研究临近空间环境下封闭方腔内自然对流、表面辐射和导热的耦合问题。重点分析了不同时刻、不同腔壁热阻和发射率对结果的影响,相关结论对工程应用具有一定的参考价值。
1 封闭方腔数学建模 1.1 封闭方腔理论分析模型 考虑临近空间环境中一含有热源的有限厚度封闭方腔,方腔内部尺寸为0.5 m×0.5 m×0.5 m,特征长度L=0.5 m,腔壁是厚度为d的保温材料。热源位于方腔底部中心处,尺寸为0.1 m×0.1 m×0.1 m,发热功率45 W。同时在方腔底部还放置有一块2 mm厚的铝板,以增加热源向腔内的传热。方腔示意图如图 1所示,X轴指向正南,Y轴指向正东。
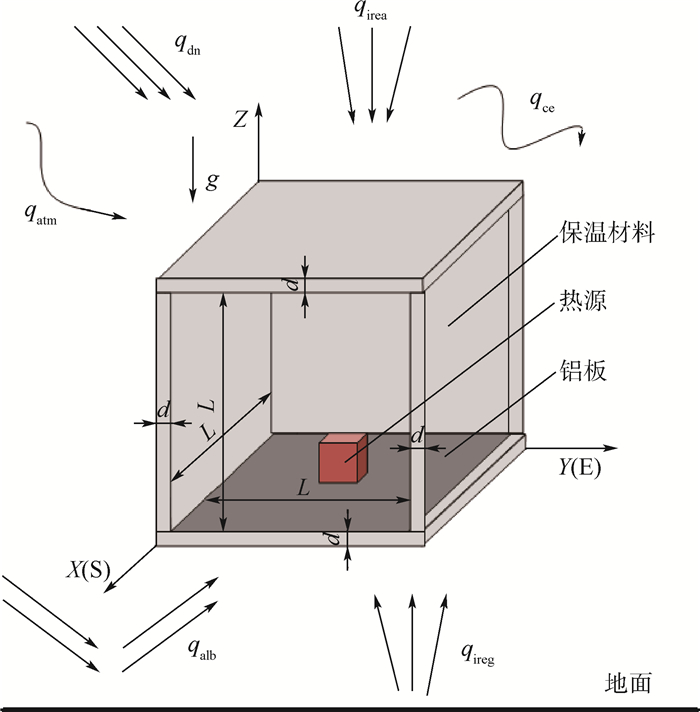 |
| 图 1 封闭方腔热分析模型 Fig. 1 Thermal analysis model of enclosure cavity |
| 图选项 |
在临近空间大气中,方腔外面非均匀的辐射-对流耦合热边界条件可以用热流表示,包括:太阳直射辐射热流qdn,太阳散射辐射热流qatm,地面反照辐射热流qalb,天空长波辐射热流qirea,地面长波辐射热流qireg,以及外部强迫对流换热热流qce。其分析模型如图 1所示,g为重力加速度。
太阳直接辐射、太阳散射辐射和地面反照辐射所得热流分别为[3]
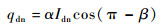 | (1) |
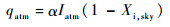 | (2) |
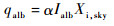 | (3) |
式中:α为壁面材料对可见光的吸收率,取0.1;β为壁面法向与太阳辐射向量夹角,当β∈(π/2, π]时,壁面能接收到太阳直接辐射,β∈[0, π/2]时,则不能;Idn、Iatm和Ialb分别为太阳直接辐射、太阳散射辐射和地面反照辐射强度,采用文献[3]中的公式计算:
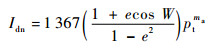 | (4) |
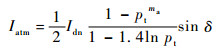 | (5) |
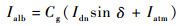 | (6) |
式中:e为地球轨道偏心率;W为真实轨道时间角;pt为大气透过率;ma为大气质量;δ为太阳高度角;Cg为地面平均反射率。各参数具体计算方法可参考文献[11]。
Xi, sky为方腔表面对空的角系数,是该表面与水平面之间夹角θi(规定上表面与水平面的夹角为0)的函数[12]:
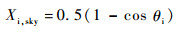 | (7) |
地面和天空的长波辐射热流可用式(8)和式(9)计算[12]:
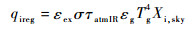 | (8) |
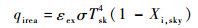 | (9) |
式中:εex为腔外壁面发射率,取0.2;σ为斯蒂芬-玻尔兹曼常数;τatmIR为地面长波辐射大气透过率,见文献[12];εg为地面长波辐射发射率;Tg为地面温度;Tsk为大气辐射等效温度[13]。
同时方腔表面也向环境辐射热量,因此方腔与外部环境的总辐射换热热流为
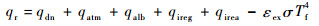 | (10) |
式中:Tf为方腔表面温度。
将外部辐射用等效热沉表示[14],等效热沉温度为
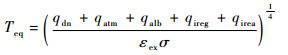 | (11) |
则方腔与外部环境的总辐射换热热流qr可以表示为
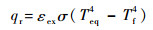 | (12) |
外部强迫对流换热系数hce采用式(13)计算[11]:
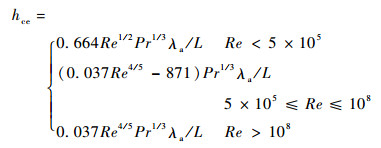 | (13) |
式中:Re为雷诺数;Pr为普朗特数;λa为空气的导热系数。
由于方腔外界热环境变化缓慢,在一定的时间段内,热边界条件变化很小,可将其视为不变,腔内自然对流非常接近稳态状况。为了计算方便,可以用多个不同热边界条件下的稳态过程来模拟腔内一昼夜的自然对流变化[15]。
1.2 封闭方腔数值分析模型 假设腔内空气为辐射透明介质,密度采用Boussinesq近似,其他物性参量为常数。流场区域控制方程的通用形式为
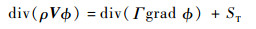 | (14) |
式中:ρ为空气密度;V为速度矢量;?为广义变量;Γ为对应于?的广义扩散系数;ST为广义源项。
腔壁的控制方程为
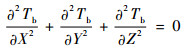 | (15) |
式中:Tb为腔壁温度。
对于由温度场不均匀,产生的自然对流,可由瑞利数判断流动强度。
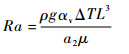 | (16) |
式中:αv为空气体积膨胀系数;μ为动力黏度;a2=λa/(ρCp)为热扩散系数,Cp为定压热容;ΔT采用文献[16]中的组合温度尺度
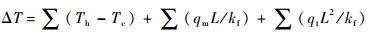 | (17) |
式中:T包含腔壁和腔内空气的温度;Th和Tc分别为热面温度和冷面温度;qm和qt分别为面热源和体热源热生成率;kf为导热系数。
由此估算Ra≥108,所以腔内自然对流为湍流。而且在具体计算时发现采用湍流模型计算所得结果比层流更符合实际情况。因此采用标准k-ε湍流模型进行模拟,近壁面用增强壁面处理。
计算时需要同时考虑方腔外的辐射热环境、对流热环境,以及方腔内部对流、辐射和导热的耦合作用。根据1.1节的处理方法,可以把临近空间热环境的影响通过Fluent混合热边界条件加入到仿真模型中,以减少计算量。辐射边界方面,给定表面发射率,热沉温度通过UDF计算得到;对流边界方面,给定换热系数,环境温度为所处的大气温度。方腔内部空气、热源及腔壁分别设定材料属性;空气与热源及壁面的交界面采用Coupled耦合边界,并给定交界面上的发射率,Fluent可以自动计算得到上面的热流密度和温度分布。腔体底部的铝板采用壳导热模型(shell conduction)进行处理。内部热源以体热源的形式施加。内壁面辐射用离散坐标模型(Do模型)计算。压力-速度耦合项使用SIMPLE算法,压力项的离散格式为Body Force Weighted,动量和能量项都使用二阶迎风格式,并适当减小亚松弛因子。
仿真计算前先进行网格无关性验证。热源、腔壁和腔内空气分别划分网格,腔内空气与固体区域接触的部分进行局部加密,如图 2所示。图 3显示了秋分日0:00时刻不同网格密度下腔内沿直线X=Y=0.28 m的温度变化,可以看出33万网格和42万网格的计算结果非常相近,能满足计算精度的要求,所以可采取33万网格进行计算。
 |
| 图 2 X=0.28 m截面的网格示意图 Fig. 2 Schematic of grid at X=0.28 m section |
| 图选项 |
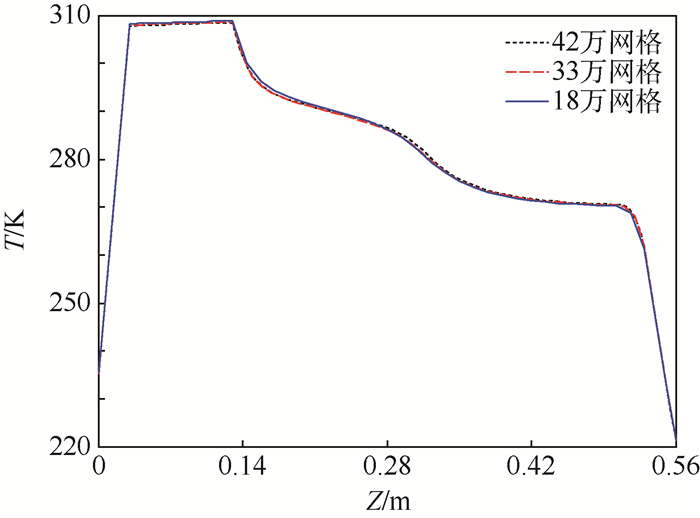 |
| 图 3 不同网格下沿直线X=Y=0.28 m的温度变化曲线 Fig. 3 Variation curves of temperature at X=Y=0.28 m for different grids |
| 图选项 |
2 计算结果分析 2.1 环境昼夜变化的影响 采用上述模型对秋分日北纬40°,东经120°20 km高空方腔内一昼夜热特性变化进行模拟。腔壁采用表面贴铝箔的聚氨酯泡沫板,壁厚d=0.03 m,腔壁导热系数取泡沫板的导热系数k=0.024 W/(m·K),腔内表面发射率取铝箔的发射率ε=0.2,计算时不考虑铝箔的厚度。假设腔内热源为体热源,热生成率为45 000 W/m3,且一直处于工作状态。一昼夜,方腔内空气温度极值和平均值的变化情况如图 4所示,腔内温度和垂直速度的分布情况如图 5所示。
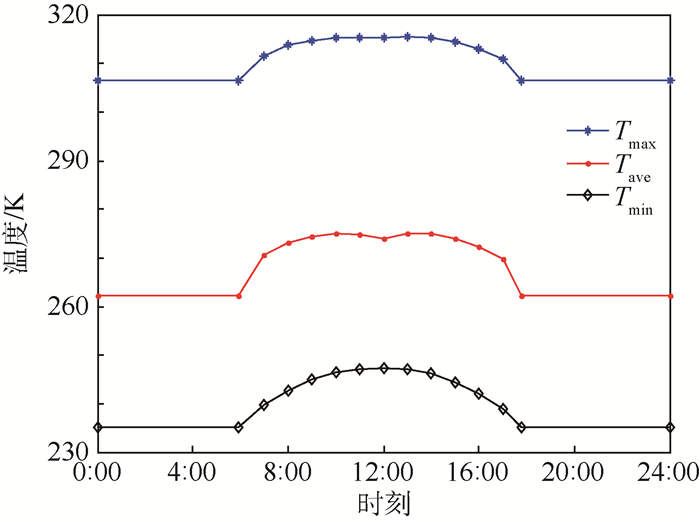 |
| 图 4 腔内温度极值和平均值随时间变化曲线 Fig. 4 Variation of extreme and average temperature in cavity with time |
| 图选项 |
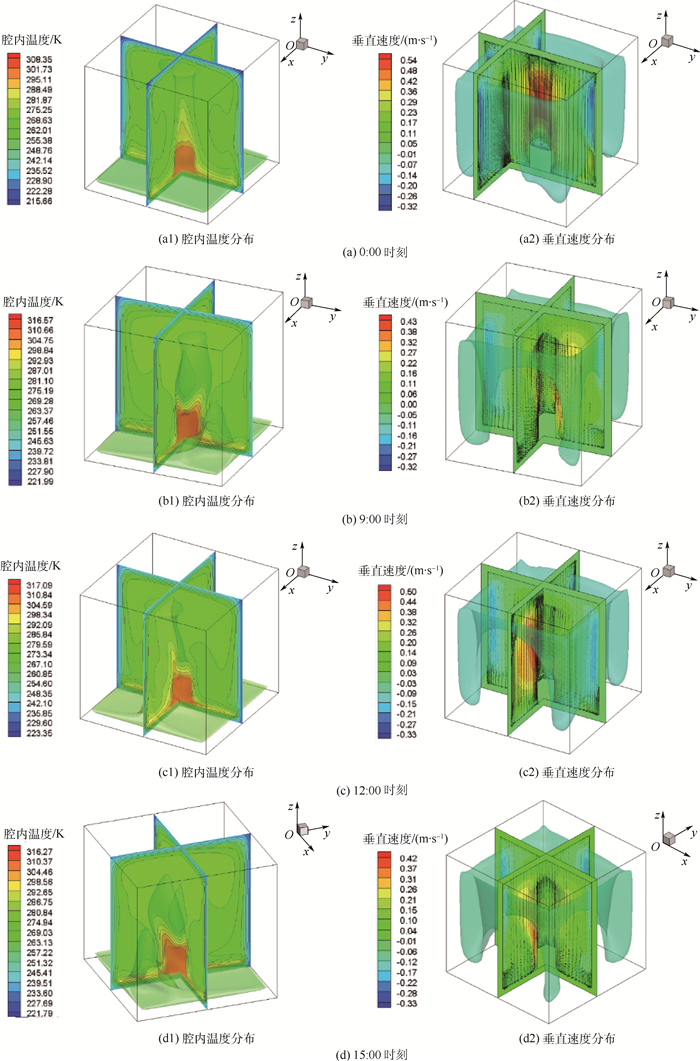 |
| 图 5 不同时刻腔内温度和垂直速度分布云图 Fig. 5 Distribution contours of temperature and vertical velocity in cavity at different time |
| 图选项 |
由图 4可知,腔内空气温度在235~315 K之间变化,其极值和平均值以12:00时刻近似成对称分布。由于腔壁为弱导热系数的保温材料,一天中腔内平均温度昼夜变化很小,约为12.9 K。但腔内自然对流较弱,同一时刻腔内温差很大,夜间温差最大,约为71.3 K,12:00时刻温差最小,约为67.9 K。对于发热量较大、工作温度要求苛刻的设备,需要采取其他措施促进腔内温度分布的均匀。腔内空气温度变化主要受到太阳高度角的影响,夜间温度最低,上午随着太阳高度角增大逐渐升高,下午温度开始下降,日落之后温度迅速下降。按照该方腔的方位假设,虽然12:00时刻太阳辐射最强,但此时方腔能接收到太阳直接辐射的面积要小于10:00时刻的面积,所以一天中腔内空气最高值和平均值的最大值并不是在12:00时刻,而是在10:00时刻左右。
由图 5可知,腔内温度在绝大部分空间中是均匀的,只在靠近热源、底面铝板和壁面处有较大温度梯度。在不同时刻腔内温度分布相差很大,随太阳高度角和方位角而变化。这与文献[9]中假设腔外边界条件为恒温边界时有很大区别。夜间无太阳辐射,腔内温度分布对称;太阳在9:00时刻处于方腔的东南方向,腔内热源上方偏东南区域的温度较高,加上铝板导热的影响,在腔内底部的东南角也有一个高温区;15:00时刻的太阳高度角与9:00时的基本相同,但方位角相反,腔内高温区偏向西南方。太阳在12:00时刻处在方腔的正南方,高温区在热源上方偏南,此时由于太阳辐射强烈,腔内整体温度都较高。
由于方腔各个面接收的辐射不同,再加上热源的影响,腔内的自然对流比较复杂。总的来讲,由于20 km高空空气密度较低,腔内自然对流较弱,在热源上方面向太阳的区域空气流速较大,但最大速度不超过0.55 m/s。从图 5中可以看出0:00和12:00时刻的流动要比9:00和15:00时刻强烈。在夜间,腔内下部温度高而上部温度低,内部形成以热源为中心向上部四周流动的大涡,热源上部的空气流速最大;太阳在12:00时刻辐射强度最高,再加上热源的影响,内部的自然对流形成不止一个涡,热源上方偏南处对流最为强烈。图 6为0:00和12:00时刻Y=0.28 m截面垂直方向的速度矢量图。
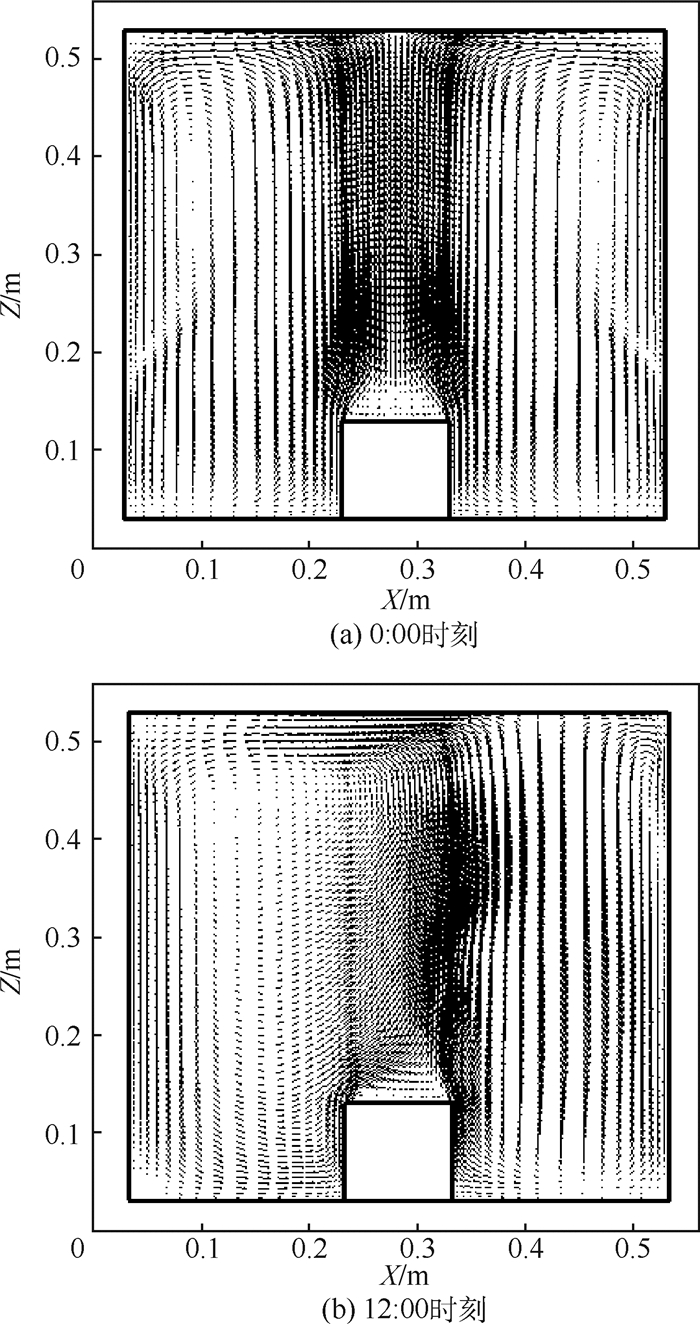 |
| 图 6 0:00和12:00时刻Y=0.28 m截面垂直方向的速度矢量图 Fig. 6 Vertical velocity vector of Y=0.28 m section at 0:00 and 12:00 |
| 图选项 |
定义方腔内表面的局部努赛尔数为
 | (18) |
平均努赛尔数Nuave为
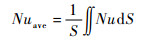 | (19) |
式中:L取腔内空间的高度;Tin为腔内表面温度;Tref为参考温度,取腔内空气平均温度;S为表面面积。
图 7给出了方腔内顶面的平均努赛尔数和空气温差的昼夜变化曲线。从中可以看出,接近12:00时刻,腔内顶面的Nuave最大,内部的自然对流使得空气的混合相对均匀,温差最小。
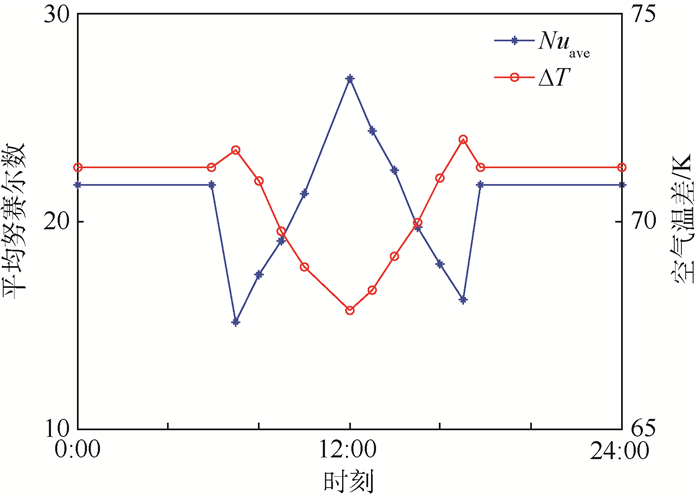 |
| 图 7 腔内顶面平均努赛尔数和空气温差变化曲线 Fig. 7 Variation curves of average Nusselt numbers and air temperature differences at top surface in cavity |
| 图选项 |
2.2 内表面发射率的影响 表 1为0:00时刻方腔内顶面的辐射和自然对流换热量大小。可以看到20 km高空腔内的辐射换热要比对流换热更强,而且随着腔内表面发射率的增加,辐射增强,而对流减弱,但总的换热量增加的。
表 1 0:00时刻腔内顶面辐射和对流换热量 Table 1 Radiation and convective heat transfer at top surface in cavity at 0:00
| 内表面发射率 | 辐射换热量/W | 对流换热量/W | 总换热量/W |
| 0.2 | 2.99 | 1.92 | 4.91 |
| 0.4 | 3.30 | 1.73 | 5.03 |
| 0.6 | 3.43 | 1.65 | 5.08 |
| 0.8 | 3.47 | 1.63 | 5.10 |
表选项
0:00时刻,在不同内表面发射率下,X=0.28 m截面的温度(单位为K)和速度(单位为m/s)等值线如图 8所示,腔内温度极值(Tmax、Tmin)和平均温度(Tave)的变化如图 9所示,沿直线X=Z=0.28 m方向垂直速度Vz的变化如图 10所示。
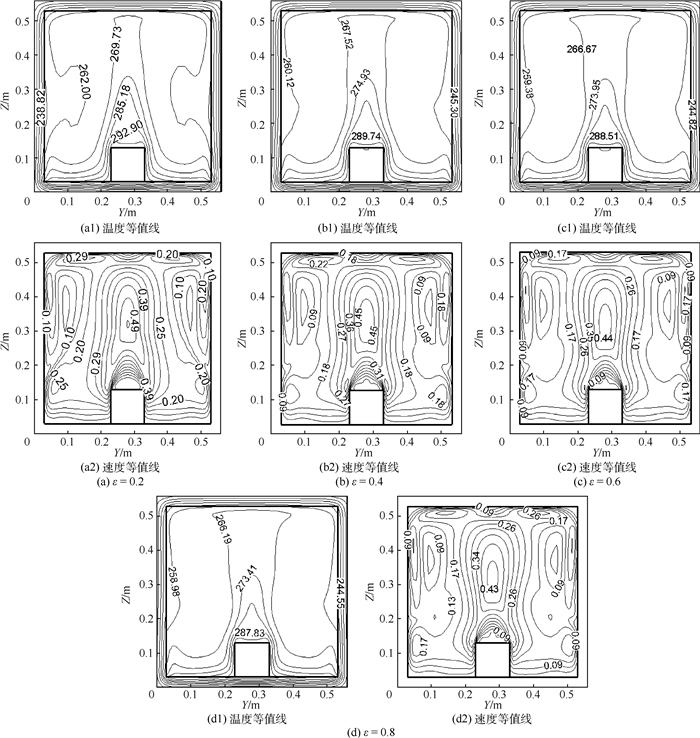 |
| 图 8 0:00时刻不同内表面发射率下X=0.28 m截面的温度和速度等值线 Fig. 8 Temperature and velocity contours at X=0.28 m section for different values of internal surface emissivity at 0:00 |
| 图选项 |
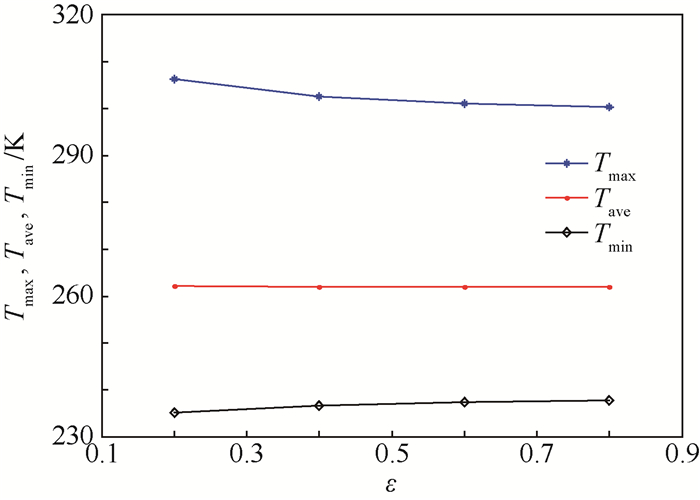 |
| 图 9 0:00时刻腔内温度极值和平均温度随内表面发射率的变化 Fig. 9 Change of extreme temperature and average temperature in cavity with internal surface emissivity at 0:00 |
| 图选项 |
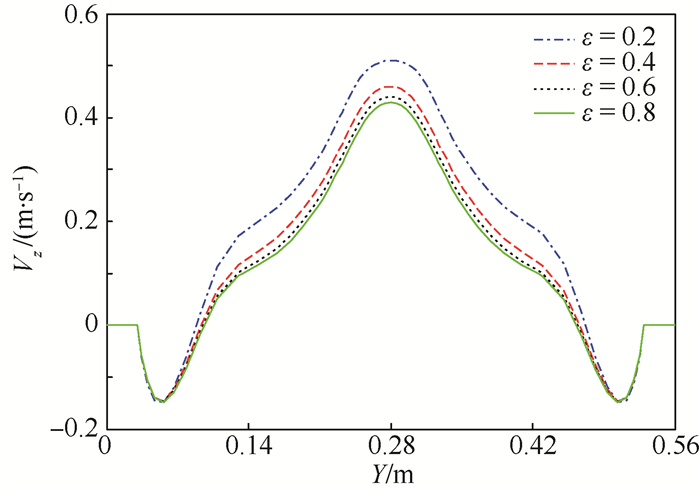 |
| 图 10 0:00时刻不同内表面发射率下直线X=Z=0.28 m方向垂直速度变化曲线 Fig. 10 Variation curve of vertical velocity at X=Z=0.28 m for different values of internal surface emissivity at 0:00 |
| 图选项 |
从图 8中可以看到腔内有3个区域的空气温度较高,分别是热源正上方、铝板上方以及腔内顶部。随着腔内表面发射率的增加,从腔内中心区域到腔壁的传热量增加,腔内顶部高温区面积变大。结合图 9可以看到,随着内表面发射率的增加,腔内温度的最大值减小,最小值增大,但平均温度变化很小,说明腔内温度分布变得更均匀。
图 10中则显示出腔内空气的流速随内表面发射率的增加而减小,因为腔内温差降低使自然对流换热的强度有所减弱,也就是说腔内辐射换热的增强,从一定程度上会抑制自然对流换热过程。此外发射率从0.2增加到0.4,腔内空气最高温度下降了3.79 K,最大速度减小了0.05 m/s,而内表面发射率从0.4增加到0.6,最高温度下降了1.47 K,最大速度减小了0.01 m/s。说明随着内表面发射率的逐渐增加,辐射换热对自然对流的抑制作用有所减弱。
2.3 腔壁导热系数的影响 在封闭方腔体内的自然对流模拟中,有限厚度的保温材料对腔内温度场和流态会产生实质性的影响。由于保温材料的热惰性非常强,在导热过程中会起到“缓冲区”的作用,如一定时间内的能量积累、防止环境影响等。选取4种不同导热系数的保温材料进行模拟,分别为聚氨酯板导热系数0.024 W/(m·K),挤塑聚苯板导热系数0.030 W/(m·K),石墨聚苯板导热系数0.033 W/(m·K),膨胀聚苯板导热系数0.041 W/(m·K)。图 11为0:00时刻不同材料腔内X=0.28 m截面的温度(单位为K)和速度(单位为m/s)等值线图。由图 11可知,随着导热系数的减小,腔内温度明显升高,外界低温环境对腔内的影响降低。图 12为0:00时刻腔内X=Z=0.28 m处温度和垂直速度沿Y轴的分布曲线,从中也可以看到,随着导热系数的减小,腔壁的温度梯度增加,保温效果增强。由于选取的4种保温材料的导热系数相差很小,最大不超过2倍,在图中导热系数对流场的影响表现的不是很明显。
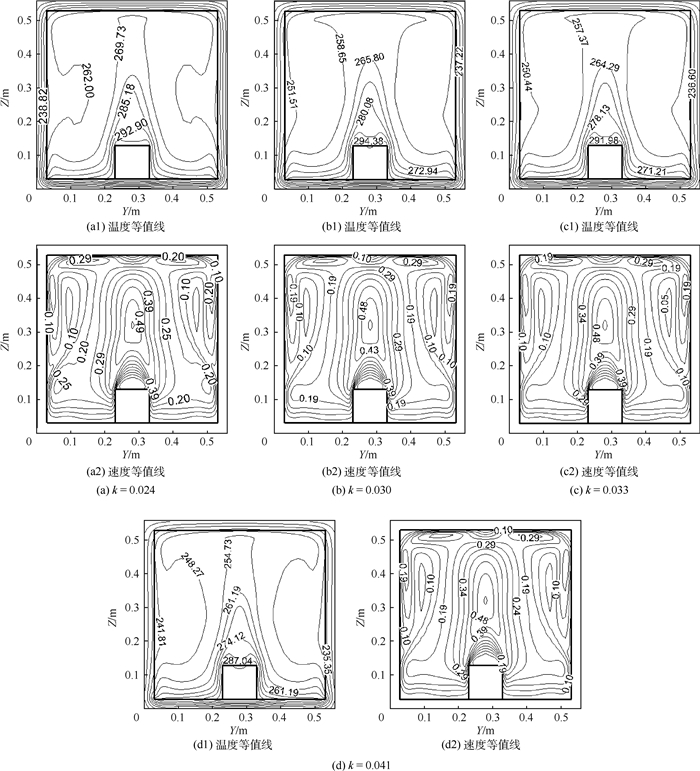 |
| 图 11 0:00时刻不同腔壁导热系数下X=0.28 m截面的温度和速度等值线 Fig. 11 Temperature and velocity contours at X=0.28 m section for different values of thermal conductivity at 0:00 |
| 图选项 |
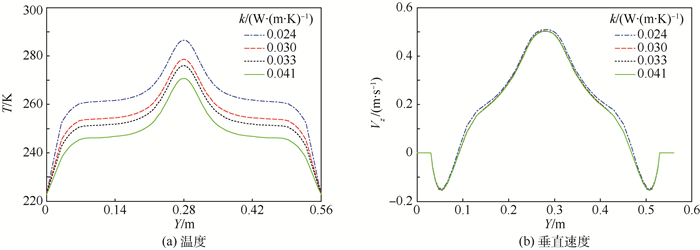 |
| 图 12 0:00时刻不同腔壁导热系数下直线X=Z=0.28 m方向温度和垂直速度的变化曲线 Fig. 12 Profiles of temperature and vertical velocity at X=Z=0.28 m for different values of thermal conductivity at 0:00 |
| 图选项 |
2.4 腔壁厚度的影响 图 13为0:00时刻不同壁厚腔内X=0.28 m截面的温度(单位为K)和速度(单位为m/s)等值线,图 14为0:00时刻腔内温度和垂直速度沿直线X=Z=0.28 m的分布曲线。由图中可以看出腔壁厚度从0.02 m逐渐增加到0.05 m,腔内流场分布变化很小,流动强度则有所减弱,最大流速从0.54 m/s减小到0.52 m/s。因为腔壁厚度增加,热阻增加,导致腔内各表面的温差减小,浮升力减弱,自然对流强度降低。腔内等温线的分布则受腔壁厚度的影响很大。腔壁厚度增加,腔内损失的热量减小,腔内整体温度都升高。腔壁厚从0.02 m增加到0.05 m,腔内平均温度上升了32.36 K。
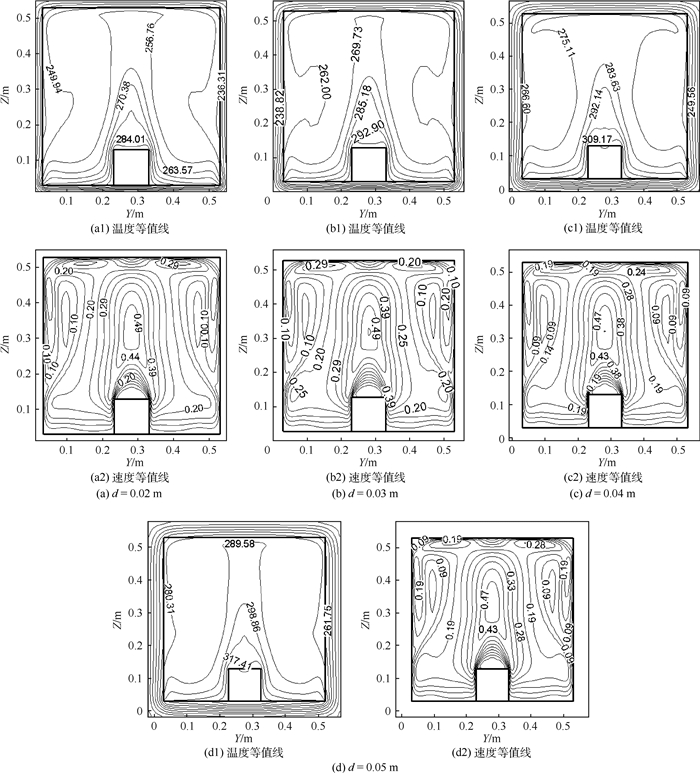 |
| 图 13 0:00时刻不同腔壁厚度下X=0.28 m截面的温度和速度等值线 Fig. 13 Temperature and velocity contours at X=0.28 m section for different values of solid wall thickness at 0:00 |
| 图选项 |
 |
| 图 14 0:00时刻不同腔壁厚度下直线X=Z=0.28 m方向温度和垂直速度的变化曲线 Fig. 14 Variation curve of temperature and vertical velocity at X=Z=0.28 m for different values of solid wall thickness at 0:00 |
| 图选项 |
对于工程应用而言,腔内温度应该维持在一定范围内,以满足电源及电子设备正常工作需求。假设腔内空气的平均温度为262 K时,能满足温度要求。图 15给出了其他条件不变腔内平均温度为262 K时,腔壁厚度和导热系数的关系。由于方腔存在棱与角,导热系数和腔壁厚度不是严格的正比关系。这与一维平板导热有所区别,但是热阻随导热系数的增加而减小,随厚度的增加而增加这个关系不变。当腔壁导热系数增加时,要维持腔内平均温度不变,相应的就需要增加腔壁的厚度。在设计过程中应综合考虑腔壁材料的各项属性,在满足温度要求的同时,尽量减小系统质量。
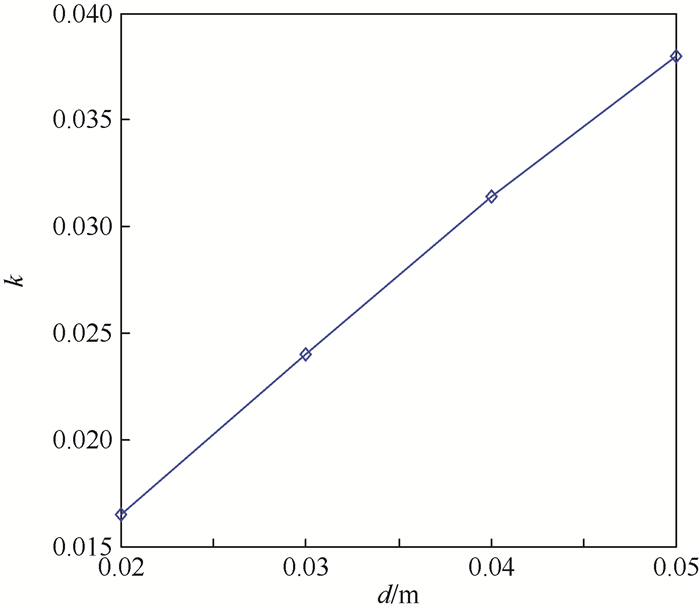 |
| 图 15 腔内平均温度为262 K时,导热系数和腔壁厚度的关系 Fig. 15 Thermal conductivity versus solid wall thickness when average temperature in cavity is 262 K |
| 图选项 |
3 结论 1) 临近空间环境中,封闭方腔外的非均匀对流-辐射耦合热边界条件及其昼夜变化对腔内热特性的影响主要体现在腔内温度分布和空气流动状态上。腔内温度分布随太阳高度角和方位角变化而变化,温度较高的区域空气流速较快。弱导热系数的保温材料能有效降低外界环境的影响,使腔内平均温度昼夜变化很小,约为12.9 K,满足大部分设备的工作要求。
2) 临近空间环境中,方腔内空气流速很低,最大不超过0.55 m/s,换热能力较弱。同一时刻,腔内大部分区域温差不大,但在靠近热源的附近存在较大温度梯度。夜间温差最大,约为71.3 K,12:00时刻温差最小,约为67.9 K。如果方腔内设备发热量较大、工作温度要求苛刻,需要采取其他措施增加其向空气的散热,促进腔内温度分布均匀。
3) 腔内表面辐射效应增强,会削弱自然对流换热的强度,但总换热量增加。方腔内表面发射率增加,对腔内平均温度影响较小,但能促进腔内温度分布的均匀。
4) 腔壁热阻增加(导热系数减小或厚度增加)会削弱腔内自然对流的强度,同时降低外界环境对腔内温度的影响。
为了更加准确地反映方腔内的热特性,需要进一步研究多体系统的耦合换热及瞬态效应,并进行试验验证。
参考文献
| [1] | 夏新林, 李德富, 杨小川. 平流层浮空器的热特性与研究现状[J].航空学报, 2009, 30(4): 577–583. XIA X L, LI D F, YANG X C. Thermal characteristics of stratospheric aerostats and their research[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(4): 577–583.(in Chinese) |
| [2] | FARLEY R E. Balloonascent: 3-D simulation tool for the ascent and float of high-altitude balloons: AIAA-2005-7412[R]. Reston: AIAA, 2005. |
| [3] | DAI Q M, FANG X D, LI X J, et al. Performance simulation of high altitude scientific balloons[J].Advances in Space Research, 2012, 49(6): 1045–1052.DOI:10.1016/j.asr.2011.12.026 |
| [4] | CHOI S K, KIM S O. Turbulence modeling of natural convection in enclosures:A review[J].Journal of Mechanical Science and Technology, 2012, 26(1): 283–297.DOI:10.1007/s12206-011-1037-0 |
| [5] | XAMáN J, ARCE J, áLVAREZ G, et al. Laminar and turbulent natural convection combined with surface thermal radiation in a square cavity with a glass wall[J].International Journal of Thermal Sciences, 2008, 47(12): 1630–1638.DOI:10.1016/j.ijthermalsci.2008.01.012 |
| [6] | KUZNETSOV G V, SHEREMET M A. Numerical simulation of turbulent natural convection in a rectangular enclosure having finite thickness walls[J].International Journal of Heat & Mass Transfer, 2010, 53(1): 163–177. |
| [7] | MARTYUSHEY S G, SHEREMET M A. Conjugate natural convection combined with surface thermal radiation in an air filled cavity with internal heat source[J].International Journal of Thermal Sciences, 2014, 76(2): 51–67. |
| [8] | MARTYUSHEY S G, SHEREMET M A. Conjugate natural convection combined with surface thermal radiation in a three-dimensional enclosure with a heat source[J].International Journal of Heat & Mass Transfer, 2014, 73(9): 340–353. |
| [9] | 许玉, 方贤德, 李小建, 等. 浮空器载荷舱热特性研究[J].科学技术与工程, 2011, 11(30): 7577–7579. XU Y, FANG X D, LI X J, et al. A study of thermal characteristics of aerostats' load cabins[J].Science Technology and Engineering, 2011, 11(30): 7577–7579.DOI:10.3969/j.issn.1671-1815.2011.30.057(in Chinese) |
| [10] | 邓丽君. 一种临近空间浮空器热控系统的研究[D]. 南京: 南京理工大学, 2009. DENG L J. Study on thermal control system of a near space vehiel[D]. Nanjing: Nanjing University of Science and Technology, 2009(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10288-2009197067.htm |
| [11] | 李小建. 临近空间浮空器热-结构耦合数值模拟研究[D]. 南京: 南京航空航天大学, 2013. LI X J. Numerical simulation of thermal-structure coupling for near space airship[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10287-1014060019.htm |
| [12] | 张贺磊, 方贤德, 戴秋敏. 临近空间飞艇内部自然对流换热计算研究[J].宇航学报, 2016, 37(7): 879–886. ZHANG H L, FANG X D, DAI Q M. Investigation on internal natural convection of stratospheric airship[J].Journal of Astronautics, 2016, 37(7): 879–886.(in Chinese) |
| [13] | 刘强, 武哲, 祝明, 等. 平流层气球热动力学仿真[J].北京航空航天大学学报, 2013, 39(12): 1578–1583. LIU Q, WU Z, ZHU M, et al. Thermal-dynamic simulation of stratospheric balloon[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12): 1578–1583.(in Chinese) |
| [14] | 徐向华, 程雪涛, 梁新刚. 平流层浮空器的热数值分析[J].清华大学学报(自然科学版), 2009, 49(11): 1848–1851. XU X H, CHENG X T, LIANG X G. Thermal analysis of a stratospheric airship[J].Journal of Tsinghua University(Science and Technology), 2009, 49(11): 1848–1851.DOI:10.3321/j.issn:1000-0054.2009.11.027(in Chinese) |
| [15] | 夏新林, 李德富, 杨小川. 复合热条件下椭球形封闭腔内低压气体的自然对流[J].航空学报, 2010, 31(3): 453–458. XIA X L, LI D F, YANG X C. Natural convection of low pressure gas in ellipsoidal enclosure induced by combined thermal conditions[J].Acta Aeronautica et Astronautica Sinica, 2010, 31(3): 453–458.(in Chinese) |
| [16] | 邓启红. 室内空气对流的特征与模拟[D]. 长沙: 湖南大学, 2003. DENG Q H. Modeling and characteristics of indoor air convection[D]. Changsha: Hunan University, 2003(in Chinese). |
