粒子滤波(Particle Filter, PF)是基于蒙特卡罗采样思想来实现状态的近似估计,理论上可以适用于任何非线性非高斯系统,因此在故障诊断领域获得了广泛的研究和应用[3-4]。但是目前存在的PF算法及其改进算法,在应用中假设噪声统计特性均为已知的高斯分布[5-6]。事实上,噪声统计特性在实际应用中很可能是未知的,且可能随系统本身或者量测环境的变化而变化,现有的PF算法难以满足诊断系统精度的要求。代价评估粒子滤波(Cost Reference Particle Filter, CRPF)不需要已知系统噪声的统计特性,便可实现状态估计[7],因此在一定程度上解决了复杂噪声背景下的状态估计问题,该方法在故障诊断和目标跟踪等领域得到了良好的应用。胡振涛和潘泉等[8]提出了一种基于CRPF的残差似然比检验故障诊断算法,克服了外界随机扰动对于滤波精度的不利影响。卢锦等[9]针对天波雷达背景噪声强度大和统计特性未知等特点,采用CRPF估计天波超视距雷达目标状态。Lim[10]采用CRPF实现未知噪声统计特性的非线性系统动态状态估计。Yu[11]提出了一种H∞和CRPF结合的滤波算法,提高了未知非高斯噪声的非线性动力学系统的状态估计精度。
CRPF是以粒子的代价或风险为参考来实现重采样及状态估计,代价和风险的计算不需要已知噪声统计特性[9],因此,在解决非线性、噪声统计特性未知问题中得到了良好应用。但在实际应用中仍然存在不足,CRPF以当前时刻的状态预测值为均值,在一定的高斯分布范围内随机选取粒子完成状态更新[10, 12],但随着时间的不断推移,状态转移密度协方差逐渐趋于恒定值,对强噪声扰动或时变噪声的修正能力将减弱甚至消失,大大降低了算法对噪声环境的适应能力,将导致较大的误诊和漏诊。对复杂噪声环境下的故障诊断方法的研究是现代复杂系统故障诊断与故障预测研究中必须解决的基础科学问题,因此,本文研究对提高诊断系统的精确性,进一步提高现代复杂设备故障诊断的可靠性具有重要意义。
本文根据噪声的变化情况自适应调整状态转移密度方差,确定状态更新的合理区域,增强算法对时变噪声的适应能力;同时,利用统计方法设计残差判别函数的自适应阈值,提高故障检测的准确性。在此基础上,对强噪声背景下的非线性非高斯系统进行了故障诊断仿真分析。
1 非线性系统状态空间模型 考虑非线性非高斯随机状态空间模型如下:
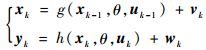 | (1) |
式中:k为采样时刻;xk为k时刻系统状态向量;uk为k时刻系统输入;θ为系统参数变量;yk为k时刻系统状态的量测向量;g(·)和h(·)分别为系统状态转移函数和量测函数,它们都可以是非线性函数;vk和wk分别为系统状态噪声和量测噪声,其统计特性未知。
假设系统可能存在S种故障模式,则共有S+1个系统模型,其中1个模型为无故障模式。采用多模型方法表示的非线性系统状态空间模型如下:
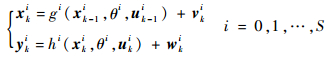 | (2) |
系统量测的预测输出为
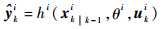 | (3) |
式中:xk|k-1i为系统状态的一步预测值;?ki为系统量测的预测输出值。
系统残差可表示为
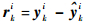 | (4) |
残差是系统实际输出和依据模型预测输出的差值,反映了实际系统和数学模型之间的不一致程度,主要由系统噪声和故障确定,当系统无故障时,残差的变化反映了系统中的噪声和干扰因素对系统输出的影响。当系统处于强噪声干扰环境,噪声会引起残差较明显的变化,可能引起故障误报或漏报。可见,获得准确的残差是提高故障诊断准确性的关键。因此,利用CRPF对未知噪声系统的状态估计优势,克服强噪声的影响而得到准确的系统状态的估计值,当估计值越接近真实值,则会减小噪声对残差信号的影响,提高故障诊断的准确性。
2 代价评估粒子滤波 在CRPF算法中用代价函数和风险函数表示粒子性能质量,同时引入遗忘因子,并基于代价最小化原则给出一种噪声统计特性未知情况下的粒子权重评价方法。
代价函数定义为
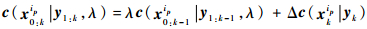 | (5) |
将式(5)简写为:ckip=λck-1ip+Δckip。式中:ip为粒子索引;λ(0≤λ≤1)为遗忘因子;Δckip=‖yk-h(xkip)‖q(q≥1)为代价增量。
风险函数定义为
 | (6) |
概率质量函数(PMF)也称类权值,计算如下:
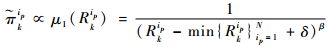 | (7) |
式中:δ, β>0,δ是为了保证分母不为0;N为粒子数。
按照以上参数定义,CRPF算法通过风险估计、选择、粒子传递和代价更新步骤,递推计算获得状态估计。算法步骤如下:
步骤1????在k=0时刻,从先验分布中获取N个样本,x0ip~P0(x0),设定初始时刻粒子的代价c0ip和状态转移密度方差σ02, ip,则k=0时刻样本和代价集合为{x0ip, c0ip}Nip=1,ip=1, 2, …, N。
步骤2????递归更新。
1) 分别按照式(6)和式(7)计算风险函数Rkip和概率质量函数
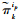
2) 重采样。根据
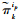
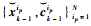
3) 粒子更新。
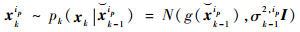 | (8) |
式中:I为维数与x相同的单位矩阵。
状态转移密度的方差为
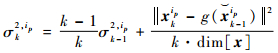 | (9) |
式中:dim[x]表示取x的维数。
可见,在CRPF算法中,σk2, ip是在线调整的。
4) 按照式(5)计算代价函数ckip,按式(10)计算πkip,并归一化πkip。
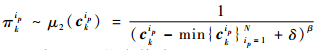 | (10) |
步骤3????状态估计。
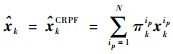 |
从以上算法步骤可见,在CRPF算法的递推估计中不涉及对过程噪声与量测噪声的计算,因此,在计算中不需要已知噪声统计特性,改善了PF中由于外界随机干扰对依据量测似然度评价的不利影响。从式(8)和式(9)的粒子更新过程可知,粒子的时间更新是在确定的概率区域中随机选取新粒子,此区域的方差σk2, ip是根据当前时刻的状态估计值与前一时刻的方差递推更新,当k→∞时,
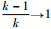
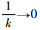
3 自适应CRPF故障诊断方法 3.1 状态转移密度的方差自适应更新 由对CRPF的递推估计过程的分析可知,状态转移密度方差直接影响着状态预测的准确性,但在CRPF算法中,方差的递归更新随着时间的推移最终趋于恒定值,对于时变噪声出现随机波动的情况下,在确定的小范围中很有可能无法获得准确的状态预测。因此,本文考虑当前观测值与先验状态之间的互相关系数的大小,自适应调整状态转移密度方差,增强算法对时变噪声的适应能力。
测量值和先验状态之间的相关系数表示为
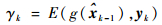 | (11) |
状态转移密度的方差按照式(12)进行修正:
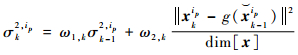 | (12) |
式中:ω1, k和ω2, k为方差的自适应调节系数,ω1, k=γk,ω2, k=1-γk。相关系数大,说明状态噪声小,则ω1, k>ω2, k,方差主要由前一时刻的方差σk-12, ip决定,这样可适当增强粒子的扰动;相关系数小,说明噪声扰动较大,这时ω1, k < ω2, k,方差主要由
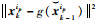
3.2 自适应阈值设计 残差是判断是否发生故障的主要依据,若k时刻的残差rk>rth,rth为所设定的阈值,则说明系统发生了故障。最简单的阈值选择方法是将阈值设定为一个固定的常数,但是实际系统不可避免地存在建模误差、复杂噪声及干扰等不确定性因素,在这种情况下若仍采用传统的固定阈值来判定故障是否发生,很容易出现故障的误报和漏报。因此,依据系统不确定性的变化,采用自适应阈值可以避免上述情况的发生。文献[13-14]将统计学中参数置信区间的思想应用于自适应阈值的设计,假设残差的统计特性符合正态分布,残差的均值和方差求取方法分别为
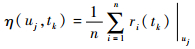 | (13) |
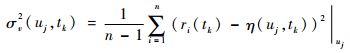 | (14) |
式中:η(uj, tk)为输入为uj时tk时刻残差的均值;σv2(uj, tk)为输入为uj时tk时刻残差的方差;n为系统重复运行并测量系统残差的次数。
置信度为1-α的残差的置信区间表示为
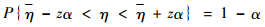 | (15) |
式中:α为置信水平,通常设定置信度为95%~98%。若设α=0.03,则置信度为97%,z=2.17,由式(16)求得自适应阈值为
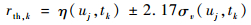 | (16) |
但采用这种方法计算自适应阈值,为了得到当前时刻残差的均值和方差,在算法迭代的每一步都需要系统重复运行n次,这样计算量近似成指数增长,很难满足实际系统的实时性要求。本文受Hashemi和Pisu[15]的启发,引入滑动窗通过求区间均值来解决上述问题。将残差的标准差表示为
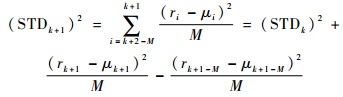 | (17) |
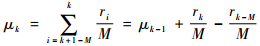 | (18) |
式中:μk为残差的均值;M为滑动窗宽度。
由式(17)和式(18)可见,在每一个采样周期,只需要在前一时刻的基础上通过当前时刻的残差对均值与方差进行更新,无需重复多次运行系统,大大减少运行时间。同时,对于随机噪声来说,在一定的时间内对某一个采样值重复执行多次,与对不同时间点的多个采样值重复执行多次,在该时间范围内噪声的分布趋于一致,因此,令σv2(uj, tk)=(STDk)2,η(uj, tk)=μk,采用式(17)和式(18)分别计算残差的方差与均值,再由式(16)求得每一时刻的残差自适应阈值。
3.3 算法步骤 步骤1????初始化x0ip~P0(x0)、c0ip和σ02, ip,生成初始样本代价集合{x0ip, c0ip}Nip=1。
步骤2????递归更新:k=1, 2, …, K(总时间步数)。
1) for ip=1, 2, …, N,计算Rkip和
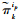
2) 重采样。根据
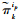
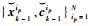
3) 根据式(8)更新状态,由式(11)计算互相关系数,然后根据式(12)修正状态转移密度协方差。
4) 计算代价函数:
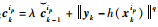
步骤3????估计状态
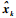
步骤4????故障检测和隔离。将获得的状态估计
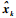
4 实例分析与讨论 采用一个160 MW燃油机组的动态模型[16]为对象,以燃油调节阀开度、汽轮机调节阀开度和给水调节阀开度为输入,选取汽包压力、汽包液体密度为状态变量,汽包水位作为观测变量,分别在伽马噪声和高斯混合噪声影响下对汽包水位传感器的3种故障进行实例分析,验证本文方法的性能。该燃油机组模型的离散方程为
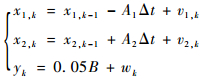 |
式中:
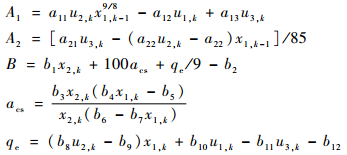 |
其中:x1为汽包压力;x2为汽包液体密度;u1为燃油调节阀开度;u2为汽轮机调节阀开度;u3为给水调节阀开度;y为汽包水位;vk为状态噪声;wk为量测噪声,它们都是统计特性未知的非高斯噪声。
针对汽包水位传感器故障进行实验,假设传感器有3种故障模态:
故障模态1????恒偏差故障,yk=0.05B+0.5+wk。
故障模态2????恒增益故障,yk=0.08B+wk。
故障模态3????卡死故障,yk=wk。
设置初始状态x0=[108??428]T,离散步长Δt=0.1 s,粒子数N=500,传感器采样频率为1 Hz,其他参数:a11=0.001 8,a12=0.9,a13=0.15,a21=141,a22=1.1,a23=0.19,b1=0.131,b2=0.068,b3=0.001 54,b4=0.8,b5=25.6,b6=1.039 4,b7=0.001 23,b8=0.854,b9=0.147,b10=45.59,b11=2.514,b12=2.096,ut=[0.3??0.4??0.5]。状态初始先验分布x0ip~N(x0, Σ0), Σ0=diag(0.01, 0.01),c0ip=0,σ02, ip=[0.01??0.01]T,滑动窗宽度M=20。
本文方法的评价指标选择平均绝对误差、故障误报率和漏报率,评价指标定义如下:
平均绝对误差MAE为
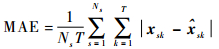 |
式中:xsk和
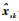
故障漏报率pm和误报率pf为
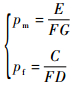 |
式中:F为系统总共的运行次数;E为发生故障时残差小于阈值的采样点总数;G为系统一次运行的总采样点数;C为系统无故障发生且残差值大于阈值的采样点总数;D为系统无故障时的采样点总数。
4.1 实验1 本文所设定的偏差故障为0.5的小偏差,增益故障的增益系数变化仅为0.03,噪声对这种小故障的检测和诊断结果影响更为严重,采用伽马噪声和高斯混合噪声来模拟工程实际中的复杂噪声,采用CRPF算法和自适应代价评估粒子滤波(ACRPF)算法对汽包压力x1和汽包液体密度x2进行估计,验证本文方法在强噪声环境下的状态估计精度。
采样周期为0.1 s,步长为3 000,总仿真时长为300 s,粒子数为500。设定0≤t≤100 s时,系统处于正常模态;100 s < t≤200 s时,系统处于故障模态1;200 s < t≤300 s时,系统处于故障模态2。
实验中所采用的噪声如下:
伽马噪声:
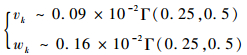 |
高斯混合噪声:
 |
图 1和图 2分别为伽马噪声和高斯混合噪声背景下,CRPF算法和改进的ACRPF算法对汽包压力x1和汽包液体密度x2的估计误差,0~100 s系统处于正常工作状态,2种算法的估计误差都比较小。可见,由于ACRPF算法能够根据状态估计误差自适应调整状态转移密度方差,增强了对强噪声扰动的自适应修正能力,因此,对x1和x2的估计精度均高于改进前的CRPF算法。尤其对于x2,在100 s系统出现故障,采用原有CRPF算法估计误差急剧增加,而本文改进算法的估计精度得到了大幅提高。表 1为图 1和图 2中x1和x2的平均绝对误差,数据同样说明了本文算法的状态估计准确性均得到了明显提高。
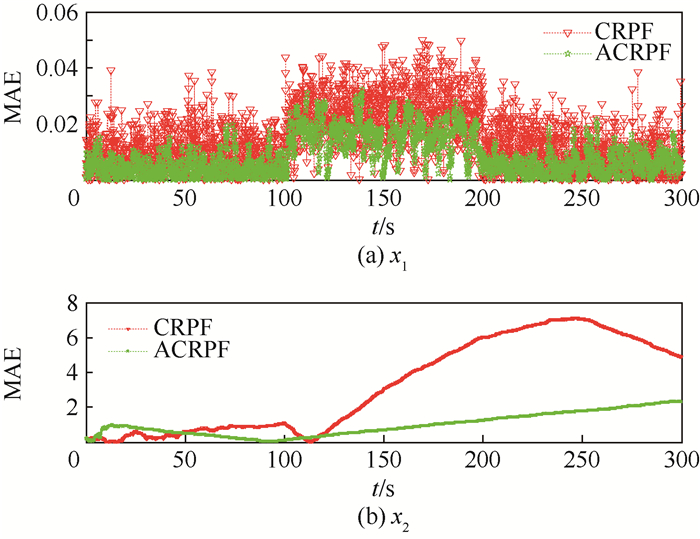 |
| 图 1 伽马噪声背景下2种算法对x1和x2的跟踪误差对比 Fig. 1 Tracking error comparison of x1 and x2 between two algorithms under condition of Gamma noise |
| 图选项 |
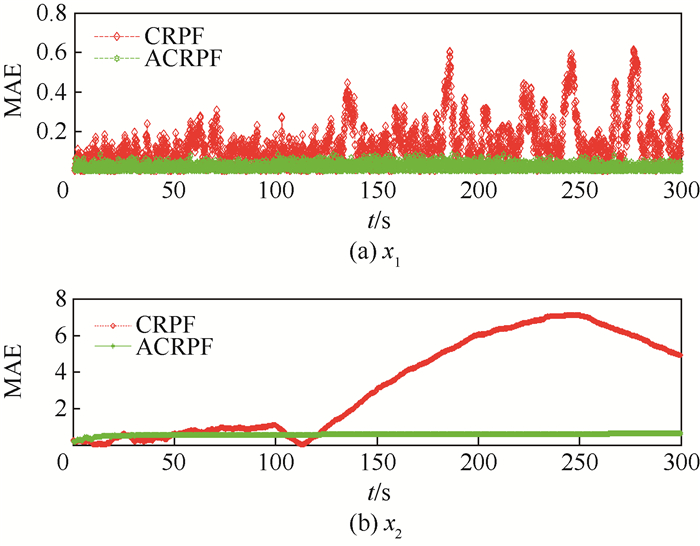 |
| 图 2 高斯混合噪声背景下2种算法对x1和x2的跟踪误差对比 Fig. 2 Tracking error comparison of x1 and x2 between two algorithms under condition of Gaussian mixture noise |
| 图选项 |
表 1 不同噪声背景下x1、x2的平均绝对误差 Table 1 Mean absolute errors of x1 and x2 under different noise conditions
| 状态 | 伽马噪声 | 高斯混合噪声 | |||
| 改进前 | 改进后 | 改进前 | 改进后 | ||
| x1 | 0.011 1 | 0.008 2 | 0.195 2 | 0.009 5 | |
| x2 | 3.575 0 | 1.707 1 | 4.365 9 | 0.886 0 | |
表选项
4.2 实验2 分别在伽马噪声和高斯混合噪声影响下对上述系统进行故障诊断,对本文ACRPF故障诊断方法的性能进行验证。设残差r0=|y-?正常|,若r0>rth,说明有故障发生;然后分别计算r1=|y-?故障1|,r2=|y-?故障2|,r3=|y-?故障3|,若ri→0(i=1, 2, 3),则说明发生了模态为i的故障。系统工作过程中的故障状态设定和噪声形式同实验1。
图 3为文献[13-14]的自适应阈值与本文自适应阈值分别在伽马噪声和高斯混合噪声下的对比。对比2种自适应阈值曲线,其变化趋势和范围均非常接近;表 2中,第2列和第3列、第4列和第5列相应的漏报率非常接近。可见,2种自适应阈值的漏报率基本相同,而误报率取近似值均为0。因此,采用本文改进的自适应阈值完全可等价文献[13-14]中的阈值,而本文自适应阈值的时间计算复杂度要比文献[13-14]小一个数量级,大大节约了计算时间。
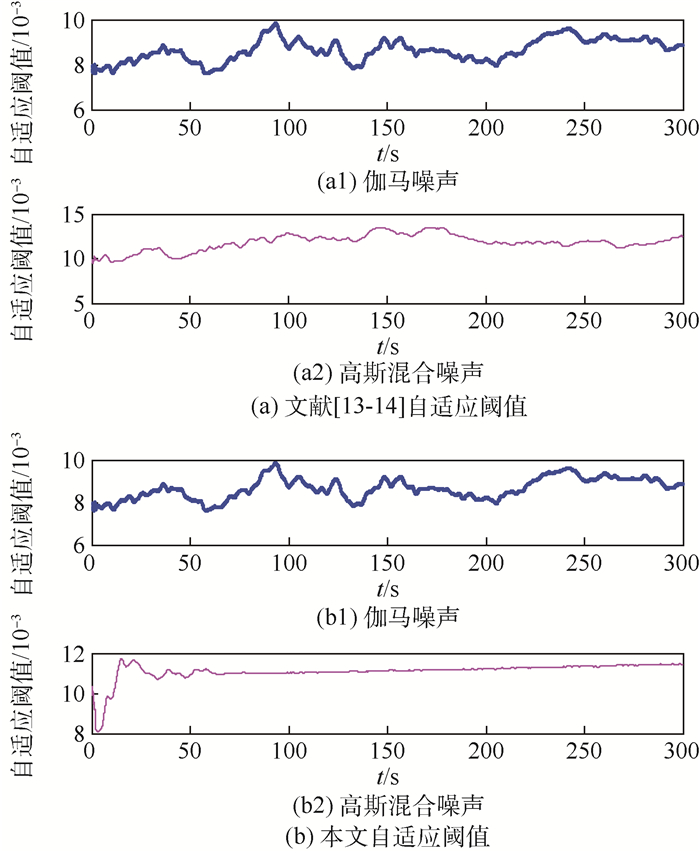 |
| 图 3 自适应阈值对比 Fig. 3 Comparison of adaptive thresholds |
| 图选项 |
表 2 故障漏报率和时间计算复杂度比较 Table 2 Comparison of missed diagnosis rates and time computation complexity
| 参数 | CRPF故障诊断方法 | ACRPF故障诊断方法 | |||
| 文献[13-14] | 本文 | 文献[13-14] | 本文 | ||
| 伽马噪声下漏报率 | 0.004 7 | 0.004 5 | 0.003 8 | 0.003 7 | |
| 高斯混合噪声下漏报率 | 0.006 3 | 0.006 1 | 0.004 5 | 0.004 6 | |
| 时间计算复杂度 | O(n3) | O(n2) | O(n3) | O(n2) | |
表选项
图 4和图 5分别为伽马噪声和高斯混合噪声背景下对160 MW燃油机组的2种故障进行检测和隔离的结果。由残差r0可判断,系统在100s以前处于正常工作状态,100 s以后均处于故障状态;为了充分说明故障检测的有效性,在图 4和图 5中0~100 s时间段内,选择残差和自适应阈值的极小值点分别标注了残差r0的坐标值以及对应的自适应阈值的坐标值。图 4中,在时刻17.3 s对应的残差r0的值为0.002 63,自适应阈值为0.008 872;在时刻98.1 s对应的r0为0.002 21,自适应阈值为0.01。图 5中,在时刻3.4 s对应的r0为0.002 876,自适应阈值为0.006 455。可见,r0的值均小于对应时刻的自适应阈值,在图 5中的25 s和84.3 s满足同样的结论,说明系统处于正常工作状态。在时间段100~200 s,比较r1~r3可见,r1更接近于0,说明系统发生了模态1故障,即恒偏差故障。为了更清楚比较残差大小,在图 4的199.3 s和图 5的180、199.6 s处分别标注了图中最接近的残差r1和r2的值,均满足r1 < r2;在时间段200~300 s,r2最接近0,说明系统发生了模态2故障,即恒增益故障。虽然在图 4的250.1 s和图 5的251.5 s处r0的值较小,但依然大于自适应阈值。可见,ACRPF故障诊断方法在不同噪声下均可实现故障的准确检测和隔离。
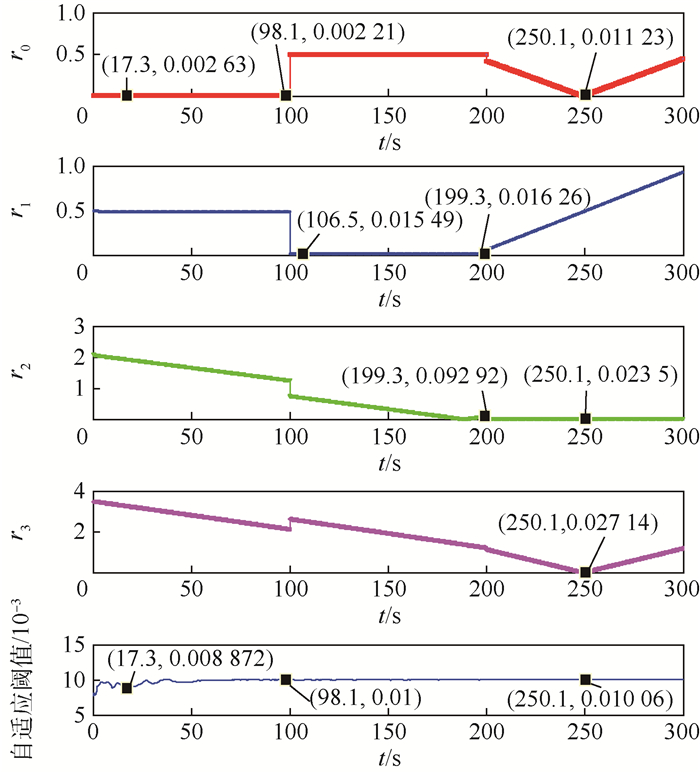 |
| 图 4 伽马噪声背景下故障检测及隔离 Fig. 4 Fault detection and isolation under condition of Gammanoise |
| 图选项 |
 |
| 图 5 高斯混合噪声背景下故障检测及隔离 Fig. 5 Fault detection and isolation under condition of Gaussian mixture noise |
| 图选项 |
表 2对比了CRPF故障诊断方法和ACRPF故障诊断方法的漏报率,实验中系统运行50次,每次运行的采样点数为3 000,通过对所有采样点在50次运行中出现漏报的采样点数进行统计,并利用漏报率公式计算得到漏报率。总体来看,ACRPF故障诊断方法在不同噪声下的漏报率均小于CRPF故障诊断方法的漏报率,分别对比表 2的前2列和后2列的数据,可见本文的改进自适应阈值和文献[13-14]所得到的故障漏报率基本相同,但本文改进自适应阈值的时间计算复杂度低。结果表明,ACRPF故障诊断方法在强噪声背景下,可提高故障诊断准确性,减少系统的运行时间。
5 结论 1) CRPF算法可在未知噪声统计特性的条件下实现对非线性非高斯系统状态的递推估计,为复杂非线性系统的故障诊断提供了一种可借鉴的方法。
2) 本文通过分析CRPF算法对强噪声干扰下状态估计的性能,设计相关性判别函数实现对CRPF的状态转移密度方差的自适应调整,克服了CRPF随着时间的递推,对强噪声及时变噪声的修正能力逐渐消失而导致的误差变大甚至发散的问题。
3) 引入滑动窗利用求区间均值的方法对残差的自适应阈值进行了改进,解决了在计算残差均值和方差时系统重复运行而导致的耗时问题。
4) 应用本文方法,在不同的强噪声背景下对非线性非高斯系统进行了故障检测和隔离,对漏报率和误报率进行了分析,提高了故障诊断准确性并可减少运行时间,具有重要的理论意义和工程应用价值。
参考文献
| [1] | JIN X H, QIAO W, PENG Y Y, et al. Quantitative evaluation of wind turbine faults under variable operational conditions[J].IEEE Transactions on Industry Applications, 2016, 52(3): 2061–2069.DOI:10.1109/TIA.2016.2519412 |
| [2] | PARK J, HA J M, OH H, et al. Model-based fault diagnosis of a planetary gear:A novel approach using transmission error[J].IEEE Transactions on Reliability, 2016, 65(4): 1830–1841.DOI:10.1109/TR.2016.2590997 |
| [3] | SUN Y S, RAN X R, LI Y M, et al. Thruster fault diagnosis method based on Gaussian particle filter for autonomous underwater vehicles[J].International Journal of Naval Architecture and Ocean Engineering, 2016, 8(3): 243–251.DOI:10.1016/j.ijnaoe.2016.03.003 |
| [4] | 万磊, 杨勇, 李岳明. 水下机器人执行器的高斯粒子滤波故障诊断方法[J].上海交通大学学报, 2013, 47(7): 1072–1076. WAN L, YANG Y, LI Y M. Actuator fault diagnosis of automa-tic under water vehicle using Gaussian particle filter[J].Journal of Shanghai Jiaotong University, 2013, 47(7): 1072–1076.(in Chinese) |
| [5] | 曹洁, 李伟, 李军, 等. 强噪声背景下鲁棒的说话人跟踪方法[J].华中科技大学学报(自然科学版), 2015, 43(10): 363–366. CAO J, LI W, LI J, et al. Robust speaker tracking under the background of strong noise[J].Journal of Huazhong University of Science and Technology(Natural Science Edition), 2015, 43(10): 363–366.(in Chinese) |
| [6] | 王强, 刘永葆, 贺星, 等. 噪声方差自适应修正的混合系统故障诊断方法[J].振动与冲击, 2016, 35(8): 14–20. WANG Q, LIU Y B, HE X, et al. A hybrid-system fault-diagnosis method based on noise-variance adaptive correction[J].Journal of Vibration and Shock, 2016, 35(8): 14–20.(in Chinese) |
| [7] | MíGUEZ J, BUGALLO M F, DJURIC'P M. A new class of particle fllters for random dynamical systems with unknown statistics[J].EURASIP Journal on Applied Signal Processing, 2004(15): 2287–2294. |
| [8] | 胡振涛, 潘泉, 杨峰, 等. 基于CRPF的残差似然比检验故障诊断算法[J].系统工程与电子技术, 2009, 31(12): 3022–3025. HU Z T, PAN Q, YANG F, et al. Residual likelihood ratio test for fault diagnosis based on cost reference particle filter[J].Systems Engineering and Electronics, 2009, 31(12): 3022–3025.DOI:10.3321/j.issn:1001-506X.2009.12.049(in Chinese) |
| [9] | 卢锦, 苏洪涛, 水鹏朗. 采用代价参考粒子滤波器估计天波雷达目标状态[J].西安电子科技大学学报, 2013, 40(5): 20–25. LU J, SU H T, SHUI P L. Target state estimation of the over-the-horizon radar using the cost reference particle filter[J].Journal of Xidian University, 2013, 40(5): 20–25.(in Chinese) |
| [10] | LIM J. Particle filtering for nonlinear dynamic state systems with unknown noise statistics[J].Nonlinear Dynamics, 2014, 78(2): 1369–1388.DOI:10.1007/s11071-014-1523-x |
| [11] | YU Y H. Combining H∞ fllter and cost-reference particle fllter for conditionally linear dynamic systems in unknown non-Gaussian noises[J].Signal Processing, 2013, 93(7): 1871–1878.DOI:10.1016/j.sigpro.2012.12.014 |
| [12] | LIM J, KIM T, HONG D. Estimating the number of competing terminals by cost-reference particle filtering in non-saturated wireless-LAN[J].Telecommunication System, 2016, 62(3): 519–527.DOI:10.1007/s11235-015-0091-9 |
| [13] | SHI Z, GU F, LENNOX B, et al. The development of an adaptive threshold for model-based fault detection of a nonlinear electro-hydraulic system[J].Control Engineering Practice, 2005, 13(11): 1357–1367.DOI:10.1016/j.conengprac.2004.11.014 |
| [14] | 蒋栋年, 李炜. 基于自适应阈值的粒子滤波非线性系统故障诊断[J].北京航空航天大学学报, 2016, 42(10): 2099–2106. JIANG D N, LI W. Fault diagnosis of particle filter nonlinear systems based on adaptive threshold[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2099–2106.(in Chinese) |
| [15] | HASHEMI A, PISU P. Adaptive threshold-based fault detection and isolation for automotive electrical systems[C]//20119th World Congress on Intelligent Control and Automation. Piscataway, NJ: IEEE Press, 2011: 1013-1018. |
| [16] | 郭健彬, 纪丁菲, 王鑫, 等. 混杂系统粒子滤波混合状态估计及故障诊断算法[J].系统工程与电子技术, 2015, 37(8): 1936–1942. GUO J B, JI D F, WANG X, et al. Hybrid state estimation and fault diagnosis algorithm of hybrid systems using particle filter[J].Systems Engineering and Electronics, 2015, 37(8): 1936–1942.DOI:10.3969/j.issn.1001-506X.2015.08.33(in Chinese) |
